2. 北京航空航天大学,北京 100191
2. Beihang University, Beijing 100191, China
直升机反潜是反潜体系的重要组成部分,是反潜能力建设的重要方向。反潜直升机可使用多种搜潜设备进行作业,其中吊放声呐是反潜直升机搜潜主要设备,也是特有的搜潜设备,使用吊放声呐进行应召搜潜,具有机动灵活、搜索速度快、使用经济等优点,是训练(或战时)使用最多的搜潜方式之一[1 − 4] 。
吊放声呐多采用悬停探测及回收的作业方式[5 − 7],若在直升机飞行过渡中完成回收动作,也即水下分机带速回收,则可减少整个探测任务的作业时间,有效提高作战效能。目前,水下分机带速回收的理论研究比较匮乏。与悬停回收相比,带速回收吊放电缆所受最大拉力、吊放电缆的偏转角以及水下分机的偏角将发生变化,上述因素将对吊放声呐系统的设计产生重要影响,因而对吊放声呐带速过程进行分析,应着重对带速回收过程中吊放电缆最大拉力、吊放电缆偏转角及水下分机偏转角的变化规律进行研究。
本文建立吊放声呐拖曳系统带速回收的动力学模型,根据风洞试验结果对模型进行标定,并基于标定好的气动力模型,仿真分析了吊放声呐带速回收过程,获得了带速回收过程吊放电缆最大拉力、吊放电缆偏转角及水下分机偏转角的变化规律,为吊放声呐拖曳系统带速回收动力学特性的深入研究提供理论支撑,为未来吊放声呐带速回收模式的应用提供参考。
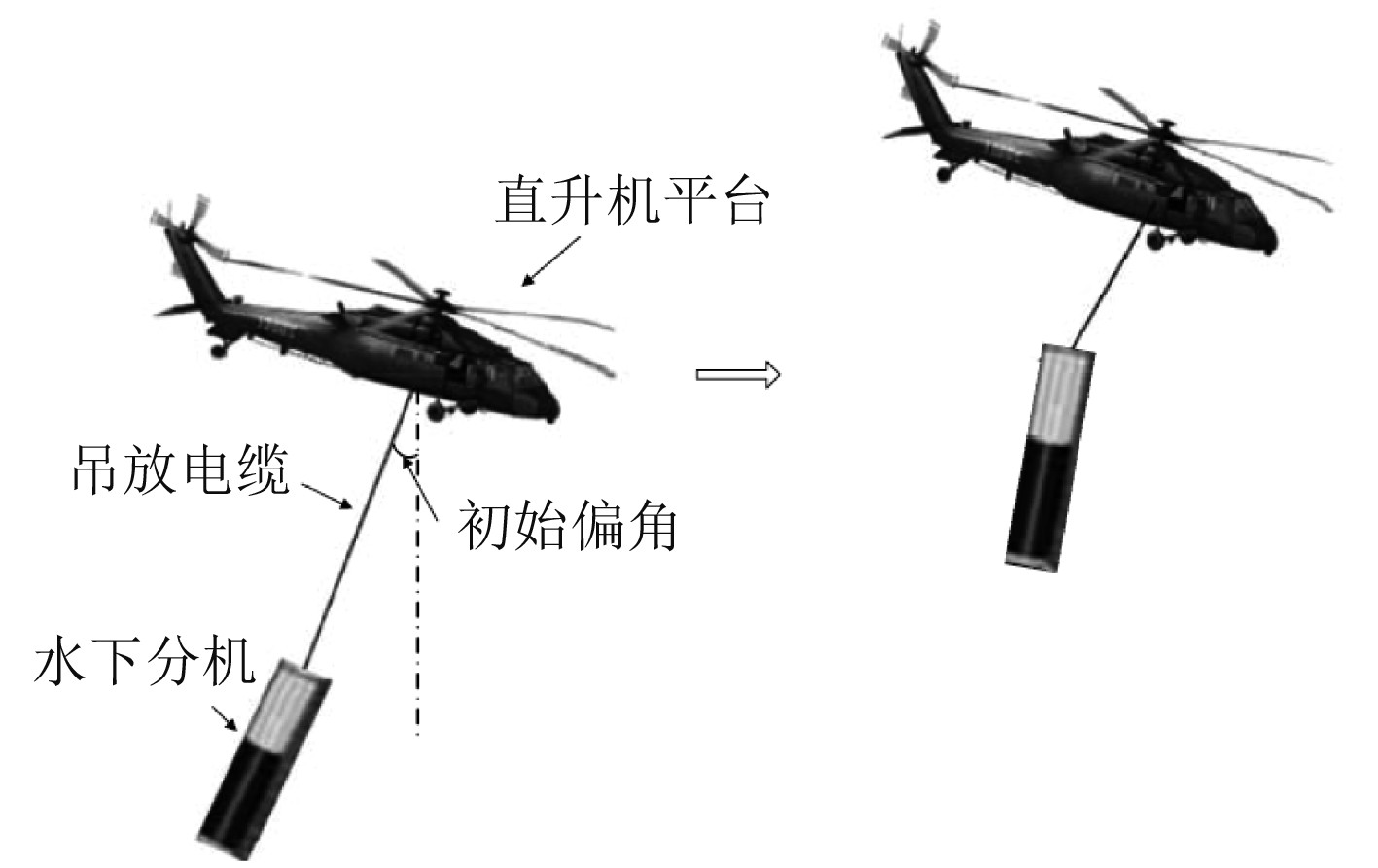
1 系统组成吊放声呐拖曳系统主要由直升机平台、吊放电缆及水下分机组成,水下分机通过吊放电缆回收至舱内,吊放电缆为柔性电缆,具有抗拉、抗扭转,允许工况下轴向基本无变形等特点。根据作业实况,水下分机提出海面时,存在一定初始偏角,同时水下分机从提出海面到回收就位的过程,直升机平台一般保持低头的姿态角斜向上飞行过渡,系统组成及回收过程示意如图1所示。
|
图 1 吊放声呐拖曳系统组成及带速回收过程示意 Fig. 1 Composition of dipping sonar towing system and schematic of speed recovery process |
本文吊放声呐拖曳系统的动力学建模,是指系统瞬态动力学建模。系统的瞬态模型,可模拟吊放电缆收放过程中,水下分机姿态及吊放电缆拉力随时间的变化过程。
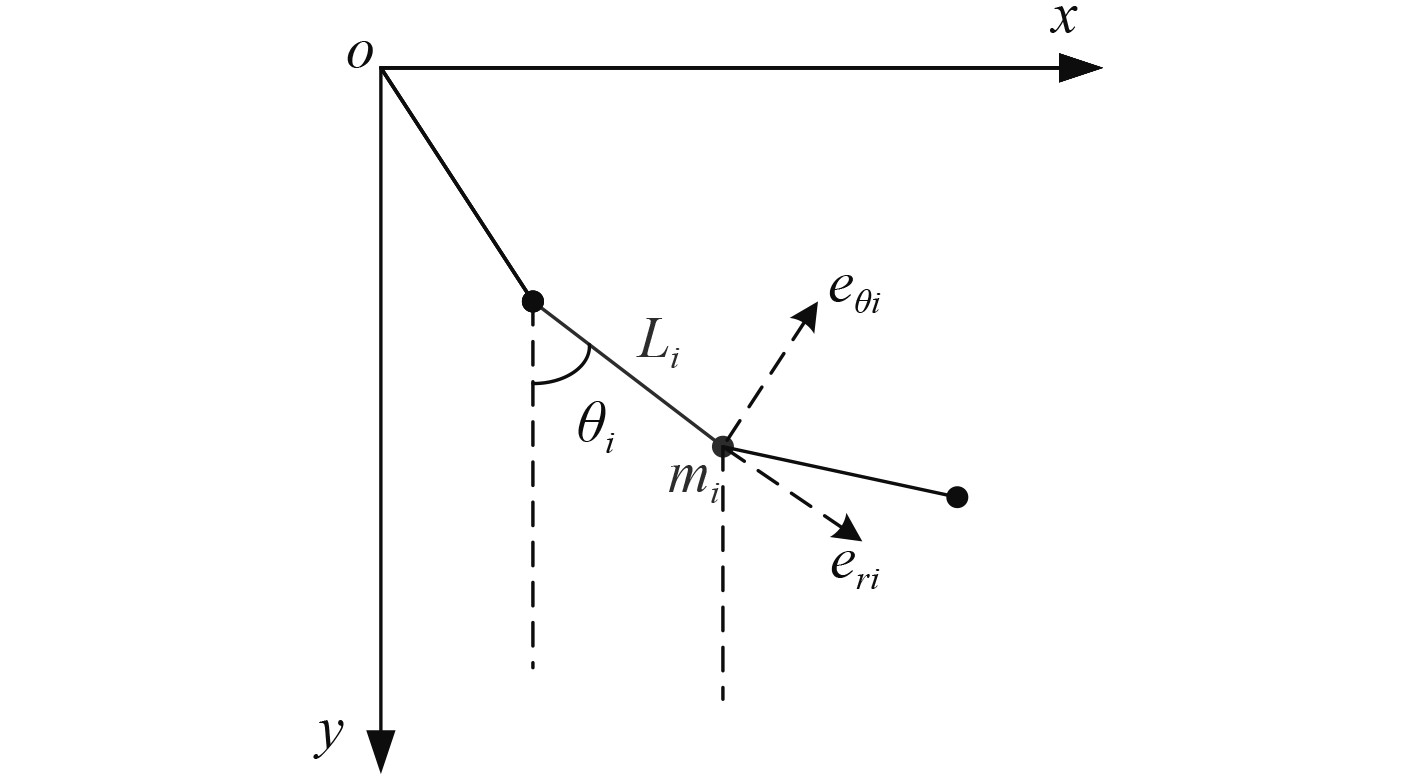
基于凯恩方法[8 − 10]建立吊放声呐拖曳系统的瞬态动力学模型,将吊放电缆离散成若干微段,假定每段质量集中在该段远离直升机一侧的端点处, 且吊放电缆各单元之间铰接。取水下分机回收到位时吊放电缆中轴线在飞机地板的投影作为坐标原点,构建吊放声呐拖曳系统多体动力学模型,如图2所示。
|
图 2 吊放声呐拖曳系统多体动力学模型 Fig. 2 Multi-body dynamics model of dipping sonar towing system |
取初始飞行器的位置为
| $ \mathbf{\mathit{R}}_i=\mathbf{\mathit{R}}_{i-1}+L_i\mathbf{\mathit{e}}_{r_i} 。$ | (1) |
式中:
上述求导,可得质点
| $ {{\boldsymbol{v}}_i} = {{\boldsymbol{v}}_{i - 1}} + {L_i}{{\boldsymbol{\dot e}}_{{r_i}}} = {{\boldsymbol{v}}_{i - 1}} + {L_i}\frac{{\partial {{\boldsymbol{e}}_{{r_i}}}}}{{\partial {\theta _i}}}{\dot \theta _i} = {{\boldsymbol{v}}_{i - 1}} + {L_i}{\omega _i}{{\boldsymbol{e}}_{{\theta _i}}} 。$ | (2) |
偏速度为
| $ \left\{\begin{array}{l} \displaystyle \frac{{\partial {{\boldsymbol{v}}_1}}}{{\partial {\omega _1}}} = \displaystyle \frac{{\partial {{\boldsymbol{v}}_2}}}{{\partial {\omega _1}}} = \displaystyle \frac{{\partial {{\boldsymbol{v}}_3}}}{{\partial {\omega _1}}} = \cdots = \displaystyle \frac{{\partial {{\boldsymbol{v}}_N}}}{{\partial {\omega _1}}} = {L_1}{{\boldsymbol{e}}_{{\theta _1}}},\\ \displaystyle \frac{{\partial {{\boldsymbol{v}}_1}}}{{\partial {\omega _2}}} = 0,\displaystyle \frac{{\partial {{\boldsymbol{v}}_2}}}{{\partial {\omega _2}}} = \displaystyle \frac{{\partial {{\boldsymbol{v}}_3}}}{{\partial {\omega _2}}} = \cdots = \displaystyle \frac{{\partial {{\boldsymbol{v}}_N}}}{{\partial {\omega _2}}} = {L_2}{{\boldsymbol{e}}_{{\theta _2}}},\\ \displaystyle \frac{{\partial {{\boldsymbol{v}}_1}}}{{\partial {\omega _3}}} = \displaystyle \frac{{\partial {{\boldsymbol{v}}_2}}}{{\partial {\omega _3}}} = 0,\displaystyle \frac{{\partial {{\boldsymbol{v}}_3}}}{{\partial {\omega _3}}} = \displaystyle \frac{{\partial {{\boldsymbol{v}}_4}}}{{\partial {\omega _3}}} = \cdots = \displaystyle \frac{{\partial {{\boldsymbol{v}}_N}}}{{\partial {\omega _3}}} = {L_3}{{\boldsymbol{e}}_{{\theta _3}}},\\ \cdots \cdots 。\end{array} \right.$ | (3) |
将式(3)写成NXN矩阵形式,并应用偏速度矩阵和偏速度矩阵导数,可将加速度表示为:
| $ \left[\begin{array}{c}{a}_{1}\\ {a}_{2}\\ \vdots \\ {a}_{N}\end{array}\right]\text=\left[\begin{array}{c}{a}_{0}\\ {a}_{0}\\ \vdots \\ {a}_{0}\end{array}\right]+{\frac{\partial {v}_{j}}{\partial {\omega }_{i}}}^{\text T}\left[\begin{array}{c}{\dot{\omega }}_{1}\\ {\dot{\omega }}_{2}\\ \vdots \\ {\dot{\omega }}_{N}\end{array}\right]+{\stackrel{·}{\frac{\partial {v}_{j}}{\partial {\omega }_{i}}}}^{\text T}\left[\begin{array}{c}{\omega }_{1}\\ {\omega }_{2}\\ \vdots \\ {\omega }_{N}\end{array}\right] 。$ | (4) |
式中:
| $ \begin{array}{l} {V_{partial}} = \displaystyle\frac{{\partial {{\boldsymbol{v}}_j}}}{{\partial {\omega _i}}} = \\ \left[ {\begin{array}{*{20}{l}} {{L_1}{{\boldsymbol{e}}_{{\theta _1}}}} & {{L_1}{{\boldsymbol{e}}_{{\theta _1}}}} & {{L_1}{{\boldsymbol{e}}_{{\theta _1}}}} & {{L_1}{{\boldsymbol{e}}_{{\theta _1}}}} & {{L_1}{{\boldsymbol{e}}_{{\theta _1}}}}\\ 0 & {{L_2}{{\boldsymbol{e}}_{{\theta _2}}}} & {{L_2}{{\boldsymbol{e}}_{{\theta _2}}}} & {{L_2}{{\boldsymbol{e}}_{{\theta _2}}}} & {{L_2}{{\boldsymbol{e}}_{{\theta _2}}}}\\ 0 & {0} & {{L_i}{{\boldsymbol{e}}_{{\theta _i}}}} & {{L_i}{{\boldsymbol{e}}_{{\theta _i}}}} & {{L_i}{{\boldsymbol{e}}_{{\theta _i}}}}\\ 0 & {0} & { \ldots } & { \ddots } & { \vdots }\\ 0 & {0} & {0} & {0} & {{L_N}{{\boldsymbol{e}}_{{\theta _N}}}} \end{array}} \right],\\ {{\dot V}_{partial}} = \mathop {\displaystyle\frac{{\partial {{\boldsymbol{v}}_j}}}{{\partial {\omega _i}}}}\limits^ \bullet = - \\ \left[ {\begin{array}{*{20}{l}} {{L_1}{\omega _1}{{\boldsymbol{e}}_{{r_1}}}} & {{L_1}{\omega _1}{{\boldsymbol{e}}_{{r_1}}}} & {{L_1}{\omega _1}{{\boldsymbol{e}}_{{r_1}}}} & {{L_1}{\omega _1}{{\boldsymbol{e}}_{{r_1}}}} & {{L_1}{\omega _1}{{\boldsymbol{e}}_{{r_1}}}} \\ 0 & {{L_2}{\omega _2}{{\boldsymbol{e}}_{{r_2}}}} & {{L_2}{\omega _2}{{\boldsymbol{e}}_{{r_2}}}} & {{L_2}{\omega _2}{{\boldsymbol{e}}_{{r_2}}}} & {{L_2}{\omega _2}{{\boldsymbol{e}}_{{r_2}}}} \\ 0 & {0} & {{L_i}{\omega _i}{{\boldsymbol{e}}_{{r_i}}}} & {{L_i}{\omega _i}{{\boldsymbol{e}}_{{r_i}}}} & {{L_i}{\omega _i}{{\boldsymbol{e}}_{{r_i}}}} \\ 0 & {0} & { \ldots } & { \ddots } & { \vdots } \\ 0 & {0} & {0} & {0} & {{L_N}{\omega _N}{{\boldsymbol{e}}_{{r_N}}}} \end{array}} \right]。\end{array} $ | (5) |
广义惯性力
| $ F_\theta ^* = - {V_{partial}}\left[ {\begin{array}{*{20}{c}} {{m_1}{{\boldsymbol{a}}_1}} \\ {{m_2}{{\boldsymbol{a}}_2}} \\ \vdots \\ {{m_i}{{\boldsymbol{a}}_i}} \\ \vdots \\ {{m_N}{{\boldsymbol{a}}_N}} \end{array}} \right] = - {V_{partial}}{{{M}}_d}\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{a}}_1}} \\ {{{\boldsymbol{a}}_2}} \\ \vdots \\ {{{\boldsymbol{a}}_i}} \\ \vdots \\ {{{\boldsymbol{a}}_N}} \end{array}} \right] ,$ | (6) |
式中:
将质点上主动力,投影到偏速度方向,得广义主动力。
| $ \begin{aligned} & {\boldsymbol{F}}_{\boldsymbol{\theta }}^{} = {V_{partial}}\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{F}}_1} + {m_1}{{\boldsymbol{g}}_1}}\\ {{{\boldsymbol{F}}_2} + {m_2}{{\boldsymbol{g}}_2}}\\ \vdots \\ {{{\boldsymbol{F}}_i} + {m_i}{{\boldsymbol{g}}_i}}\\ \vdots \\ {{{\boldsymbol{F}}_N} + {m_N}{{\boldsymbol{g}}_N}} \end{array}} \right] = \frac{{\partial {{\boldsymbol{V}}_i}}}{{\partial {\omega _i}}}\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{F}}_1} + {m_1}{{\boldsymbol{g}}_1}}\\ {{{\boldsymbol{F}}_2} + {m_2}{{\boldsymbol{g}}_2}}\\ \vdots \\ {{{\boldsymbol{F}}_i} + {m_i}{{\boldsymbol{g}}_i}}\\ \vdots \\ {{{\boldsymbol{F}}_N} + {m_N}{{\boldsymbol{g}}_N}} \end{array}} \right] = \\ & \quad\quad \quad\quad\quad \left[ {\begin{array}{*{20}{c}} {{L_1}{{\boldsymbol{e}}_{{\theta _1}}} \cdot \sum\limits_{i = 1}^N {({{\boldsymbol{F}}_i} + {m_i}{{\boldsymbol{g}}_i})} }\\ {{L_2}{{\boldsymbol{e}}_{{\theta _2}}} \cdot \sum\limits_{i = 2}^N {({{\boldsymbol{F}}_i} + {m_i}{{\boldsymbol{g}}_i})} }\\ \vdots \\ {{L_j}{{\boldsymbol{e}}_{{\theta _j}}} \cdot \sum\limits_{i = j}^N {({{\boldsymbol{F}}_i} + {m_i}{{\boldsymbol{g}}_i})} }\\ \vdots \\ {{L_N}{{\boldsymbol{e}}_{{\theta _N}}} \cdot \sum\limits_{i = N}^N {({{\boldsymbol{F}}_N} + {m_N}{{\boldsymbol{g}}_N})} } \end{array}} \right]。\end{aligned} $ | (7) |
将广义主动力和广义惯性力带入凯恩方程
| $ {\boldsymbol{M\dot \omega }} = {\boldsymbol{B}} + {{\boldsymbol{F}}_\theta } ,$ | (8) |
其中:
| $ {\boldsymbol{M}} = {V_{partial}}{{\boldsymbol{M}}_d}V_{^{partial}}^{\text T} ,$ |
| $ {\boldsymbol{B}} = - {V_{partial}}{{{M}}_d}\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{a}}_0}} \\ {{{\boldsymbol{a}}_0}} \\ \vdots \\ {{{\boldsymbol{a}}_0}} \end{array}} \right]{\text{ + }}{V_{partial}}{{{M}}_d}\dot V_{^{partial}}^{\text T}\left[ {\begin{array}{*{20}{c}} {{\omega _1}} \\ {{\omega _2}} \\ \vdots \\ {{\omega _N}} \end{array}} \right] 。$ |
当缆绳进行回收时,第一段绳索的质量
式(8)为最终求解的动力学方程,可用龙格库塔法沿时间积分求解获得角速度
根据姿态、气动力和重力以及各节点的加速度,可以构建缆绳拉力的计算公式如下:
| $ {{\boldsymbol{T}}_i} = {M_i}{\boldsymbol{a}} - {{\boldsymbol{F}}_i} - {M_i}{\boldsymbol{g}} 。$ | (9) |
式中:
对瞬态模型进行长时间的模拟仿真可获得某风阻系数一风速下稳定后的形态和姿态。
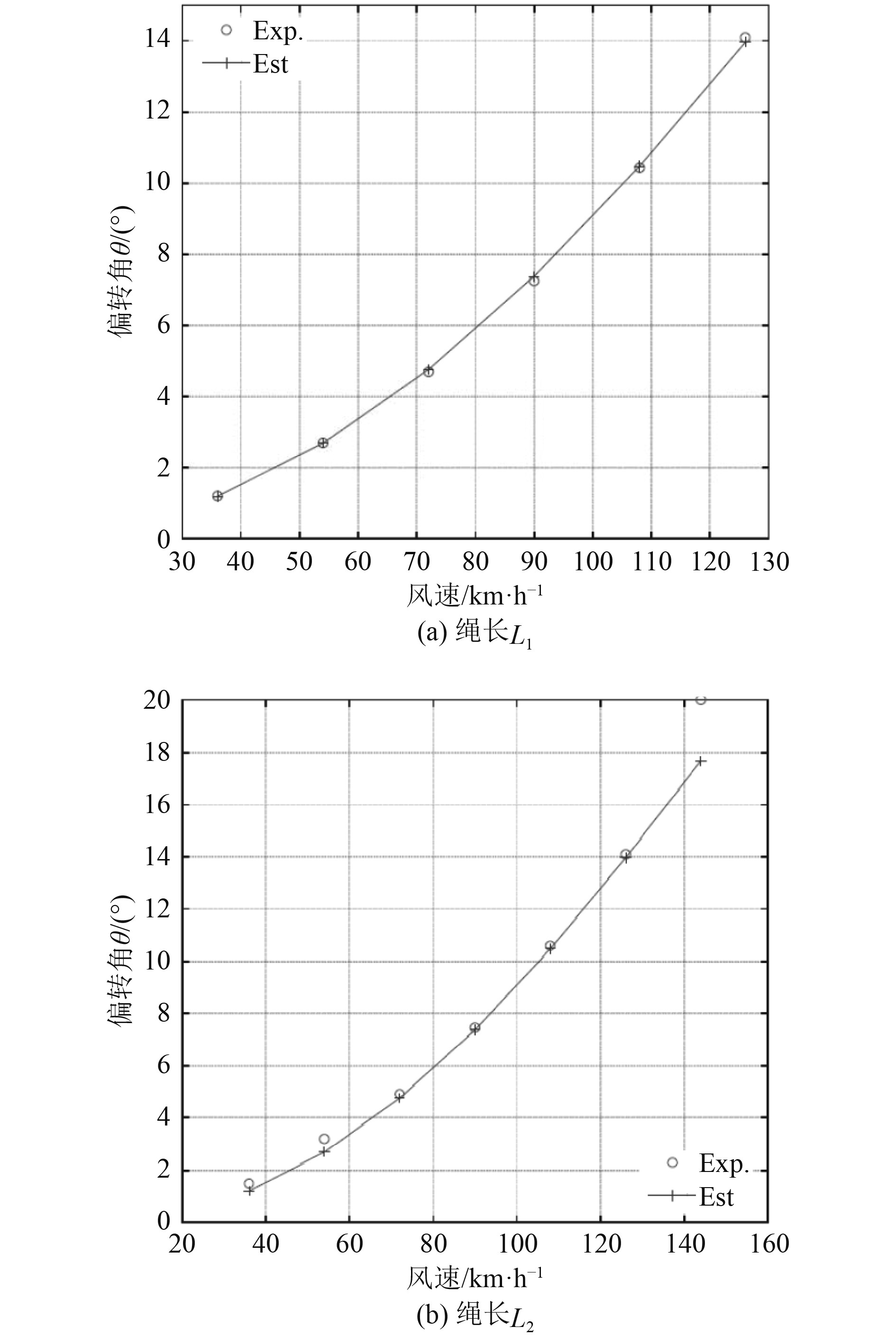
对某型吊放声呐进行风洞试验,试验测得了吊放电缆长度为L1和L2两种情况,不同风速条件下的缆绳偏角。针对试验工况,用建立好的模型进行仿真,并用最小二乘法对水下分机的风阻系数进行拟合,完成了带速回收气动力学模型的标定完善。
仿真结果与风对试验数据对比如图3所示,整体上仿真结果(Est)与实验数据(Exp)吻合较好。
|
图 3 仿真结果与风洞试验结果对比 Fig. 3 Comparison diagram of simulation results and wind tunnel test results |
吊放声呐在执行搜潜任务时,经常面临不同的海况环境,其中主要影响带速回收特性的是风速,基于建立好的动力学模型,对吊放声呐拖曳系统带速回收过程中进行仿真,对作业风速(0~5级海况)对吊放电缆最大拉力、吊放电缆偏转角以及水下分机偏转角的影响进行分析。
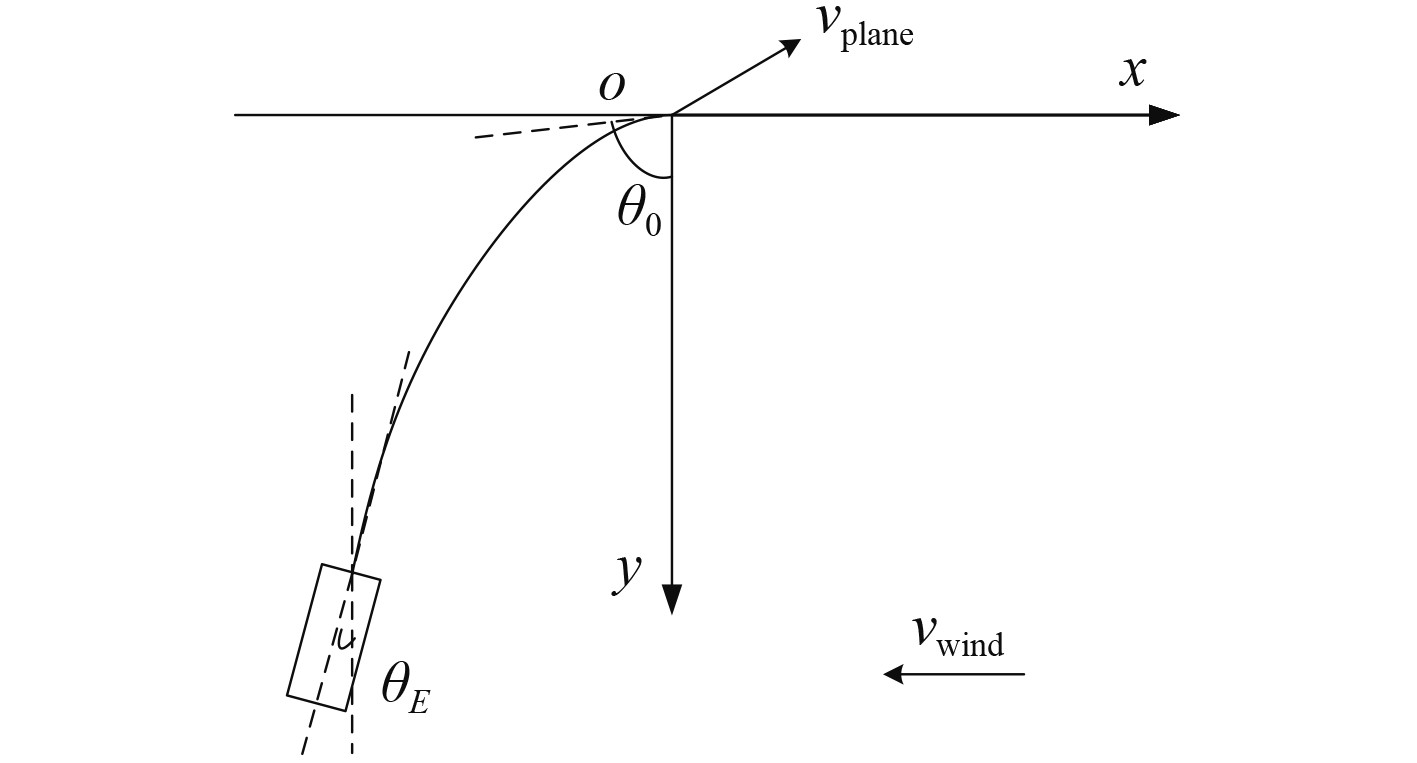
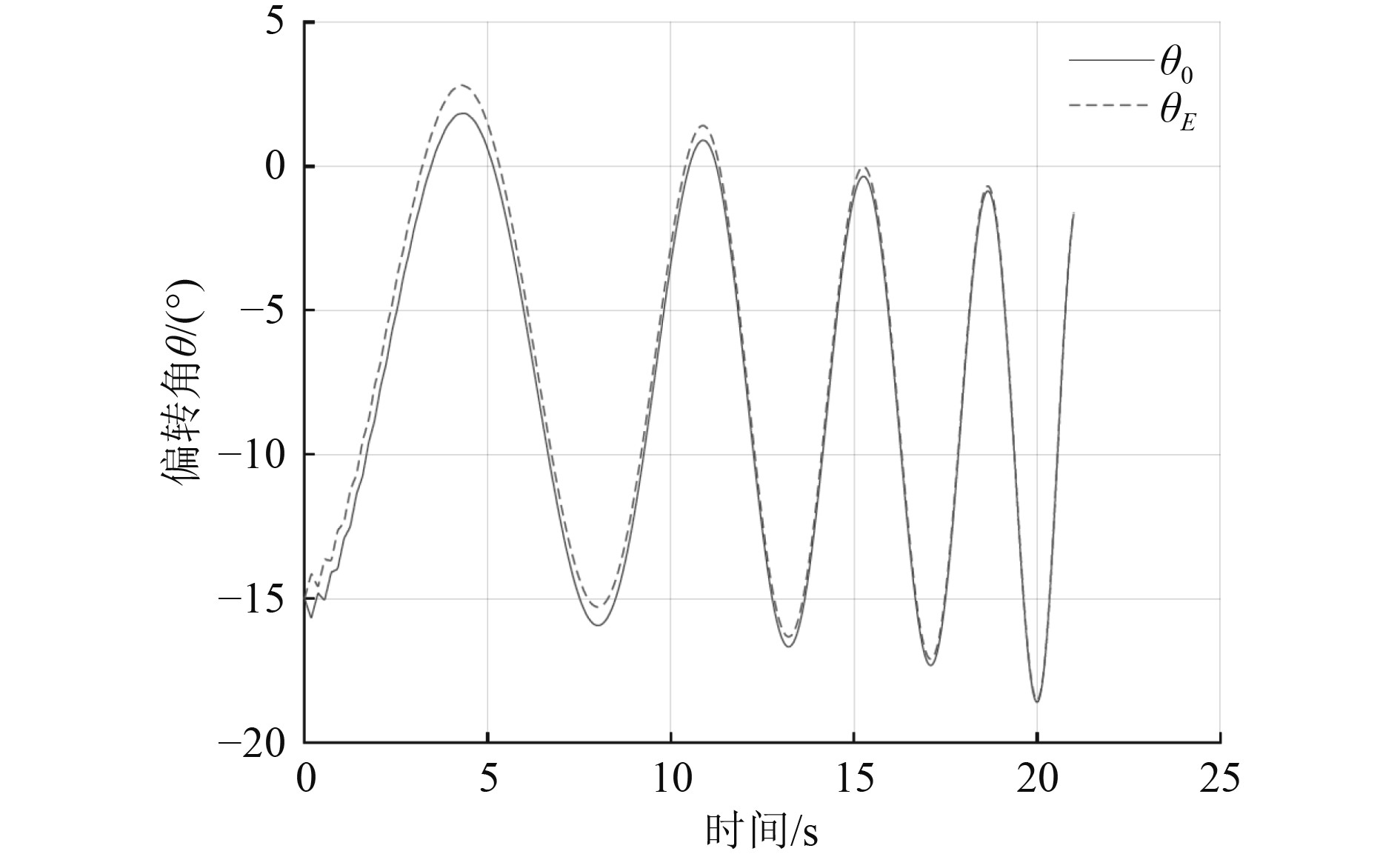
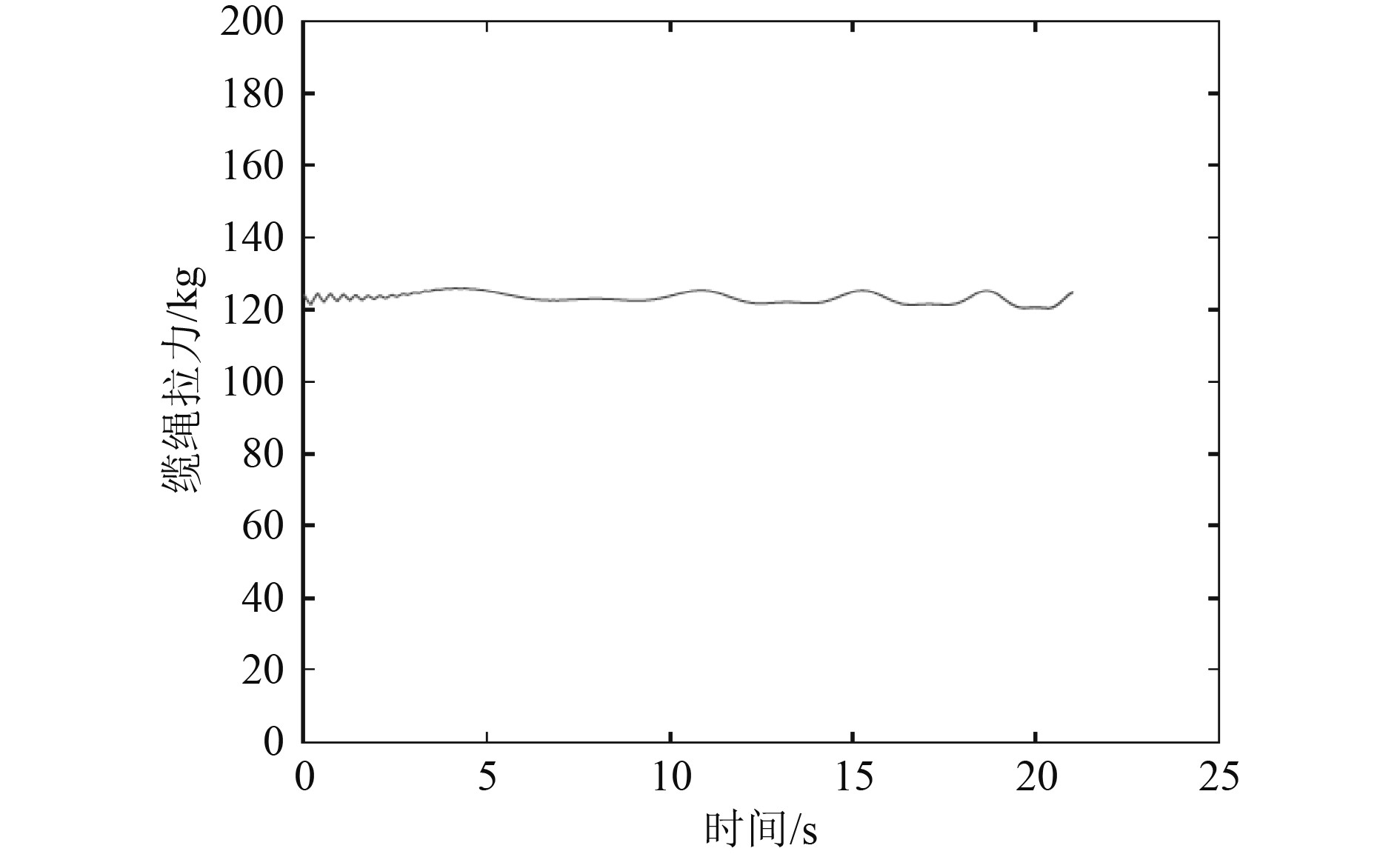
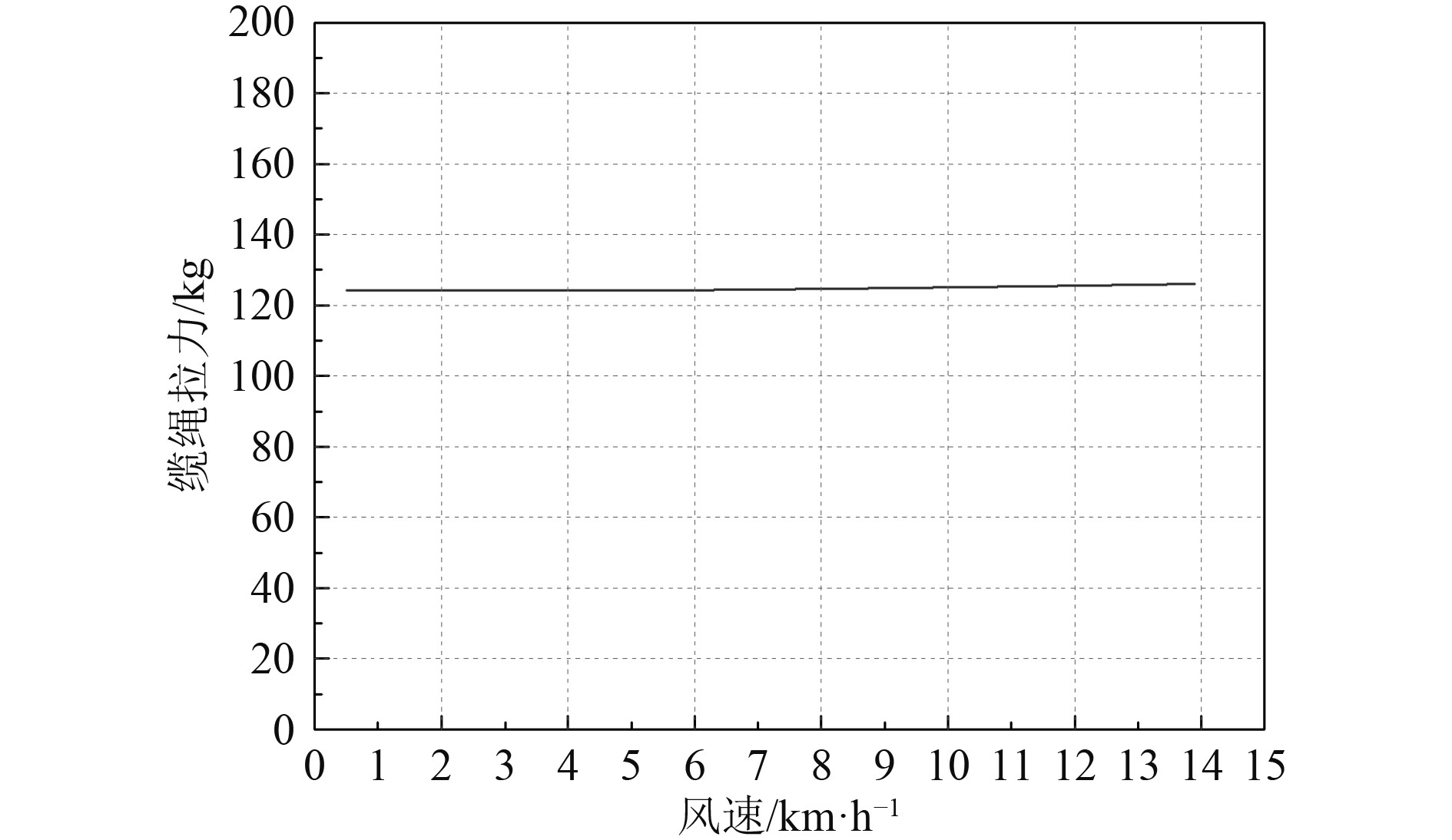
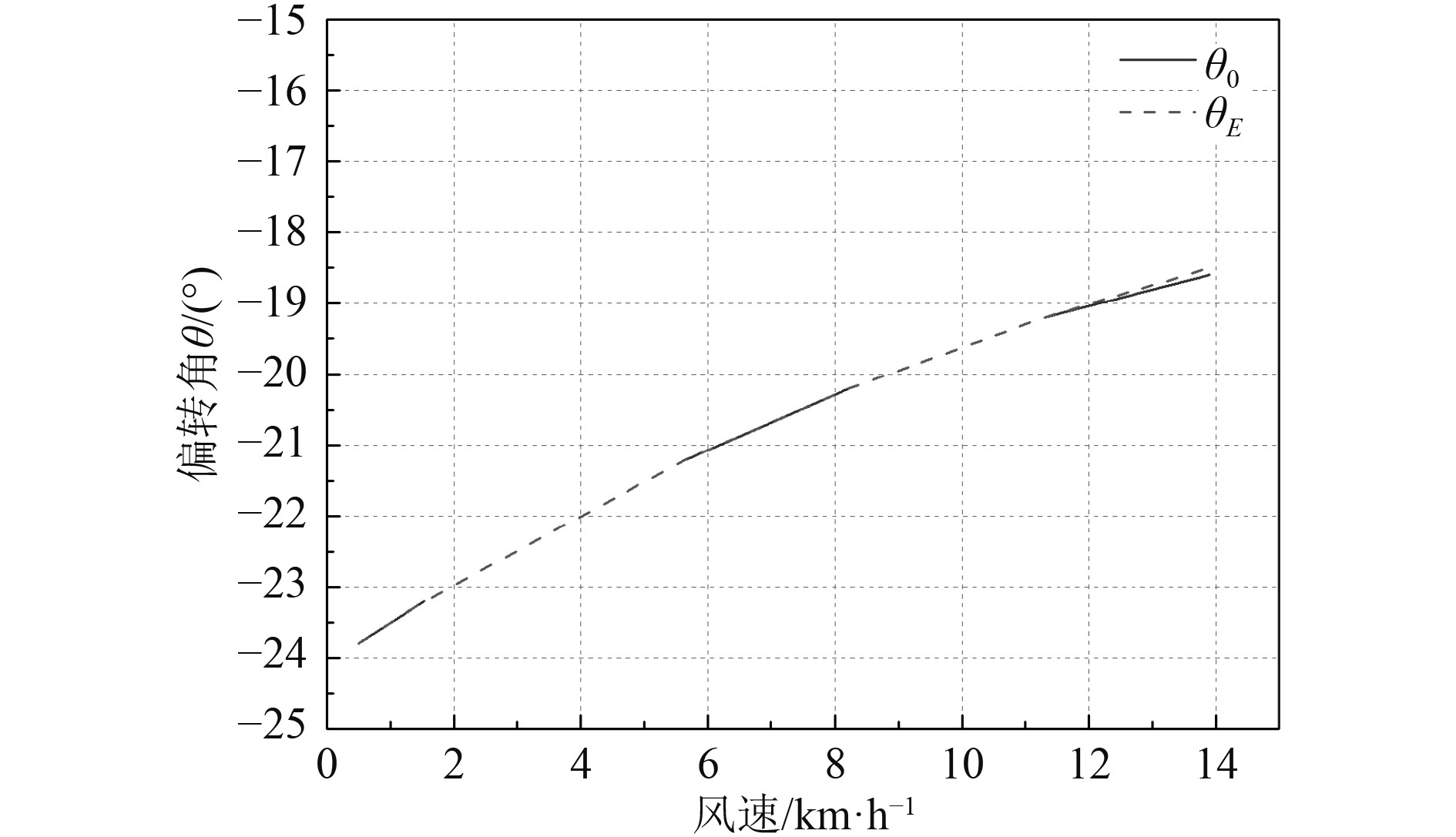
仿真算例假定直升机匀加速迎风飞行过渡,飞行渡时保持低头的5°姿态角,取初始回收高度22 m,出水初始偏角为15°,同时作业工况取5级海况风速13.9 m/s。进行仿真时各角度的定义如图4所示,θ0为缆绳偏角,θE为水下分机偏角,取向右偏移为正,则图4中对应的是向左偏移,应为负值。图5 ~ 图6分别为水下分机带速回收过程中缆绳偏角θ0及水下分机偏角θE随时间的变化曲线,及吊放电缆最大拉力随时间变化曲线。图7为不同风速下吊放电缆最大拉力变化曲线,图8为不同风速下缆绳偏角及水下分机偏角随风速的变化曲线。
|
图 4 系统角度定义 Fig. 4 System angle definition |
|
图 5 13.9 m/s风速下吊放电缆偏角θ0及水下分机偏角θE Fig. 5 The cable deflection angle θ0 and the underwater extension deflection angle θE under 13.9 m/s wind speed. |
|
图 6 13.9 m/s风速下吊放电缆拉力 Fig. 6 Cable tension under 13.9 m/s wind speed. |
|
图 7 不同风速下的吊放电缆拉力 Fig. 7 Cable tension diagram under different wind speed |
|
图 8 不同风速下电缆偏角θ0及水下分机偏角θE Fig. 8 The cable deflection angle θ0 and the underwater extension deflection angle θE under different wind speed |
根据以上仿真结果可以看出:
1)带速回收过程中,吊放电缆发生振荡运动,整个过程吊放电缆偏转角和水下分机偏角变化趋势基本一致。整个过程吊放电缆偏转角和水下分机偏角角度差不大,同时随着吊放电缆长度的变短,振荡周期变短,振荡频率变快。
2)带速回收过程,吊放电缆的最大拉力小幅超过设备重力,最大拉力值基本保持稳定。
3)不同风速条件下,带速回收过程中吊放电缆最大拉力变化很小,也即风速对带速回收过程中吊放电缆所受最大拉力影响很小。
4)0~5级海况条件下作业,随着风速的增加,吊放电缆偏转角以及水下分机偏转角的逐渐减小,偏转角越小,水下分机越容易回收至舱内就位,也即0~5级海况范围内,海风对回收有利。
4 结 语吊放声呐是直升机反潜的重要搜潜装备,吊放声呐的带速回收对搜潜效能的提升将产生有效的促进作用。目前,对吊放声呐带速回收过程的研究较少。本文以算例吊放声呐为研究对象,建立了其带速回收过程的动力学模型,根据风洞试验结果,对模型进行了标定完善,并对吊放声呐的带速回收过程进行了仿真,重点对关注的吊放电缆拉力、水下分机及吊放电缆的偏角以及风速的影响等进行了分析。仿真结果表明,带速回收过程吊放电缆和水下分机偏转角变化趋势一致,整个过程角度相差不大,回收过程中吊放电缆的最大拉力小幅超过设备重力,数值基本保持稳定,同时风速对吊放电缆最大拉力影响很小,且在0~5级海况范围内,风速越大,吊放电缆偏转角越小,越有利于回收。
本文对吊放声呐带速回收过程进行了初步研究,对未来吊放声呐带速回收模式的应用提供了参考。后续将进一步开展对该拖曳系统动力学特性的研究工作,对作业海况、回收时机、初始偏转角等参数对系统回收特性的影响进行分析。
| [1] |
王琪, 时江超, 范学满. 外军舰机反潜探测装备技术发展综述[J]. 系统仿真技术及其应用, 2022, 23: 139−142. WANG Qi, SHI Jiangchao, FAN Xueman. Review on the development of anti submarine detection equipment technology of foreign warships and aircraf [J]. CCSSTA23rd 2022, 23: 139−142. |
| [2] |
张本辉, 门金柱, 姚科明, 等. 舰载直升机反潜作战使用研究综述[J]. 电光与控制, 2019, 26(8): 60−66. ZHANG Benhui, MEN Jinzhu, YAO Keming, et al. Review of research on shipboard helicopter in antisubmarine operational application[J]. Electronics Optics & Control. 2019, 26(8) : 60−66. |
| [3] |
王祖典. 航空反潜战与反潜武器[J]. 航空兵器, 2007(1): 6-9. WANG Zudian. Airborne anti−submarine warfare and their weapons[J]. Aeroweaponry, 2007(1): 6-9. DOI:10.3969/j.issn.1673-5048.2007.01.002 |
| [4] |
孙明太. 航空反潜装备[M]. 北京: 国防工业出版社, 2012.
|
| [5] |
胡伟涛, 赵青松, 罗弋洋, 等. 基于体系结构框架的反潜作战装备体系[J]. 兵工自动化, 2021(40): 49−53 HU Weitao, ZHAO Qingsong, LUO Yiyang, et al . Architecture of anti−submarine warfare weapon equipment based on architecture framework[J]. Ordnance Industry Automation. 2021(40): 49−53. |
| [6] |
窦强, 阴启玉, 梁立. 基于吊放声呐的无人艇搜潜任务规划算法[J]. 指挥控制与仿真, 2023, 45(2): 9−16. DOU Qiang, YIN Qiyu, LIANG Li. Planning algorithm of USV antisubmarine mission based on the dipping sonar [J]. Command Control & Simulation. 45(2): 9−16. |
| [7] |
张丙飞, 孙心毅, 成建波. 单机吊放声呐应召反潜探测概率的计算与优化[J]. 航空电子技术, 2020, 51(1): 35−38. ZHANG Bingfei, SUN Xinyi, CHENG Jianbo. Probability in antisubmarine call search with sonar compute and optimize[J]. Avionics Technology, 2020 51(1): 35−38. |
| [8] |
休斯顿, 刘又午. 多体系统动力学[M]. 天津: 天津大学出版社, 1987.
|
| [9] |
顾文彬, 陆鸣, 刘建青, 等. 基于Kane方法的火箭抛绳系统飞行动力学模型[J]. 弹道学报, 2015, 27(2): 20-23. GU Wenbin, LU Ming, LIU Jianqing, et al. Dynamic model of line throwing rocket system with flight motion based on kane's method[J]. Journal of Ballistics, 2015, 27(2): 20-23. DOI:10.3969/j.issn.1004-499X.2015.02.004 |
| [10] |
HUSTON R L , KAMMAN J W . Validation of finite segment cable models[J]. Computers & Structures, 1982, 15(6): 653−660.
|
 2024, Vol. 46
2024, Vol. 46
