0 引　言

被动声呐系统进行警戒探测时，目标通常在波束形成后的方位能量谱图中以峰值形式显示，峰值以外部分即为背景噪声。因水声环境噪声在时间上的非平稳性和空间上的非均匀性，方位能量谱图中的背景噪声在时间和空间上具有不稳定、不均匀的特点，随机起伏的噪声甚至会“掩盖”较弱的目标峰值，干扰弱目标检测。为了降低背景噪声对目标检测的影响，设备中经常使用时间积分和背景均衡等方法^{[1 − 2]}。时间积分主要着重于时间上对方位能量谱做平滑，而背景均衡除了能降低背景噪声起伏，还能压缩数据的动态范围，方便显示软件的显示和控制^[3]。常见的背景均衡算法有二次循环均值 （Two-Pass Mean，TMP）算法、排序截断平均 （Order Truncate Average，OTA）算法、拆分三次循环均值 （Split Three-Pass Mean，S3PM）算法、二次循环均值加窗 （Two-Pass Split-Window，TPSW）算法^{[4 − 5]}等以及相关算法的优化算法^{[6 − 8]}。为了适应噪声门限时刻变化的特点，邱家兴等^[9]提出一种自适应门限背景均衡算法；李启虎等^[10]提出一种将中值滤波与OTA结合的波束域背景均衡算法，该方法能够去除背景中的大范围起伏，提高时间方位历程（Bearing Time Recording，BTR）显示效果。基于波束域峰值检测^[11]和数字图像处理中的特征提取思想，王晓宇等^[12]提出一种差分邻域检测均衡算法，能在均衡背景噪声同时较好保留目标信号，改善声呐显示效果。张晓勇等^[13]从数学形态学滤波（Mathematical Morphology Filter，MMF）入手，提出一种新的噪声背景归一化方法，可在保持一定检测概率的前提下，大幅降低检测虚警。蒋天立等^[14]、李伟等^{[15 − 16]}都对形态学滤波在宽带信号检测上的应用做了进一步的改进提升。

随着背景均衡算法的发展，被动声呐系统在检测目标时越来越稳定，但方位能量谱中目标峰值的高低与信号的强弱有着很强的相关性，背景均衡无法做到将弱目标的小峰值突出于背景显示，即无法直观地凸显弱目标方位，为此，本文提出一种稳定背景的局部缩放信号处理方法，能在保持方位能量谱背景基本稳定的情况下，实现目标方位处的局部缩放和突出显示。

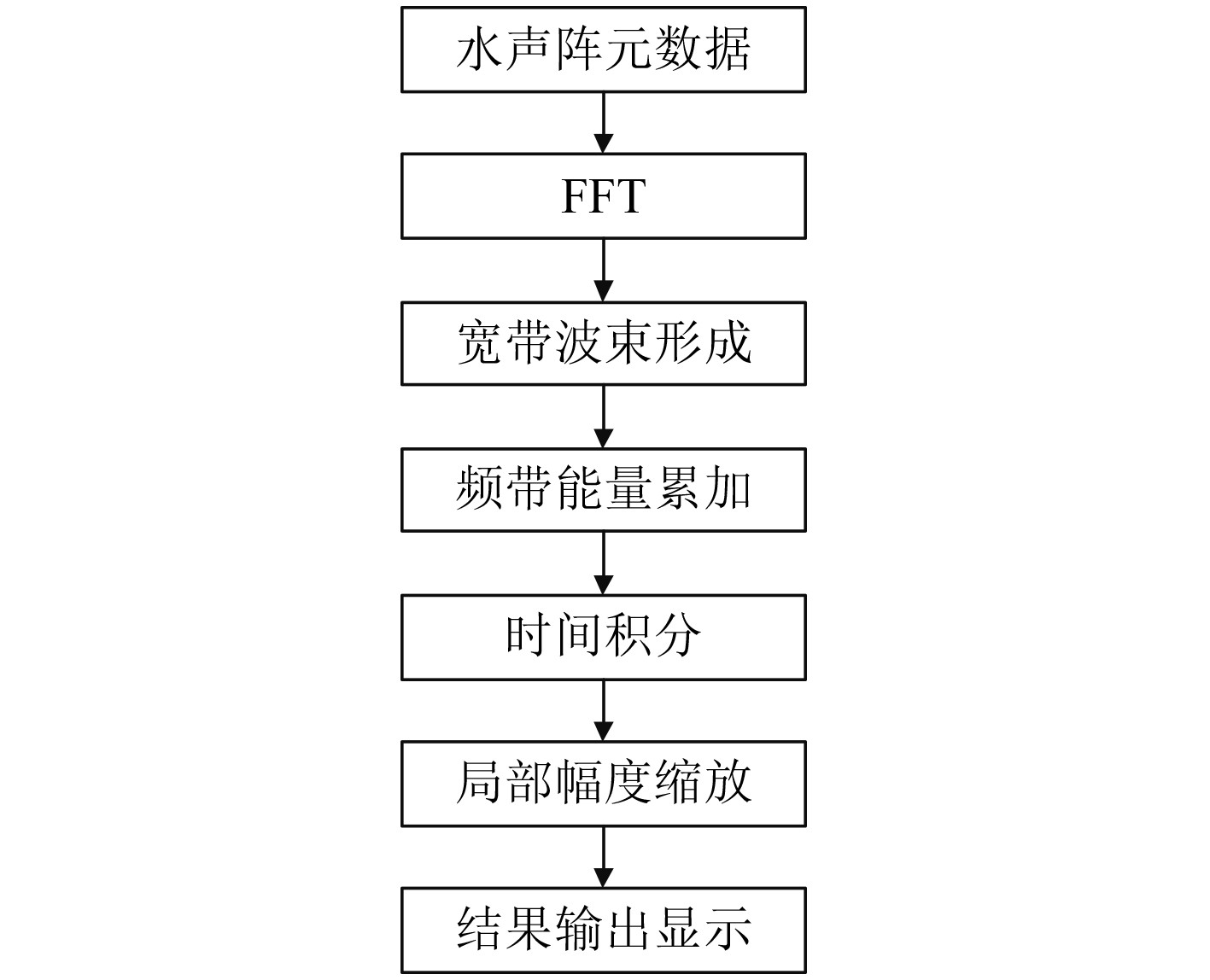
1 稳定背景的局部缩放信号处理方法 1.1 检测处理框架

被动声呐系统的检测处理框架如图1所示，通过水听器基阵采集的M个阵元的T个采样点的一帧时域数$ {s_{MT}} $，经N点FFT变换至频域，得到阵元频域数据$ {S_{MN}} $；对阵元频域数据做宽带波束形成后得到P个波束方向的频域波束数据$ {H_{PN}} $；对频域波束数据做频带能量累加后即可得到一组P点的方位能量谱$ Y(\theta ),\theta = 1,2,...,P $；为了降低噪声背景在时间上的随机抖动影响，对方位能量谱做时间积分后得到$\overline {Y(\theta )} $，此时的$\overline {Y(\theta )} $已可作为当前时刻被动声呐系统的检测结果输出，以瀑布图形式累计长时间输出结果后就组成了时间方位历程图BTR。本文所提方法是对输出的实时检测结果的进一步处理，即后置处理，不影响整个被动声呐系统检测处理的基本框架，对现有设备的更新升级改动很小，利于工程实现。

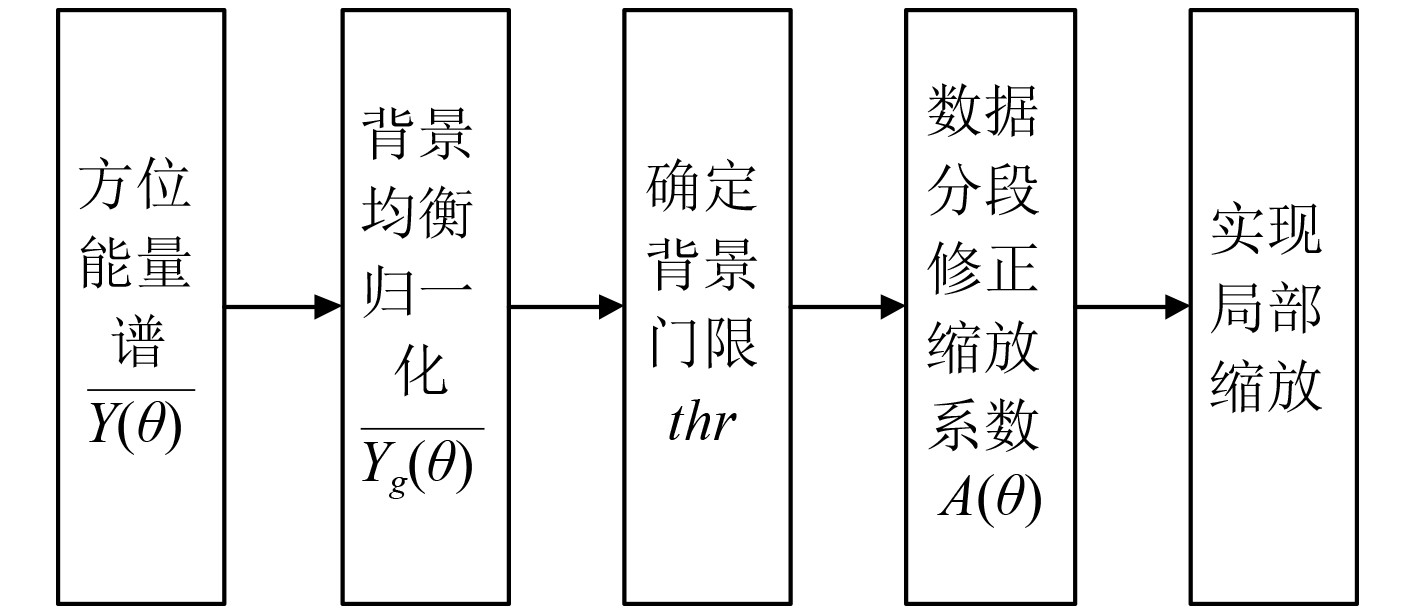
局部幅度缩放信号处理算法的具体流程如图2所示。因本方法是在方位能量谱的基础上做进一步处理，被动检测能力与所使用的波束形成方法高度相关，即本方法对前置的被动检测算法具有极高的适应性，故在本文中不再对波束形成及相关检测算法优劣做对比，仅以常规算法进行讨论。首先对方位能量谱$\overline {Y(\theta )} $做背景均衡归一化处理，压缩整个方位能量谱的动态范围，降低环境噪声或强脉冲干扰对不同时刻检测结果的影响，保持BTR在时间上的基本稳定；其次对归一化后的方位能量谱$\overline {{Y_{g}}(\theta )} $做统计分析，确定背景门限${T_{hr}}$；再次，门限将$\overline {{Y_{g}}(\theta )} $划分成2段。

$ \overline {{Y_{{g}}}(\theta )} = \left\{ {\begin{array}{*{20}{c}} \overline {{Y_{{{gl}}}}(\theta )} ，{\overline {{Y_{{g}}}(\theta )} < {T_{hr}},\theta \in [1,P]} ，\\ \overline {{Y_{{{gh}}}}(\theta )} ，{\overline {{Y_{{g}}}(\theta )} \geqslant {T_{hr}},\theta \in [1,P]}。\end{array}} \right. $

(1)

对小于门限数据$ \overline {{Y_{{{gl}}}}(\theta )} $和不小于门限数据$ \overline {{Y_{{{gh}}}}(\theta )} $采用不同指数修正缩放系数$A(\theta )$；最后根据显示控制台下发的缩放指令对$ \overline {{Y_{{g}}}(\theta )} $进行局部缩放。

1.2 背景均衡归一化

被动声呐系统某一时刻的检测结果$\overline {Y(\theta )} $为包含P个波束的一位方位能量谱，P个波束一般覆盖[0°，360°]的方位范围。背景均衡时P个波束分别要做一次均衡处理，以分析窗长为2K+1为例，“1”为当前待分析的波束点，窗内左右各选择K个波束，对原始数据$\overline {Y(\theta )} $而言，左右边界处不满足窗长条件，会导致均衡结果偏差，均衡后边界处会出现跳变。为了减轻边缘效应影响，将$\overline {Y(\theta )} $进行左右边界循环扩展，扩展后数据为：

$ \begin{gathered} \overline {Y(P - K)} ,...,\overline {Y(P)} ,\overline {Y(1)} ,\overline {Y(2)} , ...,\overline {Y(P)} ,\overline {Y(P + 1),} ...\overline {,Y(P + K)} 。\\ \end{gathered} $

(2)

每次选取扩展数据中的2K+1个数据，按从小到大升序重排为：

$ {C_\theta }(1),{C_\theta }(2),...,{C_\theta }(2K),{C_\theta }(2K + 1)。$

(3)

式中：$ {C_\theta }(K + 1) $为中值，定义截断门限$ {C_{{t}}} = a{C_\theta }(K + 1) $，a为截断常数，a>0，将$ {C_\theta } $与截断门限$ {C_{{t}}} $比较，记录小于门限数据并取均值$\mu (\theta ) = \displaystyle\frac{1}{k}\sum\nolimits_{i = 1}^k {{C_i}} $，式中k为小于门限数据个数，最后对输入数据$\overline {Y(\theta )} $做归一化处理$\overline {{Y_{\text{g}}}(\theta )} = \overline{Y(\theta)}/\mu(\theta),\theta = 1,2,...,P$。

算法中需注意的是截断常数a的选择有一定范围限制，a过大时无法起到截断作用，算法退化为均值归一化；a过小时会导致均值$\mu (\theta )$过小且失真，归一化后的结果$\overline {{Y_{\text{g}}}(\theta )} $会出现异常突起，引入虚假目标，造成虚警。实践中a取值为3～5。

半窗长K的选择与波束域主瓣宽度相关，当窗长2K+1小于主瓣宽度时，式(3)中数据都处在主瓣范围内，数据幅度都较大且与中值$ {C_\theta }(2K + 1) $近似，会造成$\mu (\theta )$偏大失真，归一化处理后压缩目标峰值，且会在主瓣附近形成虚假峰值，引入虚假目标。为取得较好归一化效果，半窗长K一般选取大于2倍主瓣宽度。

1.3 门限与缩放系数

归一化后方位能量谱的动态范围已被压缩在一个较小范围内，没有异常强信号干扰情况下，背景也被归一化在1附近，通常情况下背景门限经验值可取${T_{hr}}$=1，再确定$\overline {{Y_{{g}}}(\theta )} $的最大值$\overline {{Y_{{{gM}}}}(\theta )} $，将$\overline {{Y_{{g}}}(\theta )} $在[0，$\overline {{Y_{{{gM}}}}(\theta )} $]范围内按式(1)进行分段。为了实现背景在缩放时保持基本稳定，门限处的缩放系数应设置为1，在此前提条件下，按抛物线形式构造$ \overline {{Y_{{{gl}}}}(\theta )} $的缩放系数。

$ {A_{\text{l}}}(x) = - {\left(\frac{x}{{{T_{hr}}}}\right)^2} + 2\frac{x}{{{T_{hr}}}} 。$

(4)

式中：x为分段自变量，设[0，${T_{hr}}$]之间共分L段，则$x =\displaystyle \frac{{{T_{hr}}}}{L}i,i = 0,1,...,L - 1$。

按对数形式构造$ \overline {{Y_{{{gh}}}}(\theta )} $的缩放系数。

$ \begin{split} A_{{h}}(x)= &\frac{B-1}{\sqrt{\overline{Y_{{gM}}(\theta)}}-\sqrt{T_{hr}}}\sqrt{x}+ \\ &\left(1-\sqrt{T_{hr}}\frac{B-1}{\sqrt{\overline{Y_{{gM}}(\theta)}}-\sqrt{T_{hr}}}\right)。\end{split} $

(5)

式中：x为分段自变量，设[${T_{hr}}$，$\overline {{Y_{{gM}}}(\theta )} $]之间共分R段，则$x =\displaystyle \frac{{\overline {{Y_{{gM}}}(\theta )} - {T_{hr}}}}{{R - 1}}i + {T_{hr}},i = 0,1,...,R - 1$；B为显控指定的缩放倍数。

将2个分段序号合并，总分段为：

$ x = \left\{{\begin{aligned} & { \displaystyle\frac{T_{hr}}{L}i，{i = 0,1,\cdots,L - 1} }，\\ & {\displaystyle \frac{{\overline {{Y_{{{gM}}}}(\theta )} - {T_{hr}}}}{{R - 1}}(i - L) + {T_{hr}}}，{i = L,\cdots,L + R - 1} 。\end{aligned}} \right. $

(6)

总缩放系数为：

$ A(x) = \left\{ \begin{aligned} &{A_{{l}}}(x)，x \in [0,{T_{hr}}] ，\\ &{A_{{h}}}(x)，x \in [{T_{hr}},\overline {{Y_{{{gM}}}}(\theta )} ] 。\end{aligned} \right. $

(7)

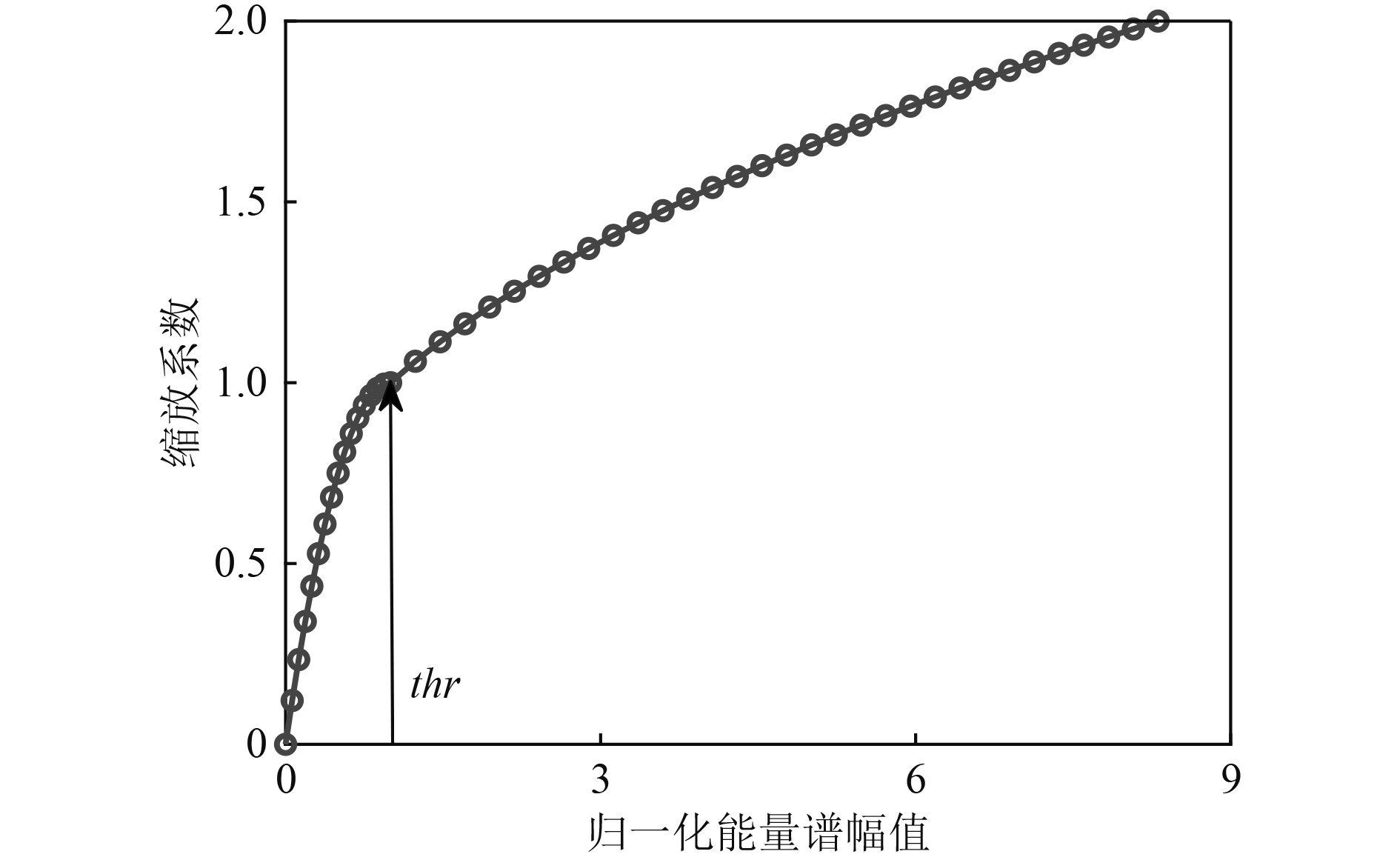
构造缩放系数示意图如图3所示。

图3中X轴为归一化能量谱幅值，Y轴为缩放系数，示意图所用参数为B=2, $ {T_{hr}} $=1，L=16，R=32。

最后，遍历$\overline {{Y_{\text{g}}}(\theta )} $中P个波束能量数据，根据式(6)判断$\overline {{Y_{\text{g}}}(\theta )} $中数据的分段序号x，再根据式(7)确定对应的缩放修正系数${A^{'}}(\theta )$，则局部缩放后的方位能量谱为$Z(\theta ) = \overline {{Y_{\text{g}}}(\theta )} {A^{'}}(\theta ),\theta = 1,2,...,P$。

2 数值仿真与验证 2.1 仿真分析

因圆环阵360°全向方位能量谱在首尾位置处能按式(2)进行循环扩展，实现平滑过渡，故本文选择圆环阵进行仿真分析。圆环阵阵元数M=64，在方位50°有一$ R_{\text{SN}}=-40\text{ dB} $弱宽带信号，在邻近方位60°处有一$ R_{\text{SN}}=-25\text{ dB} $的强干扰宽带信号，背景噪声为高斯白噪声。仿真使用常规波束形成生成全向360°共512个等角度分布波束，经10倍插值后单批次方位能量谱共长5120点。背景均衡归一化半窗长K=31，截断常数取a=3，背景门限取${T_{hr}}$=1，分段L=16，R=32，实际应用中缩放倍数B是一个可通过显控更改的可调参数，仿真中以固定数值进行对比分析。

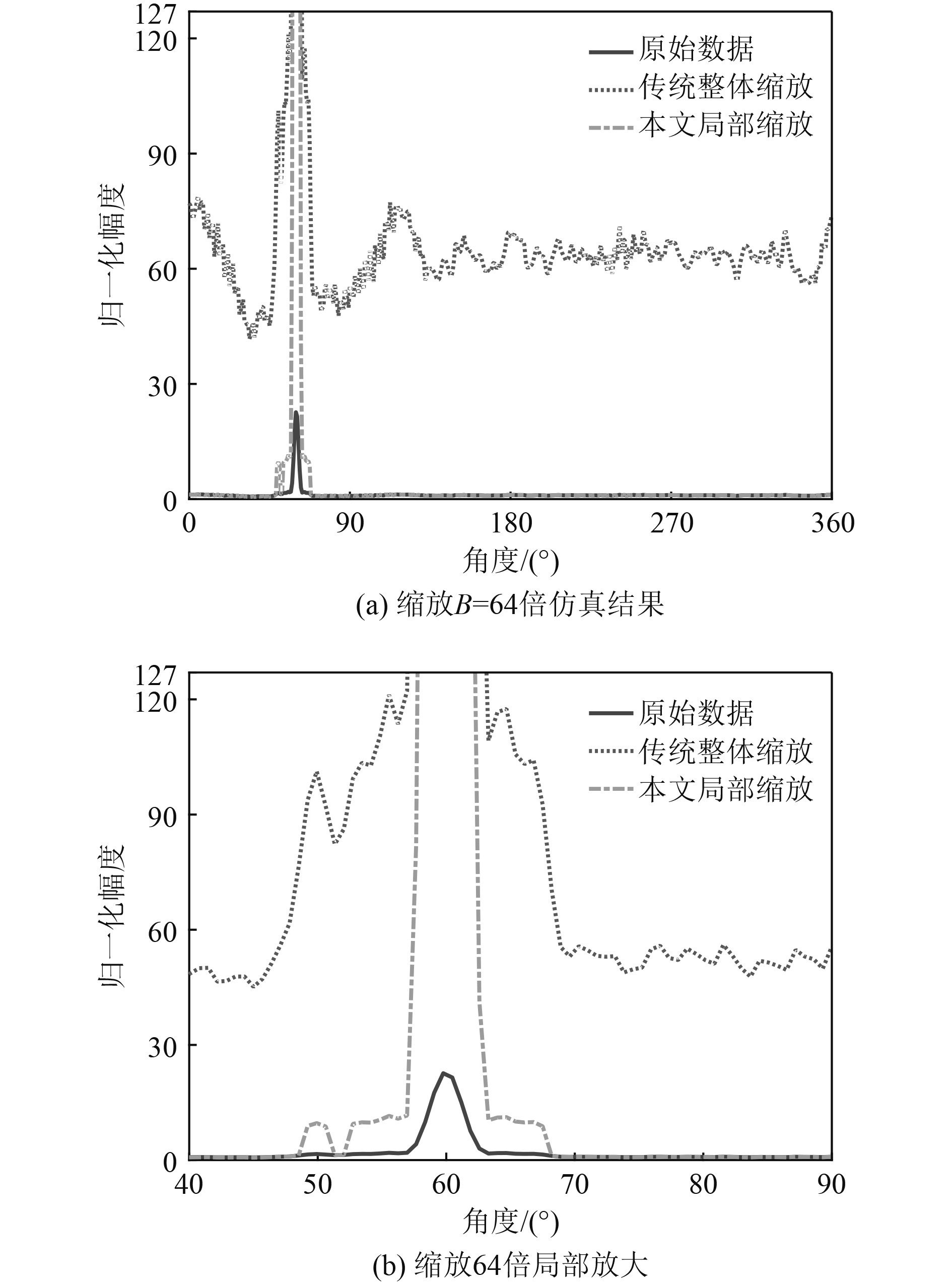
图4中X轴为方位角度，Y轴为归一化幅度，实线为原始方位能量谱，点线为传统整体缩放结果，点划线为本文局部缩放结果。图4(a)为模拟实际使用情况，Y轴做了限幅处理，只显示幅度在[0，127]数据。图4(b)为图4(a)中目标方位局部放大。图中可看出，在强目标干扰下，50°附近的弱目标在原始数据里不易分辨，经传统整体缩放后，整个背景被抬高，弱目标夹杂在起伏的背景中能被分辨，但较强的背景噪声影响目标方位识别，且无法兼顾其他方位目标；经本文所提局部缩放方法处理后，整体背景基本保持稳定，目标方位实现局部放大，50°附近的弱目标能明显分辨，且不影响其他方位目标的监测，极大地提高了目标方位识别能力。

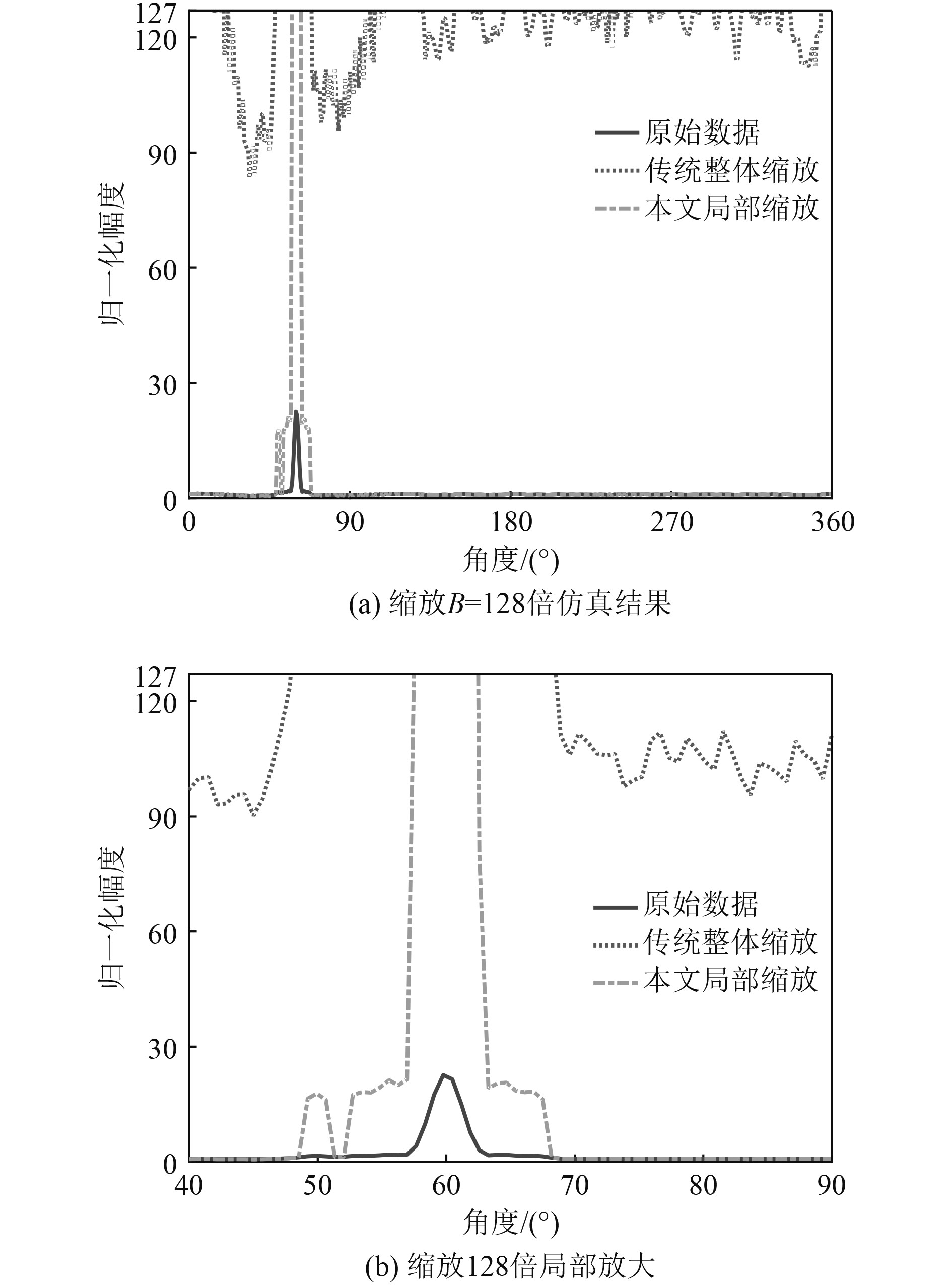
对同一批数据继续做128倍放大。结果如图5所示，在Y轴同样限幅情况下，传统整体缩放随着放大倍数的提高整个方位能量谱大部分已经超出了显示范围限制，无法观测目标方位；而经本文局部缩放处理的方位能量谱，背景保持稳定的情况下，实现了目标方位处的进一步放大，更加利于目标方位快速识别；在当前的显示限幅情况下，弱目标方位依然剩余约7倍的放大余量；而且，相比于传统整体缩放，经本文方法缩放后依然可观测其他方位，不影响全方位警戒功能。

2.2 实际数据验证

使用实际试验数据进行验证，缩放倍数B=16，采样常规波束形成，传统整体缩放所得的方位历程图如图6所示，采样本文局部缩放信号处理方法获得的方位历程图如图7所示。

图6与图7中X轴为方位[0°，360°]，Y轴为时间，数据取对数后以颜色进行区分显示，具体对应关系见图中右侧色棒。对比图6和图7这2种缩放方法下的方位历程图，强目标的轨迹2种方法在历程图上显示基本一致，但在强目标干扰下的弱目标显示有所差距。以图中黑色方框内数据为例，图6传统整体缩放因背景随着缩放被整体“抬高”，弱目标在较高的背景下被“淹没”，不易区分识别目标轨迹；而图7本文局部缩放处理后结果，背景保持在−30 dB附近，比传统方法低了近15 dB，方框中能清晰分辨2条弱目标轨迹。

3 结　语

本文针对声呐应用中遇到的缩放问题进行分析，提出一种稳定背景的局部缩放信号处理方法。该方法能在保持方位能量谱背景基本稳定的情况下，实现快速直观区分目标和背景、突出显示和识别目标方位的功能，尤其对强干扰附近的弱目标检测，相比于传统整体缩放方法，提高弱目标的检测和识别能力的同时不影响其他方位目标的监测。另外，本方法不影响整个被动声呐系统检测处理的基本框架，对现有设备的更新升级改动很小，利于工程实现。