随着我国对海洋资源的探索、研究、开发变得愈发重视,水下所需传输信息的增多,对水中发射和接受信号的装置即水声换能器的要求也越来越高[1 − 5]。纵振水声换能器是目前应用最广、发射性能较好的一种发射装置[6 − 8],它的整体结构简单并且具有较高的发射电压响应以及其他各项性能稳定等优势,但也存在着精度较低、发射电压响应起伏较大以及加工制作难度大等问题。
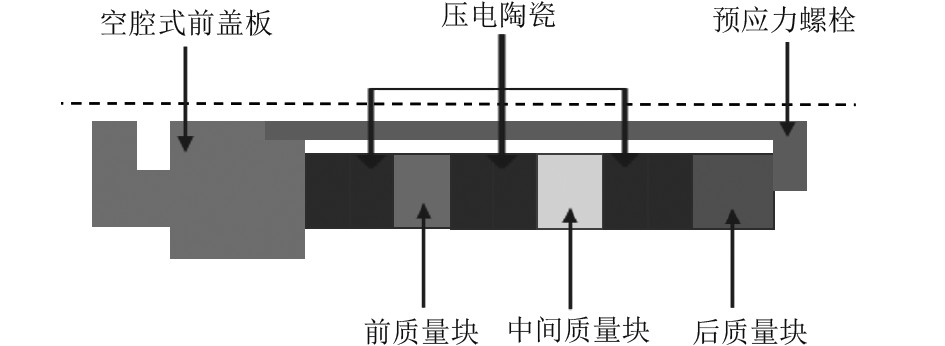
1 有限元分析 1.1 有限元仿真建模通过对实物进行一些简化处理得到其二维轴对称模型图如图1所示。
|
图 1 二维轴对称模型图 Fig. 1 Two-dimensional axisymmetric model |
在COMSOL软件中分析水声换能器时,主要分析空腔式辐射头、压电晶堆、前中后质量块、水域等。空腔式辐射头采用的是7075金属铝,压电陶瓷采用的是PZT-4,前质量块和中间质量块采用的是HT350铸铁,后质量块采用的是H59黄铜。
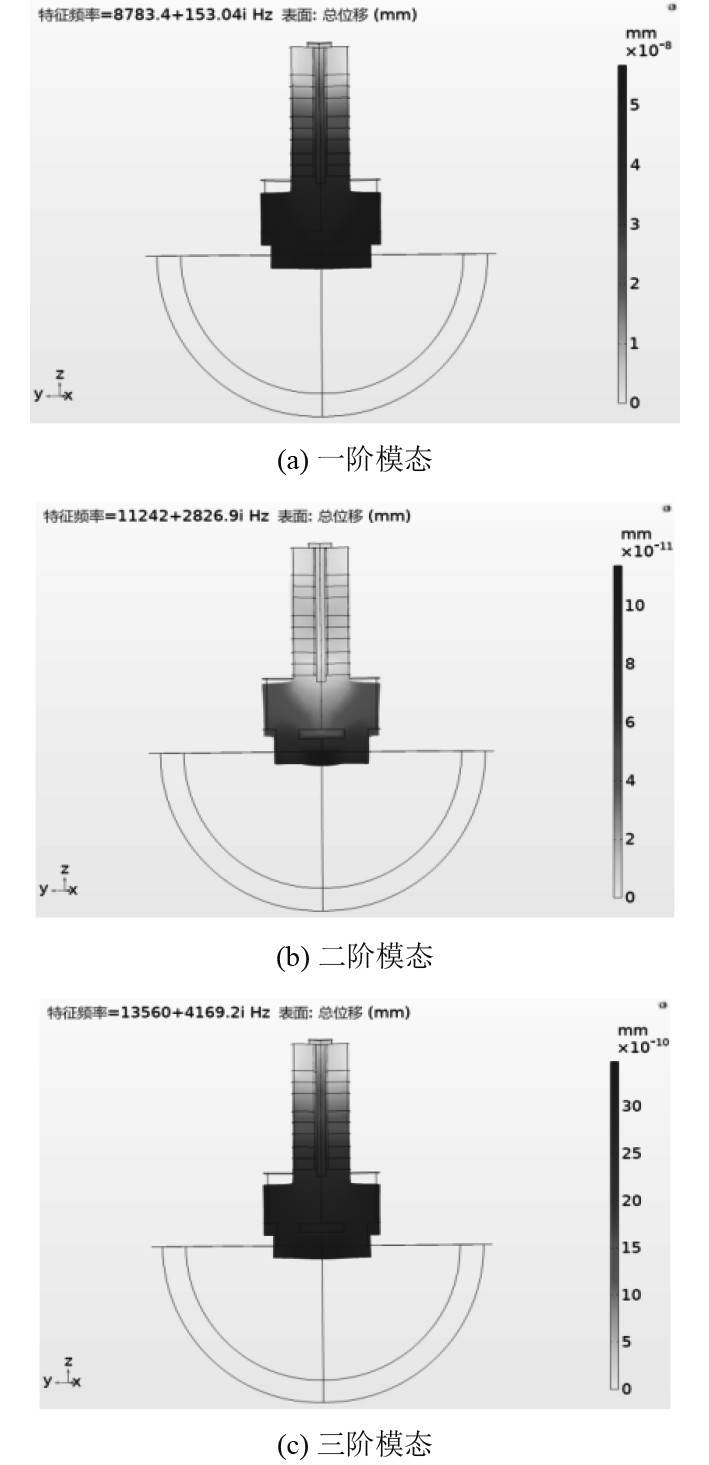
1.2 模态分析通过对换能器的特征频率求解计算,可以得到换能器在不同频率下的振动模态,如图2所示。通过分析换能器在不同特征频率下的振动模态,可以分析其在整个分析过程中振动部位随频率变化的趋势,进一步了解换能器向水中辐射声波的振动原理。
|
图 2 换能器振动模态 Fig. 2 Vibration modes of transducer |
图2(a)为换能器的一阶振动模态的云图,其特征频率为87832.4 Hz,该模态以辐射头的弯曲振动和前晶堆的径向振动为主,表面位移主要体现在辐射头,中间晶堆和后晶堆也存在轻微振动。图2(b)为换能器的二阶振动模态的云图,其特征频率为11242 Hz,该模态下主要以前盖板弯曲振动为主,辐射头和压电晶堆也存在轻微振动。图2(c)为换能器的三阶振动模态的云图,其特征频率为13560 Hz,该模态与一阶模态类似,实现了空腔式辐射头弯曲振动模态和压电晶堆纵向振动模态的耦合。
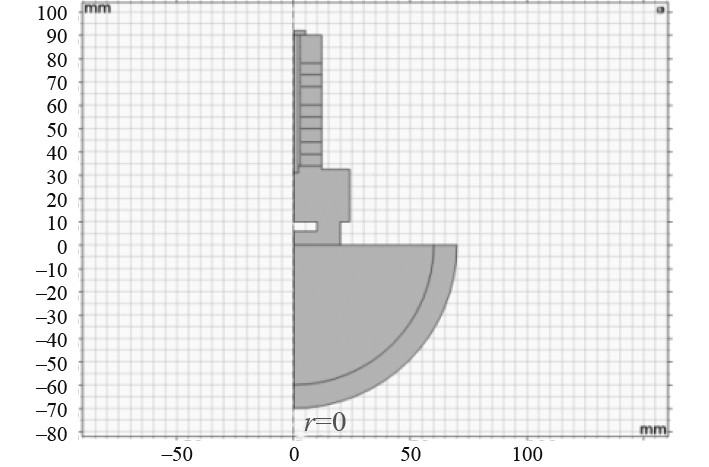
1.3 空气中谐响应分析在不影响精度并减少求解计算量的情况下构建等效二维轴对称模型,如图3所示。
|
图 3 等效二维轴对称模型 Fig. 3 Equivalent two-dimensional axisymmetric model |
分析时,更换到空气域并设置换能器的工作频率为1~60 kHz,扫描频率步进为100 Hz,得到水声换能器在空气中的导纳曲线和发射电压响应。
由图4可知,纵振水声换能器在空气中导纳曲线与空气中发射电压响应曲线的一阶谐振频率和二阶谐振频率

|
图 4 空气中研究分析曲线图 Fig. 4 Research and analysis curves in the air |
在空气介质中验证完换能器的结构模型是安全可靠后,则可进行换能器在水中的谐响应分析。换能器在水中的谐响应分析操作步骤和计算公式可参照在空气中的谐响应分析,只需将设置的材料由空气改为水域。
由图5可知,换能器在水中导纳曲线与水中发射电压响应曲线的一阶谐振频率和二阶谐振频率

|
图 5 水中研究分析曲线图 Fig. 5 Diagram of research and analysis in water |
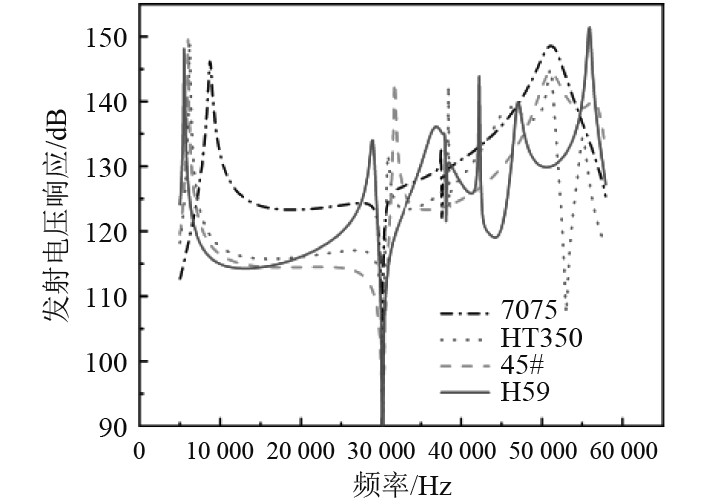
辐射头一般选用金属铝、45钢、铜、铸铁等材料。通过控制变量法,只改变辐射头使用的材料。通过对不同材料的辐射头分别求解所得到相应的发射电压响应如图6所示。
|
图 6 不同材料辐射头的发射电压响应图 Fig. 6 Emission voltage response of radiators with different materials |
可知,当辐射头材料为硬铝时,一阶谐振频率明显大于其他材料,之后的发射电压响应偏高且整体浮动较小。30 kHz频率处的中间凹谷缺陷相较于其他3种材料最小。在30~50 kHz频率范围内,硬铝材料的发射电压响应也相对光滑平缓。
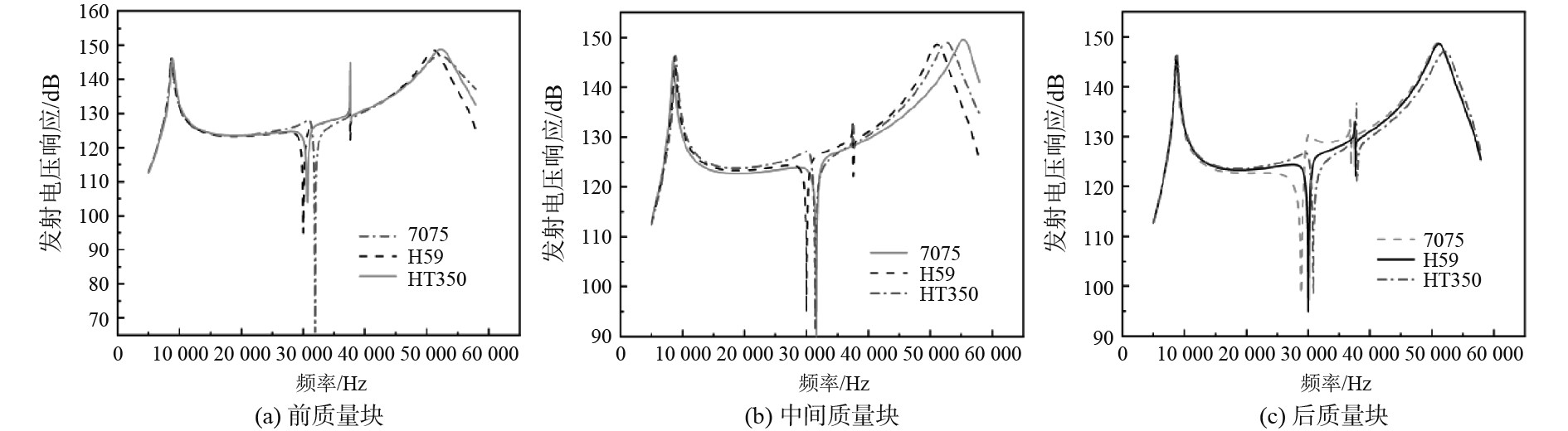
2.2 前、中、后质量块优化由图7(a)可知,HT350铸铁虽然在38 kHz处的发射电压响应波动稍大,但是其凹谷缺陷最小,综合考虑前质量块的材料选择HT350铸铁;由图7(b)可知,由于3种材料的中间凹谷缺陷差不多而HT350的发射电压响应起伏最小所以中质量块选择HT350;由图7(c)可知,H59虽然中间凹谷缺陷稍大一点,但其整体起伏波动最小且可利用波段大,因此后质量块材料选择H59。
|
图 7 质量块不同材料对发射电压响应的影响 Fig. 7 Influence of different materials of mass blocks on the response of emission voltage |
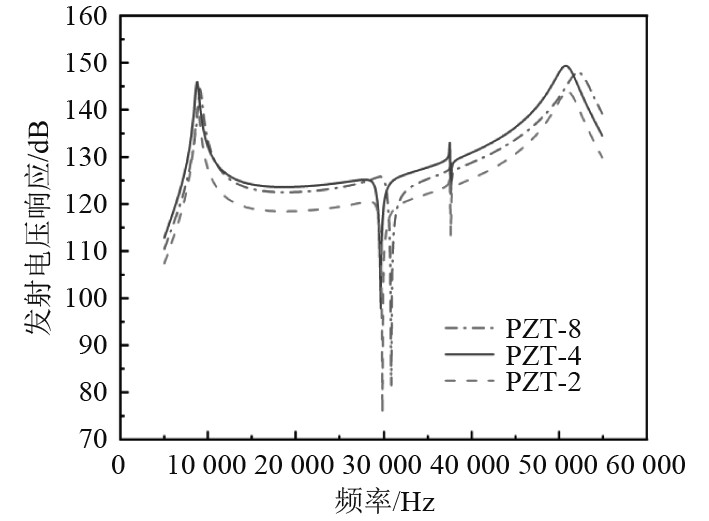
由图8可知,PZT-4型压电陶瓷的整体曲线最为平稳且起伏最小,中间凹谷缺陷最小,因此压电陶瓷材料选择使用PZT-4型压电陶瓷片。
|
图 8 不同压电陶瓷材料对发射电压响应的影响 Fig. 8 Influence of different piezoelectric ceramic materials on the emission voltage response |
通过优化最终确定辐射头材料为7075硬铝;前中质量块材料为HT350;后质量块材料为H59;压电陶瓷材料为PZT-4。通过仿真发现,此时最高压电响应值可达150 dB,可利用TVR维持在125 dB,工作频域可达20 kHz。
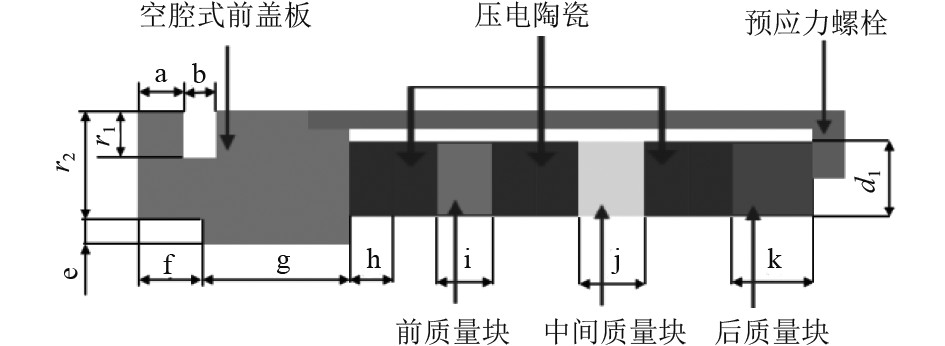
2.4 换能器结构尺寸优化通过对图9上各个结构的尺寸进行调整优化从而达到整体性能的优化效果。
|
图 9 结构尺寸优化示意图 Fig. 9 Schematic diagram of structure size optimization |
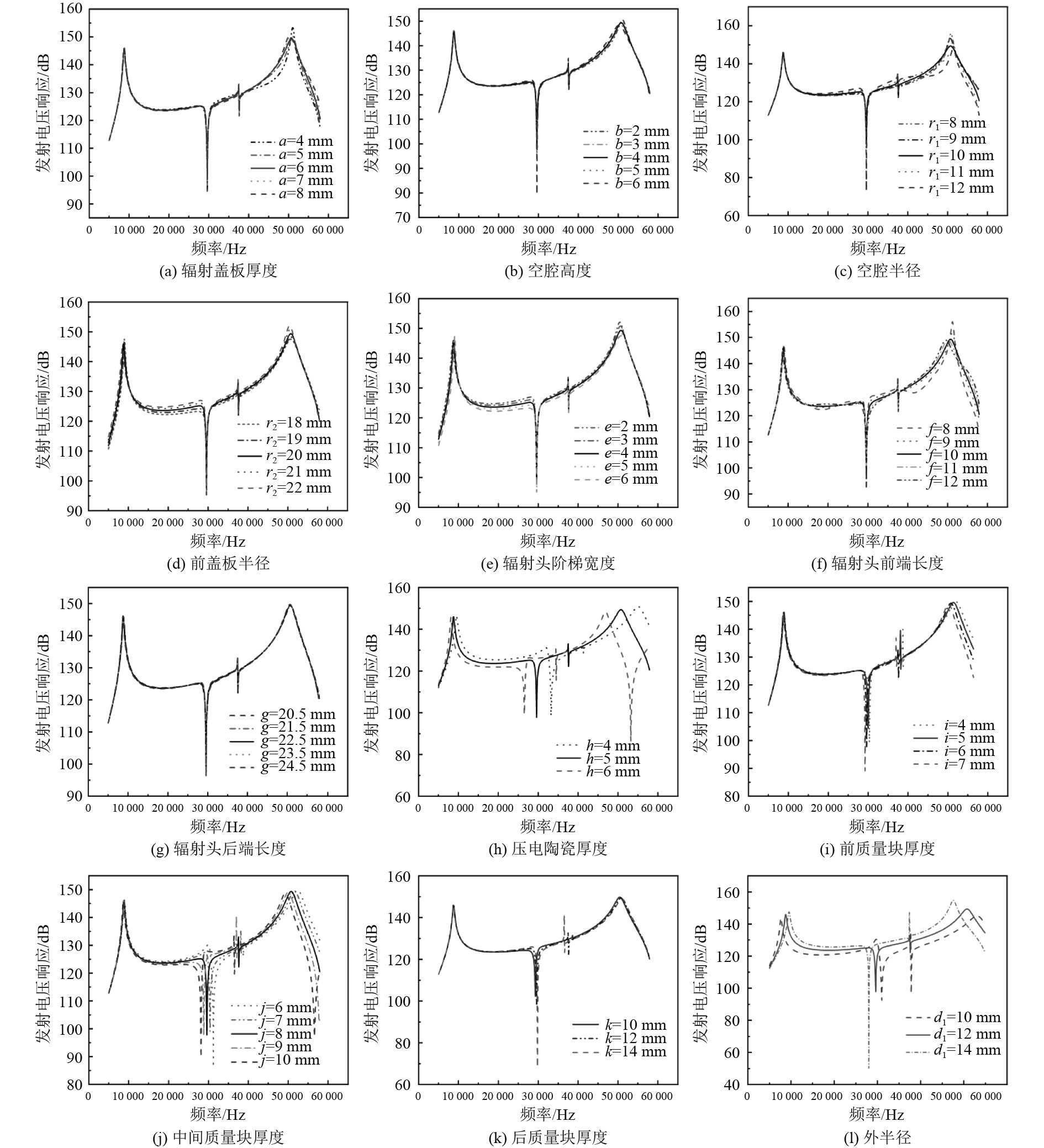
由图10(a)可知,虽然不同的辐射盖厚度对发射电压响应造成的波动整体不大,但当a=6 mm时发射电压响应整体波动最小,因此辐射盖板厚度选择6 mm;由图10(b)可知,空腔高度b在第一谐振频率差别不大但考虑到第二谐振频率,以及中间凹谷处,故选择b=4 mm;由图10(c)可知,由于中间凹谷随着r1的增大而增大,二阶谐振频率也随着空腔半径r1增大而增大,综合考虑选择r1=10 mm;由图10(d)可知,r2=20 mm时起伏较小,可用带宽较宽;由图10(e)可知,由于发射电压响应、中间凹谷随着e的增大而增大,起伏随着e增大而减小,综合考虑选择e=4 mm;由图10(f)可知,第一谐振频率、起伏程度随f增加而降低,第二谐振频率、中间凹谷随着f的增加而增加,故而选择f=10 mm,此时一阶和二阶谐振频率处的发射电压响应值也较为相近;由图10(g)可知,辐射头后端长度基本没有影响,故选g=22.5 mm;由图10(h)可知,h=5 mm时,工作带宽尚可,曲线起伏较小;由图10(i)~ 图10(k)可知,随着前质量块厚度i的增大一阶谐振频率基本不变,二阶谐振频率减小,可用带宽减小,综合考虑吧选择i=5;随着中质量块厚度j的增加一阶谐振频率基本不变,二阶谐振频率与可用带宽减少幅度明显,凹谷处缺陷也先降低后增高,故选j=7 mm此时换能器凹谷缺陷和波动都最小,工作带宽也较长;随着后质量块厚度k增大中间凹谷缺陷大幅增加,发射电压响应峰值有所下降,综合考虑选择k=10 mm;由图10(l)可知,d1=12时中间缺陷最小,可用带宽较长,起伏较小。
|
图 10 各部件优化对发射电压响应的影响 Fig. 10 Influence of component optimization on transmitting voltage response |
通过对换能器各个部件材料以及尺寸参数如图11所示,最终得到可用工作带宽为10~31.5 kHz,发射电压响应起伏为5.1 dB,发射电压响应幅值在127 dB左右。

|
图 11 优化后的发射电压响应曲线 Fig. 11 Optimized emission voltage response curve |
由于水声换能器是在水下工作,且用于探索工作,为了尽可能提高其高效性一般前端的辐射头会露出壳体所以辐射头与壳体的接触部分的也需要很好的水密性,所以采用了聚氨酯作为保护层材料。
换能器水中测试主要包括导纳测试、发射电压响应测试以及指向性测试。实验时室温17.0℃,室内相对湿度66.5%,使用水水温12.4℃。利用夹具将待测换能器固定在水深5 mm,距接收水听器1.6 m处,满足远场条件。水下检测示意图如图12所示。
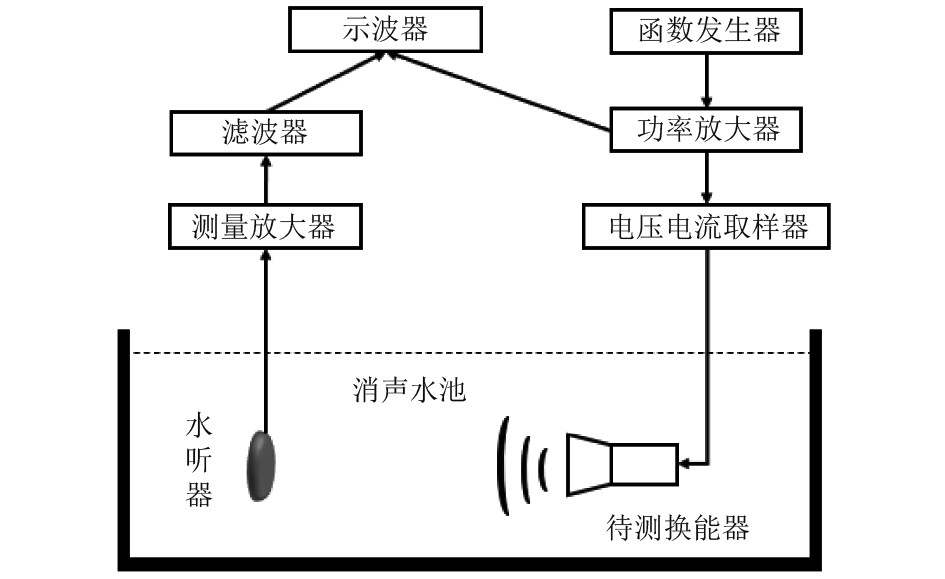
|
图 12 水下检测示意图 Fig. 12 Schematic diagram of underwater detection |
通过精密阻抗分析仪测得换能器水下导纳频响曲线如图13所示。
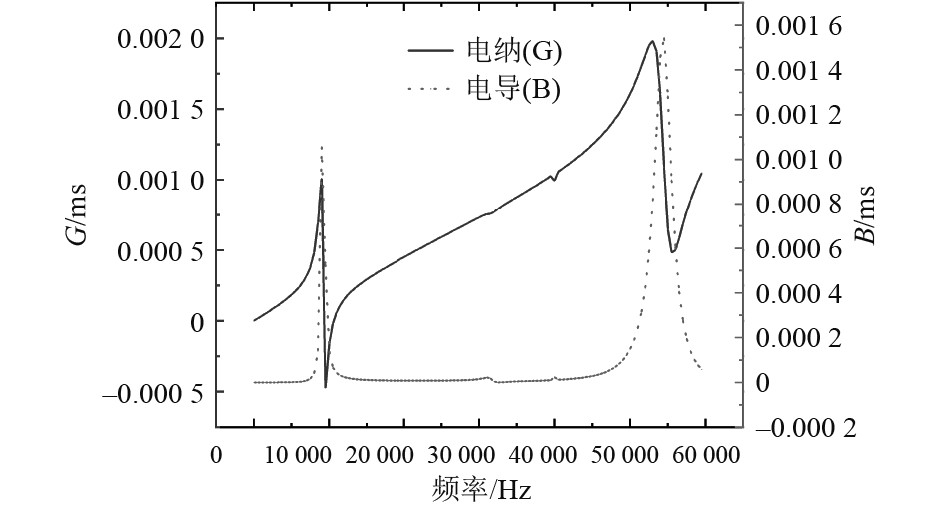
|
图 13 水中测试的导纳频响曲线 Fig. 13 Admittance frequency response curve tested in water |
可知,实际测得的换能器谐振频率与仿真结果相差不大,一阶和二阶谐振频率基本相同。但一阶谐振频率对应的电导值略小,而二阶谐振频率对应的电导值稍大,具体原因可能是实际制作的水声换能器与建立的理想化仿真模型有一定的出入、换能器加工制作时,存在一些加工误差。而且所建立的仿真模型没有考虑预应力螺钉的作用,也忽略了一些边界条件。因此实验结果与仿真结果略有出入。
4 结 语将发射电压响应的仿真数据与测试数据进行对比(见图14)可知,仿真和测试的发射电压曲线大体上趋势一致。实验测试的结果相较于仿真结果较好,实验结果的中间凹谷缺陷得到了一定程度上的改善;在整个频域范围内,换能器的可用频域在11.5~33.5 kHz之间且相较于仿真结果可用频域的起伏更小,控制在±1.5 dB,幅值为126 dB略小于仿真结果,可用工作带宽则更长,高达22 kHz,达到工作要求。
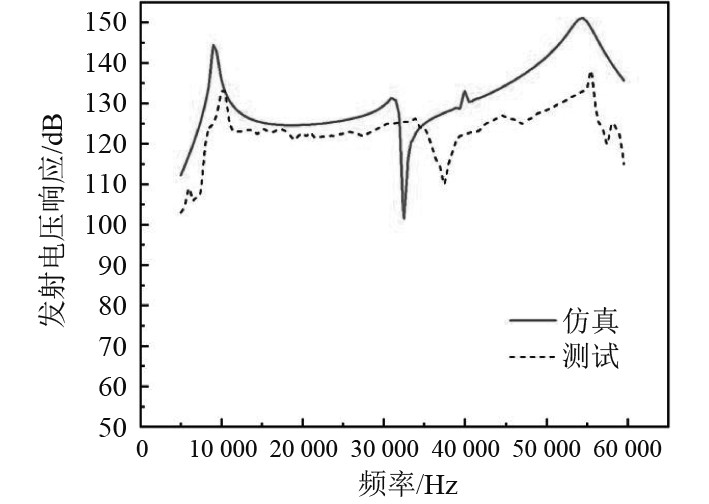
|
图 14 发射电压响应的仿真与测试图 Fig. 14 Simulation and test diagram of transmitting voltage response |
| [1] |
张庆国, 黄其培, 李兴武, 等. 宽带组合式水声换能器设计研制及应用[J]. 压电与声光, 2020, 42(2): 223-229. |
| [2] |
唐平, 鲜晓军, 刘振华, 等. 高频球面宽波束水声换能器研究[J]. 压电与声光, 2019, 41(5): 647-649. |
| [3] |
莫喜平. 我国水声换能器技术研究进展与发展机遇[J]. 中国科学院院刊, 2019, 34(3): 272-282. |
| [4] |
杜海波, 秦雷, 仲超, 等. 基于1-1-3型压电复合材料水声换能器性能分析[J]. 西北工业大学学报, 2019, 37(2): 386-392. |
| [5] |
纪京召, 黄勇军. 水声换能器灵敏度混响法校准技术研究[J]. 声学与电子工程, 2019(1): 47-49. |
| [6] |
邓皓元. 纵振宽带水声换能器的仿真及优化[D]. 武汉: 华中科技大学, 2019.
|
| [7] |
刘望生, 俞宏沛, 周利生. 纵振水声换能器发送电压响应频带展宽补偿[J]. 压电与声光, 2008(5): 577-578. |
| [8] |
滕舵, 陈航, 张允孟. 宽带纵振Tonpilz型水声换能器的优化设计[J]. 声学技术, 2005(1): 58-60. |
 2024, Vol. 46
2024, Vol. 46
