2. 中国船舶集团有限公司第七〇三研究所,黑龙江 哈尔滨 150078
2. The 703 Research Institute of CSSC, Harbin 150078, China
发电汽轮机作为热电系统中将热能转化为机械能的核心部件,其工作状态直接影响整个系统的运行稳定性和安全性[1];通过对汽轮机故障发生前运行数据的信息挖掘,可定量评估汽轮机当前运行状态并预测在接下来一段时间内可能出现的参数波动,由此实现对系统当前故障的诊断和预测[2]。
本文采用的长短期记忆模型(Long Short-Term Memory, LSTM)在处理时序问题时表现优异[3],将其与卷积神经网络(Convolution Neural Networks,CNN)结合可同时提取数据的空间和时序特征,在多特征预测领域取得了良好效果。邢红涛等[4]通过K-means聚类对氮氧化合物排放量的训练样本集进行分组,通过CNN提取排放变量的多维时序特征向量,再以此作为LSTM的训练集,构建氮氧化合物排放预测的CNN-LSTM模型;经某型电站锅炉实际数据验证,该模型对训练和测试样本的平均相对误差分别为1.76%和3.85%,远低于其他模型。闾曾怡等[5]为解决燃烧不稳定性预测问题,搭建了燃烧试验台进行多工况燃烧实验并对火焰图像随时序进行记录,得到大量各种燃烧状态的火焰图像;然后,将其作为训练集代入CNN-LSTM神经网络,得到了不稳定燃烧火焰的特征识别和状态预测模型。Ling等[6]建立了基于注意力的CNN-LSTM模型,以监控数据为训练集对风力涡轮机组的故障相关参数进行预测,取得了较好预测结果。Wang等[7]针对太阳能发电塔在不同气象条件下的热功率预测困难问题,提出一种基于机理建模和CNN-LSTM的混合预测方法,首先通过机理分析选取用于预测的主要气象因子,避免了模型输入特征选择的主观性;然后,将其代入CNN-LSTM模型提取各因子之间的时空耦合特征,最后通过完全连接的层输出预测结果;经实机数据验证,该方法的全年均方根误差和平均绝对误差分别为5.061%和2.871%,具有较高的预测精度。
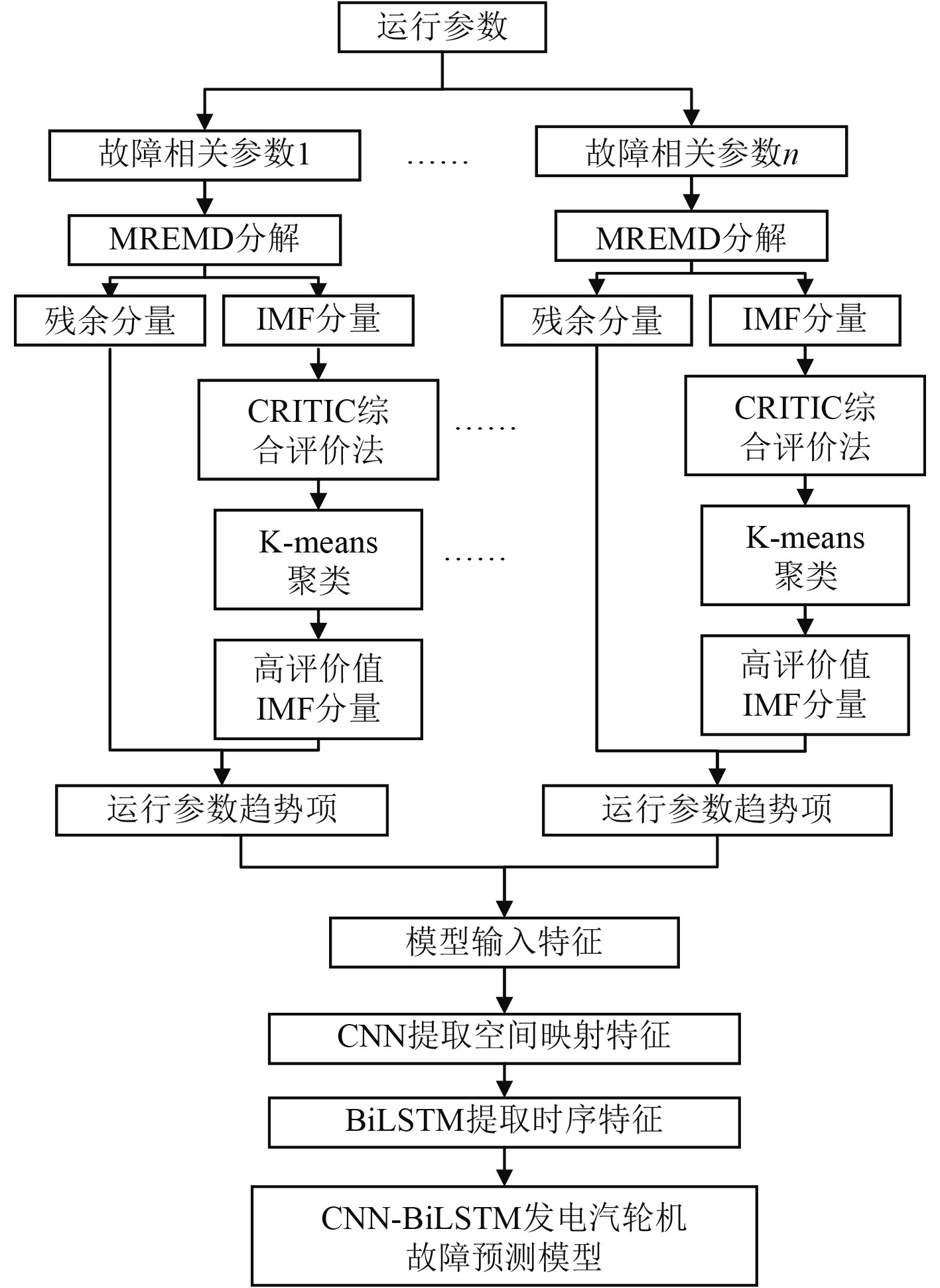
上述研究表明,CNN-LSTM模型在多特征预测领域的精准度高、应用广泛,通过优化选取输入特征可有效增加CNN-LSTM模型在提取数据时空特征方面的准确性和运算速度。本文通过对故障相关参数进行MREMD分解与筛选重构的方法提取其运行趋势,同时在传统CNN-LSTM的基础上,引入双向长短期记忆网络(Bidirectional Long Short-Term Memory, BiLSTM),以各运行参数趋势项作为神经网络训练集的输入特征构建CNN-BiLSTM模型,提取训练集的空间特征和正、逆时间序列特征,并采用麻雀搜索算法对CNN-BiLSTM模型的超参数进行优化,最终得到发电汽轮机的故障预测模型,具体流程如图1所示。
|
图 1 基于MREMD和CNN-BiLSTM的多特征故障预测流程图 Fig. 1 Multi-feature fault prediction flowchart based on MREMD and CNN-BiLSTM |
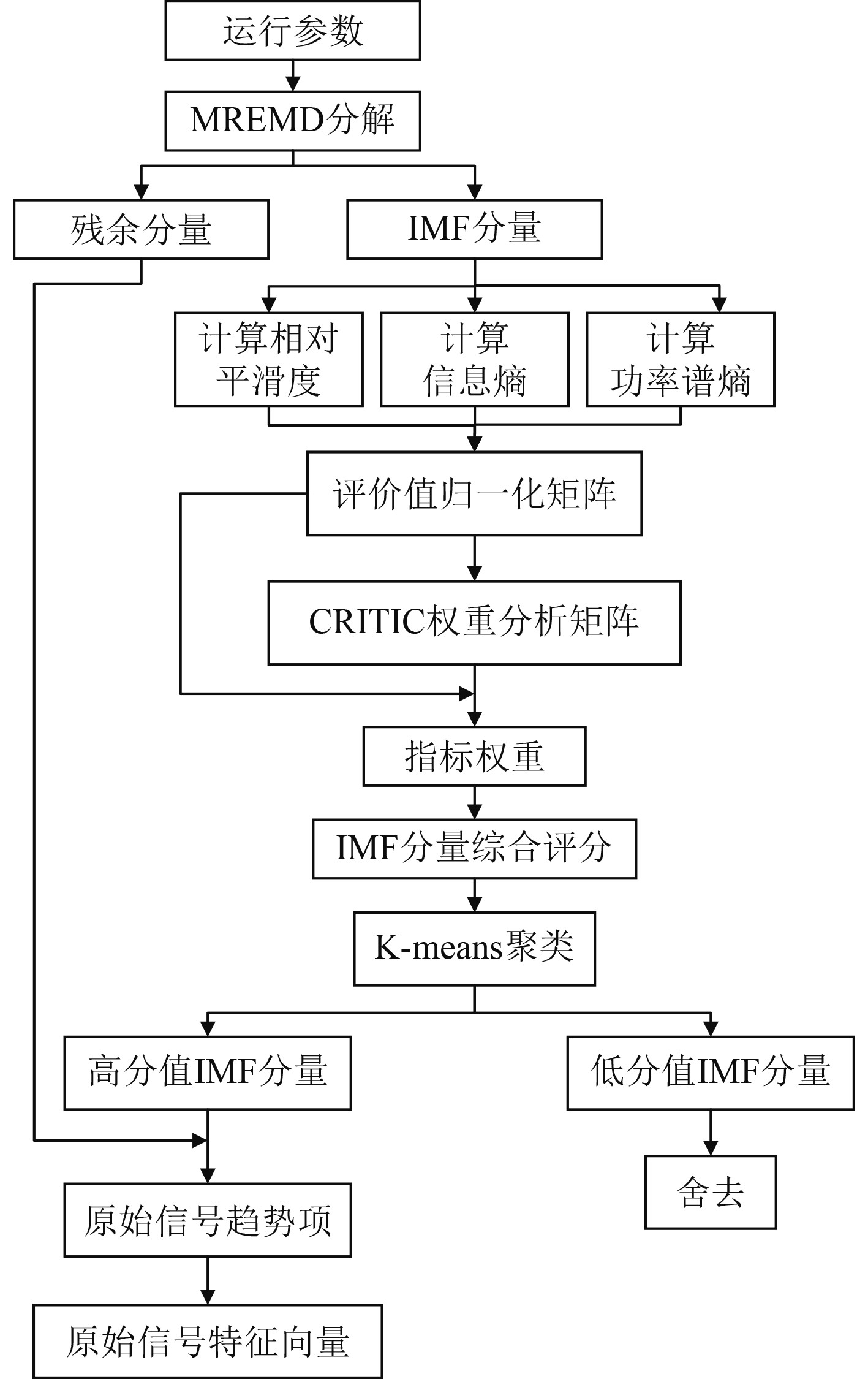
本文采用MREMD对故障相关参数的运行趋势进行提取,算法流程如图2所示。
|
图 2 基于MREMD的趋势提取流程 Fig. 2 Trend extraction process based on MREMD |
具体操作步骤如下:
步骤1 对相关参数进行MREMD分解[8],可得若干IMF分量和残余分量;
步骤2 计算各IMF分量的相对平滑度、信息熵和功率谱熵,并根据CRITIC(Criteria Importance Though Intersidereal Correlation)权重分析法计算各IMF分量的评价指标权重;
步骤3 为了在去除噪声、干扰和传感器测点异常值的同时,尽可能保留原始信号的趋势信息,各IMF分量的综合评分进行K-means聚类,划分为高评价值类IMF分量和低评价值类IMF分量;
步骤4 舍去低评价值的IMF分量,保留高评价值类的IMF分量与残余分量重构为原始数据趋势项,并以此作为故障参数的特征向量对神经网络进行训练。
1.1 MREMD分解中值回归经验模态分解(MREMD)是在经验模态分解的基础上,采用自回归(AR)模型对信号端点延拓,并用优化包络线拟合的方法改善了EMD未对有效分量和干扰分量进行定量区分,容易造成预测误差的问题。具体步骤如下:
步骤1 设研究的时间序列为s0(t),通过AR模型将s(t)两端拓延至原序列左右端点均处于延拓后时间序列的相邻2个极值点之间。
| $ s_t=\phi_0+\phi_1 s_{t-1}+\phi_2s_{t-2}+\cdots +\phi_ps_{t-p}+\mu_t 。$ | (1) |
式中:s为均值点;φ0、φ1、…φp为p+1个实数;μt(p+1,p+2,…,N)为零均值的白噪声序列。
步骤2 设延拓后的s0(t)存在k个极值点,对相邻极值点求均值得序列
| $ h_{1,0}(t)=s_0(t)-m_{1,0}(t) 。$ | (2) |
式中:m1,0(t)、s0(t)-m1,0(t)为s0(t)的信号均值序列;h1,0(t)为s0(t)的1阶信号分量。
步骤3 对h1,0(t)重复步骤1和步骤2进行迭代计算,设l次迭代后h1,l(t)满足以下终止条件,则此时停止迭代,终止条件为:
| $ \left\{ \begin{aligned} & \dfrac{| \sigma_{l-1}-\sigma_l|}{s^M_{\sigma}}\leqslant 0.2,\\ & P(\vartheta_l| \vartheta_l \leqslant \vartheta_0)\geqslant 95\text{%},\\ & P\{|s_z|(|s_z|\leqslant s_{\sigma}^M), z=1,2,\cdots,k+1\}\geqslant 68.5\text{%}。\end{aligned} \right. $\\ | (3) |
式中:σ*和σi分别为第l-1次迭代后信号分量h1,t-1(t)和第l次迭代后信号分量h1,l(t)的均值点序列标准差;sz为延拓后信序列的第z个极值点;P为条件概率;θ0和θl为初始信号和第l次迭代后的信号均值点与xM σ的比值,计算公式为:
| $ \left\{\begin{aligned} & \vartheta_0=\left(\dfrac{s^m_{1,0}}{s^M_{\sigma}}, \dfrac{s^m_{2,0}}{s^M_{\sigma}},\cdots, \dfrac{s^m_{k,0}}{s^M_{\sigma}}\right),\\ & \vartheta_0=\left(\dfrac{s^m_{1,l}}{s^M_{\sigma}}, \dfrac{s^m_{2,l}}{s^M_{\sigma}},\cdots, \dfrac{s^m_{k,l}}{s^M_{\sigma}}\right)。\end{aligned} \right. $ \\ | (4) |
式中:
步骤4 h1,l(t)即为1阶IMF分量,x0(t)-IMF1的一阶残余信号R1,将R1作为原始信号重复步骤1~步骤3,直到残余分量成为单调函数或分离不出新的IMF分量为止,计算过程为:
| $ \left\{\begin{array}{l} R_1=x_0-IMF_1,\\ R_2=R_1-IMF_2,\\ \vdots\\ R_n=R_{n-1}-IMF_n。\end{array} \right. $ \\ | (5) |
式中:n为能分解的最大IMF分量个数;Rn为原始信号s0(t)的n阶残余信号,称为残余分量
经过上述分解后,原始信号s0(t)可表示为所有IMF分量和残余分量之和,表达式为:
| $ s_0(t)=\sum^n_{i=1}IMF_i+R_n。$ | (6) |
由于MREMD分解所得的IMF分量与原始信号之间的量纲差距较大,采用传统以量纲为基础的评价标准(例如均方根误差等),不能有效评价IMF分量的优劣;所以,在构建分量综合评价体系时,选取相对平滑度、信息熵、功率谱熵等表征IMF信号质量的指标,用于表征各分量波动性的相对强弱、所含信息量大小和功率谱所含信息价值等,如下式:
| $ PH=10\times \log \left(\frac{\displaystyle\sum^n_{i=2}(y_{(i)}-y_{(i-1)})^2}{\displaystyle\sum^n_{j=2}(y'_{(j)}-y'_{(j-1)})^2}\right) ,$ | (7) |
| $ H(x)=-\sum^n_{i=1}p(x_i)\log p(x_i),$ | (8) |
| $ psdE(x)=-\sum^n_{i=1}p(x'_i)\log p(x'_i) 。$ | (9) |
式中:y(i)为原始数据第i个数值;y'(i)为IMF分量第i个数值;n为原始数据长度;p(xi)为IMF分量占原始信号的概率密度函数;p(x'i)为IMF分量功率谱占原始数据功率谱的概率密度函数;
为实现各指标的数据融合和综合评价,采用CRITIC权重分析法[9] ,通过对指标间对比强度(标准差)和冲突性(相关性)的分析,确定各指标权重,计算步骤如下:
步骤1 假设某信号经分解后有m个IMF分量,将其相对平滑度、信息熵,功率谱熵作为评价指标,可构建一个m×3的数据矩阵X,如下式:
| $ {\boldsymbol{X}}=\left(\begin{array}{ccc}x_{11},& x_{12}, & x_{13}\\ \vdots, & \vdots, &\vdots\\ x_{m1}, & x_{m2}, & x_{m3} \end{array} \right)。$ | (10) |
式中:Xm1为第m个IMF分量的相对平滑度;Xm2为第m个IMF分量的信息熵;Xm3为第m个IMF分量的功率谱熵。
步骤2 对数据进行标准化,PH、H(x)、psdE(x)为负向指标,标准化过程如下式:
| $ x'_{ij}=\frac{\min (x_j)-x_{ij}}{\max (x_j)-\min (x_j)}。$ | (11) |
步骤3 计算信息承载量,用标准差表示指标间波动性,具体如下式:
| $ b_j=\sqrt{\frac{\displaystyle\sum^m_{i=1}(x_{ij}-\overline{x_j})^2}{n-1}} 。$ | (12) |
式中:
步骤4 用相关系数的大小表示指标间冲突性,计算式为:
| $ R=\frac{\displaystyle\sum_{j, k=1}^{n}\left(x_{\bar{j}}-\overline{x_{j}}\right)\left(x_{\bar{k}}-\overline{x_{k}}\right)}{\sqrt{\displaystyle\sum_{j=1}^{n}\left(x_{\bar{j}}-\overline{x_{j}}\right)^{2} \sum_{k=1}^{n}\left(x_{\bar{k}}-\overline{x_{k}}\right)^{2}}} ,$ | (13) |
| $ A_{j}=\sum_{i=1}^{n}\left(1-r_{i j}\right)。$ | (14) |
式中:R为指标的相关性矩阵;rij为第i个指标与第j个指标的相关系数;n为评价指标个数,本文设3个评价指标,故n=3。
步骤5 设信息量为Cj如式(15)所示,各评价指标的权重如式(16)所示。
| $ C_{j}=b_{j} \times A_{j} ,$ | (15) |
| $ w_{j}=\frac{C_{j}}{\displaystyle\sum_{j=1}^{n} C_{j}}。$ | (16) |
式中:wj为第j评价指标权重。
步骤6 各IMF分量综合评价值计算式为:
| $ s_{i}=\sum_{j=1}^{n} x_{i j}^{\prime} \times w_{j} 。$ | (17) |
式中:si为第i个IMF分量的综合评价值。
此外,为了在去除噪声、干扰和传感器测点异常值的同时,尽可能保留原始信号的趋势信息,还需对各综合评价值进行K-means聚类,舍去综合评价值较低类的IMF分量,选取综合评价值较高的IMF分量和各参数的残余分量重构为各参数趋势项,并作为神经网络的训练集,计算步骤如下:
步骤1 首先从综合评价s中随机选取2个初始聚类中心ρi,计算其余数据对象与聚类中心的欧氏距离,如下式:
| $ \begin{array}{l} d(s, 2)=\left|s-\rho_{i}\right|,i=1, 2。\end{array} $ | (18) |
步骤2 找出离目标数据对象最近的聚类中心ρi,并将数据对象分配到聚类中心ρi所对应的簇中。
步骤3 计算每个簇中数据对象的平均值作为新的聚类中心,进行下一次迭代,直到聚类中心不再变化或达到最大的迭代次数时停止。
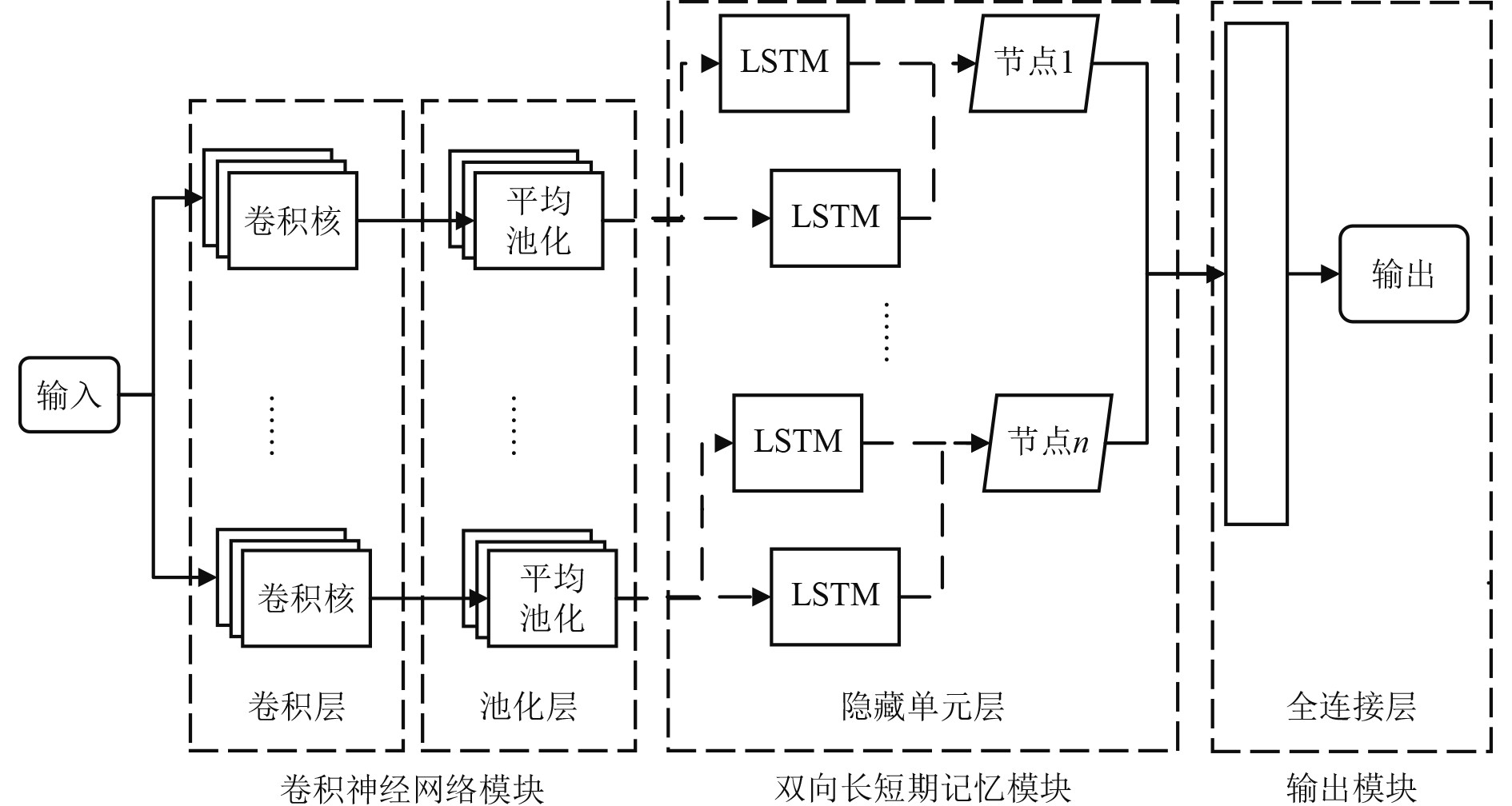
2 预测模型本文构建的卷积-双向长短期记忆(CNN-BiLSTM)预测模型,由CNN模块、BiLSTM模块和输出模块3个部分组成,结构如图3所示。
|
图 3 CNN-BiLSTM模型结构图 Fig. 3 CNN-BiLSTM model structure diagram |
由于本文研究对象的训练集是由多列具有相关性的一维时序构成,故CNN模块第一部分选取2-D卷积层,第二部分为均值池化层;这样可在有效识别数据时序特征和特征相关性的基础上,降低网络复杂度,提高模型运算速度。BiLSTM网络的主体隐藏层结构是由正向输入运算的LSTM网络和反向输入运算的LSTM网络上下叠加而成,弥补了传统单向LSTM无法关注数据的前后关联性,从而导致时序特征提取不完全的问题。CNN-BiLSTM的模型输出由全连接神经网络构成,输入向量为特征向量的时序特征和空间特征,输出结果由故障参数的维度确定。
2.1 卷积神经网络(CNN)模块CNN模块由卷积层、池化层、全连接层和输出层(作为输出模块与BiLSTM模块共用)等组成,其中卷积层计算式为:
| $ F \otimes w=\sum_{k=1}^{c} \sum_{j=1}^{W_{j}} \sum_{i=1}^{H_{f}}\left(F^{k}(i, j) w^{k}(i, j)\right) 。$ | (19) |
式中:
池化层的作用是在对卷积层进一步特征提取和降低网络复杂度,一般分为对目标区域求最大值或平均值,即最大池化和均值池化;时序特征的组合通过全连接层实现,如下式:
| $ o_{d}=f_{d}\left(o_{p} \times W_{d}+b_{d}\right) 。$ | (20) |
式中:Wd为全连接层的权值矩阵;bd为偏置;激活函数fd一般为ReLu、Tanh和Sig-moid这3种[10-11]。
全连接层的结果由输出层输出,如下式:
| $ o_{d}=f_{0}\left(o_{d} \times W_{0}+b_{0}\right)。$ | (21) |
式中:Wo为输出层的权值矩阵;bo为偏置;fo为激活函数。
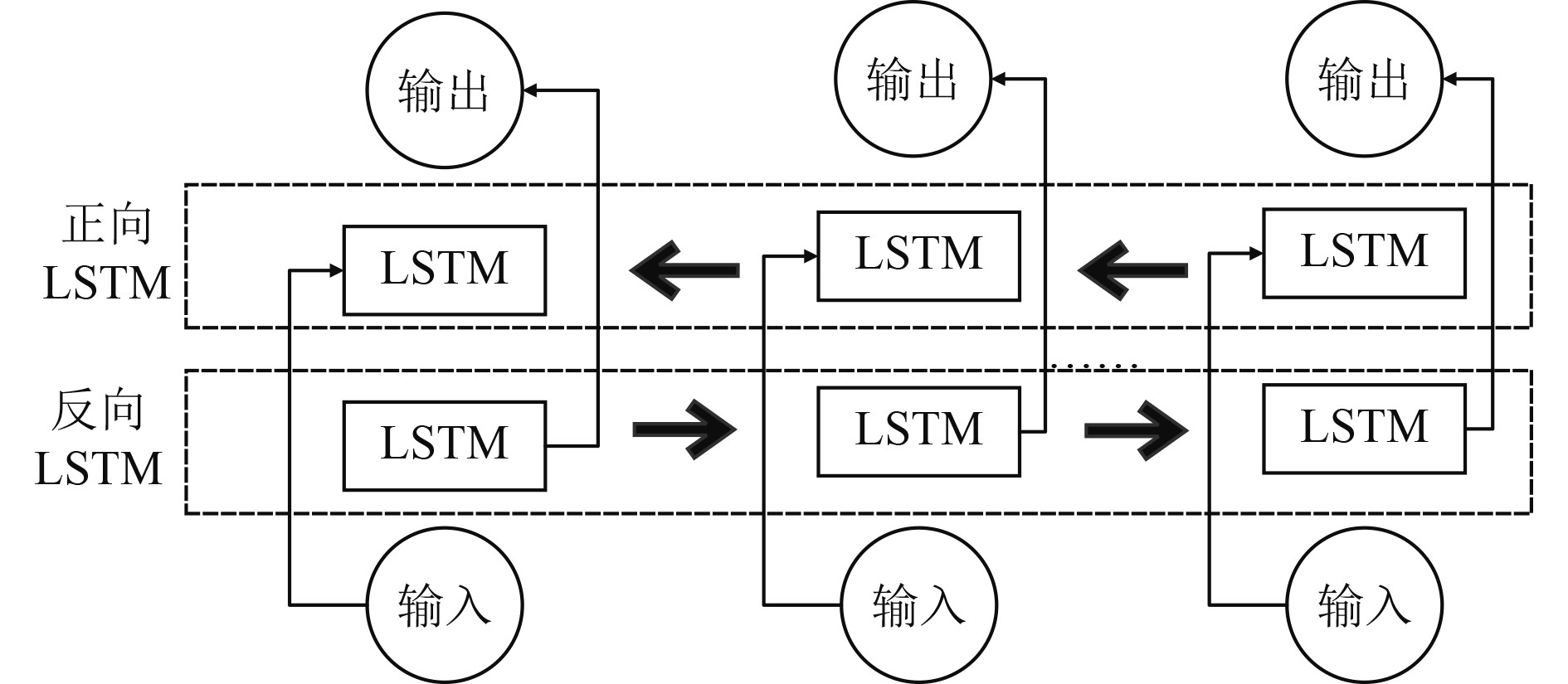
2.2 双向长短期记忆(BiLSTM) 模块BiLSTM是在传统正向LSTM的基础上引入反向LSTM结构,从而获取信号从后到前的信息,有利于模型对双向时序特征的提取[12],结构如图4所示。
|
图 4 双向长短期记忆模型(BiLSTM)结构 Fig. 4 Framework of BiLSTM |
在BiLSTM模块中设计了三类机制门,分别为输入门i、遗忘门 f 和输出门 o,用于引入或去除细胞状态 Ct中的信息[13];假设细胞状态为C ,隐藏单元为h,计算步骤如下:
步骤1 由遗忘门的 Sigmoid 函数控制历史信息的保留程度,如下式:
| $ f_{t}=\sigma\left(W_{f} \times\left[h_{t-1}, x_{t}\right]+b_{f}\right) 。$ | (22) |
式中:Wf 为 bf 和 ft 的权重矩阵和偏执。
步骤2 由输入门的 Sigmoid 函数控制当前信息的保留程度,如下式:
| $ i_{t}=\sigma\left(W_{i} \times\left[h_{t-1}, x_{t}\right]+b_{i}\right)。$ | (23) |
式中:Wi 和 bi 为 it 的权重矩阵和偏执。
步骤3 通过tanh 函数建立新的候选矢量,如下式:
| $ \overline{C_{t}}=\operatorname{tanh}\left(W_{t} \times\left[h_{t-1}, x_{t}\right]+b_{t}\right) 。$ | (24) |
式中:Wc为 tanh的权重矩阵;bc为偏置项。
步骤4 将当前信息和历史信息合并,更新当前状态如下式:
| $ C_{t}=f_{t} \times C_{t-1}+i_{t} \times \bar{C}_{t}。$ | (25) |
步骤5 由输出门的 Sigmoid 函数输出最新信息,如下式:
| $ o_{t}=\delta\left(W_{0} \times\left[h_{t-1}, x_{t}\right]+b_{0}\right) ,$ | (26) |
| $ h_{t}=O_{t} \times \operatorname{Tanh}\left(C_{t}\right)。$ | (27) |
式中:ot为输出门输出结果;ht为隐藏单元输出结果。
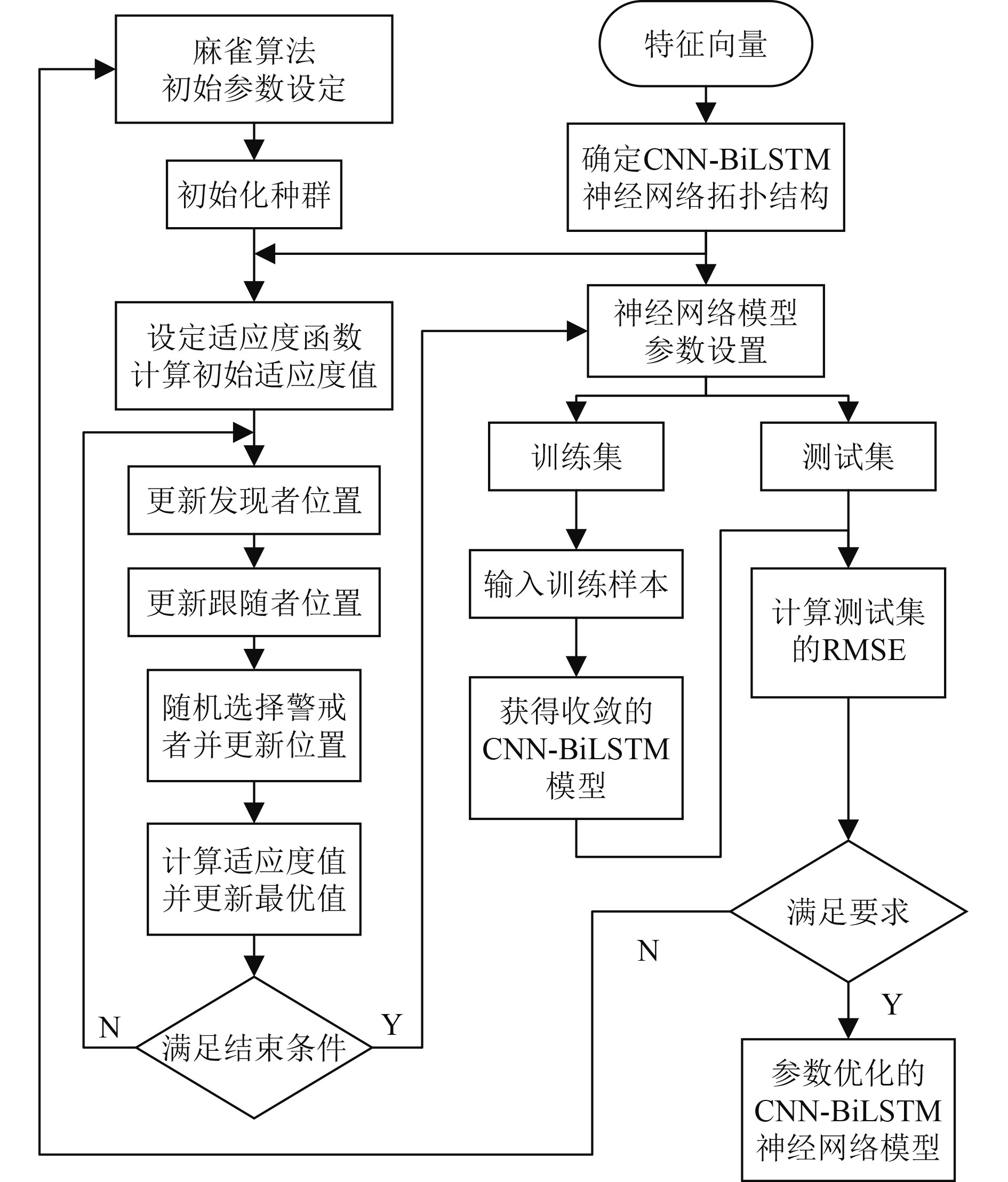
2.3 模型的超参数优化卷积-双向长短期记忆(CNN-BiLSTM)模型的超参数决定了神经网络计算的准确性和计算速度,通过经验选取会造成收敛困难,甚至过拟合等问题。麻雀搜索算法(SSA)是受麻雀的觅食行为和反捕食行为启发提出的智能优化算法,具有寻优能力强、收敛速度快的优点[14]。所以,本文采用SSA对模型参数进行全局寻优,算法流程如图5所示。
|
图 5 SSA算法优化CNN-BiLSTM模型流程图 Fig. 5 Flowchart of the SSA algorithm optimizes the CNN-BiLSTM mode |
以某型船发电汽轮机的转速波动为例,对本文所提的故障预测方法进行验证。
1)MREMD分解
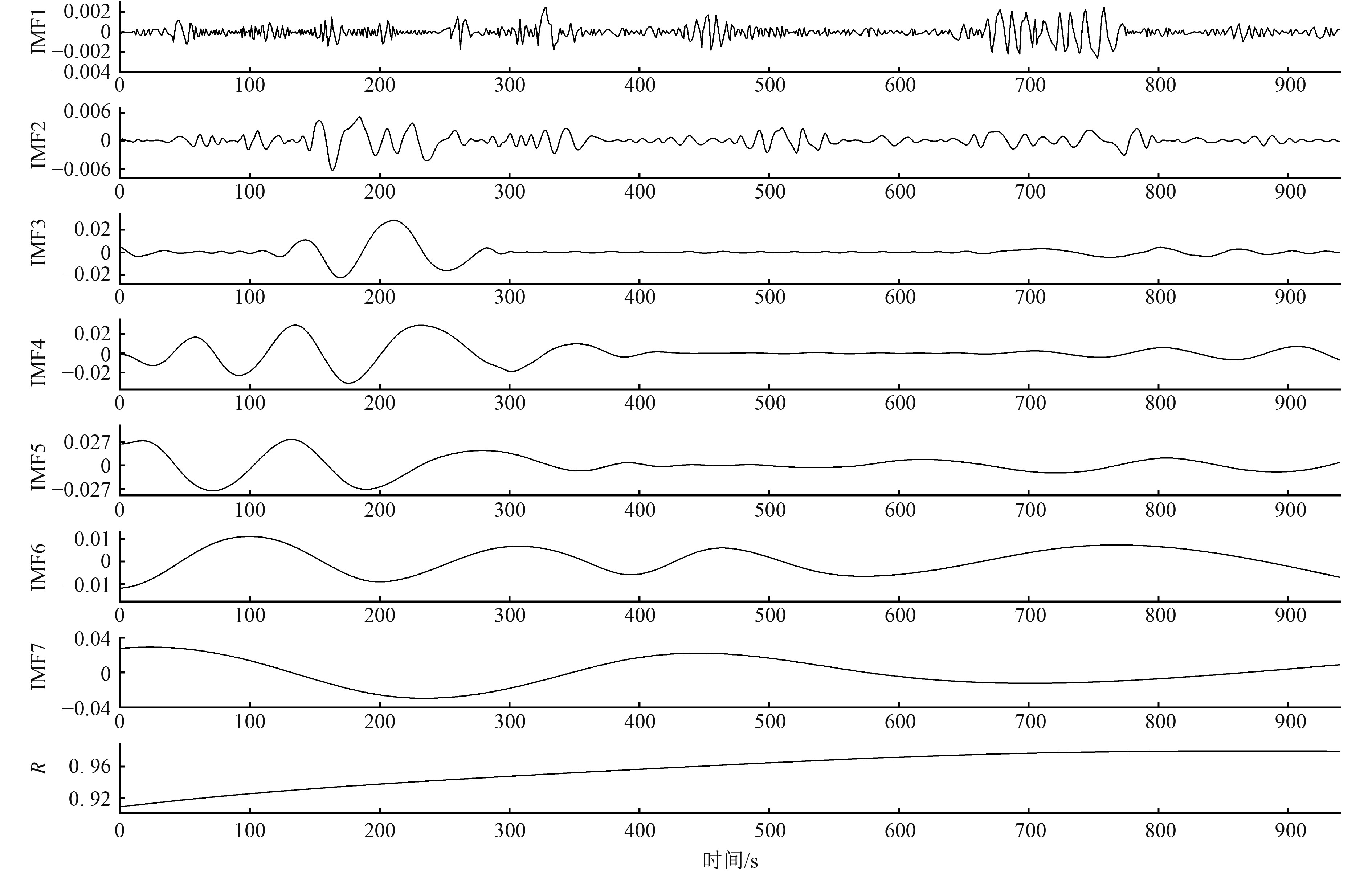
选取汽轮机速关阀前蒸汽压力、调节级后压力、主冷凝器真空作为汽轮机转速波动的故障相关参数,分别进行式(1)~式(6)的MREMD分解,结果如图6~ 图8所示。
|
图 6 汽轮机速关阀前压力分解得到的IMF分量和残余分量R Fig. 6 Decomposed IMF and residual components of front pressure of main inlet throttle-stop valve |
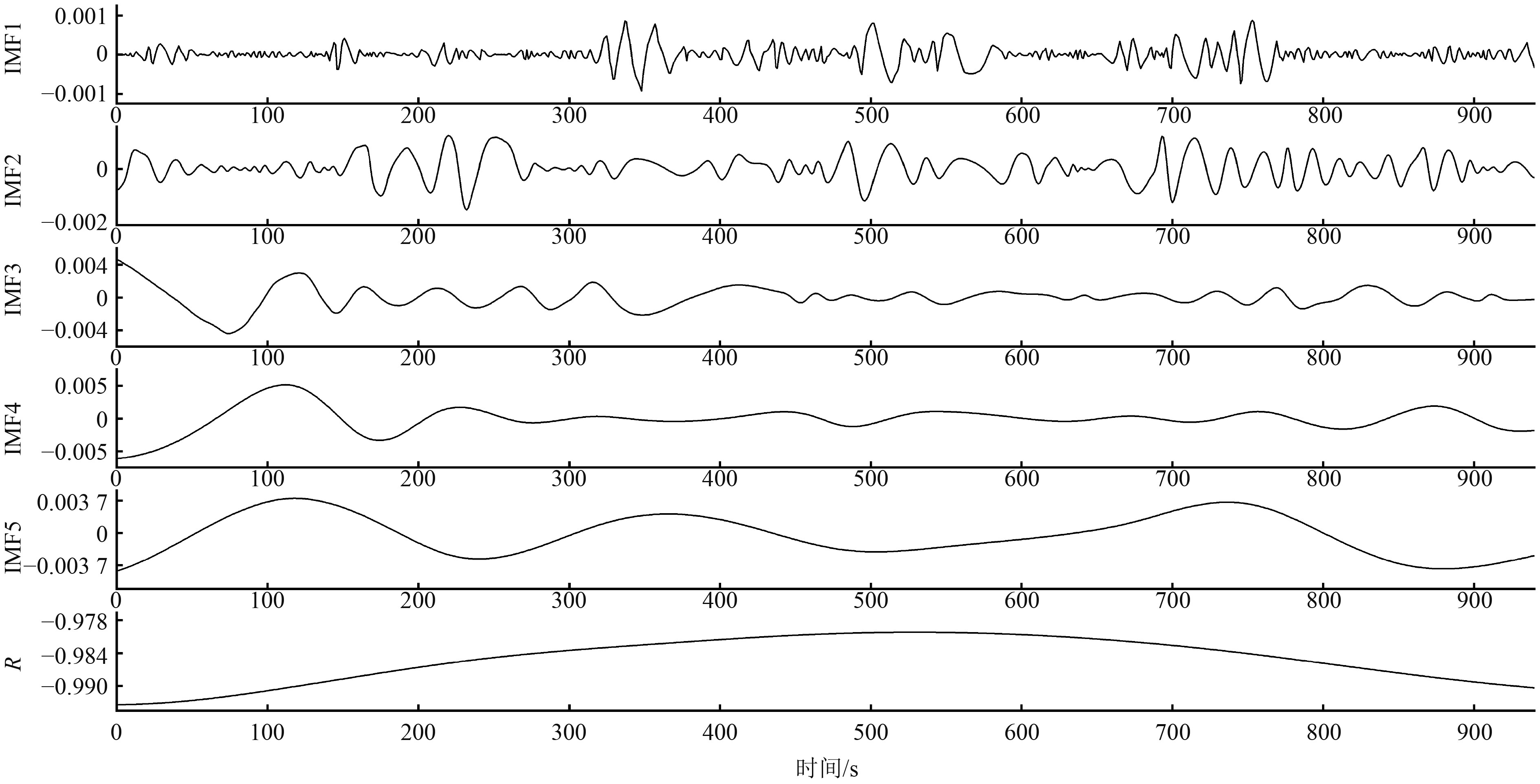
|
图 8 主冷凝器真空分解得到的IMF分量和残余分量R Fig. 8 Decomposed IMF and residual components of main condenser vacuum |
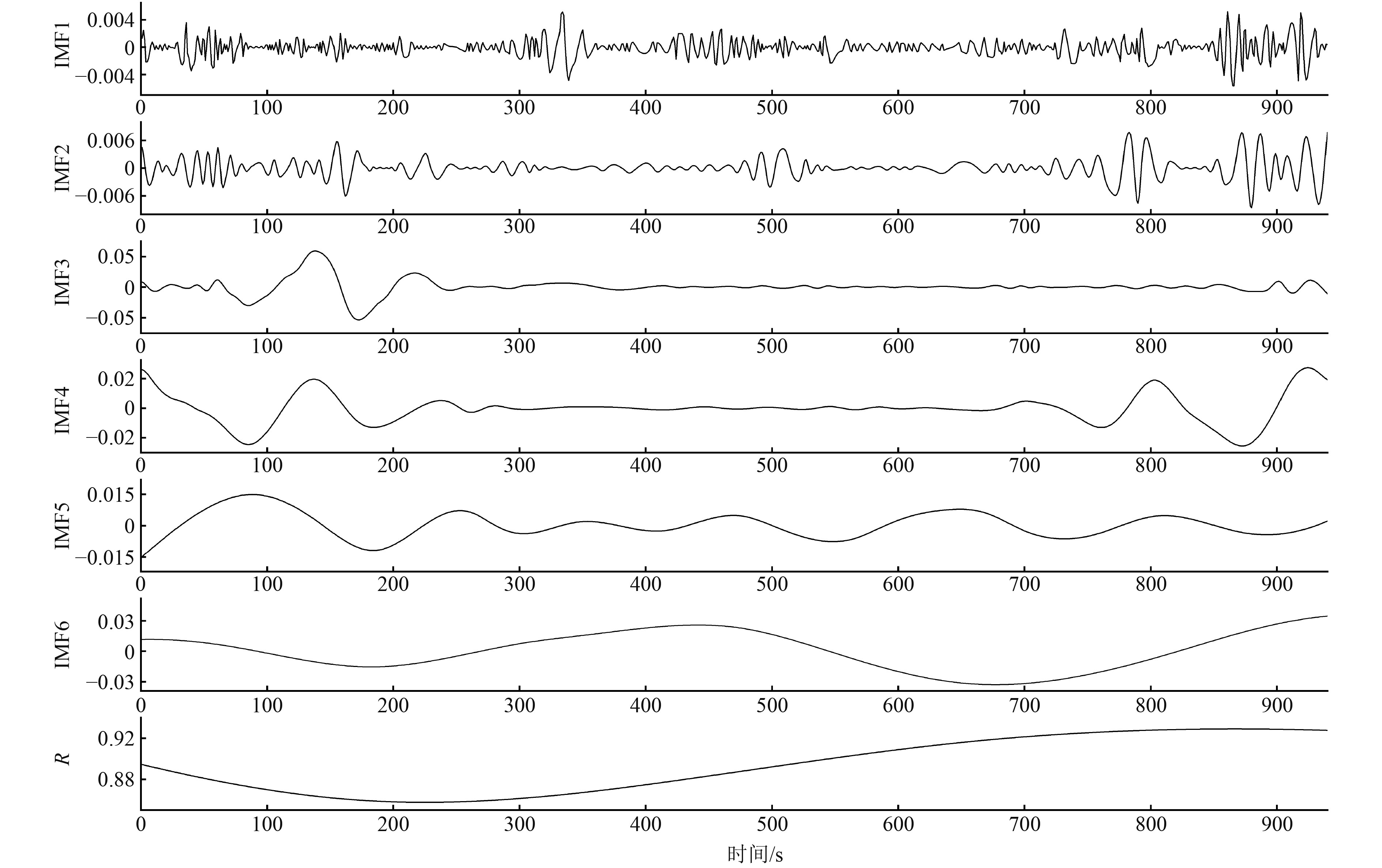
|
图 7 调节级后压力分解得到的IMF分量和残余分量R Fig. 7 Decomposed IMF and residual components of regulating stage outlet pressure |
2)质量指标计算
由式(7)~式(17)计算各参数IMF分量的质量指标和综合评价值,结果如表1所示。
|
|
表 1 各参数IMF分量的相对平滑度、信息熵、功率谱熵和综合评价值 Tab.1 The relative smoothness, energy entropy, power spectral entropy and comprehensive valuation of IMF components of every parameters |
3)趋势项重构
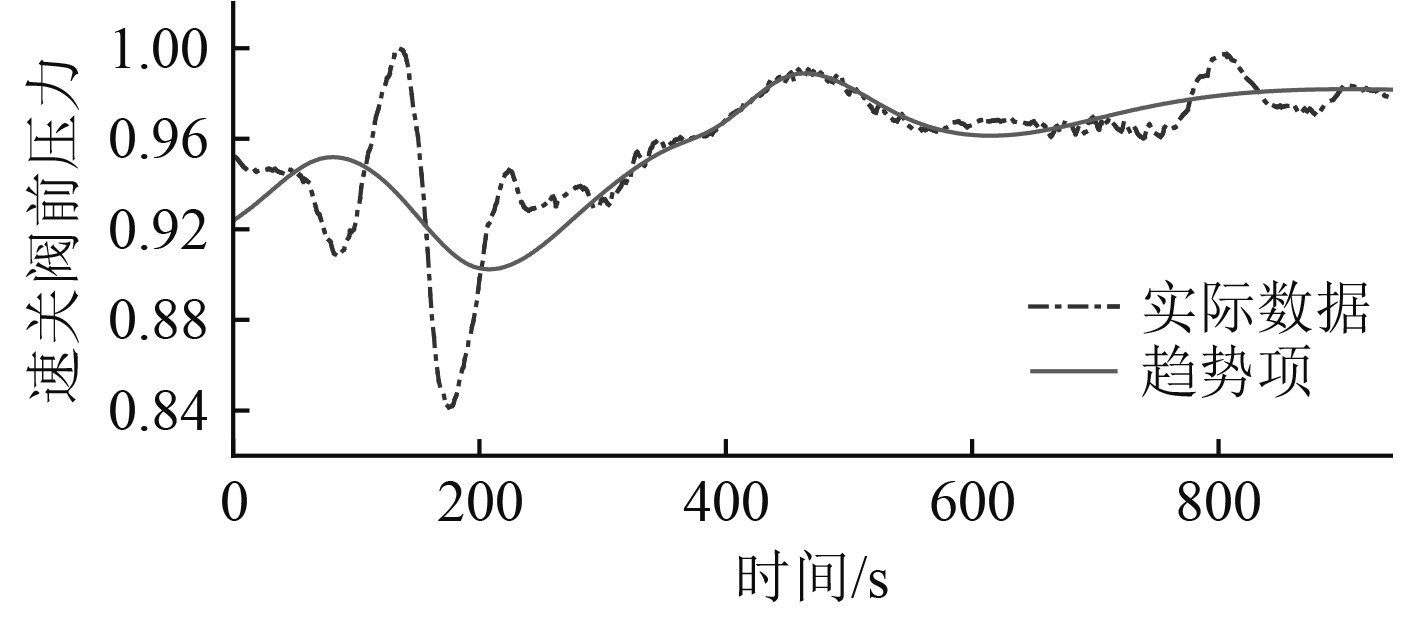
由表1可知,对于速关阀前蒸汽压力,综合评价值较高的为IMF5、IMF6和IMF7分量;对于调节级后压力,综合评价值较高的为IMF4、IMF5和IMF6分量;对于主冷凝器真空度,综合评价值较高的为IMF4和IMF5分量;将上述综合评价值较高的分量与各参数的残余分量重构为各参数的趋势项,与原始信号的对比如图9~图11所示。
|
图 9 速关阀前蒸汽压力的实际数据与趋势项 Fig. 9 Actual data and trend items of front pressure of main inlet throttle-stop valve |
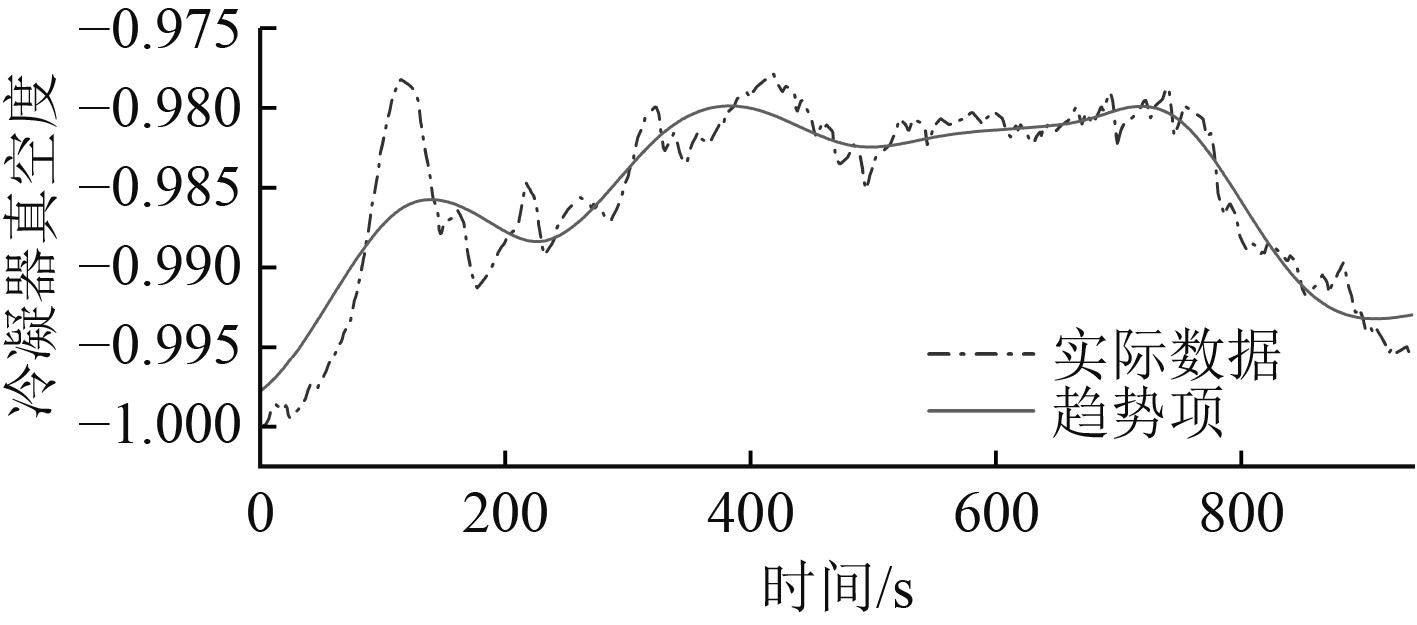
|
图 11 主冷凝器真空的实际数据与趋势项 Fig. 11 Actual data and trend item of main condenser vacuum |
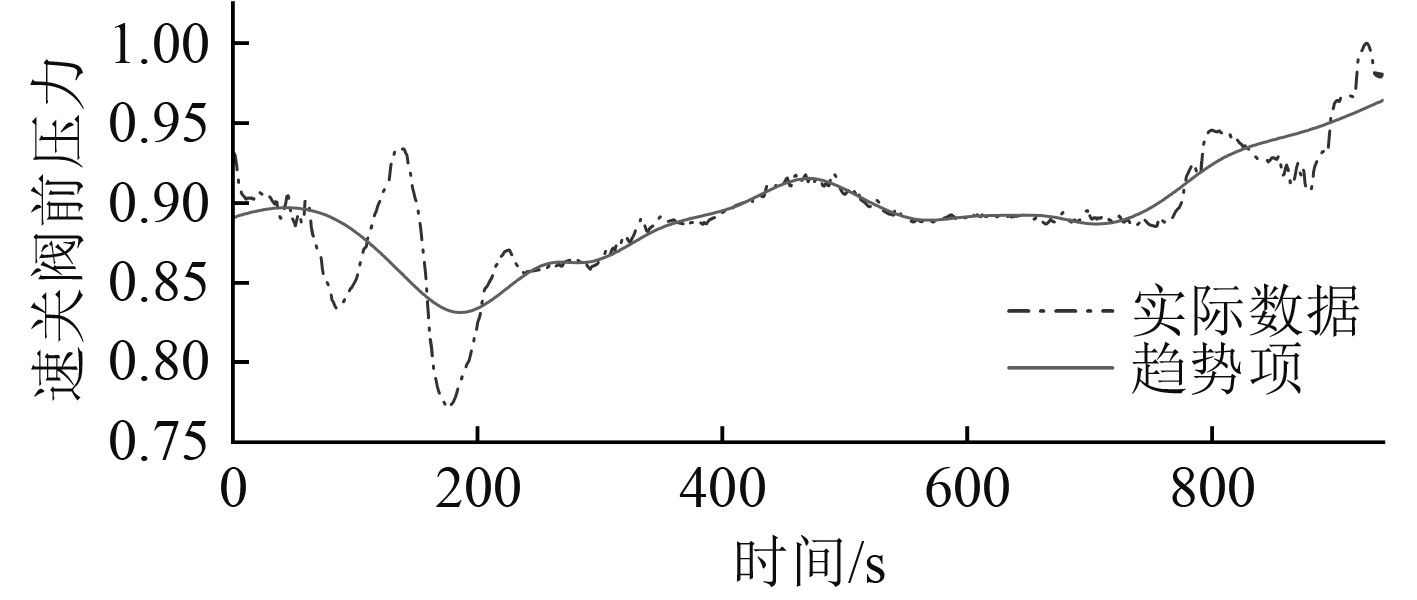
|
图 10 调节级后压力的实际数据与趋势项 Fig. 10 Actual data and trend item of regulating stage outlet pressure |
4)超参数优化
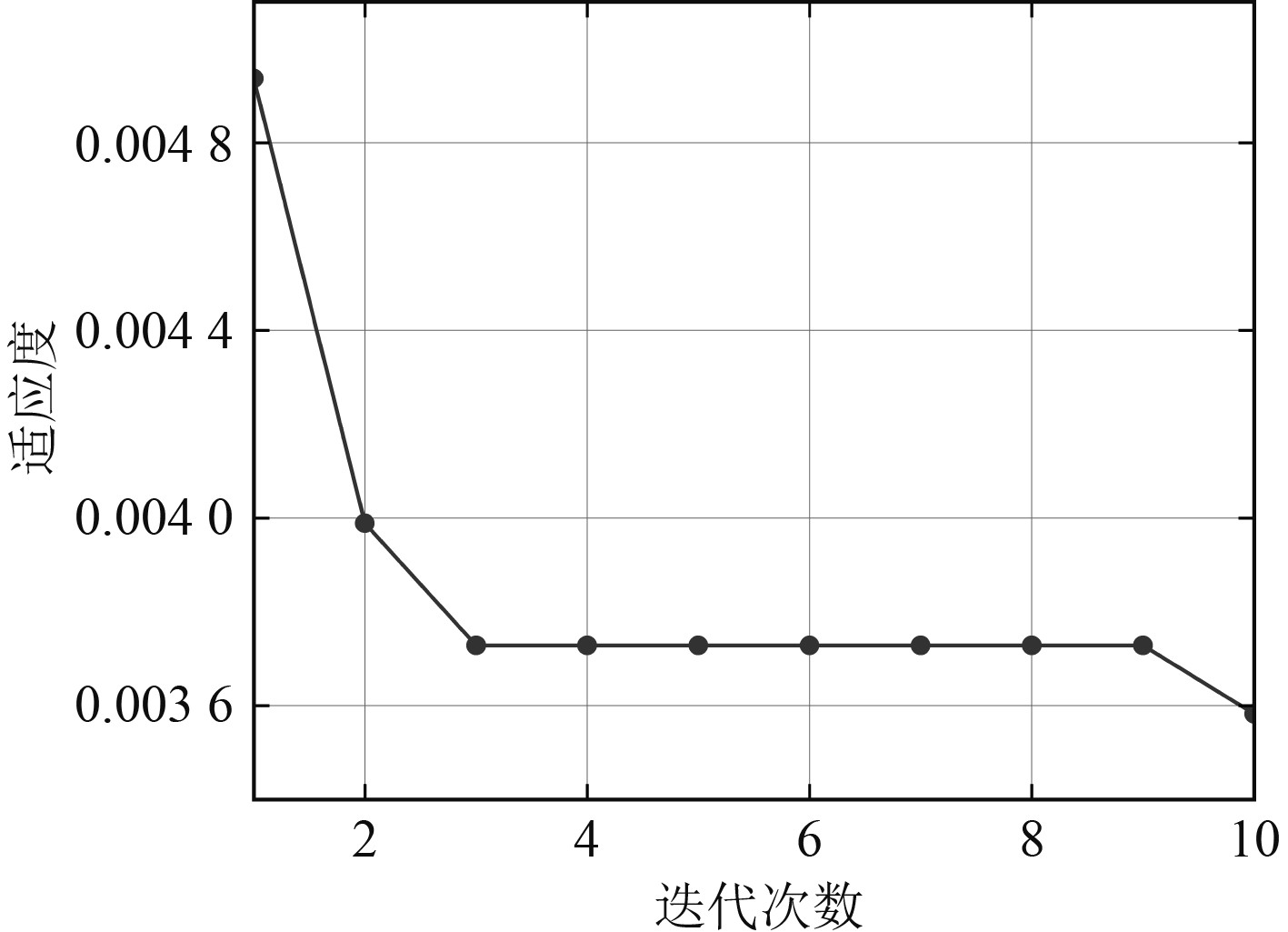
使用SSA算法对第2节中构建的CNN-BiLSTM预测模型的隐藏单元数目、卷积层的核大小、迭代次数、初始学习率等4个超参数进行优化,种群数量和迭代次数取10、发现者比例为0.7、警戒者比例选0.2,训练过程的适应度曲线如图12所示。
|
图 12 迭代过程适应度变化 Fig. 12 Fitness change of iterative process |
经过SSA算法10次迭代,最优结果如下:模型隐藏单元数目为75、卷积核大小为 [1,1]、迭代次数为50、初始学习率为0.0046。
5)模型训练与验证
将如图9~图11所示的各参数趋势项作为特征集输入向量,汽轮机转速作为特征集输出向量,取前90%作为训练集,后10%作为验证集,对第2节中构建的CNN-BiLSTM预测模型进行训练。训练集的实际数据、趋势项和预测结果如图13所示,验证集的实际数据、趋势项和预测结果如图14所示,预测结果的相对误差如图15所示。
|
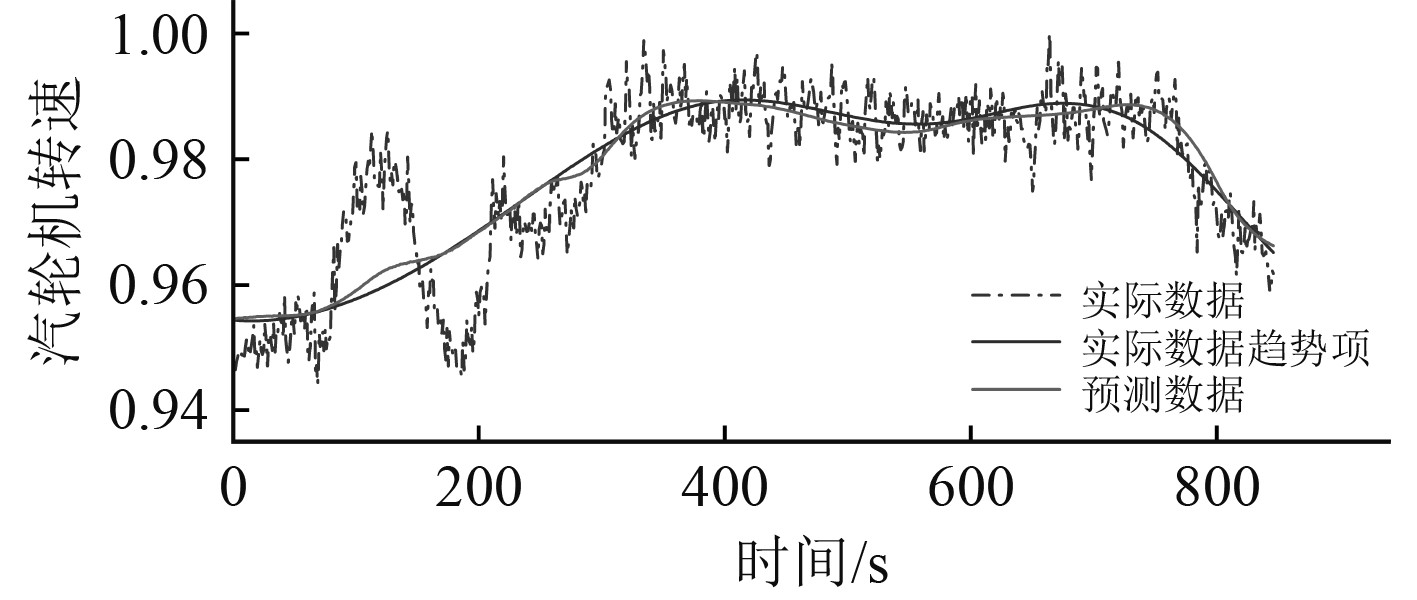
图 13 汽轮机转速训练集的实际数据、趋势项和预测数据 Fig. 13 Actual data, trend terms and forecast data of training set |
|
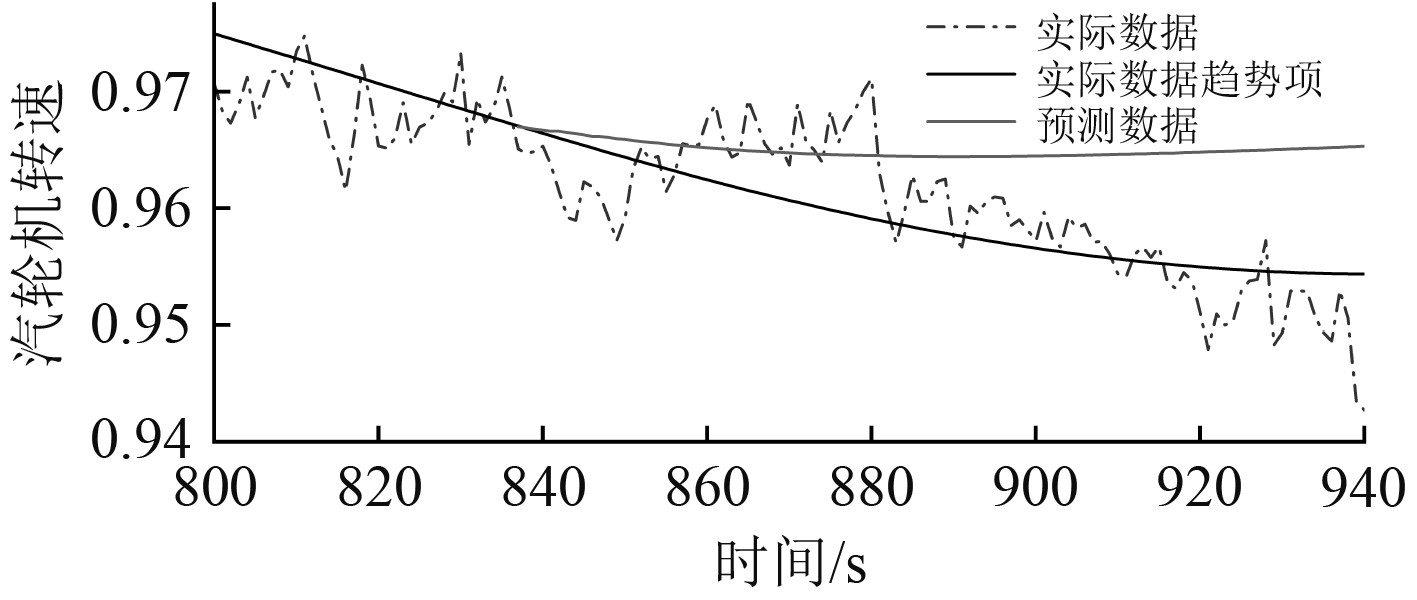
图 14 汽轮机转速验证集的实际数据、趋势项和预测数据 Fig. 14 Actual data, trend items and forecast data of verification set |
|
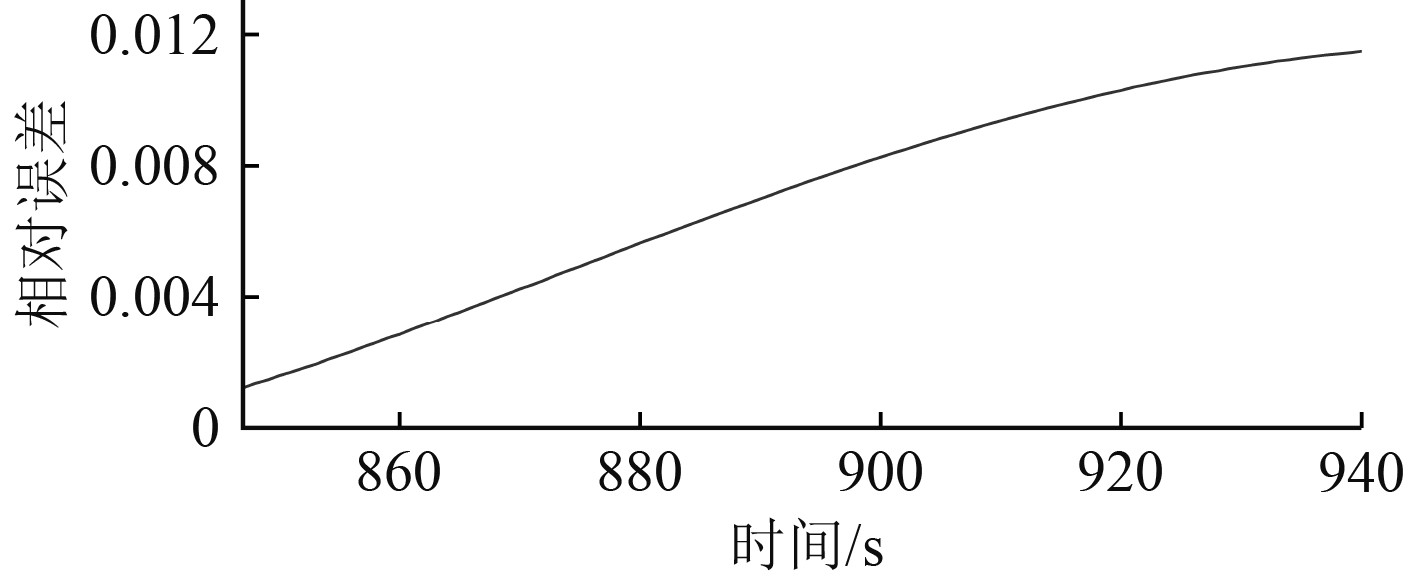
图 15 预测数据随时间的相对误差变化 Fig. 15 Forecast data over time change in relative error |
可知,随着预测时间的增加,预测误差也逐渐增大,但预测趋势与原始数据的变化趋势相同。经计算,预测结果的平均绝对误差为0.0071、均方根误差为0.0074,符合工程预测的需要。
4 结 语针对发电汽轮机多特征耦合故障预测问题,首先提出一种基于MREMD和CRITIC权重分析矩阵的热力信号趋势提取方法;其次将传统CNN-LSTM模型的LSTM更换为可提取逆向时序特征的BiLSTM;然后以故障相关参数的趋势项作为训练集特征向量,构建基于CNN-BiLSTM的多特征故障预测模型;最后采用SSA算法优化对CNN-BiLSTM模型超参数进行优化以避免发生过拟合,提高CNN-BiLSTM模型预测的准确性,经实例验证,本文所构建的MREMD-CNN-BiLSTM模型可通过故障相关参数的变化,忽略系统短时波动,有效预测出故障参数的发展趋势。
| [1] |
KARIM S, MAJID S K, MOJTABA K. Fault detection and diagnosis of an industrial steam turbine using a distributed configuration of adaptive neuro-fuzzy inference systems[J]. Simulation Modelling Practice and Theory, 2011, 19(5): 1280-1293.. DOI:10.1016/j.simpat.2011.01.005 |
| [2] |
郑奕扬, 倪何, 金家善. 基于MSOP的蒸汽动力系统单参数运行稳定性评估方法[J]. 上海交通大学学报, 2021, 55(11): 1438-1444.. ZHENG Yiyang. NI He, JIN Jiashan. An operation stability assessment method of a single-parameter in steam power system based on MSOP[J]. Journal of Shanghai Jiao Tong University, 2021, 55(11): 1438-1444.. |
| [3] |
孟忍, 董学平, 甘敏. 基于KPCA和BiLSTM的分解炉出口温度预测[J]. 合肥工业大学学报(自然科学版), 2023, 46(2): 169-174.. MENG Ren, DONG Xueping, GAN Min. Prediction of calciner outlet temperature based on KPCA and BiLSTM[J]. Journal of Hefei University of Technology (natural science), 2023, 46(2): 169-174.. |
| [4] |
邢红涛, 郭江龙, 刘书安, 等. 基于CNN-LSTM混合神经网络模型的NOx排放预测[J]. 电子测量技术, 2022, 45(2): 98-103.. XING Hongtao, GUO Jiangjiang, LIU Shuan, et al. NOx emission forecasting based on CNN-LSTM hybrid neural network[J]. Electronic Measurement Technology, 2022, 45(2): 98-103.. |
| [5] |
闾曾怡, 王高峰, 杨瑶, 等. 基于CNN-LSTM 深度学习的燃烧不稳定性检测方法研究[J]. 燃烧科学与技术, 2022, 28(2): 119-125. LV Zengyi, WANG Gaofeng, YANG Yao , et al. Combustion instability detection method based on CNN-LSTM deep learning[J]. Journal of Combustion Science and Technology, 2022, 28(2): 119−125. |
| [6] |
XIANG Ling, WANG Penghe, YANG Xin, et al. Fault detection of wind turbine based on SCADA data analysis using CNN and LSTM with attention mechanism[J]. Measurement, 2021(175): 1−8.
|
| [7] |
WANG Jianxing, GUO Lili, ZHANG Chengying, et al. Thermal power forecasting of solar power tower system by combining mechanism modeling and deep learning method[J]. Energy, 2020(208): 1−16.
|
| [8] |
肖鹏飞, 倪何, 金家善. 基于MWSA的热力系统单参数时序预测方法[J]. 上海交通大学学报, 2023, 57(1): 36-44. XIAO Pengfei, NI He, JIN Jiashan. Sequential prediction method of single parameter for thermal system based on MWSA[J]. Journal of Shanghai Jiao Tong University, 2023, 57(1): 36-44. |
| [9] |
王敏, 邹婕, 王惠琳, 等. 基于改进的AHP-CRITIC-MARCOS配电网设备风险评估方法[J]. 电力系统保护与控制, 2023, 51(3): 164-172.. WANG Min, ZOU Jie, WANG Huilin, et al. Improved AHP-CRITIC-MARCOS-based risk assessment method for distribution network equipment[J]. Power System Protection and Control, 2023, 51(3): 164-172.. |
| [10] |
董渊博, 茅大钧, 章明明. 基于CNN-LSTM的燃气轮机NOx排放预测研究[J]. 热能动力工程, 2021, 36(9): 132-138. DONG Yuanbo, MAO Dajun, ZHANG Mingming. Research on NOx emission prediction of gas turbine based on CNN-LSTM[J]. Jouranl of Engineering for Thermal Energy and Power, 2021, 36(9): 132-138. |
| [11] |
CARLOS I G, FRANCESCO G, ANTONIO L. A comparison of power quality disturbance detection and classification methods using CNN, LSTM and CNN-LSTM[J]. Applied Sciences, 2020, 10(19): 6755.
|
| [12] |
任建吉, 位慧慧, 邹卓霖, 等. 基于 CNN-BiLSTM-Attention 的超短期电力负荷预测[J]. 电力系统保护与控制, 2022, 50(8): 108-116. REN Jianji, WEI Huihui, ZOU Zhuolin, et al. Ultra-short-term power load forecasting based on CNN-BiLSTM-Attention[J]. Power System Protection and Control, 2022, 50(8): 108-116. |
| [13] |
张加劲. 基于注意力机制和CNN-BiLSTM 模型的航空发动机剩余寿命预测[J]. 电子测量与仪器学报, 2022, 36(8): 231-237.. ZHANG Jiajing. Remaining useful life estimation of aeroengine based on CNN-BiLSTM and attention mechanism[J]. Jouranl of Electronic Measurement and Instrumentation, 2022, 36(8): 231-237.. |
| [14] |
XUE Jiankai, SHEN Bo. A novel swarm intelligence optimization approach: sparrow search algorithm[J]. Systems Science & Control Engineering an Open Access Journal, 2020, 8(1): 22-34.. |
 2024, Vol. 46
2024, Vol. 46
