0 引　言

水下无人航行器是一种能够在水下自主执行任务的无人机器人。它使用船体设计合理的结构，搭载各类传感器、动力设备和通信系统，能够在水下环境中进行自主导航、数据采集、测量调查、监测控制等任务。水下无人航行器可以通过自主潜水、漂浮或者水下推进等方式在水面和水下大深度区域进行工作。它具有灵活多样的功能和应用，常见的任务包括海洋科学研究、海底资源勘探、水下生态监测、水下考古、海洋环境监测、海底管线巡检、搜救与打捞等。水下无人航行器在海洋工程、海洋科学研究和海底探索领域有着广泛的应用和重要意义。然而，水下无人航行器受复杂环境的影响，使得航行准确度降低^[1]，为此，通过实时轨迹跟踪控制的研究，可以使水下无人航行器在复杂的环境中更精准地航行，从而提高航行的效率，降低航行错误率^{[2 − 3]}。

对于水下无人航行器轨迹跟踪控制方法有很多，滕建平等^[4]提出无人水下航行器全局路径规划及有限时间跟踪控制方法，采用改进人工势场法，得到全局路径，利用Serret-Frenet坐标系，设计用于路径规划的视线制导方法。使用非奇异终端滑模控制，对无人水下航行器控制律进行设计，运用李雅普诺夫稳定性理论，验证控制方法的稳定性。李文魁等^[5]提出自主水下航行器自适应S面三维轨迹跟踪方法，对三维轨迹变前视距离视线导引律进行设计，采用李雅普诺夫稳定性判据，证明该导引律的稳定性，利用自适应S面控制算法，控制自主水下航行器的航向角、纵倾角以及纵向速度，并通过仿真实验验证所提导引律的有效性。但是上述方法操作困难，而且泛化性低，所以控制过程存在漏洞。

贝叶斯神经网络具有很高的泛化性和适应性^[6]，将其运用到水下无人航行器实时轨迹跟踪控制中，并结合水下无人航行器运动学模型，形成基于贝叶斯神经网络的水下无人航行器自适应控制器，完成水下无人航行器实时轨迹跟踪控制，提高其在实时轨迹跟踪控制中的实用性。

1 水下无人航行器运动学分析

水下无人航行器的机械结构由机器人主体、传感器、处理器、执行器等多个组成部分构成。水下无人航行器当前移动速度和旋转的角速度分别用${v_c}$和${\beta _c}$表示，机器人中心坐标用${\left[ {{x_c}\ {y_c}} \right]^\text T}$表示，$\theta$为$x$轴和机器人移动方向的夹角，${\left[ {{x_t}\ {y_t}\ {\theta _t}} \right]^\text T}$为航行前部$t$的位置，航行的目标位置是$r$点，${\left[ {{v_r}\ {\beta _r}} \right]^\text T}$为$r$点的参照速度。将航行目前伸出的长度设成$l$，则目前航行前部和预设航行位误差为：

$\left[ \begin{gathered} {{\dot e}_x} \\ {{\dot e}_y} \\ {{\dot e}_\theta } \\ \end{gathered} \right] = \left[ \begin{gathered} {v_r}\cos {e_\theta } - {v_c} + \left( {l + {e_y}} \right){\beta _c} \\ \mathop {}\limits^{} \mathop {}\limits^{} {v_r}\sin {e_\theta } - l - {e_x}{\beta _c} \\ \mathop {}\limits^{} \mathop {}\limits^{} \mathop {}\limits^{} \mathop {}\limits^{} \mathop {}\limits^{} {\beta _r} - {\beta _c} \\ \end{gathered} \right] 。$

(1)

用${p_t} = {\left[ {{x_t}\ {y_t}\ {\theta _t}} \right]^\text T}$、${p_r} = {\left[ {{x_r}\ {y_r}\ {\theta _r}} \right]^\text T}$、${v_k} = {\left[ {{v_r}\ {\beta _r}\ {v_1}} \right]^\text T}$（${v_1}$表示十字滑块的移动速度）分别表示水下无人航行器航行前部的最初预设航行位、轨迹跟踪目标位置的预设航行位以及参考速度，则基于水下无人航行器运动学模型的轨迹跟踪问题就是建立一个实时轨迹跟踪控制系统，以$v = {\left[ {{v_c}\ {\beta} \ {v_1}} \right]^\text T}$作为输入值，能确保水下无人航行器的航行点与预设航行位误差${e_p} = {\left[ {{e_x}\ {e_y}\ {e_\theta }} \right]^\text T}$符合$\mathop {\lim }\limits_{t \to \infty } {e_p} \leqslant \delta$，式中$\delta$是趋近0的正数。

根据实际操作，并且使运算和理解容易，设定已知航行的参考速度${v_k}$和轨迹的方向${e_\theta }$，轨迹（切线）和航行伸缩方向一直可以相交，即${e_x}{\text{ = }}0$，$e{\text{ = }}{e_y}$。则水下无人航行器速度跟踪误差为：

${e_o} = {o_d} - o 。$

(2)

式中，${o_d}$和$o$分别为水下无人航行器的参考速度信号和实际速度信号。以此为依据，将水下无人航行器的参考速度信号设为：

${o_d}\left( t \right) = {e_o} - {v_1}t。$

(3)

设水下无人航行器动力学参数$\mu = \left[ {{m^{}}^{}{I^{}}^{}{f_x}{{^{}}^{}}{f_y}} \right]$，由机器人质量、摩擦系数以及惯量等组成。不能精确确定矢量$\mu$是因为水下无人航行器不确定的动力学参数，那么能够将最优未知参数预估为：

${e_\mu } = {\mu _0} - \mu。$

(4)

式中，水下无人航行器动力学参数预估值为${\mu _0} = \left[ {{m_0}{{^{}}^{}}{I_0}{{^{}}^{}}{f_{x0}}{{^{}}^{}}{f_{y0}}} \right]$，则依据速度误差信号的水下无人航行器动力学方程表达式为：

$M = {e_o}{e_x} + {o_d}\left( t \right){e_y} + {e_\mu }{e_\theta }。$

(5)

2 实时轨迹跟踪控制方法设计

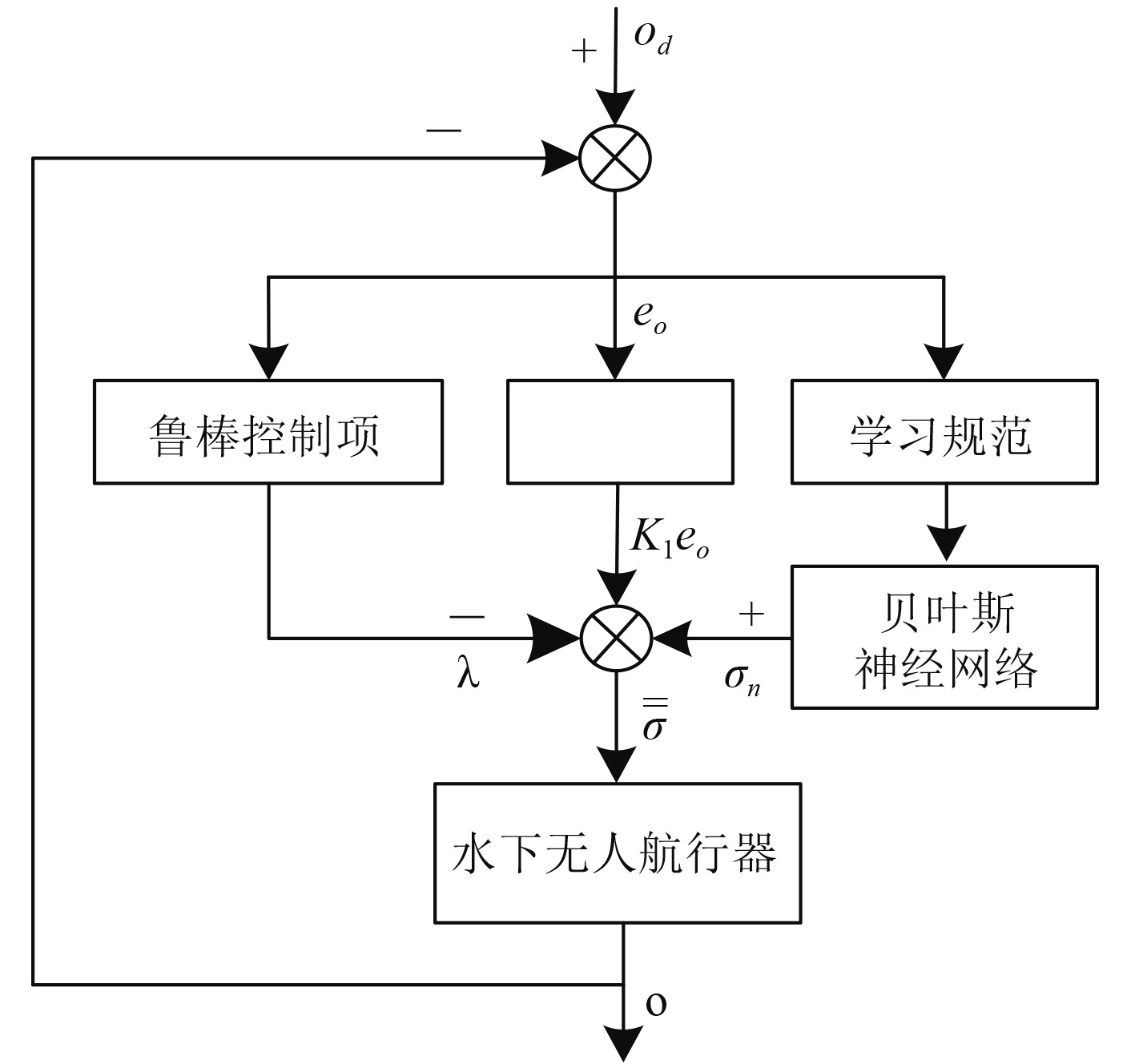
水下无人航行器运动学分析为实时轨迹跟踪控制方法设计提供了运动轨迹和预设航行位的基础，通过分析其运动过程，设计自适应控制器调整机器人的运动轨迹和航行参数，以保证航行质量。基于贝叶斯神经网络^{[7 − 8]}的水下无人航行器自适应控制器如图1所示。

图中，$\lambda$为补偿水下无人航行器动力学系统中未建模的扰动量的补偿量，${\sigma _n}$和${K_1}$分别为贝叶斯神经网络的输出力矩、正定对角增益矩阵。

控制系统复杂性在于，输入量由指定输入量与扰动量组成，按图1所示，输出是贝叶斯神经网络的输出力矩${\sigma _n}$，与${o_d}$之间的关系可由下式描述：

${\sigma _n} = Mn\left( {{o_d} + {\sigma _d}} \right) 。$

(6)

式中，$n$为扰动因子。则贝叶斯神经网络的训练性能函数为：

${E_0} = \frac{1}{2}\sum\limits_{n = 1}^Q {{{\left( {{\sigma _n} - {{\sigma '}_n}} \right)}^2}} 。$

(7)

式中：$Q$为贝叶斯神经网络输出量个数；${\sigma '_n}$为网络预期输出力矩。由此可知，贝叶斯神经网络的训练性能目标函数表达为：

${E_D} = E\varphi 。$

(8)

式中：$E = \left[ {{E_X},{E_0}} \right]$，${E_X} = \displaystyle\frac{1}{2}\sum\limits_{i = 1}^W {\left( {w_i^2 - u_i^2} \right)}$为更新项用；${w_i}$、${u_i}$和$W$分别为贝叶斯神经网络的权值、阈值以及两者的个数；${E_0}$为网络的输出值与预期值两者差的平方；$\varphi = \left[ {{\varphi _1},{\varphi _2}} \right]$为超参数，权值和阈值的分布样式以及网络训练的性能目标函数都由超参数控制。在确保网络训练误差尽量小的同时让网络有用权值以及阈值尽量少，是新的目标性能函数的作用。根据贝叶斯公式，超参数在有样本集$D = \left[ {o_d^{^{\left( N \right)}},\sigma _n^{^{\left( N \right)}}} \right]$以后的后验分布概率符合下式：

$P\left( {{\varphi _1},{\varphi _2}\left| D \right.,{N_h}} \right) = {E_D}\frac{{P\left( {D\left| {{\varphi _1},{\varphi _2},{N_h}} \right.} \right)P\left( {{\varphi _1},{\varphi _2}\left| {{N_h}} \right.} \right)}}{{P\left( {D\left| {{N_h}} \right.} \right)}}。$

(9)

式中：$P\left( {{\varphi _1},{\varphi _2}\left| {{N_h}} \right.} \right)$、${N_h}$、$P\left( {D\left| {{N_h}} \right.} \right)$、$P\left( {D\left| {{\varphi _1},{\varphi _2},{N_h}} \right.} \right)$分别为超参数先验概率、神经网络隐藏层节点数、归一化因子、似然函数。最高显著性的超参值式（10）通过对${\varphi _1}$和${\varphi _2}$求偏导得出。

${\varphi _{1MP}} = \frac{\rho }{{2{E_D}\left( {{W_{MP}}} \right)}},{\varphi _{2MP}} = \frac{{N - \rho }}{{2{E_D}\left( {{W_{MP}}} \right)}} 。$

(10)

式中：${W_{MP}}$为${E_D}$取最小值时相对应的权值以及阈值组：$\rho$为网络里能够使性能指标函数下降的参数个数$\left( {0{ \sim }W} \right)$。得到最高显著性的超参值${\varphi _1}$和${\varphi _2}$后，再次推断${E_D}$收敛情况。实现具有最高显著性的最优神经网络模型，需要经过多次的更新推断。当网络具有最高显著性时，水下无人航行器航行速度和参考速度趋于一致，当方向和速度都和轨迹趋于相同时，则完成了实时轨迹跟踪控制。

3 实验分析

为验证本文实时轨迹跟踪控制方法的精确性和稳定性，将某水下无人航行器作为实验对象，选取船上450个轨迹特征点用于实验。水下无人航行器动力学参数以及基于贝叶斯神经网络的水下无人航行器自适应控制器参数如表1所示。

3.1 轨迹跟踪控制分析

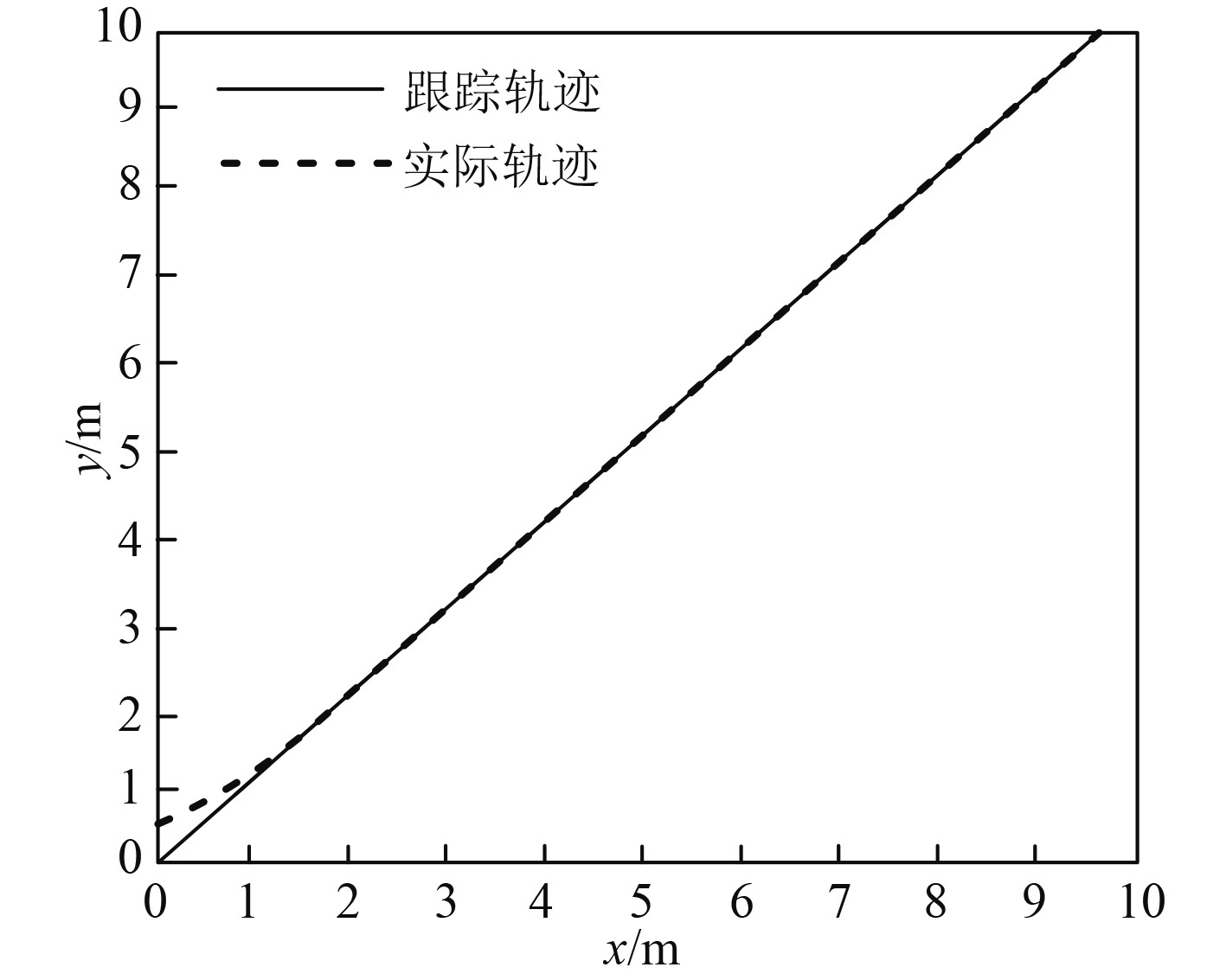
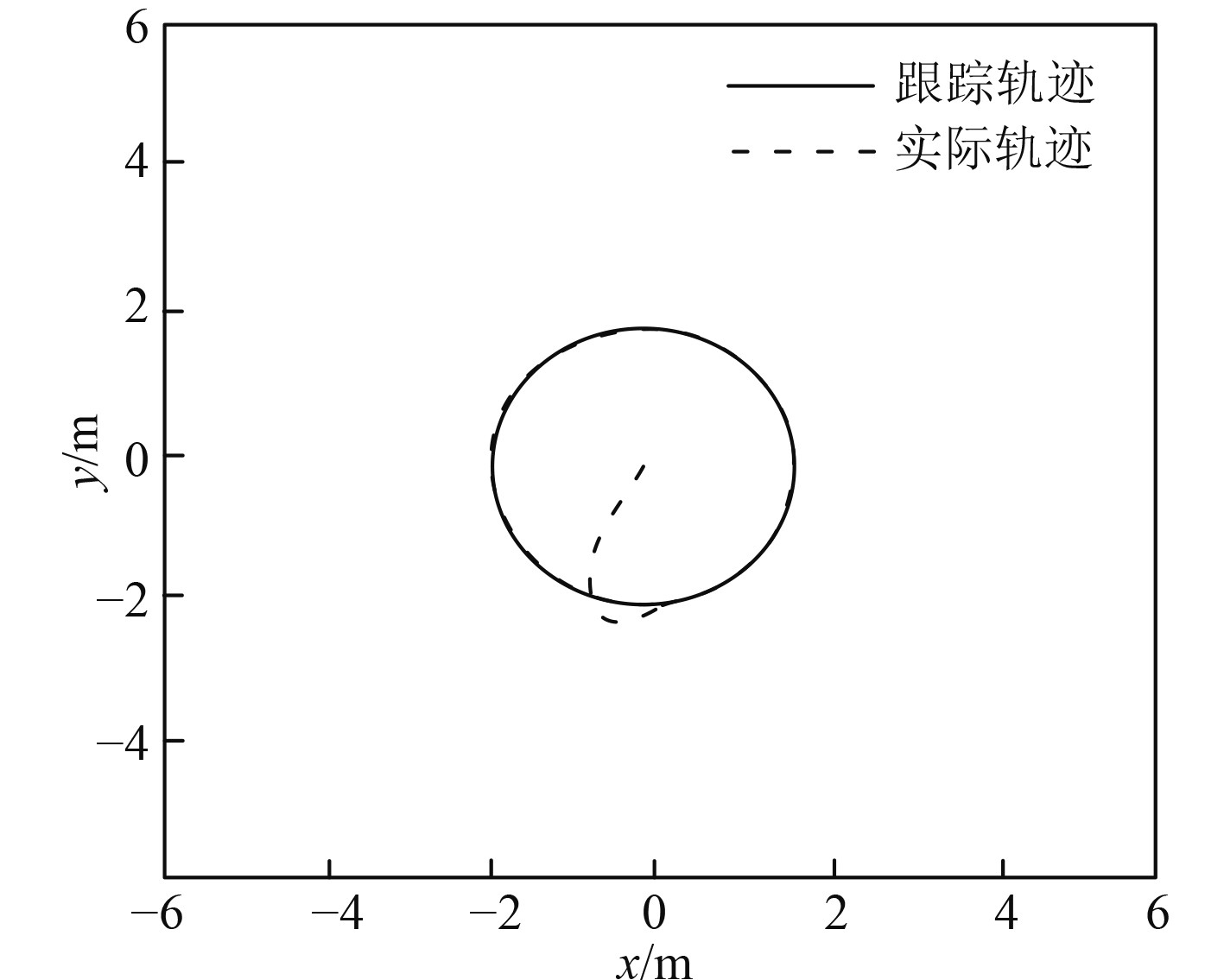
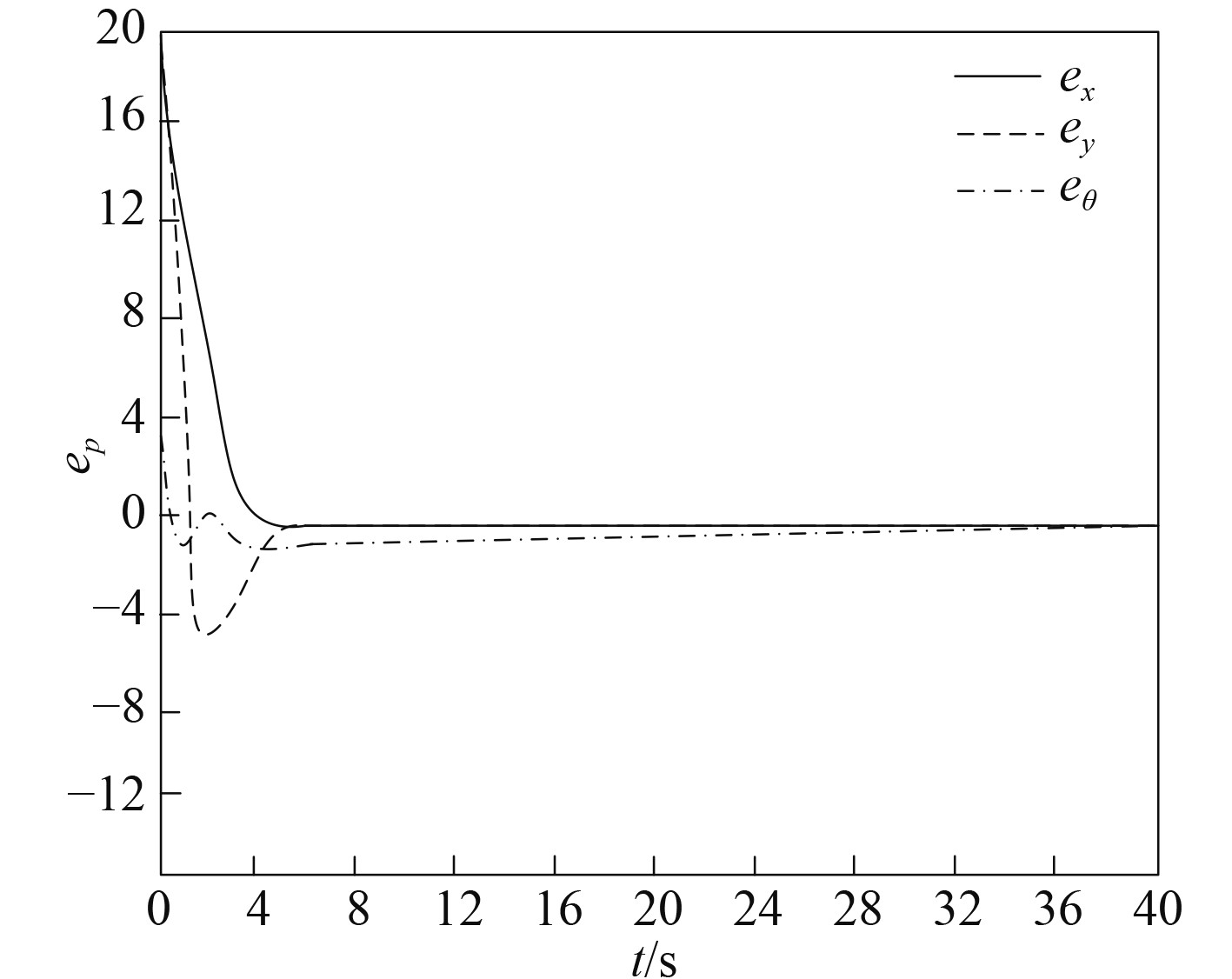
由图2可知，基于贝叶斯神经网络的水下无人航行器自适应控制器的直线实时轨迹跟踪控制稳定，跟踪轨迹精确，而且跟踪控制的速度很快。由图3可知，水下无人航行器在曲线实时轨迹跟踪控制时，跟踪轨迹也很快与跟踪轨迹吻合，并具有很高的鲁棒性。图4结果表明在贝叶斯神经网络的水下无人航行器自适应控制作用下，预设航行位误差曲线能很快收敛，且曲线平滑，波动次数少。结合图2～图4，可看出贝叶斯神经网络具有很好的泛化能力，基于贝叶斯神经网络的水下无人航行器实时轨迹跟踪控制方法实用性好，能精确稳定地实现实时轨迹跟踪控制。

3.2 轨迹跟踪控制误差分析

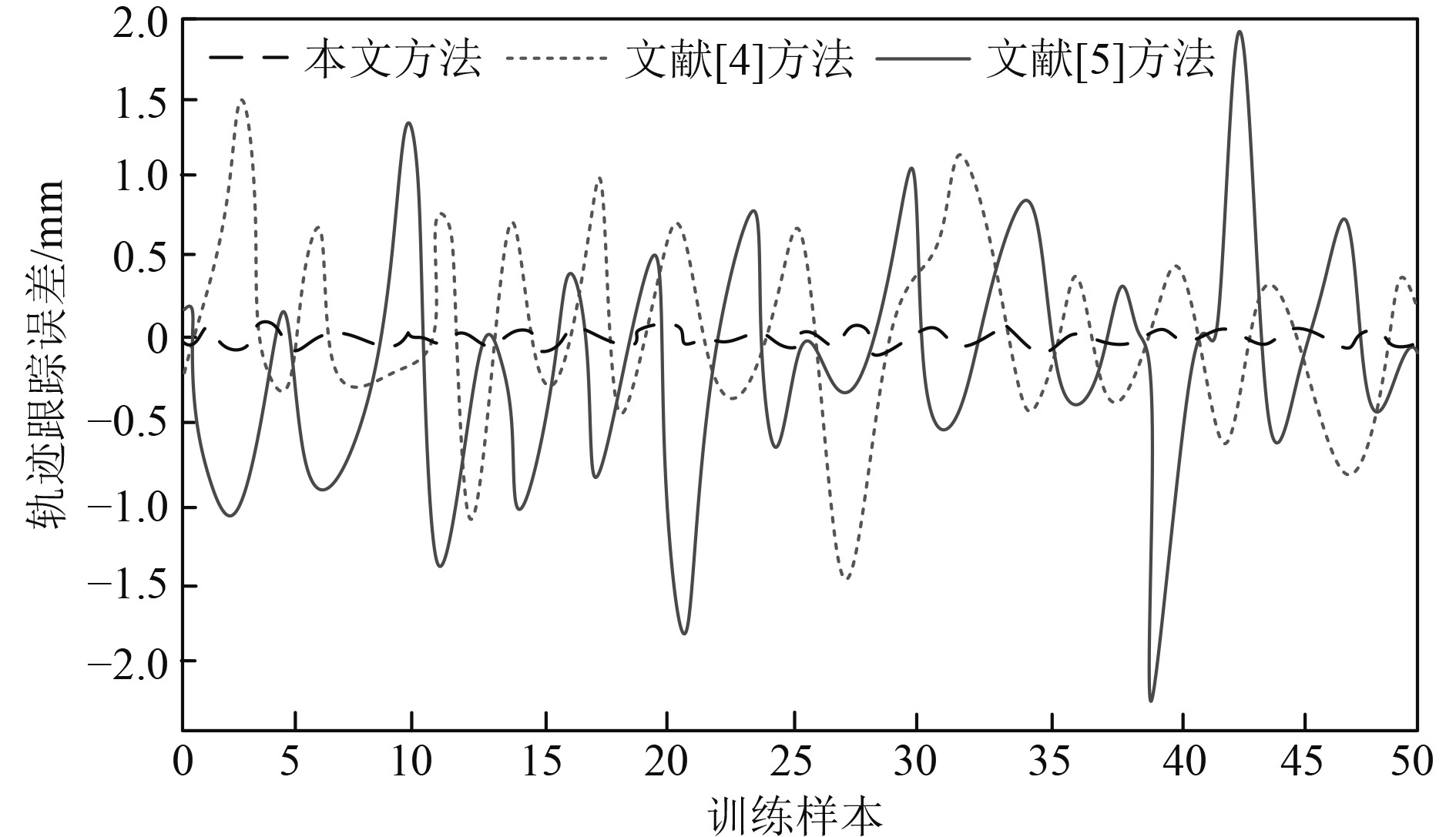
为验证本文方法中贝叶斯神经网络的抗干扰能力，对比本文方法、文献[4-5]方法，在相同噪音、湿度和气压干扰因素下轨迹跟踪控制误差，对比结果如图5所示。

可以看出，本文方法的贝叶斯神经网络在干扰因素影响下，水下无人航行器实时轨迹跟踪控制误差波动范围很小，控制在−0.1～0.1 mm内。而对比方法的波动范围较大，由此说明，本文控制方法的精确性很高，其控制有效。

因为现实中轨迹具有多样性，轨迹特征点多种多样，为验证本文方法对复杂轨迹跟踪控制的适应能力，根据航行规范，航行误差低于0.31 mm时，符合要求。现采用上述3种不同方法，针对450个轨迹特征点进行跟踪控制实验，对比结果如表2所示。

分析可知，本文方法有415个轨迹特征点的跟踪控制误差低于0.31 mm，符合航行要求。而对比方法的轨迹特征点跟踪控制误差普遍高于本文方法。由以上可得，本文方法对复杂轨迹跟踪控制的适应能力强，能适应多种环境的要求，泛化性和适应性高。

4 结　语

针对水下无人航行器轨迹跟踪控制问题，本文依据水下无人航行器运动学模型，利用贝叶斯神经网络的泛化能力和抗干扰能力强的优点，建立了基于贝叶斯神经网络的水下无人航行器自适应控制器，用于实现水下无人航行器实时轨迹跟踪控制。实验证明此控制方法的实用性和有效性。