多自主水下航行器(Autonomous Underuater Vehicle, AUV)系统在作业效率、经济性方面相较单AUV系统具有很大优势,是近年来AUV装备的研究热点之一。目前已经有多种AUV系统编队控制方法实际应用,如基于领航者-跟随者的编队控制[1 − 3]、基于虚拟结构的编队控制[4]、基于势函数的编队控制[5]、基于一致性的编队控制[4 − 6]、基于行为的编队控制[7]、基于路径跟随的编队控制[7 − 9]等。其中,基于领航者-跟随者的编队控制方法由于自身简洁实用的特点,被广泛应用。
基于领航者-跟随者的编队控制中,领航AUV按期望路径航行,跟随AUV根据设定的相对领航AUV的位置关系,执行点跟随航行即可实现编队控制。领航AUV切换航向时,跟随AUV跟踪的目标点位置快速变化,位于切换航向内侧的跟随者需减速,位于外侧的需加速,以适应切换点处航行距离差异导致的队形保持问题。该方法的关键是获取领航者的位置和航向信息及在路径切换出的队形保持。
相较于通过水声通信设备获取领航AUV的目标和航向信息,本文聚焦于AUV编队的队形保持问题,提出基于B样条曲线对规划航路切换点处做局部B样条拟合优化,平滑领航AUV在路径切换时的理想航向角过渡,一定程度改善多AUV编队的队形保持难度。在此基础上,通过数值仿真开展基于领航跟随编队控制方法在不同AUV平台上的控制效果研究。为突出对比,本文选用500 kg的“海翔500”AUV与 5000 kg的“NPS”AUV进行对比。AUV对边采用3节点编队航行,对比分析了基于领航跟随编队控制方法下的2种AUV的队形距离偏差、队形角度偏差。
1 坐标系定义及模型建立 1.1 AUV模型建立大地坐标系为
AUV的运动学方程可表示为:
| $ \dot{\mathit{\eta }}=\mathit{J}\left(\mathit{\eta }\right)\mathit{v} 。$ | (1) |
式中:
| $ \begin{aligned} {\boldsymbol{R}}_{b}^{n}\left(\mathrm{\varTheta }\right)=&{\mathit{R}}_{z,\psi }{\mathit{R}}_{y,\theta }{\mathit{R}}_{x,\varphi } = \\ &\left[\begin{array}{ccc}\cos\psi \cos\theta & -\sin\psi \cos\varphi +\cos\psi \sin\theta \sin\varphi \\ \sin\psi \cos\theta & \cos\psi \cos\varphi +\sin\psi \sin\theta \sin\varphi \\ -\sin\theta & \cos\theta \sin\varphi \end{array}\right. \\& \left.\begin{array}{ccc} \sin\psi \sin\varphi +\cos\psi \sin\theta \cos\varphi \\ -\cos\psi \sin\varphi +\sin\psi \sin\theta \cos\varphi \\ \cos\theta \cos\varphi \end{array}\right],\end{aligned}$ |
| $ \begin{aligned} &{\mathit{T}}_{\mathrm{\varTheta }}\left(\mathrm{\varTheta }\right)=\left[\begin{array}{ccc}1& \sin\varphi \tan\theta & \cos\varphi \tan\theta \\ 0& \cos\varphi & -\sin\varphi \\ 0& \sin\varphi /\cos\theta & \cos\varphi /\cos\theta \end{array}\right], \\ &\theta \ne \pm 9{0}^{{\mathrm{o}}},{\mathit{T}}_{\mathrm{\varTheta }}^{-1}\left(\mathrm{\varTheta }\right) = \left[ \begin{array}{ccc}1& 0& -\sin\theta \\ 0& \cos\varphi & \cos\theta \sin\varphi \\ 0& -\sin\varphi & \cos\theta \cos\varphi \end{array} \right],\theta \ne \pm 9{0}^{{\mathrm{o}}} 。\end{aligned}$ |
动力学方程可表示为:
| $ \boldsymbol{M}\dot{v}+\boldsymbol{C}\left(v\right)v+\boldsymbol{D}\left(v\right)v+\mathit{g}\left(\eta \right)=\mathit{\tau } 。$ | (2) |
式中:
“海翔500”AUV为中国船舶科学研究中心研发的重490 kg、长3.7 m的中小型AUV。“NPS”AUV为美国海军研究生院研发的重 5450 kg、长5.3 m的中大型AUV。2型AUV均采用尾部双推进器、扁平体结构,在操纵特性上类似,以该2型平台开展领航跟随编队控制方法在不同重量AUV下编队队形控制效果比较研究较为合理。“海翔500”AUV和“NPS”AUV的数学模型详见文献[10,11],其外形如图1所示。

|
图 1 “海翔500”AUV与“NPS”AUV样机对比 Fig. 1 Comparison of "HX500" AUV and "NPS" AUV prototypes |
基于领航者-跟随者的编队控制中,一般领航AUV执行路径跟随任务,路径跟随任务一般通过组成路径的路径点序列发送给领航者AUV。跟随者AUV通过接收领航者AUV的位置和航向,并根据队形设定计算跟踪位置点,进行点跟综,从而实现编队控制。一般将AUV编队控制限定在水平面内,路径由路径点序列P表示:
| $ \mathit{P}=\left[{P}_{1},{P}_{2},\cdots {P}_{i},{P}_{i+1},{P}_{i+2},\cdots {P}_{n}\right],i=\mathrm{1,2},...,n-2。$ |
跟随者AUV位置记为
| $ {p}_{f}^{d}={p}_{a}+{R}^{bo}\left({\phi }_{a}\right)\left[\begin{array}{c}\rho {\cos}\left(\theta \right)\\ \rho {\sin}\left(\theta \right)\end{array}\right]。$ |
式中:
领航者AUV采用改进视线法进行路径跟随任务时,在转换点前领航AUV的理想航向角为
| $ \left|{\widehat{p}}_{f}^{d}-{p}_{f}^{d}\right|={\rho }_{k}\sqrt{2-2\rm{cos}{\alpha }_{i+1}}。$ |
式中:
考虑AUV在经济航速2 kn下完成给定路径的编队航向任务。2型AUV的航向控制均采用比例微分控制,深度和纵倾采用滑膜分步控制,最大舵角限制30°。基于改进视线法进行路径跟随。航行路径点序列设置为(单位m):
| $ \begin{aligned} &{P}_{1}=\left(\mathrm{0,0}\right),{P}_{2}=\left(\mathrm{1450,0}\right),{P}_{3}=\left(\mathrm{1450,1300}\right),\quad\quad\ \ \\ &{P}_{4}=\left(\mathrm{500,1300}\right),{P}_{5}=\left(\mathrm{500,500}\right), \end{aligned}$ |
| $ \begin{aligned}&{P}_{6}=\left(\mathrm{0,500}\right),{P}_{7}=\left(-\mathrm{500,1800}\right),{P}_{8}=\left(\mathrm{1000,1800}\right),\\ &{P}_{9}=\left(\mathrm{2000,1800}\right),{P}_{10}=\left(\mathrm{2500,180}\right) 。\end{aligned} $ |
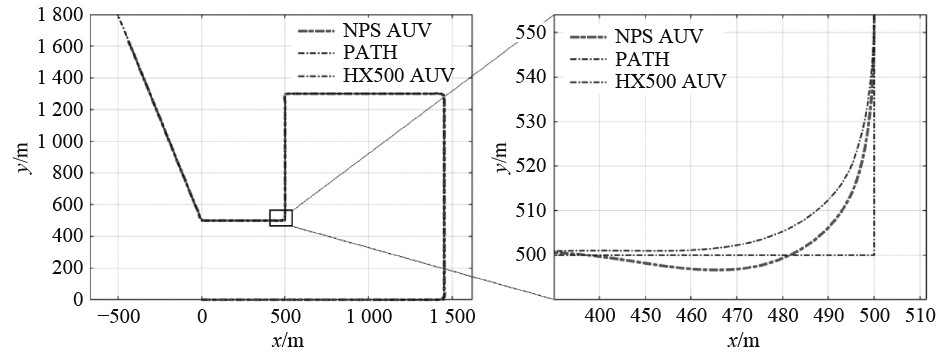
仿真时间 6000 s,航行距离约6.2 km,仿真可得2型AUV在路径跟随任务中的航行轨迹如图2所示,其航向及法向偏差距离时间历程图如图3所示。
|
图 2 2型AUV在路径跟随任务中的航行轨迹对比 Fig. 2 Comparison of trajectories of 2 AUVs in path following tasks |
|
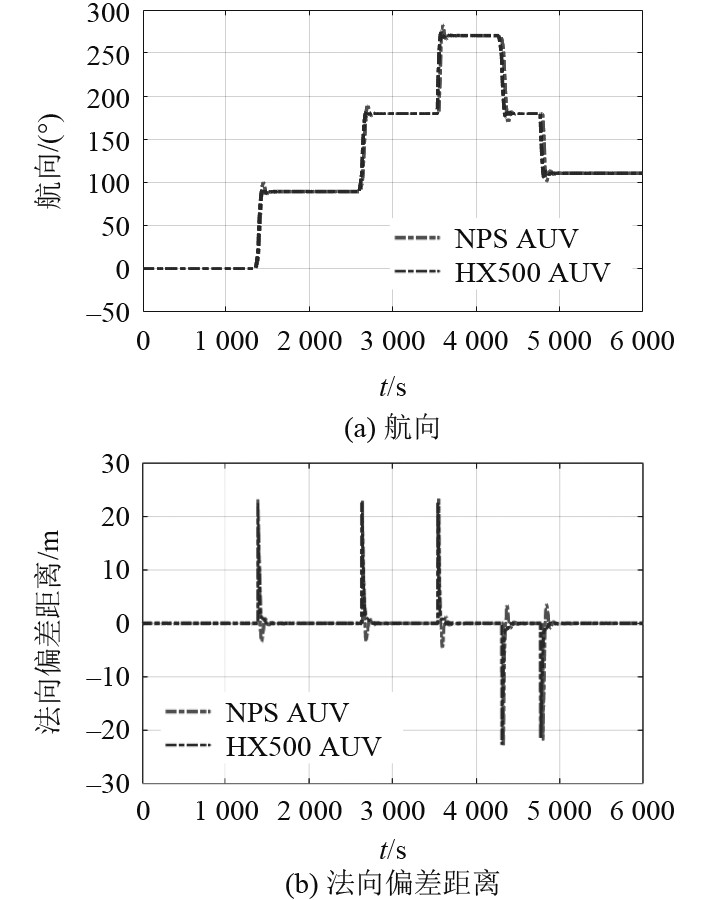
图 3 2型AUV在路径跟随任务中的航向及法向偏差距离对比 Fig. 3 Comparison of heading and normal deviation distance of 2 AUVs in path following tasks |
从仿真结果可知2型AUV均具备较好的路径跟随能力,稳定航行段的法向偏差距离控制在1 m以内。切换点处设定了路径切换距离20 m,计算法向距离的参照路径发生变化。实际的最大法向偏差距离从图2局部放大图可以看出在10 m左右。其中“NPS”AUV在设定参数下航向调整的超调量更大,调整时间较长,但从路径偏差距离上比较,两者在设定参数下的路径跟随性能比较接近。
2.2 基于领航跟随控制的“海翔500”AUV编队仿真设定2个跟随AUV与领航者AUV的相对位置分别为(
|
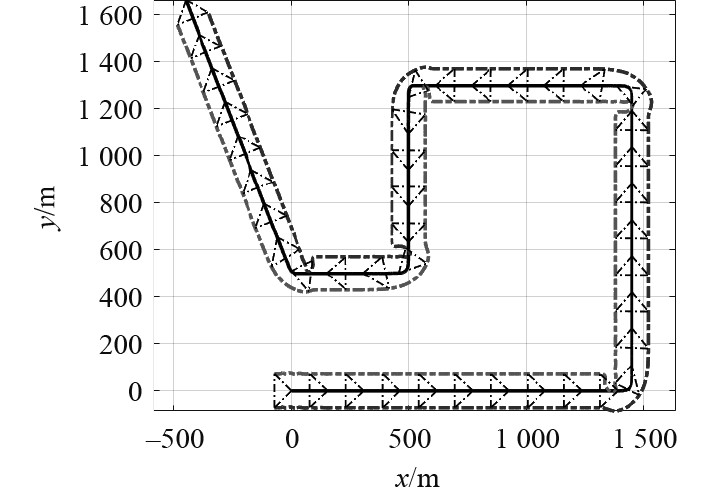
图 4 基于领航者跟随者控制的“HX500”AUV编队轨迹 Fig. 4 The formation trajectory of "HX500" AUVs based on leader follower control |
|
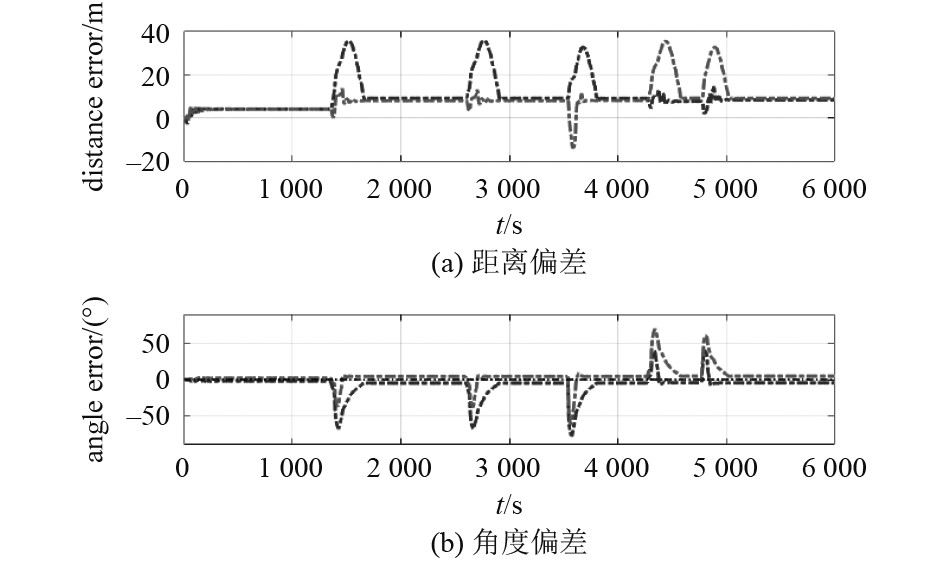
图 5 “HX500”AUV编队中跟随者与领航者距离偏差、角度偏差时间历程 Fig. 5 Time history of distance deviation and angle deviation between follower and leader in the"HX500"AUVs formation |
由图4可知,在切换点处AUV编队队形的保持较差,但在内外侧AUV的航速调整的基础上很快能恢复编队队形。由图5可知在切换点转弯内侧的AUV最大距离偏差13 m,而转弯外侧的AUV与领航AUV的相对距离偏差最大达到35 m附近。在稳定段,“HX500”AUV编队中跟随AUV与领航AUV的距离偏差保持在8 m左右(小于判断距离10 m),角度偏差保持在5°以内。
2.3 基于领航跟随控制的NPS AUV编队仿真设定2个跟随AUV与领航者AUV的相对位置分别为(
|
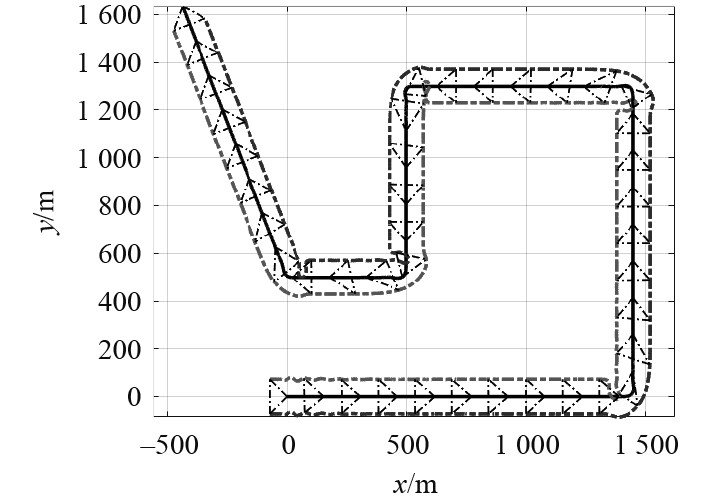
图 6 基于领航者跟随者控制的“NPS”AUV编队轨迹 Fig. 6 The formation trajectory of “NPS” AUVs based on leader follower control |
|
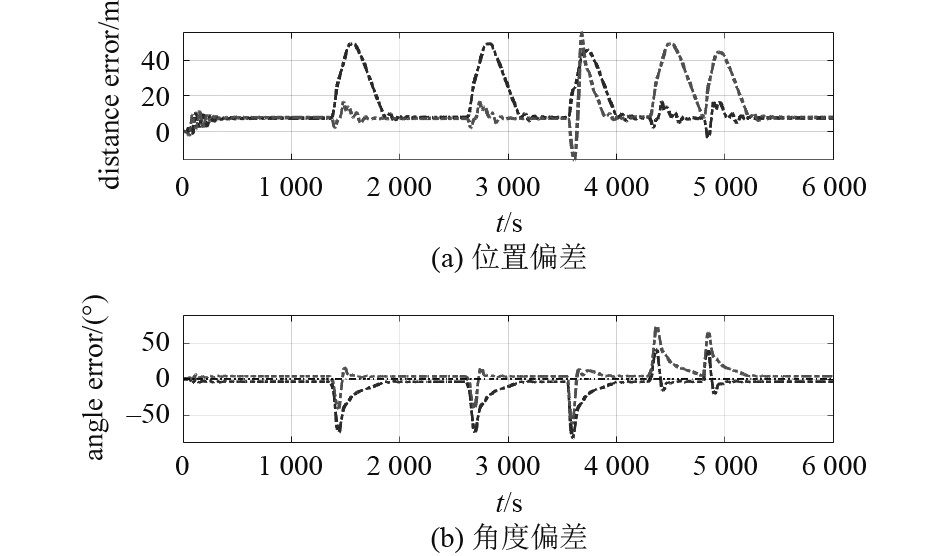
图 7 NPS AUV编队中跟随者与领航者距离偏差、角度偏差时间历程 Fig. 7 Time history of distance deviation and angle deviation between follower and leader in the NPS AUVs formation |
由图6可知,在切换点处AUV编队队形的保持较差,可以通过内外侧AUV的航速调整可恢复队形。由图7可知,转弯外侧的AUV与领航AUV的相对距离偏差最大达到50 m。在稳定段,“NPS”AUV编队中跟随AUV与领航AUV的距离偏差保持在8 m左右(小于10 m),角度偏差保持在5°以内。
2.4 不同AUV编队的队形保持效果对比通过上述基于领航跟随的编队控制仿真,“海翔500”AUV编队和“NPS”AUV编队虽然个体平台在重量、尺寸上具有较大差异,但在相同的控制策略下均能较好实现地实现AUV路径跟随和编队航行任务。在路径跟随任务上,“NPS”AUV由于惯性大等缘故,航向调整超调大、时间较长,但从路径偏差距离上比较2型AUV路径跟随性能比较接近。
编队航行任务上,“HX500”与“NPS” AUV编队中1号跟随者、2号跟随者与领航者的距离偏差、角度偏差时间历程对比如图8和图9所示。可知在2型AUV在路径跟随任务上性能接近,但在基于领航跟随编队控制实现编队航行时,更大重量和体积的“NPS”AUV编队的队形保持效果明显比“HX500” AUV编队的队形保持效果差。

|
图 8 “HX500”与NPS AUV编队中1号跟随者与领航者的距离偏差、角度偏差时间历程对比 Fig. 8 Comparison of the time history of distance deviation and angle deviation between follower-1 and leader in the "HX500" AUV formation and NPS AUV formation |

|
图 9 “HX500”与NPS AUV编队中2号跟随者与领航者的距离偏差、角度偏差时间历程对比 Fig. 9 Comparison of the time history of distance deviation and angle deviation between follower-2 and leader in the "HX500" AUV formation and NPS AUV formation |
本文基于领航跟随编队控制方法,采用500 kg的“海翔500”AUV与 5000 kg的“NPS”AUV开展AUV编队航行仿真研究,对领航跟随编队控制方法在不同AUV平台上的控制效果进了研究,对比分析了基于领航跟随编队控制方法下的2型AUV在队形距离偏差、队形角度偏差。结论如下:
1)500 kg的“海翔500”AUV与 5000 kg的“NPS”AUV在路径跟随上的航行能力接近,且基于领航跟随的编队控制方法对500 kg与5000 kg级别的AUV编队均具有较好的控制效果,稳定航行段跟随者与领航者的距离偏差保持在10 m以内,角度偏差保持在5°以内。
2)基于领航跟随的编队控制方法在切换点处,由于队形相对位置的约束,对平台的加减速性能有一定要求,重量尺寸更大的NPS AUV在直角拐弯处跟随者与领航者的距离偏差较“海翔500”AUV增大50%左右。
| [1] |
EDWARDS D B, BEAN T, ODELL D, et al. A leader-follower lgorithm for multiple AUV formations[C]// Autonomous Underwater Vehicles, Sebasco, Maine, The United State, 2004. IEEE, 2004: 501−509.
|
| [2] |
CALADO P, SOUSA J. Leader-follower control of underwater vehicles over acoustic communications[C]//OCEANS, Santander, Spain, 2011. IEEE, 2011: 501−506P.
|
| [3] |
姜成林, 徐会希. 面向复杂地形海洋勘探的Multi-AUV编队协同控制策略[J]. 舰船科学技术, 2021, 43(3): 93-100. JIANG Chenglin, XU Huixi. Multi-autonomous underwater vehicles formation control and strategy for complex terrain oceanographic exploration[J]. Ship Science and Technology, 2021, 43(3): 93-100. DOI:10.3404/j.issn.1672-7649.2021.02.020 |
| [4] |
袁健, 唐功友. 采用一致性算法与虚拟结构的多自主水下航行器编队控制[J]. 智能系统学报, 2011, 6(3): 248-253. YUAN Jian, TANG Gongyou. Formation control of autonomous underwater vehicles with consensus algorithms and virtual structure[J]. CAAI Transactions on Intelligent Systems, 2011, 6(3): 248-253. DOI:10.3969/j.issn.1673-4785.2011.03.009 |
| [5] |
潘无为, 姜大鹏, 庞永杰, 等. 人工势场和虚拟结构相结合的多水下机器人编队控制[J]. 兵工学报. 2017(2): 326−334. PAN Wuwei, JIANG Dapeng, PANG Yongjie. et al. A multi-AUV formation algorithm combining artificial potential field and virtual structure[J]. ACTA Armamentarii, 2017(2): 326−334. |
| [6] |
王银涛, 严卫生. 多自主水下航行器系统一致性编队跟踪控制[J]. 控制理论与应用. 2013, 30(3): 379−384. WANG Yintao,YAN Weisheng. Consensus formation tracking control of multiple autonomous underwater vehicle systems[J]. Control Theory & Applications, 2013, 30(3): 379−384. |
| [7] |
何斌. 多AUV编队控制与协同搜索技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2017.
|
| [8] |
GHABCHELLO R. Coordinated path following of multiple autonomous vehicles[D]. Lisbon: Ph. D Thesis of Technical University of Lisbon, 2007: 23−64.
|
| [9] |
边信黔, 牟春晖, 严浙平. 多UUV沿多条给定路径运动的协调编队控制[J]. 哈尔滨工业大学学报. 2013, 45(1): 106−111. BIAN Xinqian, MU ChunLui, YAN Zheping. Coordinated control for multi-UUV formation motion on a set of given paths[J]. Journal of Harbin Institute of Technology, 2013, 45(1): 106−111. |
| [10] |
ZHANG C, ZHANG H, ZHANG Y, et al. Parameter identification of hybrid-driven underwater glider based on differential evolution algorithm[C]// International Conference on Artificial Intelligence and Electromechanical Automation. IEEE, 2021.
|
| [11] |
HEALEY A J, LIENARD D. Multivariable sliding mode control for autonomous diving and steering of unmanned underwater vehicles[J]. IEEE Journal of Oceanic Engineering, 1993, 18(3): 327-339. DOI:10.1109/JOE.1993.236372 |
 2024, Vol. 46
2024, Vol. 46
