0 引　言

随着全球航运业快速发展，船舶靠泊作业的安全性和效率问题日益凸显。由于欠驱动船舶在动力配置上的特殊性，其靠泊控制相较于全驱动船舶更为复杂^[1]。传统的船舶靠泊控制方法多依赖于人工经验和操作技巧，不仅劳动强度大，而且难以保证在各种环境条件下的控制效果^[2]。因此，研发一种能够适应不同环境条件、自动化程度高、且控制效果稳定的船舶靠泊自动控制方法具有重要的现实意义和应用价值^[3]。

近年来，众多研究学者针对船舶靠泊控制进行研究。赵永生等^[4]针对船舶在未知时变扰动下的靠泊控制进行研究，充分考虑船舶在自动靠泊过程中，可能受到各种未知的时变扰动的影响，实时调整控制策略，确保船舶能够安全、准确地完成靠泊。但是船舶靠泊控制的实际应用中，由于各种因素的影响，如传感器故障等，可能导致船舶靠泊控制的可靠性降低。黄立文等^[5]充分考虑了船舶舵机延时性，研究船舶靠泊的最优航向控制。由于该方法考虑了船舶的舵机延时，控制器能够更准确地预测船舶响应，提前调整控制信号以补偿控制延时，有助于减少因延时引起的误差，提高船舶靠泊的航向控制精度。考虑舵机延时的控制器，能够更好地应对船舶靠泊时的动态变化，尤其是船舶受到外部扰动或模型参数不确定时。该方法可以减少船舶靠泊航行的振荡和不稳定性，提高船舶靠泊控制的稳定性。但是考虑舵机延时的船舶靠泊控制器，通常基于精确的船舶模型。如果船舶模型不准确或存在不确定性，控制器的控制性能可能会受到影响。针对以上方法在船舶靠泊控制中存在的问题，研究基于模糊自适应PID的欠驱动船舶靠泊自动控制方法。本次结合欠驱动船舶的动力学模型、模糊逻辑推理方法和PID控制算法，构建能够自适应调整控制参数、实现精准靠泊的自动控制方法。希望可通过本次研究，可为提升欠驱动船舶靠泊作业的安全性和效率提供技术支撑。

1 欠驱动船舶靠泊自动控制方法 1.1 构建欠驱动船舶动力学模型

考虑欠驱动船舶靠泊航行时的前向自由度、横荡自由度、首摇自由度以及船舶的水平面运动状况^[6]，构建受外界环境干扰情况下欠驱动船舶的运动学模型，其表达式如下：

$ \begin{aligned} Q = \sqrt {{x^2} + {y^2}} ，\qquad\qquad\\ \left\{ {\begin{aligned} & {x = a\cos \zeta - b\sin \zeta }，\\ & {y = a\sin \zeta - b\cos \zeta }，\\ & {a = {f_a}\left( {a,b,c} \right) + {\tau _a}/{m_{11}}}，\\ & {b = {f_b}\left( {a,b,c} \right)}，\\ & {c = {f_c}\left( {a,b,c} \right) + {\tau _c}/{m_{33}}}。\end{aligned}} \right. \end{aligned} $

(1)

式中：$ x $、$ y $分别为惯性坐标系下欠驱动船舶的横向位移与纵向位移；$ \zeta $、$ c $分别为欠驱动船舶的靠泊航向角与首摇角速度；$ b $、$ a $分别为欠驱动船舶靠泊航行的横漂速度以及前向速度；$ {m_{ii}} $为考虑附加质量时欠驱动船舶的惯性参数；$ {\tau _a} $、$ {\tau _c} $分别为欠驱动船舶的转向力度与纵向推进力，该船舶属于典型的欠驱动系统，未设置横向推进器，因此无需考虑靠泊航行时的横向推进力；$ \Delta f = {\left[ {{f_a},{f_b},{f_c}} \right]^{\rm T}} $表示欠驱动船舶的参数不确定项。综上，完成欠驱动船舶靠泊动力学模型。

1.2 基于视线角导航的欠驱动船舶靠泊路径确定

在完成前驱动船舶动力学模型设计后，利用视线角导航算法，确定欠驱动船舶靠泊自动控制的航行轨迹，进而利用欠驱动船舶航行的视线角与期望靠泊目标点的轨迹偏差，确定船舶靠泊航行的参考首向角。最后利用模糊自适应PID控制算法，控制欠驱动船舶依据参考首向角航行，以到达理想的船舶靠泊位置。设$ {Q_t} $、$ {Q_{t + 1}} $表示时间为$ t $与$ t + 1 $时欠驱动船舶的靠泊航路点，$ \left( {{x_s},{y_s}} \right) $表示生成的虚拟点。欠驱动船舶航路点生成的虚拟点即为欠驱动船舶的靠泊运动目标点。利用$ {Q_t} $与$ {Q_{t + 1}} $两点生成船舶靠泊路径，将船舶航行区域的大地坐标系转换为船舶的附体坐标系，用$ {Q_t} $表示坐标系原点，则坐标系$ x $轴的旋转正角度表达式如下：

$ {\alpha _t}_Q^{} = 2\tan \left( {{y_{t + 1}} - {y_t},{x_{t + 1}} - {x_t}} \right) 。$

(2)

在固定路径的参考坐标系上，船舶位置的表达式如下：

$ \left\{ {\begin{array}{*{20}{c}} {x'\left( t \right) = {x_t}{\rm cos} \left( {{\alpha _t}_Q} \right) + {y_t}{\rm sin}\left( {{\alpha _{tQ}}} \right)}，\\ {y'\left( t \right) = {x_t}{\rm sin}\left( {{\alpha _{tQ}}} \right) + {y_t}{\rm cos}\left( {{\alpha _{tQ}}} \right)} 。\end{array}} \right. $

(3)

综合上述，确定欠驱动船舶的靠泊目标点。令船舶的横漂距离偏差趋于0，即令$ \mathop {\lim }\limits_{t \to \infty } x'\left( t \right) = 0 $，以及欠驱动船舶靠泊行驶的期望航向角$ \zeta \left( t \right) $趋于$ {\alpha _t} $，则船舶靠泊行驶的期望航向角表达式如下：

$ \zeta '\left( t \right) = {\alpha _t}_Q \cdot \delta {\left( t \right)_{x'\left( t \right)y'\left( t \right)}} 。$

(4)

式中，$ \delta {\left( t \right)_{x'\left( t \right)y'\left( t \right)}} $为船舶靠泊行驶的路径速率相对角。

设模糊自适应PID控制算法的比例系数为$ {K_p}\left( t \right) = \displaystyle\frac{1}{{\Delta \left( t \right)}} $，由此可得其路径速率相对角$ \delta \left( t \right) $的表达式如下：

$ \delta {\left( t \right)_{x'\left( t \right)y'\left( t \right)}} = \arctan \left( { - {K_p}e - {K_i}\int\limits_0^t {e\left( t \right){\text d}t} } \right)。$

(5)

式中：$ {K_i} $为PID控制器的积分系数，该系数可降低欠驱动船舶受复杂环境的影响，同时有效跟踪靠泊路径，降低船舶靠泊的跟踪误差。当欠驱动船舶的航行速度与视线角处于一条直线时，船舶的航向角转化为首向角，此时船舶靠泊自动控制目标即为船舶航行的实际艏向角无限接近期望首向角。

1.3 基于模糊自适应PID的船舶靠泊自动控制

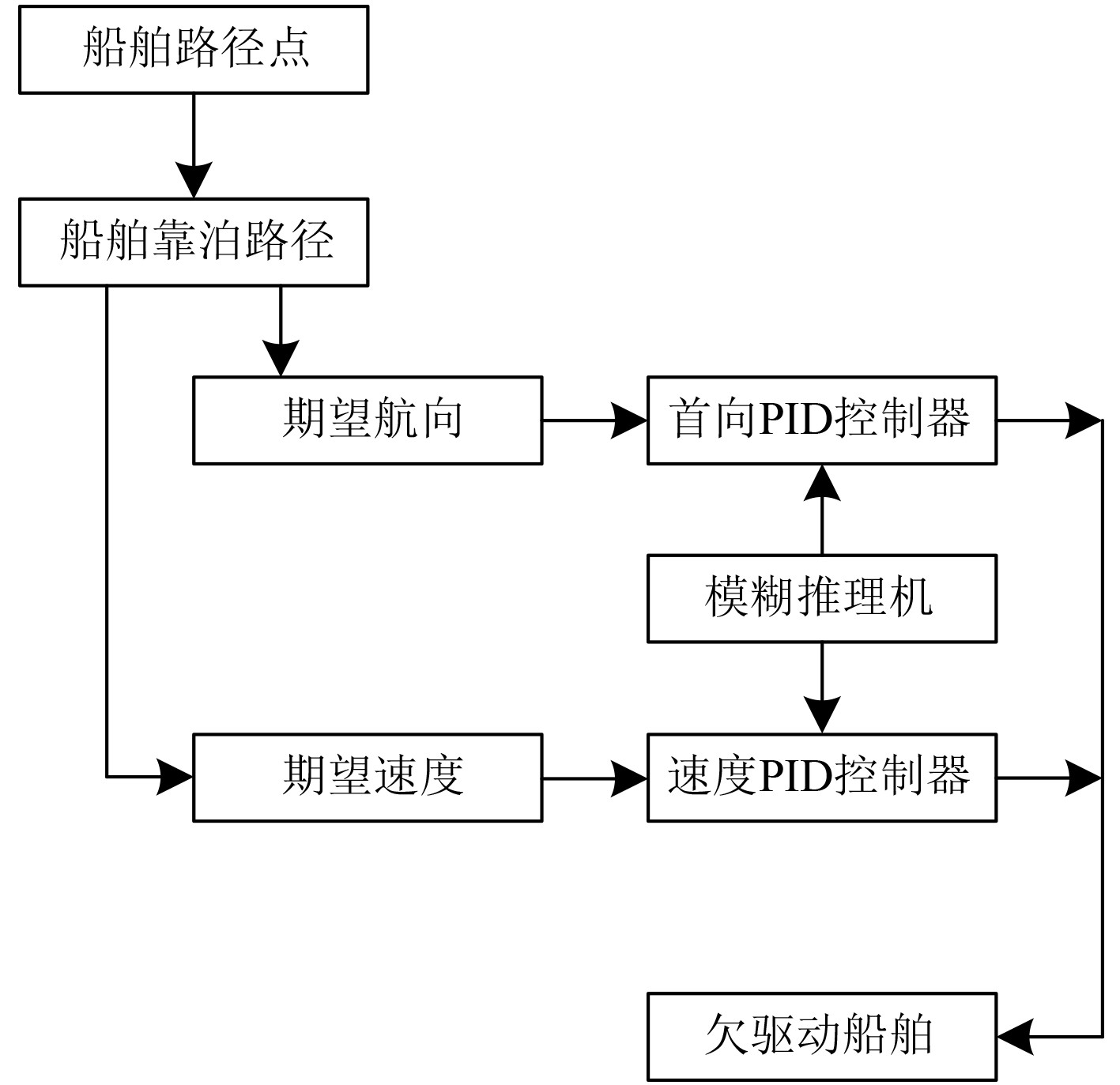
欠驱动船舶靠泊自动控制包括首向控制和速度控制两部分。本次在完成船舶靠泊路径确定后，将模糊自适应PID控制算法的控制输出，传送至欠驱动船舶的执行机构，实现船舶靠泊的自动控制。常规PID控制器的控制参数固定，不具备参数自整定功能，过于依赖所构建的欠驱动船舶数学模型，靠泊控制性能并不理想。故本次结合模糊推理算法，构建应用于欠驱动船舶靠泊自动控制的总体结构图，具体如图1所示。

在该控制中引入模糊自适应PID控制器，即将将模糊推理环节加入常规PID控制器中。设置船舶靠泊航行的实时偏差$ e\left( t \right) $与偏差变化律$ \Delta e\left( t \right) $，作为模糊推理机的输入。利用模糊规则在线整定PID控制器的参数，以满足不同时刻的$ e\left( t \right) $与$ \Delta e\left( t \right) $对PID控制器的控制参数整定需求。

船舶靠泊自动控制的常规离散PID控制器的表达式如下：

$ U\left( k \right) = {K_p}e\left( t \right) + \sum\limits_{i = 0}^k {{T_i}e\left( t \right)} \delta {\left( t \right)_{x'\left( t \right)y'\left( t \right)}} + {T_d}\frac{{\Delta e\left( t \right)}}{T} 。$

(6)

式中：$ T $与$ {T_i} $分别为船舶靠泊自动控制的采样周期以及积分时间常数；$ {T_d} $为微分时间常数。

利用船舶靠泊自动控制的模糊控制规则，通过实时推理获取最佳的PID控制参数。利用正态高斯型模糊变量，描述船舶靠泊自动控制的模糊概念。设置高斯正态分布作为模糊控制器的输入，用$ \eta $表示$ e\left( t \right) $与$ \Delta e\left( t \right) $语言变量的隶属函数。将$ e\left( t \right) $与$ \Delta e\left( t \right) $，经过模糊化处理后形成3个模糊集合。通过解模糊化处理，将欠驱动船舶靠泊自动控制的模糊量转化为精度量。本次选取重心法进行船舶靠泊自动控制的解模糊化处理。重心法具有更高的控制精度与更平滑的控制输出，设置隶属度函数与横坐标围成的面积的重心，设置为模糊自适应PID控制器，可自动控制船舶靠泊的模糊推理最终输出值。本次采用重心法对船舶靠泊自动控制解模糊化处理，其表达式如下：

$ {v_{U\left( k \right)}} = \frac{{\displaystyle\sum\limits_{i = 1}^n {{v_i}} {\eta _i}\left( {{v_i}} \right)}}{{\displaystyle\sum\limits_{i = 1}^n {{\eta _i}\left( {{v_i}} \right)} }} 。$

(7)

式中：$ {v_i} $与$ {\eta _i}\left( v \right) $分别为欠驱动船舶靠泊自动控制模糊集的输出及其对应的隶属度函数。通过式（7）的船舶靠泊自动控制解模糊化处理，获取船舶靠泊的控制误差与PID控制器的修正量。利用模糊控制器将控制修正值输入至PID控制器，可实现欠驱动船舶靠泊的自适应控制。

2 实验分析 2.1 实验环境设置

为验证所研究欠驱动船舶靠泊自动控制方法的自动控制性能，将该方法应用于某港口的船舶靠泊自动控制中。利用Matlab仿真软件，模拟分析船舶靠泊自动控制的全过程。实验所采用的欠驱动船舶的参数设置如表1所示。

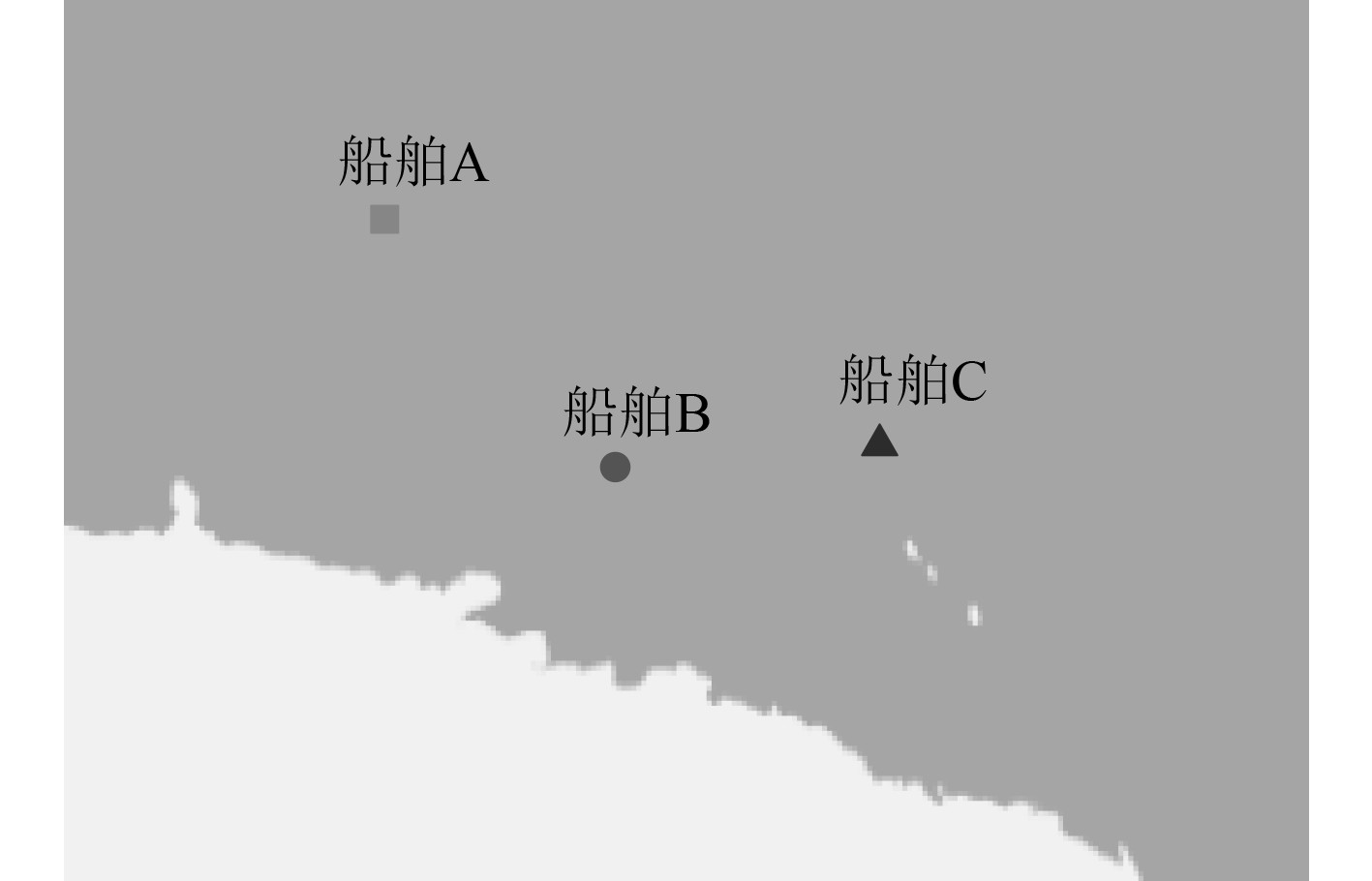
船舶靠泊自动控制仿真实验中，船舶靠泊航行的停泊区域如图2所示。以此为基础，开展实验研究。

2.2 实验结果分析

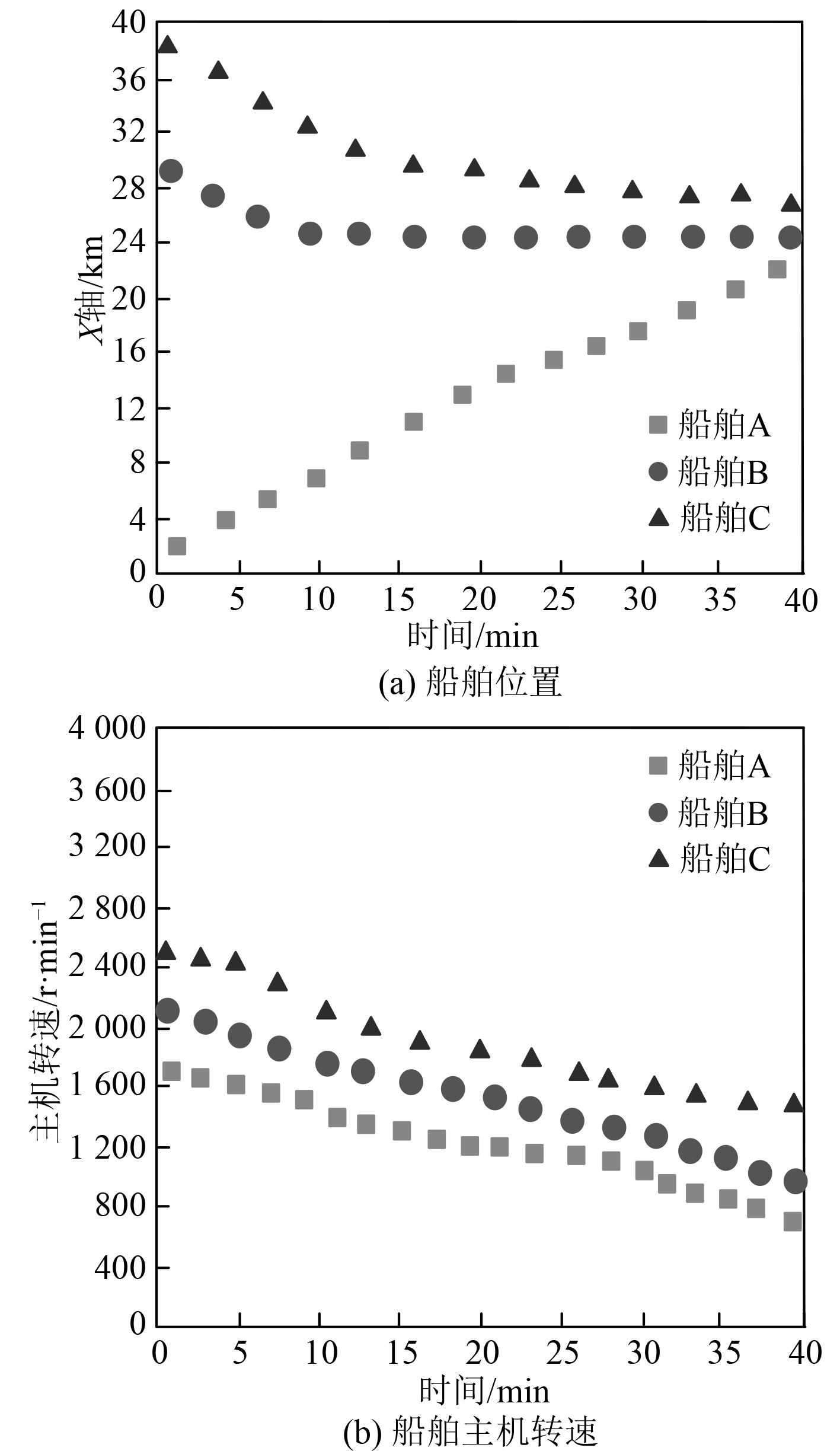
开展船舶靠泊自动控制实验时，依据图2中各船舶的当前位置，利用本文方法进行欠驱动船舶的靠泊控制，得到船舶位置与船舶主机转速的模拟结果如图3所示。

可以看出，应用本文方法可有效控制船舶靠泊航行，伴随船舶靠泊航行位置不断变化，船舶缓慢向着理想的停泊位置移动。

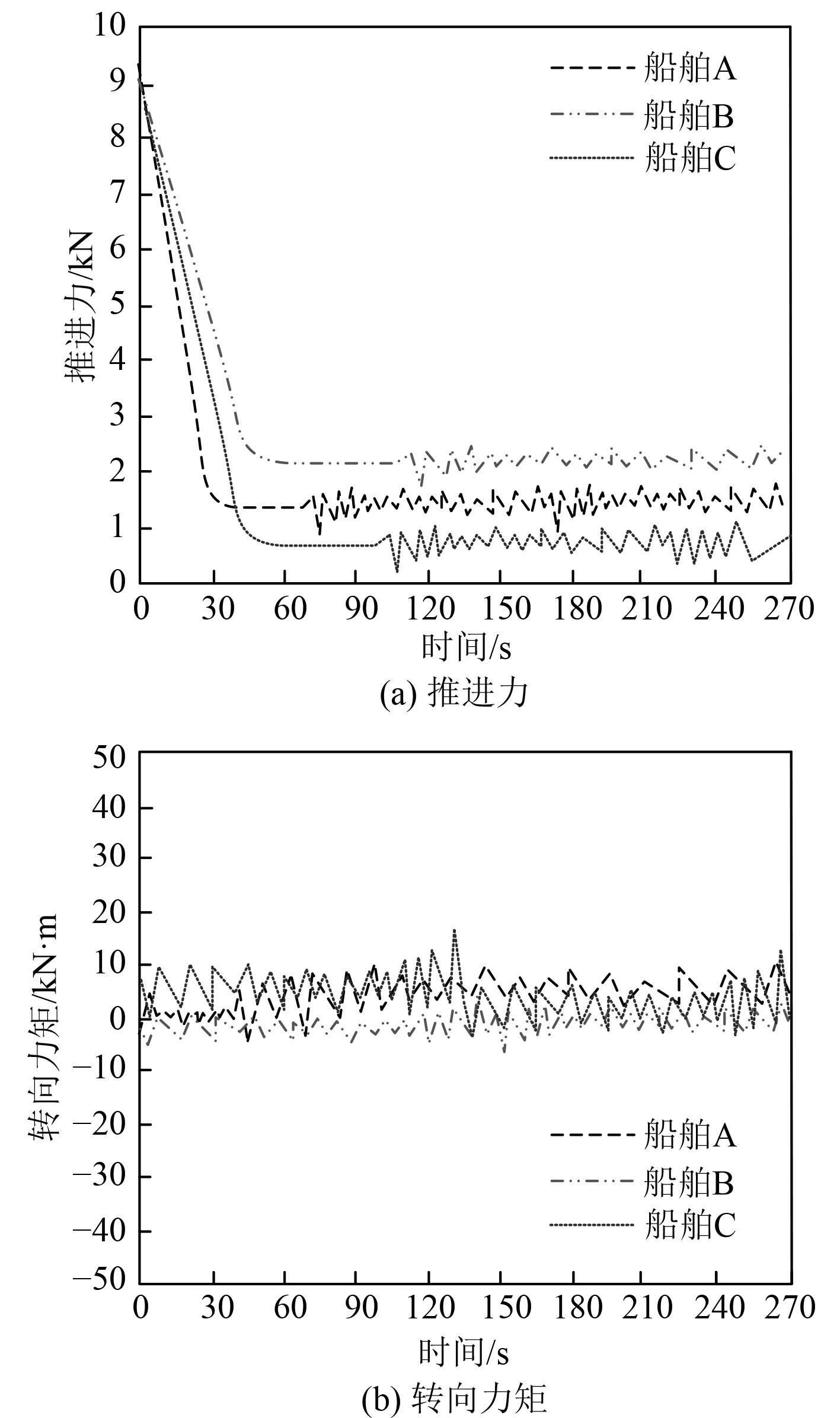
采用本文方法控制欠驱动船舶靠泊行驶，欠驱动船舶的执行机构接收的控制输入如图4所示。可以看出，本文方法能够依据船舶的靠泊需求，确定最佳的船舶靠泊航行轨迹。依据船舶靠泊航行轨迹规划结果，确定相应的船舶航行推进力以及转向力矩，控制船舶航行至最佳的靠泊位置。

选取船舶A作为分析对象，采用本文方法控制欠驱动船舶靠泊，船舶靠泊航行的航向角与靠岸速度变化情况如表2所示。从航向角的变化来看，船舶A在开始靠泊时，航向角为141°，随后在最初的几个时间点内（0～15 min），航向角呈现出波动，但总体趋势是朝向泊位方向调整。随着时间的推移，航向角逐渐减小，显示出船舶正在逐渐靠近泊位，并调整其航向以与泊位保持适当的角度。特别是在45 min之后，航向角迅速减小，这表明船舶已经接近泊位，并正在进行最后的微调以确保准确靠泊。从船舶航行速度的变化来看，最初船舶以15.0 kn的速度航行。在靠泊过程的前半段（0～40 min），船舶速度保持不变，这表明船舶在接近泊位之前需要保持一定的速度以维持航向的稳定性。然而，在45 min时，船舶速度突然下降到7.5 kn，这反映了船舶在接近泊位时开始减速，以确保能够平稳、安全地靠岸。随着船舶进一步靠近泊位，速度继续降低，特别是在最后阶段（60～90 min），速度降至4.1 kn，并最终稳定在0.8 kn，这表明船舶正在进行微调，以确保最终能够准确地停靠在泊位上。

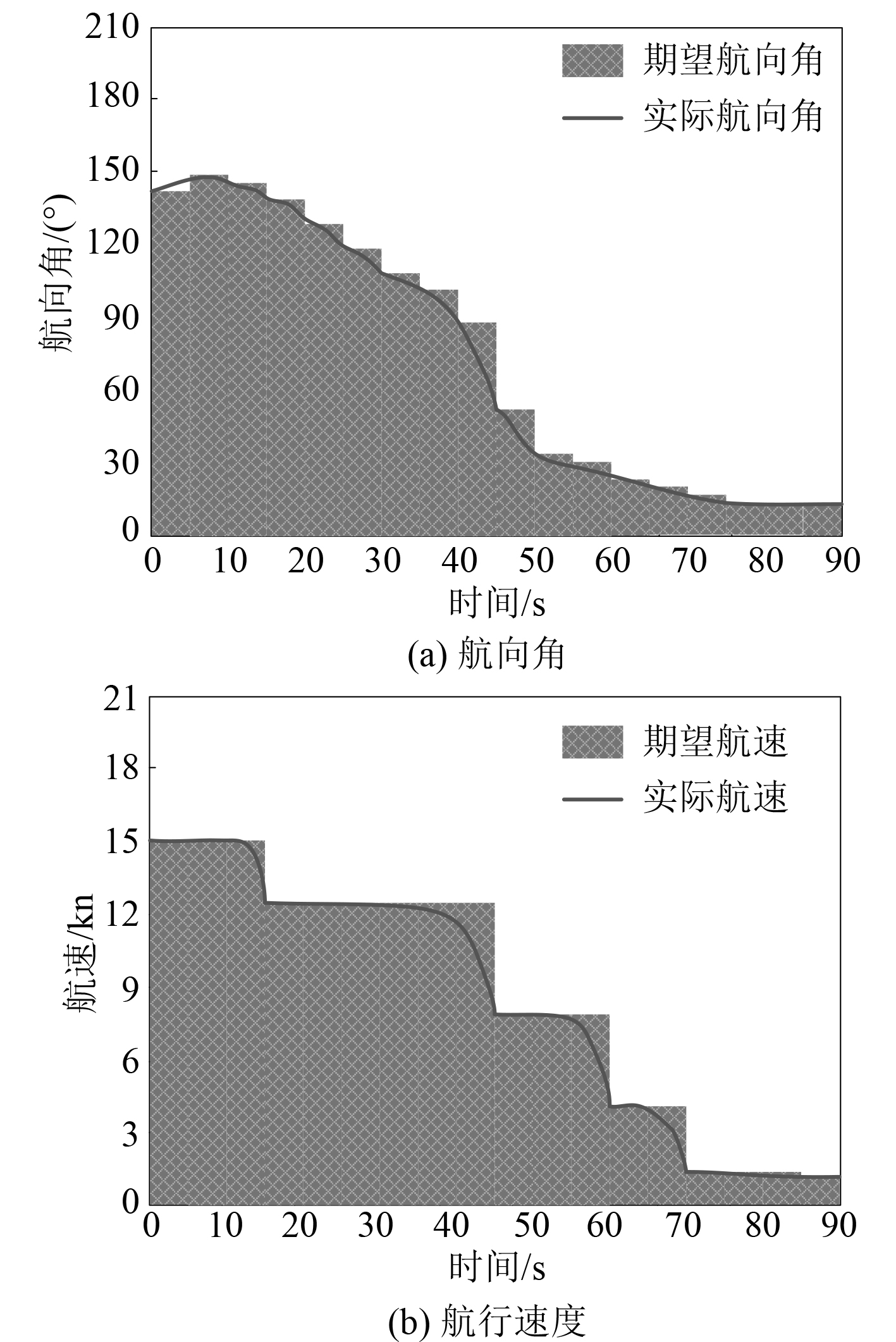
依据表2中数据，绘制本文方法控制下船舶靠泊航行的航向角与靠岸速度变化时序图如图5所示。

可以看出，采用本文方法自动控制船舶靠泊，欠驱动船舶的航向角与船舶航速与期望航向角以及期望航速极为接近。由此可证明本文方法对于欠驱动船舶，具有较高的靠泊自动控制有效性。造成这一现象的原因在于应用所提方法，其可实时根据外界环境和船舶状态的变化，通过模糊自适应PID控制算法动态调整PID控制参数，确保船舶的航向角和航速始终保持在期望范围内。此外，视线角导航算法的运用也为船舶提供了精确的航行轨迹，进一步提高了靠泊的准确性和稳定性，使其具有良好的控制性能。

3 结　语

将模糊自适应PID控制器应用于欠驱动船舶靠泊自动控制中，旨在通过智能控制算法实现更加精准和灵活的欠驱动船舶靠泊控制。模糊自适应PID控制结合了模糊逻辑和PID控制器的优点，能够根据船舶的实际运动状态和环境条件实时调整控制参数，从而实现更加精准和稳定的靠泊自动控制效果。实验结果表明，应用所提方法，可对前驱动船舶靠泊进行控制，且其应用具有一定有效性和稳定性。该方法在船舶靠泊作业的实际应用中可行性高，显著提高了欠驱动船舶靠泊作业效率，具有重要的应用价值。