远程投送水下攻击武器为了能突破敌方空中拦截,需攻击武器搭载的载荷在空中进行高速突防,导致载荷在抛伞后仍具有较高余速,以及一定散布范围的滚动、俯仰和偏航角速度,且速度方向与载荷轴向间有较大合成攻角。
高速载荷的入水瞬间对系统结构产生强烈的冲击过载。研究表明,载荷在入水前会存在一定合成攻角,如果合成攻角过大会导致载荷结构性损坏。因此在高速载荷从抛伞到触水前瞬时内,需实现载荷姿态快速调整,以实现载荷在允许的合成攻角范围内入水。在控制方法确定的前提下,较好的控制参数是决定高速载荷能否在合理的合成攻角范围内入水的关键。因此,这需对高速载荷瞬时姿态控制参数进行优化,以期达到较好的控制效果。针对此类复杂和缺少信息的优化问题,智能优化算法提供了新的方法和思路[1 − 4]。
智能优化算法的主要思想是借鉴自然界各种动物种群的生存行为,将这些行为抽象为各种数学模型,并选取适当的评价函数进行评价[1 − 5]。其中,遗传算法和粒子群算法是使用最为广泛的2种智能优化算法。
美国的Holland教授[6]于1975年在《自然界和人工系统的适应性》中首次提出遗传算法,其通过学习生物界自然选择和自然遗传机制而设计的一种随机搜索算法,该算法可实现问题解空间上的全局搜索,但在解决恶劣初始条件下高速载荷瞬时姿态控制参数寻优问题上存在收敛速度慢、局部寻优能力较差的问题。Kennedy等[7]提出粒子群优化算法,类似于遗传算法,其是一种基于群体的随机优化技术。粒子群优化算法主要的不同点在于结合种群中各个体的经验信息来迭代产生最优解。粒子群算法具有概念简单、容易实现、算法参数偏少、收敛迅速等优点,但在恶劣初始条件下,高速载荷瞬时姿态控制参数寻优问题上存在早熟现象,优化参数容易陷入局部极值,从而可能导致无法实现恶劣初始条件下高速载荷瞬时姿态控制。
1 高速载荷瞬时姿态控制参数优化高速载荷瞬时姿态控制的目的是在短时间内将载荷的合成攻角控制在合理误差范围内,其通过设计载荷俯仰、偏航和横滚3条通道各自独立的控制器实现载荷合成攻角的控制。其中,俯仰通道控制的状态变量是载荷的攻角
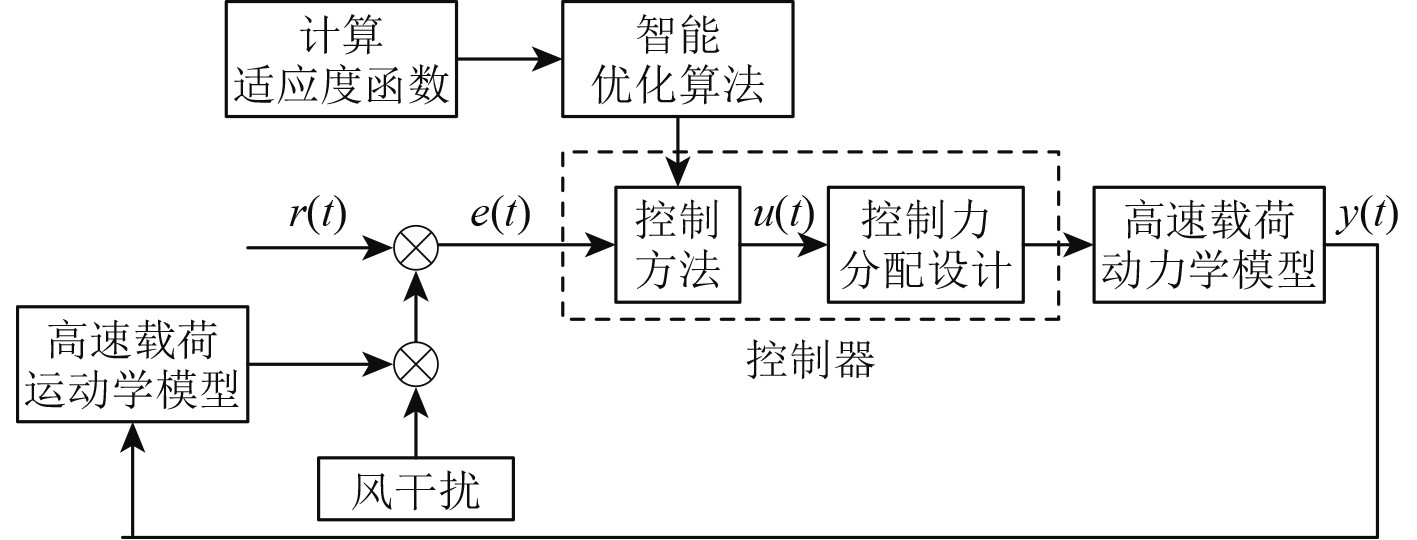
|
图 1 高速载荷姿态控制流程 Fig. 1 High-speed load attitude control process |
以载荷的俯仰通道为例,其控制方法的控制律为:
| $ U(s) = \left(K_P^\alpha + K_D^\alpha \dfrac{1}{{1 + K_N^\alpha \dfrac{1}{s}}}\right)(R(s) - R\_tar) 。$ | (1) |
其中,
在高速载荷物理参数以及控制方法确定的情况下,高速载荷瞬时姿态控制效果主要由高速载荷初始条件和控制方法的控制参数决定。其中,高速载荷的初始条件主要包括高速载荷的初始速度、初始角速度、合成攻角。当高速载荷的初始速度、初始角速度以及合成攻角较小,即常规初始条件时,传统的遗传算法和基本粒子群算法均可寻优得到较好的控制参数,实现高速载荷瞬时姿态的稳定控制。但当高速载荷的初始速度、初始角速度以及合成攻角较大,即恶劣初始条件时,传统的遗传算法和基本粒子群算法随机进行控制参数寻优,其无法实现较高的高速载荷瞬时姿态稳定控制次数,即不具备较高的寻优成功率。因此,本文设计一种改进的粒子群优化算法,以实现较高的高速载荷瞬时姿态寻优成功率。
2 粒子群优化算法的改进 2.1 基本粒子群优化算法基本粒子群优化算法的迭代规则为:
| $ \left\{ {\begin{gathered} \begin{gathered} {v_{ij}}(t + 1) = \omega {v_{ij}}(t) + {c_1}{r_1}\left[ {pbes{t_{ij}} - {x_{ij}}(t)} \right] + \\ {c_2}{r_2}\left[ {gbes{t_j} - {x_{ij}}(t)} \right] ,\\ \end{gathered} \\ {{x_{ij}}(t + 1) = {x_{ij}}(t) + {v_{ij}}(t)} 。\qquad\qquad\qquad\ \ \end{gathered}} \right. $ | (2) |
式中:
本文主要从设计惯性权重和引入遗传算法2个方面改进粒子群优化算法在恶劣初始条件下高速载荷瞬时,姿态控制参数优化问题上的性能,以达到提高寻优成功率的目的。
1)设计惯性权重
影响粒子群优化算法性能的一个主要方面是粒子群的搜索能力,其反映在每一次迭代的粒子速度中。粒子速度由惯性部分、自身部分和社会部分组成。其中,参数
惯性权重
| $ \omega (i) = {\omega _{\max }} - ({\omega _{\max }} - {\omega _{\min }})\times \displaystyle\frac{i}{{\max \_{\mathrm{iteration}}}} 。$ | (3) |
其中,
李会荣等[9]提出了惯性权重的非线性调整策略。王生亮等[10]利用Sigmoid型函数呈现的非线性平滑性对种群粒子的惯性权重进行生成,提出了一种基于Sigmoid惯性权重自适应调整的粒子群优化算法。
以上算法在一定程度上改善了粒子群算法的搜索性能,但在解决提高恶劣初始条件下高速载荷瞬时姿态控制参数优化的寻优成功率问题上仍然存在以下不足:
①粒子群具有较大惯性权重。若种群中的粒子发现了某些较好的位置,但因粒子具有较大惯性权重,粒子的迭代搜索步长较大,使粒子无法在可能的最优解局部位置进行细致搜索,从而错过最优解。
②粒子群具有较小的惯性权重。种群中的粒子迭代步长较小时,会导致粒子只能在当前最优解的局部范围内搜索。但如果前期粒子群没有对全局进行较好的搜索,粒子群会过早陷入局部极值,从而造成当前的最优解与全局最优解有较大差距。
因此,较好的惯性权重调整方式为影响粒子群搜索性能的重要因素。针对上述2个问题,本文设计一种自适应惯性权重的调整方式。其对具备不同自身进化速度的粒子计算不同的惯性权值,使每个粒子能尽可能保证在进行细致的局部搜索时,整个粒子群进行较全面的全局搜索,在维持算法复杂度的前提下,提升了粒子群的搜索能力。
本文设计的惯性权重调整方式为:
| $ \left\{\begin{aligned} &{{\omega _j}(i) = {\omega _{\min }} + ({\omega _{\max }} - {\omega _{\min }}) \times \displaystyle\frac{1}{{1 + 0.5 \cdot \exp [ - h({f_j}(i))]}}},\\ &{h({f_j}(i)) = {{\tanh }^{ - 1}}[\frac{2}{{b - a}}({f_j}(i) - a) - 1]} 。\end{aligned} \right. $ | (4) |
定义适应度值边界:
| $ \left\{ {\begin{array}{*{20}{c}} {a = f{{(i)}_{\min }}} ,\\ {b = f{{(i)}_{\max }}} 。\end{array}} \right. $ | (5) |
式中:
2)引入遗传算法
即使设计了新的惯性权重调整方式,但也只是延缓了粒子群在迭代过程中搜索空间不断缩小的趋势,为了使粒子群始终保持较大的解空间搜索能力,需在粒子群每一次迭代后,以一定概率重新初始化粒子群的位置,最简单的做法是设定一个重置参数,每次迭代后产生一个随机数,如果随机数大于重置参数,则对当前粒子群的位置重新初始化。但这种方法无法保留迭代后的粒子群信息,而遗传算法的变异和交叉操作可在保留部分迭代信息的同时扩大粒子群的全局搜索能力。因此,引入遗传算法的变异、交叉和选择操作,重新设计了粒子群优化算法的迭代规则。其中变异、交叉和选择操作的原理如下:
①变异操作
对种群中每个个体的参数(每个个体定义为一组待优化的9个参数)进行遍历,设置常值变异概率,生成随机数与变异概率作比较,如果随机数小于等于变异概率代表该个体的此参数进行变异。产生变异步长,即:
| ${\rm{mut}}\_{\mathrm{step}} = rand\times{(1 - i/\max \_{\mathrm{iteration}})^2}。$ | (6) |
式中:
设置正向变异概率,默认为0.5。生成随机数与正向变异概率作比较,如果随机数大于正向变异概率,代表该个体的此参数向数值增大的方向变异,否则代表该个体的此参数向数值减小的方向变异,即:
| $ populatio{n_{ij}} = populatio{n_{ij}}\times(1 \pm {\mathrm{mut}}\_{\mathrm{step}})。$ | (7) |
其中,
每个个体的当前节点完成变异操作后,判断当前节点是否超出其取值范围。如果超出,设置为其取值范围的边界。
②交叉操作
对种群中个体进行遍历,设置常值交叉概率,生成随机数与交叉概率作比较,如果随机数小于等于交叉概率代表该个体进行交叉。随机寻找需进行交叉的个体,随机生成需进行交叉的参数,然后进行交叉操作。
③选择操作
设置当前迭代种群的选择界限,即:
| $ ({f_{\max }} - {f_{\min }})\times0.8 + {f_{\min }} 。$ | (8) |
式中:
| $ f = \int_{0.5}^{1.5} {t(\arccos (\cos \left( \alpha \right)\cos \left( \beta \right)))} {\mathrm{d}t} 。$ | (9) |
遍历当前迭代种群,将大于选择界限的个体替换为当前迭代种群适应度最小值所对应的个体。
2.3 基于改进粒子群算法的控制参数优化过程基于改进粒子群算法的控制参数优化具体步骤为:
步骤1 设置初始参数。确定种群中个体数、个体参数个数、最大迭代数、精度终止迭代数、惯性权重取值区间的上下限、个体学习因子、社会学习因子、变异概率、交叉概率、速度区间、位置区间、误差精度。
步骤2 初始化种群,计算初始种群适应度值,比较得到最小的适应度值,与之对应的个体设置为最优个体。
步骤3 根据式(4)和式(5)确定当前迭代数的粒子群惯性权重。根据式(2)确定当前迭代数的粒子群更新速度,并进行速度越界操作,即如果粒子速度超过速度区间,则将粒子速度取为速度区间边界。
步骤4 根据变异操作和步骤3计算得到的粒子速度初步更新粒子位置,其步骤如下:遍历每个粒子的每个优化变量,如果
步骤5 采用交叉操作进行粒子位置的随机更新,然后计算当前粒子群的适应度值及最优适应度值,将当前粒子群的最优适应度值与上一次迭代的粒子群最优适应度值作比较,如果当前粒子群的最优适应度值小于上一次迭代的粒子群最优适应度值,则将最优解替换为当前粒子群最优适应度值和与最优适应度值对应的粒子位置,否则保持不变。
步骤6 根据最优解采用选择操作再次更新粒子位置,并计算选择操作更新的各个粒子适应度值,与各个粒子自身的历史最优适应度值作比较,如果更新的粒子适应度值小于该粒子历史最优适应度值,则将该粒子历史最优解替换为更新的粒子位置,否则保持不变。
步骤7 判定迭代终止条件。达到最大迭代次数或前后两次迭代最小适应度值的绝对误差小于误差精度并且持续迭代次数大于精度终止迭代数,否则返回执行步骤3。具体流程如图2所示。
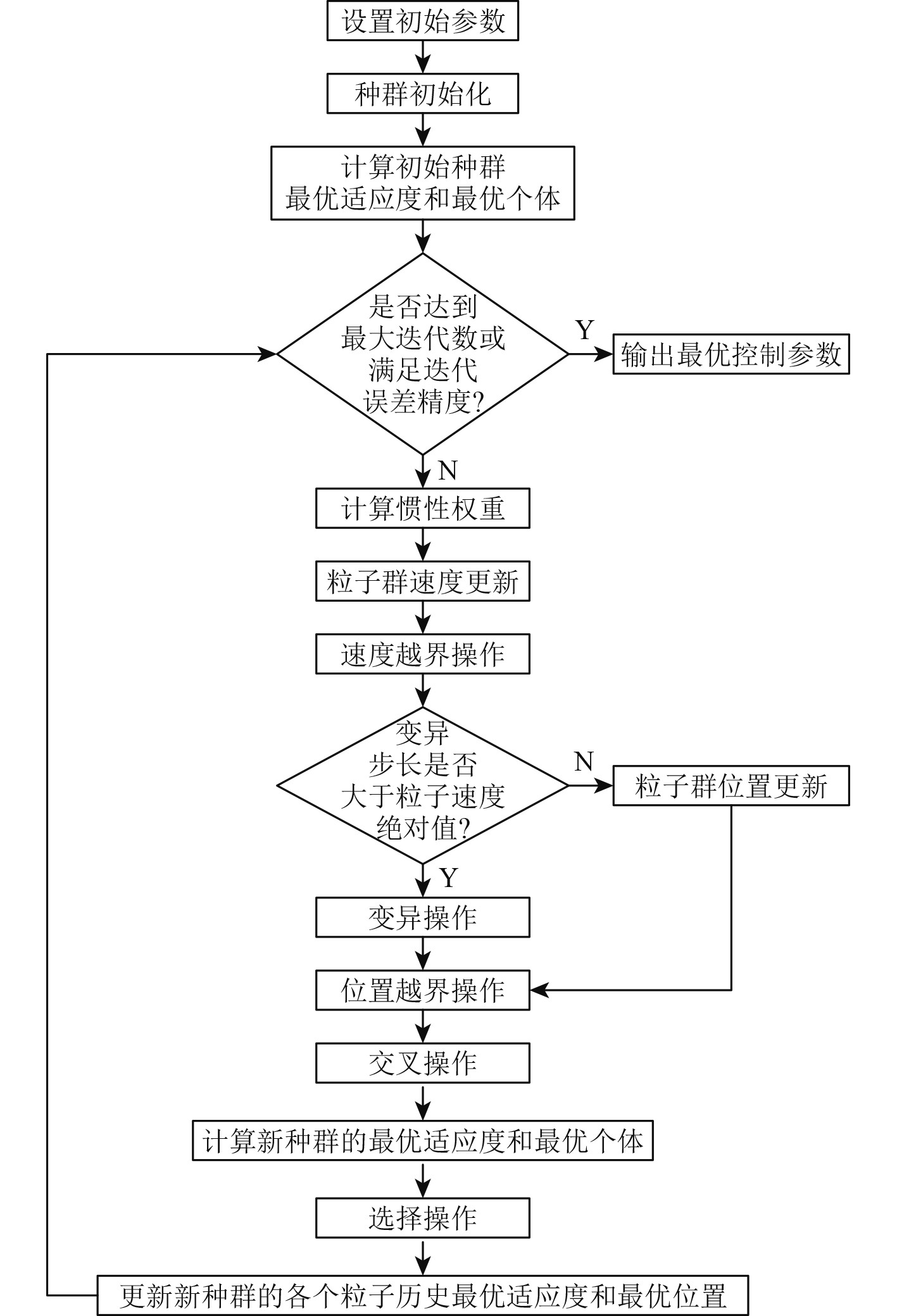
|
图 2 基于改进粒子群优化算法的控制参数优化流程 Fig. 2 Control parameters optimization process based on improved particle swarm optimization algorithm |
本节验证改进粒子群优化算法的有效性,针对恶劣初始条件下,高速载荷瞬时姿态控制问题对比遗传算法、基本粒子群算法和改进粒子群算法的寻优成功率。
高速载荷的初始条件如表1所示。各算法的仿真参数如表2所示。遗传算法仿真结果如图3所示。基本粒子群算法仿真结果如图4所示。改进粒子群算法仿真结果如图5所示。
|
|
表 1 载荷参数设置 Tab.1 Load parameter settings |
|
|
表 2 算法参数设置 Tab.2 Algorithm parameters settings |
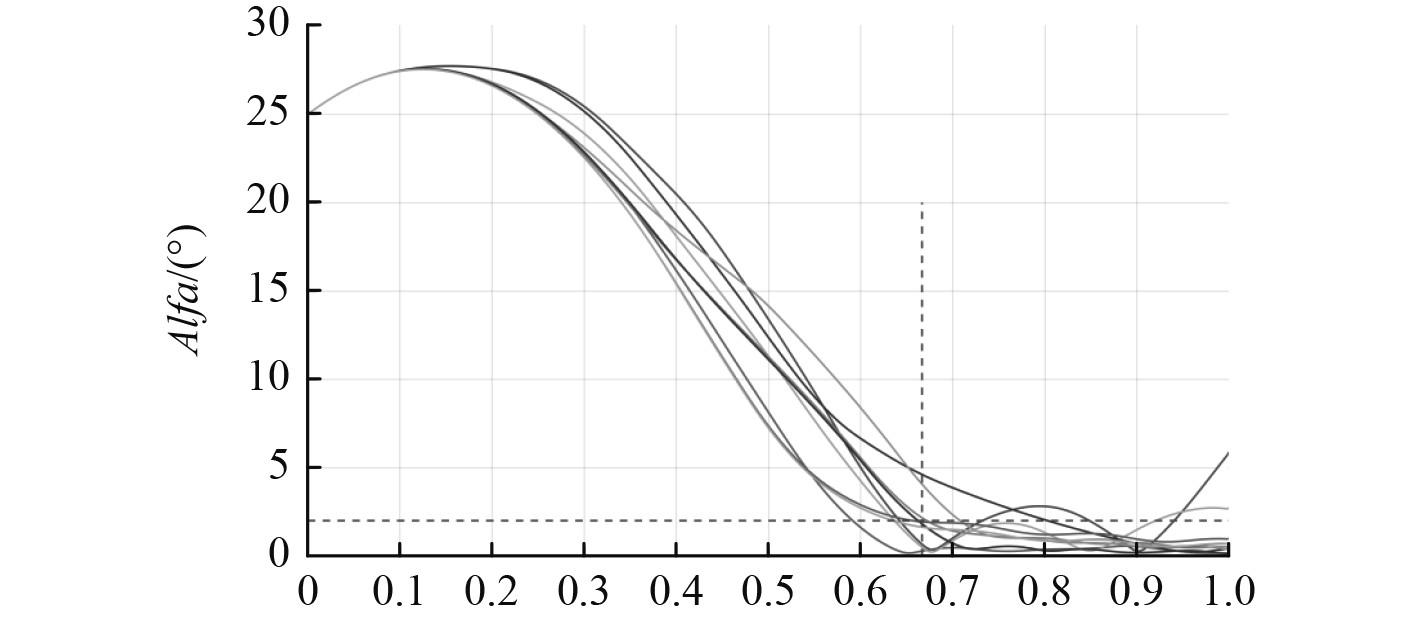
|
图 3 遗传算法仿真结果 Fig. 3 Simulation results of genetic algorithm |
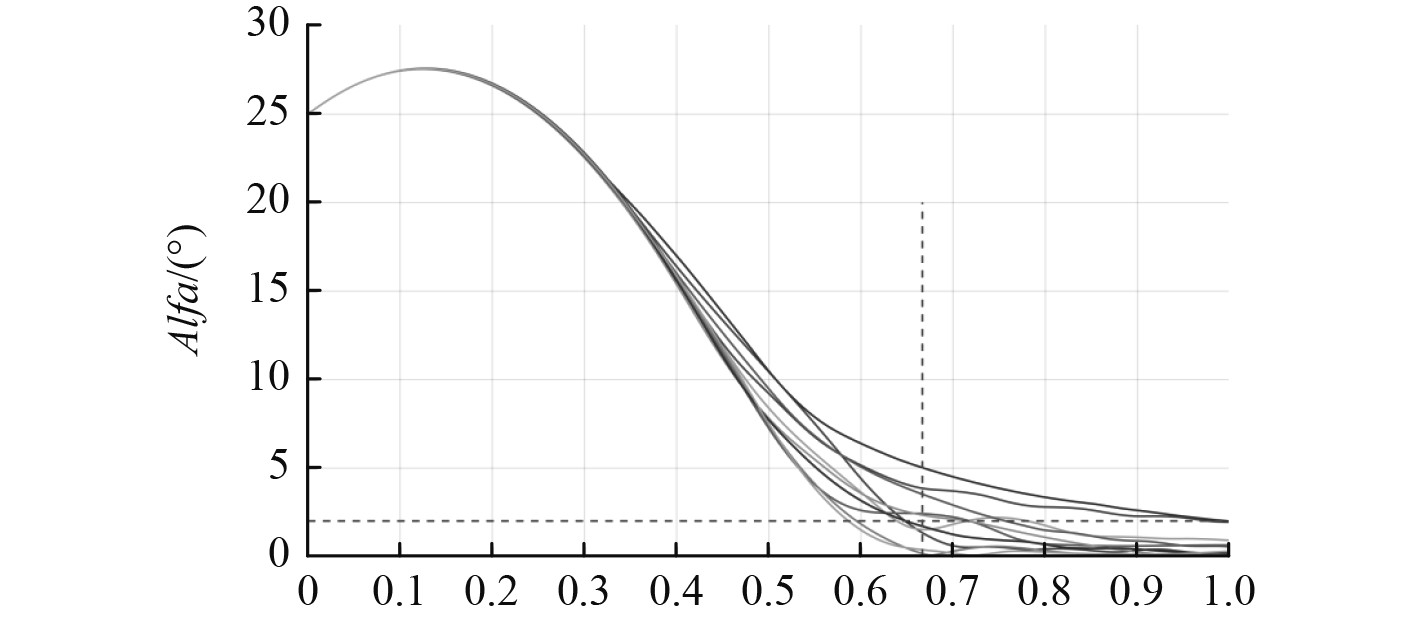
|
图 4 基本粒子群算法仿真结果 Fig. 4 Simulation results of elementary particle swarm algorithm |
|
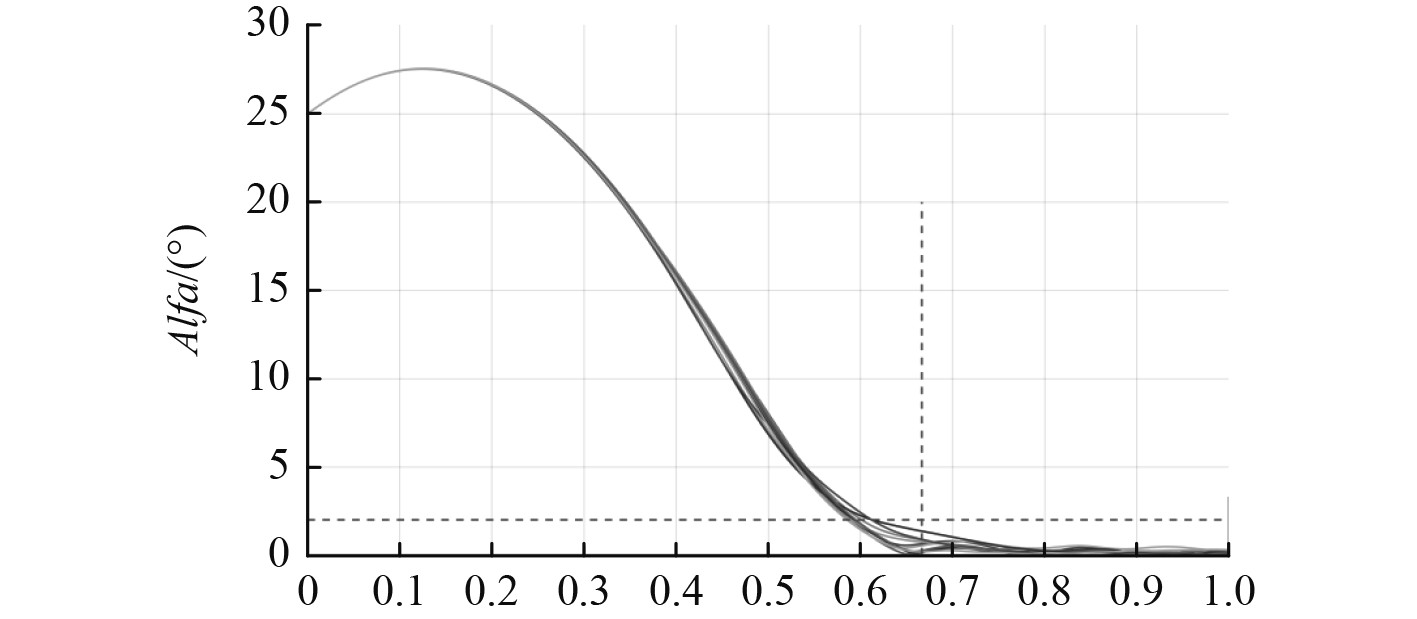
图 5 改进粒子群算法仿真结果 Fig. 5 Simulation results of improved particle swarm algorithm |
为了更有效地验证算法的性能效果,所以各算法采取随机运行多次,对比各算法的寻优成功率,如表3所示。可以看出,改进粒子群算法相较于遗传算法和基本粒子群算法,针对恶劣初始条件的高速载荷瞬时姿态控制问题具有更好的寻优成功率。
|
|
表 3 优化算法性能对比 Tab.3 Performance comparison of optimization algorithms |
本文针对恶劣初始条件下,高速载荷瞬时姿态控制问题设计了一种改进的粒子群优化算法,实现高速载荷在要求的控制时间内将合成攻角控制在合理范围内,该算法设计了一种惯性权重自适应调整方式和引入了遗传算法的选择、变异和交叉操作的思想构建新的粒子群更新规则,提高粒子群算法的寻优能力。仿真结果表明,相比于传统的遗传算法和基本粒子群算法,改进粒子群算法在恶劣初始条件的高速载荷瞬时姿态控制问题的寻优成功率上有所提升,从而保证随机运行一次优化算法找到可行解的概率大大提高。
| [1] |
智慧. 群智能优化算法的研究及应用[D]. 西安:西安电子科技大学, 2020.
|
| [2] |
高岳林, 杨钦文, 王晓峰, 等. 新型群体智能优化算法综述[J]. 郑州大学学报(工学版), 2022, 43(3): 21-30. |
| [3] |
安家乐, 刘晓楠, 何明, 等. 量子群智能优化算法综述[J]. 计算机工程与应用, 2022, 58(7): 31-42. DOI:10.3778/j.issn.1002-8331.2110-0141 |
| [4] |
张九龙, 王晓峰, 芦磊, 等. 若干新型智能优化算法对比分析研究[J]. 计算机科学与探索, 2022, 16(1): 88-105. |
| [5] |
韩礼红. 影响力最大化智能优化算法及应用研究[D]. 兰州:兰州大学, 2021.
|
| [6] |
HOLLAND J H. Adaptation in natural and artificial systems: an introductory analysis with applications to biology, control, and artificial intelligence[M]. 2nd ed. Cambridge: MIT Press, 1992.
|
| [7] |
KENNEDY J, EBERHART R. Particle swarm optimization[C]// IEEE International Conference on Neural Network. New Jersey, USA: IEEE, 1995, (4): 1942−1948.
|
| [8] |
杨博雯. 粒子群优化算法的惯性权重研究[D]. 锦州:渤海大学, 2021.
|
| [9] |
李会荣, 彭娇. 带有非线性惯性权重和柯西变异的粒子群优化算法[J]. 计算机与数字工程, 2021, 49(7): 1325-1329+1362. |
| [10] |
王生亮, 刘根友. 一种非线性动态自适应惯性权重PSO算法[J]. 计算机仿真, 2021, 38(4): 249-253+451. |
 2024, Vol. 46
2024, Vol. 46
