船舶在海面航行过程中遇到特别大的风浪时,由于货物可能会向一侧移动,导致船舶失稳,此时可能会发生倾覆风险。另外船舶在航行过程中排、压水操作不当也有可能导致压载水泄露,进而引发船舶倾覆。船舶倾覆严重影响船舶运输安全,会带来极大的财产损失和人员伤亡,因而在船舶设计时就需要考虑船体的形状、大小、重量分布以及船体材料的选择等[1 − 2]。合理的船体设计可以减小船舶受到外力的影响,提高船舶的稳定性。船体的宽度、高度、重心位置等参数都需要经过精确计算,以确保船舶在不同航行情况下都能保持平衡。但是船舶设计只能针对正常航行时的情况,在应急情况下,特别是遭遇特大风浪时需要启动自动应急抗倾覆装置来防止船舶出现倾覆[3]。
船舶自动应急抗倾覆装置可以及时监测和调整船舶的倾斜状态,防止船舶因各种原因而倾覆,从而避免造成人员伤亡和财产损失。此外,通过预防和监控倾覆事故,还可以提高船舶的可靠性和稳定性,降低运营成本,提高经济效益。在船舶倾覆的诸多案例中,船舶横摇幅度过大是造成船舶倾覆的重要原因,这是由于船舶横摇阻尼小,为了增大横摇阻尼,一般在大型船舶上会设计减摇鳍,通过操纵机构转动,利用水流在鳍的上部产生作用力,形成减摇力矩,以此来减少船体的横向摇晃。对于大型高速轮船来说,减摇鳍的效果尤为明显,且航速越高,其抗倾覆效果越好。液压系统是减摇鳍的动力来源,通过对液压装置的控制,可以帮助船舶在应急状态下快速调整状态,防止船舶出现倾覆[4]。
本文在上述研究基础上对船舶自动抗倾覆装置进行研究,主要方法为设计一种大型船舶的减摇鳍装置,并对船舶在航行过程中的减摇鳍液压控制方式进行研究,以达到抗倾覆的目的。
1 船舶横摇模型 1.1 Conolly船舶横摇模型为了更好地对船舶自动应急抗倾覆装置进行设计,首先需要对船舶横摇运动进行研究。船舶的横摇运动是一种受到波浪的影响下的无规则运动,而为了防止船舶倾覆,就需要对船舶的横摇运动进行预测和跟踪,因而建立船舶横摇模型就显得尤为重要。
将船舶横摇运动从非线性运动简化为线性运动,建立船舶横摇运动的运动方程。这个方程通常是一个二阶常微分方程,描述了船舶横摇的惯性、阻尼和恢复力之间的关系。本文使用Conolly船舶横摇模型来计算船舶横摇的运动过程,Conolly船舶横摇模型是用于描述和分析船舶在波浪中受到横摇(侧倾)运动的数学模型。这个模型基于船舶运动学和流体动力学的原理,考虑了波浪对船体的作用以及船体自身的动力学特性,假设船舶是刚性的并且波浪是线性的,模型的准确性取决于输入参数(如波浪谱、船体几何形状等)的准确性[5]。
建立的船舶横摇运动线性表达式如下:
| $ D\text{h}\theta +\sigma \theta +({J}_{x}+\Delta {J}_{x})=-(\Delta {J}_{x}{\beta }_{1}+\sigma {\beta }_{1}+Dh{\beta }_{2})。$ | (1) |
式中:D为目标船舶的排水量;h为船舶的横稳心高度;θ为船舶的横摇角;δ为阻尼系数;Jx为船舶转动惯量[6]。对β1、β2作如下定义:
| $ {\beta _1} = {\beta _{11}}\sin {\omega _e}t \text{,} $ | (2) |
| $ {\beta _2} = {\beta _{22}}\sin {\omega _e}t \text{。} $ | (3) |
式中:ωe为海浪频率;β11为海浪波倾角对应的最大有义波倾角;β22为海浪波倾角加速度对应的最大有义波倾角。
模型首先确定波浪对船体的激励力。这通常基于波浪的谱密度和船体的几何形状来计算。然后,模型计算船体对波浪激励的响应。这涉及到船体的惯性、阻尼和恢复力(如浮力)等因素。对上述模型进行拉式变化可以得到:
| $ G(S) = \frac{{\theta (s)}}{{{\beta _2}(s)}} = \frac{1}{{1 + T_\theta ^2{s^2} + 2{T_\theta }\sigma s}} \text{。} $ | (4) |
最终获得船舶横摇运动方程:
| $ \theta ={\theta }_{u}\mathrm{sin}({\omega }_{t}-{\epsilon }_{\theta }) 。$ | (5) |
根据此模型就可以实现对船舶横摇运动的预测,包括横摇的幅度、频率和相位等参数。
1.2 P-M谱在Conolly船舶横摇模型中合适的波浪谱函数对船舶横摇影响较大,本文选择P-M谱,P-M谱是一个经验模型,它根据实际海洋波浪的观测数据总结而来,它适用于深水或中等水深的海域。P-M谱对于浅水区域的适用性则需要考虑其他因素,对于海浪的模拟、海浪对结构物的作用力分析、船舶设计和海洋资源开发等方面都有重要应用。
P-M谱的数学表达式为:
| $ S(\zeta)=\frac{0.78}{{\zeta }^{5}}\text{exp}\left(-\frac{3.11}{{\zeta }^{4}{H}_{S}^{2}}\right) \text{。} $ | (6) |
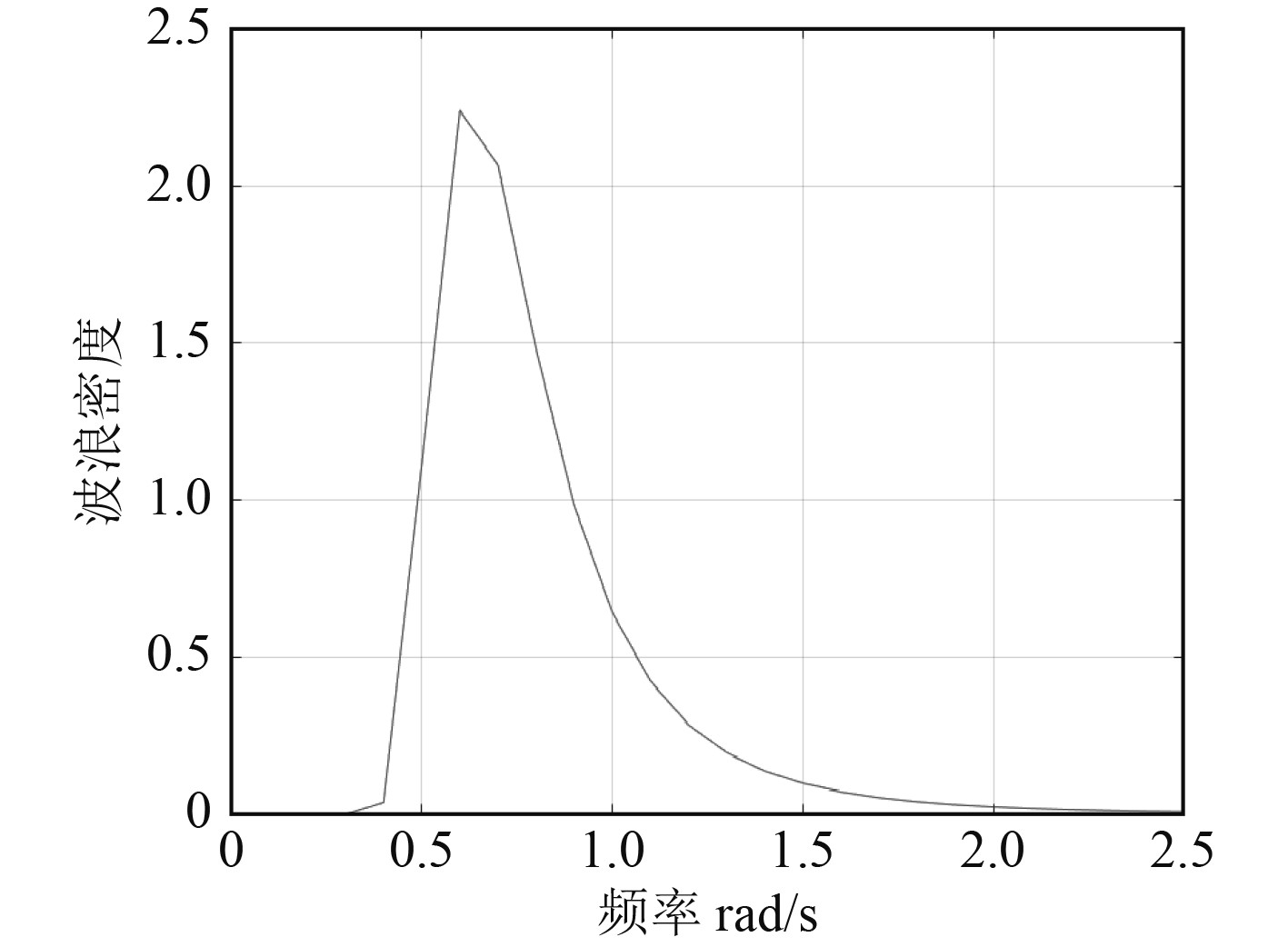
式中:S(ξ)为船舶横摇频率为ξ时的谱密度,ξ为圆频率。图1为P-M谱的分布情况。
|
图 1 P-M谱分布情况 Fig. 1 The distribution of P-M spectrum |
在实际船舶横摇运动中需要结合实验数据或现场观测数据来验证模型的预测结果,并根据需要进行调整和优化。
2 基于液压控制技术的自动应急抗倾覆装置设计 2.1 减摇鳍基本结构应急抗倾覆主要是通过设计一种特殊的减摇鳍来实现,其剖面类似机翼,从船体中部两舭伸出机翼型翼片,且能够通过控制其攻角来产生减摇力矩。其工作原理是利用流体动力学效应,即当船舶在航行时,减摇鳍在水中运动产生升力,这个升力与船舶的横摇运动方向相反,从而产生减摇效果。当船在风浪中横摇时,在自动控制系统的控制下,根据横摇情况,不断改变鳍角,使鳍上产生的升力在左右两舷方向始终相反,达到减小横摇的目的。
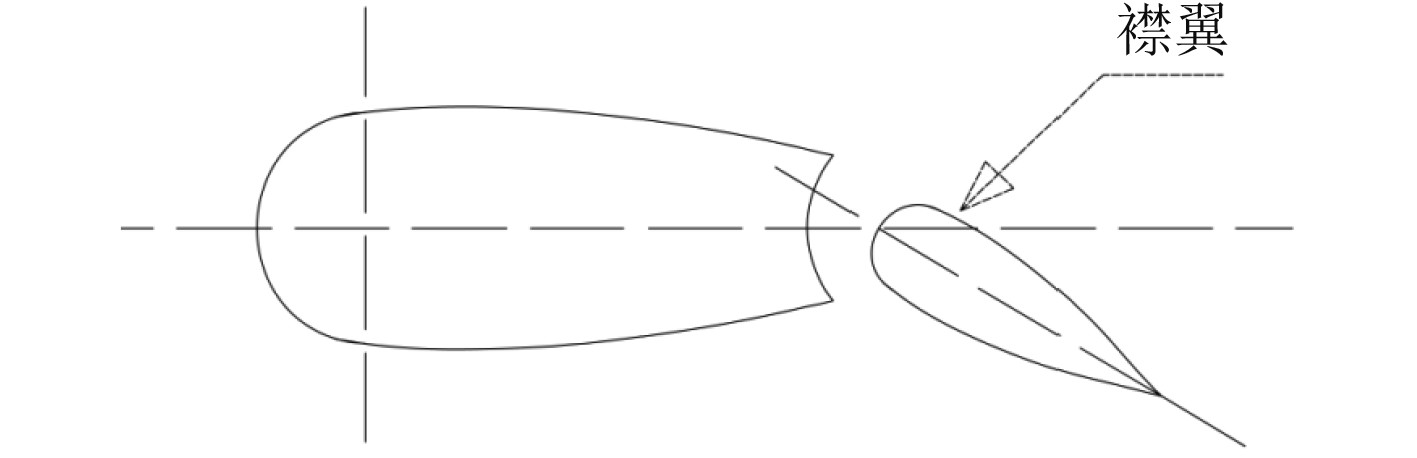
根据伯努利原理,快速流动的水对鳍产生的压力小于静止或流动慢的水的压力,从而在鳍的两侧产生压力差,形成升力。这个升力与船舶的横摇运动方向相反,因此,当船舶开始倾覆时,减摇鳍产生的升力力矩会抵抗这种倾覆运动。使用液压系统+运动控制模型对减摇鳍进行控制,能够根据船舶的横摇速度和加速度反馈信号,自动调整鳍的攻角,以实现最佳的减摇效果。并且可以显著减小船舶的横摇角度,减少船舶因海浪造成的摇摆,从而提高船舶的稳定性,避免因横摇幅度过大而导致的倾覆危险。图2为一种开襟式减摇鳍的基本结构。
|
图 2 开襟式减摇鳍结构 Fig. 2 Cardigan fin structure |
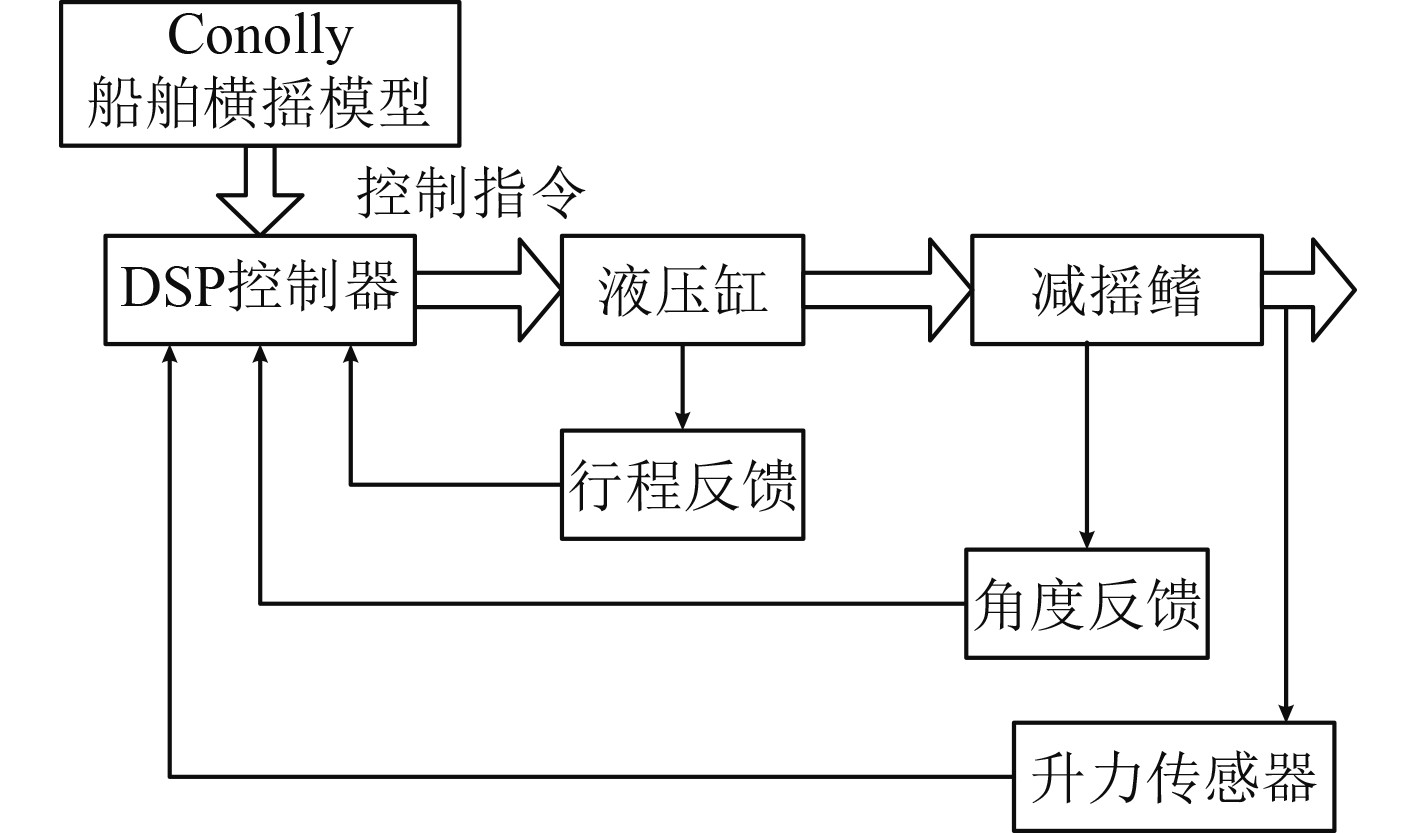
对基于液压控制技术的船舶自动应急抗倾覆装置进行设计,系统结构如图3所示。系统通过DSP控制器接收来自升力传感器、行程反馈和角度反馈的信号,然后计算出最优的控制信号发送给液压缸,以驱动减摇鳍,产生与船舶横摇方向相反的力矩,最终达到船舶自动应急抗倾覆的目的。这种闭环控制系统能够动态响应海况变化和船舶运动,提供更为稳定的船舶航行控制。
|
图 3 船舶自动应急抗倾覆装置结构 Fig. 3 Structure of ship automatic emergency anti-capsizing device |
1)Conolly船舶横摇模型。用于模拟船舶在海浪中横摇行为的数学模型。该模型用于预测船舶在不同海况下的横摇响应,以及评估减摇系统的效果,在初始化后将得到的结果输入到DSP控制器,实现对船舶抗倾覆装置的控制。
2)DSP控制器。DSP代表数字信号处理器(Digital Signal Processor),这是一种专门为快速数字信号处理而设计的微处理器。在船舶自动应急抗倾覆装置中,DSP控制器负责接收船舶运动的实时数据(如横摇角度、升力传感器、行程、船舶速度等),并根据预设的控制算法快速计算出控制信号,以调节自动应急抗倾覆装置的工作状态。
3)液压缸。液压缸是一种将液压能转换为直线运动机械能的设备。在船舶自动应急抗倾覆装置中,液压缸是核心元件,用于驱动减摇鳍以产生与船舶横摇运动相反的力矩,从而减少船舶的横摇,提升船舶的稳定性。
4)减摇鳍。减摇鳍是一种广泛使用的船舶减摇装置,通常安装在船体两侧。通过调整减摇鳍的角度,可以产生升力,这个升力与船舶的横摇方向相反,有助于减少船舶的摇摆。
5)行程反馈、角度反馈以及升力传感器。行程反馈用于监测液压缸或减摇鳍的移动距离或“行程”,角度反馈监测的是减摇鳍或其他减摇装置的当前角度,升力传感器用于测量减摇鳍产生的升力大小。通过行程反馈、角度反馈以及升力传感器,控制系统可以精确地知道减摇装置的当前位置、角度以及升力情况,这个信息可以反馈给DSP控制器,以便进一步根据实际的信号变化来调整控制算法,优化控制信号,确保减摇鳍以最有效的方式工作。
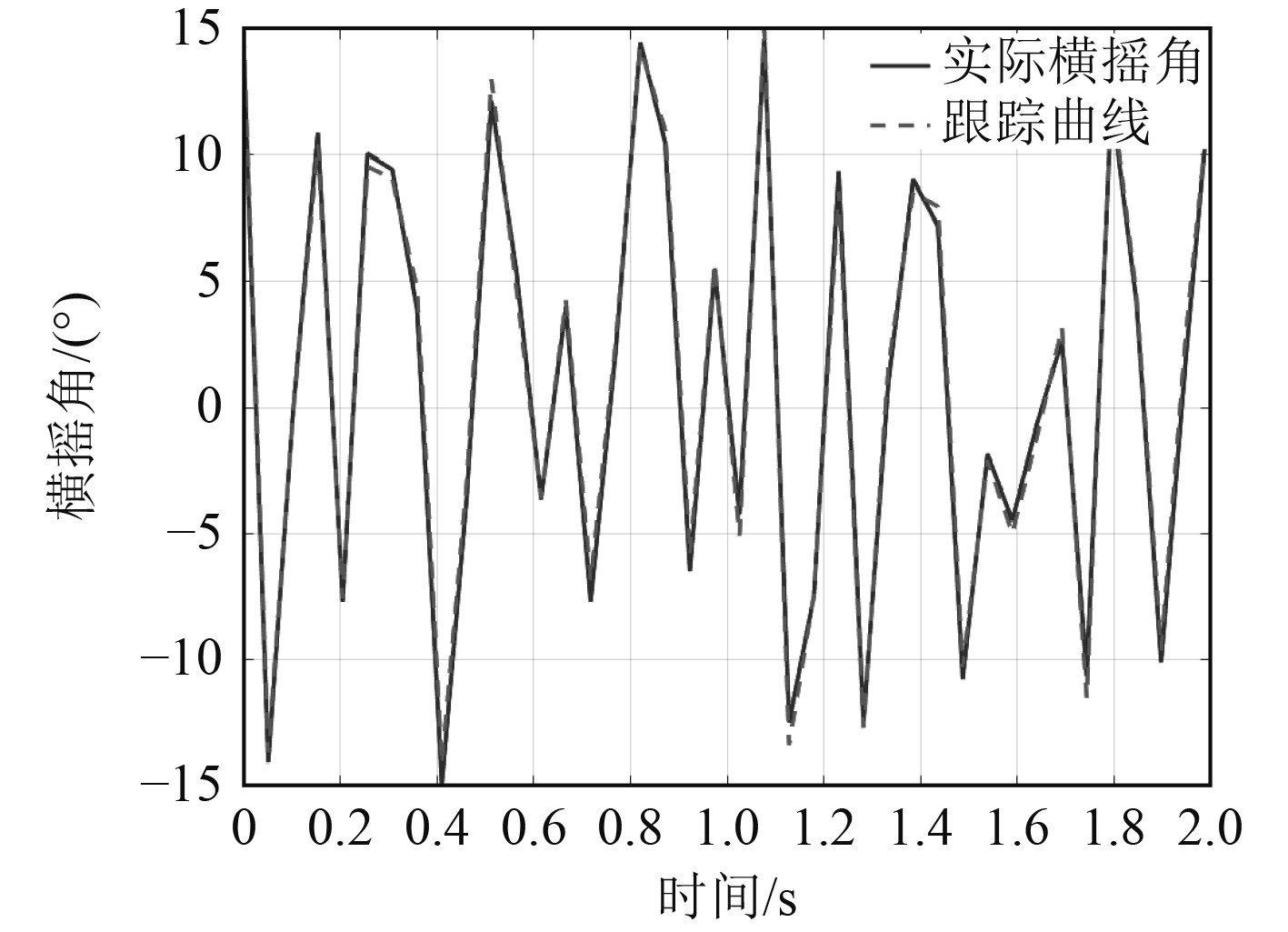
2.3 系统仿真对本文设计的船舶自动应急抗倾覆装置进行仿真,设置船舶速度为22 kn,波浪高4 m,船舶和波浪之间遭遇的角度为90°。本文从两方面来说明系统的应急抗倾覆效果,一个是Conolly船舶横摇模型对横摇角的跟踪精度,另外一个是系统对液压装置的控制精度。图4为船舶横摇角跟踪仿真曲线,可以发现,模型能够跟踪横摇角的变化,且具有较好的适应性和实时性,同时可以发现系统跟踪的误差较小,在不同航行条件下仍然能够实现对横摇角的实时跟踪。
|
图 4 船舶横摇角跟踪仿真 Fig. 4 Simulation of ship roll angle tracking |
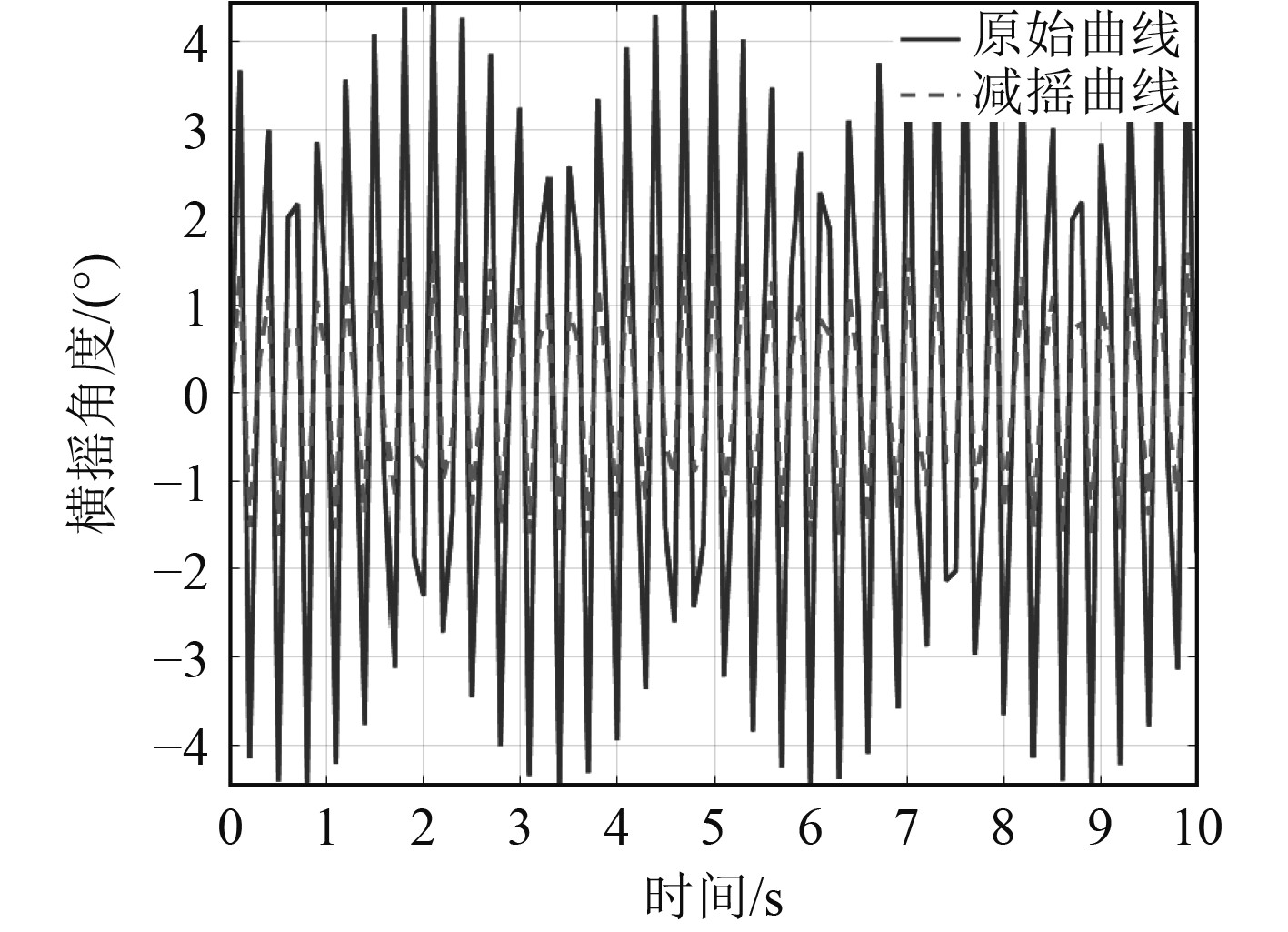
图5为船舶横摇角控制效果仿真,通过对比可以发现,在船舶自动应急抗倾覆装置作用后,船舶的横摇角幅值得到明显控制,从原有的±4.5°减小到±2°,控制效果明显。因而在船舶实际航行过程中可以有效抑制船舶的横摇运动,并在出现大的横摇运动时通过即时调整DSP控制器的输出,以达到自动抗倾覆的目的。
|
图 5 船舶横摇角控制效果仿真 Fig. 5 Simulation of ship roll angle control effect |
传统的抗倾覆装置大多数为被动抗倾覆,在船舶航行过程中使用基于液压控制技术的自动应急抗倾覆可以有效缩短反应时间,系统会根据当前船舶横摇角的变化来改变控制液压装置的输出信号,从而提升船舶航行的稳定性。本文得到的结论主要包括:
1)Conolly船舶横摇模型可以有效对船舶横摇情况进行计算,进而对船舶横摇的情况进行跟踪,是实现船舶自动应急抗倾覆功能的重要组成部分。
2)DSP控制器通过接收来自升力传感器、行程反馈和角度反馈的信号,可以计算出最优的控制信号发送给液压缸,以驱动减摇鳍实现对减摇鳍的闭环控制。
3)系统仿真结果表明系统能够实现对船舶横摇角的实时跟踪,可以有效减少船舶横摇角的幅值,实现船舶自动应急抗倾覆的目的,系统具有较好的适应性和实时性。
| [1] |
崇健斌. 全航速减摇鳍仿真与控制研究[D]. 镇江: 江苏科技大学, 2023.
|
| [2] |
孙云, 金方银, 曾启盛, 等. 大型减摇鳍液压机组隔振装置设计与试验[J]. 机电设备, 2022, 39(4): 1-6. SUN Yun, JIN Fangyin, ZENG Qisheng, et al. Design and test of vibration isolation device for large fin stabilizer hydraulic unit[J]. Mechanical and Electrical Equipment, 2022, 39(4): 1-6. |
| [3] |
曹长水, 蒋衡捷, 司黎明, 等. 零航速减摇鳍节能型液压系统研究[J]. 机电设备, 2020, 37(3): 11-14+34. CAO Changshui, JIANG Hengjie, SI Liming, et al. Research on energy-saving hydraulic system of zero-speed fin stabilizer[J]. Mechanical and Electrical Equipment, 2020, 37(3): 11-14+34. |
| [4] |
吴建林, 卜锋斌, 张亮, 等. 零航速减摇鳍水动力特性分析[J]. 船舶工程, 2017, 39(9): 11-14+30. WU Jianlin, BU Fengbin, ZHANG Liang, et al. Analysis of hydrodynamic characteristics of zero-speed fin stabilizer[J]. Ship Engineering, 2017, 39(9): 11-14+30. |
| [5] |
赵树培, 盛兴. 基于SolidWorks的非收放式减摇鳍摇臂结构优化分析[J]. 公安海警学院学报, 2016, 15(3): 64-67. ZHAO Shupei, SHENG Xing. Optimization analysis of non-retractable fin stabilizer rocker arm structure based on solidWorks[J]. Journal of Maritime Police College, 2016, 15(3): 64-67. |
| [6] |
刘隽瑶. 减摇鳍在船舶横纵摇控制中的应用研究[D]. 哈尔滨: 哈尔滨工程大学, 2016.
|
 2024, Vol. 46
2024, Vol. 46
