2. 海军工程大学 振动与噪声研究所,湖北 武汉 430033;
3. 船舶振动噪声重点实验室,湖北 武汉 430033
2. Institute of Noise and Vibration, Naval University of Engineer, Wuhan 430033, China;
3. National Key Laboratory on Ship Vibration and Nosie, Wuhan 430033, China
船舶在航行中受到海风、海浪和水流等外部激励和螺旋桨等船舶设备等内部激励,不可避免地会出现振动现象。船体结构振动水平已经成为船舶设计建造的一个重要参数。过大的振动会影响结构的稳定性,甚至会破环船体结构;同时船体振动也会降低舒适性,影响船员的生活和工作。
工程振动分析方法主要分为有限元分析法(Finite Element Analysis,FEA)、传统试验模态分析法(Experimental Modal Analysis,EMA)和运行模态分析法(Operational Modal Analysis,OMA)。有限元分析法可直接利用结构模型,借助于计算机分析结构的模态。随着高性能计算机和有限元商业软件的发展,有限元分析法广泛地应用于大型结构的模态分析。但部分结构存在边界条件无法准确描述,材料的物理参数无法确定等问题,使得有限元分析法无法达到较高的精度。
传统实验模态分析基于真实的物理结构,测试振动数据,求得频响曲线,分析得到准确的模态参数。其原理是测试得到系统的输入激励源以及输出响应,利用频响函数进行参数识别。在实际操作中,一般在非工作状态下的结构上施加人工激励,通过测量结构的输入和输出信号,求得频响函数,识别分析得到结构的模态参数。但许多结构由于其物理尺寸、形状和位置的原因,尤其是船舶这种大型复杂结构,很难通过人工激励激起结构总体共振系统。另外,在工程实践中,一些大型结构会受到环境激励,想要通过测试得到激励的完整信息是比较困难的。
运行模态分析不需要输入激励源的完整信息,解决了传统实验模态分析需要测量激励源信号的问题。它只需要利用工作状态下结构自身激励产生的响应信号,就能够得到实际工况的结构模态参数。以船舶为例,使用运行模态分析可以直接在航行状态下测试分析得到结构的模态参数,比较船舶的主要激励源频率是否和船舶的固有频率接近,从而引起系统共振,或者进一步参考船舶振型,对结构振幅较大处进行有效的加强或者对结构进行修改。
为弥补了传统试验模态分析法的不足,在运行模态分析领域国内外学者已经提出了多种成熟理论,其中包括时间序列方法、随机减量技术、ITD(IbrahimTime Domain)类方法和自然激励法(Natural Excitation Technology,NExT)。Akaile等[1]首次利用自回归移动均值模型识别结构的模态参数,并将其与传统方法比较,发现其在识别结构的模型参数时有较大的潜力。Box等[2]将时间序列模型预测方法运用于结构模态参数识别,但是该预测成本较高,不利于广泛使用。Gautier等[3]基于自回归移动均值模型,利用系统响应信号的相关函数提高了该方法的稳定性。Cole[4]提出随机减量技术,并在模型试验中取得了较好的效果。Ibrahim[5]随后在多通道信号领域利用随机减量技术成功提取振动实验响应。张西宁等[6]针对随机减量法存在的问题,采用正、负阈值同时截取的提取方法,提高了提取信号的质量。黄方林等[7]利用随机减量技术成功识别拉索桥的模态参数,证明了该方法的有效性。Ibrahim等[8]提出了精度较高的ITD方法,但该方法只适合线性结构和弱非线性机构。James等[9 − 10]提出了自然激励法,将其应用于涡轮机振动的测量,并成功识别了涡轮机的模态频率和振型。自然激励法[11]的基本思想是白噪声环境激励下结构两点之间响应的互相关函数的表达式和脉冲响应函数的表达式相似,求得两点之间响应的互相关函数后,运用时域中模态识别方法进行模态参数识别。孙乐[12]基于自然激励法对板架结构进行了研究,结果表明该方法的识别精度良好。李长玉等[13]基于自然激励法,识别车身模态参数,研究汽车的动态特性。卞超[14]基于自然激励法提出了一套预测方法,并用该方法对飞机进行模态分析,结果显示该测验方法能有效提高模态参数识别的准确性。目前,自然激励法已经广泛应用于汽车、船舶和飞机的工作模态参数识别。
1 理论推导 1.1 自然激励法(NExT)理论NExT的理论成立需要证明系统在随机激励下产生的两点响应之间的互相关函数的表达式和脉冲响应函数的表达式相似,均可展开为正弦函数的和。本文仅给出激励力为白噪声时的证明过程。
对于一般粘性阻尼系统:
| $ \left[ {\boldsymbol{M}} \right]\left\{ {\ddot x(t)} \right\} + \left[ {\boldsymbol{C}} \right]\left\{ {\dot x(t)} \right\} + \left[ {\boldsymbol{K}} \right]\left\{ {x(t)} \right\} = \left\{ {f(t)} \right\}。$ | (1) |
式中:
在模态坐标下,
| $ \left\{ {x(t)} \right\} = \left[ {\boldsymbol{\varPhi }} \right]\left\{ {q(t)} \right\} = \sum\limits_{r = 1}^n {\left\{ {{\phi ^r}} \right\}{q^r}(t)}。$ | (2) |
式中:
将式(2)代入式(1),同时对式(1)左乘
| $ {\ddot q^r}(t) + 2{\zeta ^r}\omega _n^r{\dot q^r}(t) + \omega _n^{{r^2}}{q^r}(t) = \frac{1}{{{m^r}}}{\{ {\phi ^r}\} ^{\mathbf{T}}}\left\{ {f(t)} \right\}。$ | (3) |
式中:
零初始条件时,式(3)的解为:
| $ {q^r}(t) = \int_{ - \infty }^t {{{\{ {\phi ^r}\} }^{\mathbf{T}}}\left\{ {f(\tau )} \right\}} {g^r}(t - \tau ){\mathrm{d}}\tau 。$ | (4) |
式中:
将式(4)代入式(2),记
| $ {x_{ik}}(t) = \sum\limits_{r = 1}^n {\phi _i^r\phi _k^r\int_{ - \infty }^t {{f_k}(\tau ){g^r}(t - \tau ){\mathrm{d}}\tau } } 。$ | (5) |
式中:
当
| $ {x_{ik}}(t) = \sum\limits_{r = 1}^n {\frac{{\phi _i^r\phi _k^r}}{{{m^r}\omega _d^r}}\exp ( - {\zeta ^r}\omega _n^rt)\sin (\omega _d^rt)}。$ | (6) |
接下来推导激励点k施加白噪声激励时,响应点i和响应点j的互相关函数表达式。记i点响应为
| $ {R_{ijk}}(T) = {E} [{x_{ik}}(t + T){x_{jk}}(t)]。$ | (7) |
式中:E为期望算子。
将式(5)代入式(7)可得:
| $\begin{split} {R_{ijk}}(T) =& \sum\limits_{r = 1}^n {\sum\limits_{s = 1}^n {\phi _i^r\phi _k^r\phi _j^s\phi _k^s\int_{ - \infty }^t{\int_{ - \infty }^{t + T}{\{ {g^r}(t + T - \sigma ) \cdot } } } }\\ &{g^s}(t - \tau )E[{f_k}(\sigma ){f_k}(\tau )]\} {\mathrm{d}}\sigma {\mathrm{d}}\tau 。\end{split}$ | (8) |
假设激励为白噪声,故而:
| $ E[{f_k}(\tau ){f_k}(\sigma )] = {\alpha _k}\delta (\tau - \sigma )。$ | (9) |
式(9)代入式(8),可得
| $ {R_{ijk}}(T) = \sum\limits_{r = 1}^n {\sum\limits_{s = 1}^n {{\alpha _k}\phi _i^r\phi _k^r\phi _j^s\phi _k^s\int_{ - \infty }^t {[{g^r}(t + T - \tau )} } } \cdot {g^s}(t - \tau )]{\mathrm{d}}\tau。$ | (10) |
为了进一步化简,令
| $ {R_{ijk}}(T) = \sum\limits_{r = 1}^n {\sum\limits_{s = 1}^n {{\alpha _k}\phi _i^r\phi _k^r\phi _j^s\phi _k^s\int_0^{ + \infty } {[ - {g^r}(\lambda + T)} } } \cdot {g^s}(\lambda )]{\mathrm{d}}\lambda,$ | (11) |
根据
| $\begin{split} {R_{ijk}}(T) =& \sum\limits_{r = 1}^n {[G_{ijk}^r\exp ( - {\zeta ^r}\omega _n^rT)\cos (\omega _d^rT) + }\\ &H_{ijk}^r\exp ( - {\zeta ^r}\omega _n^rT)\sin (\omega _d^rT)] 。\end{split}$ | (12) |
其中,
| $\begin{split}\left\{ {\begin{array}{*{20}{c}} {G_{ijk}^r} \\ {H_{ijk}^r} \end{array}} \right\} =& \sum\limits_{s = 1}^n {\frac{{{\alpha _k}\phi _i^r\phi _k^r\phi _j^s\phi _k^s}}{{{m^r}\omega _d^r{m^s}\omega _d^s}}\int_0^{ + \infty }{ - \exp ( - {\zeta ^r}\omega _n^r\lambda - } } \\ &{\zeta ^s}\omega _n^s\lambda )\sin (\omega _d^s\lambda )\left\{ {\begin{array}{*{20}{c}} {\sin (\omega _d^r\lambda )} \\ {\cos (\omega _d^r\lambda )} \end{array}} \right\}{\mathrm{d}}\lambda 。\end{split}$ | (13) |
对式(13)进行积分可得:
式中:
定义
| $ \begin{split} {R_{ijk}}(T) =& \sum\limits_{r = 1}^n {\frac{{\phi _i^r}}{{{m^r}\omega _d^r}}\sum\limits_{s = 1}^n {\sum\limits_{k = 1}^m {\beta _{jk}^{rs}{{(J_{rs}^2 + I_{rs}^2)}^{ - 1/2}}} } } \\ & \exp ( - {\zeta ^r}\omega _n^rT)\sin (\omega _d^rT) 。\\ \end{split} $ | (14) |
上述求和式中的正弦函数幅值不同、相位不同但频率相同,可以使用三角函数进行求和,式(14)可以改写为:
| $ {R_{ijk}}(T) = \sum\limits_{r = 1}^n {\frac{{\phi _i^rA_j^r}}{{{m^r}\omega _d^r}}\exp ( - {\zeta ^r}\omega _n^rT)\sin (\omega _d^rT + {\theta ^r})}。$ | (15) |
式中:
白噪声激励下两点响应间的互相关函数表达式如式(15),根据前文,脉冲响应函数表达式如下:
| $ {x_{ik}}(t) = \sum\limits_{r = 1}^n {\frac{{\phi _i^r\phi _k^r}}{{{m^r}\omega _d^r}}\exp ( - {\zeta ^r}\omega _n^rt)\sin (\omega _d^rt)} 。$ |
对比分析可得,互相关函数与脉冲响应函数都是由一系列衰减正弦函数的和构成,且频率相同,两者有相似的表达式。
1.2 特征系统实现法(ERA)理论特征系统实现法(ERA)以脉冲响应函数为基本模型,通过构造广义Hankel矩阵,利用奇异值分解技术,得到系统的最小实现,从而得到最小阶数的系统矩阵,以此为基础进一步识别系统的模态参数。
对于n自由度一般粘性阻尼系统,设系统响应点数为M,激励点数为L,式(1)引入辅助方程:
| $ [{\boldsymbol{M}}]\{ \dot x(t)\} - [{\boldsymbol{M}}]\{ \dot x(t)\} = 0 。$ | (16) |
那么,可得系统状态方程如下:
| $ \{ \dot y(t)\} = {\boldsymbol{A}}\{ y(t)\} + {\boldsymbol{B}}\{ f(t)\} 。$ | (17) |
式中:y(t)为状态向量,表达式为
系统观测方程为:
| $ \{ z(t)\} = {\boldsymbol{G}}\{ y(t)\}。$ | (18) |
式中:
系统状态方程式(17)的解的表达式为:
| $ \{ y(t)\} = {e^{{\boldsymbol{A}}t}}y(0) + \int_0^t {{e^{{\boldsymbol{A}}(t - \tau )}}{\boldsymbol{B}}\{ f(\tau )\} {\mathrm{d}}\tau }。$ | (19) |
令
| $ y((k + 1)\Delta t) = {e^{{\boldsymbol{A}}\Delta t}}y(k\Delta t) + {e^{{\boldsymbol{A}}\Delta t}}{\boldsymbol{B}}f(k\Delta t)\Delta t 。$ | (20) |
令
| $ y(k + 1) = {{\boldsymbol{A}}_1}y(k) + {{\boldsymbol{B}}_1}f(k) 。$ | (21) |
式中:A1为系统矩阵,B1为输入矩阵。
系统观测方程的离散形式为:
| $ z(k) = {\boldsymbol{G}}y(k)。$ | (22) |
[A1,B1,G]为时间离散系统的一个实现。已知观测向量
为构造系统的最小实现,脉冲响应函数
| $ {\boldsymbol{h}}(k) = {\boldsymbol{GA}}_1^{k - 1}{{\boldsymbol{{\boldsymbol B}}}_1}。$ | (23) |
根据
| $ \begin{aligned} & {\boldsymbol{H}}(k - 1) = \\ & \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{h}}(k)}&{{\boldsymbol{h}}(k + {t_1})}& \cdots &{{\boldsymbol{h}}(k + {t_{\beta - 1}})}\\ {{\boldsymbol{h}}(k + {s_1})}&{{\boldsymbol{h}}(k + {s_1} + {t_1})}& \cdots &{{\boldsymbol{h}}(k + {s_1} + {t_{\beta - 1}})}\\ \vdots & \vdots & \ddots & \vdots \\ {{\boldsymbol{h}}(k + {s_{\alpha - 1}})}&{{\boldsymbol{h}}(k + {s_{\alpha - 1}} + {t_1})}& \cdots &{{\boldsymbol{h}}(k + {s_{\alpha - 1}} + {t_{\beta - 1}})} \end{array}} \right]。\end{aligned} $ | (24) |
其中:
通常取
| $ \begin{aligned} & {\boldsymbol{H}}(k - 1) = \\ & \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{h}}(k)}&{{\boldsymbol{h}}(k + 1)}&{}& \cdots &{{\boldsymbol{h}}(k + \beta - 1)}\\ {{\boldsymbol{h}}(k + 1)}&{{\boldsymbol{h}}(k + 2)}&{}& \cdots &{{\boldsymbol{h}}(k + \beta )}\\ {{\boldsymbol{h}}(k + 2)}&{{\boldsymbol{h}}(k + 3)}&{}& \cdots &{{\boldsymbol{h}}(k + \beta + 1)}\\ \vdots & \vdots &{}& \ddots & \vdots \\ {{\boldsymbol{h}}(k + \alpha - 1)}&{{\boldsymbol{h}}(k + \alpha )}&{}& \cdots &{{\boldsymbol{h}}(k + \alpha + \beta - 2)} \end{array}} \right]。\end{aligned} $ | (25) |
构造矩阵P、Q如下:
同时根据式(23),式(25)可化为:
| $ {\boldsymbol{H}}(k - 1) = {\boldsymbol{PA}}_1^{k - 1}{\boldsymbol{Q}} ,$ | (26) |
显然:
| $ {\boldsymbol{H}}(0) = {\boldsymbol{PQ}},$ | (27) |
对
| $ {\boldsymbol{H}}(0) = {\boldsymbol{US}}{{\boldsymbol{V}}^{{\mathrm{T}}}}。$ | (28) |
其中:
U、V均为列正交矩阵,即:
定义
| $ {\boldsymbol{H}}(0){{\boldsymbol{H}}^{\mathbf{\# }}}{\boldsymbol{H}}(0) = {\boldsymbol{PQ}}{{\boldsymbol{H}}^{\mathbf{\# }}}{\boldsymbol{PQ}} = {\boldsymbol{PQ}} = {\boldsymbol{H}}(0),$ |
求取H#的表达,根据式(27)、式(28),
| $ {\boldsymbol{H}}(0) = {\boldsymbol{PQ}} = {\boldsymbol{US}}{{\boldsymbol{V}}^{{\mathrm{T}}}}。$ |
令
构造2n×2n方阵
对照前文定义,
| $ {{\boldsymbol{H}}^{\mathbf{\# }}} = {\boldsymbol{V}}{{\boldsymbol{S}}^{{\mathbf{ - 1}}}}{{\boldsymbol{U}}^{\mathrm{T}}},$ | (29) |
设
结合式(25),可得:
将式(26)代入可得:
| $ {\boldsymbol{h}}(k) = {{\boldsymbol{E}}_{\boldsymbol{M}}}{\boldsymbol{PA}}_1^{k - 1}{\boldsymbol{Q}}{{\boldsymbol{E}}_{\boldsymbol{L}}}。$ |
在上式
| $\begin{split} {\boldsymbol{h}}(k) = &{{\boldsymbol{E}}_{\boldsymbol{M}}}{\boldsymbol{P}}({\boldsymbol{Q}}{{\boldsymbol{H}}^{\mathbf{\# }}}{\boldsymbol{P}}){\boldsymbol{A}}_1^{k - 1}({\boldsymbol{Q}}{{\boldsymbol{H}}^{\mathbf{\# }}}{\boldsymbol{P}}){\boldsymbol{Q}}{{\boldsymbol{E}}_{\boldsymbol{L}}} =\\ &{{\boldsymbol{E}}_{\boldsymbol{M}}}{\boldsymbol{H}}(0)({{\boldsymbol{H}}^{\mathbf{\# }}}{\boldsymbol{PA}}_1^{k - 1}{\boldsymbol{Q}}){{\boldsymbol{H}}^{\mathbf{\# }}}{\boldsymbol{H}}(0){{\boldsymbol{E}}_{\boldsymbol{L}}} 。\end{split}$ |
对于
| $\begin{split} {H}^{\#}P{A}_{1}^{k-1}Q=&\underset{k-1个}{\underbrace{{H}^{\#}P{A}_{1}Q\cdot {H}^{\#}P{A}_{1}Q\cdot \cdots \cdot {H}^{\#}P{A}_{1}Q}}\text{=}\\ &({H}^{\#}P{A}_{1}Q{)}^{k-1}={\text{(}{H}^{\#}H(1))}^{k-1} 。\end{split}$ |
根据式(29),那么:
| $ \begin{split} {\boldsymbol{h}}(k) =& {{\boldsymbol{E}}_{\boldsymbol{M}}}{\boldsymbol{H}}(0) \cdot {({\boldsymbol{V}}{{\boldsymbol{S}}^{{\mathbf{ - 1}}}}{{\boldsymbol{U}}^{\mathrm{T}}}{\boldsymbol{H}}(1))^{k - 1}} \cdot {\boldsymbol{V}}{{\boldsymbol{S}}^{{\mathbf{ - 1}}}}{{\boldsymbol{U}}^{\mathrm{T}}} \cdot {\boldsymbol{H}}(0){{\boldsymbol{E}}_{\boldsymbol{L}}}= \\ & {{\boldsymbol{E}}_{\boldsymbol{M}}}{\boldsymbol{H}}(0){\boldsymbol{V}} \cdot {({{\boldsymbol{S}}^{{\mathbf{ - 1}}}}{{\boldsymbol{U}}^{\mathrm{T}}}{\boldsymbol{H}}(1){\boldsymbol{V}})^{k - 1}} \cdot {{\boldsymbol{S}}^{{\mathbf{ - 1}}}}{{\boldsymbol{U}}^{\mathrm{T}}}{\boldsymbol{H}}(0){{\boldsymbol{E}}_{\boldsymbol{L}}}= \\ & {{\boldsymbol{E}}_{\boldsymbol{M}}}{\boldsymbol{H}}(0){\boldsymbol{V}}{{\boldsymbol{S}}^{{\mathbf{ - 1}}/2}} \cdot {({{\boldsymbol{S}}^{{\mathbf{ - 1}}/2}}{{\boldsymbol{U}}^{\mathrm{T}}}{\boldsymbol{H}}(1){\boldsymbol{V}}{{\boldsymbol{S}}^{{\mathbf{ - 1}}/2}})^{k - 1}} \cdot\\ &{{\boldsymbol{S}}^{{\mathbf{ - 1}}/2}}{{\boldsymbol{U}}^{\mathrm{T}}}{\boldsymbol{H}}(0){{\boldsymbol{E}}_{\boldsymbol{L}}}。\\ \end{split} $ |
考虑到式(28),进一步化简上式:
| $ {\boldsymbol{h}}(k) = \underbrace {{{\boldsymbol{E}}_{\boldsymbol{M}}}{\boldsymbol{U}}{{\boldsymbol{S}}^{{\mathbf{1}}/2}}}_{\mathbf{G}} \cdot {(\underbrace {{{\boldsymbol{S}}^{{\mathbf{ - 1}}/2}}{{\boldsymbol{U}}^{\mathrm{T}}}{\boldsymbol{H}}(1){\boldsymbol{V}}{{\boldsymbol{S}}^{{\mathbf{ - 1}}/2}}}_{{{\mathbf{A}}_1}})^{k - 1}} \cdot \underbrace {{{\boldsymbol{S}}^{{\mathbf{1}}/2}}{{\boldsymbol{V}}^{\mathrm{T}}}{{\boldsymbol{E}}_{\boldsymbol{L}}}}_{{{\mathbf{B}}_1}},$ |
对比式(23)
| $ {\boldsymbol{G}} = {{\boldsymbol{E}}_{\mathbf{M}}}{\boldsymbol{U}}{{\boldsymbol{S}}^{{\mathbf{1}}/2}} ,$ | (30) |
| $ {{\boldsymbol{A}}}_1 = {{\boldsymbol{S}}^{{{ - 1}}/2}}{{\boldsymbol{U}}^{\mathrm{T}}}{\boldsymbol{H}}(1){\boldsymbol{V}}{{\boldsymbol{S}}^{{{ - 1}}/2}},$ | (31) |
| $ {{\boldsymbol{B}}_1} = {{\boldsymbol{S}}^{{{1}}/2}}{{\boldsymbol{V}}^{\mathrm{T}}}{{\boldsymbol{E}}_{\mathbf{L}}}。$ | (32) |
式中:S为2n×2n矩阵,可以得到G为M×2n矩阵,A1为2n×2n矩阵,B1为2n×L矩阵,为系统的最小实现为[A1,B1,G]。
设系统矩阵A的特征值矩阵为
由前文
因此,A1的特征向量与A相同,A1的特征值矩阵为
ERA模态参数识别的步骤如下:
步骤1 根据特征值分解,求解A1的特征值矩阵Z和特征向量矩阵
步骤2 求解系统矩阵A的特征值矩阵
| $ {\lambda _i} = \frac{1}{{\Delta t}}\ln {z_i},{\text{ (}}i = 1,2, \cdots ,2n{\text{)}}。$ | (33) |
步骤3 根据模态理论,得到系统的模态频率和阻尼比:
| $ {\omega _i} = \sqrt {{Re} {{({\lambda _i})}^2} + {Im} {{({\lambda _i})}^2}},$ | (34) |
| $ {\zeta _i} = - \frac{{{Re} ({\lambda _i})}}{{{\omega _i}}}{\text{ }},(i = 1,2, \cdots ,2n)。$ | (35) |
步骤4 计算系统振型:
| $ {\boldsymbol{\varPhi }} = {\boldsymbol{G\varPsi }} 。$ | (36) |
NExT-ERA模态识别方法将自然激励法和特征系统实现法二者结合,实现仅利用响应数据识别分析得到模态参数。
1.4 模态评判引入模态幅值相干系数MAC和模态相位共线性系数MPC来区分NExT-ERA模态识别中的有效模态和噪声模态。
1)模态幅值相干系数MAC
第i阶模态运动的理想模态幅值时间序列为
第i阶模态运动的实测模态幅值时间序列为
模态幅值相干系数MAC为:
| $ MA{C_i} = \frac{{\left| {{{\boldsymbol{q}}_i}{{\boldsymbol{p}}_i}} \right|}}{{{{(\left| {{{\boldsymbol{q}}_i}{\boldsymbol{q}}_i^{\mathbf{H}}} \right|\left| {{\boldsymbol{p}}_i^{\mathbf{H}}{{\boldsymbol{p}}_i}} \right|)}^{1/2}}}}\begin{array}{*{20}{c}},\end{array}(i = 1,2, \cdots ,2n)。$ |
2)模态相位共线性系数MPC
系统振型矩阵为:
| $ {\boldsymbol{\varPhi }} = [\begin{array}{*{20}{c}} {{{\boldsymbol{\varPhi }}_1}}&{{{\boldsymbol{\varPhi }}_2}}& \cdots &{{{\boldsymbol{\varPhi }}_{2n}}} \end{array}]。$ |
定义以下各式:
| $ {C_{xx}} = {Re} {({{{\boldsymbol{\varPhi }}}_i})^{\mathrm{T}}}{Re} ({{{\boldsymbol{\varPhi }}}_i}),$ |
| $ {C_{yy}} = {Im} {({{{\boldsymbol{\varPhi }}}_i})^{\mathrm{T}}}{Im} ({{{\boldsymbol{\varPhi }}}_i}),$ |
| $ {C_{xy}} = {Re} {({{{\boldsymbol{\varPhi }}}_i})^{\mathrm{T}}}{Im} ({{{\boldsymbol{\varPhi }}}_i})。$ |
式中:
令
| $ MP{C_i} = {\left( {\frac{{{\chi _1} - {\chi _2}}}{{{\chi _1} + {\chi _2}}}} \right)^2} 。$ |
MPCi表示的是模态振型实虚部之间的关系,反映了识别模态振型距离0或180°的相位偏差。当MPCi值趋近1时表示第i阶模态为系统模态。
2 试验分析 2.1 试验流程试验所用自由板尺寸为590 mm×370 mm ×8 mm,测点布置如图1所示,共设置35个测点,激振点为25号测点,安装激振器和加速度传感器,搭建振动测试平台。试验采用DHDAS5927N动态信号采集分析系统,采样频率 5120 Hz。激励力为扫频信号,频带为10~1000 Hz。

|
图 1 自由板测点、激振点位置示意图 Fig. 1 The free plate with measuring point and excitation point |
在Ansys中对自由板进行仿真分析,参数设置见表1。选取solid185单元,按实测尺寸590 mm×370 mm ×8 mm建立模型,网格尺寸设为4 mm,进行模态计算。
|
|
表 1 仿真计算参数设置 Tab.1 parameters of simulation analysis |
根据以上参数设置,计算得到自由板仿真分析频率如表2所示。
|
|
表 2 EMA、NExT-ERA、仿真分析结果对比 Tab.2 comparison of EMA、NExT-ERA and simulation analysis |
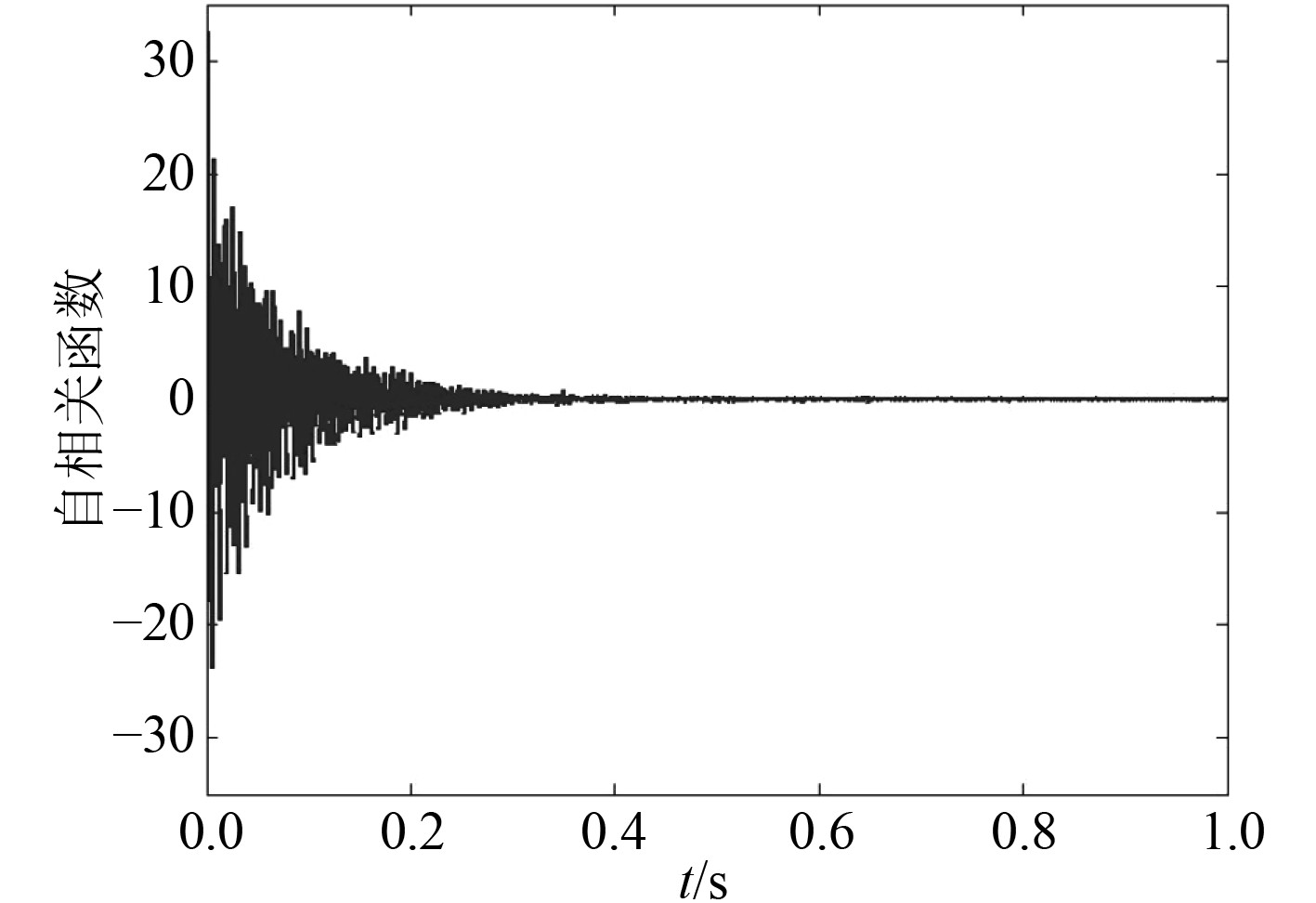
NExT-ERA模态分析在Matlab中编程完成。根据采集到的时域信号,分段进行自相关、互相关计算后平均,得到35个测点两两之间的互相关函数,图2为25号的测点的自相关函数。
|
图 2 25号测点自相关函数 Fig. 2 The auto-correlation function of No.25 measure point |
选取
| $ {\boldsymbol{H}}(0) = {{\boldsymbol{U}}_0}{{\boldsymbol{S}}_0}{{\boldsymbol{V}}_0}^{\mathrm{T}} 。$ |
取系统阶数n=50,那么取

|
图 3 1阶振型 Fig. 3 The shape of the first order |
|
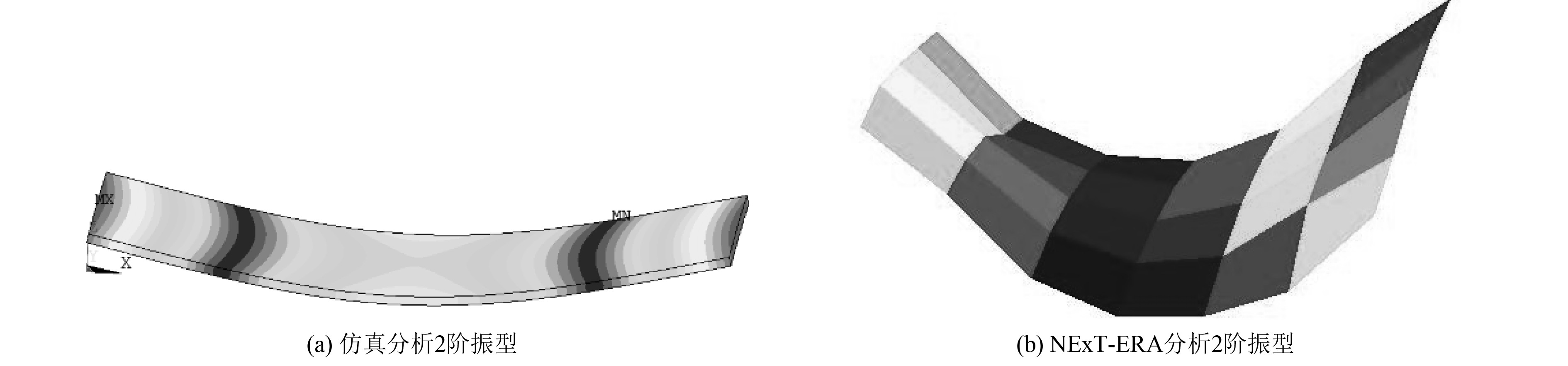
图 4 2阶振型 Fig. 4 The shape of the second order |
|
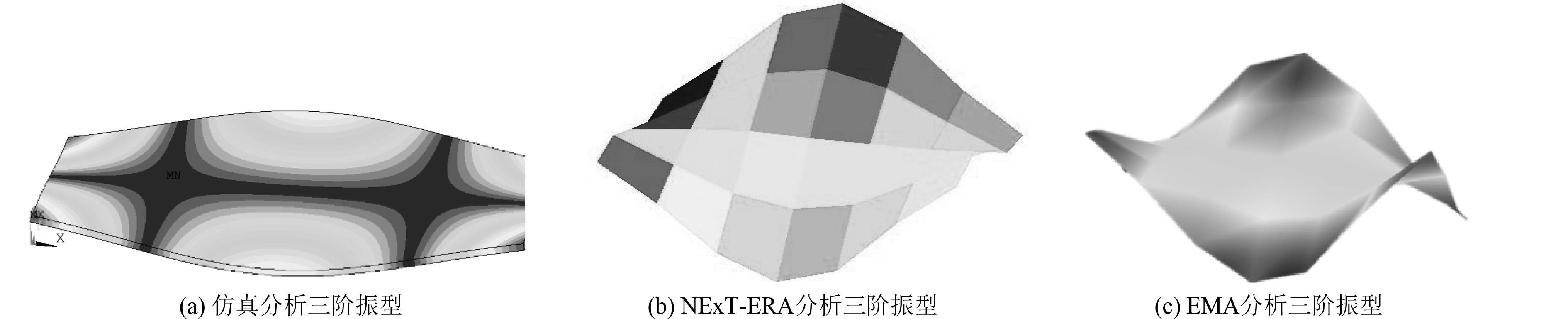
图 5 3阶振型 Fig. 5 The shape of the third order |

|
图 6 4阶振型 Fig. 6 The shape of the forth order |

|
图 7 5阶振型 Fig. 7 The shape of the fifth order |

|
图 8 6阶振型 Fig. 8 The shape of the sixth order |
观察图3~图8,NExT-ERA法振型识别结果与Ansys仿真模拟相似,从1阶到6阶振型识别良好,没有缺失振型。反观,EMA法振型识别结果,其1阶、3阶至6阶振型与仿真结果相似,但是,缺失2阶振型。
以Ansys模拟仿真结果为标准,对比分析NExT-ERA法、EMA法频率识别误差,如表3所示。可知,NExT-ERA法、EMA法频率识别精度误差在5%以内。NExT-ERA法前三阶模态频率误差小于3%,且随模态阶数的增长,频率误差基本呈现增大趋势。EMA法1阶、3阶、4阶模态小于3%,但其缺失2阶模态。同NExT-ERA法相仿,频率误差基本随模态阶数增大而增大。
|
|
表 3 EMA、NExT-ERA频率误差分析 Tab.3 error analysis of EMA、NExT-ERA on frequencies |
根据自由板振动模态试验及结果分析,可得出以下结论:
1)实验表明NExT-ERA模态识别理论成立,可以只利用结构的响应进行模态参数识别。在运行模态分析中,用互相关函数代替脉冲响应函数的做法可行。
2)NExT-ERA法对EMA法没有识别出的模态仍具有良好的识别效果,反映了NExT-ERA法具有更强的适应性和广阔的应用前景。
3)NExT-ERA法识别出的模态频率精确,与仿真分析频率相比,前六阶模态频率误差5%以内,前三阶频率误差可降至3%以内,满足模态识别对频率的精度要求。
4)NExT-ERA法识别出的振型良好,能够准确的反应结构振动。
5)NExT-ERA法模态识别精度随着模态阶数的增大呈现恶化趋势。
| [1] |
AKAIKE H. Power spectrum estimation through autoregressive model fitting[J]. Annals of the Institute of Statistical Mathematics, 1969, 21(1): 407-419. DOI:10.1007/BF02532269 |
| [2] |
BOX G E P, JENKINS G M. Time series analysis: Forecasting and control[J]. Holden-Day Series in Time Series Analysis, 1976, 14(2): 199-201. |
| [3] |
GAUTIER P E, GONTIER C, SMAIL M. Robustness of an arma identification method for modal analysis of mechanical systems in the presence of noise[J]. Journal of Sound & Vibration, 1995, 179(2): 227-242. |
| [4] |
COLE H A. Method and apparatus for measuring the damping characteristic of structure[J]. United State patent, 1971 (3): 620 069
|
| [5] |
IBRAHIM S R. Random decrement technique for modal identification of structures[J]. Journal of Spacecraft & Rockets, 1977, 14(11): 696. |
| [6] |
张西宁, 屈梁生. 一种改进的随机减量信号提取方法[J]. 西安交通大学学报, 2000, (34): 106-107+110. DOI:10.3321/j.issn:0253-987X.2000.03.025 |
| [7] |
黄方林, 何旭辉, 陈政清, 等. 随机减量法在斜拉桥拉索模态参数识别中的应用[J]. 机械强度, 2002, (3): 331−334.
|
| [8] |
IBRAHIM S R, MIKULCIK E C. A method for the direct identification of vibration parameters from the free response[J]. Shock and Vibration Bulletin, 1977, 47: 183−198.
|
| [9] |
JAMES G H. Extraction of modal parameter from an operating hawt using the natural excitation technique (NexT)[C]// 13th ASME Wind Energy Symposium, New Orleans, L A , 1994.
|
| [10] |
JAMES G H, CARNE T G, EDMUNDS R S. STARS missile-modal analysis of first- flight data using the natural excitation technique, NexT Proceeding of SPIE[J]. The International Societr of Optical Engineering, 1993, 154(4): 749−757
|
| [11] |
李华新. 环境激励下工程结构模态参数辨识研究[D]. 重庆: 重庆大学, 2013.
|
| [12] |
孙乐. 基于运行模态分析的板架结构模态识别研究[D]. 武汉: 华中科技大学, 2017.
|
| [13] |
李长玉, 余莎丽, 林子涵, 等. 自然激励下某电动汽车白车身模态参数识别[J]. 电子测量与仪器学报, 2020, 34(8): 167-173. |
| [14] |
卞超. 飞机紊流激励下的模态分析和颤振边界预测方法研究[D]. 南京: 南京航空航天大学, 2021.
|
 2024, Vol. 46
2024, Vol. 46
