2. 郑州科技学院 大数据与人工智能学院,河南 郑州 450064
2. College of Big Data and Artificial Intelligence, Zhengzhou University of Science and Technology, Zhengzhou 450064, China
随着船舶制造强国对船舶模块化技术的不断开发以及应用,船舶模块化设计方法已经可以极大地缩短新型武器及装备从设计制造到舾装的时间,促使船舶的设计制造能够快速地应对现代快速变化的战争需求,因此基于船舶的模块化设计技术,海军可以根据具体的战争情况对已有的船舶进行快速的改装,以应对临时修改的任务需求[1]。针对我国船舶种类多、任务量大以及经费有限等问题,模块化的船舶设计方法可以解决这些问题[2]。利用模块化的设计方法将各类设备以及武器设计成独立的单元,可以实现不同的任务需求、提升船舶在作战过程中的生存率、降低船舶在制造过程中的成本、缩短新型船舶的研发周期等[3]。由于我国的模块化设计技术起步比较晚,因此主要是对船舶的功能和标准化方面进行模块设计,没有全面系统地考虑船舶模块化设计的制造环境以及建造方法[4]。本文基于船舶的模块化空间设计,分析了船舶结构相关性,这有助于我国船舶结构设计技术的快速发展。
1 模块化空间设计 1.1 模块划分方法在对船舶空间进行模块化分割的过程中,需要考虑到功能、几何以及物理等方面的相关性,其相关矩阵见下式:
| $ {{\boldsymbol{R}}_g}\left( {i,j} \right) = \left[ {\begin{array}{*{20}{c}} {{R_g}\left( {1,1} \right)}&{{R_g}\left( {1,2} \right)}& \ldots &{{R_g}\left( {1,n} \right)} \\ {{R_g}\left( {2,1} \right)}&{{R_g}\left( {2,2} \right)}& \ldots &{{R_g}\left( {2,n} \right)} \\ \vdots & \vdots & \ddots & \vdots \\ {{R_g}\left( {n,1} \right)}&{{R_g}\left( {n,2} \right)}& \ldots &{{R_g}\left( {n,n} \right)} \end{array}} \right]\text{。} $ | (1) |
子相关矩阵构建的零部件i和零部件j之间的相关矩阵如下式:
| $ {\boldsymbol{R}}\left( {i,j} \right) = {{\boldsymbol{R}}_g}\left( {i,j} \right){\mu _g} + {{\boldsymbol{R}}_j}\left( {i,j} \right){\mu _i} + {{\boldsymbol{R}}_w}\left( {i,j} \right){\mu _w}\text{。} $ | (2) |
式中:μg、μi、μw分别为功能、几何以及物理的相关性比例系数。当船舶结构设计中存在n个量纲或者量级不同的指标的时候,在模块划分计算的时候可能会出现偏向于数量级比较大的指标,而忽略数量级比较小的指标,这使得船舶结构模块划分没有统一的指标分类尺度[5]。为了能够降低由于船舶结构模块特性的数量级不同而产生的影响,本文对船舶结构模块的各类指标进行标幺化处理,这样可以将船舶结构模块的每一个指标统一到相同的数据特征范围内,标幺化的方法如式(3)所示,可知,其结果范围为[0, 1]。
| $ x = \frac{{x' - {{x'}_{\min }}}}{{{{x'}_{\max }} - {{x'}_{\min }}}}\text{。} $ | (3) |
式中:x′为实际数据,如果x′=x′max,那么x=1;如果x′=x′min,那么x=0。通常以夹角的余弦值来计算统计量rij,假定2个分类对象xi和xj之间的夹角为αij,并且规定该夹角的取值范围为0°≤α≤180o,则夹角αij的余弦值计算式为:
| $ \cos {\alpha _{ij}} = \frac{{\left( {{x_i},{x_j}} \right)}}{{\left\| {{x_i}} \right\| \cdot \left\| {{x_j}} \right\|}}\text{。} $ | (4) |
式中:
| $ \left( {{x_i},{x_j}} \right) = \sum\limits_{k = 1}^m {{x_{ik}}{x_{jk}}} \text{,} $ | (5) |
| $ \left\| {{x_i}} \right\| = \sqrt {\sum\limits_{k = 1}^m {x_{ik}^2} } \text{,} $ | (6) |
| $ \left\| {{x_j}} \right\| = \sqrt {\sum\limits_{k = 1}^m {x_{jk}^2} } \text{。} $ | (7) |
通过式(4)中的夹角余弦值,可以对不同的船舶模块化样本之间的差异进行描述,很明显,当2个样本的所有指标都一样的时候,式(4)计算得到的结果等于1,即式(4)的结果越接近1,则表示2个船舶模块的样本差异越小;式(4)的结果越接近−1,则表示2个船舶模块的样本差异越大。因此该余弦值又被称为不同样本间的相似系数。通过标定可以得到模糊矩阵,如式(8)所示。
| $ \tilde R = \left[\begin{array}{llll} r_{11} & r_{12}& \cdots & r_{1n}\\ r_{21} & r_{22}& \cdots & r_{2n}\\ \vdots & \vdots& \ddots & \vdots\\ r_{n1} & r_{n2}& \cdots & r_{nn}\end{array}\right]\text{,} $ | (8) |
通过式(8)的模糊矩阵,可以对船舶模块样本之间的相似关系进行描述,但是该矩阵只存在自反性以及对称性,没有传递性。基于模糊数学理论可以知道,将模糊相似矩阵转换成模糊等价矩阵则可以实现聚类,其方法如式(9)所示。
| $ \tilde R^2_{ij} = \vee (r_{ij}\wedge r_{ji})\text{,} $ | (9) |
基于式(9),设置不同的阈值,则可以获得不同的截矩阵,进一步则可以获得动态聚类结果。
1.2 模糊综合评判因素集的表示方法如下式:
| $ U = \left\{ {{u_1},{u_2},\cdots,{u_n}} \right\}\text{。} $ | (10) |
式中:un为影响因素。所有权重系数构成的集合为:
| $ \tilde A = \left( {{a_1},{a_2},\cdots,{a_n}} \right)\text{。} $ | (11) |
式中:an为因素un的权重系数,体现了因素un在评判过程中的重要程度,并且所有权重系数需要满足:
| $ {\sum\limits_{i = 1}^n {{a_i} = 1} },{{a_i} \geqslant 0} \text{。} $ | (12) |
一般可以使用穷尽成对比较法来确定权重系数,将任意2个因素的重要性进行比较,其结果主要有3种,如式(13)所示。为了避开某些因素的权重值等于0的情况,一般假定存在一个虚拟的因素,使得所有的实际因素都比该虚拟因素重要。
| $ {u}_{i,j}=\left\{\begin{array}{ll}1,{u}_{i}比{u}_{j}重要,\\ 0.5,{u}_{i}和{u}_{j}同等重要,\\ 0,{u}_{i}没有{u}_{j}重要。\end{array} \right.$ | (13) |
如果将所有的比较结果都考虑进去,那么所有因素的比较结果的和计算式为:
| $ \sum\limits_{i = 1}^{n + 1} {\sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne i \end{subarray}} ^{n + 1} {{u_{i,j}}} = \frac{{n\left( {n + 1} \right)}}{2}} 。$ | (14) |
每个因素的权重值计算式为:
| $ {a_i} = \frac{{\displaystyle\sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne i \end{subarray}} ^{n + 1} {{u_{i,j}}} }}{{\displaystyle\sum\limits_{i = 1}^{n + 1} {\displaystyle\sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne i \end{subarray}} ^{N + 1} {{u_{i,j}}} } }}\text{。} $ | (15) |
当因素比较多的时候,穷尽成对比较法的计算量将会很大,在这种情况下,可以采用排序成对比较法,该方法先将所有因素按照重要性进行排序,然后当前因素只和前一个因素进行比较,则每个权重值可以用式(16)来表示。
| $ {a'_i} = \frac{\overline u}{\displaystyle\sum\limits_{i = 1}^{n} \overline u_i }\text{,} $ | (16) |
基于自由速度理论可知,机械设备的内源激振力存在不变性,利用面板加速度以及振动响应,可以反演出一定加速度情况下的机械设备的内源激振力[6]。由强迫振动理论可以知道,非平衡激振力系统的动力学数学模型计算式为:
| $ m\ddot x + c\dot x + kx = F\text{。} $ | (17) |
反演力的计算方法如式(18)所示。基于单位作用力对面板加速度响应进行解算,则可以得到船舶模块化设备中内源激振力。
| $ {F_T} = \frac{{{a_T}}}{{{a_1}}}\text{。} $ | (18) |
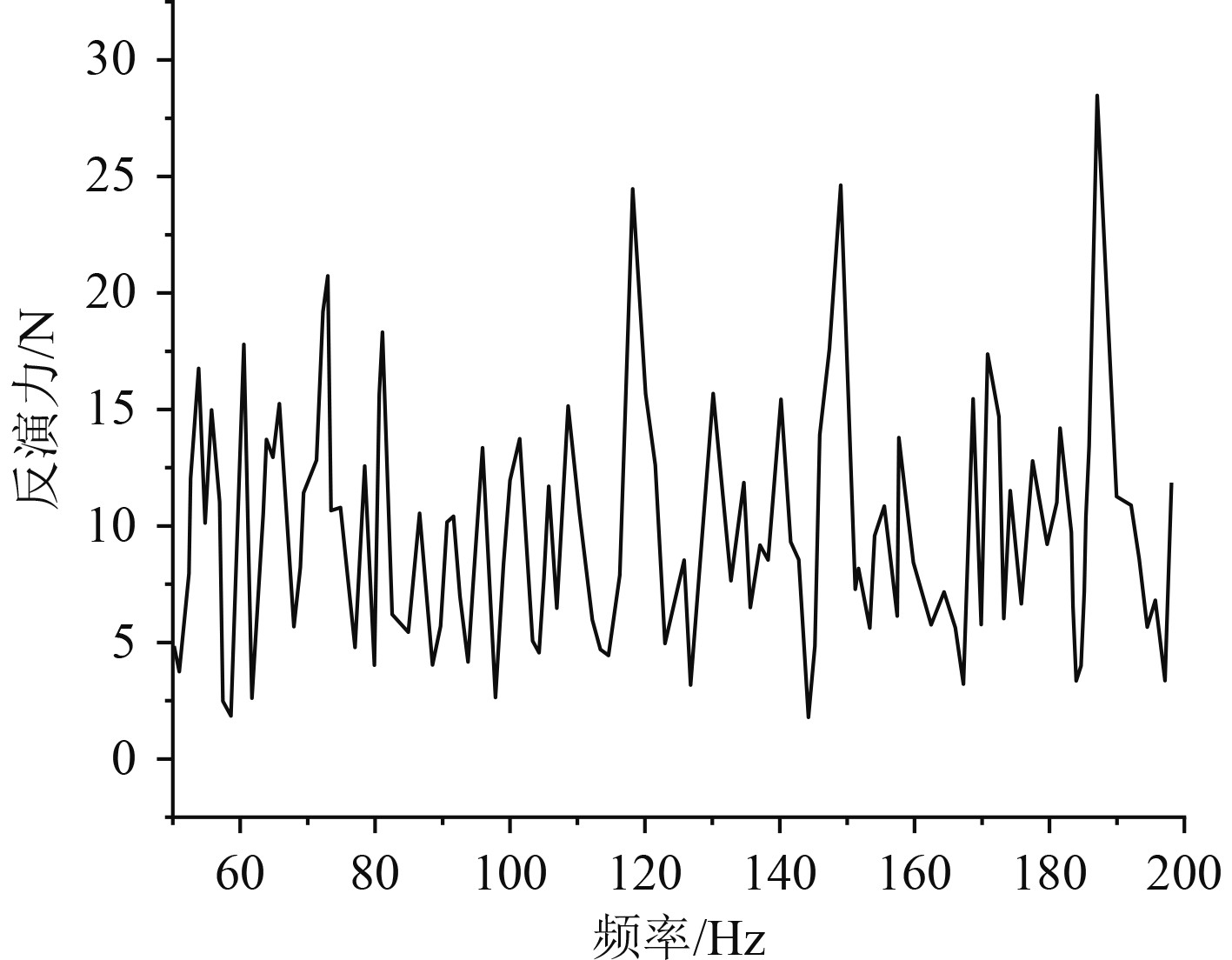
不同频率下反演力的变化曲线如图1所示,从图中能够看出,反演力的最大值可以达到27.5 N。
|
图 1 反演力随频率的变化曲线 Fig. 1 Inversion force versus frequency variation curve |
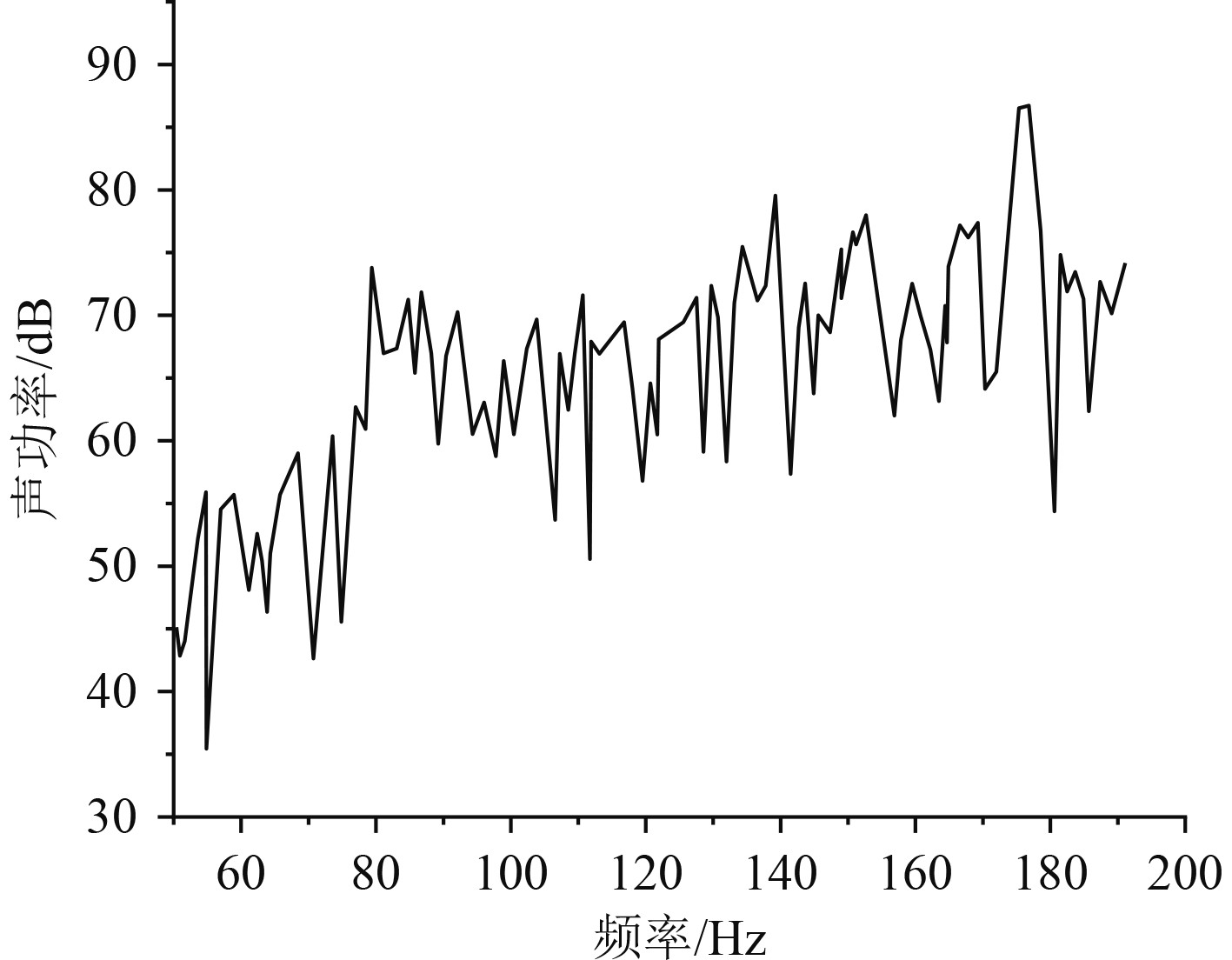
不同频率下声功率的变化曲线如图2所示,可知,随着频率的增大,声功率有着变大的趋势,最大值可以达到85 dB。本文基于有限元频谱技术对船舶模块化结构进行低频振动分析。船舶的模块化结构利用六面体单元进行构建。本文设置船舶舱外板厚度为0.012 m,弹性模量为210 GPa,泊松比为0.3,密度为7850 kg/m3。
|
图 2 声功率随频率的变化曲线 Fig. 2 The curve of sound power variation with frequency |
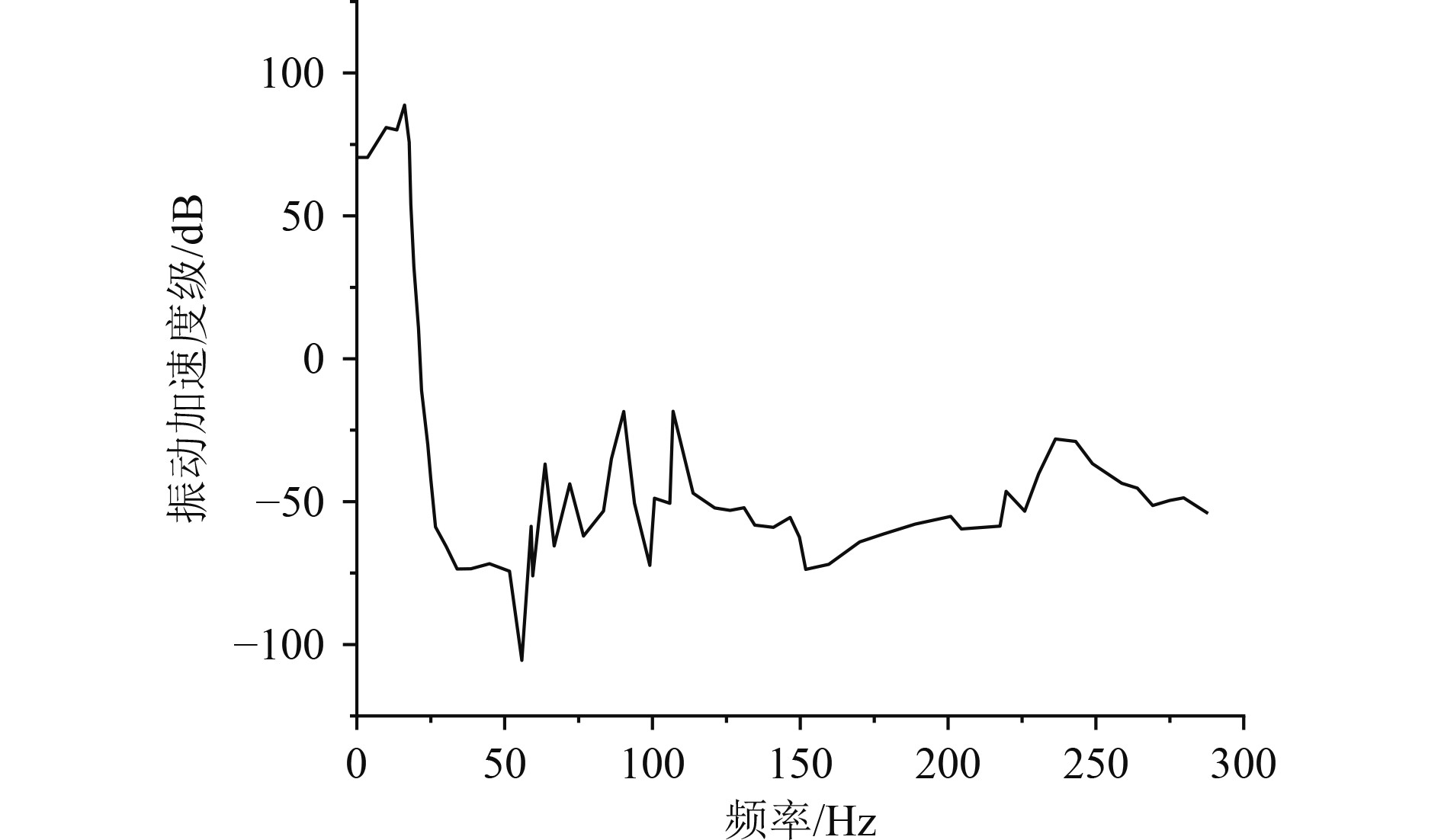
本文基于有限元软件构建的船舶模块化的舱段模型,其最大的单元尺寸是50 mm,并且整个模块一共划分出了56622个单元,有49393个节点数,并且其阻尼系数为0.01。在一定的加速度载荷情况下,使用大质量法对船舶舱段面板的振动加速度响应进行解算,图3为获得的不同频率下的振动加速度级曲线,可知,振动加速度级一开始会上升,然后迅速降低,然后在−50 dB附近上下震荡。
|
图 3 不同频率下振动加速度级的变化曲线 Fig. 3 The variation curve of vibration acceleration level at different frequencies |
以10 N振幅的作用力为基础,对船舶模块化的舱段模型进行重构,并进行动力学响应分析,将振级落差作为评价指标,船舶模块化的舱段模型中任意2个点之间的振级落差计算式为:
| $ VLD_{\alpha \beta }^i = 20\lg \left( {\frac{{a_\alpha ^i}}{{a_\beta ^i}}} \right)\text{。} $ | (19) |
式中:
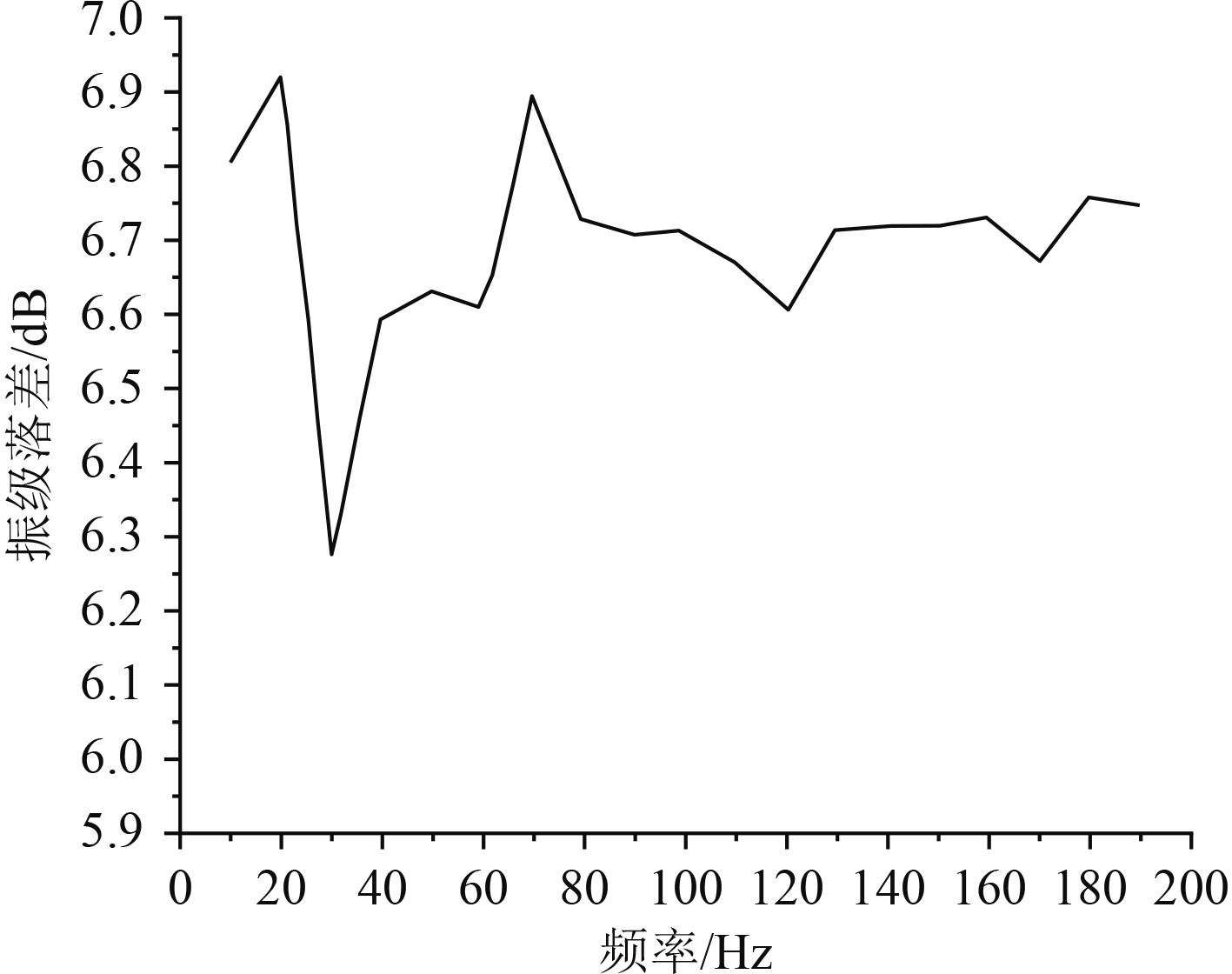
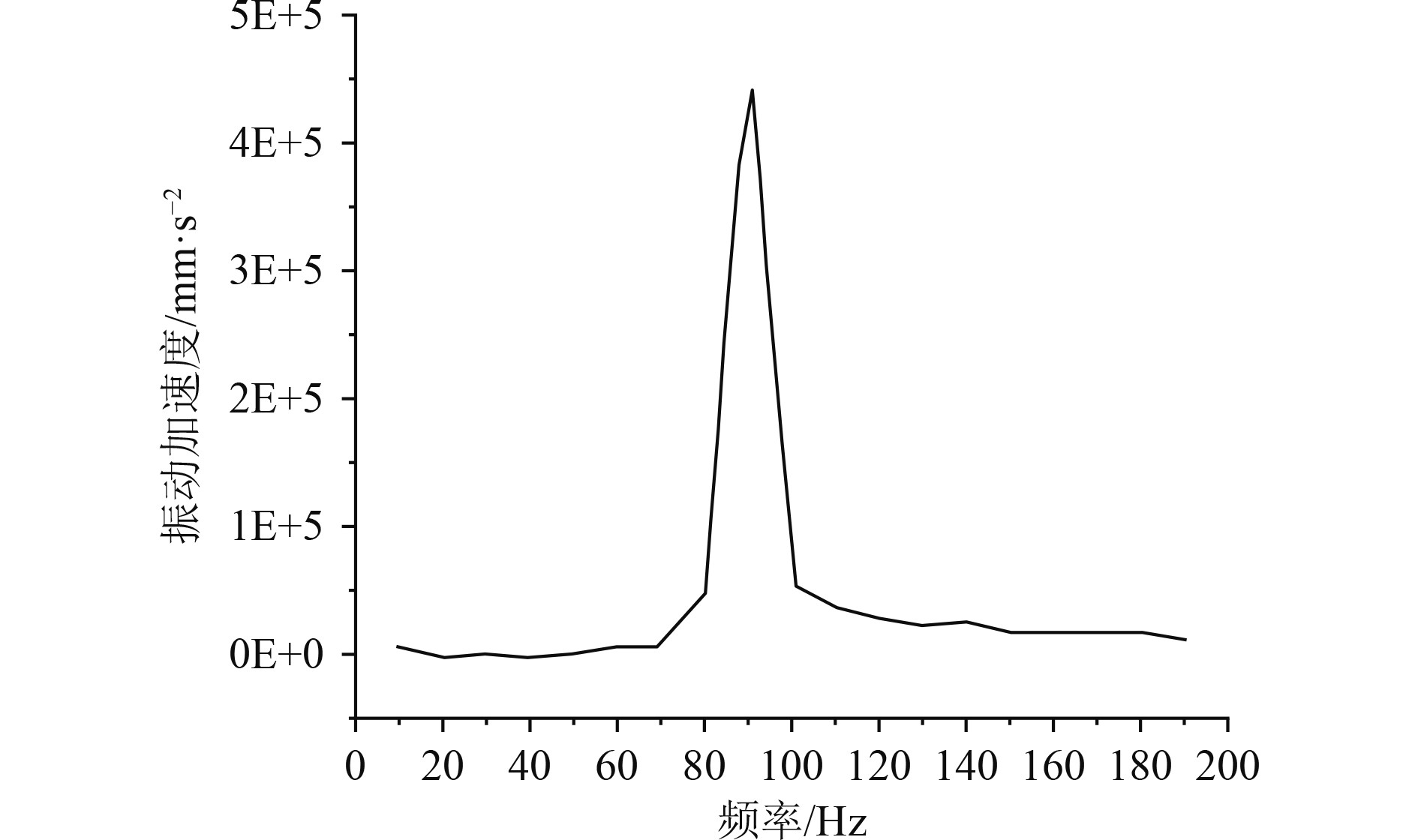
船舶模块化舱段的振级落差随频率的变化曲线如图4所示。可知,最小振级落差出现在频率为30 Hz的地方,最小值为6.25 dB。图5为不同频率下的振动加速度曲线,可以看出,最大的振动加速度约为4.5×105 mm/s2。
|
图 4 振级落差随频率的变化曲线 Fig. 4 The curve of vibration level drop with frequency |
|
图 5 不同频率下振动加速度的变化曲线 Fig. 5 The variation curve of vibration acceleration at different frequencies |
武器在水下爆炸的时候会产生气泡状的冲击波,约53%的能量以冲击波的能量散发出去,剩余的能量则以气泡脉动的形式释放[7]。实战显示,船舶上的模块化设备的破坏,主要是由冲击波造成。冲击波压力的计算式为:
| $ P\left( t \right) = {P_m} \cdot {e^{ - \frac{1}{\lambda }}}\text{。} $ | (20) |
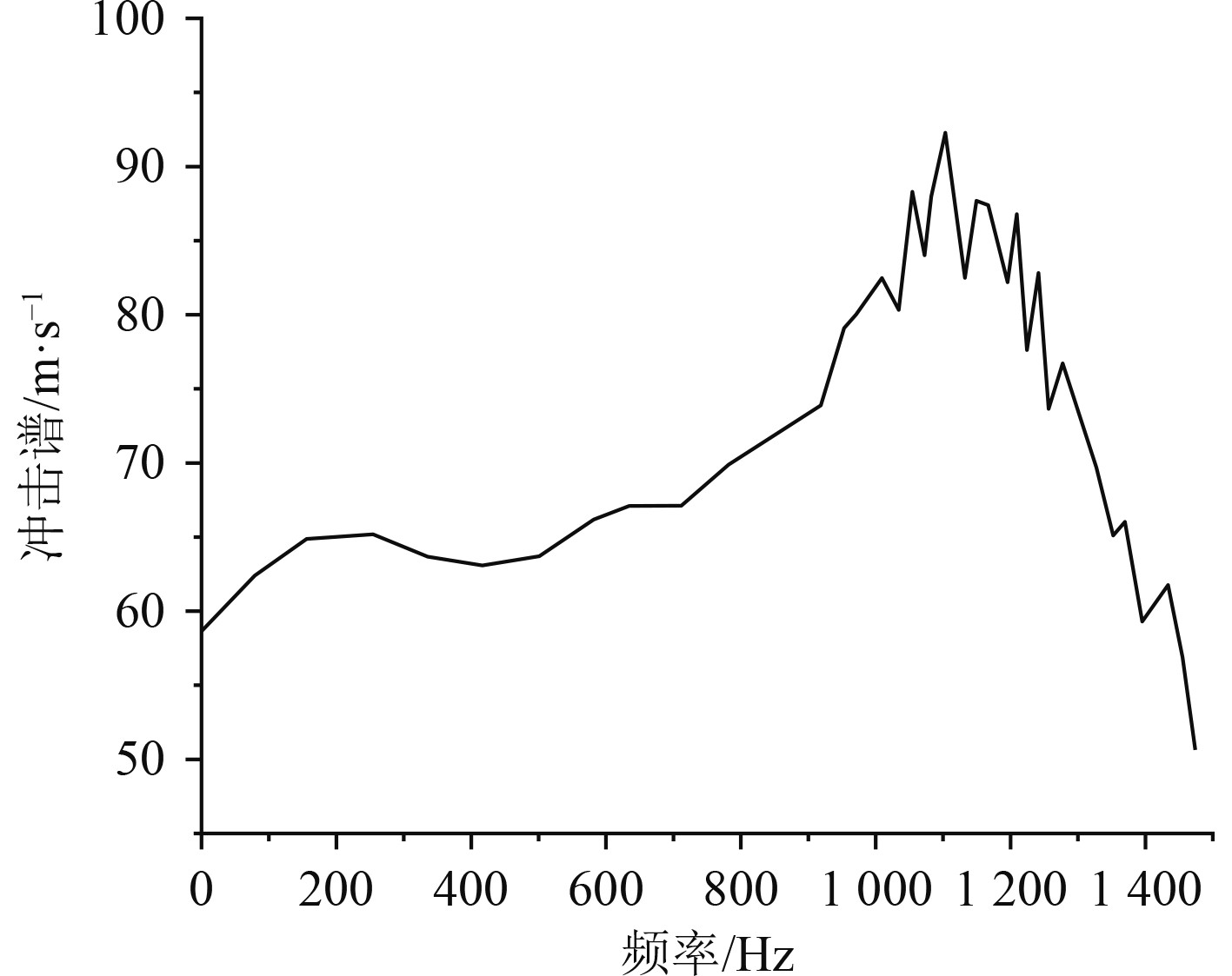
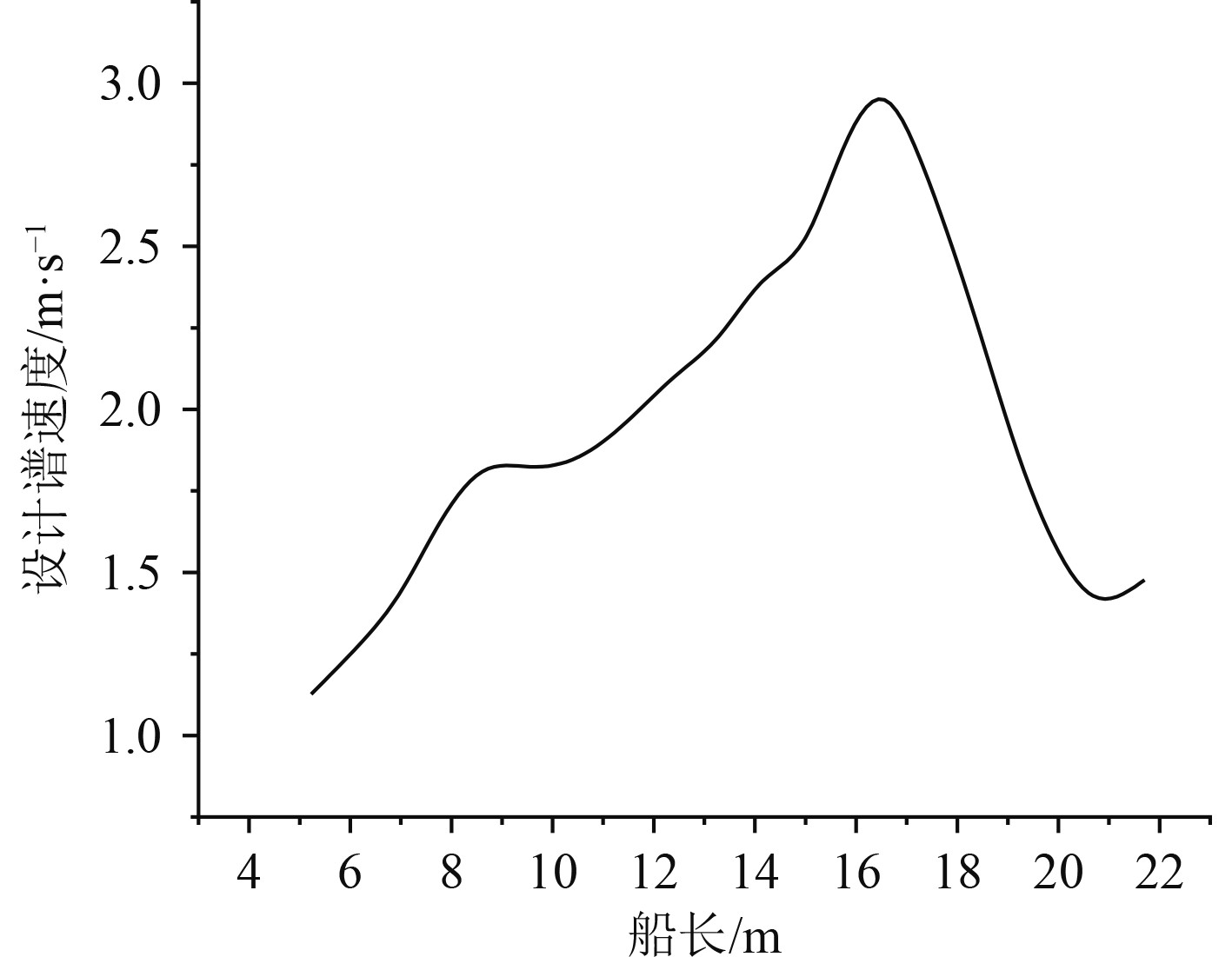
本文基于Abaqus软件对水下爆炸进行模拟分析,同时选择炸药量为1000 kgTNT。不同频率下冲击谱的变化曲线如图6所示,可知,最大冲击谱约为90 m/s。图7设计为谱速度随船舶长度的变化曲线,可知,最大的设计谱速度出现在船长约16.5 m的地方,最大值约为3 m/s。
|
图 6 冲击谱随频率的变化曲线 Fig. 6 The variation curve of shock spectrum with frequency |
|
图 7 设计谱速度随船舶长度的变化曲线 Fig. 7 Design the curve of spectral velocity variation with ship length |
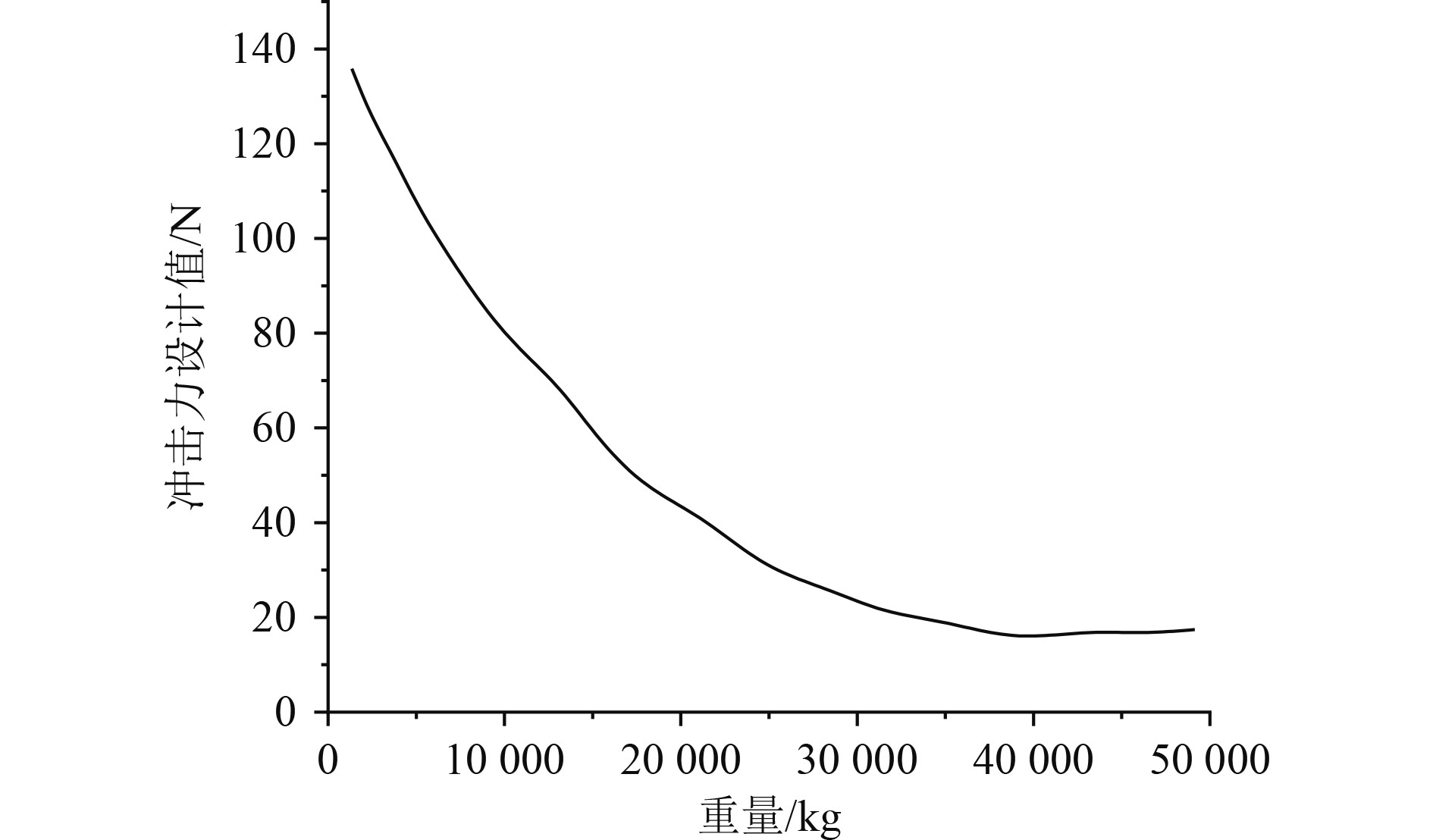
本文对船舶的冲击环境预测模型进行预测学习。得到的预测收敛值随迭代次数的曲线如图8所示,可知,预测收敛值随着迭代次数的增加会迅速降低,在迭代次数700左右,达到收敛的目的。不同重量下冲击力设计值的变化曲线如图9所示,可知,冲击设计值随着重量的变大而逐渐降低。

|
图 8 不同迭代次数下预测收敛值的变化曲线 Fig. 8 The variation curve of predicted convergence value under different iteration times |
|
图 9 冲击力设计值随重量的变化情况 Fig. 9 The variation of impact force design value with weight |
船舶的制造生产过程十分复杂,并且随着现代电子信息技术的快速升级,船舶的设计制造技术也在不断的更迭创新,其目的是为了利用先进的集成制造方法提升船舶运输业的经济效益,本文基于模块化空间设计,对船舶结构相关性进行分析,这有助于我国船舶技术的快速发展。
| [1] |
李威, 杨德庆, 刘西安, 等. 船舶水下辐射噪声抑制的声振相关性方法[J]. 振动与冲击, 2023(42): 1-7+22. LI Wei, YANG Deqing, LIU Xian, et al. Acoustic-vibration correlation method for suppressing underwater radiated noise from ships[J]. Journal of Vibration and Shock, 2023(42): 1-7+22. |
| [2] |
金洪禹. 船舶系统声学性能影响因素研究[J]. 电声技术, 2023(1): 12-16. JIN Hongyu. Study on influencing factors of acoustic performance of ship system[J]. Audio Engineering, 2023(1): 12-16. |
| [3] |
朱全华, 张涛, 汪雪良, 等. 结构应力逆向推演模型及其不确定度定量分析[J]. 装备环境工程, 2023(31): 69-76. ZHU Quanhua, ZHANG Tao, WANG Xueliang, et al. Reverse deduction model of structural stress and quantitative analysis of its uncertainty[J]. Equipment Environmental Engineering, 2023(31): 69-76. |
| [4] |
毛致远, 段超伟, 宋浦, 等. 基于有效冲量的水下爆炸冲击波对平板结构的毁伤准则[J]. 高压物理学报, 2023(2): 1-10. MAO Zhiyuan, DUAN Chaowei, SONG Pu, et al. Criterion of Plate Structure Damage Caused by Underwater Explosion Shock Wave Based on Effective Impulse[J]. Chinse Journal of High Pressure Physics, 2023(2): 1-10. |
| [5] |
王凯, 王中一, 黄连忠, 等. 基于大数据及人工智能的船舶能效智能优化研究综述[J]. 中国航海, 2023(1): 155-162. WANG Kai, WANG Zhongyi, HUANG Lianzhong, et al. Advances in intelligent ship energy efficiency optimization with big data and AI[J]. Navigation of China, 2023(1): 155-162. DOI:10.3969/j.issn.1000-4653.2023.01.022 |
| [6] |
祝捍皓, 薛洋洋, 崔智强, 等. 船舶辐射噪声贝叶斯方法反演浅海底层结构及地声参数[J]. 声学学报, 2022(6): 765-776. ZHU Hanhao, XUE Yangyang, CUI Zhiqiangm, et al. Inversion of shallow seabed structure and geoacoustic parmeters with ship radiated noise Bayesian method[J]. ACta Acustica, 2022(6): 765-776. |
| [7] |
郑智育, 涂文晏, 廖金山. 船舶火灾爆炸危险性评估与预警系统[J]. 船舶科学技术, 2024(20): 165-169. ZHENG Zhiyu, TU Wenyan, LIAO Jinshan. Risk assessment and early warning system for ship fire and explosion[J]. Ship Science and Technology, 2024(20): 165-169. |
 2024, Vol. 46
2024, Vol. 46
