现有船舶大多以柴油和重油为主要燃料,会产生氮氧化物(NOx)、硫氧化物(SOx)和固体颗粒物等诸多大气污染物质,造成严重的环境污染。因此,需要引进更环保的替代性燃料[1 − 3]。氢能作为来源广、可再生的清洁能源,是未来船舶燃料的重要选择。相比于传统动力船舶,氢燃料电池船具有零排放、无污染、低噪音、高能效、易操作、维护成本低等诸多优势,具有极大的发展潜力[4 − 6]。但是,氢气是一种易燃、易爆气体,在制备、储存、运输和使用过程中均有潜在的泄漏爆炸风险[7]。近年来,国内外氢安全事故频发,甚至造成了重大的人员伤亡和财产损失,其安全问题不容忽视[8]。迄今为止,国内外学者研究了许多因素对氢气爆炸特性的影响,其中障碍物是研究最广泛的影响因素之一。
氢气意外泄漏后发生爆炸,湍流火焰传播过程中可能遇到各种障碍物(如舱室内放置的仪器设备等),火焰与障碍物之间会产生复杂的相互作用。丁信伟等[9]在半球形容器中进行了可燃气云爆炸实验。结果表明,障碍物会显著增强爆炸压力,峰值超压可达无障碍物时的10倍以上。Masri等[10]研究了氢气、液化石油气和压缩天然气通过障碍物时湍流火焰的压力变化,发现氢气火焰的峰值压力比其他燃料高一个数量级以上。Lv等[11]在方形管道内进行了氢气爆炸实验,得出了氢气当量比和障碍物位置对爆炸超压的影响。段强领等[12]研究了障碍物对高压氢气泄漏自燃特性的影响,发现三角形障碍物会提高氢气自燃的可能性。李西贵等[13]采用CFD模拟讨论了不同障碍物位置对高压氢气泄漏自燃过程的影响,发现障碍物产生的反射激波会使氢气自燃机制发生改变。李雪等[14]采用实验和数值模拟结合的方法研究了内置障碍物的封闭管道内氢-空气混合气的燃爆过程。Sheng等[15 − 16]利用大涡模拟(LES)研究了不同障碍物对爆燃火焰的影响,发现三角形障碍物引起的峰值超压比方形和圆形障碍物高7%和30%,障碍物布置在管道中心和管道四周分别导致了最大和最小的火焰传播速度和超压。以上研究为理解障碍物对氢气爆炸特性的影响提供了理论依据。此外,在实际应用中氢气意外泄漏,在重力场的作用下,空间中的氢气易形成具有浓度梯度的分层混合气[17],这种非均匀浓度场也会对氢气火焰传播和加速产生显著的影响。
综上所述,尽管已有学者开展了障碍物对氢气爆炸影响的研究,但对于具有浓度梯度的氢−空气混合物在有障碍物的管道内爆炸火焰行为的研究较少。本文使用非稳态雷诺平均纳维−斯托克斯方程技术研究了不同障碍物排列方式对非均匀氢气−空气混合物爆炸火焰形态和超压的影响。该研究可以为氢燃料电池船舶的安全规划和防爆提供理论参考。
1 数值方法 1.1 数学模型 1.1.1 控制方程本文采用非稳态压缩流雷诺平均纳维−斯托克斯方程组对氢气爆炸过程进行描述,该方程组包括质量、动量、能量守恒方程[18],分别表述如下:
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{\partial }{{\partial {x_i}}}\left( {\rho {u_i}} \right) = 0,$ | (1) |
| $ \frac{\partial }{{\partial t}}\left( {\rho {u_i}} \right) + \frac{\partial }{{\partial {x_j}}}\left( {\rho {u_j}{u_i}} \right) = - \frac{{\partial p}}{{\partial {x_j}}} + \frac{{\partial {\tau _{ij}}}}{{\partial {x_j}}} + \rho {g_i},$ | (2) |
| $ \frac{\partial }{{\partial t}}\left( {\rho E} \right) + \frac{\partial }{{\partial {x_j}}}\left( {\rho {u_j}{c_p}T + p} \right) = {\mu _i}\left( {\frac{{\partial p}}{{\partial {x_i}}}} \right) + \frac{{\partial {u_i}}}{{\partial {x_i}}}{\left( {{\tau _{ij}}} \right)_{e f f}} - \frac{{\partial {q_i}}}{{\partial {x_i}}} ,$ | (3) |
| $ pM = \rho RT 。$ | (4) |
式中:
使用SST (Shear-Stress Transport) k-ω湍流模型,湍流动能和耗散率由以下输运方程求得[19]:
| $ \frac{\partial }{{\partial t}}\left( {\rho k} \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho k{u_i}} \right) = \frac{\partial }{{\partial {x_j}}}\left( {{\Gamma _k}\frac{{\partial k}}{{\partial {x_j}}}} \right) + {G_k} - {Y_k} + {S_k} + {G_b},$ | (5) |
| $ \frac{\partial }{{\partial t}} \left( {\rho \omega } \right) + \frac{\partial }{{\partial {x_i}}} \left( {\rho \omega {u_i}} \right) = \frac{\partial }{{\partial {x_j}}} \left( {{\Gamma _\omega } \frac{{{\partial _\omega }}}{{\partial {x _j}}}} \right) + {G_\omega } - {Y_\omega } + {D_\omega } + {S_\omega } + {G_{\omega b}} ,$ | (6) |
式中:
| $ {D_\omega } = 2\left( {1 - {F_1}} \right)\rho \frac{1}{{\omega {\sigma _{\omega ,2}}}}\frac{{\partial k}}{{\partial {x_j}}}\frac{{\partial \omega }}{{\partial {x_j}}},$ | (7) |
| $ {F_1} = \tan {\text h} \left( {\varPhi _1^4} \right) ,$ | (8) |
| $ {\Phi _1} = \min \left[ {\max \left( {\frac{{\sqrt k }}{{0.09\omega y}},\frac{{500\mu }}{{\rho {y^2}\omega }}} \right),\frac{{4\rho k}}{{{\sigma _{\omega ,2}}D_\omega ^ + {y^2}}}} \right] ,$ | (9) |
| $ D_\omega ^ + = \max \left[ {2\rho \frac{1}{{{\sigma _{\omega ,2}}}}\frac{1}{\omega }\frac{{\partial k}}{{\partial {x_j}}}\frac{{\partial \omega }}{{\partial {x_j}}},{{10}^{ - 10}}} \right] 。$ | (10) |
式中:
湍流粘度由以下方程求得[20]:
| $ {\mu _t} = \frac{{\rho k}}{\omega }\frac{1}{{\max \displaystyle \left[ {\frac{1}{{{\alpha ^*}}},\frac{{S{F_2}}}{{{a_1}\omega }}} \right]}} ,$ | (11) |
| $ {F_2} = \tan {\text h} \left( {\varPhi _2^2} \right),$ | (12) |
| $ {\varPhi _2} = \max \left[ {2\frac{{\sqrt k }}{{0.09\omega y}},\frac{{500\mu }}{{\rho {y^2}\omega }}} \right] 。$ | (13) |
式中:
火焰传播过程可以通过求解反应进程变量
| $ \frac{\partial }{{\partial t}}\left( {\rho c} \right) + \nabla \cdot \left( {\rho {u_j}c} \right) = \nabla \cdot \left( {\left( {\frac{k}{{{C_p}}} + \frac{{{\mu _t}}}{{S{c_t}}}} \right)\nabla c} \right) + {\rho _u}{U_t}\left| {\nabla c} \right|。$ | (14) |
式中:
| $ {U_t} = A{\left( {{u^{'}}} \right)^{3/4}}U_l^{1/2}{\alpha ^{ - 1/4}}\ell _t^{1/4}。$ | (15) |
式中:
如图1所示,本文参考Lv等[11]的实验装置,建立了一个500 mm×100 mm的二维计算域,点火位置在管道左侧壁面中心。设计了3种不同排列方式的障碍物,分别为管道底部布置、管道两侧布置以及管道顶部布置。障碍物厚度为10 mm,阻塞比均为0.5,障碍物中心距点火源200 mm。参考Boeck等[23]的实验对氢气浓度梯度进行了模拟和验证。氢气从管道顶部注入,使管内混合物中氢气含量为化学计量比,随后氢气自由扩散形成具有浓度梯度的混合气。随着氢气不断扩散,浓度梯度越来越小,扩散一段时间后为均匀混合物。图2为扩散20 s时氢气浓度梯度分布曲线。混合物初始反应进程变量为0,初始压力为大气压力,初始温度为300 K。设置管道右侧为压力出口,障碍物边界和管壁为绝热无滑移壁面。
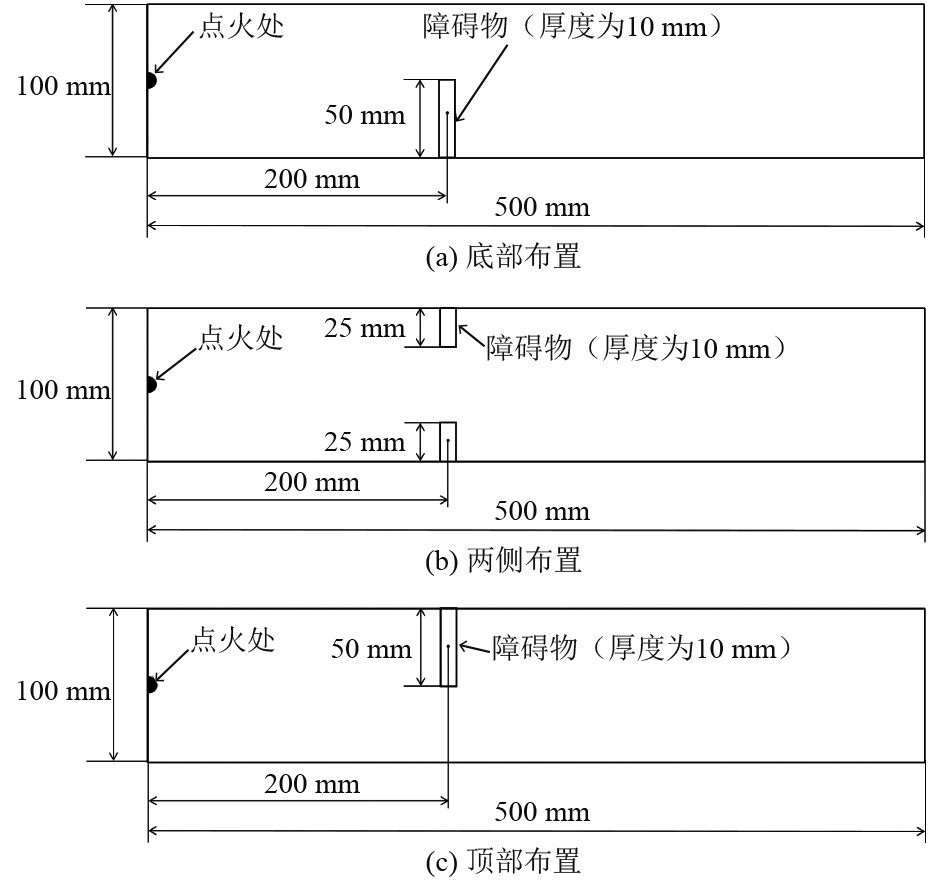
|
图 1 不同障碍物排列方式管道几何模型图 Fig. 1 Geometric model diagram of ducts with different obstacle arrangements |
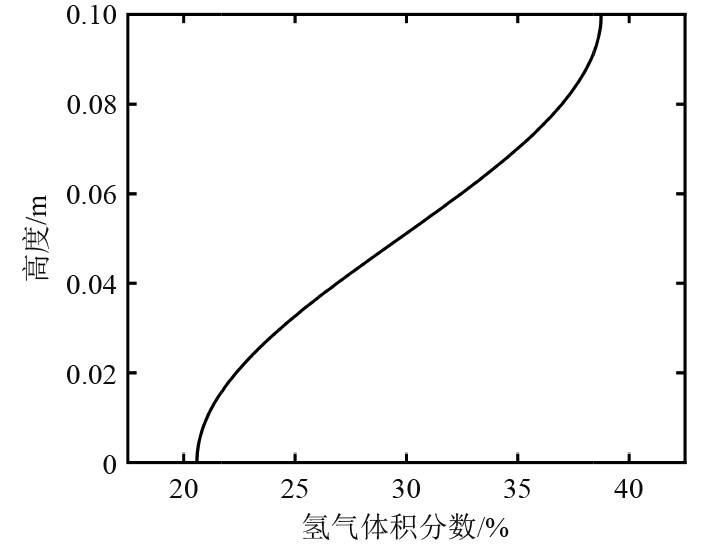
|
图 2 氢气浓度梯度分布 Fig. 2 Hydrogen concentration gradient distribution |
使用Fluent求解器进行数值计算,有限体积法被用于二维计算域的离散化,采用基于压力隐式分裂算子(PISO)方法对速度场和压力场进行解耦,空间离散化使用二阶逆风格式。在模拟计算过程中各方程的残差小于1E-3,能量方程残差小于1E-6。为保证计算稳定,计算步长采用自适应时间步长,Courant数设置为0.5。
1.4 网格划分本文使用mesh软件进行模型的网格划分,验证了4种尺寸0.5 mm、1 mm、2 mm、4 mm的网格对求解结果的影响,得到了混合物爆炸后火焰锋面位置随时间的变化曲线,如图3所示。可以看出,随着网格尺寸的降低,模拟结果的差异不断减小,并且0.5 mm网格与1 mm网格的模拟结果非常接近。为节约计算成本,最终选择1 mm网格进行计算。
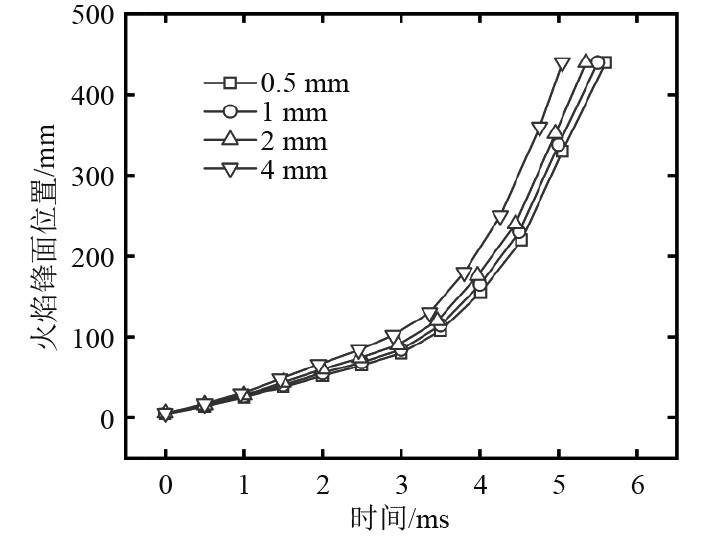
|
图 3 网格独立性验证 Fig. 3 Grid independence verification |
为确保模拟结果的准确性,将均匀氢-空气混合物在障碍物距点火处100 mm的管道中爆炸的模拟结果与Lv等[11]的实验结果进行比较,如图4所示。火焰传播过程中,预混火焰由球形火焰演变为指形火焰,最后演变为分叉火焰,这与Lv等[11]的实验结果一致。由图4(b)和图4(c)可知,发现模拟预测的火焰传播速度和超压与实验存在一定差异,其主要原因是忽略了管道壁面的影响。总体而言,数值模拟结果与实验结果基本吻合,表明本文采用的数值计算方法可靠。
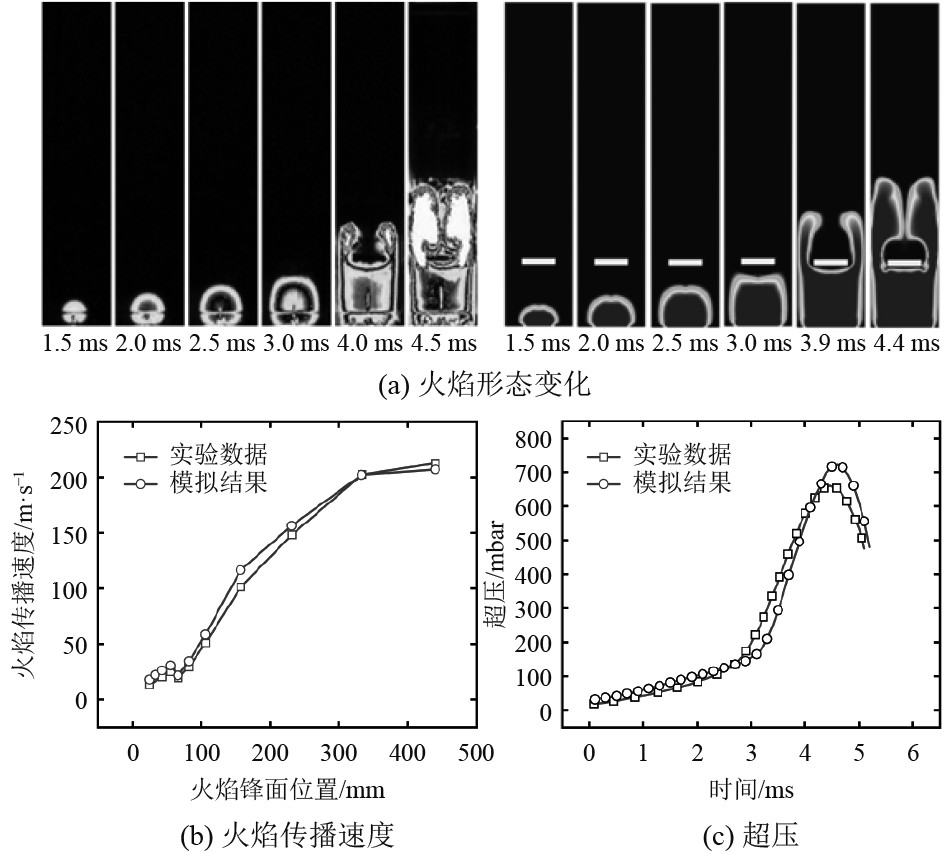
|
图 4 数值模拟与实验结果的比较 Fig. 4 Comparison of numerical simulation and experimental results |
图5为3种障碍物排列方式下火焰结构和流场变化情况。可以看出,火焰穿过障碍物前,每种情况下火焰形态变化基本相同。点火后t=2 ms时,火焰呈球形。在t=4 ms时,球形火焰转变为指形火焰,这表明点火初期火焰形态演变不受障碍物的影响。然而t=5 ms时,火焰遇到障碍物后,各种排列方式下火焰结构出现明显差异。在图5(a)中,障碍物布置在管道底部,t=5 ms时,火焰结构呈现为锥形火焰,原因是在浮力作用下管道顶部氢气浓度较高,从而产生更剧烈的化学反应和更快的局部火焰速度。在t=6 ms时,随着燃烧气体的膨胀,未燃烧的混合物被迫穿过障碍物,在障碍物后形成涡流。随后预混火焰在涡流的作用下向管道底部扩散,最终到达管道末端(t=7 ms)。如图5(b)所示,障碍物在管道两侧布置,并且两侧障碍物高度相同。可以看出,预混火焰穿过障碍物后发生畸变,在涡流的作用下被拉长,在管道末端呈现为絮状火焰。在图5(c)中,即障碍物布置在管道顶部,t=5 ms时,在障碍物的影响下火焰锋面逐渐扁平,随后火焰从底部穿过障碍物并逐渐被拉长,主要原因是障碍物的存在导致管道截面减小,燃烧产物的膨胀推动未燃混合物穿过障碍物,火焰穿过障碍物后需要维持一段距离才能摆脱这种干扰[24]。可以发现,当障碍物布置在管道顶部时,火焰形态发生更剧烈的变化,表明顶部障碍物对火焰传播过程有更显著的影响。
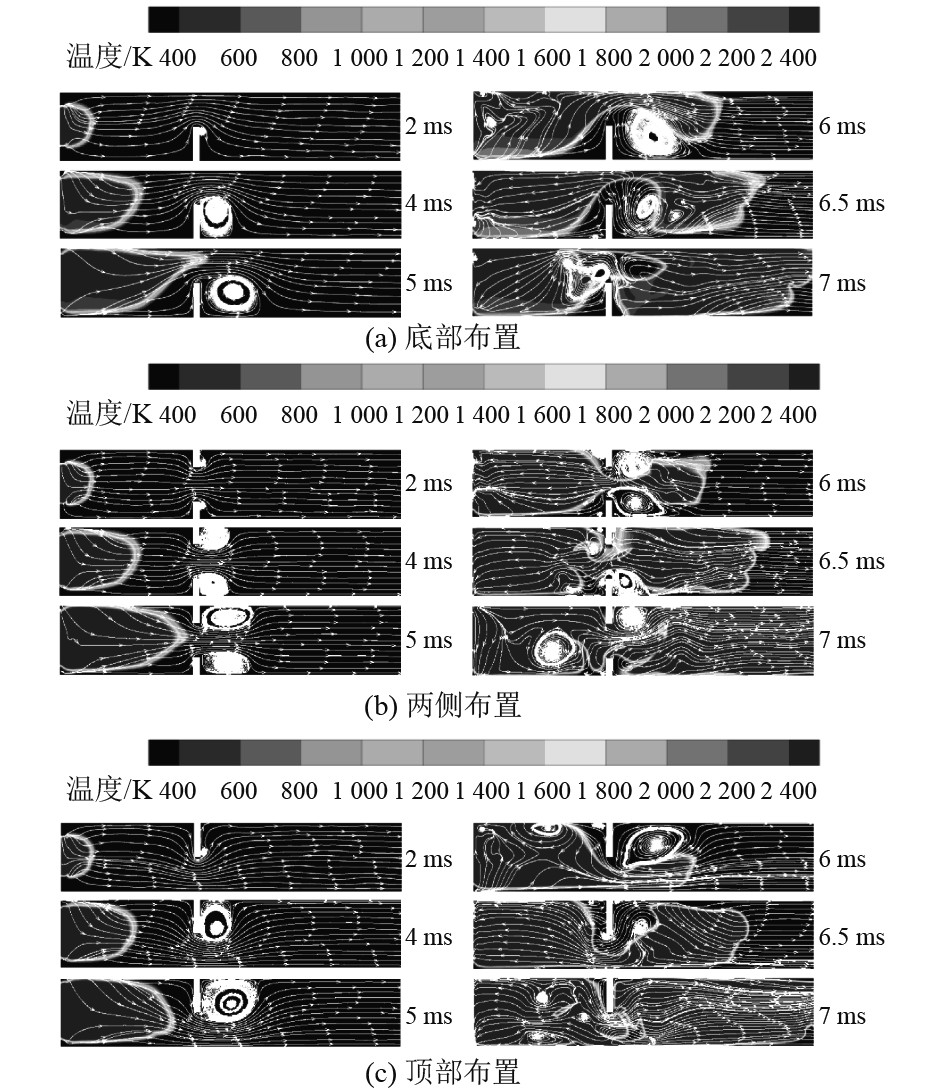
|
图 5 不同障碍物排列方式管道内火焰结构和流场变化 Fig. 5 Variations of flame structure and flow field in ducts with different obstacle arrangements |
图6为3种障碍物排列方式下火焰锋面位置和火焰传播速度随时间的变化。可以看出,在点火初期(t=4 ms前),各种障碍物布置条件下火焰的传播情况差异不大。在t=5 ms,火焰传播到障碍物附近时,障碍物的存在阻碍了可燃气体扩散,并且反射燃烧产生的压力波形成反向压力梯度,从而抑制了火焰的传播。与底部布置相比,障碍物在管道顶部和两侧布置时火焰传播速度较低,这表明这2种排列方式下障碍物对火焰的抑制作用更强。在t=5.5 ms时,在涡流的扰动作用下,火焰穿过障碍物后与未燃气体快速混合,促进了火焰的传播,火焰传播速度快速上升。最终3种障碍物排列方式下火焰锋面几乎同时到达管道出口。值得注意的是,与其他情况相比,障碍物在管道两侧布置时,火焰到达管道出口时的速度最快。
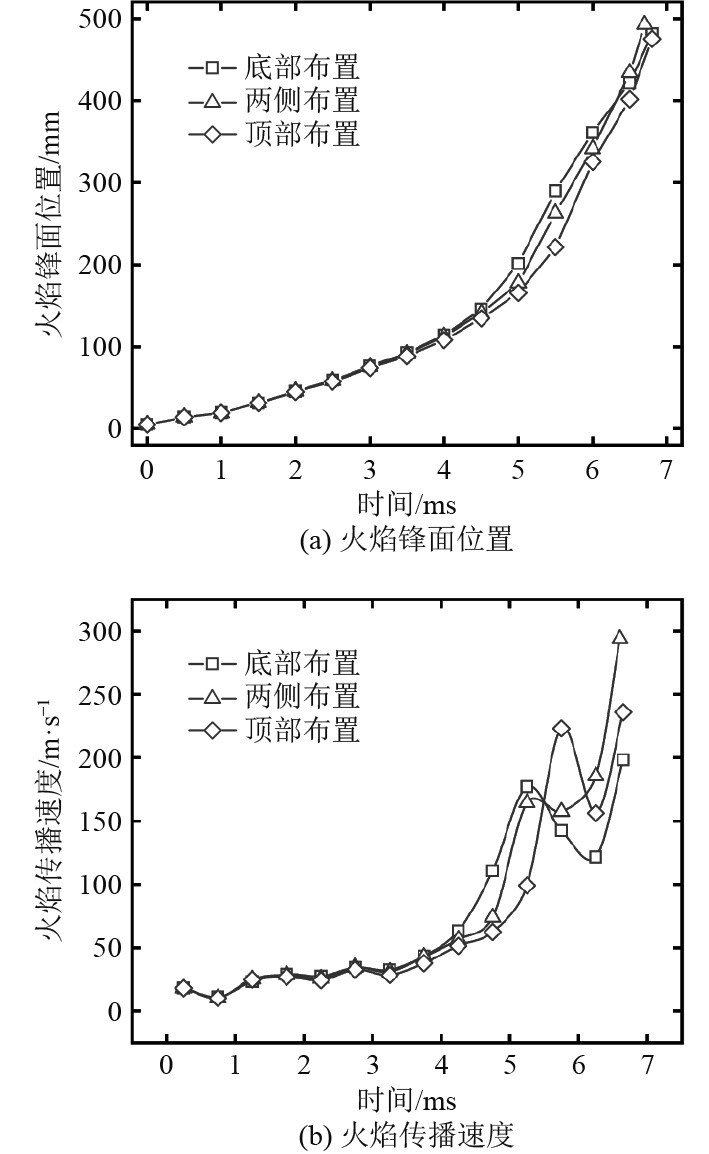
|
图 6 不同障碍物排列方式管道内火焰锋面位置和火焰传播速度随时间的变化 Fig. 6 Variations of flame front position and flame propagation velocity with time in ducts with different obstacle arrangements |
图7为3种障碍物排列方式下非均匀氢-空气混合物爆炸超压和超压增长率的变化曲线。预混气体点燃后释放大量能量,使管道内的压力快速上升,达到峰值压力后下降。可知,所有情况下压力的变化趋势相似,但峰值压力和达到峰值压力的时间有所不同。当障碍物在管道底部布置时,混合物爆炸峰值超压为58.85 kPa,压力达到峰值的时间最长。当障碍物在两侧布置时,压力达到峰值的时间最短,爆炸峰值压力为72.4 kPa。当障碍物位于管道顶部时,混合物爆炸峰值超压达到102.36 kPa。显然,与底部布置相比,两侧布置和顶部布置时的峰值超压分别增加了23%和74%,这表明管道顶部障碍物能极大地激发非均匀氢-空气混合物的爆炸威力。
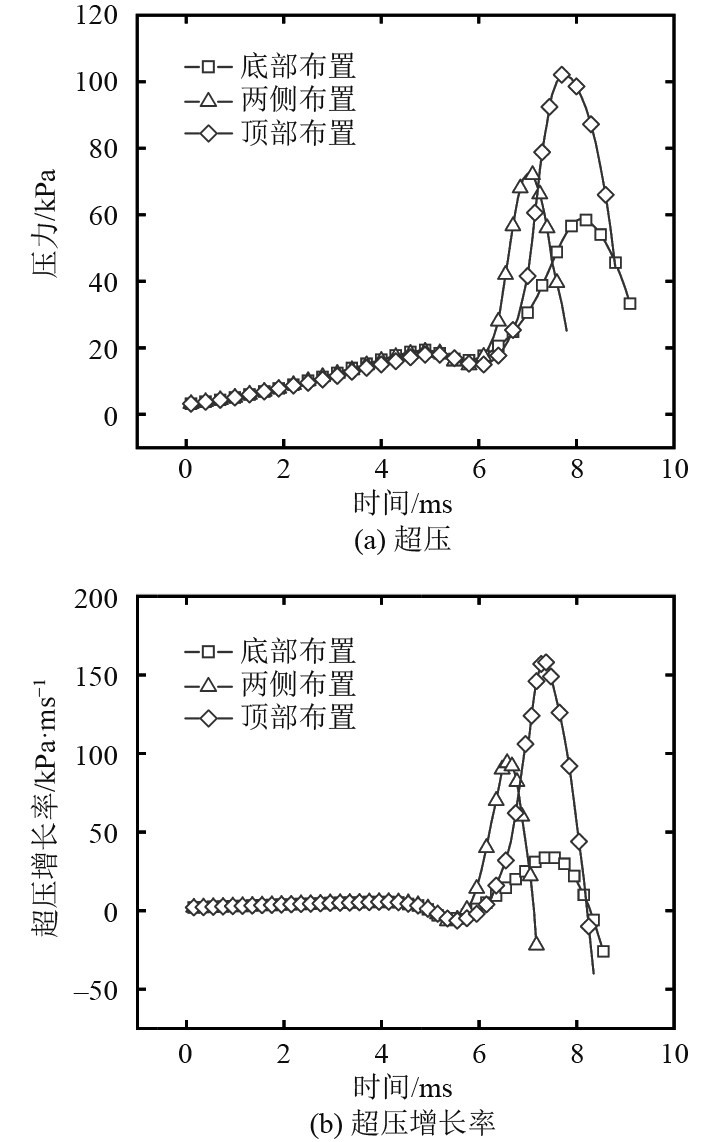
|
图 7 不同障碍物排列方式管道内爆炸超压和超压增长率随时间的变化 Fig. 7 Variations of explosion overpressure and growth rate of overpressure with time in ducts with different obstacle arrangements |
本文研究了障碍物排列方式对非均匀氢-空气混合物爆炸特性的影响。主要结论如下:
1)在不同障碍物排列方式情况下,火焰传播过程中经历了球形火焰、指形火焰、锥形火焰和絮状火焰4个阶段。当火焰穿过障碍物时,涡流的扰动作用是火焰形态变化的主要原因。
2)障碍物对早期火焰传播的影响不大。障碍物布置在管道顶部时,火焰锋面靠近障碍物时受到的抑制作用更强,穿过障碍物后的火焰传播速度更快。
3)随着顶部障碍物高度的增加,混合物爆炸峰值压力显著提高。障碍物布置在管道两侧和顶部时的峰值压力分别比底部布置时高23%和74%。
| [1] |
杨发财, 李世安, 沈秋婉, 等. 绿色航运发展趋势和燃料电池船舶的应用前景[J]. 船舶工程, 2020, 42(4): 1-7. YANG Facai, LI Shian, SHEN Qiuwan, et al. Development trend of green shipping and application prospect of fuel cell ships[J]. Ship Engineering, 2020, 42(4): 1-7. |
| [2] |
周洋, 杨发财, 李世安, 等. 燃料电池动力船舶安全问题及对策探讨[J]. 舰船科学技术, 2022, 44(4): 91-96. ZHOU Yang, YANG Facai, LI Shian, et al. Discussion on safety problems and countermeasures of fuel cell powered ships[J]. Ship Science and Technology, 2022, 44(4): 91-96. DOI:10.3404/j.issn.1672-7649.2022.04.019 |
| [3] |
马峻峰, 杨国刚, 李世安, 等. 燃料电池船舶储氢方式研究现状与展望[J]. 舰船科学技术, 2023, 45(3): 6-12. MA Junfeng, YANG Guogang, LI Shian, et al. Research status and prospect of fuel cell ship hydrogen storage technology[J]. Ship Science and Technology, 2023, 45(3): 6-12. DOI:10.3404/j.issn.1672-7649.2023.03.002 |
| [4] |
刘继海, 肖金超, 魏三喜, 等. 绿色船舶的现状和发展趋势分析[J]. 船舶工程, 2016, 38(S2): 33-37. LIU Jihai, XIAO Jinchao, WEI Sanxi, et al. The status quo and development tendency analysis of green ship[J]. Ship Engineering, 2016, 38(S2): 33-37. |
| [5] |
于全虎. 氢能和燃料电池及其船舶应用进展[J]. 船舶, 2020, 31(5): 69-76. YU Quanhu. Hydrogen, fuel cells and their application on ship[J]. Ship & Boat, 2020, 31(5): 69-76. |
| [6] |
杨庆勇. 氢燃料在船舶上的应用分析[J]. 青岛远洋船员职业学院学报, 2020, 41(4): 41-44. YANG Qingyong. On the application of hydrogen energy in ships[J]. Journal of Qingdao Ocean Shipping Mariners College, 2020, 41(4): 41-44. DOI:10.3969/j.issn.2095-3747.2020.04.010 |
| [7] |
郑津洋, 刘自亮, 花争立, 等. 氢安全研究现状及面临的挑战[J]. 安全与环境学报, 2020, 20(1): 106-115. |
| [8] |
邝辰, 刘迪, 杨昊, 等. 氢气泄漏后燃爆风险研究现状综述[J]. 安全, 健康和环境, 2021, 21(9): 1-5. |
| [9] |
丁信伟, 杨国刚, 毕明树, 等. 环栅条形障碍物对可燃气云爆炸影响的数值模拟与实验研究[J]. 天然气工业, 2004, 24(4): 81-83. DOI:10.3321/j.issn:1000-0976.2004.04.027 |
| [10] |
MASRI A R, ALHARBI A, MEARES S, et al. A comparative study of turbulent premixed flames propagating past repeated obstacles[J]. Industrial & Engineering Chemistry Research, 2012, 51(22): 7690-7703. |
| [11] |
LV Xiangshu, ZHENG Ligang, ZHANG Yugui, et al. Combined effects of obstacle position and equivalence ratio on overpressure of premixed hydrogen-air explosion[J]. International Journal of Hydrogen Energy, 2016, 41(39): 17740-17749. DOI:10.1016/j.ijhydene.2016.07.263 |
| [12] |
段强领, 曾倩, 李萍, 等. 管道内障碍物对高压氢泄漏自燃特性的影响研究[J]. 中国安全科学学报, 2020, 39(9): 164-170. |
| [13] |
李西贵, 滕霖, 李卫东, 等. 管内障碍物位置对高压氢气泄漏自燃影响的数值模拟[J]. 运行与管理, 2021, 40(11): 1306-1313. |
| [14] |
李雪, 王腾, 陈兵, 等 . 燃料电池动力船舶安全问题及对策探讨[J/OL]. 油气储运, 2021: 1−8(2021-04-08)[2023-07-24].
|
| [15] |
SHENG Z H, YANG G G, LI S A, et al. Modeling of turbulent deflagration behaviors of premixed hydrogen-air in closed space with obstacles[J]. Process Safety and Environmental Protection, 2022, 161: 506-519. DOI:10.1016/j.psep.2022.03.044 |
| [16] |
SHENG Z H, YANG G G, CAO W, et al. Study on the dynamic process of premixed hydrogen-air deflagration flame propagating in a closed space with obstacles[J]. Fuel, 2023, 334: 126542. DOI:10.1016/j.fuel.2022.126542 |
| [17] |
PUNETHA M, CHOUDHARY A, KHANDEKAR S. Stratification and mixing dynamics of helium in an air filled confined enclosure[J]. International Journal of Hydrogen Energy, 2018, 43(42): 19792-19809. DOI:10.1016/j.ijhydene.2018.08.168 |
| [18] |
徐莹莹 . 受限空间内氢气_空气燃爆特性数值研究[D]. 常州: 常州大学, 2021.
|
| [19] |
SAEID M H S, KHADEM J, EMAMI S. Numerical investigation of the mechanism behind the deflagration to detonation transition inhomogeneous and inhomogeneous mixtures of H2-air in an obstructed channel[J]. International Journal of Hydrogen Energy, 2021, 46(41): 21657-21671. DOI:10.1016/j.ijhydene.2021.04.006 |
| [20] |
ZHENG J Y, BIE H Y, XU P, et al. Numerical simulation of hydrogen release from high-pressure storage vessel [J]. 2009[2023-07-24].
|
| [21] |
CHERBA´NSK R, MOLGA E. CFD simulations of hydrogen deflagration in slow and fast combustion regime [J]. Combustion Theory and Modelling, 2020[2023-07-24].
|
| [22] |
MEI Y, SHUAI J, LI Y, et al. Flame acceleration process of premixed hydrogen in confined space with different obstacle shapes[J]. International Journal of Hydrogen Energy, 2018, 43(42): 19792-19809. DOI:10.1016/j.ijhydene.2018.08.168 |
| [23] |
BOECK L R, BERGER F M, HASSLBERGER J, et al. Detonation propagation in hydrogen–air mixtures with transverse concentration gradients[J]. Shock Waves, 2016, 26(2): 181-192. DOI:10.1007/s00193-015-0598-8 |
| [24] |
BOECK L R, HASSLBERGER J, SATTELMAYER T. Flame acceleration in hydrogen/air mixtures with concentration gradients[J]. Combustion Science and Technology, 2014, 186(10-11): 1650-1661. DOI:10.1080/00102202.2014.935619 |
 2024, Vol. 46
2024, Vol. 46
