2. 中国人民解放军 92857部队,北京 100161
2. No. 92857 Unit of PLA, Beijing 100161, China
船舶破损进水过程涉及到复杂的现象,水进入舱室,舱室内空气发生变化。在完全封闭或通风部位已因进水失去作用的舱室,随着舱室进水,空气被困住并压缩,形成气压很高的气穴,对船舶破损舱室进水过程和最终状态产生较大负面影响,因此,在研究船舶破损进水的过程中,应考虑空气压缩效应的影响。
同时,为实现复杂舱室进水的准确时域模拟,需考虑非水密门对水蔓延的影响。非水密门破损坍塌前,会阻碍水的蔓延,复杂舱室系统中两者之间存在耦合效应,对船舶渐进式进水过程产生影响。
自20世纪90年代以来,针对船舶破损进水过程中的耦合计算问题,许多研究人员采用计算流体力学(CFD)方法开展了船舶破损进水过程相关研究。Gao等[1]为研究船舶破损舱室进水的复杂过程,将流体体积法和动网络技术相结合,建立了一种Navier -Stoker(NS)求解器,采用动态网格技术处理船舶破损的进水过程研究;在此基础上,针对国内缺少舱内空气对进水影响研究的情况,刘强等[2]应用Fluent软件对大量计算模型进行了破舱进水的时域模拟,探讨了空气流对进水过程的影响;Gao等[3]采用CFD方法对湍流模型与层流模型,空气可压缩模型与不可压缩模型进行了计算,分析了气流对船舶进水和下沉的影响;陈振等[4]建立了基于求解RANS方程的船舶破舱进水计算模型,研究了空气压缩性对船舶破舱进水过程的影响;吴家俊等[5]基于STAR-CCM+软件研究了不同姿态下破损舱室在密闭和通风2种情况下的进水过程。
上述方法依然存在计算时间长、所需硬件设备较高的缺点。为提高船舶破损进水过程计算效率,Pekka 等[6]基于伯努利方程,采用数值计算方法开展破舱进水研究,在提高计算速度的基础上,保证了一定的计算效率;为进一步提升计算的可靠性,预测船舶破损进水后的情况,Hirotada等[7]通过半隐式运动粒子模拟和势流理论来求解船舶破损进水运动方程;考虑到破损船舶进水是一个时域过程,受到舱内非水密结构的影响明显,Risto等[8]采用全尺寸试验和有限元分析,对各种非水密结构在水压作用下的泄露和倒塌特性进行分析,提出一种可用于时域进水模拟的非水密结构简化建模方法;为将船舶运动与进水过程相结合以更贴近实际情况,Bu等[9]提出一种非线性时域统一粘性势预测方法,可以很好地预测船舶的运动动态并大幅减少计算时间;在此基础上,为了将相关研究情况应用于实际船舶破损进水预报,Luca等[10-11]提出一种能独立考虑舱室内进水过程的微分代数过程新方法,可通过调整时间步长有效提升模拟过程的计算效率,并将相关研究结合,在简化部分建模的基础上,构建了船舶进水损管决策支持系统,为现实中船舶破损进水后相关决策支持。
本文基于伯努利原理和波义耳定律,采用准静态法建立了考虑空气压缩效应的船舶破损进水数值计算模型,以ITTC标准驳船模型为对象,分析了空气压缩效应对舱室压力、进水速度、水面高度的影响,并进一步考虑了非水密门对破损舱室进水特性的影响。
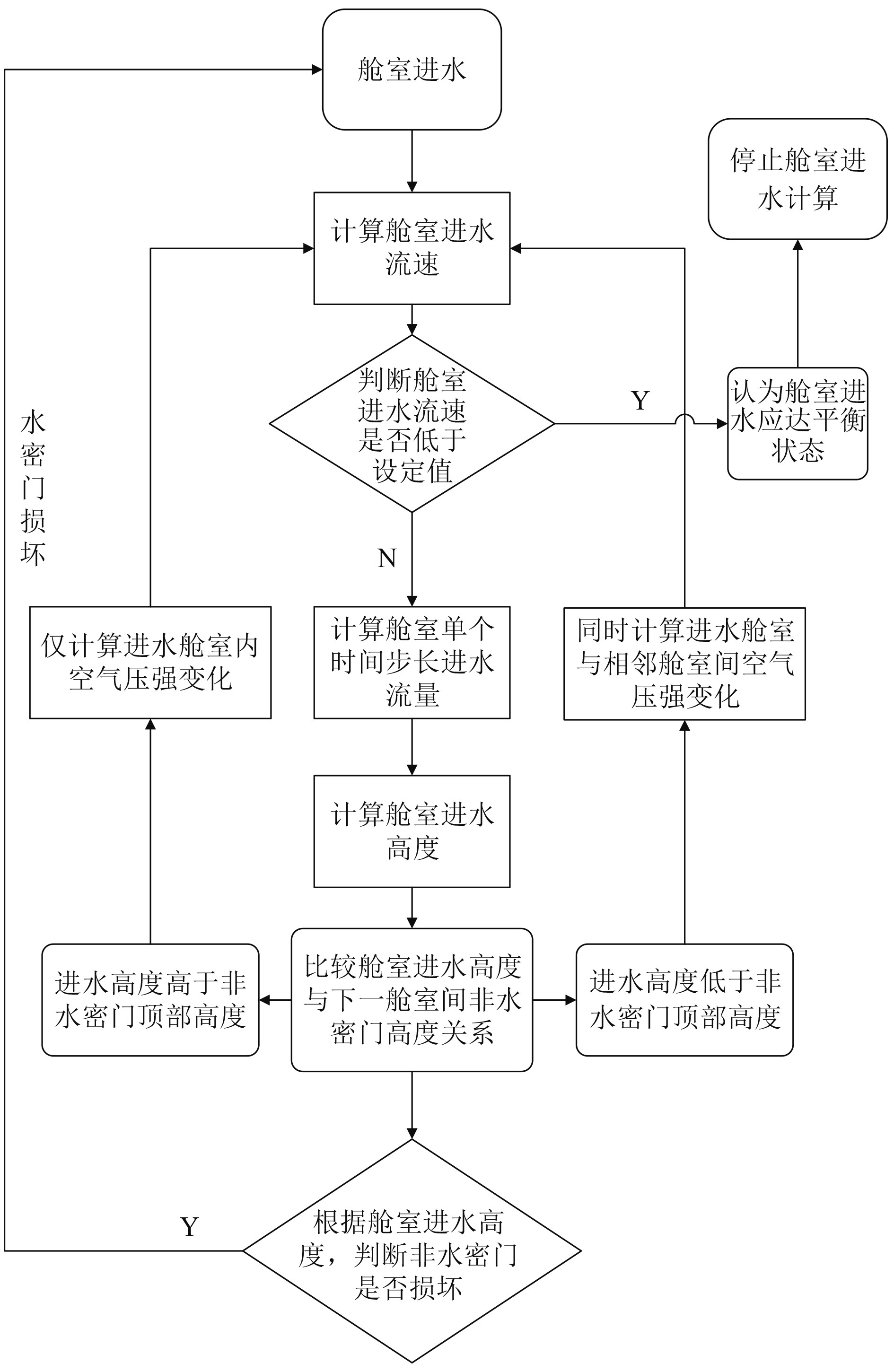
1 数值计算方法舱室进水、空气压缩与非水密门受力之间存在耦合关系,为采用数值计算方法开展舱室进水研究,需对三者开展迭代计算。在简化相关影响条件的基础上,采用图1思路开展舱室进水迭代计算。
|
图 1 舱室进水计算流程示意图 Fig. 1 Schematic diagram of the calculation process of cabin water flooding |
采用准静态法对船舶破损进水进行时域模拟,舱室内进水可简化为瞬时与海平面平行的液面,忽略舱室进水的动能效应,该简化已被证明合理并广泛使用[12]。为简化计算流程,减少计算时间,假设舱室破口为一维破口,即具有给定面积和流量系数的点。同时,该方法也可扩展处理复杂形状的破口[6]。
水是不可压缩流体,密度恒定,水通过破口的体积流量可认为是水的速度与破口面积的点积,破损进水过程满足连续方程:
| $ {\rho _w}\frac{{{\text d}{V_{w,i}}}}{{{\text d}t}} = - {\rho _w}\sum\limits_k {{Q_{w,k}}} 。$ | (1) |
式中:
假设水是理想流体,在破口处应用伯努利方程:
| $ \int\nolimits_A^B {\frac{{{\text d}p}}{\rho }} + \frac{1}{2}\left( {u_B^2 - u_A^2} \right) + g\left( {{h_B} - {h_A}} \right) = 0 ,$ | (2) |
式中:
式(2)考虑的流线连接了水面中部的A点和位于破口的B点。实际的水有粘性,流动过程存在能量损失,因此式(2)中加入压力损失项,可以半经验地考虑在实际破损进水过程中的压力损失[6]。因此,修正后的伯努利方程如下:
| $ \int\nolimits_A^B {\frac{{{\mathrm{d}}p}}{\rho }} + \frac{1}{2}\left( {u_B^2 - u_A^2} \right) + g\left( {{h_B} - {h_A}} \right) + \frac{1}{2}{K_L}u_B^2 = 0 。$ | (3) |
式中:
由式(3)可求得破口处水的流速为:
| $ {u_B} = \frac{1}{{\sqrt {1 + {K_L}} }}\sqrt {2g\left( {{h_A} - {h_B}} \right) - 2\int\nolimits_A^B {\frac{{{\mathrm{d}}p}}{\rho }} } 。$ | (4) |
定义流量系数
| $ {C_d} = \frac{1}{{\sqrt {1 + {K_L}} }} 。$ | (5) |
显然,破口处水的流速与恒定的流量系数成正比。
根据式(4)可求得通过破口的水的体积流量:
| $ {\text d}Q = {u_B}{\mathrm{d}}A = {\mathrm{sign}}\left( {{h_A} - {h_B}} \right) \cdot \sqrt {2g\left| {{h_A} - {h_B}} \right| - 2\int\nolimits_A^B {\frac{{{\mathrm{d}}p}}{\rho }} } \cdot {\mathrm{d}}A。$ | (6) |
式中:
考虑空气的压缩效应,破口处的有效压力等于舱室空气压力和静水压力之和,即:
| $ P = p + \rho gh 。$ | (7) |
式中:
以上述内容为基础,考虑舱内的空气压缩效应,海水从第
| $ {Q_{ji}}{\text{ = }}{C_d}{A_{ji}} \cdot {\text{sgn}} \left( {{{\hat z}_j} - {{\hat z}_i}} \right)\sqrt {2g\left| {{{\hat z}_j} - {{\hat z}_i}} \right| + 2\left( {{P_i} - {P_j}} \right)} 。$ | (8) |
其中,
| $ {\hat z_j} = \max \left( {{z_j} - {z_{\min ji}}} \right)。$ | (9) |
式中:
密闭舱室中,随着舱室进水,空气体积减小,压强增大,进而对舱室进水产生影响。为开展舱室空气压强计算,假定空气为理想的可压缩气体,在压缩的过程中不考虑温度的变化,因此在计算空气压强时应用波义耳定律得:
| $ {p_1}{V_1}{\text{ = }}{p_2}{V_2} 。$ | (10) |
考虑舱室内空气流通及空气压缩效应,假设在密闭性良好的舱室内,水面高度未高于破口最高处时,认为舱室内空气可自由流通;水面高度高于破口最高处时,认为舱室内空气无法流通,并开展后续计算。
空气压强迭代计算与舱室进水量迭代计算之间属于高度耦合关系。根据舱室进水量计算舱室进水高度,再依据舱室进水高度和舱室之间破口高度判断相连通舱室之间的空气压缩情况,进而对下一阶段舱室进水流速产生影响。
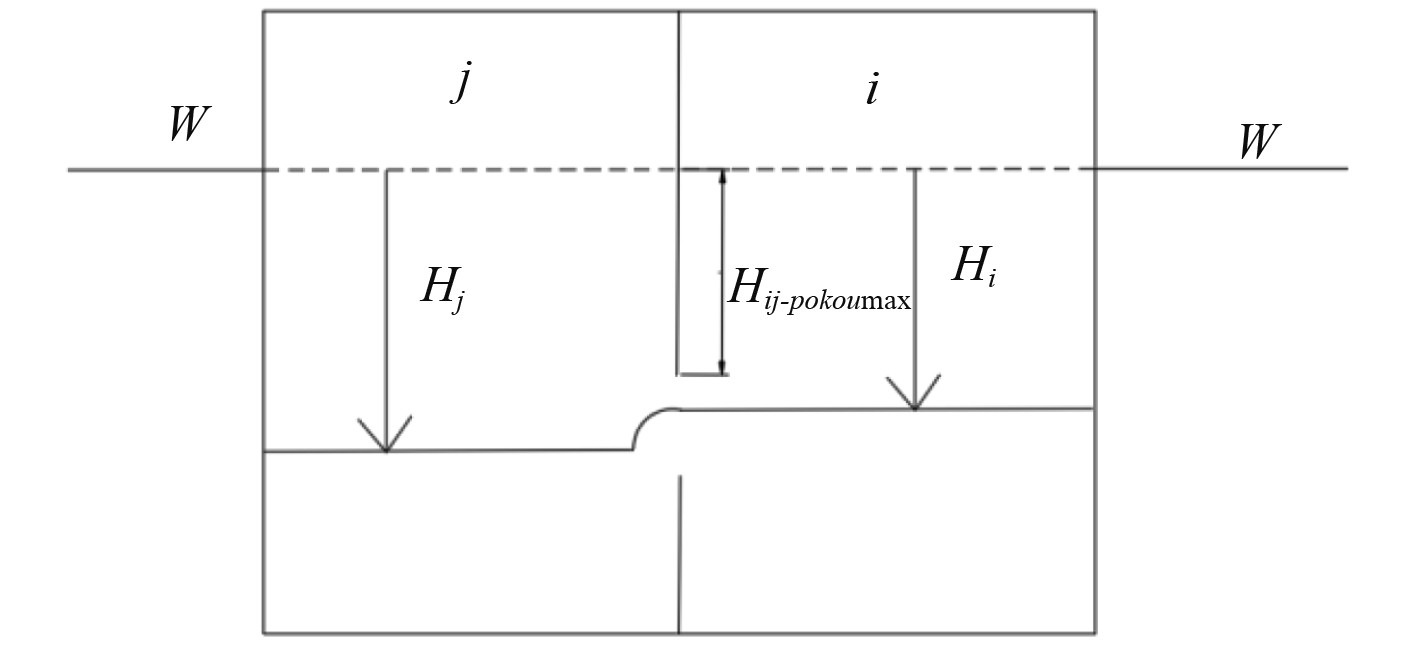
如图2所示,根据舱室之间破口高度及舱室进水高度可得舱室内不同情况下空气压缩状态:
|
图 2 空气压强计算示意图 Fig. 2 Schematic diagram of air pressure calculation |
| $ P_i^t = \left\{ {\begin{aligned} & {p_i^{t - 1} \cdot \left( {\frac{{V_i^t + V_j^t}}{{V_i^{t - 1} + V_j^{t - 1}}}} \right)},{{H_i} \leqslant {H_{ij - pokou{\text{max}}}} },\\ & {p_i^{t - 1} \cdot \left( {\frac{{V_i^t}}{{V_i^{t - 1}}}} \right)},{{H_i} \geqslant {H_{ij - pokou{\text{max}}}} } ,\end{aligned}} \right. $ | (11) |
式中:
非水密门对舱室进水存在阻碍作用,在其未损坏前,可阻止海水蔓延。假定非水密门在未被水淹没前可保持空气正常流通。未达到受力临界值前可阻止水的流通,所受压力达到临界值瞬间被完全破坏,被破坏后水可流通。非水密门受力计算公式为:
| $ F = P \cdot A{\text{ = }}\int\nolimits_{{h_1}}^{{h_2}} {\rho gh \cdot B{\mathrm{d}}h}。$ | (12) |
式中:
此时可根据非水密门受力情况开展舱室间海水流速计算:
| $ {Q_{ij}} = \left\{ {\begin{array}{l} 0,F < {F_{\max }},\\ {{C_d}{A_{ji}}{{\mathrm{sgn}}} \left( {{{\hat z}_j} - {{\hat z}_i}} \right) \sqrt {2g\left|{{{\hat z}_j} - {{\hat z}_i}} \right| + 2\sqrt {\left( {{P_i} - {P_j}} \right)} } },{F \geqslant {F_{\max }}}。\end{array}} \right. $ | (13) |
式中:
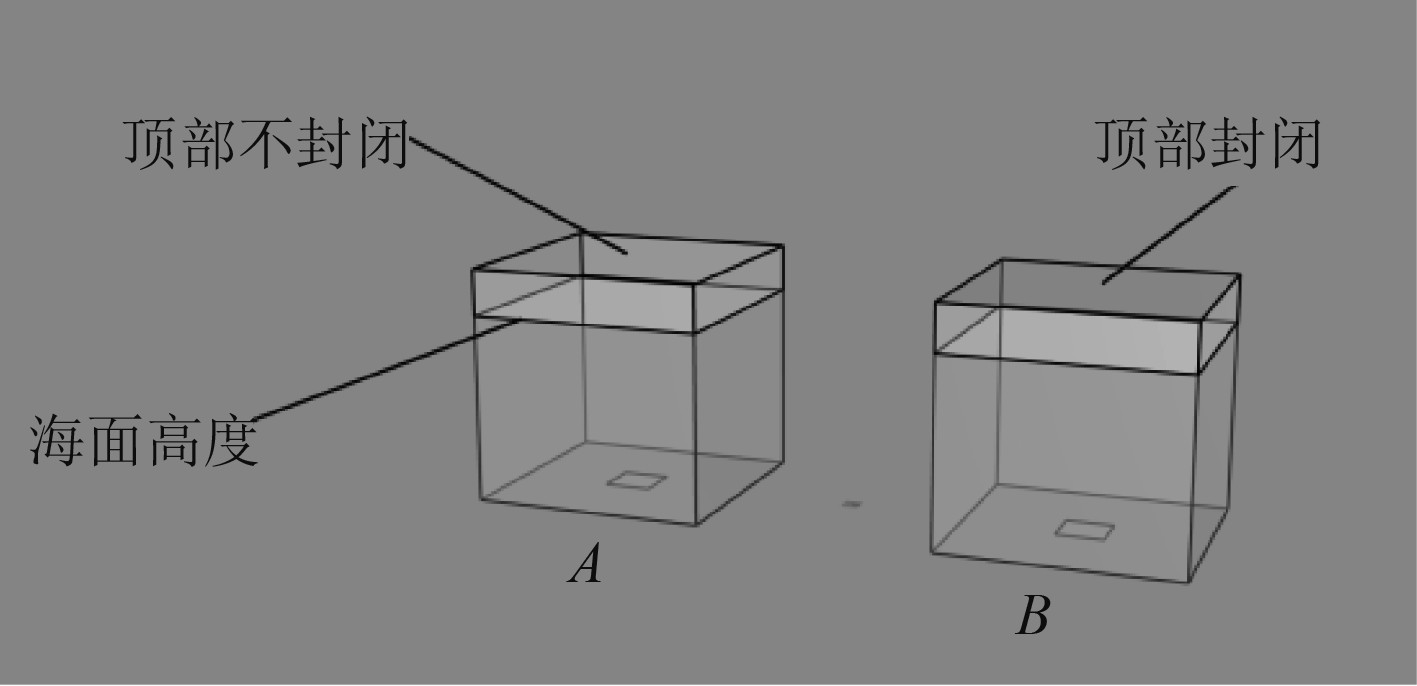
以Ruponen的简易测试模型[6]为对象,如图3所示,模型尺寸见表1,采用Matlab编写程序开展时域模拟。
|
图 3 测试模型示意图 Fig. 3 Test model schematic |
|
|
表 1 测试模型中舱室尺寸 Tab.1 Test the dimensions of the cabin in the model |
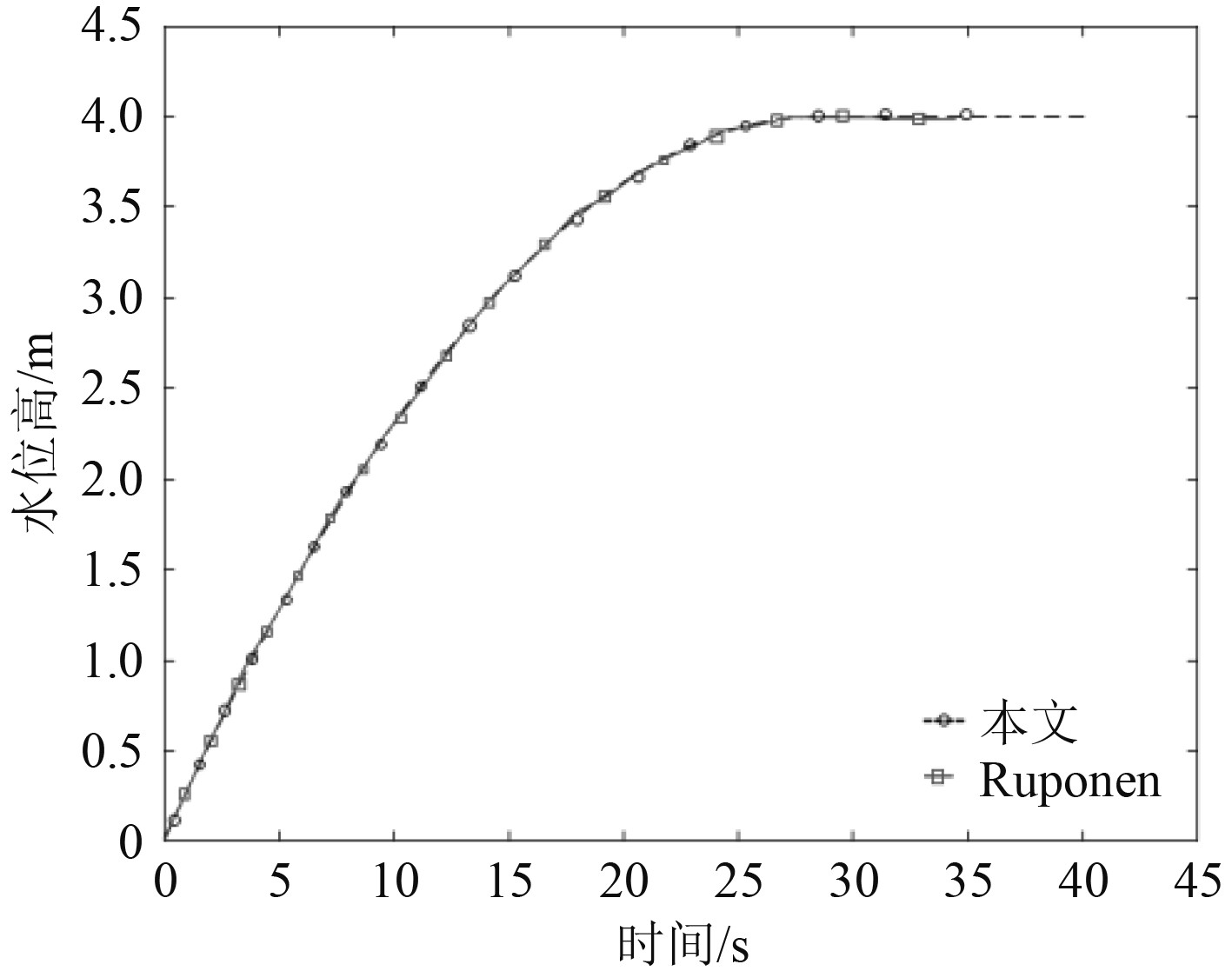
数值计算时,海平面高度恒定,舱室位置恒定,初始条件为舱室内部干燥,空气压力等于大气初始压强。其中A舱室为顶部与外界完全相通,在舱室进水期间不考虑空气压缩效应;B舱室为完全封闭,舱室进水期间需要考虑空气压缩效应。数值计算结果与Ruponen计算结果[6]的对比如图4 ~图6所示。
|
图 4 模拟A舱室中舱室进水高度变化情况 Fig. 4 Simulate the change in the water ingress of the cabin in cabin A |
|
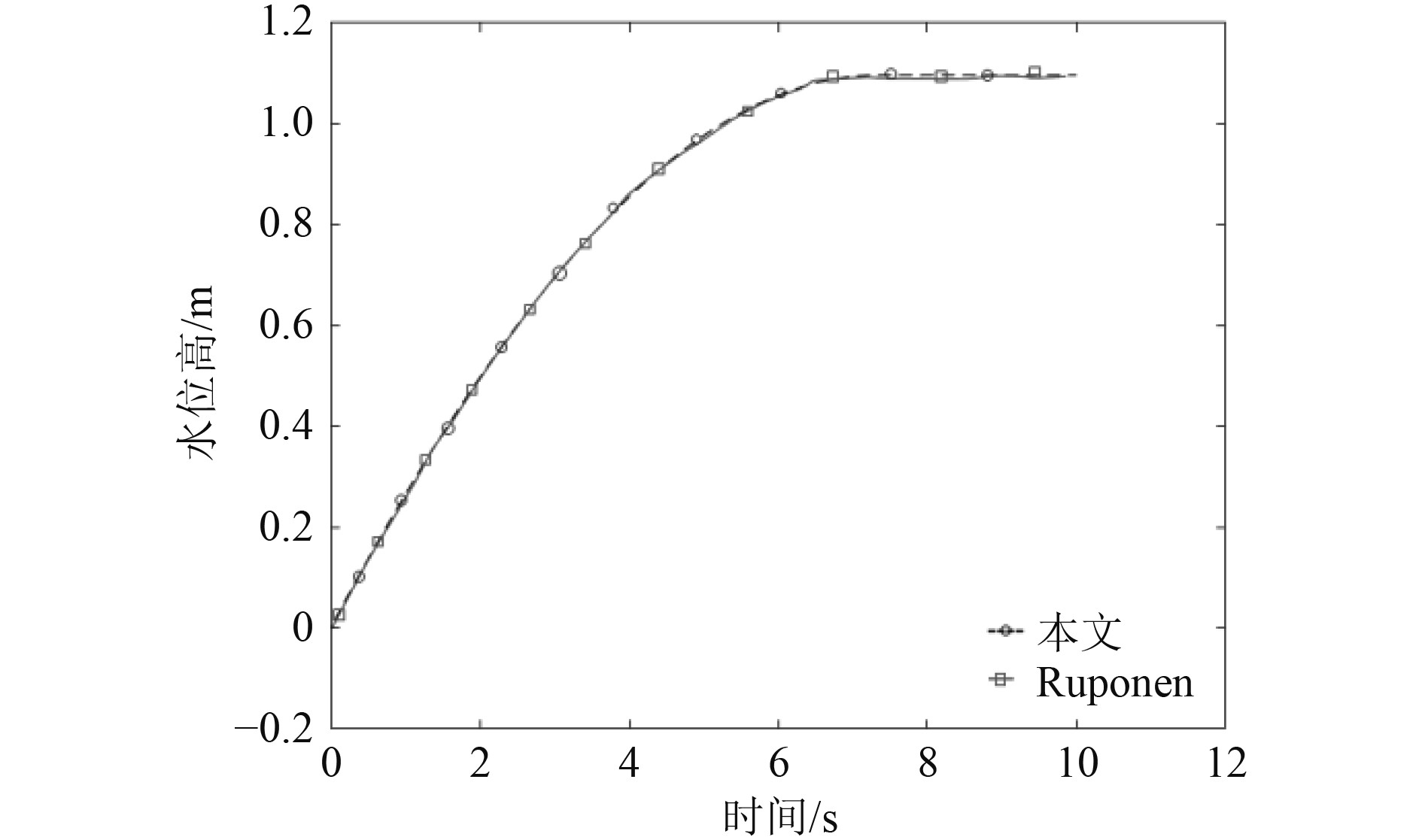
图 6 B舱室中舱室进水高度变化 Fig. 6 The water height of the cabin changes in cabin B |

|
图 5 B舱室中舱室内压强变化 Fig. 5 Change in pressure in cabin B |
可知,数值计算结果不论是舱室内压强变化还是进水高度变化均吻合良好,表明本文采用的时域计算方法可准确模拟考虑空气压缩效应时舱室内进水高度和压强变化。
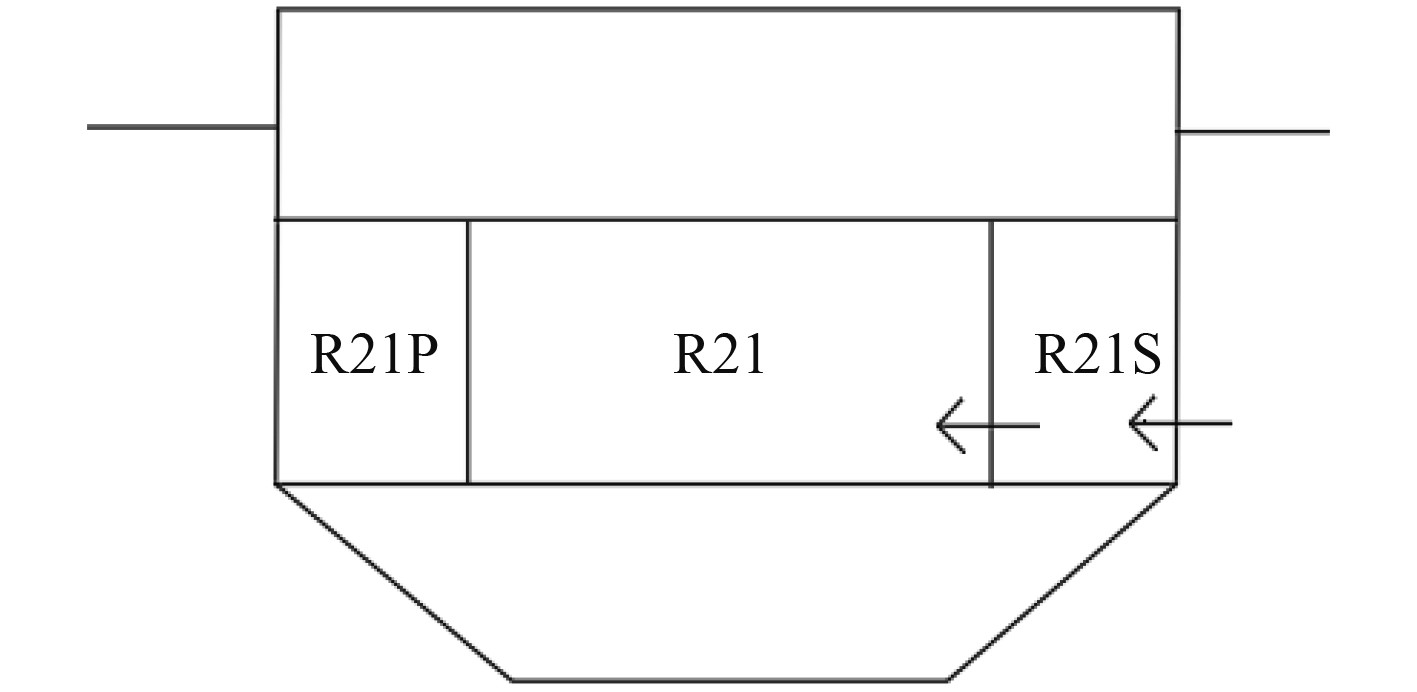
2.2 非水密门模型为研究非水密门对船舶破损进水的影响,以ITTC标准驳船模型为对象测试计算方法的正确性。该模型三维模型如图7所示,舱室进水横截面如图8所示,图中箭头表示舱室进水方向,相关数据如表2所示。R21S/R21舱室间添加非水密门,研究不考虑空气压缩效应下舱室中存在非水密门的船舶破损进水特性。

|
图 7 ITTC标准驳船模型示意图 Fig. 7 Schematic diagram of the ITTC standard barge model |
|
图 8 ITTC标准驳船模型中舱室进水横截面示意图 Fig. 8 Schematic diagram of the cross-section of the water ingress in the cabin in the ITTC standard barge model |
|
|
表 2 ITTC标准驳船模型舱室数据 Tab.2 ITTC standard barge model cabin data |
数值计算时,R21S舱室与外界海洋相连通,进水舱室顺序为R21S-R21,其中R21S与R21舱室之间存在非水密门。非水密门所受压力未达临界值前,R21舱室未进水;达到临界值后,认为该非水密门破损,R21舱室开始进水。在考虑非水密门受到压力作用的前提下,对舱室进水进行计算,设定计算时间步长为0.05 s。数值计算结果如图9 ~ 图11所示。
|
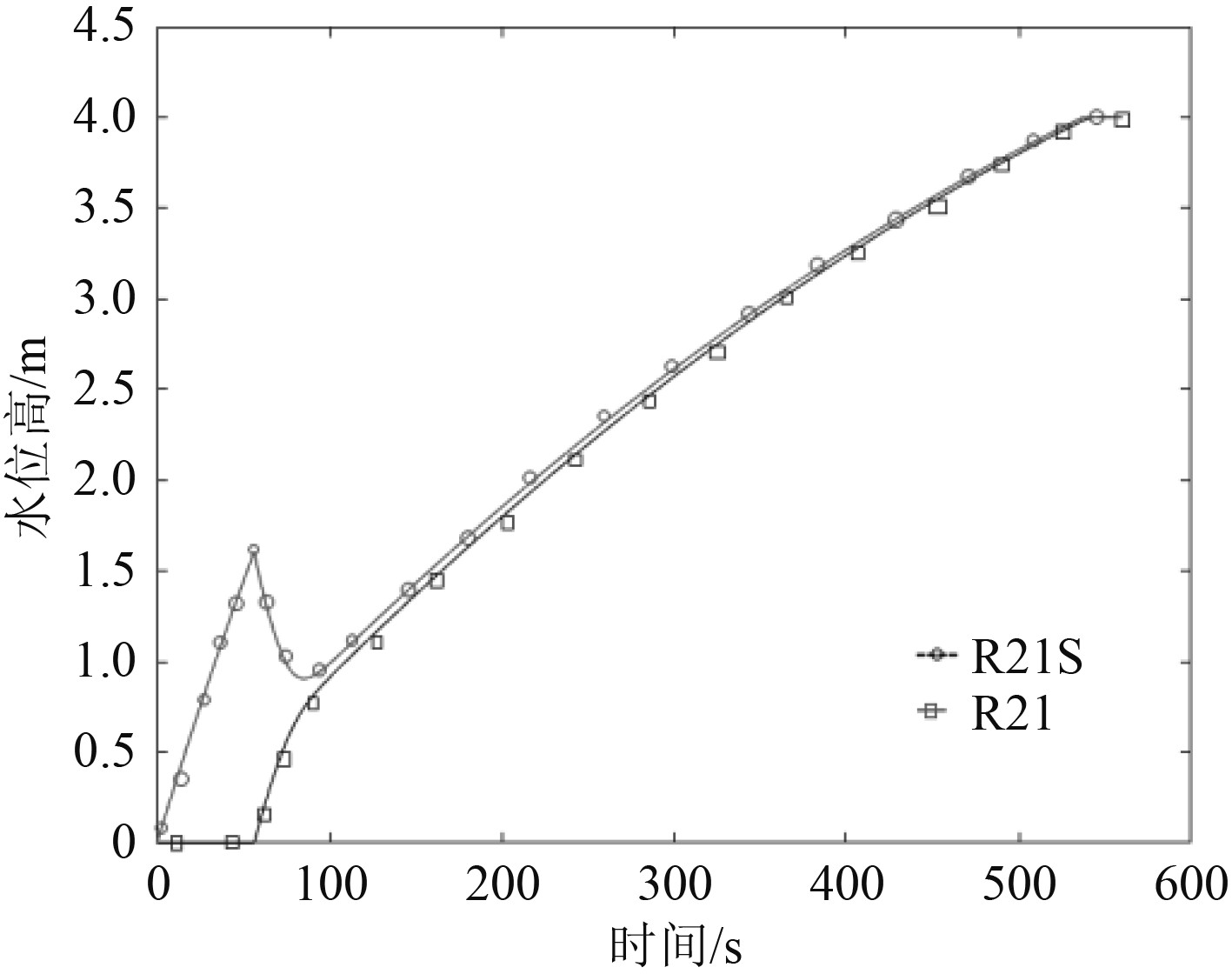
图 9 考虑非水密门影响时舱室水面高度随时间的变化 Fig. 9 Consider the change in the water height of the cabin over time when the non-watertight door is affected |
|
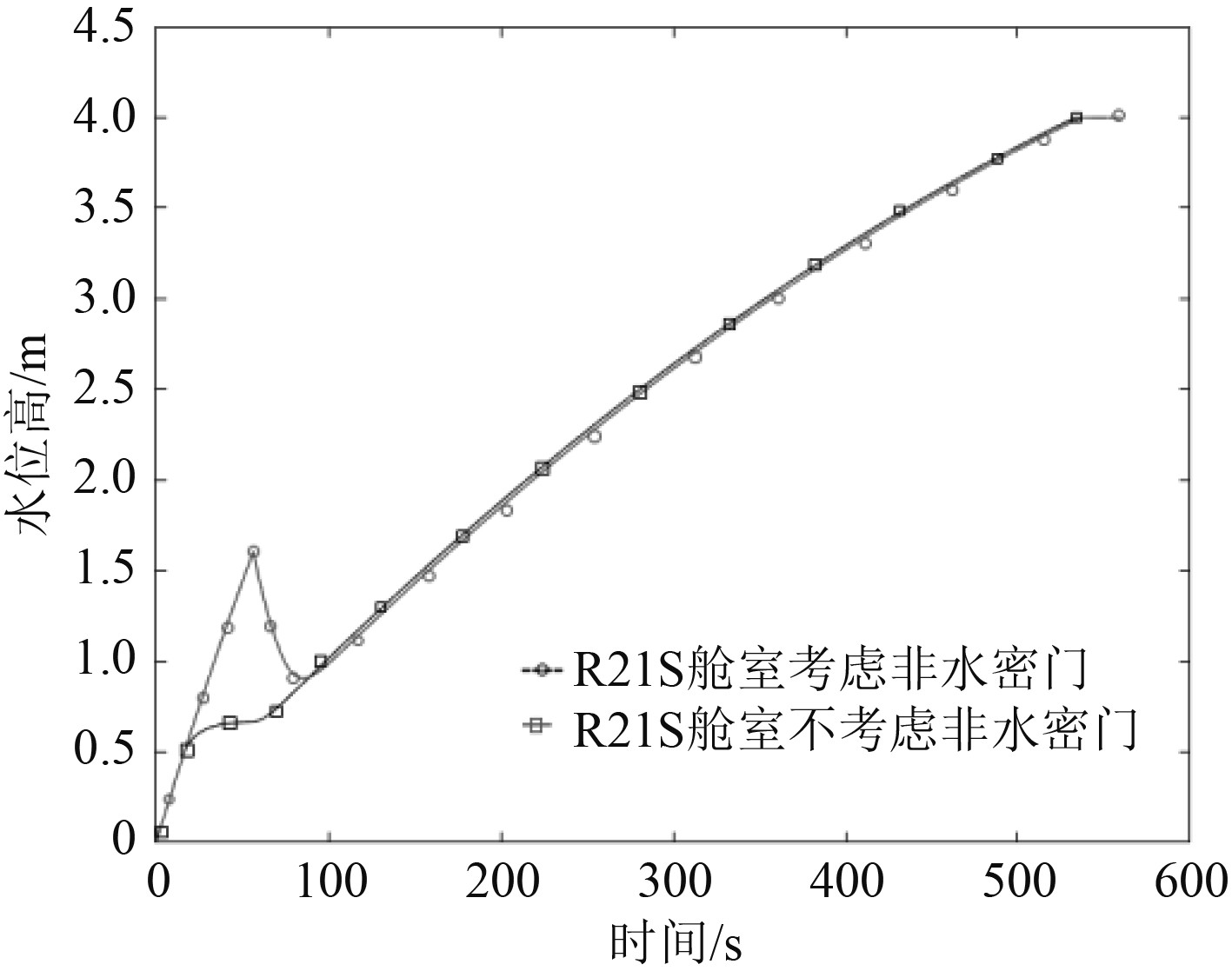
图 10 R21S舱室是否考虑非水密门影响时舱室水面高度随时间的变化 Fig. 10 Whether the R21S cabin takes into account the change in the water height of the cabin with time when the non-watertight door is affected |
|
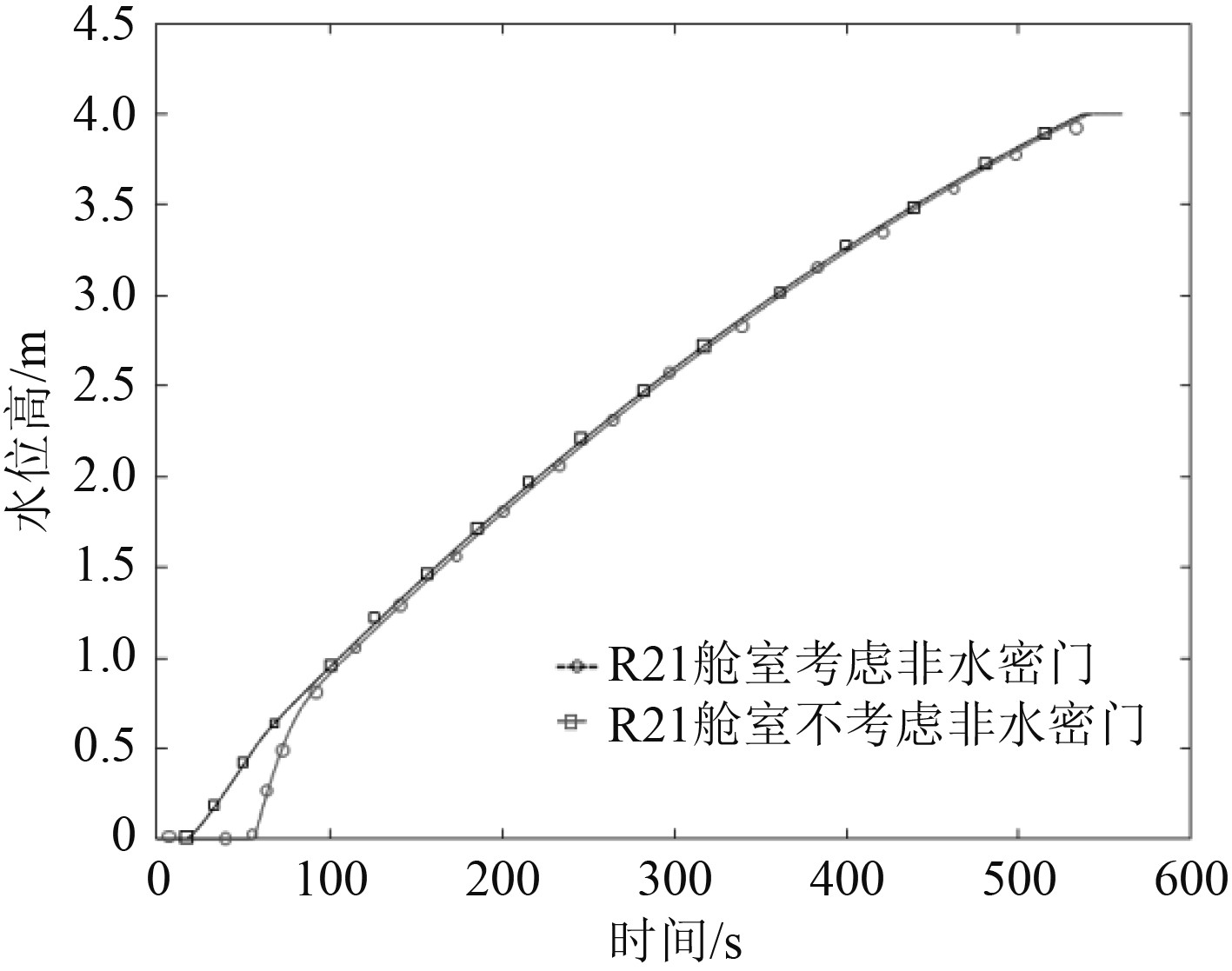
图 11 R21舱室是否考虑非水密门影响时舱室水面高度随时间的变化 Fig. 11 Whether the R21 cabin takes into account the change of the water height of the cabin over time when the non-watertight door is affected |
可知,受非水密门的影响,在进水后10~90 s期间R21S舱室水面高度较高,且开始进水后约50 s水面高度达到1.6 m后才开始下降,意味进水前期在未达到非水密门临界压力前,R21S舱室中液体未进入R21舱室,导致R21舱室进水时间滞后约40 s。
由图11可知,当舱室进水淹没时,受非水密门影响,舱室进水过程存在滞后情况;非水密门形成破口后,舱室水面高度先突降后正常升高,对准确计算船舶浮稳性产生一定影响。
2.3 复杂舱室系统进水模拟模型为研究空气压缩效应和非水密门对复杂舱室破损进水特性的影响规律,如图12所示,以ITTC标准驳船模型为对象进行测试,其模型横截面如图13所示,相关数据如表3所示。

|
图 12 ITTC标准驳船模型示意图 Fig. 12 Schematic illustration of ITTC standard barge mode |

|
图 13 ITTC标准驳船模型中舱室进水示意图 Fig. 13 Schematic diagram of chamber water ingress in ITTC standard barge model |
|
|
表 3 ITTC标准驳船模型舱室数据 Tab.3 ITTC standard barge model cabin data |
数值计算时,R21S舱室破口与外界海洋相连通,进水舱室顺序为R21S-R21-R21P。在是否考虑空气压缩效应和非水密门影响的多种情况下对舱室进水情况进行计算,设定计算时间步长为0.05 s;数值计算过程中,考虑空气压缩效应时,R21S舱室与外界大气连通,R21/R21P舱室与外界空气密闭性良好。R21S-R21,R21-R21P舱室之间非水密门在破损前仅隔离水的进入,空气可自由流通。数值计算结果如图14~图17所示。可知:
|
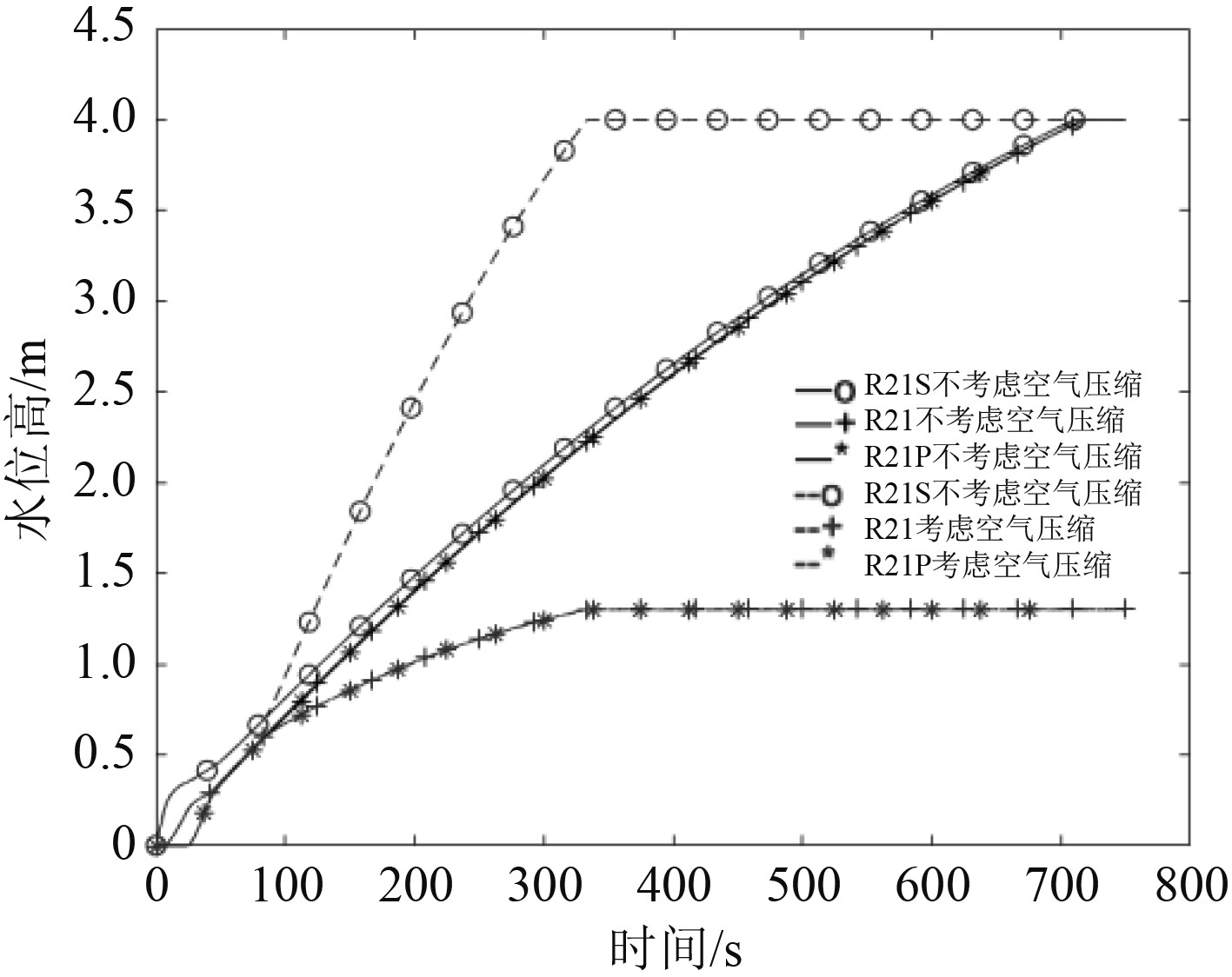
图 14 不同情况下舱室水面高度随时间的变化 Fig. 14 The height of the cabin water changes over time under different circumstances |
|
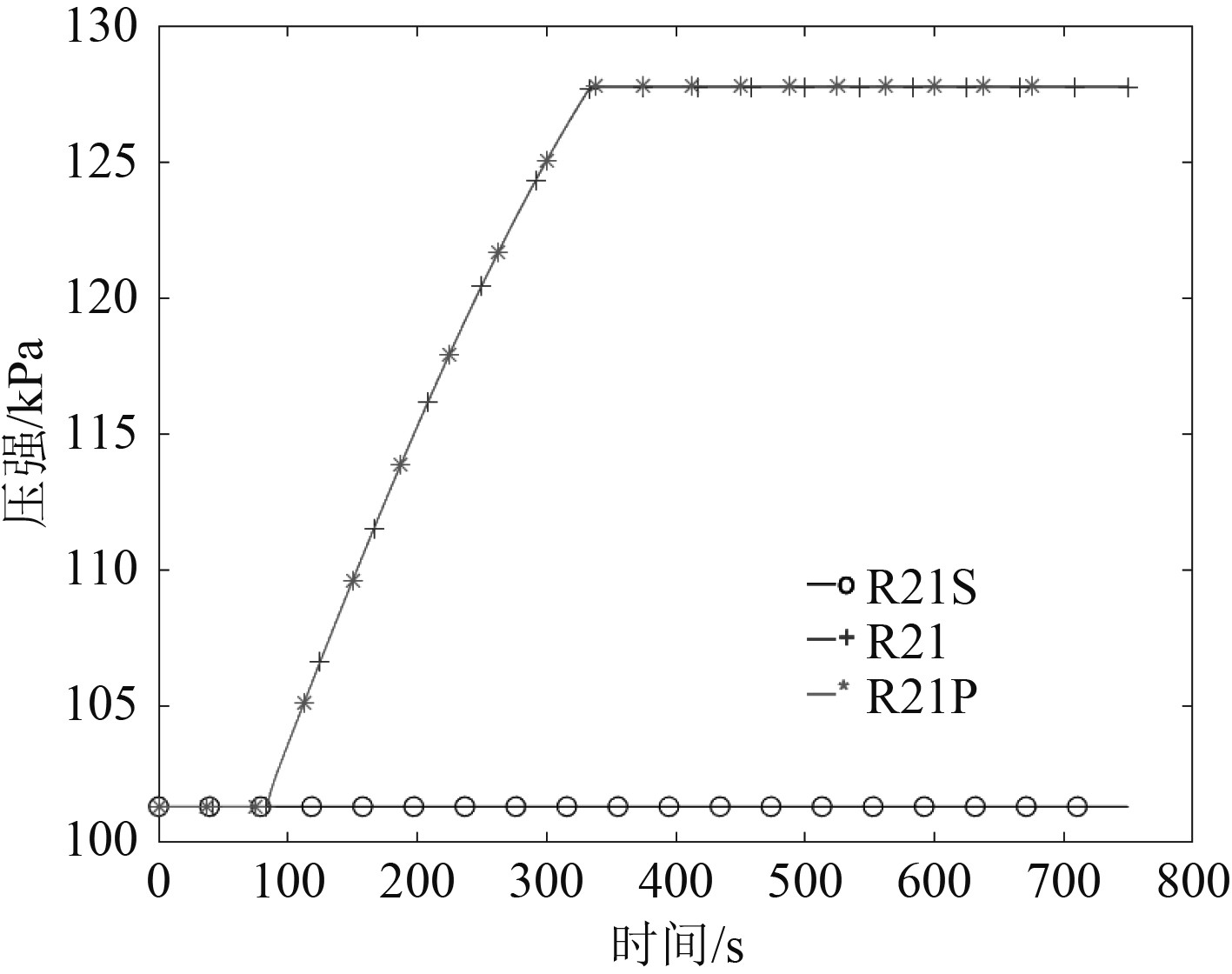
图 15 考虑空气压缩效应时舱室内压强随时间变化 Fig. 15 When considering the air compression effect the cabin pressure changes with time |
|
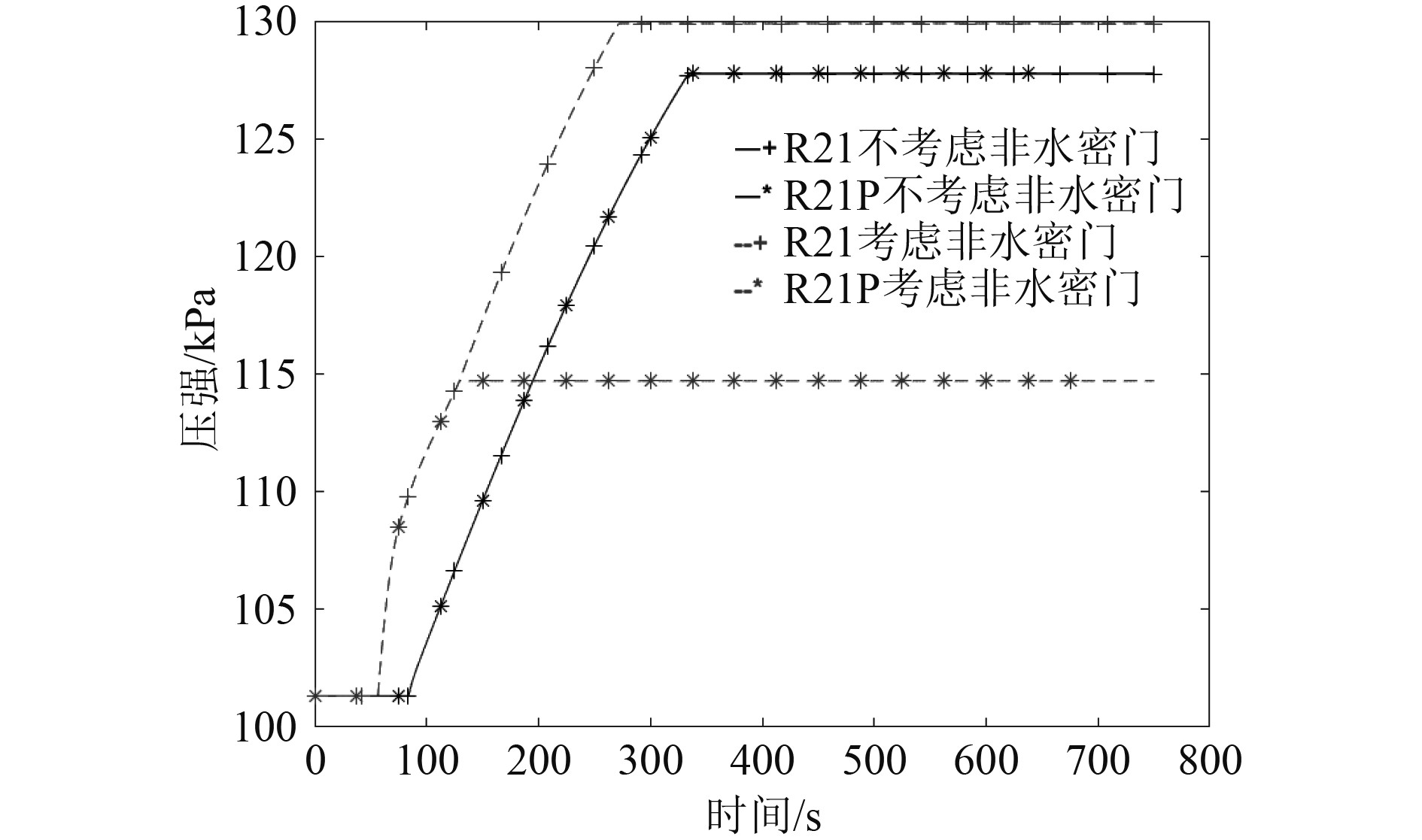
图 17 考虑空气压缩效应时是否考虑非水密门影响时舱室压强随时间的变化 Fig. 17 When considering the air compression effect, whether to consider the change of cabin pressure over time under the influence of non-watertight doors |
1)对比是否考虑空气压缩效应时的舱室平衡状态,达到进水平衡时水面高度有明显减小,由4 m减少至1.2 m。
2)舱室达到进水平衡时间明显减少,由数值计算结果可得:不考虑空气压缩效应时,开始进水后约700 s舱室进水达到平衡;考虑空气压缩效应时,开始进水后约320 s舱室进水达到平衡。数值计算得到的舱室平衡时间比不考虑空气压缩性效应时快约380 s。
3)图16表明,考虑空气压缩效应时,受到非水密门影响,R21S舱室进水达到平衡时间由320 s减少至280 s;R21舱室达到平衡时,水面高度由1.2 m减少至1.0 m,且达到平衡时间由320 s减少至280 s;R21P舱室中未进水。分析原因为:不考虑非水密门影响时,R21舱室进水高度达到0.2 m(R21-R21P舱室破口底部与舱室底部高度)后即引起R21P进水,随后R21/R21P同步进水且压强同步上升;考虑非水密门影响时,R21舱室开始进水后,R21/R21P舱室压强同步上升,但R21舱室进水高度达到0.7 m后,在R21-R21P间非水密门破损前R21P舱室压强停止变化,仅R21舱室压强随R21舱室进水的影响上升。
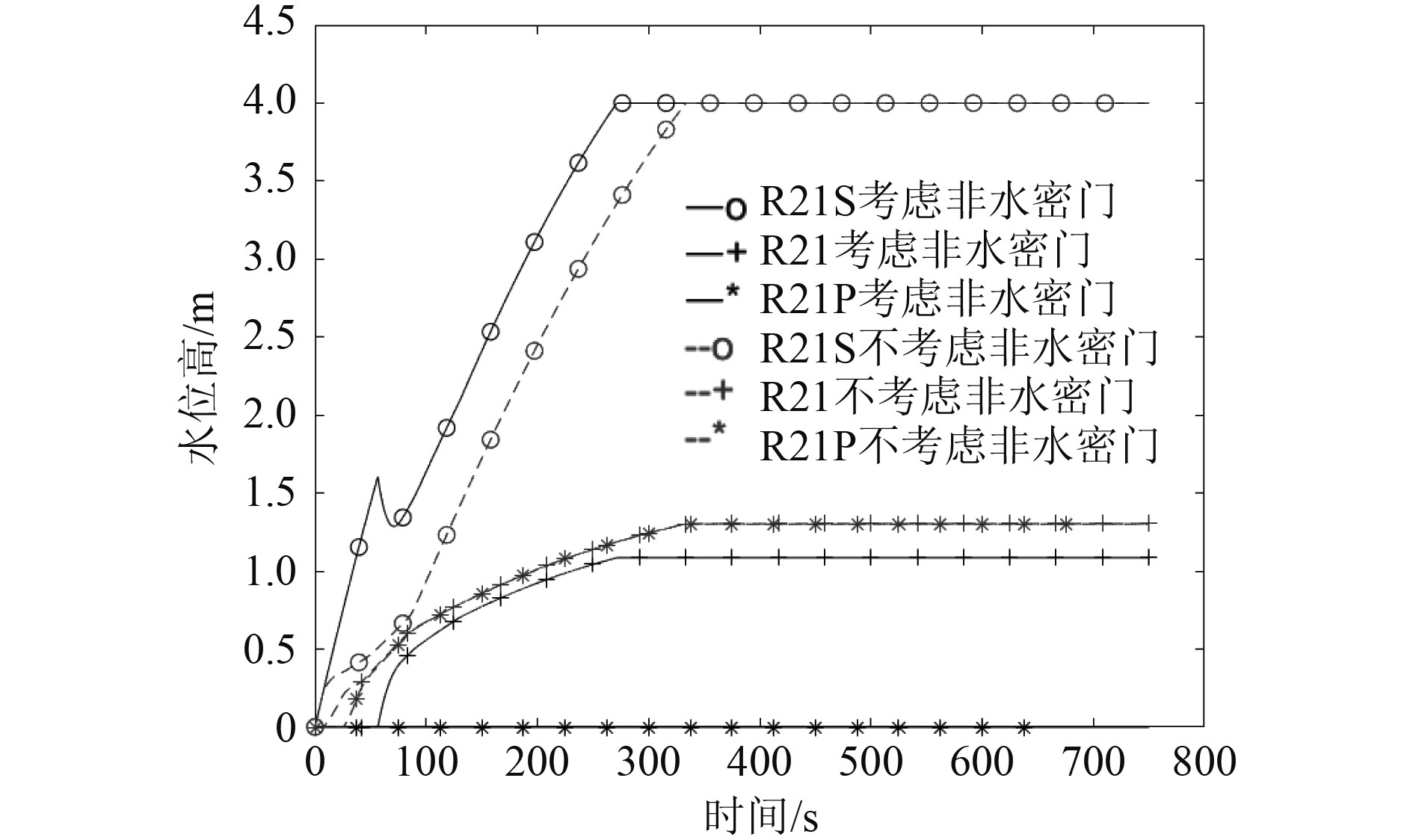
|
图 16 考虑空气压缩效应时是否考虑非水密门影响时舱室水面高度随时间的变化 Fig. 16 When considering the effect of air compression, whether to consider the change of cabin water surface height over time under the influence of non-watertight doors |
4)图17表明,考虑空气压缩效应时,受到非水密门影响,R21舱室达到平衡状态时间由320 s减少至260 s,平衡时舱室内压强由128 kPa提升至130 kPa;R21P舱室达到平衡状态时间由320 s减少至130 s,平衡时舱室内压强由128 kPa降低至115 kPa;R21与R21P舱室压强发生变化时间由90 s提升至60 s,提前30 s舱室内压强发生变化。分析原因为:受到非水密门影响R21舱室开始进水前,R21S舱室水面高度已超过R21S-R21非水密门,R21舱室开始进水即引起R21与R21P舱室压强变化;受空气压缩效应及非水密门影响,R21舱室达到平衡状态时水面高度为1.0 m,未能产生足够压力使R21-R21P非水密门损坏,导致R21P舱室压强提升至115 kPa后即达到平衡。
综上所述。当舱室被淹没时,若浸水速度很快,隔室的通风水平降低,则空气压缩效应变得显著,压缩空气将延迟溢流,严重影响破损舱室的进水过程;当舱室浸水考虑非水密门影响时,非水密门对舱室进水存在阻碍作用,将影响舱室液体流入下一个舱室,对船舶进水存在阻碍作用,对船舶进水最终状态产生影响。本文采用的数值计算方法能在较短时间内较好地模拟考虑空气压缩效应的船舶破损进水过程,为准确计算破损船舶进水特性,准确预报破损船舶浮性稳性奠定基础。
3 结 语在复杂舱室进水条件下,舱室内空气压缩形成的气穴对舱室进水速度、达到平衡时间、最终平衡状态产生较大影响;舱室之间的非水密门对船舶进水过程产生阻碍影响;在舱室密闭性良好和非水密门受力临界值较大的情况下,会阻碍水对下一个舱室的蔓延,进而对船舶破损最终状态产生影响。当舱室气体密封性较好时,空气压缩性有明显减小舱室进水量、减缓舱室进水的作用;非水密门的存在也一定程度影响舱室的进水特性。因此,在计算破损船舶稳性时,若考虑完全排出空气会过于保守,可能高估破损船舶的稳性,从而对破损后船舶状态产生乐观估计;若完全不考虑非水密门影响,可能对舱室进水过程计算产生不良影响,对破损后船舶状态产生错误估计。
此外,当前针对空气压缩效应的影响研究,主要采用CFD方法进行研究,计算时间较长,不利于破损船舶的应急决策。本文根据流体力学相关原理,采用Matlab开展程序编写与数值计算,可在极短时间内计算考虑空气压缩效应与非水密门影响的破损船舶舱室进水,并为后续相关实际应用提供基础。
下一步需要将空气压缩效应和非水密门影响与复杂系统下船舶进水浮性稳性精确计算相结合,开展破损船舶准确计算和浮稳性准确预报的数学建模和实验研究。
| [1] |
GAO Zhiliang, GAO Qiuxin, VASSALOS D. Numerical simulation of flooding of a damaged ship[J]. Ocean Engineering, 2011, 38(14-15): 1649-1662. DOI:10.1016/j.oceaneng.2011.07.020 |
| [2] |
刘强, 段文洋. 舰船破舱进水过程时域模拟[J]. 舰船科学技术, 2012, 34(3): 45−49. LIU Qiang, DUAN Wenyang. Time-domain simulation of the flooding pracess of damaged warships[J]. Ship Science and Technology, 2012, 34(3): 45−49. |
| [3] |
GAO Zhiliang, WANG Yaling, SU Yangyang, et al. Numerical study of damaged ship's compartment sinking with air compression effect[J]. Ocean Engineering, 2018, 147: 68-76. DOI:10.1016/j.oceaneng.2017.10.035 |
| [4] |
陈振, 高志亮, 刘虎. 空气可压缩性对船舶破舱进水的影响[J]. 船舶工程, 2019, 41(5): 15-19+33. CHEN Zhen, GAO Zhi-liang, LIU Hu. Influence of air compressibility on ship damaged flooding[J]. Ship Engineering, 2019, 41(5): 15-19+33. |
| [5] |
吴家俊, 李廷秋, 李杰. 基于CFD的破舱进水数值研究[J]. 中国造船, 2023, 64(2): 25−35. WU Jia-jun, LI Ting-qiu, LI Jie. Numerical study of water inflow in broken tank based on CFD[J]. Shipbuliding of China, 64(2): 25−35. |
| [6] |
RUPONEN P, TECHNOLOGY H U O. Pressure-correction method for simulation of progressive flooding and internal air flows[J]. Ship Technology Research, 2006, 53(2): 63-73. DOI:10.1179/str.2006.53.2.003 |
| [7] |
HASHIMOTO H, KAWAMURA K, SUEYOSHI M. A numerical simulation method for transient behavior of damaged ships associated with flooding[J]. Ocean Engineering, 2017, 143: 282-294. DOI:10.1016/j.oceaneng.2017.08.006 |
| [8] |
JALONEN R, RUPONEN P, WERYK M, et al. A study on leakage and collapse of non-watertight ship doors under floodwater pressure[J]. Marine Structures, 2017, 51: 188-201. DOI:10.1016/j.marstruc.2016.10.010 |
| [9] |
BU Shuxia, GU Min. Unified viscous and potential prediction method for the coupled motion of damaged ship and floodwater in calm water[J]. Ocean Engineering, 2020, 210: 107441. DOI:10.1016/j.oceaneng.2020.107441 |
| [10] |
BRAIDOTTI L, MAURO F. A fast algorithm for onboard progressive flooding simulation[J]. Journal of Marine Science and Engineering, 2020, 8(5): 369. DOI:10.3390/jmse8050369 |
| [11] |
BRAIDOTTI L. The assessment of ship damage consequences by a fast simulation of compartments flooding[D]. University of Rijeka. Faculty of Engineering, 2021.
|
| [12] |
PALAZZI L, KAT J O D. Model experiments and simulations of a damaged ship with air flow taken into account[J]. Marine Technology and Sname News, 2004, 41: 38-44. DOI:10.5957/mt1.2004.41.1.38 |
 2024, Vol. 46
2024, Vol. 46
