2. 深海技术科学太湖实验室,江苏 无锡 214082;
3. 深海载人装备国家重点实验室,江苏 无锡 214082
2. Taihu Laboratory of Deepsea Technological Science,Wuxi 214082, China;
3. State Key Laboratory of Deep-sea Manned Vehicles, Wuxi 214082, China
深海载人潜水器充分发挥了专业人员在现场的主观能动性和创造力,并具有大范围机动能力,是深海进入、探测、开发和保护的重要技术手段和装备[1],已成为海洋开发技术领域的前沿与制高点之一,极大推动了深海探测作业能力的发展[2 − 11]。
无动力潜浮是深海载人潜水器下潜和上浮的首选方式,可以大大节省潜水器的能源,提高潜水器在水下的作业时间,是潜水器水下作业能力的重要基础之一。在无动力潜浮运动研究方面,刘正元等[12-13]以标准运动模型为基础,建立潜水器大攻角运动数学模型,对载人潜水器的无动力潜浮运动进行了预报;潘彬彬等[14]在文献[12]的基础上,引入可变体积收缩率的概念,对运动数学模型进一步改进,开发了 “蛟龙号”载人潜水器的无动力潜浮运动分析系统。上述方法均建立在标准运动模型的基础上,其中的流体动力项多采用常规的多项式表达或水动力模型试验结果,由于深海载人潜水器无动力潜浮运动具有大攻角、非线性的特点,采用常规的多项式表达方式一次性表示作用于潜水器的流体动力已超出了多项式展开的适用条件,进而导致流体动力预报存在较大的误差,使得潜水器无动力潜浮运动预报存在较大偏差;如采用水动力模型试验结果,虽然可以避免流体动力项的多项式展开的影响,但由于实艇与模型之间的尺度效应,将对模型试验提出较高要求。
本文以载人潜水器受力分析为基础,基于几何相似性理论,获取载人潜水器潜浮速度与潜水器水中重力之间的关系,建立载人潜水器无动力潜浮运动预报模型。以“蛟龙”号载人潜水器为例,基于5000 m海上试验数据,训练获得“蛟龙”号潜浮运动预报模型,采用所建立的潜浮运动预报模型对7000 m无动力潜浮运动进行了预报,通过将预报结果同海上试验结果进行对比,验证了本文所建立模型的可行性和有效性,为在实际应用中对无动力潜浮运动的准确预报提供了可靠的技术手段。
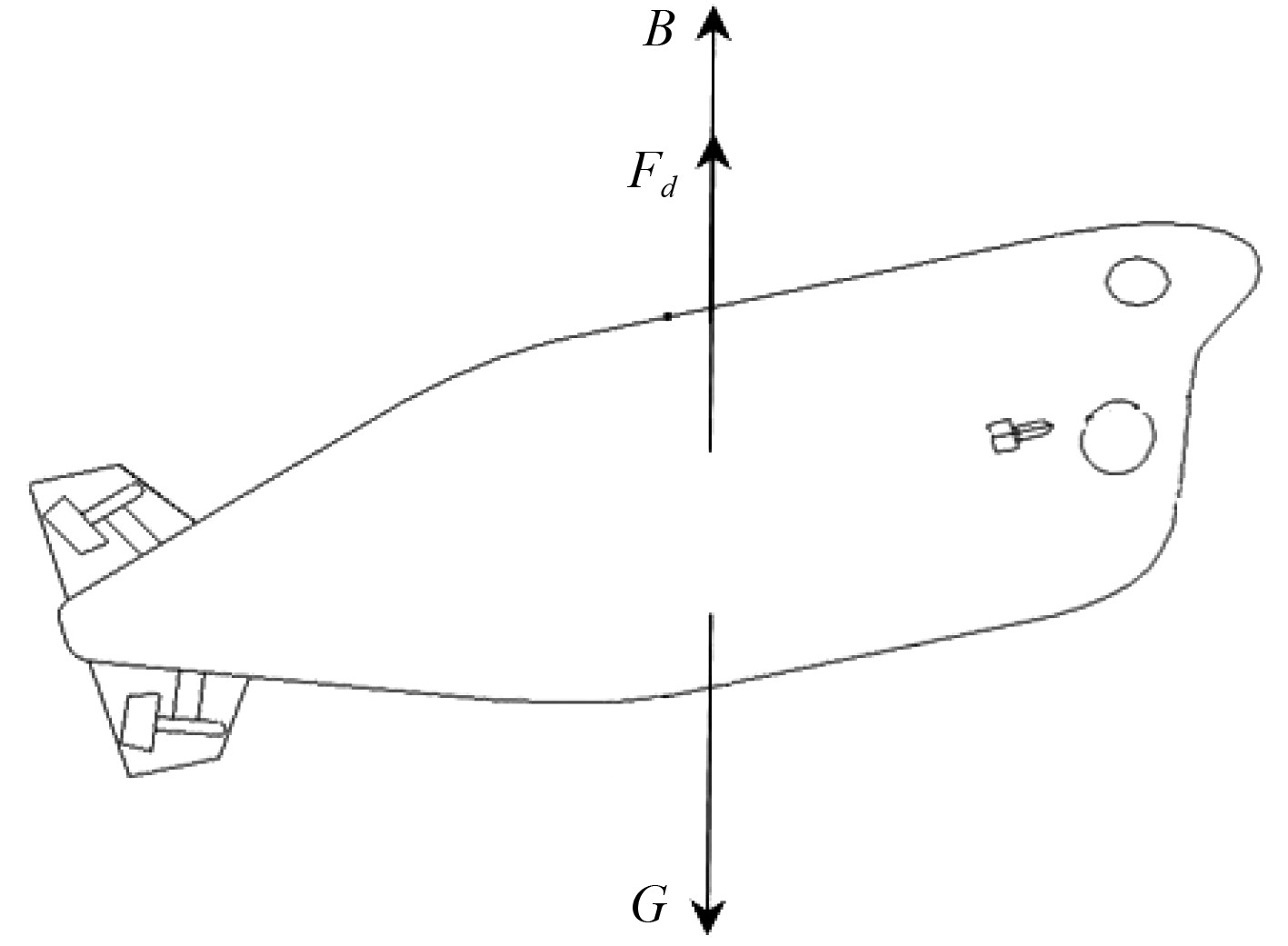
1 基于几何相似性的运动预报模型 1.1 受力分析载人潜水器在无动力潜浮运动过程中的受力情况见图1。
|
图 1 受力分析 Fig. 1 Force analysis |
可知,载人潜水器在无动力潜浮运动过程中,作用在载人潜水器上的力包括重力G、浮力B和流体动力Fd。各力之间的关系为:
| $ G + B + {F_d} = Ma 。$ | (1) |
式中:M为载人潜水器的质量;
载人潜水器的质量M由潜水器固定重量M0、可变重量(人员、舱内耗材等重量)Mc和潜浮压载重量Mad组成,可表示为:
| $ M = {M_0} + {M_c} + {M_{ad}} 。$ | (2) |
在潜浮过程中,受海水密度变化和排水体积变化的综合影响,载人潜水器的浮力可表示为:
| $ B = \rho \cdot g \cdot \left( {1 - k} \right) \cdot V 。$ | (3) |
式中:ρ为海水密度;g为重力加速度;V为载人潜水器的初始排水体积;k为排水体积损失系数。
1.2 预报模型为简化预报模型,提出如下假设:
1)深海载人潜水器的无动力潜浮运动为弱机动,属于垂直面运动;
2)载人潜水器在无动力下潜/上浮运动过程中,其运动均可近似为平稳运动,即近似认为下潜/上浮平稳阶段载人潜水器的加速度为0;
3)计算过程中,只考虑载人潜水器平稳下潜阶段和平稳上浮阶段。
结合上述假设,式(1)简化为:
| $ \left\{ \begin{gathered} {{G}_s} = -{{F}_d},\\ {{G}_s} = G + B。\\ \end{gathered} \right. $ | (4) |
式中,Gs为载人潜水器的水中重力。
由文献[15]可知,载人潜水器所受到的流体动力Fd与载人潜水器湿表面积S、潜浮速度v之间的关系为:
| $ {F_d} \propto S{v^2}。$ | (5) |
由几何相似性可知,载人潜水器的湿表面积S、排水体积V与其特征长度l之间的关系为:
| $ S \propto {l^2} ,$ | (6) |
| $ V \propto {l^3}。$ | (7) |
由式(6)和式(7)可得载人潜水器湿表面积S和排水体积V之间的关系为:
| $ S \propto {V^{2/3}}。$ | (8) |
根据几何相似中的比例性传递规则,可得载人潜水器湿表面积S与其水中重力Gs之间的关系为
| $ S \propto G_s^{2/3} 。$ | (9) |
将式(5)~式(9)代入式(4)可得:
| $ v \propto {\left( {G + B} \right)^{1/6}}。$ | (10) |
可知,载人潜水器的潜浮速度v与其水中重力的六分之一次方成比例关系,由此,可建立载人潜水器的潜浮速度v的预报模型为
| $ \left\{ \begin{gathered} v = b \cdot {\left( {Mg + B} \right)^{1/6}} + c ,\\ M = {M_0} + {M_c} + {M_{ad}} ,\\ B = \rho \cdot g \cdot \left( {1 - k} \right) \cdot V 。\\ \end{gathered} \right. $ | (11) |
式中:参数b和c通过训练样本辨识获得。
2 模型参数辨识方法运用最小二乘法对式(11)中的参数b和c进行辨识,令
| $ \left\{ \begin{gathered} x = {\left( {Mg + B} \right)^{1/6}},\\ y = v。\\ \end{gathered} \right. $ | (12) |
将式(12)代入式(11)可得:
| $ y = b \cdot x + c。$ | (13) |
假设训练样本数量为n,对于给定的n个样本
| $ R = \sum\limits_{i = 1}^n {{{\left( {{y_i} - b \cdot {x_i} - c} \right)}^2}} 。$ | (14) |
根据最小二乘准则可得:
| $ \left\{ \begin{gathered} \sum\limits_{i = 1}^n {\left( {{y_i} - b \cdot {x_i} - c} \right){x_i}} = 0 ,\\ \sum\limits_{i = 1}^n {\left( {{y_i} - b \cdot {x_i} - c} \right)} = 0 。\\ \end{gathered} \right. $ | (15) |
由式(15)可得:
| $ \left\{ \begin{gathered} b = \frac{{n\displaystyle\sum {{x_i}{y_i}} - \displaystyle\sum {{x_i}} \displaystyle\sum {{y_i}} }}{{n\displaystyle\sum {x_i^2 - {{\left( {\displaystyle\sum {{x_i}} } \right)}^2}} }} ,\\ c = \frac{{\displaystyle\sum {x_i^2\displaystyle\sum {{y_i}} } - \displaystyle\sum {{x_i}{y_i}} \displaystyle\sum {{x_i}} }}{{n\displaystyle\sum {x_i^2 - {{\left( {\displaystyle\sum {{x_i}} } \right)}^2}} }}。\\ \end{gathered} \right. $ | (16) |
以“蛟龙”号载人潜水器为研究对象,采用建立的预报模型对潜浮运动进行预报,并与海试数据比较。以“蛟龙”号载人潜水器第44潜次5000 m下潜试验数据作为训练样本,以第50潜次7000 m下潜试验数据作为对比样本。
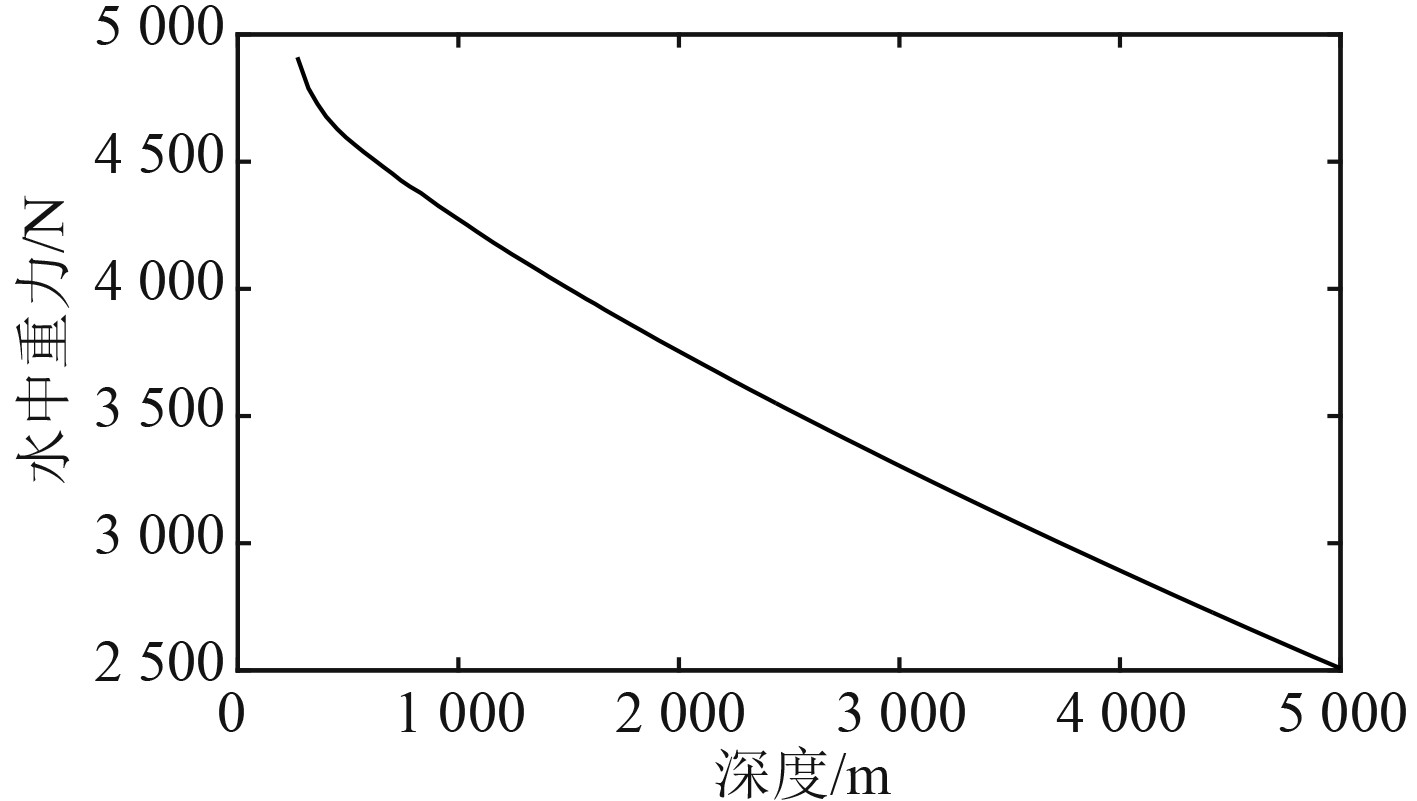
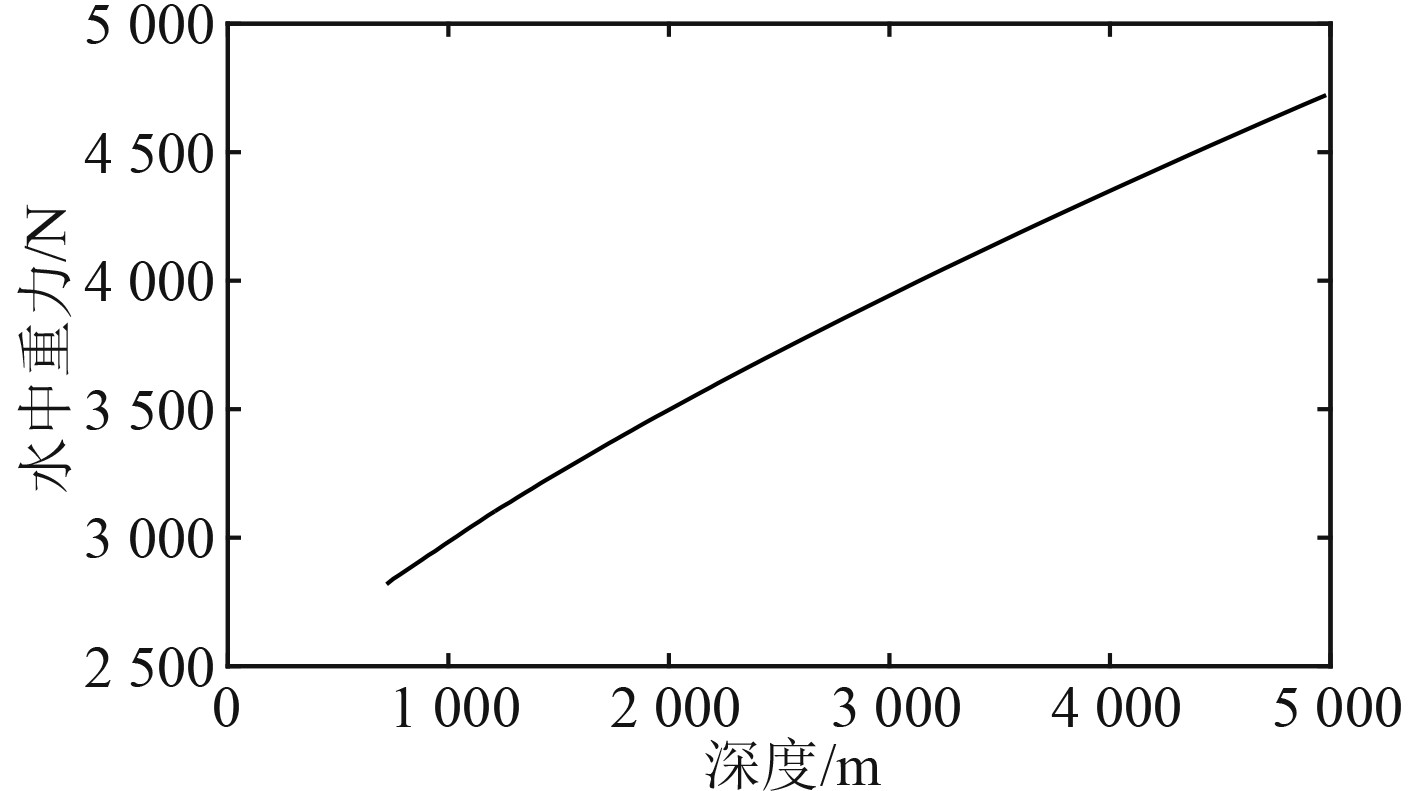
3.1 参数辨识文献[16]采用标准运动模型对“蛟龙”号载人潜水器的无动力潜浮运动进行了预报。本文根据文献[16]中的“蛟龙”号载人潜水器第44潜次5 000 m下潜试验数据,对预报模型式(11)中的参数进行辨识。在第44潜次5 000 m下潜试验中,“蛟龙”号载人潜水器潜浮运动过程中的水中重力随深度的变化曲线见图2和图3。
|
图 2 下潜过程中水中重力随深度变化曲线 Fig. 2 Gravity in water varies with depth during diving |
|
图 3 上浮过程中水中重力随深度变化曲线 Fig. 3 Gravity in water varies with depth during floating |
采用最小二乘法对预报模型式(11)中的参数进行辨识,辨识结果见表1。
|
|
表 1 预报模型参数辨识结果 Tab.1 Prediction model parameter identification results |
将辨识得到的参数导入式(11)得到“蛟龙”号载人潜水器的潜浮运动预报模型为:
| $ V = \left\{ {\begin{aligned} & {0.3171 \cdot {{\left( {Mg - B} \right)}^{1/6}} - 0.621,{\rm{下潜阶段}}},\\ & {0.3842 \cdot {{\left( {Mg - B} \right)}^{1/6}} - 0.9442,{\rm{上浮阶段}}}。\end{aligned}} \right. $ | (17) |
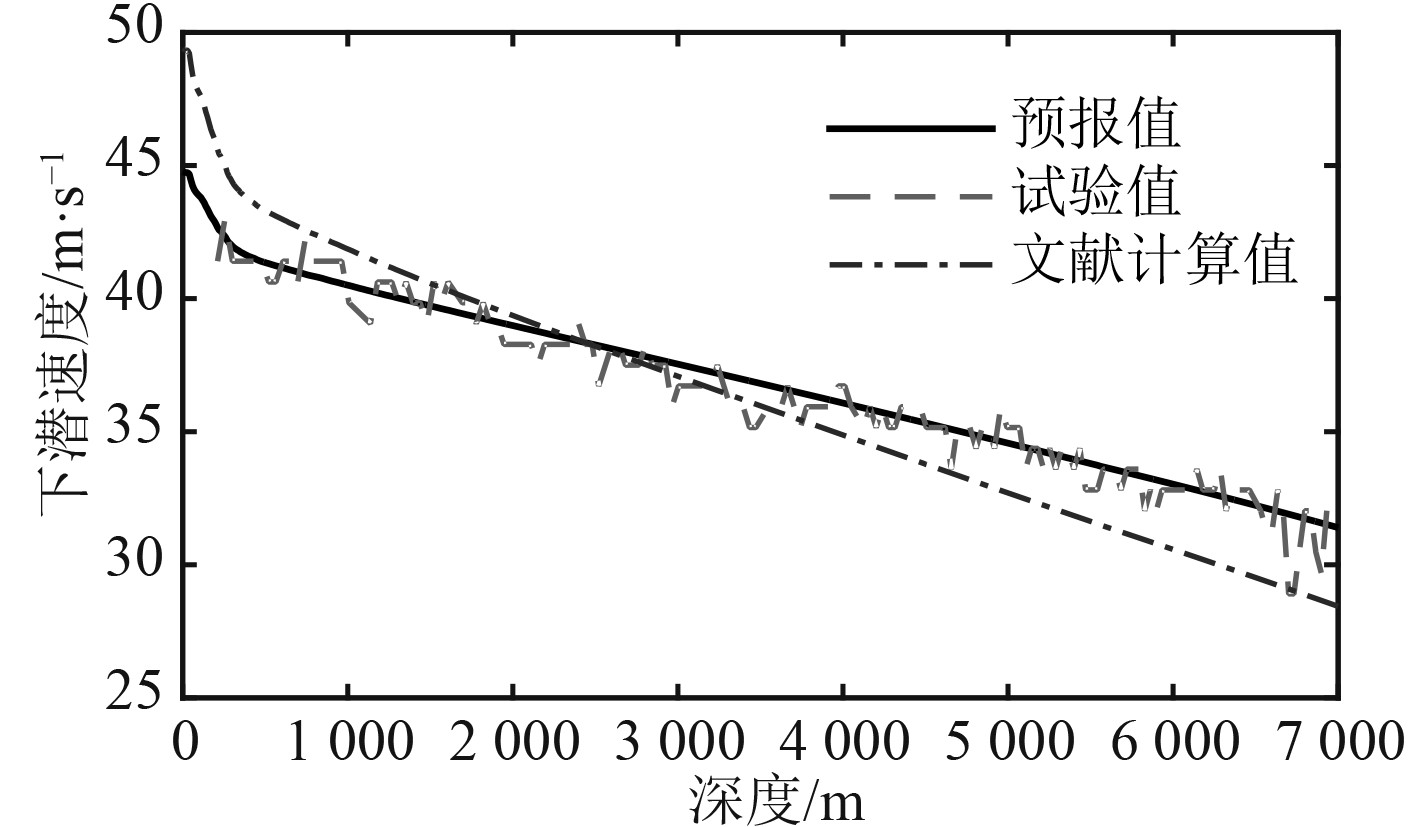
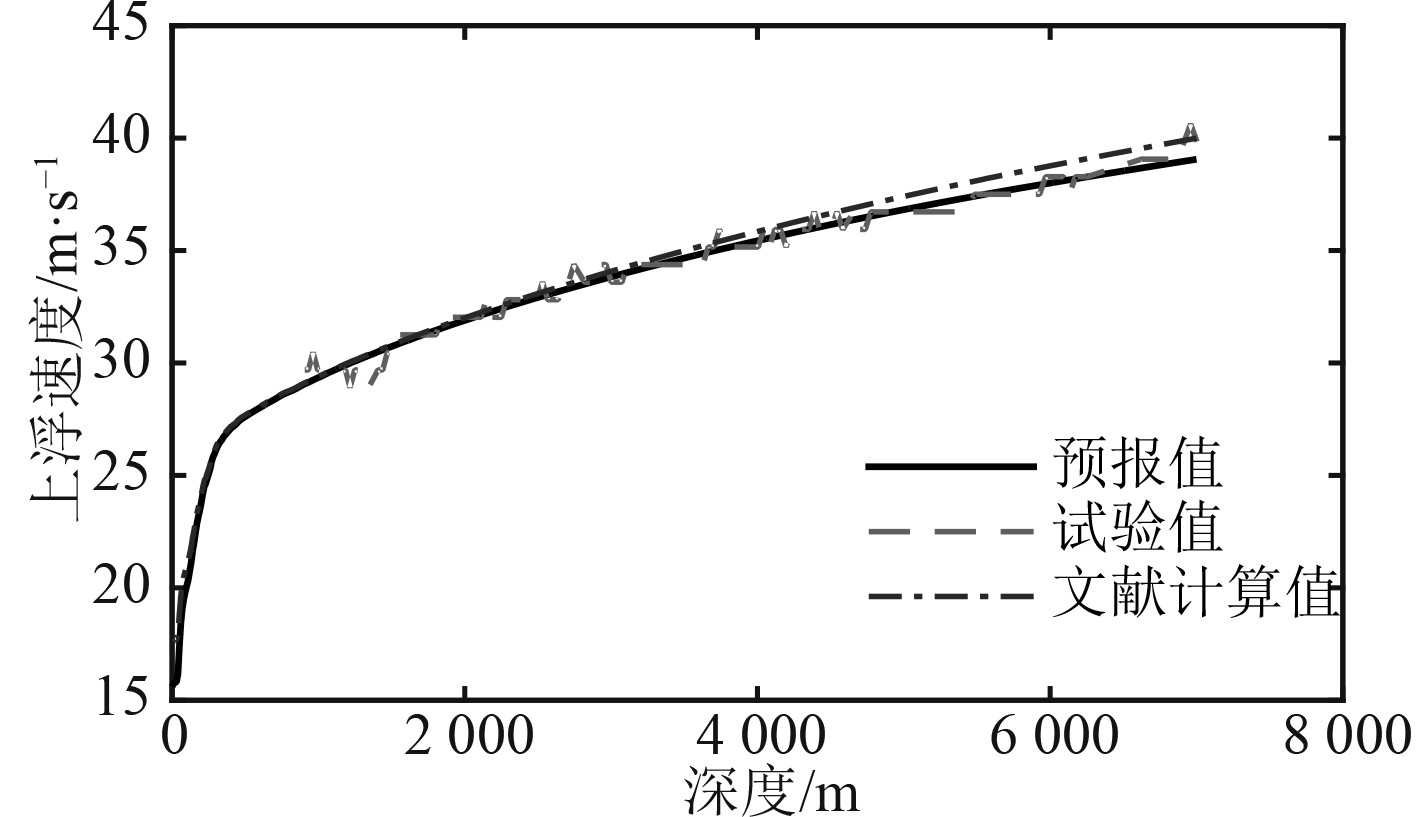
采用式(17)对“蛟龙”号载人潜水器的7 000 m潜浮运动进行预报,并与海试数据以及文献[16]中的预报结果进行对比,结果见图4和图5。
|
图 4 下潜速度预报曲线 Fig. 4 Diving speed forecast curve |
|
图 5 上浮速度预报曲线 Fig. 5 Floating speed forecast curve |
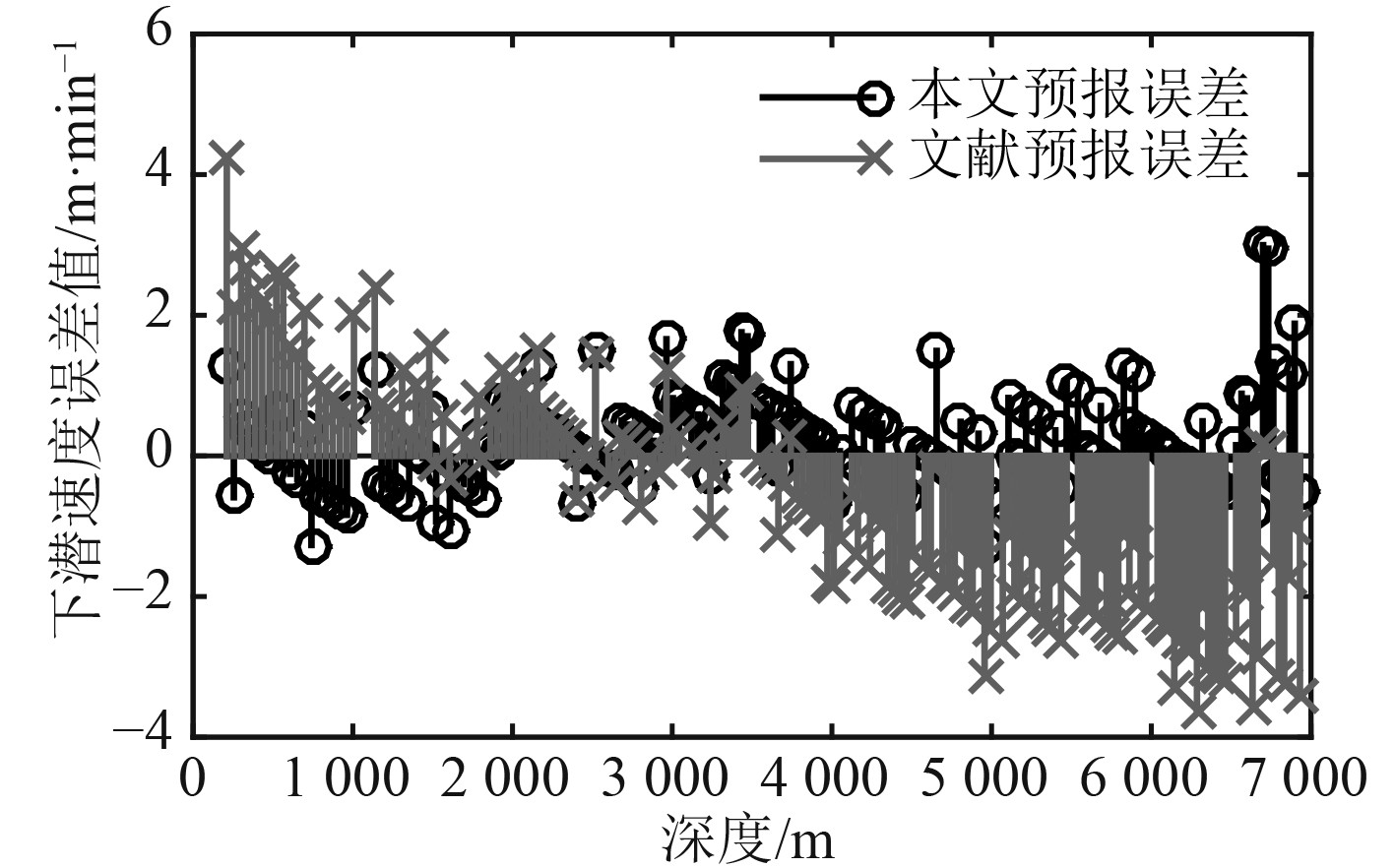
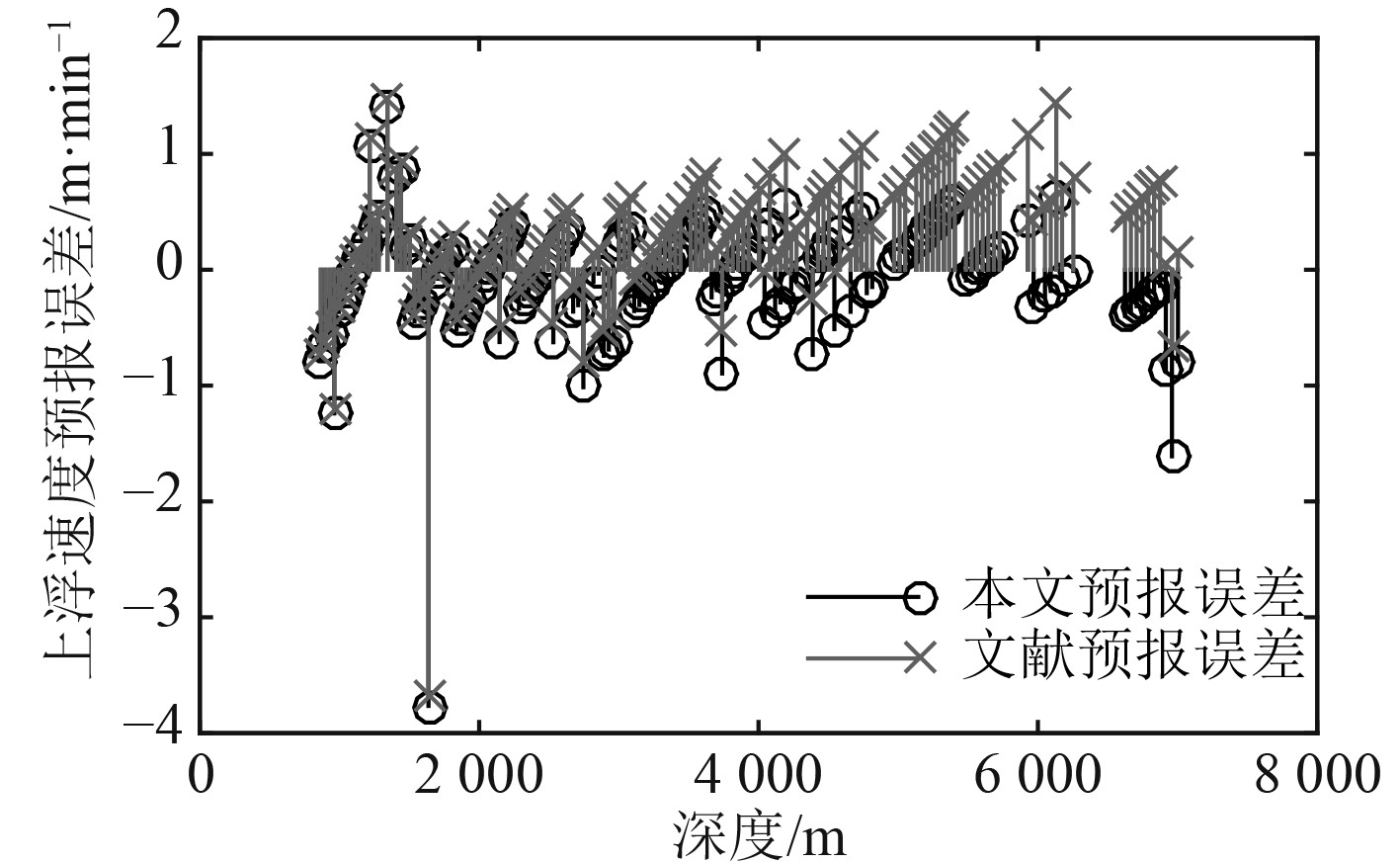
本文和文献[16]的预报结果的误差对比见图6和图7。预报均方根误差对比见表2。
|
图 6 下潜速度预报误差对比 Fig. 6 Comparison of error in prediction of diving speed |
|
图 7 上浮速度预报误差对比 Fig. 7 Comparison of error in prediction of floating speed |
|
|
表 2 2种模型的预报均方根误差对比 Tab.2 Comparison of EMS error of prediction between two model |
由图4和图5可知,采用本文建立的预报模型的预报结果与海试结果的变化趋势一致,其吻合度优于采用标准运动模型的预报结果。由图6、图7及表2可知,本文的预报误差整体小于标准运动模型的预报误差,预报精度更高,验证了本文建立的无动力潜浮运动预报模型的可行性和有效性,可以对载人潜水器的潜浮运动进行准确的预报。
4 结 语以载人潜水器受力分析为基础,引入几何相似性理论,建立了载人潜水器无动力潜浮运动预报模型。以“蛟龙”号载人潜水器为研究对象,基于5000 m海上试验数据,采用最小二乘法辨识了预报模型中的参数,并对7000 m无动力潜浮运动进行了预报,由预报结果与海上试验结果和标准运动模型预报结果的对比可知,本文建立的预报模型的预报精度优于标准运动模型的预报精度,验证了本文所建立模型的可行性和有效性,为在实际应用中对无动力潜浮运动的准确预报提供了可靠的技术手段。
| [1] |
曹俊, 胡震, 刘涛, 等. 深海潜水器装备体系现状及发展分析[J]. 中国造船, 2020, 61(1): 204-217. DOI:10.3969/j.issn.1000-4882.2020.01.021 |
| [2] |
SAGALEVITCH A. Experience of the use of manned submersibles in PP Shirshov institute of oceanology of russian academy of sciences[C]//Underwater Technology, 1988. Proceeding of the 1988 International Symposium on. IEEE, 1988: 403-407.
|
| [3] |
SAGALEVITCH A. From the bathyscaph trieste to the submersibles mir[J]. Marine Technology Society Journal, 2009, 43(5): 79-86. DOI:10.4031/MTSJ.43.5.3 |
| [4] |
NANBA N, MARIHANA H, NAKAMURA E, et al. Development of deep submergence research vehicle “SHINKAI 6500”[R]. Technology Review Mitsubish Heavy Industry Ltd, 1990, 27: 157-168.
|
| [5] |
MOMMA H. Deep ocean technology at JAMSTEC[J]. Marine Technology Society Journal, 1999, 33(4): 49-64. DOI:10.4031/MTSJ.33.4.6 |
| [6] |
崔维成, 徐芑南, 刘涛, 等. 7000 m载人潜水器研发简介[J]. 上海造船, 2008(1): 14-17. |
| [7] |
胡震, 叶聪, 杨申申, 等. 4500米载人潜水器研制[J]. 科技成果管理与研究, 2019(4): 50-51. |
| [8] |
刘涛, 王璇, 王帅, 等. 深海载人潜水器发展现状及技术进展[J]. 中国造船, 2012, 53(3): 233-243. |
| [9] |
刘保华, 丁忠军, 史先鹏, 等. 载人潜水器在深海科学考察中的应用研究进展[J]. 海洋学报, 2015, 37(10): 1-10. |
| [10] |
崔维成. 我国载人深渊器的发展策略及当前进展[J]. 江苏科技大学学报(自然科学版), 2015, 29(1): 1-9. |
| [11] |
徐伟哲, 张庆勇. 全海深潜水器的技术现状和发展综述[J]. 中国造船, 2016, 57(2): 206-221. |
| [12] |
刘正元, 沈明学, 刘涛. 深水潜器运动的非解析式数学模型[J]. 中国造船, 2010, 51(2): 92-98. |
| [13] |
MORTON G, GRANT R H. Standard equations of motion for submarine simulation [R]. AD-653861, 1967.
|
| [14] |
潘彬彬, 崔维成, 叶聪, 等. 蛟龙号载人潜水器无动力潜浮运动分析系统开发[J]. 船舶力学, 2012, 16(2): 58-71. |
| [15] |
FRANK R, WILLIAM P, STEVEN B. A first course in mathematical modeling[M]. USA: Cengage Learning, lnc, 2013.
|
| [16] |
胡中惠, 曲文新, 刘帅, 等. 载人潜水器无动力潜浮运动压载匹配方法研究[J]. 船舶力学, 2020, 24(11): 1422-1432. |
 2024, Vol. 46
2024, Vol. 46
