现代新兴科学技术以及理论的快速发展,人们从未放弃对更高性能船舶的探索和研究,水翼船、穿浪船等均是科技者不断创新研究的成果[1]。虽然船舶技术不断更新,但是现代的船舶技术距离人类的目标期盼还有很远的距离[2]。部分船舶的设计目标之间相互矛盾,船舶系统和环境之间存在信息以及能量的交换,船舶上的子系统结构也会随着船舶系统的变化而变化,并且人们的经验知识对船舶系统的影响十分明显[3]。传统的船舶设计方法基本使用母型船改造技术,这种方法只能对船舶的某些指标进行优化设计,无法使船舶的性能达到最优[4]。
1 仿生学 1.1 海豚尾部摆动运动学分析海豚在水中游行的时候,其尾部会不停的摆动以形成推进行波,海豚靠着这个行波在水中前行[5]。这种行波可以通过一条从海豚头部到尾部的正弦曲线来描述,并且该正弦曲线的幅值会随着时间的推移而增大,通过二次样条曲线拟合方法可以得到海豚的鱼体波曲线,其方程如下式。
| $ \left\{ {\begin{array}{*{20}{l}} {y = \left( {{c_1}x + {c_2}{x^2}} \right)\sin \left( {kx + \omega t} \right)},\\ {k = \dfrac{{2{\text{π}} }}{\lambda } = \dfrac{{2{\text{π}} R}}{L}} ,\\ {\omega = 2{\text{π}} f} 。\end{array}} \right. $ | (1) |
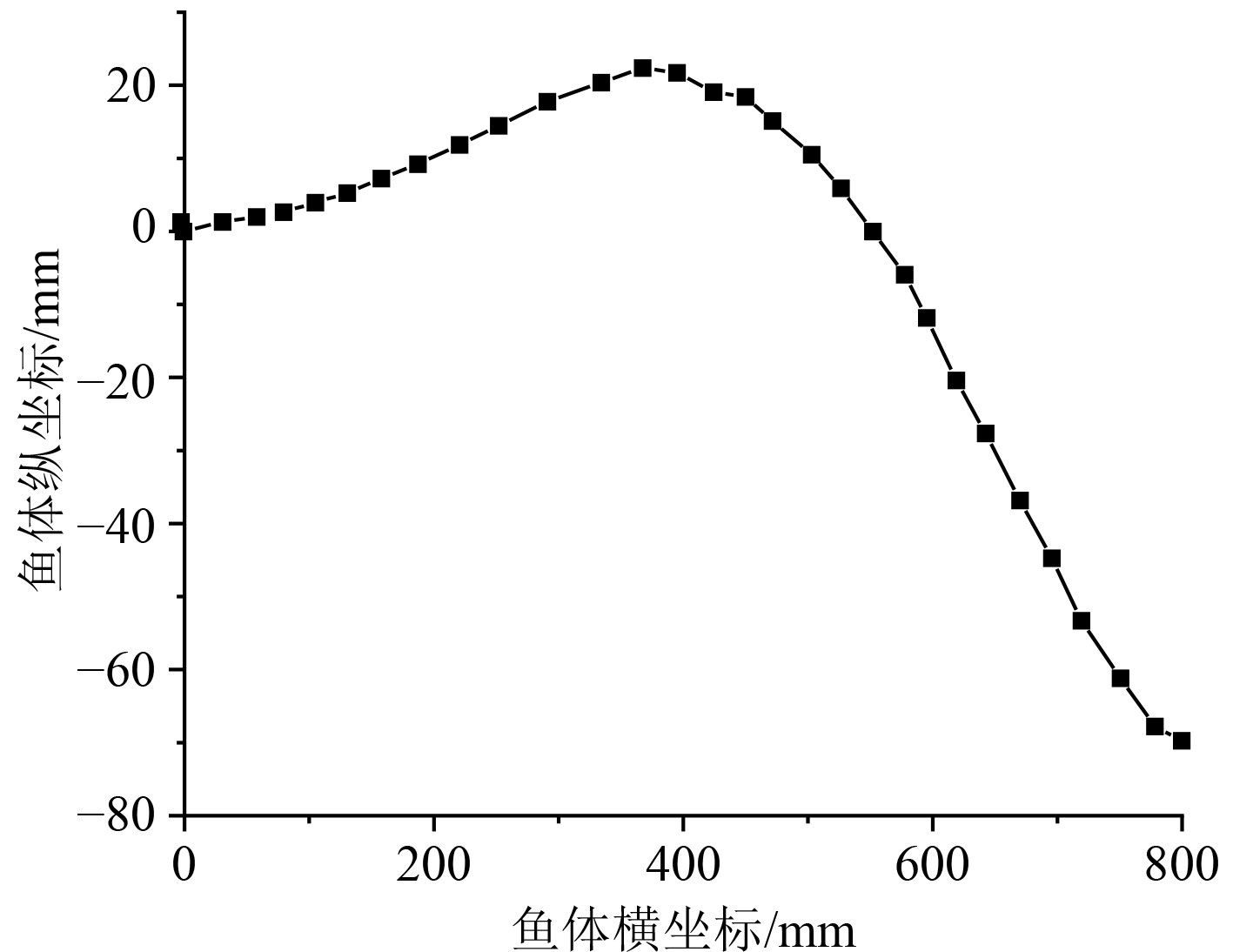
式中:R为波数;L为体长;ω为角速度;f为频率。本文c1和c2分别取值为0.4和0.6,λ取值为1。将海豚在一个摆动周期中的时间进行离散化处理,则可以得到海豚的鱼体波幅曲线,如图1所示。可以看出,海豚的鱼体波幅从头部到尾部幅值先缓慢增加然后急剧减小。
|
图 1 海豚鱼体波幅曲线 Fig. 1 Dolphin fish body wave amplitude curve |
通过学者们对海豚游泳姿态的长期分析以及大量试验,得到了海豚在水中的运动规律,该运动规律可以表示为:
| $ {Y_{\rm{body}}}\left( {x,t} \right) = {H_{\max }}g\left( x \right)\sin \left( {2{\text{π}} ft} \right)\text{。} $ | (2) |
式中:Hmax为最大摆幅;f为尾部摆动频率;g(x)为波动幅度方程;海豚在游泳的过程中,其波动幅度方程可以表示为:
| $ g\left( x \right) = 0.21 - 0.66x + 1.1{x^2} + 0.35{x^8}。$ | (3) |
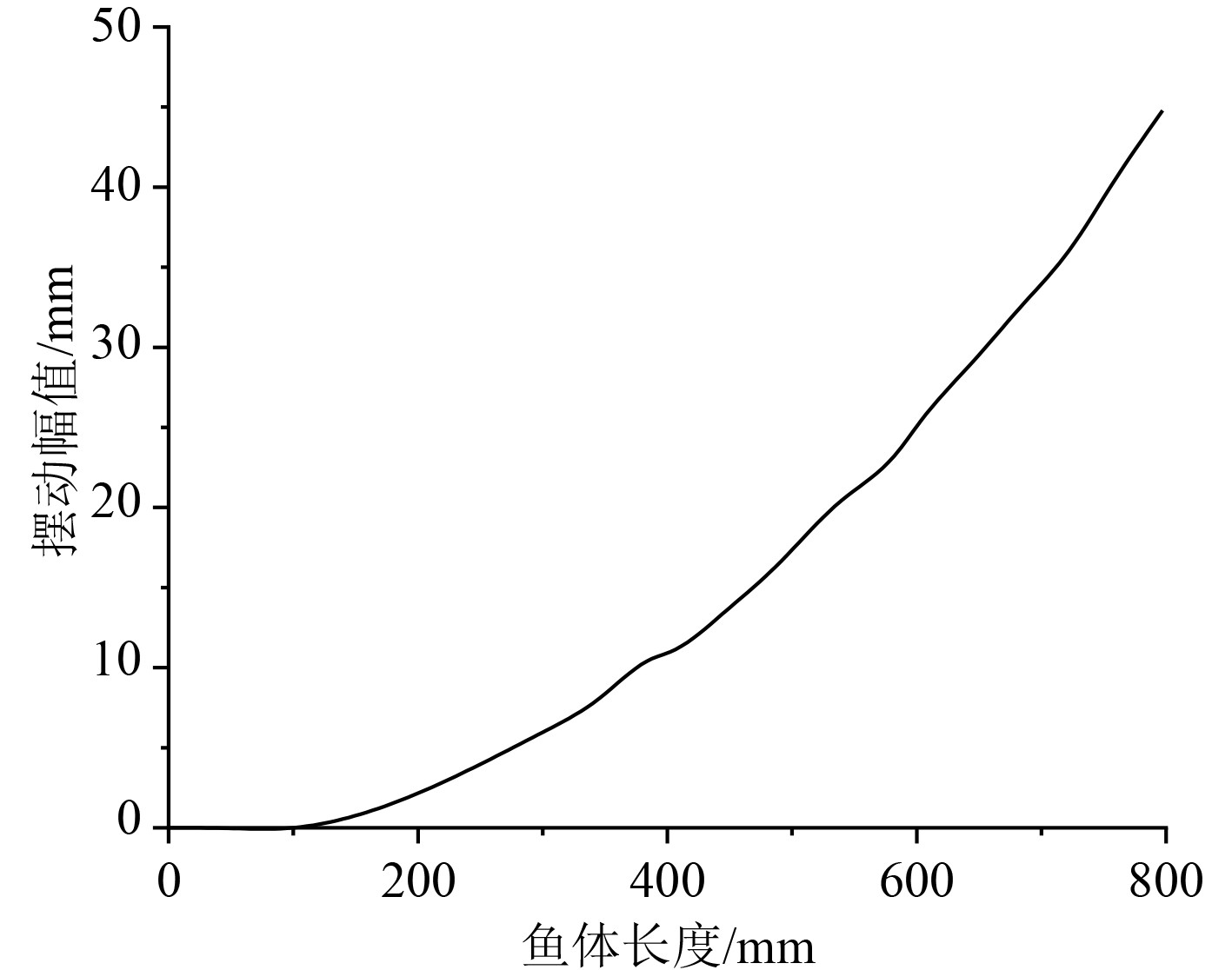
为了可以对海豚的鱼体波的曲线方程进行简化,本文提出了更加简洁的鱼体波方程,如式(4)所示。本文拟合出的海豚运动曲线如图2所示。可以看出,越靠近海豚尾部其摆动幅度越大。
|
图 2 海豚运动曲线 Fig. 2 Dolphin movement curve |
| $ g\left(x\right)=0.1-1.3x-2x^2\text{。} $ | (4) |
利用坐标变换的方法,可以构造出海豚的俯仰沉浮运动模型,其方程如下式:
| $ \left\{ {\begin{array}{*{20}{l}} {x = Ut - d\cos \left[ {\left( {\dfrac{{2{\text{π}} fH}}{U} - {\alpha _{\max }}} \right)\sin \left( {2{\text{π}} ft + \psi } \right)} \right]},\\ {y = H\sin \left( {2{\text{π}} ft} \right) - d\sin \left[ {\left( {\dfrac{{2{\text{π}} fH}}{U} - {\alpha _{\max }}} \right)\sin \left( {2{\text{π}} ft + \psi } \right)} \right]}。\end{array}} \right.$ | (5) |
式中:f为拍动的频率;H为摆动的幅度;U为游动速度;αmax为最大的击水角。利用坐标变换法可以构造出海豚做沉浮运动时的数学模型,如式(6)所示,海豚的摆动以及平动的数学模型,如式(7)所示。
| $ {y}_{尾鳍}=H\mathrm{sin}\left(2{\text{π}} ft\right)-\left(x-{x}_{\alpha }\right)\mathrm{sin}\left(2{\text{π}} ft+\psi \right) \text{,} $ | (6) |
| $ \left\{\begin{array}{*{20}{l}}Y\mathrm{_{body}}\left(x_{\alpha},t\right)=a\left(t\right)A\left(x_a\right)\sin\left[2\text{π}\left(\dfrac{t}{T}-\dfrac{x_a}{\lambda}\right)\right],\\ a\left(t\right)=\left\{\begin{array}{*{20}{l}}\dfrac{t}{T}-\dfrac{1}{2\text{π}}\sin\left(\dfrac{2\text{π}t}{T}\right),0\leqslant t\leqslant T,\\ 1,t > T。\end{array}\right.\end{array}\right. $ | (7) |
根据流体力学理论可以知道,海豚在水中游行的过程中会受到流水阻力的影响,该阻力可以表示为:
| $ {F_D} = \frac{1}{2}{C_D}{\rho _f}{\mu ^2}S。$ | (8) |
式中:CD为阻力系数;ρf为水流密度;μ为海豚游行速度;S为海豚和流水的接触面积。海豚在向前游行的过程中会出现拨水的动作,以此从水流中得到相反的作用力,然后产生诱导速度,因此可以通过动量定理对海豚的水动力性能进行研究。由于海豚的摆尾动作是唯一的前行动力来源,根据动量定理,可以得到海豚驱动模型为:
| $ {F_i}\Delta t = {m_{ft}}{v_{\alpha i}}\text{。} $ | (9) |
式中:Fi为海豚第i次摆尾产生的推力;∆t为摆尾时间;mft为推动的水流质量,其计算方法如式(10)所示;vαi为拍动速度,其计算方法如式(11)所示。海豚第i次摆尾之后的运动方程如式(12)所示。
| $ {m_{ft}} = {\rho _f}{V_i}\text{,} $ | (10) |
| $ {v_{\alpha i}} = 2{\text{π}} f{A_i}\cos \left( {2{\text{π}} ft} \right)\text{,} $ | (11) |
| $ \left\{ {\begin{array}{*{20}{l}} {{l_i} = {A_i}\sin \left( {\omega t} \right)},\\ {{\xi _i} = {\psi _i}\sin \left( {\omega t - {\phi _i}} \right)} 。\end{array}} \right. $ | (12) |
式中:li为海豚第i次摆动的位移;ω为摆动的角速度。海豚在向前游行过程中的动力学模型为:
| $ \left\{ {\begin{array}{*{20}{l}} {M{{\ddot X}_C} = F - {F_D}} ,\\ {F = \displaystyle\sum\limits_{i = 1}^4 {{F_i}} },\\ {u = {{\dot X}_C}} 。\end{array}} \right. $ | (13) |
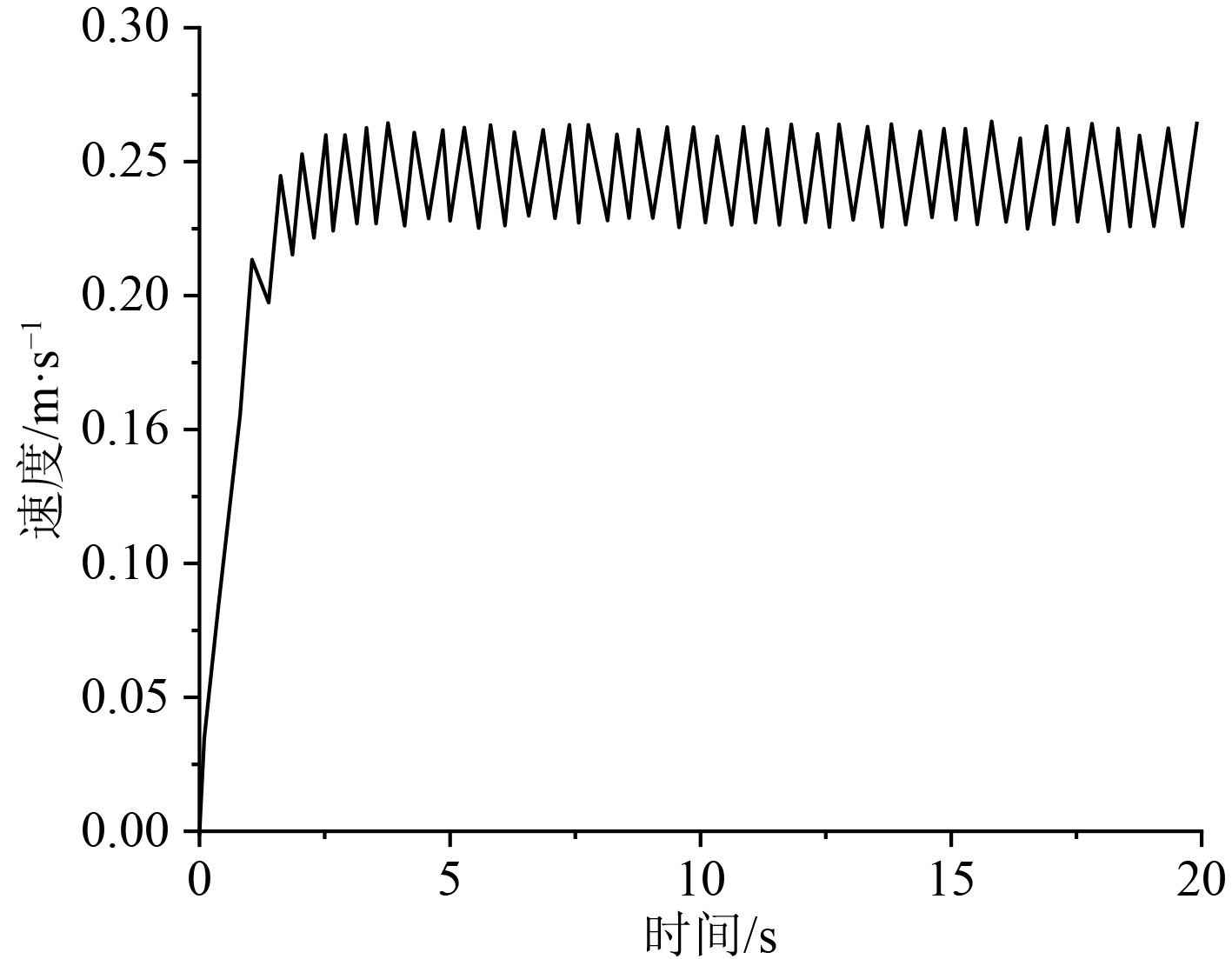
对海豚在游行过程中的动力学模型进行仿真求解,得到的瞬态速度曲线如图3所示。可以看出,海豚的游行速度一开始增长速度很快,随后趋于稳定。
|
图 3 瞬态速度变化曲线 Fig. 3 Transient velocity variation curve |
随着现代科学技术的快速发展,船舶技术研究人员想通过计算机技术进行精确且光顺的船体型线设计,以便更好地进行船舶外型设计,因此开发出了船舶的参数化设计方法[6]。船舶的参数化设计方法主要有融合技术、叠加扰动面技术以及横剖面移动技术3种[7]。这3种方法可以对船体外型进行各类变换,以构造出不同类型的船舶。融合技术的原理可以表示为:
| $ x_i^k = \sum\limits_{j = 1}^N {{w_j}x_i^j} \text{。} \\ $ | (14) |
式中,wj为融合系数,其满足:
| $ \sum\limits_{j = 1}^N {{w_j} = 1} \text{。} $ | (15) |
船体外形曲面上的控制节点可以表示为:
| $ {\xi _n}\left( {u,v} \right) = \sum\limits_{i = 0}^{{N_n} - 1} {\sum\limits_{j = 0}^{{M_n} - 1} {{J_{{N_x},i}}\left( u \right)} } {K_{M,j}}\left( v \right){\xi _{i,j}}\text{,} $ | (16) |
| $ {J_{N,i}} = \left( {\begin{array}{*{20}{c}} {{N_x} - 1} \\ i \end{array}} \right){\left( {1 - u} \right)^{{N_x} - 1 - i}}{u^i}\text{,} $ | (17) |
| $ {K_{{N_x},j}} = \left( {\begin{array}{*{20}{c}} {{M_x} - 1} \\ j \end{array}} \right){\left( {1 - v} \right)^{{M_x} - 1 - j}}{v^i}\text{。} $ | (18) |
对式(16)中的ξi,j进行调整,则可以对扰动曲面进行优化,然后利用叠加法可以得到各类船体外型。通过线性映射的关系,船舶在物理空间上的节点都能够映射到u、v空间上的某个点,其扰动矢量可以通过式(19)来解算,将该扰动矢量添加到网格点X0中之后,则可以得到扰动之后的位置值,如式(20)所示。
| $ {\wp _B} = \left( {{\xi _B},{\eta _B},{\zeta _B}} \right)\text{,} $ | (19) |
| $ {X_{{\mathrm{mod}} }} = {X_0} + {\wp _B}\text{。} $ | (20) |
假定存在n+1个控制顶点,并且节点的矢量如式(21)所示,那么其k次NURBS曲线可以用式(22)来表示。
| $ u = [{u_0},{u_1},...,{u_{n + k + 1}}]\text{,} $ | (21) |
| $ \vec p\left( u \right) = \frac{{\displaystyle\sum\limits_{i = 0}^n {{w_i}{{\bar d}_i}{N_{i,k}}\left( u \right)} }}{{\displaystyle\sum\limits_{i - 0}^n {{w_i}{N_{i,k}}\left( u \right)} }}\text{。} $ | (22) |
式中:wi为控制顶点的权重系数;Ni,k(u)为基函数。式(21)中的NURBS曲线具备局部性。NURBS曲面在u、v参数方向上的数学模型如式(23)所示。
| $ \vec p\left( {u,v} \right) = \frac{{\displaystyle\sum\limits_{i = 0}^n {\displaystyle\sum\limits_{j = 0}^m {{w_{i,j}}{{\vec d}_{ij}}{N_{i,k}}\left( u \right){N_{j,l}}\left( v \right)} } }}{{\displaystyle\sum\limits_{i = 0}^n {\displaystyle\sum\limits_{j = 0}^m {{w_{ij}}{N_{i,k}}\left( u \right){N_{j,l}}\left( v \right)} } }}\text{。} $ | (23) |
式中:wi,j为控制顶点di,j的权重系数,并且四角上的权重系数为正数,即w0,0、wm,0、w0,n、wm,n均大于0,其余权重系数的取值不小于0;Ni,k(u)为u向k次基函数;Nj,l(v)为v向l次基函数。光顺的曲线需要满足:
| $ {{\mathrm{d}}^2}z = \frac{{{\partial ^2}z}}{{\partial {x^2}}}{{{\mathrm{d}}}}{x^2} + 2\frac{{{\partial ^2}z}}{{\partial x\partial y}}{\rm{d}}x{\rm{d}}y + \frac{{{\partial ^2}z}}{{\partial {y^2}}}{\rm{d}}{y^2}\text{。} $ | (24) |
为了能够降低船舶曲线生成过程中涉及到的参数数量,本文提出一种船舶修改的融合方法。在融合过程中需要确保权重系数之和等于1,融合公式可以表示为:
| $ p = \sum\limits_{i = 1}^n {{C_i} \times {P_i}} \text{。} $ | (25) |
式中:n为母型船舶的个数;Ci为权重系数,并且需满足
| $ \sum\limits_{i = 1}^n {{C_i} = 1} \text{。} $ | (26) |
采用Shipflow软件对船舶阻力进行解算,船舶在航行过程中受到的总阻力:
| $ {R_t} = {R_{vp}} + {R_f} + {R_w}\text{。} $ | (27) |
船舶受到的总阻力中的摩擦阻力和粘压阻力的和可以用式(28)来表示,k为形状因子,可以使用式(29)来估算。
| $ {R_f} + {R_{vp}} = {R_f}(1 + k)\text{,} $ | (28) |
| $ 1 + k = {c_1}\left\{ {0.93 + {c_2}{{\left( {\frac{B}{{{L_R}}}} \right)}^{0.93}}{{\left( {0.95 - {C_p}} \right)}^{ - 0.52}}} \right\}\text{。} $ | (29) |
式中,LR为流段长度,其值可以通过式(30)估算。
| $ \frac{{{L_R}}}{L} = 1 - {C_p} + \frac{{0.06{C_p}{l_{cb}}}}{{4{C_p} - 1}}\text{。} $ | (30) |
船舶的粗糙度补贴系数可以使用式(31)来计算,ks取值为150×10−3。
| $ \Delta {C_f} = \left[ {105 \times {{\left( {\frac{{{k_s}}}{L}} \right)}^{\frac{1}{3}}} - 0.64} \right] \times {10^{ - 3}}\text{。} $ | (31) |
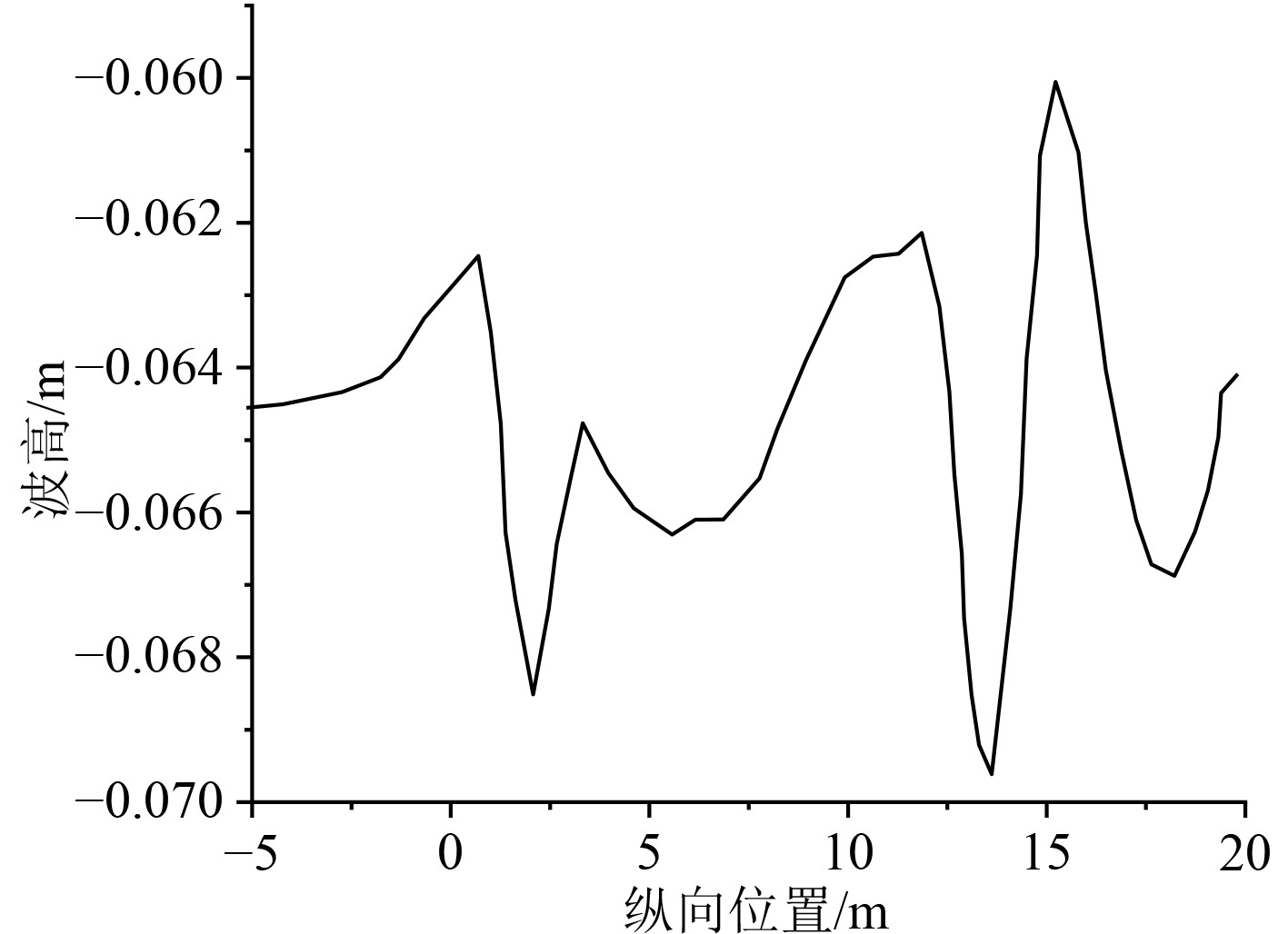
船舶受到的兴波阻力可以通过式(32)来计算。仿真得到的船舶舷侧纵切波形曲线如图4所示,可以看出,最小的波高出现在纵向位置约为14 m的地方。
|
图 4 船舶舷侧纵切波形曲线 Fig. 4 Ship side longitudinal shear waveform curve |
| $ {R_w} = {C_w} \cdot \frac{1}{2}\rho {V^2}S\text{。} $ | (32) |
船舶在航行过程中受到的阻力随船舶航速的变化曲线如图5所示。可以看出,随着船舶航速的提升,船舶受到的阻力也会变大,并且当船舶的航行速度超过19 km/h之后,其受到的阻力上升速度会明显加快。

|
图 5 不同航速下阻力的变化曲线 Fig. 5 The variation curve of resistance under different sailing speeds |
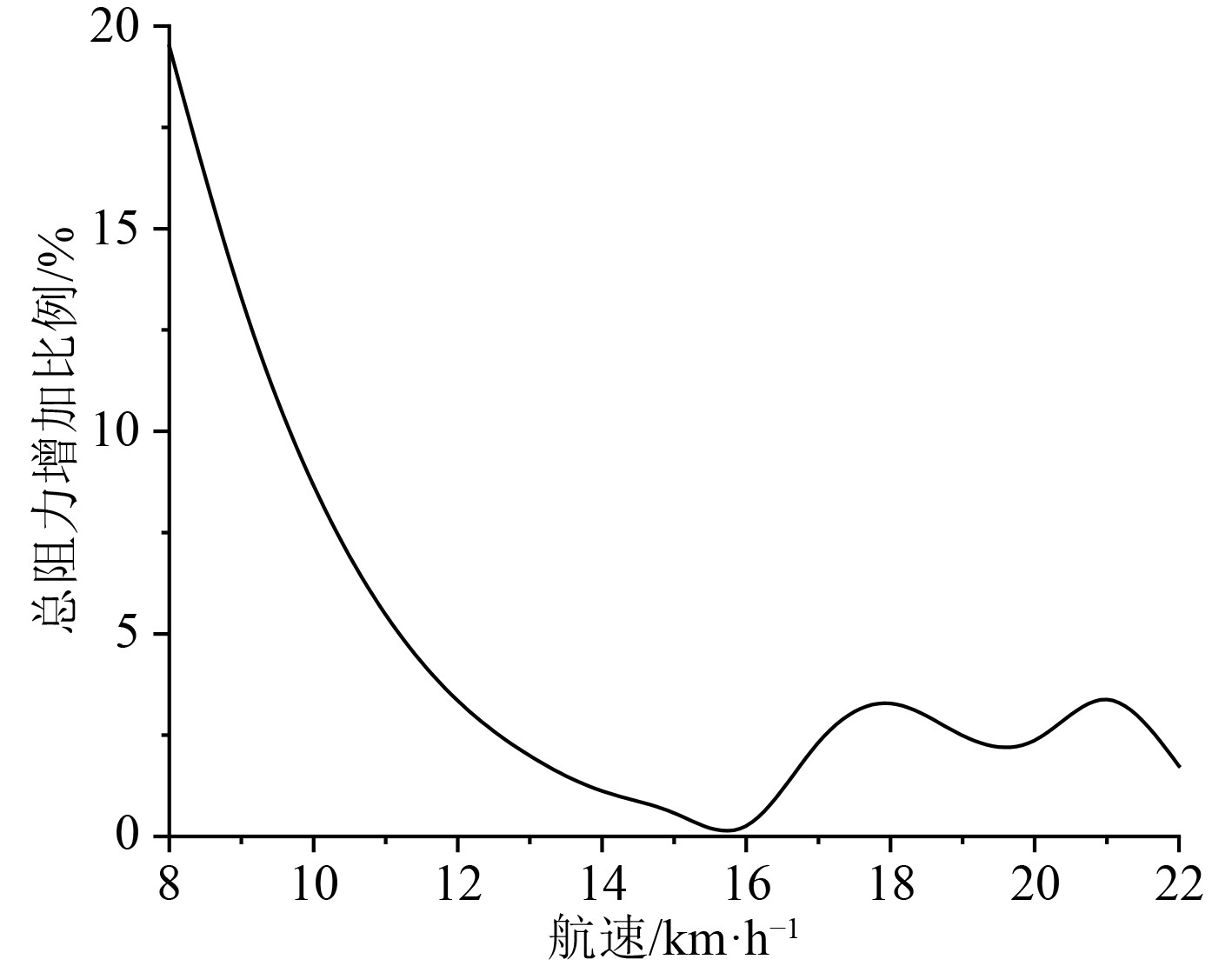
船舶外型优化之后的阻力增加比例随船舶航速的变化曲线如图6所示,刚开始的时候,随着航速的提升,阻力增长比例会快速的降低。
|
图 6 不同航速下阻力增加比例的变化曲线 Fig. 6 The variation curve of the proportion of resistance increase at different speeds |
船舶技术不断前进的动力主要来自对新设计方法的不断探索。构成船舶复杂系统的各个子系统之间相互依存并且高度集成,因此船舶上的某个子系统一旦发生变化,则会引起其他子系统的连锁反应,子系统之间的这种强耦合性极大地增加了船舶设计者解决问题的难度,同样也使得船舶的系统数量变得很大。因此船舶的结构设计是一种多属性的复杂工程。本文基于仿生学,对船舶的外型设计进行研究,这有助于简化船舶系统设计结构,以促进我国船舶外型设计技术的快速发展。
| [1] |
孙久荣, 戴振东. 仿生学的现状和未来[J]. 生物物理学报, 2007(23): 109-115. SUN Jiu-rong, DAI Zhen-dong. Bionics today and tomottow[J]. Acta Biophysica Sinica, 2007(23): 109-115. |
| [2] |
马楷东, 张瑞荣, 郭鑫, 等. 仿双髻鲨头部的仿生机器鱼外型设计及其流场特性[J]. 力学学报, 2021(12): 3389-3398. MA Kai-dong, ZHANG Rui-dong, GUO Xin, et al. Shape design and flow field characteristics of a robotic fish imitating the head of a hammerhead[J]. Chinese Joutnal of Theoretical and Applied Mechanics, 2021(12): 3389-3398. |
| [3] |
金鸿章, 巩晋, 李冬松. 仿驼背鲸减摇鳍升力数值计算[J]. 中国造船, 2009(4): 22-27. JIN Hong-zhang, GONG Jin, LI Dong-song. Numerical simulation on imitation humpback whale fin stabilizer lift[J]. Shipbuilding of China, 2009(4): 22-27. |
| [4] |
褚福锋. 基于NURBS曲线与曲面光顺理论的船体设计与优化[J]. 舰船科学技术, 2022(11): 27-30. CHU Fu-feng. Hull design and optimization based on NURBS curve and surface fairing theory[J]. Ship Science and Technology, 2022(11): 27-30. |
| [5] |
孙华, 李鹏展, 齐方利, 等. 双体船不同状态流场特性与力学性能仿真[J]. 舰船科学技术, 2022(23): 6-11. SUN Hua, LI Peng-zhan, QI Fang-li, et al. Numerical simulation of flow field charcateristics and mechanical properties of catamarian in different states[J]. Ship Science and Technology, 2022(23): 6-11. |
| [6] |
刁宏伟, 李宗吉, 王世哲, 等. 水下滑翔机研究现状及发展[J]. 舰船科学技术, 2022, 44(6): 8−12. DIAO Hong-wei, LI Zong-ji, WANG Shi-zhe, et al. The research status and development trend of underwater glider[J]. Ship Science and Technology, 2022, 44(6): 8−12. |
| [7] |
吕帮俊, 黄斌, 彭利坤. 水下航行器模型参数辨识技术[J]. 舰船科学技术, 2023(15): 81-86. LV Bang-jin, HUANG Bin, PENG Li-kun. Underwater vehicle model parameters identification technology[J]. Ship Science and Technology, 2023(15): 81-86. |
 2024, Vol. 46
2024, Vol. 46
