0 引　言

船舶在海洋中航行会受到多种因素的影响，如海浪、海风和海流等，这些因素会导致船舶偏离预定的航向。为了确保安全并优化航行效率，需要尽量减少航向偏差。因此，船舶航向控制是船舶控制中的重要环节^[1-2]。

针对航向控制问题，李伟等^[3]使用分数阶滑膜控制方法，根据船舶的动态特性自适应地调整航向控制策略，提高航向的控制精度和稳定性。此方法具有快速响应的特点，能够快速跟踪船舶的目标航向，减小航向偏差。但分数阶滑模控制方法涉及复杂的数学理论和计算，实现起来相对复杂，需要较高的技术水平。陆潇杨等^[4]在航向控制问题中，引入漂角修正，可以减小因船舶重力速度方向与航向不一致而导致的航向偏差，提高航向控制的精度。并采用输入饱和限制，可以确保控制输入力矩始终保持在较小值范围内，避免过大的控制力矩对船舶造成不利影响。虽然该方法考虑了外部干扰对航向的影响，但在极端天气或复杂海洋环境下，外部干扰可能超出系统的处理能力，导致航向控制性能下降。Islam等^[5]研究了基于深度Q网络算法的航向控制方法，可通过学习大量数据优化航向控制策略，可快速适应新的海况，并减少对人工干预的需求。但深度Q网络算法需要大量数据进行训练和优化，而这在某些情况下可能难以获得。Sivaraj等^[6]研究基于粒子群优化的船舶航向控制方法，粒子群优化算法能够通过迭代搜索，找到最优的航向保持控制参数，提高船舶的航向保持性能。但粒子群优化算法的计算复杂度较高，需要大量计算资源。对于资源受限的船舶系统，可能难以实现高效的优化。

为此，本文研究一种考虑横向风浪干扰的舰船航向稳定性自动控制算法，并设计船舶航向控制效果分析实验，分析其可用性。

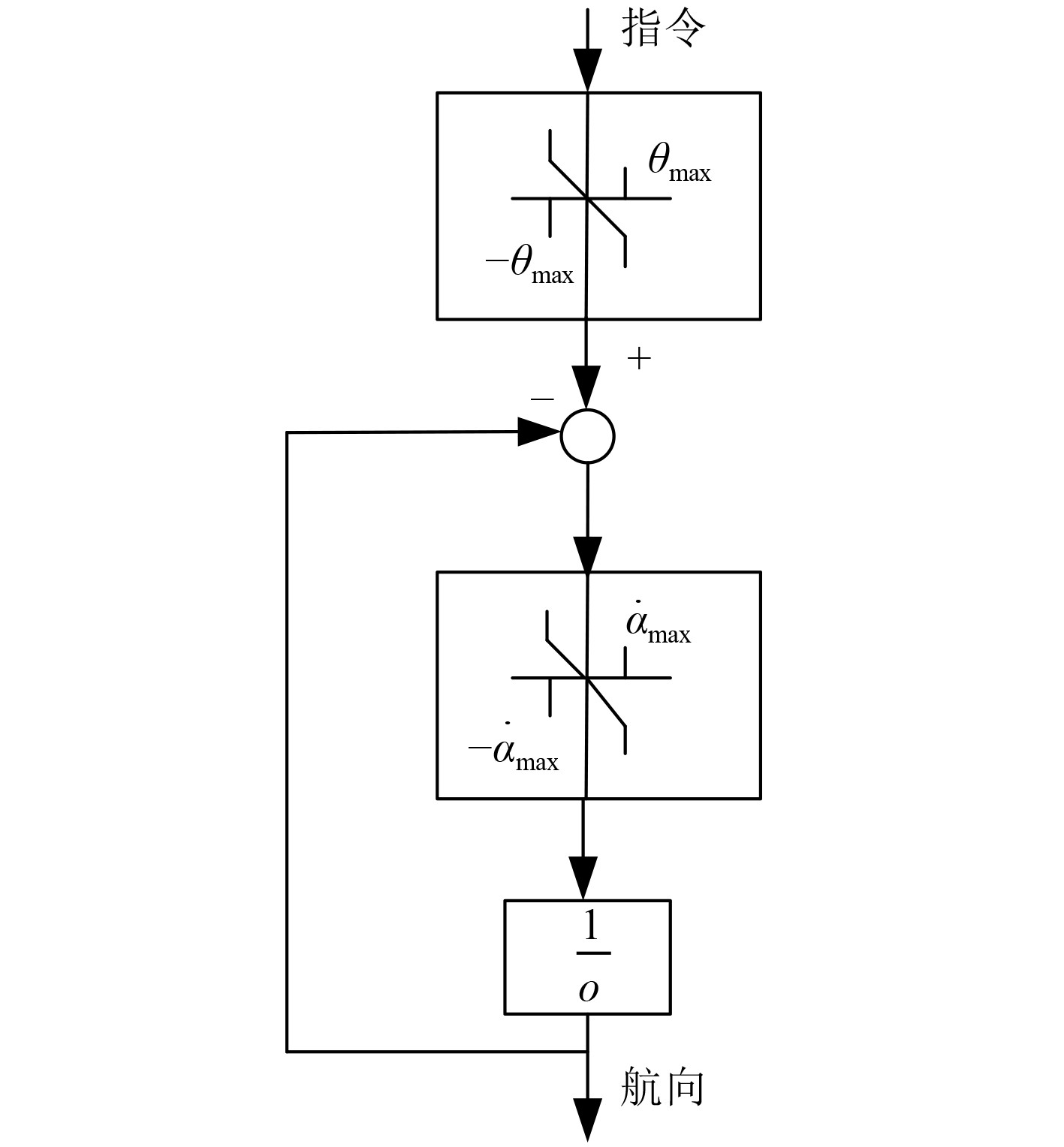
1 舰船航向稳定性自动控制算法 1.1 舵机模型设计

舰船航向稳定性自动控制，主要通过舰船的舵机系统完成，图1为舵机控制回路结构图。

主要描述舰船在遭遇横向风浪干扰时，操作控制回路的运行状态^[7]。主要受极限舵角$ {\theta _{\max }} $、极限舵速$ {\dot \alpha _{\max }} $所约束。当舵机处于不饱和状态时，舵机的动态性能$ o $可表达为一阶惯性，则饱和特征表达为饱和函数$ {\mathrm{sat}}\left( \cdot \right) $：

$ {\text{sat}}\left( o \right) = \left\{ {\begin{array}{*{20}{c}} {\Delta ,}&{{\rm{if}}}\;{o > \Delta }，\\ {o,}&{{\rm{if}}}\;{\left| o \right| ＝ \Delta ,}\\ { - \Delta ,}&{{\rm{if}}}\;{o < \Delta 。} \end{array}} \right. $

(1)

1.2 横向风浪干扰建模

舰船航行时，若海面出现横向风浪干扰，此时舰船会出现横摇运动状态。在舵机模型中使用线性化海浪模型，对横向风浪干扰建模：

$ {\varpi _a}\left( t \right) = \frac{{2\beta {\varpi _0}{\delta _1}t}}{{{t^2} + 2\beta {\varpi _0}t + \varpi _0^2}}\varpi \left( t \right) ，$

(2)

$ {\varpi _b}\left( t \right) = \frac{{2\beta {\varpi _0}{\delta _2}t}}{{{t^2} + 2\beta {\varpi _0}t + \varpi _0^2}}\varpi \left( t \right)。$

(3)

式中：$ \varpi \left( t \right) $为$ t $时刻零均值的Gaussian白噪声；$ {\delta _j} = \left\{ {{\delta _1},{\delta _2}} \right\} $、$ {\varpi _0} $分别为横向风浪强度、主导海浪频率；$ \beta $为阻尼系数；$ {\varpi _a}\left( t \right) $、$ {\varpi _b}\left( t \right) $分别为$ t $时刻横向风浪对舰船横摇、首摇的扰动。

1.3 考虑横向风浪干扰的舰船航向控制算法 1.3.1 期望航向分析

横向风浪干扰下，设置舰船的期望航向$ {\varepsilon _s} $为：

$ {\varepsilon _s} = {\tan ^{ - 1}}\left( {\frac{{{X_B} - {X_A}}}{{{Y_B} - {Y_A}}}} \right)。$

(4)

式中：$ {X_A} $、$ {X_B} $分别为舰船起点与终点的横坐标；$ {Y_A} $、$ {Y_B} $分别为舰船起点与终点的纵坐标。

舰船的航向偏差是其和航迹线之间的垂直距离，为防止舰船多次打舵，设置其航行过程中，准许的航向误差是$ \Delta e $。考虑横向风浪干扰时，为控制舰船航向稳定，引入航向修正角$ \Delta \varepsilon $，此时期望的航向角$ {\varepsilon _{{M_s}}} $为：

$ {\varepsilon _{{M_s}}} = {\varepsilon _s} + \Delta \varepsilon。$

(5)

1.3.2 航向控制器设计

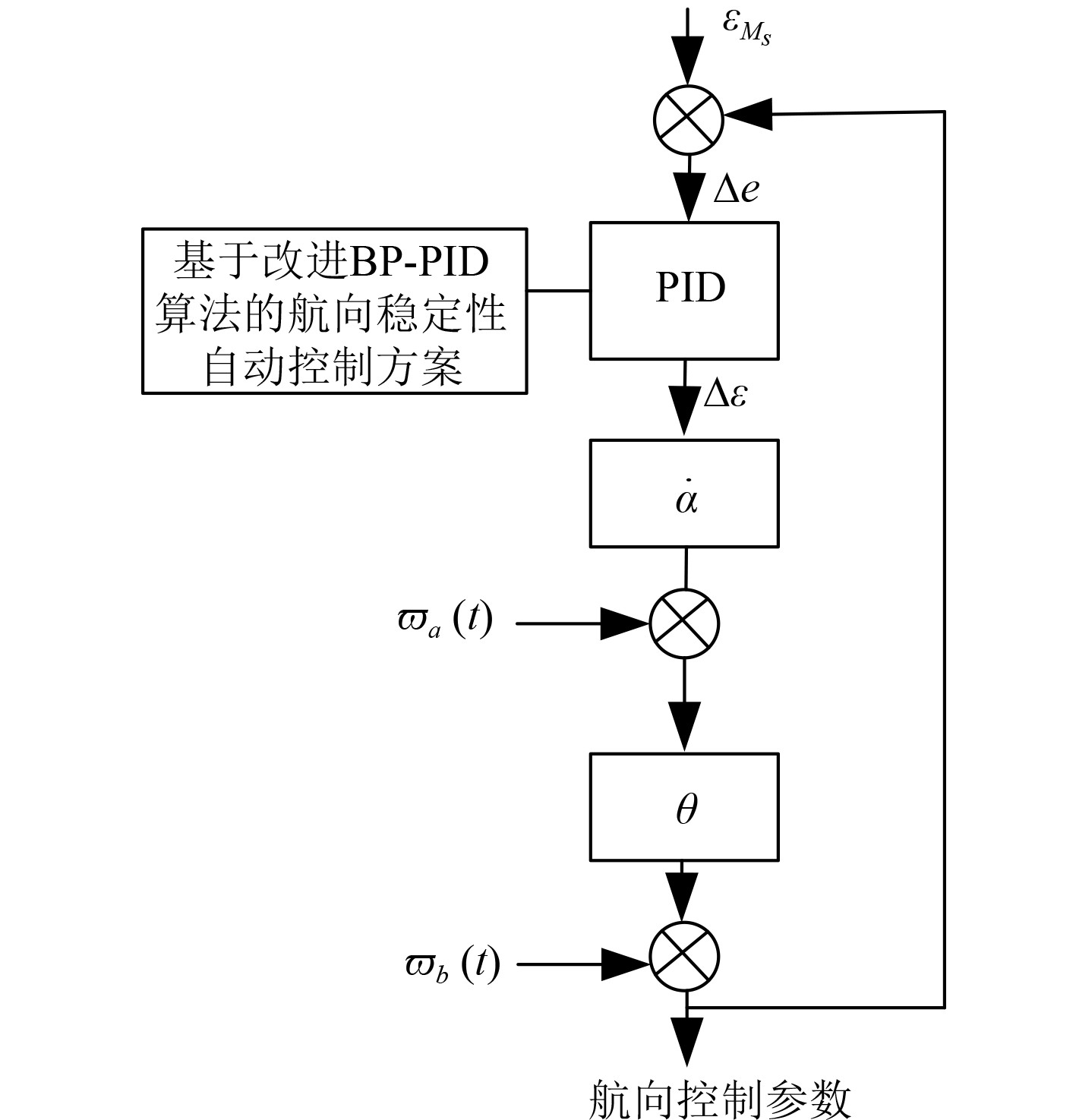
在期望航向的设定下，设计航向控制器。图2为考虑横向风浪干扰的舰船航向稳定控制器结构，$ \dot \alpha $、$ \theta $分别为舵速与舵角。

1.3.3 基于改进BP-PID算法的航向稳定性自动控制方案设计

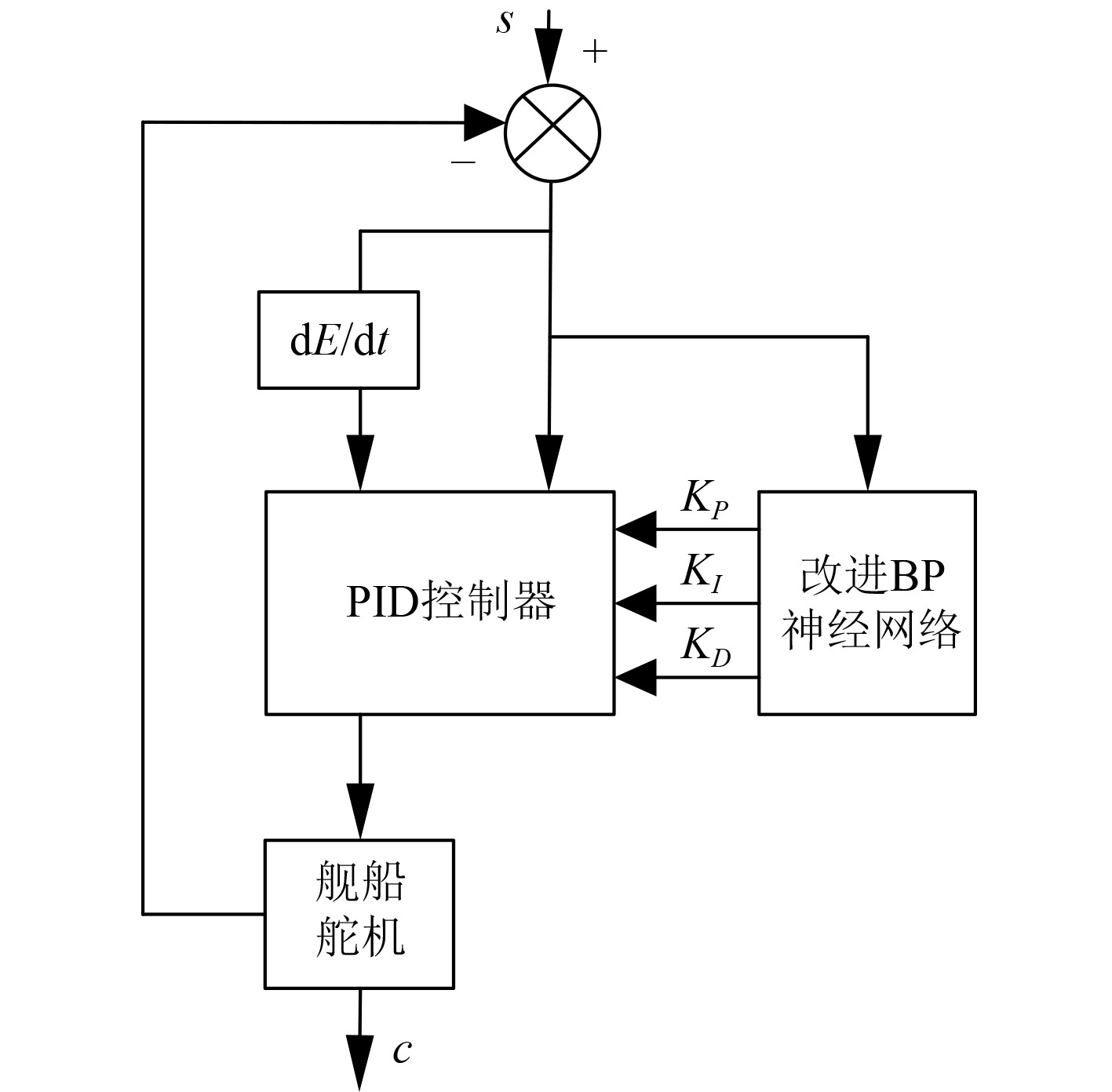
图2中，PID控制器为考虑横向风浪干扰的舰船航向稳定控制器的核心设备^[8]。为了实现航向稳定性自动控制，在PID控制器中引入基于改进BP-PID算法的航向稳定性自动控制方案，其运行原理如图3所示。

BP神经网络中存在4个神经元，依次是PID控制器的理想输出$ s $、实际输出$ c $、偏差$ E = s - c $、航向偏差对时间的导数$ \mathrm{d}E/\mathrm{d}t $。输出层存在3个神经元，依次是PID控制器的比例系数$ {K_P} $、积分系数$ {K_I} $、微分系数$ {K_D} $。PID控制器的离散化公式为：

$ \begin{split} c\left( t \right) = & c\left( {t - 1} \right) + {K_P}\left[ {E\left( t \right) - E\left( {t - 1} \right)} \right] + \\ & {K_I}E\left( t \right) + {K_D}\left[ {E\left( t \right) - 2E\left( {t - 1} \right) + E\left( {t - 2} \right)} \right]，\end{split} $

(6)

$ E\left( t \right) = s\left( t \right) - c\left( t \right)。$

(7)

式中：$ c\left( t \right) $为$ t $时刻控制器的控制量，该变量可调节$ {K_P} $、$ {K_I} $、$ {K_D} $的值。

为寻找PID控制器的最优控制率，本文使用改进BP神经网络，整定PID控制参数。传统式BP神经网络使用固定的学习率，会出现收敛效率低这一问题，导致舰船航向控制效率受到影响。为此，引入动量项，改进BP神经网络的学习率调节方法，用于修正BP神经网络连接权重$ \Omega $的变化状态，修正公式为：

$ \Delta\Omega\left(t\right)=-g\frac{\mathrm{\partial}E\left(t\right)}{\mathrm{\partial}\Omega}+\rho_1\Delta\Omega\left(t-1\right)。$

(8)

式中：$ \Delta \Omega \left( t \right) $、$ E\left( t \right) $依次为$ t $时刻的权重变化量、误差项；$ {\rho _1} $为动量因子；$ g $为学习率。为提高BP神经网络的收敛效率，降低PID控制参数的振荡变化幅度，引入$ \left( {t - 2} \right) $的权重变化量，则权重更新为：

$ \Delta\Omega\left(t\right) = -\left(1 + \rho_1\right)g\frac{\mathrm{\partial}E\left(t\right)}{\mathrm{\partial}\Omega} + \rho_1\Delta\Omega\left(t - 1\right) + \rho_2\Delta\Omega\left(t - 2\right)。$

(9)

基于改进BP-PID算法的航向稳定性自动控制方案的步骤为：

步骤1　使用式（8）、式（9）运算改进BP神经网络结构，设置输入层节点数、隐含层节点数。

步骤2　对PID控制器输入航向控制时，理想航向中，舵速与舵角的理想输出$ s = \left\{ {\dot \alpha ,\theta } \right\} $，以及实际输出$ c $。

步骤3　运算改进BP神经网络每层神经元的输入、输出。输出即为PID控制器的$ {K_P} $、$ {K_I} $、$ {K_D} $。

步骤4　由式（6）运算提取PID控制器的输出。结合式（6）提取的$ {K_P} $、$ {K_I} $、$ {K_D} $，调节横向风量干扰时舰船航行的舵速与舵角，完成考虑横向风浪干扰的舰船航向稳定性自动控制。

2 实验分析 2.1 实验参数设计

为测试本文算法的使用效果，使用舰船运动模拟器模拟测试本文算法在舰船航向稳定性控制中的使用效果。表1和表2为在舰船运动模拟器设置的舰船模型参数信息。

2.2 航向控制效果测试

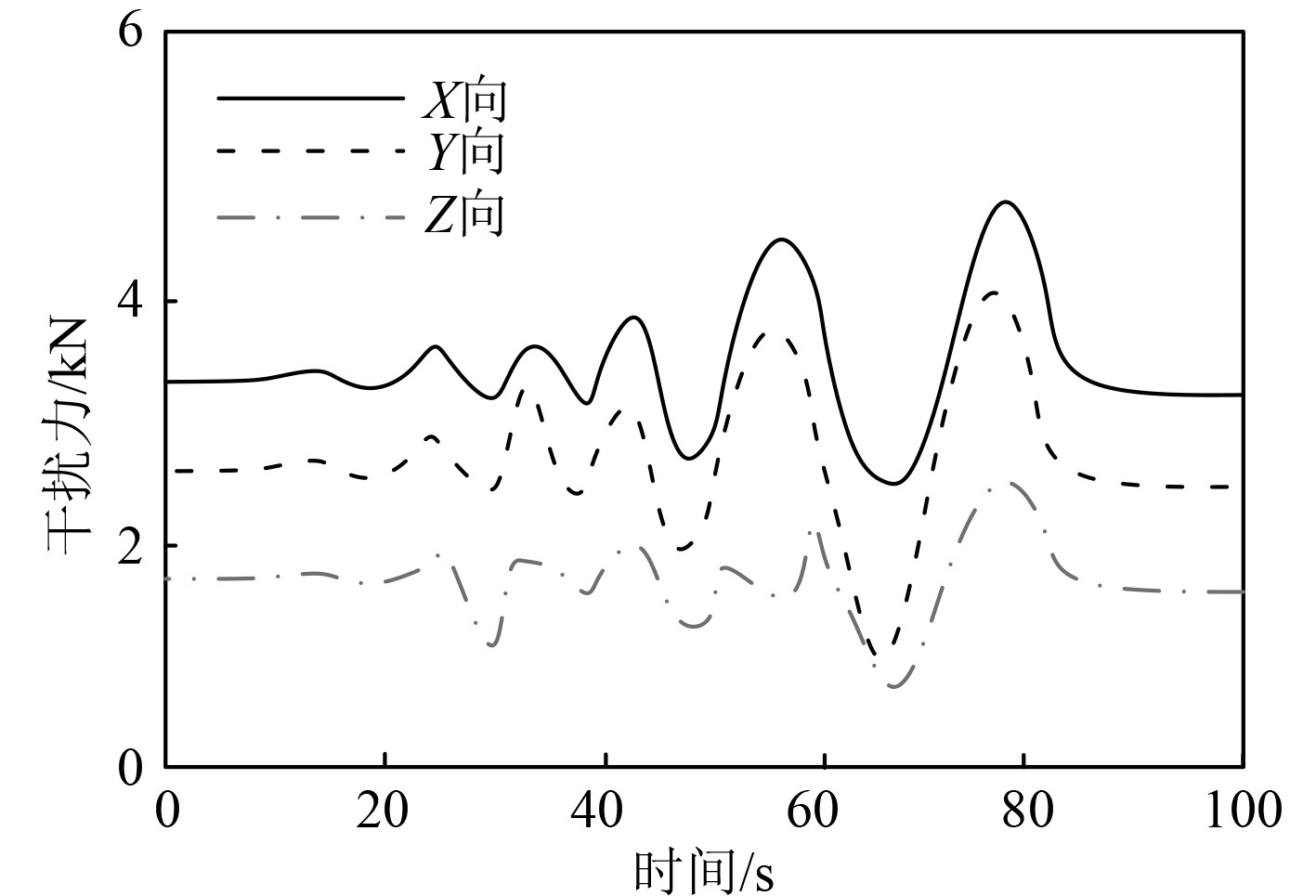
在舰船运动模拟器中，设置海面高度为20 m的横向风速为5 m/s，浪向角设为10°，航速为20 kn，此时海浪功率谱能量聚集于低频[0.25,1.55]Hz范围内，模拟器时域控制回路时间是0.001 s，采样频率是550 Hz，图4为模拟的横向风浪出现时，舰船受到的干扰力状态示意图。

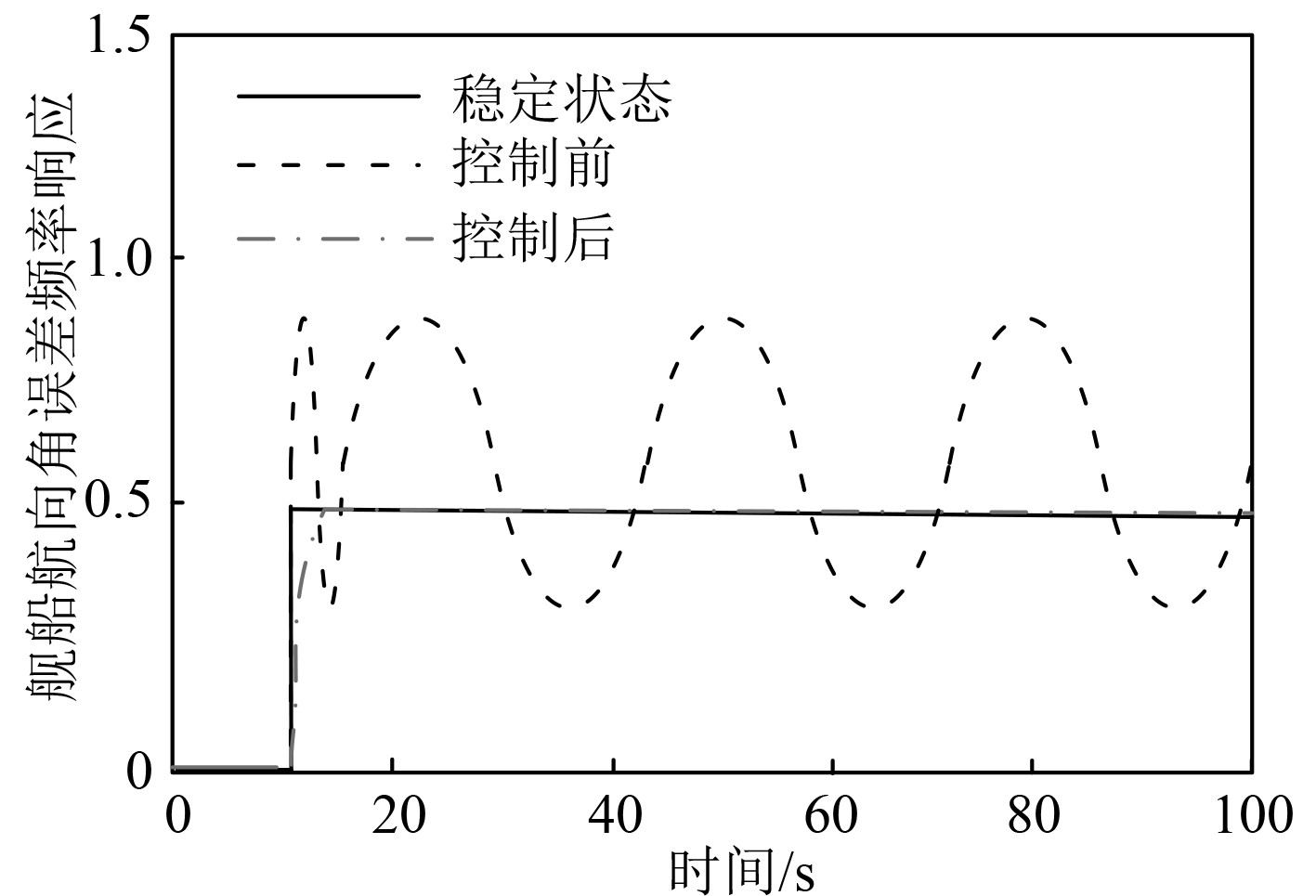
在此工况中，本文算法使用前后，舰船航向稳定性如图5所示。可知，横向风浪出现时，使用本文算法控制舰船航向之前，舰船航向稳定性较差，此时舰船航行航向的误差频率波动明显，且始终没有满足稳定状态标准。本文算法控制舰船航向之后，在20 s之内便可完成舰船航向稳定性自动控制。由此证明，本文算法在舰船航向稳定性控制中存在可用价值。

通过实验可知，本文算法对直线式、交叉式航线中舰船航向的控制效果可满足应用需求，在航向控制过程中，舰船航向未出现偏离状态。

将横向风浪出现后，浪向角分别设成15°、30°、45°，航速为20 kn，在此工况中，测试本文算法使用前后，舰船首摇角、横摇角、鳍角的均方差。测试结果如表3所示。

可知，不同浪向角影响下，使用本文算法控制舰船航向后，浪向角是15°、30°、45°的工况中，本文算法可有效降低舰船航行时首摇角、横摇角、鳍角的均方差，从而控制舰船按照期望航向稳定航行。

3 结　语

本文研究一种考虑横向风浪干扰的舰船航向稳定性自动控制算法，此算法将横向风浪干扰因素作为舰船航向控制的考虑目标，将PID控制器与改进BP神经网络相结合，有效完成了不同横向风浪干扰强度下舰船航向的稳定性自动控制，具体使用价值如下：

1）本文算法控制舰船航向之后，在20 s之内便可完成舰船航向稳定性自动控制。

2）本文算法对直线式、交叉式航线中舰船航向的控制效果可满足应用需求，在航向控制过程中，舰船航向未出现偏离状态。

3）浪向角是15°、30°、45°的工况中，本文算法可有效降低舰船航行时首摇角、横摇角、鳍角的均方差，控制舰船按照期望航向稳定航行。