0 引　言

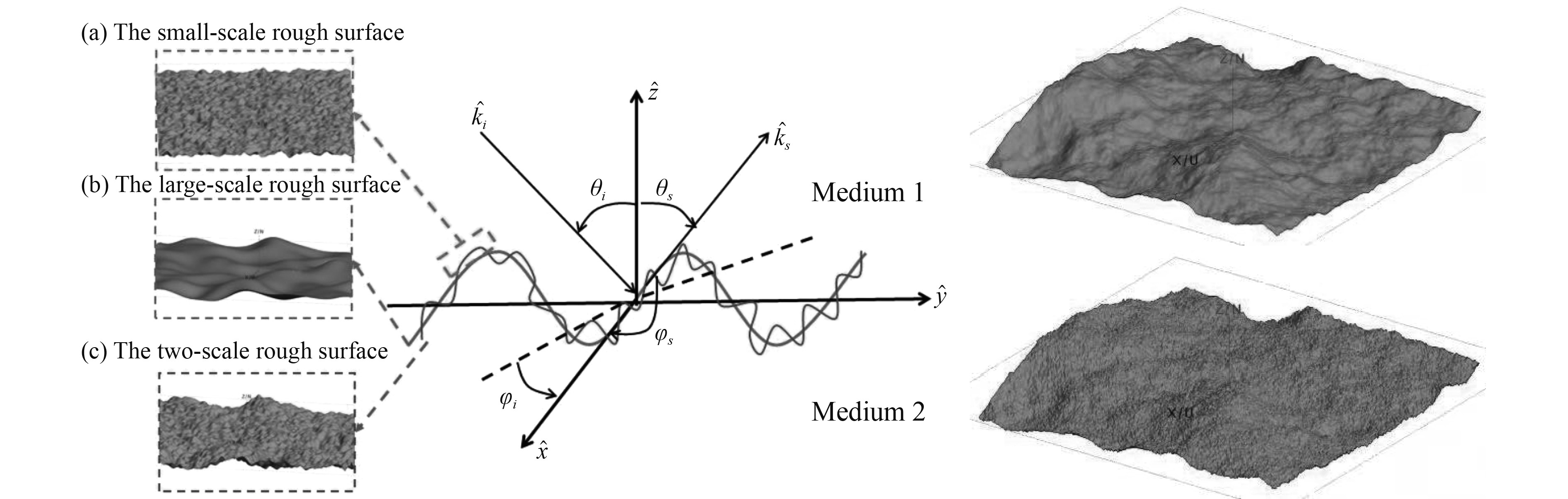
复杂环境下，动态海面环境下武器装备目标复合电磁散射特性机理能反映目标本身或关联平台特征，可为战时推演目标的行为或预测其在态势中的发展变化提供理论依据和数据支持。由于复合散射问题本身的复杂性，如何建立经过测量数据验证的地海环境中复杂目标的复合电磁散射模型，并用于解决实际工程问题，从而高效获取有效地海面目标复合散射特性数据，仍迫切需要开展多方面研究。随着计算电磁学和计算机技术的迅猛发展，国外研究人员对海洋背景与舰船复合电磁散射特性的模化技术研究越来越重视。海面可看作由稍粗糙（小尺度）表面叠加在大波浪结构上构成的一种复合粗糙表面，大波浪（大尺度）结构造成稍粗糙表面的倾斜，这就是“双尺度模型”^[1]。通常情况下，高斯粗糙面和卷浪模型模拟小尺度波浪，卷浪模型在成长过程中的形态不是一成不变的，海面形态随着时间在一直改变。

1 双尺度海面海谱模型构建与几何建模

受风和洋流的影响，海面是随机形成的粗糙面，任意截取2个海面的轮廓均不一样。计算随机海面的电磁散射，或在海面背景下进行目标的探测与识别，均需对随机粗糙的海面进行建模。从随机理论的角度看，海面可理解为特定比例的高斯随机变量谐波叠加而成的粗糙表面。具体的变量可表示如下：

建模过程中，将粗糙面的长宽分别设置为L_x、L_y，用$ \Delta x $、$ \Delta y $来表示长和宽的离散间隔，随机数矩阵$ {{\boldsymbol{\alpha}} _{mn}} $和$ {{\boldsymbol{\beta}} _{mn}} $是均值为0、方差为1的标准正态分布^[2]。其中，$ m=0\sim 2M $，$ n = 0\sim 2N $，$ M = \dfrac{{{L_x}}}{{2\Delta x}} $，$ N = \dfrac{{{L_y}}}{{2\Delta y}} $。

通过组合随机数矩阵，则形成复随机数：

$ \gamma_{m0}=\alpha_{m0}/2,\left(m=0\sim2M\right)，$

(1)

$ \gamma_{0n}=\alpha_{0n}/2,\left(n=0\sim2N\right)，$

(2)

$ \gamma_{mn}=\alpha_{mn}+j\beta_{mn}，\left(m=1\sim2M,n=1\sim2N\right)。$

(3)

展开系数为：

$ \chi_{mn}=W\left(\frac{2\text{π}m}{L_x},\frac{2\text{π}n}{L_y}\right),m=0\sim M,n=0\sim N，$

(4)

$ \chi{\left(2M - m\right)\left(2N - n\right)} = \chi{m\left(2N - n\right)} = \chi{\left(2M - m\right)n} = \chi{mn}，$

(5)

$ b_{mn}=\text{π}\sqrt{\frac{\chi_{mn}}{L_xL_y}}\gamma_{mn。} $

(6)

DFT计算：

$ \hat{f}\left(x,y\right)=\sum\limits_{m=0}^{2M}\sum\limits_{n=0}^{2N}b_{mn}e^{j\left(\frac{2\text{π}}{M}mx+\frac{2\text{π}}{N}ny\right)}。$

(7)

最后，随机粗糙面的高度表示为：

$ f\left(x,y\right)=2Re\left\{\hat{f}\left(x,y\right)\right\}。$

(8)

随机粗糙面的特性由功率谱密度函数决定，在生成随机粗糙面的过程中，代入不同的功率谱密度函数$ W\left( {{K_x},{K_y}} \right) $，即生成了不同随机特性的粗糙面。针对高海情海面建模难题，采用了双尺度方法海面模型的建模仿真，近垂直入射时的镜面反射可用来仿真大尺度长波分量，斜入射时的Bragg散射可用来仿真小尺度的毛细波分量。本文分别用JONSWA海谱+GAUSS谱模型双尺度结合来构建海面模型，效果如图1所示。

2 体-面复合结构的自适应弹跳射线法

基于几何光学理论的弹跳射线法^[3]，是用一系列相对独立的密集光学射线管来模拟电磁波入射到目标的效果，在复杂金属目标表面会发生的多次反射后，光学射线管离开物体表面射向无穷远处，最后用几何光学理论求解远区散射场。

2.1 射线路径追踪

电磁波照射到物体表面，会沿着物体继续传播。然而实际物体的表面会存在无数个小的二面角、三面角或不同大小的腔体，此时根据射线传播理论，电磁会在物体表面多次弹射。射线传播的路径是根据几何光学理论按照基本原理进行，因此可对射线的传播路径进行光学追踪进而得到射线的出射点和射出的方向。根据几何光学原理，射线管在均匀各向同性介质中沿着直线进行传播，因而可用直线方程来表示射线传播的路径：

$ \vec{r}(x,y,z)=\vec{r}_0(x_0,y_0,z_0)+\vec{s}(s_x,s_y,s_z)t。$

(9)

式中：$ \vec s $为射线的传播方向；$ {\vec r_0} $为射线传播的起始点，从起始点到交点之间的传播向量通过参数$t$与射线的传播矢量相乘来表示。

通常用平面三角形表示离散的散射目标，用${\vec r_1}({x_1},{y_1},{z_1})$、${\vec r_2}({x_2},{y_2},{z_2})$、${\vec r_3}({x_3},{y_3},{z_3})$来表示三角形面元的3个节点坐标，通过三节点坐标就可构建三角形所在的平面方程：

$ \left(\vec{r}-\vec{r}_3\right)\cdot\vec{n}=0。$

(10)

式中，$\vec n$为三角形面元的法向量，$\vec n = ({\vec r_1} - {\vec r_2}) \times ({\vec r_2} - {\vec r_3})$，$\vec r(x,y,z)$为三角形面元上任意一点。可得：

$ t=\frac{(\vec{r}_3-\vec{r}_0)\cdot\vec{n}}{\vec{s}\cdot\vec{n}}。$

(11)

在射线追踪的过程中，出现反射情况时，反射方向即可看作下一次射线的出射方向，该反射交点为下一次射线的出射点。将求出的$t$代入直线方程求出射线与物体表面的交点，所在的三角形法向为交点处的法向方向，求出反射射线后，即可对下一次射线弹跳进行路径追踪，反射线求解如图2所示。

图中${\hat k_i}$为入射射线方向矢量，$\hat n$为反射点处法向矢量，根据Snell定律可知入射角${\theta _i}$等于反射角${\theta _r}$，可得反射射线方向矢量${\hat k_s}$为：

$ \hat{k}_r=\hat{k}_i-2(\hat{k}_i\cdot\hat{n})\hat{n}。$

(12)

2.2 射线场强追踪

射线在物体表面传播的过程中，随着传播距离不同，射线管内的电场相位会发生变化，进而在每次反射后电场幅值也会发生相应变化。当射线与物体表面在第$ i $个交点$ {\vec r_i}(i = 1,2,\cdots ,N) $处的电场场强为$ \vec E({\vec r_i}) $，则在第$ i + 1 $个交点$ {\vec r_{i + 1}} $处可得到射线与物体表面的场强$ \vec E({\vec r_{i + 1}}) $为：

$ \vec{E}\left(\vec{r}_{i+1}\right)=\left(DF\right)_i\left(R\right)_i\vec{E}\left(\vec{r}_i\right)e^{-jk\cdot d}。$

(13)

式中，$\vec E\left( {{{\vec r}_i}} \right)$为$ {\vec r_i} $处的入射电场；$ {\left( {DF} \right)_i} $为射线从第$i$次反射点到第$i + 1$次反射点的散度因子；$ \boldsymbol{R}_i $为第$i$次反射的反射系数矩阵；$d = \left| {{{\vec r}_{i + 1}} - {{\vec r}_i}} \right|$为2个交点之间射线传播的距离。

2.3 远场积分

射线在物体表面完成追踪过程，最后离开物体表面时，电磁波获得了相应的场和出射方向，需要确定积分口径面来计算远区散射场。弹跳射线的积分口径面的确定，可通过射线离开物体表面时，射线管在物体表面的相交面来表示，在对物体表面进行网格剖分时将射线管尺寸设置的足够小时，就能取得很好的计算结果。

如图3所示，物体表面剖分的积分区域为$ {\left( {\Delta A} \right)_{exit}} $，当$ {\left( {\Delta A} \right)_{exit}} $足够小，散射场就可表示为：

$ \left[\begin{array}{*{20}{c}}A_{\theta} \\ A_{\phi}\end{array}\right]\approx\left[\begin{array}{*{20}{c}}B_{\theta} \\ B_{\phi}\end{array}\right]\left(\frac{jk}{2\text{π}}\right)\left[\frac{\left(\Delta A\right)_{exit}}{\hat{n}\cdot\hat{s}}\right]e^{jk\hat{k}\cdot\vec{r}_A}P\left(\theta,\phi\right)。$

(14)

式中，$\hat s = {s_1}\hat x + {s_2}\hat y + {s_3}\hat z$为射线离开目标的出射方向；${\vec r_A}$为$ {\left( {\Delta A} \right)_{exit}} $的中心点$A$处的位置矢量；$\hat n$为物体表面法向量；$\hat k$为观察方向。

3 海面舰船目标仿真实测数据比对验证 3.1 海谱模型仿真结果

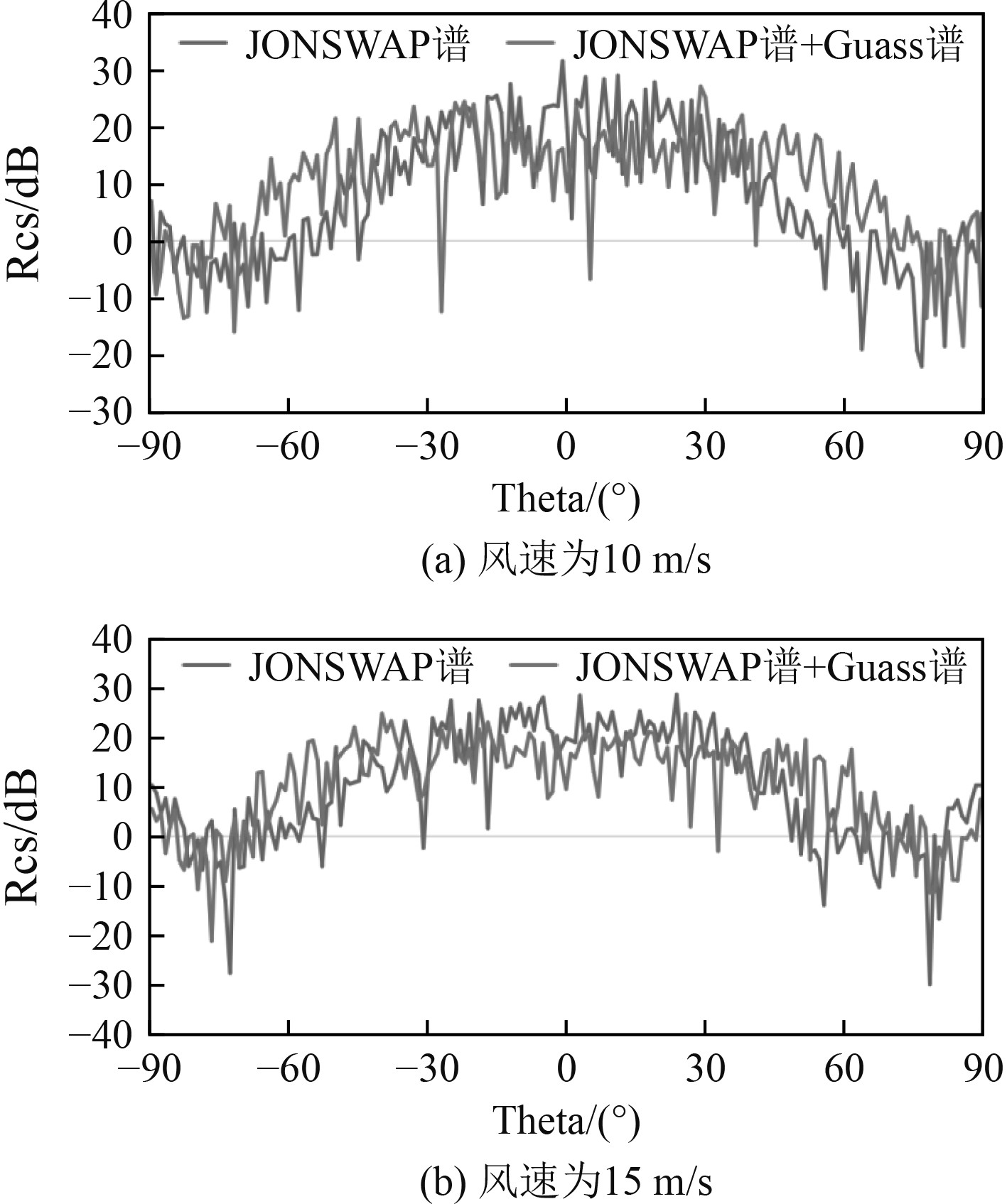
针对高海情海面建模难题，根据对实际海浪运动特点，考虑了卷浪在顺风面与逆风面的形状有差异，实现了双尺度方法海面模型的建模仿真，模拟了不同风速下的单尺度海面（JONSWA海谱模型）与双尺度海面（JONSWA海谱+GAUSS谱模型）的RCS，频率为5 GHz，单站雷达观测角度为Theta=−90°～90°，Phi=0°。

从仿真结果中可看出，对比于单尺度海面回波而言，双尺度海面粗糙度变大，在俯仰角Theta为大角度时（约0°～30°），雷达回波变小，而在俯仰角Theta约30°～60°附近观测到的雷达后向散射贡献增强。发生这一现象的原因归结为：1）海面在雷达俯仰角Theta小角度时粗糙度变大导致漫反射作用增强，后向反射的回波减弱；2）雷达俯仰角Theta在30°～60°周围观测时现成了更多的二面角结构，使得后向散射作用更强。由于双尺度模型将细微结构考虑了进来，所以模拟的高海情更加逼真。

3.2 海面目标实测仿真比对

本文利用RCS测量雷达对海面目标进行实际测量实验，测得了海上目标电磁散射回波，完成了外场实验验证工作，该工作测试目标如图5所示。该模型为某港口货轮，货轮吃水深度约为6 m，测量时海面风速为8 m/s，对测量的船舶模型进行了等比例建模，船长为320 m，宽为29 m，建立了海谱模型，长为500 m、宽为500 m。雷达测试角度为方位角90°入射，俯仰角91°、92°入射。基于本文研究的仿真方法对该海上目标场景进行仿真，对测量的船舶模型进行外形还原，仿真舰船如图6所示。

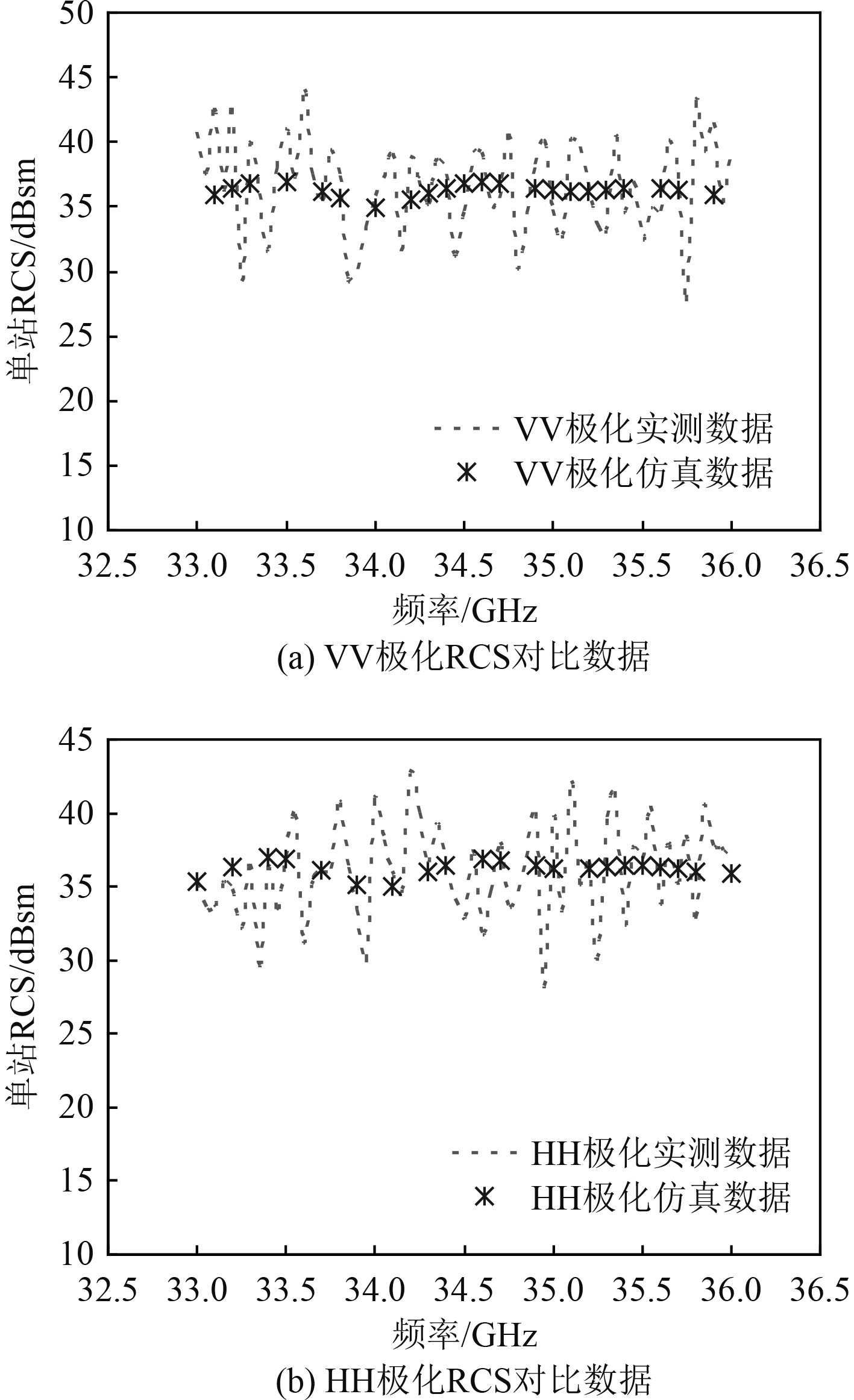
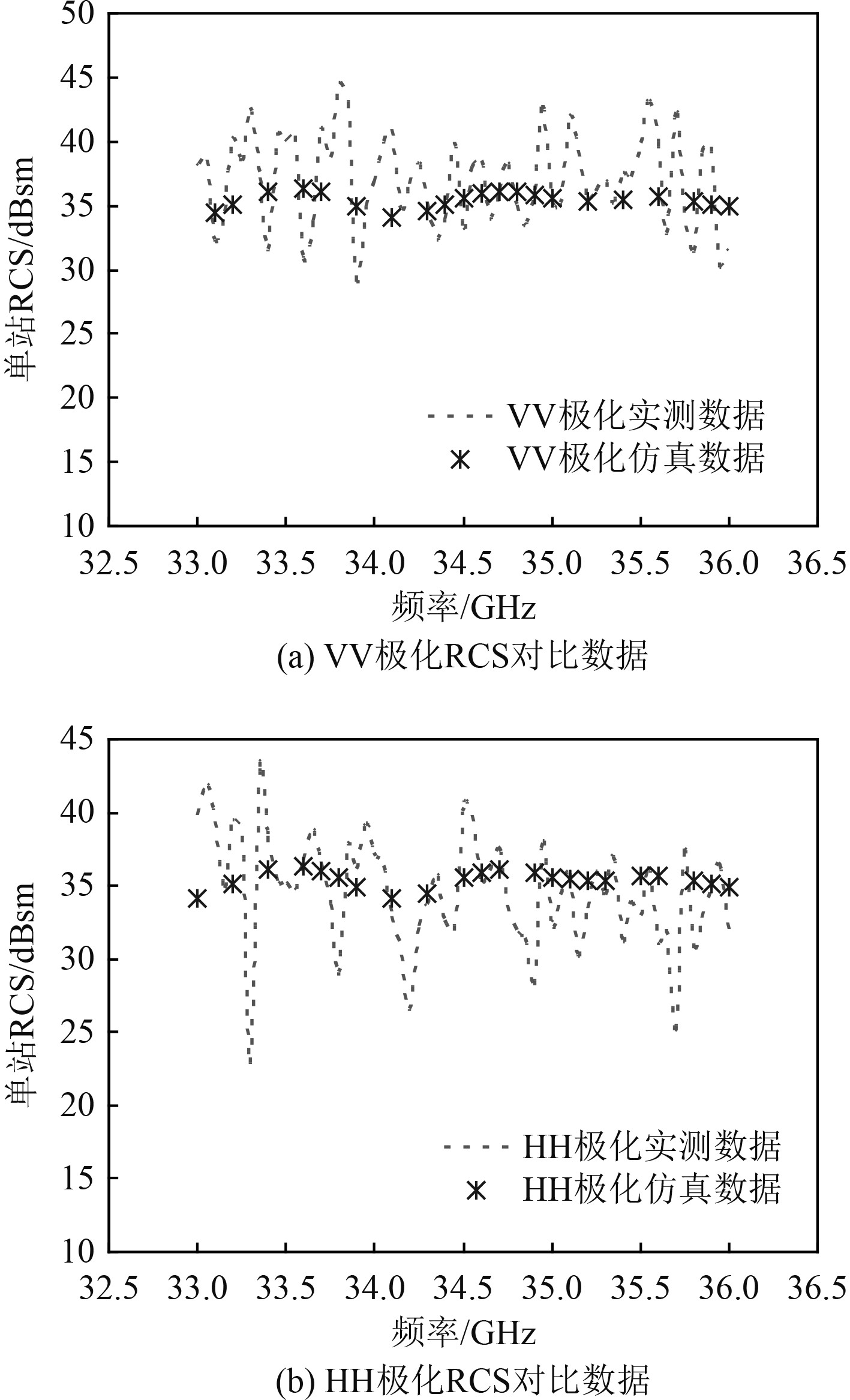
本工作利用测量得到的回波数据与仿真数据进行对比验证，回波数据如图7与图8所示。

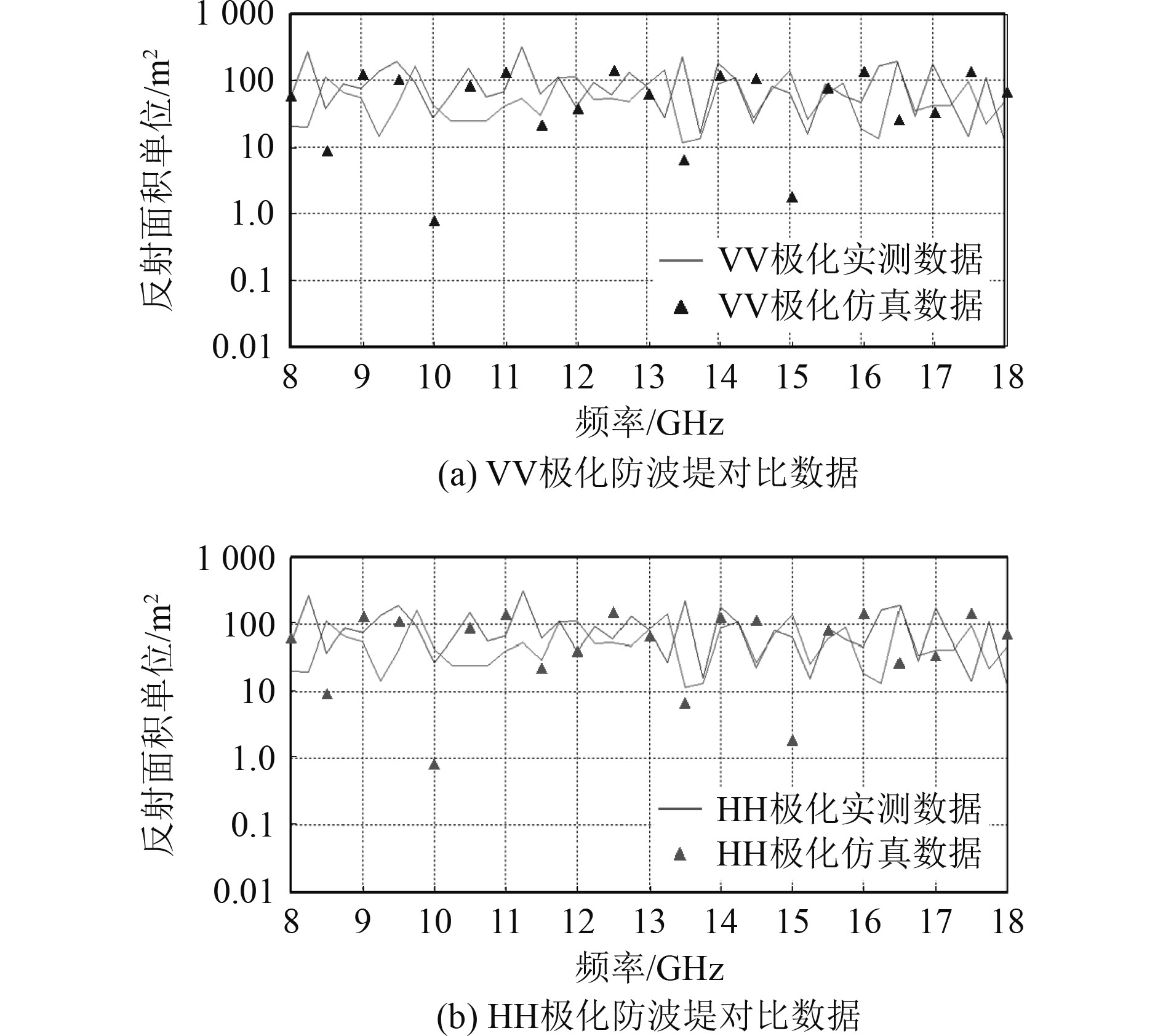
同时，利用RCS测量雷达测得了海岸防波堤电磁散射回波，测试目标如图9所示，该防波堤长度为460 m，雷达测试角度为俯仰角90°。雷达照射方向与防波堤长轴为30°夹角。基于本文研究的仿真方法对该防波堤场景进行了仿真，设置防波堤材质为水泥，介电参数为$ {\varepsilon _r} = \left( {4, - j0.5} \right) $，防波堤模型长为460 m，宽为5 m，海面模型长度为600 m×600 m，海水介电参数设置为$ {\varepsilon _r} = \left( {30.2, - j32.3} \right) $，如图10所示。

由图7、图8和图11可以看出，本文研究的仿真建模方法计算得到的民用船舶和防波堤的回波数据与测量得到的实验数据量级一致，误差产生的原因可能是受舰船姿态、海杂波影响与建模误差引起的。

4 结　语

目前，开展的海面运动目标电磁建模中，动态海面模型与运动舰船模型相互独立，虽然依据海洋运动学方程在散射建模时考虑了目标六自由度运动，但在实际仿真过程中，海面模型随机生成，无法确定海面瞬态运动变化与海面目标受力的关系。在后续的研究工作中，针对这一问题，需对运动学方程与电磁场方程共同求解，建立相互关联的物理模型，利用海面瞬态运动状态对海面进行几何建模。同时从几何模型出发推导目标受力关系，得到瞬态目标运动方程，获得目标瞬态回波表达式，最终实现海面目标关联的运动电磁散射特征模型。