水声目标检测中,主动发射信号,利用接收到的回波信号进行检测,获得目标的距离、方位、速度信息,是一种广泛使用的检测手段[1]。水下环境复杂,和发射信号高度相关的混响以及时变非平稳的噪声干扰大大提高了精确检测水下目标的难度[2]。特别是,在对UUV、鱼雷、水雷等水中小目标探测过程中,由于目标尺度小、回波信号弱,混响与噪声干扰严重影响了水中小目标信号检测的有效性与可靠性。因此,水中小目标信号检测一直是水声目标探测的难题,研究强混响、非平稳噪声干扰条件下有效抑制混响与噪声干扰而实现目标信号检测的方法,对于水中小目标探测有重要意义。
本文针对水下小目标探测的应用环境,分别研究了低信噪比和低信混比条件下降低噪声及抑制强混响的方法,并以此构建了一种水中小目标恒虚警检测方法。恒虚警检测(Constant False Alarm Detection,CFAR)是一种广泛使用的目标检测方法,可以在低虚警率下准确地判别目标是否存在。单元平均(Cell Averaging,CA)-CFAR算法是其中最经典的一种算法,其运算复杂度低,在均匀环境中表现良好,但当背景环境起伏较大时,其检测性能受到很大影响。因此在CA-CFAR算法的基础上又提出了最大选择(Greatest of,GO)-CFAR算法,解决了CA-CFAR算法在杂波边缘虚警率过高的问题。但是仍然受到信噪比与信混比的约束,对于弱目标的检测概率还有待提高。因此本文提出一种基于自相关预处理(Data Preprocessing)降噪与奇异值分解的最大选择恒虚警检测器(DP-SVD-GO-CFAR), 有效解决了复杂海洋环境下水中小目标的检测问题。首先,利用主动发射探测信号与噪声对自相关处理的差异性,通过对接收信号进行自相关处理可降低噪声干扰。同时,利用混响与发射信号强相关、频域能量集中但相对于目标回波信号能量强而且奇异值大等特性,通过对接收信号进行矩阵重构与奇异值分解,并采用对较大奇异值置零的方法可抑制混响干扰。在此基础上,采用恒虚警检测算法,可有效检测弱目标信号,降低虚警概率。为验证本文所提检测器的检测性能,利用计算机进行仿真,并与自相关奇异值单元平均恒虚警(DP-SVD-CA-CFAR)检测器、奇异值分解最大选择恒虚警(SVD-GO-CFAR)检测器、奇异值分解单元平均恒虚警(SVD-CA-CFAR)检测器这3种恒虚警检测器相对比,同时利用外场探测试验的实际试验数据进行了验证。仿真和试验结果表明,该方法可有效减小噪声并抑制强混响干扰,能够提高弱目标回波的信号干扰比,算法计算量小,可实际应用于实现对水中小目标的弱信号检测。
1 自相关处理降低噪声干扰CW信号是水声目标探测的常用信号波形之一,其接收信号可表示为:
| $ x(t)=s(t)+n(t)=A \cos \left(2 {\text{π}} f_{0} t+\varphi\right)+n(t) ,0 \leqslant t \leqslant T 。$ | (1) |
式中:
则信号的自相关函数为:
| $ \begin{aligned} R(t) =&R_{s}(t)+R_{s n}(t)+R_{n s}(t)+R_{n}(t) \approx\\ & R_{s}(t)+R_{n}(t)。\end{aligned} $ | (2) |
由于信号和噪声相互独立,所以
| $ R_{s}(t)=\left\{\begin{array}{l} \displaystyle\frac{A^{2}}{2}(T+t) \cos \left(2 {\text π} f_{0} t\right),-T \leqslant t \leqslant 0 ,\\ \displaystyle\frac{A^{2}}{2}(T-t) \cos \left(2 {\text π} f_{0} t\right), 0 \leqslant t \leqslant T。\end{array}\right. $ | (3) |
假设高斯白噪声的功率谱密度为
| $ R_{n}(t)=N_{0} \delta(t) 。$ | (4) |
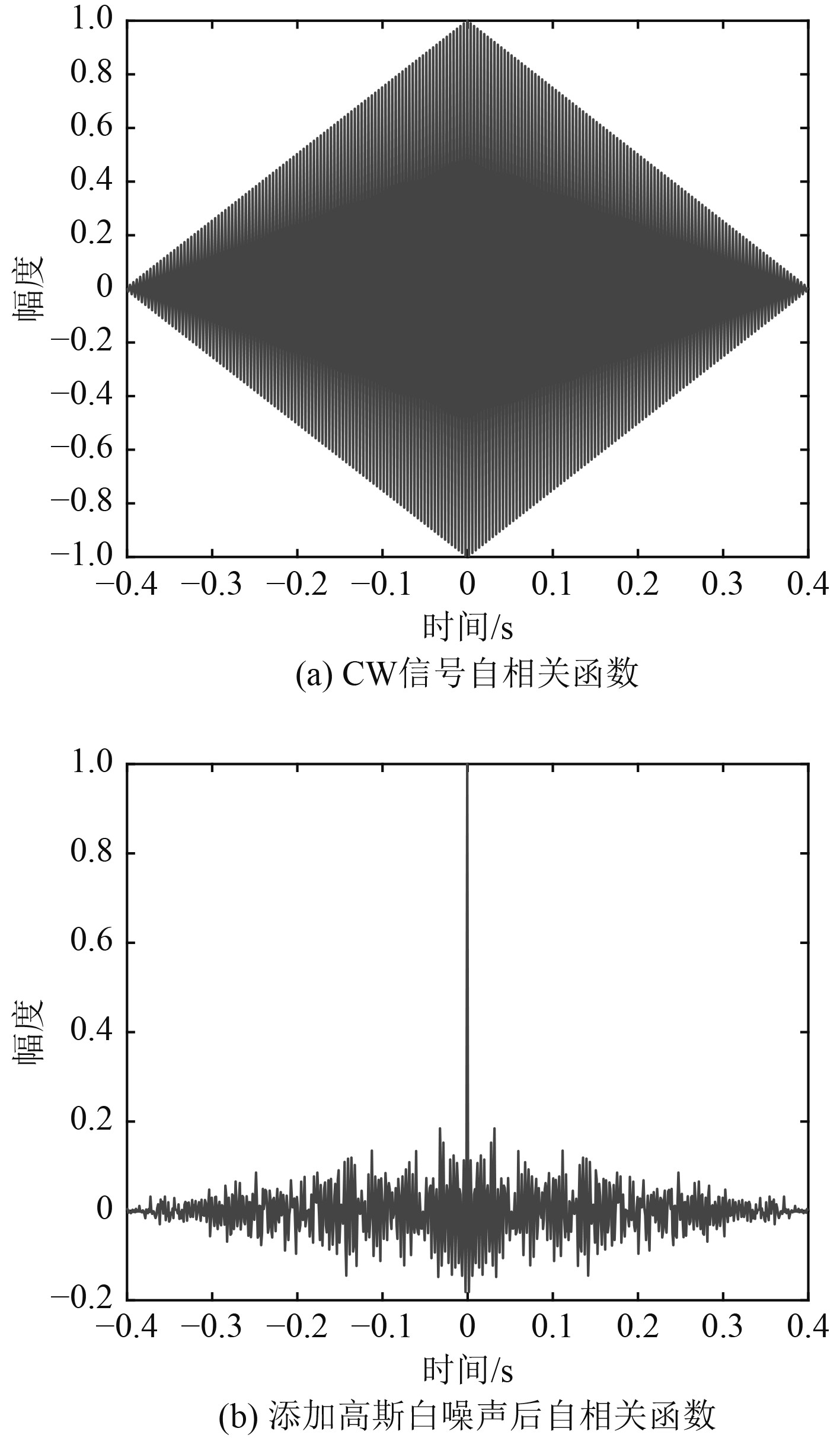
由式(3)和式(4)可知,CW信号的自相关函数为一载波频率为
|
图 1 自相关函数图 Fig. 1 Autocorrelation function graph |
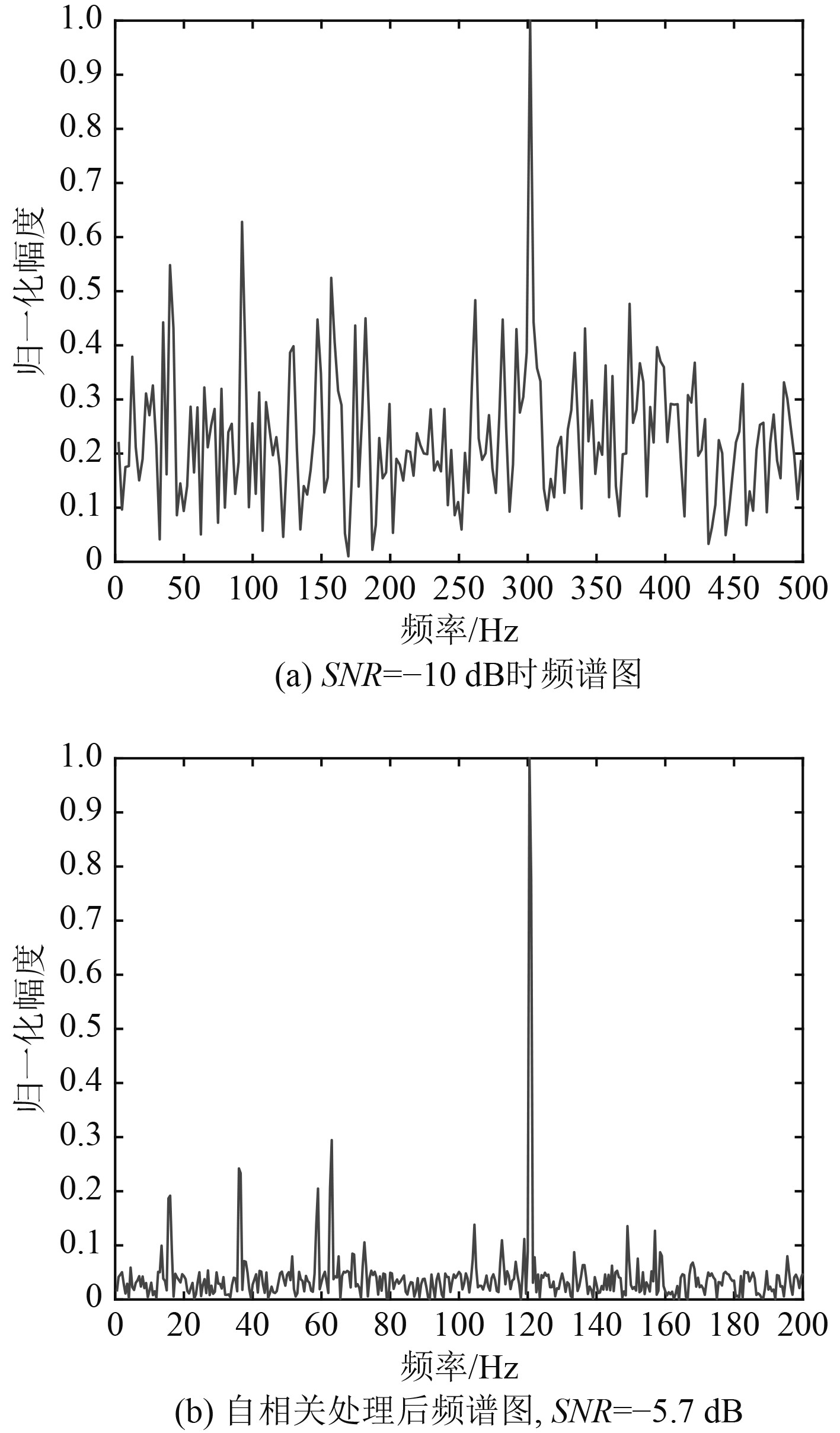
针对中心频率300 Hz、信噪比−10 dB的CW信号进行了仿真,该CW信号的频域波形如图2(a)所示,自相关降噪处理后的频域波形如图2(b)所示,自相关处理后信噪比达到−5.7 dB,由图1和图2对比可知,自相关处理明显提高了信噪比。
|
图 2 自相关降噪效果对比 Fig. 2 Comparison of autocorrelation noise reduction effects |
对于一个秩为r的m×n 维矩阵
| $ \mathbf{\mathit{X}}=U\left[\begin{array}{ll}\Sigma & 0 \\ 0 & 0\end{array}\right]V^H。$ | (5) |
式中:U、V 分别为
矩阵X 的每一个行向量都可通过U,V矩阵进行重构:
| $ x_{i}=\sigma_{i} u_{i} v_{i}^{\rm H}。$ | (6) |
式中:
对于接收信号
| ${\boldsymbol{A}}=\left[\begin{array}{cccc} x(1) & x(2) & \cdots & x(N-L+1) \\ x(2) & x(3) & \cdots & x(N-L+2) \\ \vdots & \vdots & \vdots & \vdots \\ x(L) & x(L+1) & \cdots & x(N) \end{array}\right]。$ | (7) |
再根据式(5)对重构接收信号矩阵进行奇异值分解,得到一组非零奇异值
再根据式(5)对重构接收信号矩阵进行奇异值分解,得到一组非零奇异值
根据文献[6],大奇异值的个数是接收信号中主频率成分个数的2倍,并且恒定不变,即每2个大特征值对应频谱上的一个主频率。实际应用中,一般可根据特征值的递减差来判断需要置零的特征值个数,能得到较为理想的效果。
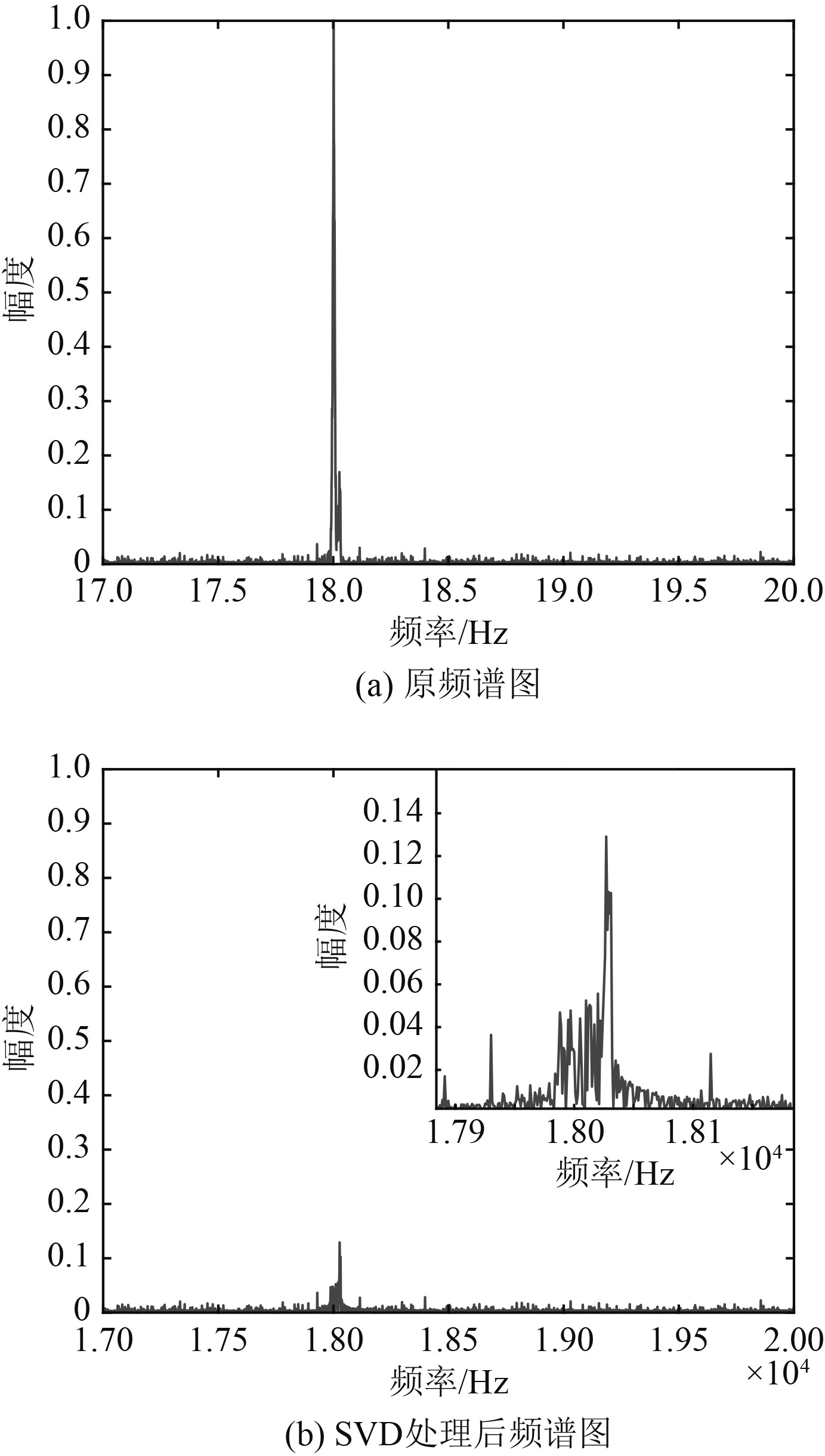
对于目标速度4 kn、信混比−10 dB、中心频率为18 kHz的目标信号,利用该方法抑制混响的仿真效果对比分别如图3所示。可知,接收信号中的强混响干扰被有效抑制,目标回波信号凸显,可以进行目标信号检测。
|
图 3 v=4 kn, 信混比为−10 dB Fig. 3 v=4 kn, signal-to-mix ratio is−10 dB |
采用SVD算法对不同目标速度下不同信混比的回波信号进行目标提取。发现当信混比为−10 dB时,若波信号进行目标提取。发现当信混比为−10 dB时,若相对运动速度小于4 kn,该方法不能有效地将目标回波与混响进行分离。对于如何在更低信混比、更低相对速度下提取目标信号,还有待进一步的研究。
3 基于GO-CFAR算法的恒虚警检测方法经过自相关降噪与奇异值分解抑制强混响后,待检测信号可表示为:
| $ \left\{\begin{array}{l} x(t)=n(t), H_{0},\\ x(t)=n(t)+s(t), H_{1}。\end{array}\right. $ | (8) |
式中:n(t)为噪声与部分未滤除的混响信号;s(t)为目标回波信号。假设
恒虚警检测(Constant False Alarm Rate,CFAR)通过临近参考单元对背景杂波进行估计,给出恒定虚警概率下的自适应门限[7]。将待检测信号与门限值进行比较,就可判断出目标是由否存在。其中应用最为广泛的2种CFAR算法为单元平均恒虚警检测器(CA-CFAR)和最大选择恒虚警检测器(GO-CFAR)[8] 。
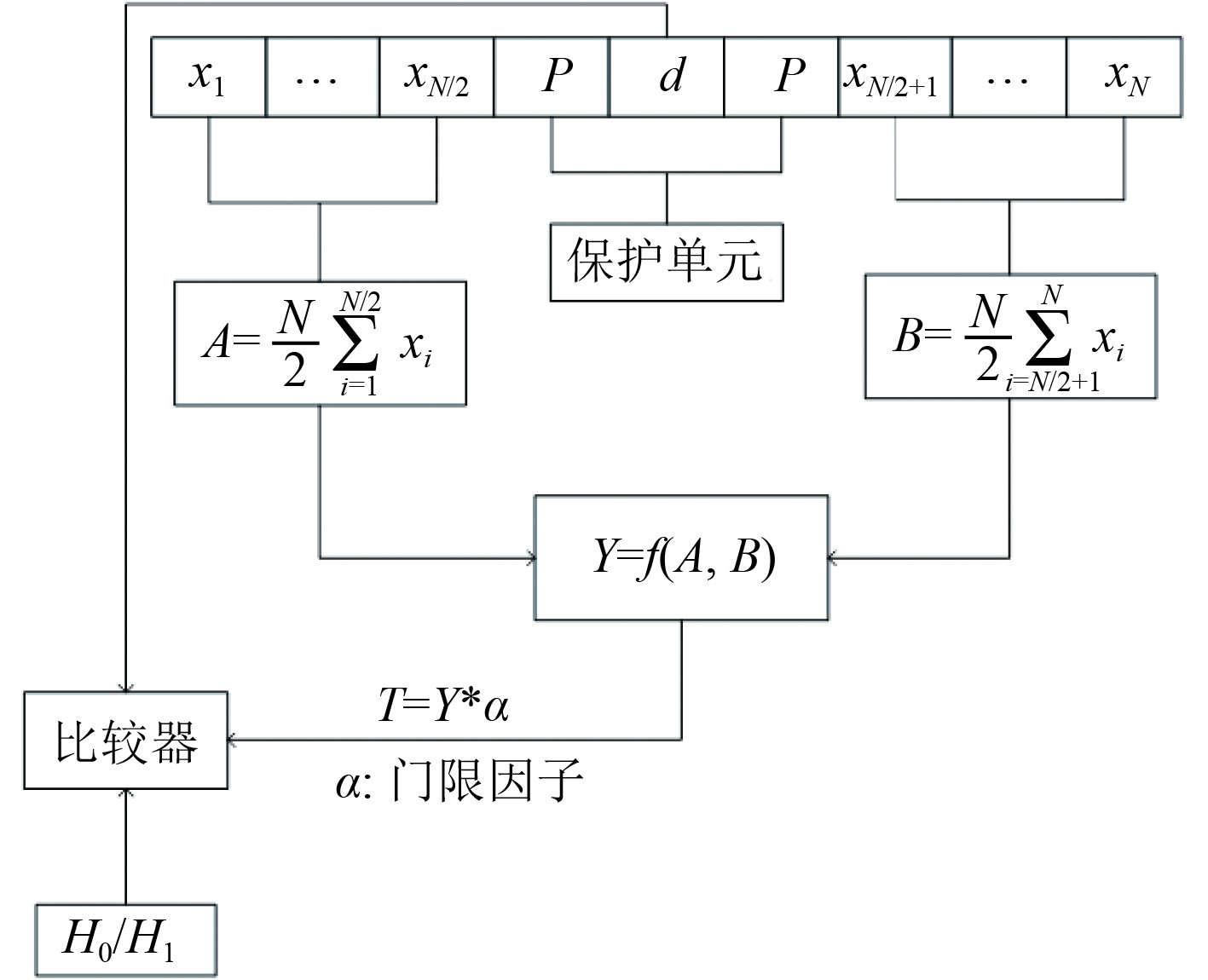
在图4的CFAR算法流程中,d为待检测单元。为防止临近单元出现能量泄露导致检测效果下降,设定临近待检测单元的k个单元为保护单元P。通过滑动窗选取除保护单元外的N个相邻的参考单元对背景功率进行估计。自适应门限T由门限因子
|
图 4 CFAR算法流程 Fig. 4 CFAR algorithm flow |
| $ \left\{\begin{array}{l} d \leqslant T, H_{0},\\ d>T, H_{1}。\end{array}\right. $ | (9) |
当待检测单元幅值大于检测门限时,假设 H1 成立,表示检测到目标信号;否则,假设 H0成立,未检测到目标信号。
CA-CFAR算法通过对左右参考单元的均值取平均来实现背景功率的估计:
| $ Y=\frac{A+B}{2}。$ | (10) |
式中,A、B分别为左右参考单元的均值;Y为背景功率的估计值。
CA-CFAR算法的门限因子
| $ \alpha=P_{f a}{ }^{-1 / N}-1。$ | (11) |
其中,N为参考单元的总数目。
CA-CFAR算法的门限值T由背景功率估计值Y与门限因子
| $ T=Y^{*} \alpha 。$ | (12) |
GO-CFAR算法通过计算左右滑窗中参考单元的均值,并取其中的最大值对背景功率估计:
| $ Y=\max (A, B)。$ | (13) |
GO-CFAR的门限因子
| $ P_{f a} = 2(1+\alpha)^{-N / 2} - 2 \sum_{i=1}^{N / 2}\left(\begin{array}{c} n+i-1 \\ i \end{array}\right)(2 + \alpha)^{-(N / 2+i)}。$ | (14) |
在均匀杂波背景下,CA-CFAR获得接近最优的检测性能,但在杂波边缘场景会有虚警或者漏警[10];而GO-CFAR能有效地避免杂波边缘的虚警[11]。对于水下低信噪比和信混比的小目标的检测而言,背景噪声起伏较大且要求虚警概率相对较低,选择GO-CFAR算法可以获得更优的检测结果。
基于前述自相关降噪及强混响抑制处理,构建水下小目标恒虚警检测的整体算法流程如图5所示。
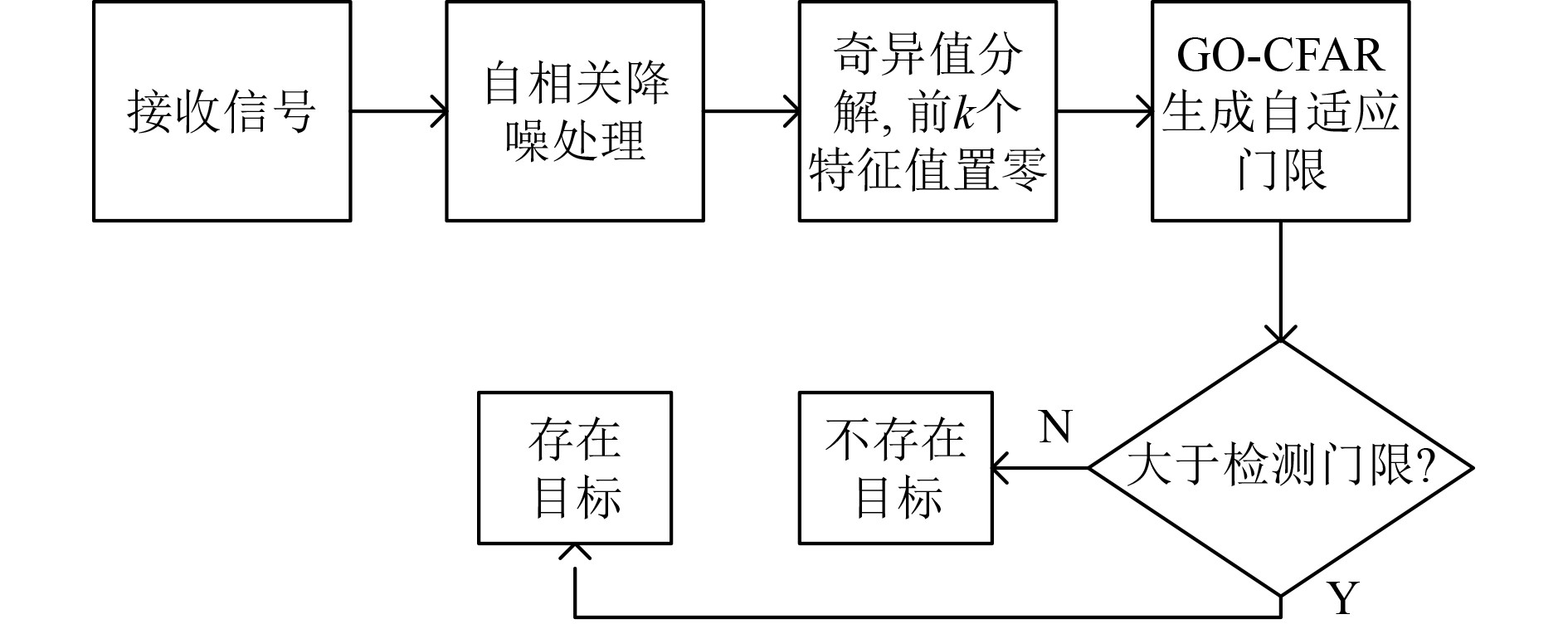
|
图 5 信号检测流程图 Fig. 5 Signal detection flowchart |
可知,对于接收到的目标信号,首先通过自相关处理,可以有效去除信号中的非相关噪声,降低噪声干扰。其次,通过构建信号矩阵并进行奇异值分解处理,可以有效去除能量强而且集中的混响,从而达到抑制强混响干扰、保留小目标回波信号的目的。在此基础上,进一步利用恒虚警检测算法,实现对弱目标信号的有效检测,给出有无目标信号的准确判决。
4 仿真及试验验证 4.1 计算机仿真假设发射中心频率为20 kHz的单频脉冲信号,采样频率为100 kHz,信号脉宽为10 ms,信混比−10 dB,环境噪声为高斯白噪声。不同雷目相对运动速度条件下的检测结果分别如图6和图7所示。可知,分别经过自相关降噪和强混响抑制处理后,利用恒虚警检测方法生成了自适应检测门限,有效实现了弱目标信号检测。
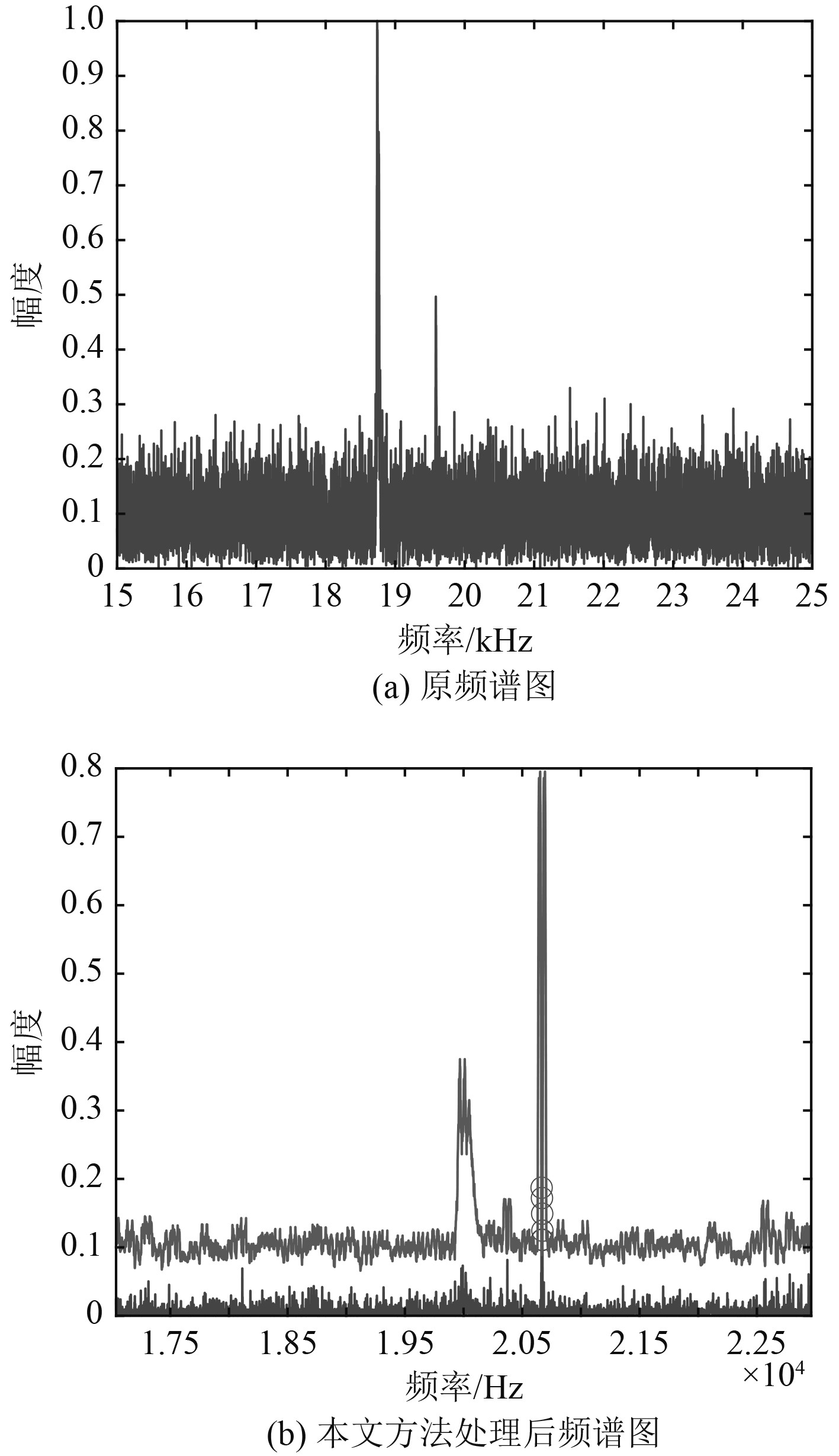
|
图 6 v=50 kn, SNR=-15 dB Fig. 6 v=50 kn, SNR=-15 dB |
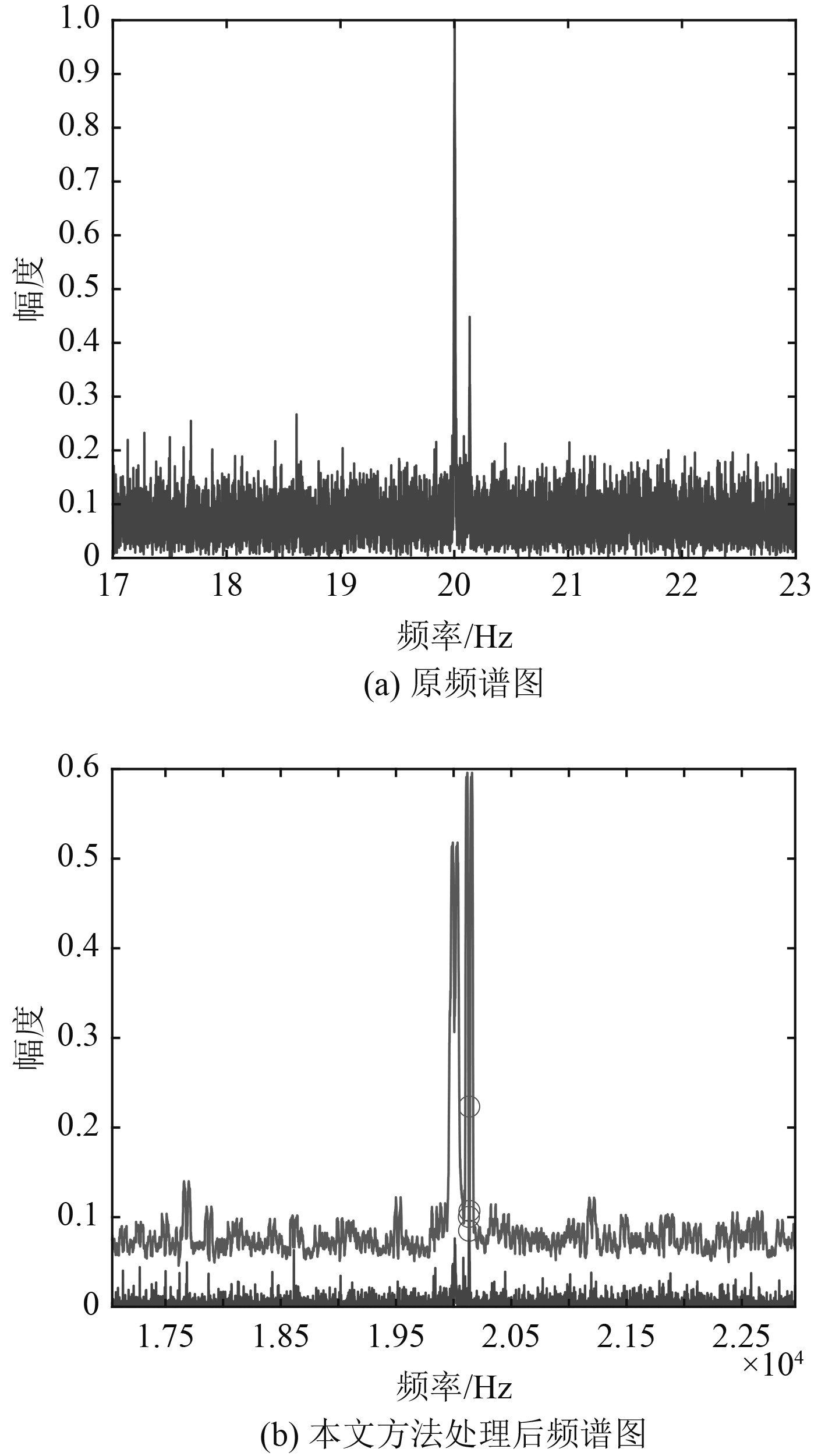
|
图 7 v=10 kn, SNR=-15 dB Fig. 7 v=10 kn, SNR=-15 dB |
可以看到,在不同的信噪比、相对运动速度下,本文提出的检测算法均能达到较好的检测效果,可以准确的检测到目标。
为在多维度下进行对比分析,本文选取SVD-CA-CFAR、DP-SVD-CA-CFAR、SVD-GO-CFAR、DP-SVD-GO-CFAR检测器进行仿真比较。
相对运动速度为50 kn时,4种检测算法的ROC曲线如图8(a)所示。可以看到,未预处理时,在同一信噪比下,SVD-CA-CFAR的检测概率要明显高于SVD-GO-CFAR,这是因为背景噪声相对平稳,且相对运动速度较高,目标与混响易于分辨。而经过自相关降噪后,虽然提升了接收信号的信噪比,但背景噪声的起伏则变得较大、不再平稳。因此DP-SVD-CA-CFAR在同一信噪比下的检测概率相比DP-SVD-GO-CFAR较低,但整体优于SVD-CA-CFAR与SVD-GO-CFAR。综上,本文提出的DP-SVD-GO-CFAR检测器可以实现对弱目标的有效检测,达到理想的检测概率。
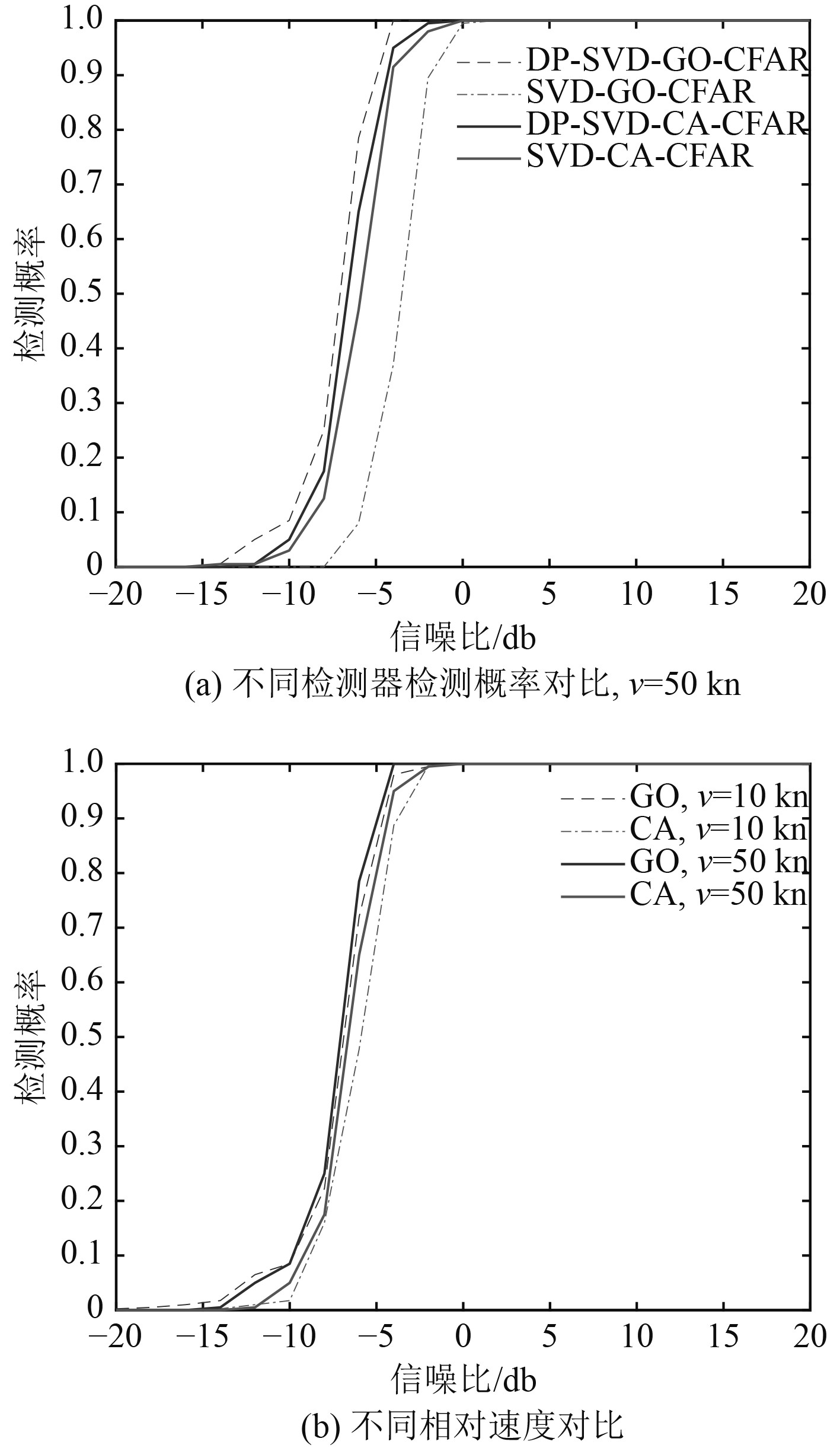
|
图 8 不同方法下检测性能对比 Fig. 8 Comparison of detection performance under different methods |
图8(b)为雷目相对速度v=10 kn与v=50 kn下 DP-SVD-CA-CFAR与DP-SVD-GO-CFAR检测器的 ROC 检测曲线,对比不同检测算法对低速目标的检测能力。低速时,混响与目标较难分辨,对检测算法的要求更高。可知,在不同速度下,DP-SVD-GO-CFAR 的检测效果均优于 DP-SVD-CA-CFAR。且在−10~0 dB之间,DP-SVD-GO-CFAR在同一信噪比条件下的检测概率较DP-SVD-CA-CFAR受速度的影响更小,更加稳定可靠。综合不同条件下的仿真结果,可以看到本文提出的检测方法可以有效地检测出低速小目标。
4.2 试验验证为了进一步验证本文所提方法的有效性,针对鱼雷目标检测开展了外场试验验证。
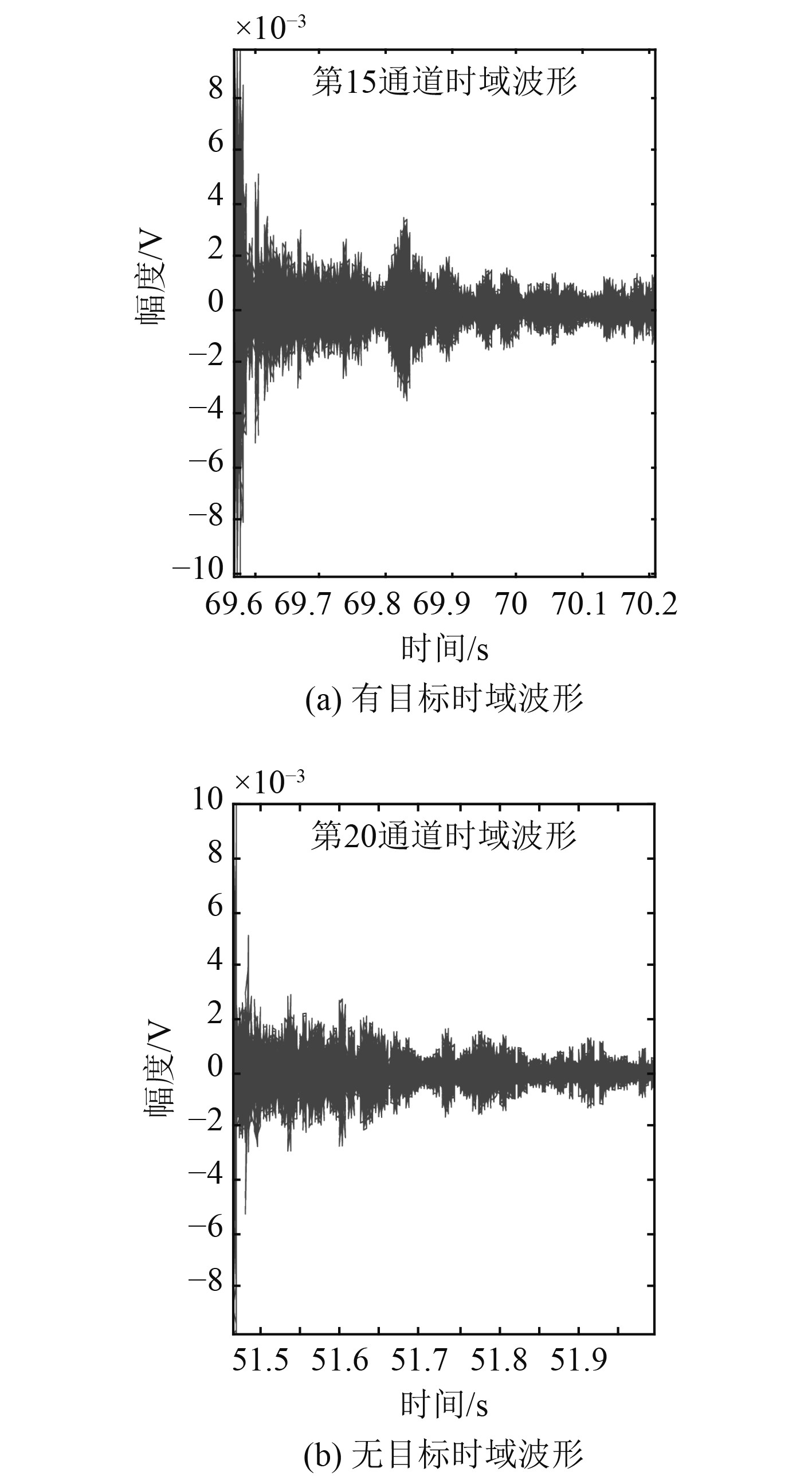
试验中,检测目标为直径533 mm的重型鱼雷,其航行速度50 kn。发射探测信号为脉宽100 ms的CW信号,典型接收信号的时域波形如图9所示。可知,时域混响较强,无法分辨目标回波信号。从频域变换结果也明显可见,混响强度远远超过目标信号,目标回波的信号干扰比不高。
|
图 9 接收信号波形图 Fig. 9 Waveform plot of the received signal |
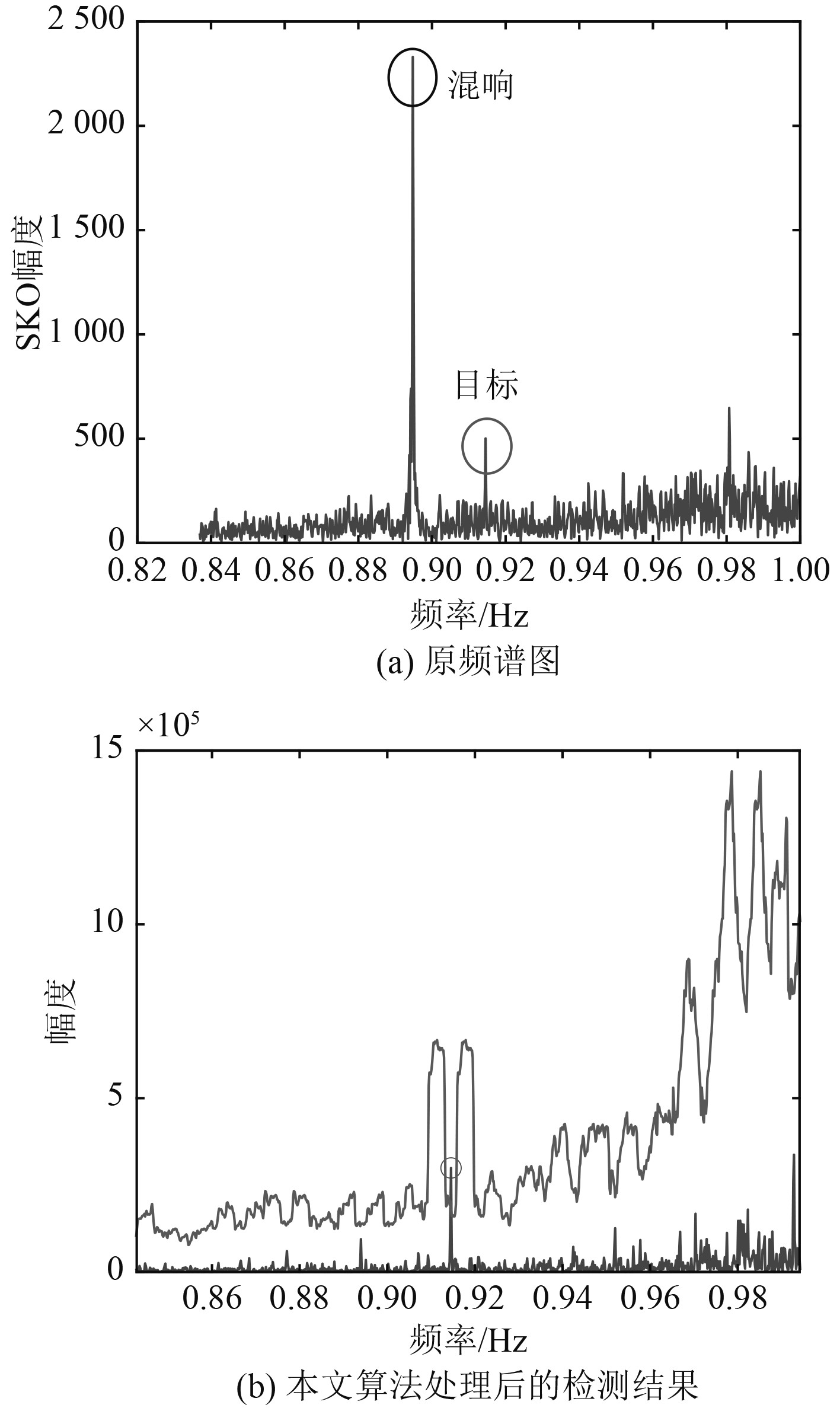
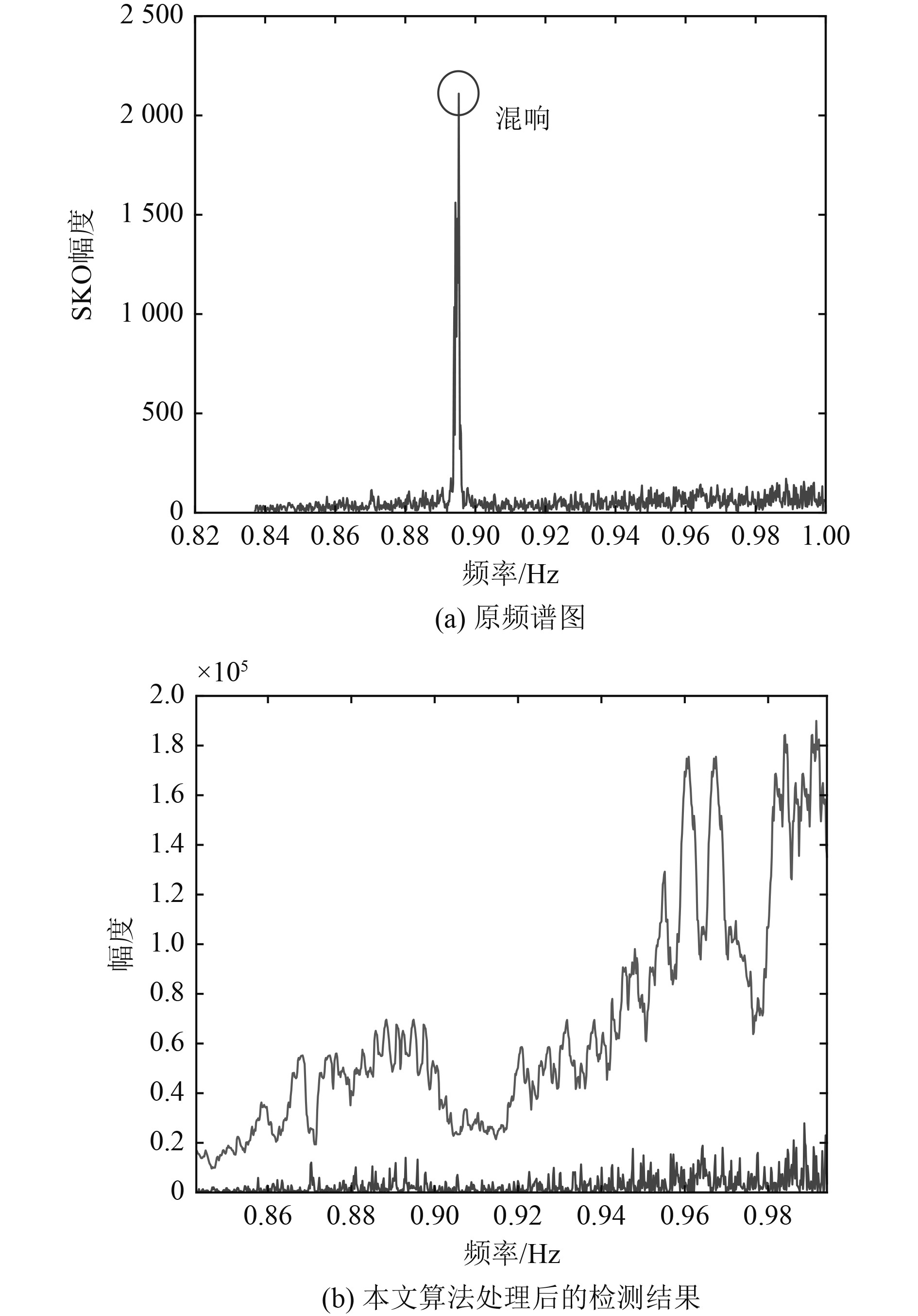
利用本文方法分别进行降噪和抑制混响处理后的波形如图10和图11所示。可知,本文算法有效抑制了强混响,充分保留了目标回波信号,明显提升了信号干扰比。同时,利用恒虚警算法也有效生成了自适应检测门限,目标信号明显超过检测门限,很好地实现了目标检测。
|
图 10 有目标时检测结果 Fig. 10 Detect results when there is a target |
|
图 11 无目标时检测结果 Fig. 11 Detect results when there is no target |
针对水下小目标回波信号弱、受混响及噪声干扰影响大而难以检测的问题,本文提出了一种基于自相关与奇异值分解的恒虚警检测的方法。首先通过对接收信号进行自相关处理降低不相关噪声以提高信噪比,其次利用混响在频域强度大、能量集中的特点,通过对信号进行奇异值分解处理抑制混响,在此基础上,采用GO-CFAR恒虚警检测算法生成自适应检测门限,降低虚警概率,实现稳定的目标信号检测。计算机仿真验证了该方法对于降低噪声和抑制混响干扰的有效性,同时,通过对实航重型鱼雷目标的外场检测试验,验证了算法在实际应用中对于小目标检测的可行性和有效性。试验结果表明,该方法可以有效抑制强混响,能够有效提高信号干扰比,有利于强干扰条件下的弱目标信号检测,可以应用于水中小目标探测。
| [1] |
葛春莎. 水下小目标主动检测与跟踪算法研究[D]. 哈尔滨: 哈尔滨工程大学, 2019.
|
| [2] |
朱埜. 主动声呐检测信息原理[M]. 北京: 北京海洋出版社, 2014.
|
| [3] |
马凯, 王易川, 陈喆, 等. 混响背景下基于分数阶傅里叶变换的自适应LMS滤波算法[J]. 声学技术, 2020, 39(6): 769−773.
|
| [4] |
XU Wen-hua, TAN Li-hui, Lin Rongrong, et al. Weighted singular value decomposition basis of Szegő kernel and its applications to signal reconstruction and denoising[J]. Journal of Computational and Applied Mathematics, 2023(7):377−427.
|
| [5] |
钱征文, 程礼, 李应红, 等. 利用奇异值分解的信号降噪方法[J]. 振动、测试与诊断, 2011, 31(4): 459−463. |
| [6] |
张文斌. 奇异值能量差分谱在信号降噪中的应用[J]. 工矿自动化, 2014, 40(10): 25-28. |
| [7] |
ZHANG Lijuan, SUN onglai, WANG Zhengbo, et al. Fast target detection algorithm based on CFAR and target variance characteristics[J]. Wireless Communications and Mobile Computing, 2022, 47(3): 1685−1697.
|
| [8] |
殷超然, 闫林杰, 郝程鹏, 等. 均匀混响背景下抗多目标干扰恒虚警检测器设计[J]. 水下无人系统学报, 2019, 27(4): 434-441. YIN Chao-ran, YAN Lin-jie, HAO Cheng-peng, et al. Design of a multi-target interference resistant constant false alarm rate detector for homogeneous reverberation background[J]. Journal of Unmanned Undersea Systems, 2019, 27(4): 434-441. |
| [9] |
LI Bowen, LIU Xiaoming, DU Shasha, et al. CFAR detector based on the identification of sea clutter distribution characteristics[J]. Journal of Physics: Conference Series, 2022, 43(9): 2703−2710.
|
| [10] |
LIU Kaixuan, LI Yue, WANG Peng, et al. A CFAR detection algorithm based on clutter knowledge for cognitive radar[J]. IEICE Transactions on Fundamentals of Electronics, 2023, 22(1): 590−599.
|
| [11] |
YANG Zhiqing, TANG Jianjiang, ZHOU Hao, et al. Joint ship detection based on time-frequency domain and CFAR methods with HF radar[J]. Remote Sensing, 2021, 13(8): 1548.
|
 2024, Vol. 46
2024, Vol. 46
