宽带信号携带的目标信息量大、混响背景相关性弱,有利于水下目标检测,因此研究宽带波束形成技术在水下的应用具有重要意义[1]。宽带波束形成可分别在频域和时域上实现,频域上常用基于离散傅里叶变换(Discrete Fourier Transform,DFT)的波束形成方法;时域上多采用基于有限冲激响应(Finite Impulse Response,FIR)结构的波束形成方法[2]。在实际应用中发现,基于FIR结构的波束形成精度远高于基于DFT的波束形成,因此,之后的一系列波束优化方法基本都是针对基于FIR结构的波束形成器提出的。为了在环境噪声中获得期望信号,要求宽带波束形成算法可以适应不同情况下对主瓣宽度、旁瓣峰值和稳健性等指标的要求,同时给出阵列加权系数进行空、频域的滤波。
为了实现在约束旁瓣峰值的同时降低宽带恒定主瓣的误差,本文研究了一种基于二阶锥规划的最小差异恒定束宽波束形成器设计方法,进行宽带波束形成器各个频率的波束宽度和旁瓣峰值控制,并利用主瓣空间响应差异(Mainlobe Spatial Response Variation,MSRV)来衡量设计的宽带波束形成器的主瓣响应误差大小,同时适当约束加权范数,以达到最小差异恒定束宽、低旁瓣和高稳健性的目的。
1 基于FIR结构的高精度宽带波束形成基于FIR结构的时域宽带波束形成器的实现图如图1所示[3]。
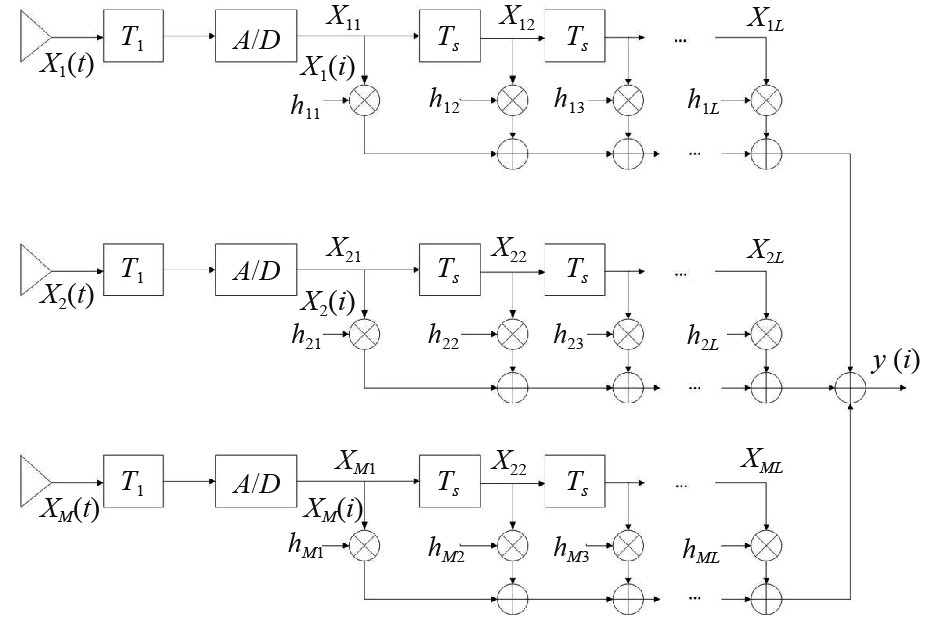
|
图 1 时域FIR波束形成器 Fig. 1 Time-domain FIR beamformer |
设各阵元经过预延迟之后的采样数据为
| $ y(i) = \sum\limits_{m = 1}^M {\sum\limits_{l = 1}^L {{h_{ml}}{x_m}[i - (l - 1)]} } 。$ | (1) |
在信号不确定的情况下,无法进行非整数倍采样周期的时延,故采用整数倍采样周期的时延和小数时延FIR滤波器共同来实现。整数倍采样周期的时延通过数字延迟实现[4],所以小数时延延迟量只需处于
| $ {H_d}({f_d}) = {e^{ - i2{\text{π}} {f_d}(D + \tau /{T_s})}}。$ | (2) |
式中:
| $ D = \left\{ \begin{array}{ccc}(L-1)/2, & L为奇数,& \tau \in [-0.5{T}_{s},0.5{T}_{s}) ,\\ L/2-1\text{,} & L为偶数,& \tau \in [\text{0},0.5{T}_{s}) ,\\ L/2+1\text{,} & L为偶数,& \tau \in [-0.5{T}_{s},0) 。\end{array}\right. $ | (3) |
为得到理想的频率响应,可以使期望频率响应与设计的FIR滤波器频率响应之间的误差范数最小。误差范数可表示为:
| $ {\delta _q} = ||{{\mathbf{\lambda }}^{1/q}} \circ ({\boldsymbol{H}} - {{\boldsymbol{H}}_d})|{|_q}。$ | (4) |
式中:
设滤波器长度
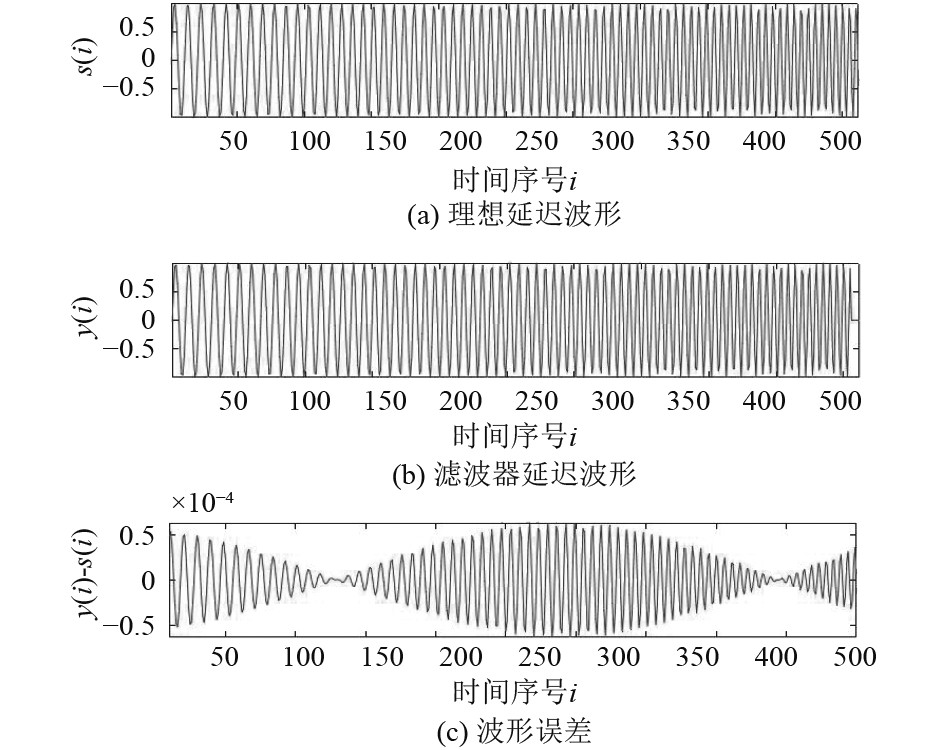
|
图 2 小数时延FIR波束形成器时域误差 Fig. 2 Fractional delay FIR beamformer time domain error |
| $ \mathop {\min }\limits_h \sum\limits_{k = 1}^K {[{\lambda _k}|{e^{\text{T}}}({f_k})h - {H_d}({f_k}){|^2}]}。$ | (5) |
通过最小加权误差准则设计的高精度小数时延FIR滤波器,具有较好的滤波性能,有效时域信号的误差在10−4级,有效提高了宽带波束形成器的精度。
2 基于SOCP的恒定主瓣波束形成 2.1 二阶锥规划二阶锥规划(Second-order Cone Programming,SOCP)本质上属于凸优化问题[6],在一定二阶锥约束及线性等式与不等式约束条件下,可求解某线性函数最小化问题,具体表述为:
| $ \left\{\begin{array}{*{20}{l}}\min_y\boldsymbol{b}^{\text{T}}\boldsymbol{y} ,\\ \mathrm{s}.\mathrm{t}.\begin{array}{*{20}{c}}\end{array}||\boldsymbol{A}_i\boldsymbol{y}+\boldsymbol{b}_i||\leqslant\boldsymbol{c}_i^{\text{T}}\boldsymbol{y}+\boldsymbol{d}_i,\\ \boldsymbol{Fy}=\boldsymbol{g} ,\\ \boldsymbol{Py}\leqslant\boldsymbol{q}。\end{array}\right. $ | (6) |
式中:
每个约束可表示为:
| $ \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{c}}_i^{\text{T}}} \\ {{{\boldsymbol{A}}_i}} \end{array}} \right]{\boldsymbol{y}} + \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{d}}_i}} \\ {{{\boldsymbol{b}}_i}} \end{array}} \right] \in cone_i^{{q_i}} \text{,} i = 1,2, \cdots ,N 。$ | (7) |
其中,
SeDuMi工具箱可专门用于求解二阶锥规划问题,求解步骤如下:
步骤1 将优化问题写为式(6)所示的标准形式。
步骤2 分别求出
其中,
| $ {\boldsymbol{\tilde b}} = - {\boldsymbol{b}} \text{;} {{\boldsymbol{\tilde c}}_{\boldsymbol{1}}} = {\boldsymbol{q}} \text{,} {{\boldsymbol{\tilde c}}_{\boldsymbol{2}}} = {\boldsymbol{g}} \text{,} {{\boldsymbol{\tilde c}}_{{\boldsymbol{2}} + {\boldsymbol{i}}}} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{d}}_{\boldsymbol{i}}}} \\ {{{\boldsymbol{b}}_{\boldsymbol{i}}}} \end{array}} \right] \text{。} $ |
步骤3 将
首先将工作频带分为若干窄带,用每个窄带的中心频率代表此窄带。在某一参考频率(不一定是某个子带频率)下,利用某一优化准则来设计期望波束响应[7]。再针对每个子带,在控制旁瓣的条件下,以最小均方主瓣逼近准则设计加权向量
| $ \left\{\begin{array}{*{20}{l}}\min_w\sum\limits_{j=1}^{N_{ML}}[\lambda_j|\boldsymbol{w}^{\text{H}}\boldsymbol{p}(\theta_j)-\boldsymbol{B}_d(\theta_j)|^2],\\ \mathrm{s}.\mathrm{t}.|\boldsymbol{w}^{\text{H}}\boldsymbol{p}(\theta_j)|\leqslant\xi_{\text{0}i} ,\\ \text{||}\boldsymbol{w}^2||\leqslant\xi_0。\end{array}\right. $ | (8) |
式中:
波束形成器中各通道FIR滤波器的期望频率响应就是该通道在该频率下的复加权,以第m个通道为例,滤波器系数为
| $ {H_{d,m}}({f_k}) = w_m^*({f_k})\exp ({i{2}}{\text{π}} {f_k}{T_m})。$ | (9) |
式中:
| $ {T_m} = - {int} [{\tau _m}({\theta _0})/T{}_s] \cdot {T_s}。$ | (10) |
以均匀32阵元线列阵,期望指向角度10°为例设计FIR恒定主瓣波束形成器。在频域中,将工作频带
步骤1 以子带内任意频率处的常规波束形成作为期望主瓣响应,在旁瓣控制最小均方主瓣逼近准则下求得各阵元在各频率下的复加权向量
步骤2 设计各通道滤波器响应,并验证是否符合期望频率响应。
步骤3 采用
步骤4 构造FIR波束形成器的等效加权向量,用该等效加权向量计算FIR波束形成器在各子带的波束响应。
通过将式(8)转换为二阶锥规划问题,利用SeDuMi工具箱求解出的各阵元复加权值,在空间域上实现了波束形成的要求,由图3可知,旁瓣峰值控制在−25 dB以下,同时各子带符合规定的主瓣宽度。图4为第8阵元滤波器的频率响应,阻带值控制在−40 dB以下,保证在频域上滤除非工作频带的信号,并同时将小数时延转化为对应的相移,实现高精度波束形成。将实际滤波器等效为各阵元加权值后求解FIR波束形成器的波束响应图,如图5所示,其中旁瓣峰值为−22.95 dB,相比设计的波束响应图有所升高,主瓣均方根误差达0.2045。
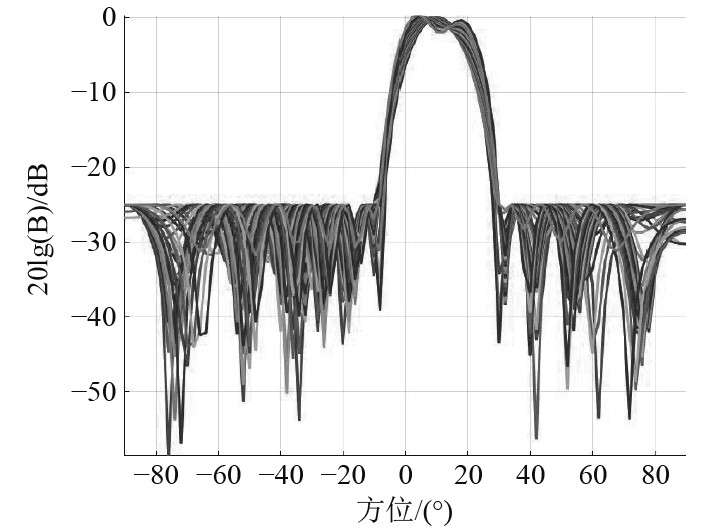
|
图 3 子带设计恒定主瓣波束响应图 Fig. 3 Subband-design constant mainlobe beam response diagram |
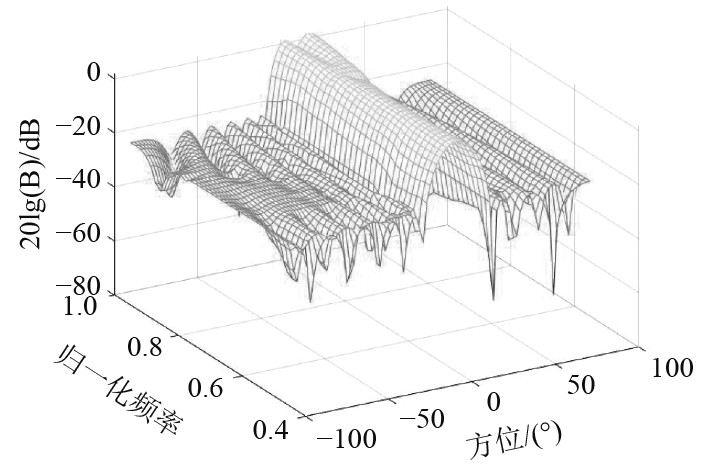
|
图 4 子带设计恒定主瓣波束响应图(三维) Fig. 4 Subband-design constant mainlobe beam response diagram (3D) |
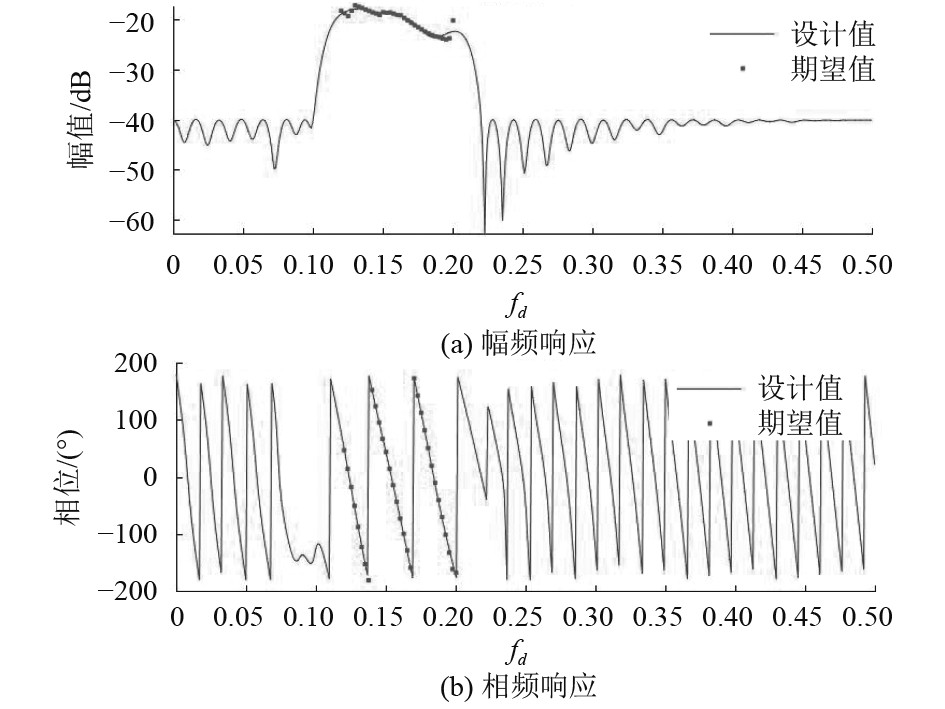
|
图 5 某通道滤波器频率响应 Fig. 5 Frequency response of a certain channel filter |
分析上述基于SOCP的恒定主瓣波束形成方法可知,上述在求解子带加权值和FIR滤波器系数时,2个优化问题都为凸优化,均可借助二阶锥规划在一定约束条件下获得最优解[11]。虽然FIR结构保证了高精度宽带波束形成,但存在一定缺陷:
1)在频域上没有对过渡带进行约束,如图6所示。
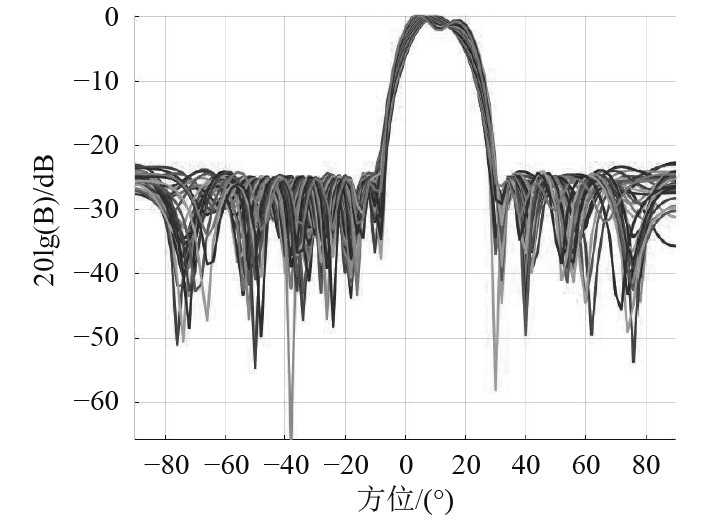
|
图 6 FIR波束形成器波束响应 Fig. 6 The FIR beamformer beam response |
2)无法直接根据旁瓣级约束确定FIR滤波器的阻带衰减级。
3)2个问题的最优解,并非全局综合的最优值。
根据图7,为控制波束形成的空、频域旁瓣,且使工作频带内的主瓣响应逼近于期望响应,最小合成误差全局优化的恒定主瓣波束响应FIR波束形成器设计如下:
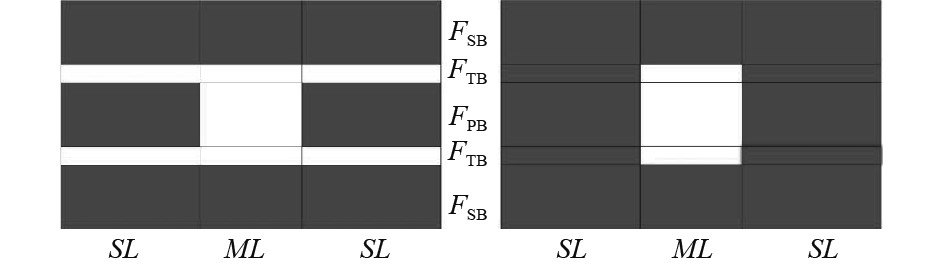
|
图 7 过渡带约束示意图 Fig. 7 Diagram of the transition zone constraints |
| $ \left\{ {\begin{array}{*{20}{l}} {{{\min }_h}{{\max }_{k,j}}|B({f_k},{\theta _j}) - {B_d}(\theta {}_j)|},\\ {{\text{s}}{\text{.t}}{\text{.|}}B({f_k},{\theta _i})| \leqslant {\xi _{0ki}}} ,\\ {|B({f_t},{\theta _i})| \leqslant {\xi _{0ti}}},\\ {|B({f_p},{\theta _q})| \leqslant {\xi _{0pq}}} 。\end{array}} \right. $ | (11) |
式中:
| $ \sum\limits_{m = 1}^M {\sum\limits_{l = 1}^L {||{h_{ml}}|{|^2} \leqslant \Delta _0^2} }。$ | (12) |
式中,
与仿真实验条件完全相同,旁瓣峰值约束均为−25 dB。
3.2 最小差异恒定主瓣波束响应就全局优化法而言,需要预先对期望主瓣响应
基于上述缺点提出用主瓣空间响应差异(Mainlobe Spatial Response Variation,MSRV)来衡量设计的宽带波束形成器的主瓣响应误差。
定义波束响应误差:
| $ {\delta _{MSRV}}({f_k},{\theta _j}) = |B({f_k},{\theta _j}) - B({f_0},{\theta _j})|。$ | (13) |
由式(9)可以推导出,FIR波束形成器在某一频率
| $ {\hat w_m}(f) = conj[h_m^{\text{T}}e(f)\exp ( - {\text{i}}2{\text{π}} f{T_m})]。$ | (14) |
其中,
| $ e(f) = {[1,\exp ( - {\text{i2}}{\text{π}} f{T_s}), \cdots ,\exp ( - {\text{i2}}{\text{π}} (L - 1)f{T_s})]^{\text{T}}} 。$ | (15) |
因此,FIR波束形成器的波束响应为:
| $\begin{split}B(f,\theta ) =& {\hat {\boldsymbol{w}}^{\text{H}}}(f){\boldsymbol{p}}(f,\theta ) = \{{\boldsymbol{e}}(f) \otimes [{\boldsymbol{p}}(f,\theta ) \circ \\ &\exp ( - {\text{i2}}{\text{π}} f{T_m})]\} ^{\text{T}}{\boldsymbol{h}} = {{\boldsymbol{u}}^{\text{T}}}(f,\theta ){\boldsymbol{h}}\end{split} 。$ | (16) |
则式(13)可变为:
| $ {\delta _{MSRV}}({f_k},{\theta _j}) = |{{\boldsymbol{u}}^{\text{T}}}({f_k},{\theta _j}){\boldsymbol{h}} - {{\boldsymbol{u}}^{\text{T}}}({f_0},{\theta _j}){\boldsymbol{h}}| 。$ | (17) |
式中:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathop {\min }\limits_h {{\max }_{k,j}}|{{\boldsymbol{u}}^{\text{T}}}({f_k},{\theta _j}){\boldsymbol{h}} - {{\boldsymbol{u}}^{\text{T}}}({f_0},{\theta _j}){\boldsymbol{h}}|} ,\\ {\mathrm{s}.\mathrm{t}.\begin{array}{*{20}{c}} {} \end{array}{{\boldsymbol{u}}^{\text{T}}}({f_0},{\theta _s}){\boldsymbol{h}} = 1} ,\\ {{{\boldsymbol{u}}^{\text{T}}}({f_k},{\theta _i}){\boldsymbol{h}} \leqslant {\xi _0}} 。\end{array}} \right. $ | (18) |
其中:
除旁瓣峰值约束提升为−30 dB外,其他与2中仿真条件完全相同,参考频率可随意选择,此处选取工作频带的下限为参考频率,代入式(18)的优化问题中,结果如下。
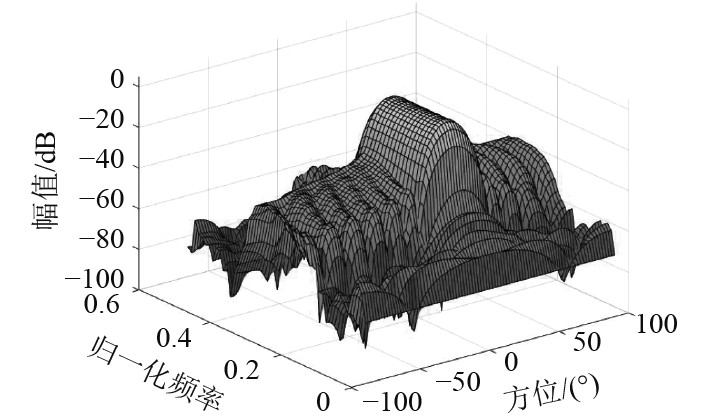
通过全局优化设计的波束形成器,在空、频域上的表现明显优于传统的FIR子带设计波束形成器,具体表现为:增加了对过渡带的约束后,空间域中在规定的主瓣范围之外,均低于设定值−25 dB,如图8所示;在频域中,工作频带之外的频率处的波束响应峰值均低于设定值−25 dB,且在过渡带与工频带的交界处可实现快速衰减,使过渡带更窄,如图9所示;综合结果如表1所示,就各频带在主瓣中的波束响应而言,相较于子带设计波束形成法的0.2045主瓣均方根误差,全局优化的主瓣均方根误差为0.1174。
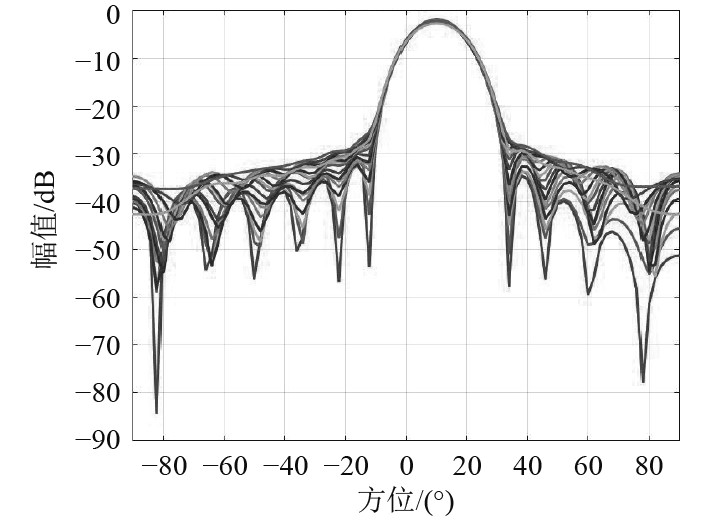
|
图 8 全局优化波束形成图 Fig. 8 Globally optimized beamforming diagram |
|
图 9 全局优化波束形成图(三维) Fig. 9 Globally optimized beamforming diagram (3D) |
|
|
表 1 性能比较 Tab.1 Parameters of flexible intercepting net |
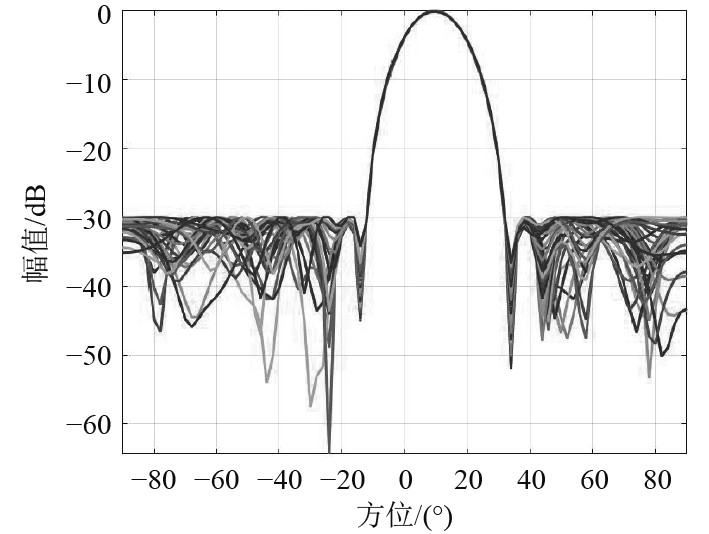
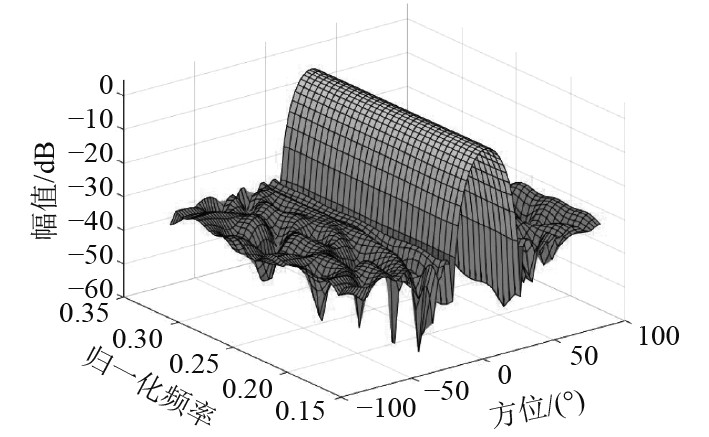
更进一步,在克服了全局优化波束形成法在主瓣参考波束响应的选择后,最小差异恒定主瓣波束响应法可将旁瓣峰值完全控制−30 dB以下,如图10所示。频域中,过渡带与工频带交接处更陡且主瓣均方根误差为0.0175,可认为各工作频带在主瓣中的波束响应完全一致,如图11所示。
|
图 10 最小差异恒定主瓣波束响应图 Fig. 10 Minimum difference constant mainlobe beam response diagram |
|
图 11 最小差异恒定主瓣波束响应图(三维) Fig. 11 Minimum difference constant mainlobe beam response diagram (3D) |
为解决传统波束形成器在空、频、时域上的表现不佳问题,本文引入了一种基于二阶锥规划的FIR最小差异恒定主瓣波束形成方法。首先采用基于FIR滤波器结构设计出的波束形成器,在实现了高精度小数时延的同时,将传统方法中的小数预延迟改进为整数预延迟与FIR滤波器的结合,使整数倍的预延迟可直接采用数字延迟线实现,避免了在工程实际中使用昂贵的电子延迟器或机械扫描器,为之后宽带波束形成器的实现奠定了良好的基础。然后,通过引入滤波器系数h,将旁瓣级与FIR滤波器的阻带衰减级联系在一起,并且采用全局优化的方法将传统方法中的2个凸优化问题合为一个凸优化问题,直接利用二阶锥规划解决,确保了所得解是综合最优解。最后,重新定义了主瓣响应误差,将原有固定参考频率处的波束响应修改为某频率处h的函数,因为最终求解的未知数也是h,提出了基于旁瓣峰值约束Minimax主瓣差异的FIR波束形成器设计准则。
仿真结果表明,在时域中,该波束形成器采用的FIR滤波器时延波形与理想时延波形之间的误差为10−4量级;在空间域中,根据所提方法可在期望信号方向获得主瓣均方根误差极小的恒定波束响应,同时对旁瓣方向信号的抑制可在−30 dB以下,可将期望信号无失真输出;在频域中,可将工频带与过渡带的交接处处理的更陡,同时控制过渡带旁瓣峰值在−30 dB以下。同时该方法的部分功能已在FPGA中得到初步验证。
| [1] |
王剑书, 樊养余, 杜瑞, 等. 改进的基于本征滤波的时域宽带波束形成[J]. 北京航空航天大学学报, 2015, 41(10): 1830-1835. |
| [2] |
祝鹏, 杜金香. 随机错位组合阵列分级波束旁瓣控制方法[J]. 水下无人系统学报, 2021, 29(2): 183-188. ZHU Peng, DU Jin-xiang. Side lobe control method in subarray beamforming based on randomly staggered combination array[J]. Journal of Unmanned Undersea Systems, 2021, 29(2): 183-188. |
| [3] |
JIANG Feng, LI Qinghua, CHEN Xiaogang. Channel smoothing for 802.11ax beamformed MIMO-OFDM[J]. IEEE Communications Letters, 2021, 25 (10): 3413−3417.
|
| [4] |
岳雷, 姜春华, 罗松, 等. 低频宽带多波束声呐系统设计及试验研究[J]. 水下无人系统学报, 2020, 28(1): 97-106. YUE Lei, JIANG Chun-hua, LUO Song, et al. Design and experimental research of low-frequency broadband multi-beam sonar system[J]. Journal of Unmanned Undersea Systems, 2020, 28(1): 97-106. |
| [5] |
石钰. 矢量拖曳阵MVDR波束形成及本舰干扰抵消方法研究[D]. 哈尔滨:哈尔滨工程大学, 2012.
|
| [6] |
鄢社锋, 马远良. 二阶锥规划方法对于时空域滤波器的优化设计与验证[J]. 中国科学E辑:信息科学, 2006(2): 153-171. |
| [7] |
柯小梅. 宽带波束形成算法研究[D]. 西安:西安电子科技大学, 2018.
|
| [8] |
HU X , PENG M , ZHONG C . Low-complexity beamforming design for IRS-aided communication systems[J]. Science China(Information Sciences), 2022, 65(10): 305−306.
|
| [9] |
JAFAR N, PAEIZ A, MAHDI N. Feasibility of a novel beamforming algorithm via retrieving spatial harmonics[J]. Journal of Systems Engineering and Electronics, 2022, 33(1): 38−46.
|
| [10] |
刘潇, 刘宝蕊, 窦修全, 等. 大规模面阵分级波束形成算法研究[J]. 河北工业科技, 2022, 39(1): 16-23. |
| [11] |
SHEN Che chou, TU Kuan lin. Ultrasound DMAS beamforming for estimation of tissue speed of sound in multi-angle plane-wave imaging[C]//IEEE International Ultrasonics Symposium. 2020.
|
| [12] |
SHI Yunmei, KONAR , SIDIROPOULOS NICHOLAS D, et al. Learning to beamform for minimum outage[J]. IEEE Transactions on Signal Processing, 2018, 66(19): 5180−5193.
|
| [13] |
XU Y, LIU J, LIU Z. Focused Widely Linear Beamforming[J]. Journal of Beijing Institute of Technology, 2019, 28(4): 744−749.
|
| [14] |
吴敏, 黎子皓, 郝程鹏,等. 基于压缩感知的低复杂度超分辨角度估计方法[J/OL]. 系统工程与电子技术: 1−9.
|
| [15] |
王子豪, 王安国, 冷文. 基于协方差矩阵重构和导向矢量优化的波束形成算法[J]. 重庆大学学报, 2022, 45(7): 79-92. |
 2024, Vol. 46
2024, Vol. 46
