2. 海军大连舰艇学院,辽宁 大连 116018
2. Dalian Naval Academy, Dalian 116018, China
在信息技术不断发展的今天,现代战争形式早已演变成信息化对抗。对于水下通信对抗场景而言,通信信号的体制、调制样式愈加多样复杂,信号环境也愈发密集,构成一个复杂多变环境。通信对抗侦察为通信对抗的重要环节,它是指利用通信侦察设备探测、搜索和截获敌方通信信号,对其进行信号测量、分析、识别与监视,同时对敌通信设备进行测向与定位,从而获得信号频率、电平、调制方式等技术参数以及电台位置、通信方式、通信网结构等信息的过程[1]。在现代战争战场不断扩大的今天,海洋毫无疑问地成为未来战争的一个重要战场,而水声通信信号识别方法作为水声通信侦察和对抗中的一种关键方法值得去着重探讨。
传统通信信号识别方式一般以特征提取为基础进行统计模式识别,这就要求人工观测这些特征之间的差异性才能完成对信号的识别。国外,Polydoros等[2]提出一种基于载波频率、符号速率和初始相位等特征,采用决策理论的方法,对BPSK和QPSK完成识别。Mobasseri[3]提出了基于星座图的数字信号模式识别方法。Sanderson等[4]采用二阶循环累积量的特征,利用盲识别算法对水声环境下BPSK、QPSK和16QAM信号进行识别。国内,曾创展等[5]于根据信号相关特性提取了信号的瞬时相关峰值数、延迟相关期望值和一阶瞬时相关谱峰位置标准差为特征,建立适当的决策阈值,对MASK、MPSK和MFSK信号进行调制识别。
近年来,伴随着机器学习理论研究的不断深入,许多基于机器学习的信号识别分类器相继提出。史文娟等[6]利用功率谱特征和支持向量机方法,实现了加性高斯白噪声信道下包括正交频分复用在内的9种调制样式的识别。巩克现等[7]用自回归模型的极点来提取信号短时频率峰值,并应用改进聚类算法将峰值序列聚类处理,依据不同阶数FSK信号在不同聚类中心局部密度和距离乘积上的差异,用支持向量机分类完成MFSK调制识别。周青等[8]利用小波变换模值的方差特性,利用支持向量机实现了对水声信号多种调制方式的识别,并在此基础上提出一种新的识别方法。
然而,基于机器学习调制方式辨识方法为人工设计判据,再依据以上判据进行特征选择。特征提取和最终预测模型学习是分离的,所以学习到的特征并不一定能改善最终模型性能并确保其泛化能力。针对这一情况,本文提出一种基于深度学习调制类型辨识方法,该方法通过深度神经网络实现信号抽象特征的自动抽取,从而完成信号调制类型辨识。
1 基于高阶累积量的识别方法 1.1 信号与信道模型本文所研究对象为水声通信信号,对于水声通信信号的调制通过正交调制来实现。正交调制的时域表达式为:
| $ s(t) = I(t)\cos ({\omega _c}t) + Q(t)\sin ({\omega _c}t) 。$ | (1) |
式中:
一般情况下,通信信号经过信道的过程公式为:
| $ r(t) = h(t) \otimes s(t) + n(t) 。$ | (2) |
式中:
为了评估水声信号各调制方式识别算法的性能,需模拟水下环境,并对水声信道进行建模。
水声信号在水下传播时,会受到海面、海底等的反射和折射,导致声波在接收端到达时经过了多条路径。这种现象称为多径效应。多径效应会对水声信号的波形产生影响,并使信号变得复杂。水声信号经多径传播通过水声信道到达接收端的波形
| $ y(t) = \sum\limits_{i = 1}^N {{A_i} \cdot s(t - {\tau _i})} 。$ | (3) |
式中:
在水声信道(见表1)中,多普勒频移主要由声源和接收机的相对运动引起。例如,当声源向接收机移动时,接收到的声波频率会升高;当声源远离接收机移动时,接收到的声波频率会降低。多普勒频移计算公式为:
|
|
表 1 水声信道参数 Tab.1 Underwater acoustic channel parameters |
| $ \Delta f = \frac{v}{c} \cdot f \cdot \cos \theta 。$ | (4) |
式中:
为了模拟水声通信信号经过多径信道的过程,本文使用射线声学理论和 BELLHOP 模型。首先,设计了浅海海域测量的数据,水深为 20 m。然后,设置了环境文件,将海底建模为声学半空间(声速为 1500 m/s,密度均匀)。声源深度为 10 m,接收器深度为 10 m。最后,调用 BELLHOP 模型,计算了声场到达结构,如图1 所示。
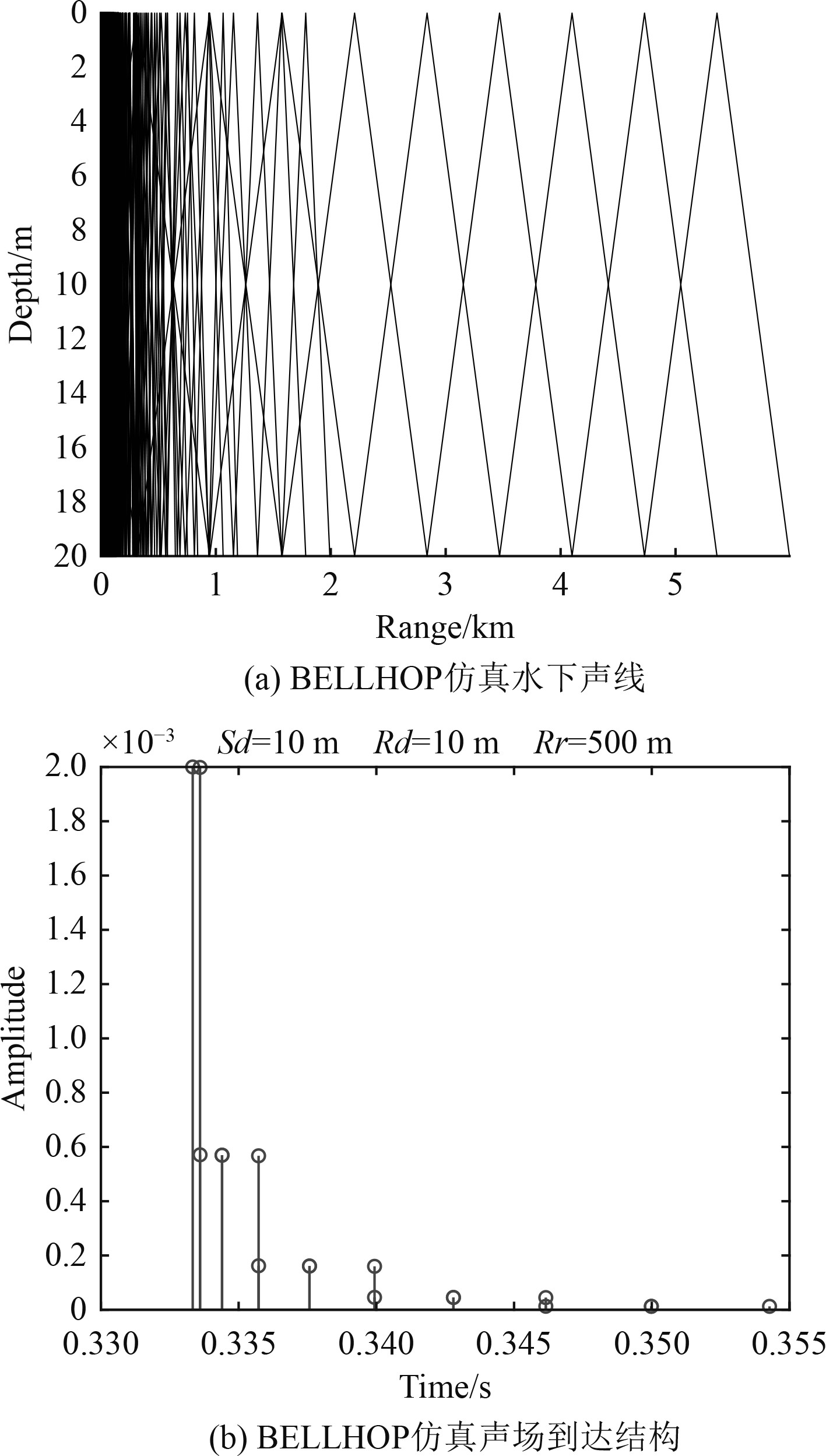
|
图 1 水声信道仿真 Fig. 1 Underwater acoustic channel simulation |
高阶累积量(Higher Order Cumulant,HOC)是描述随机过程高阶统计特性的一种数学工具,可用来描述随机过程的各种统计特性,例如协方差、相关性和自相关性。HOC 还可用于设计新的信号处理算法,例如波形分离和噪声消除算法。
通常来说,一个零均值的实平稳随机过程
| $\begin{split} & {c_{mx}}({\tau _1},{\tau _2}, \cdots {\tau _{m - 1}}) = \\ & {\text{cum}}(x(i),x(i + {\tau _1}), \cdots ,x(i + {\tau _{m - 1}})) 。\end{split}$ | (5) |
式中:
通常来说,一个零均值的平稳复随机过程
| $ {\boldsymbol M_{pq}} = E\left[ {X{{(k)}^{p - q}}{X^ * }{{(k)}^q}} \right] 。$ | (6) |
式中:
| $ \small\left\{ {\begin{array}{*{20}{l}} {{C_{20}} = {\boldsymbol M_{20}}},\\ {{C_{21}} = {\boldsymbol M_{21}}},\\ {{C_{40}} = {\boldsymbol M_{40}} - 3\boldsymbol M_{20}^2} ,\\ {{C_{41}} = {\boldsymbol M_{41}} - 3\boldsymbol M_{21}^{}{\boldsymbol M_{20}}},\\ {{C_{42}} = {\boldsymbol M_{42}} - |{\boldsymbol M_{20}}{|^2} - 2\boldsymbol M_{21}^2} ,\\ {{C_{60}} = {\boldsymbol M_{60}} - 15{\boldsymbol M_{40}}{\boldsymbol M_{20}} + 30\boldsymbol M_{20}^3},\\ {{C_{63}} = {\boldsymbol M_{63}} - 6{\boldsymbol M_{20}} {\boldsymbol M_{41}} - 9{\boldsymbol M_{42}} {\boldsymbol M_{21}} + 18\boldsymbol M_{20} ^2{\boldsymbol M_{21}} + 12\boldsymbol M_{21}^3} ,\\ {{C_{80}} = {\boldsymbol M_{80}} - 28{\boldsymbol M_{60}} {\boldsymbol M_{20}} - 35\boldsymbol M_{40}^2 + 420\boldsymbol M_{40}^{} \boldsymbol M_{20}^2 - 630\boldsymbol M_{20}^4} 。\end{array}} \right. $ | (7) |
现代信号处理理论表明,高斯噪声大于二阶的累积量均恒等于0[10]。这表明通过计算信号的高阶累积量,可几乎不考虑高斯噪声对信号识别分类的影响。将水声通信调制信号的能量设为
|
|
表 2 各累积量理论值 Tab.2 The theoretical value of each cumulant |
可知,除了2FSK和4FSK,对水声通信调制信号所计算的不同高阶累积量的值不同,这可作为信号调制类别识别过程中的重要特征,针对MFSK信号,其各个高阶累积量的理论值接近,对此,构造组合特征参数来区分,具体为对MFSK先求导,再计算高阶累积量,如表3所示。
|
|
表 3 MFSK高阶累积量 Tab.3 MFSK high-order cumulant |
对7种水声通信信号的调制识别流程如图2所示。
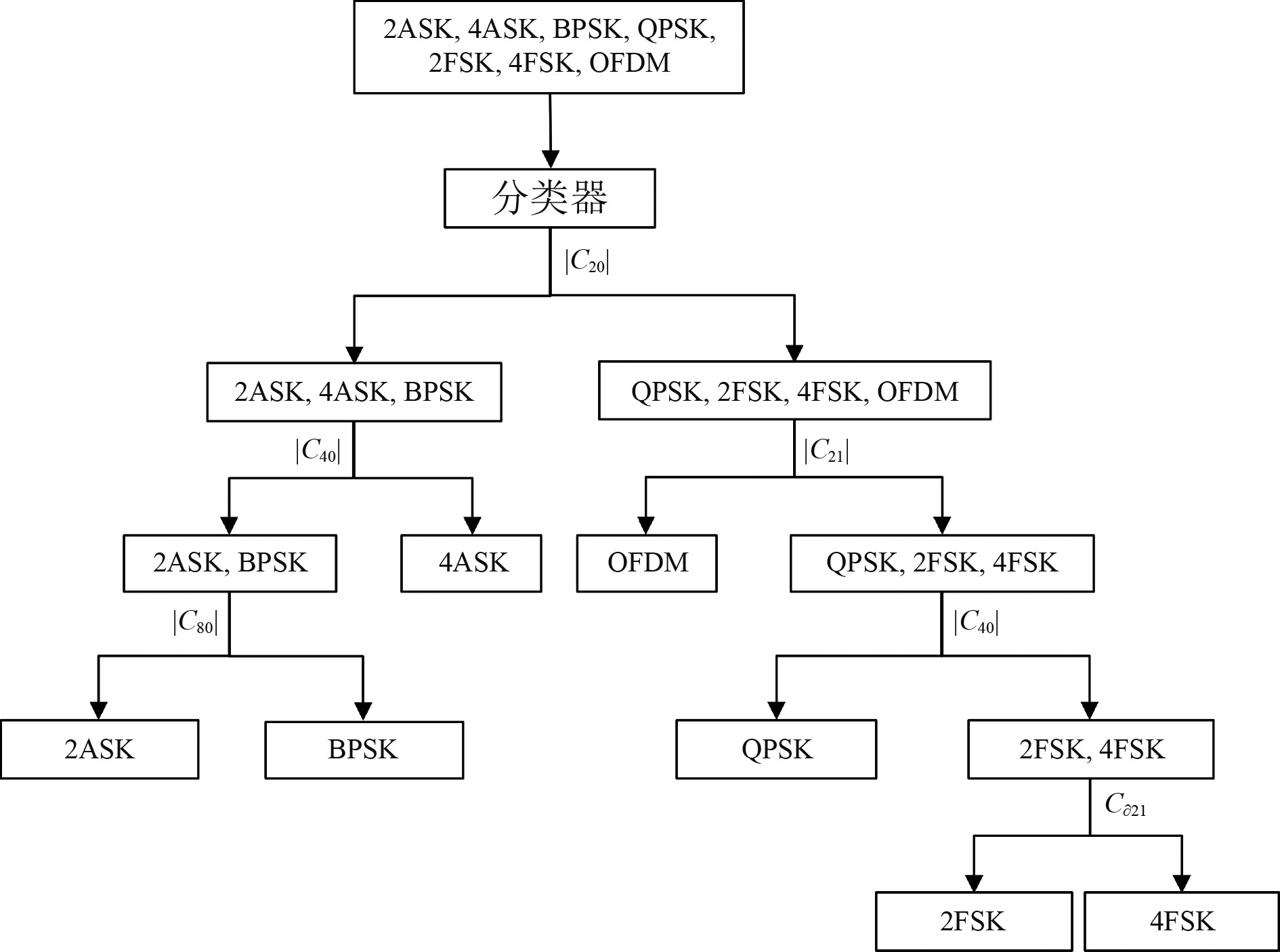
|
图 2 基于高阶累积量识别流程 Fig. 2 High-order cumulant-based identification process |
基于上述各阶累积量参数的差异性,对7种信号的累积量进行仿真,如图3所示,横坐标是信噪比,纵坐标为各个累积量特征。对比发现不同信号的特征曲线仅靠单一特征无法对其区分,需利用不同的累积量特征有针对性的展开识别,特征选取和确定十分困难。
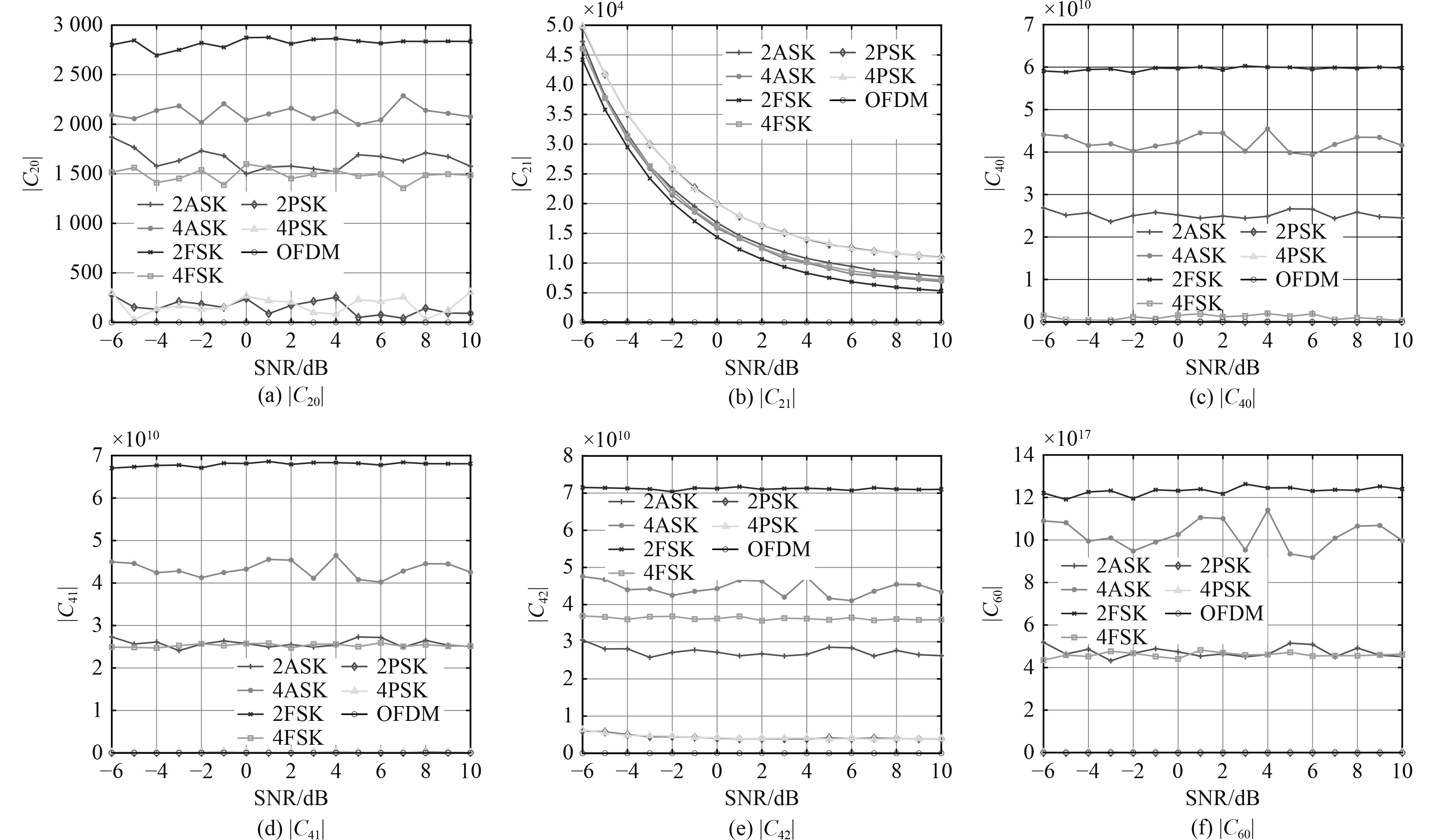
|
图 3 高阶累积量仿真曲线 Fig. 3 Higher-order cumulant simulation curve |
对于水声通信信号来说,通常难以获取大规模的信号数据,因此,利用仿真软件来生成所需的信号数据。对于信号参数的选取也可借助仿真软件来设定。本文所使用的水声通信信号数据集仿真步骤如下:
步骤1 通信信号的种类和参数,参数有采样率、载波频率、传码率等。
步骤2 生成二进制随机序列,序列承载着水声通信信号所传输的信息。
步骤3 每种信号进行载波调制,按照步骤1中确定的种类和参数对信号调制。
步骤4 将已调信号与仿真信道结合,模拟真实情况会遇到的时钟偏移、频率偏移和多径效应。
步骤5 信号采样,在采用定理允许范围内设置合适的采样速率对调制信号采样。
步骤6 将所得的信号数据存储。
仿真所用信号参数如表4所示,采样率为100 kHz。
|
|
表 4 仿真信号参数 Tab.4 Parameters of simulation signals |
将I/Q样本按行放置在输出帧中。输出帧的大小为[2×1024×1],其中第一行为同相采样,第二行为正交采样。为每种不同的调制信号生成10000个样本,8000个样本用来训练,验证使用1000个样本,剩下的1000个样本用于测试。通过确保标签(调制类型)分布均匀,避免训练数据中的类别不平衡。绘制标签分布图,以检查生成的标签是否分布均匀,仿真数据集如图4所示。
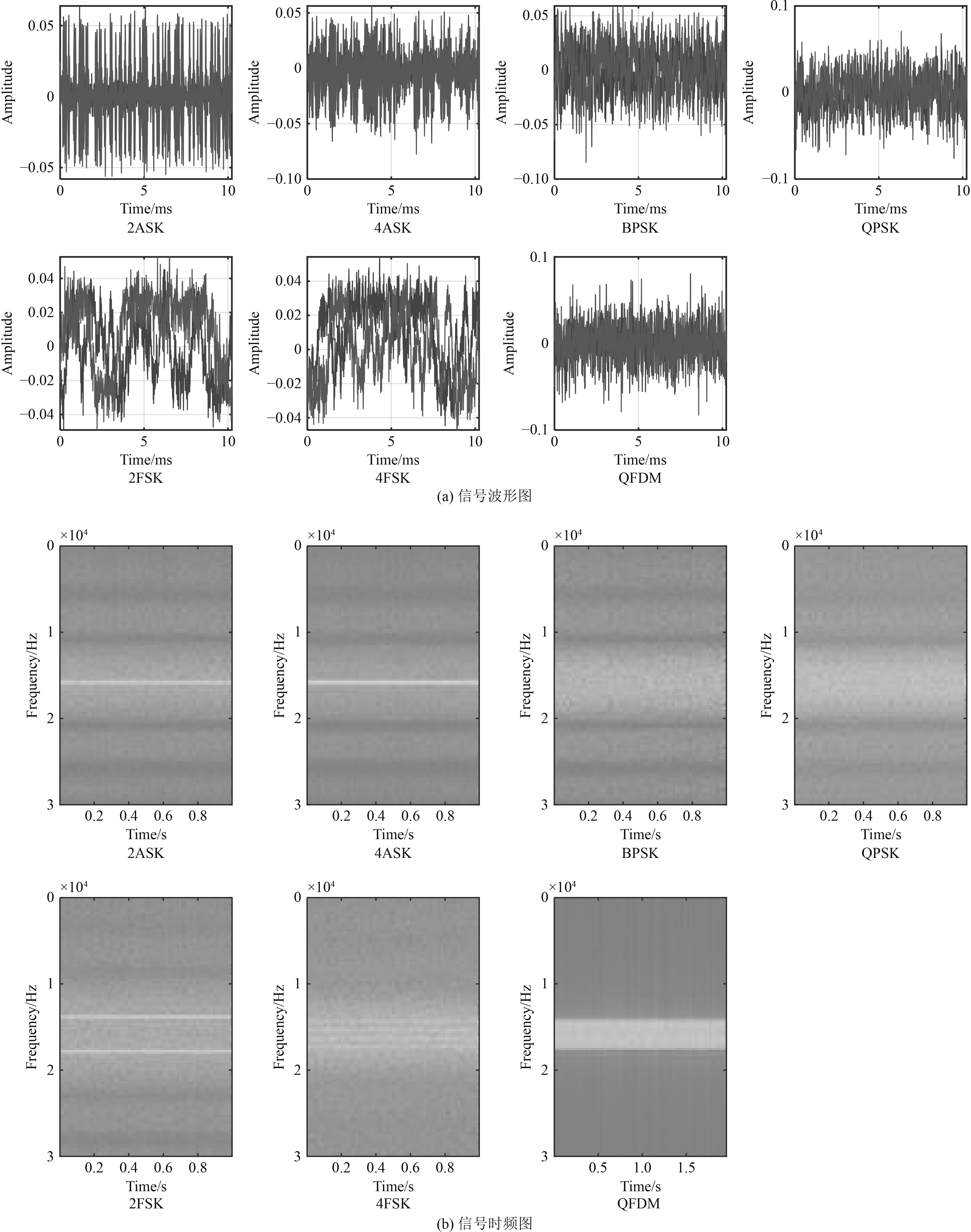
|
图 4 仿真信号数据集 Fig. 4 Simulation signal dataset |
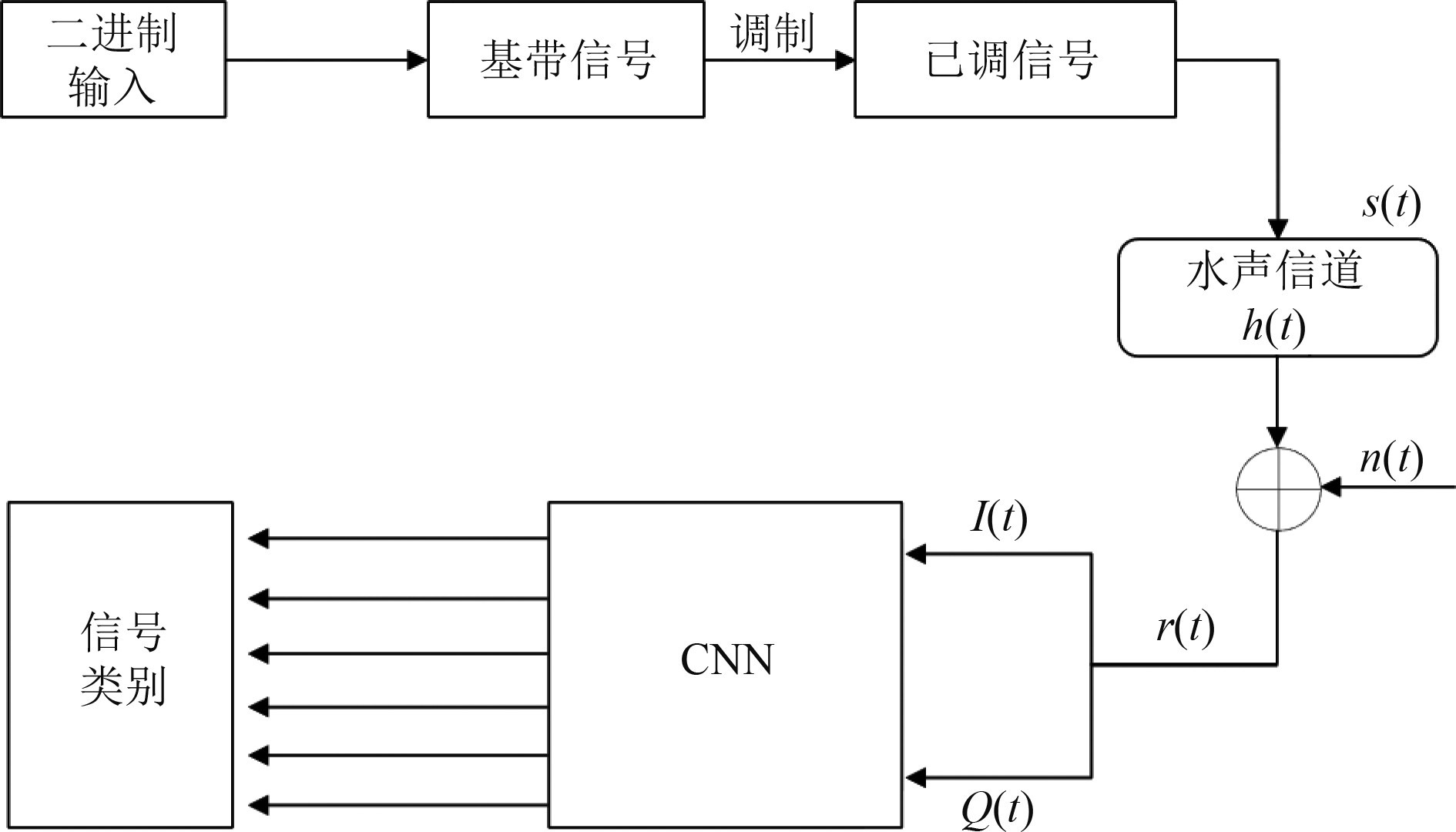
基于卷积神经网络(Convolutional Neural Network,CNN)的水声通信信号调制识别系统框图如图5所示。在发送端,随机生成的二进制比特序列首先映射为基带信号;基带信号经过不同的调制方式后,将已调信号输送至水声信道,经过水声信道后,将接收到的
|
图 5 CNN识别系统框图 Fig. 5 Block diagram of CNN recognition system |
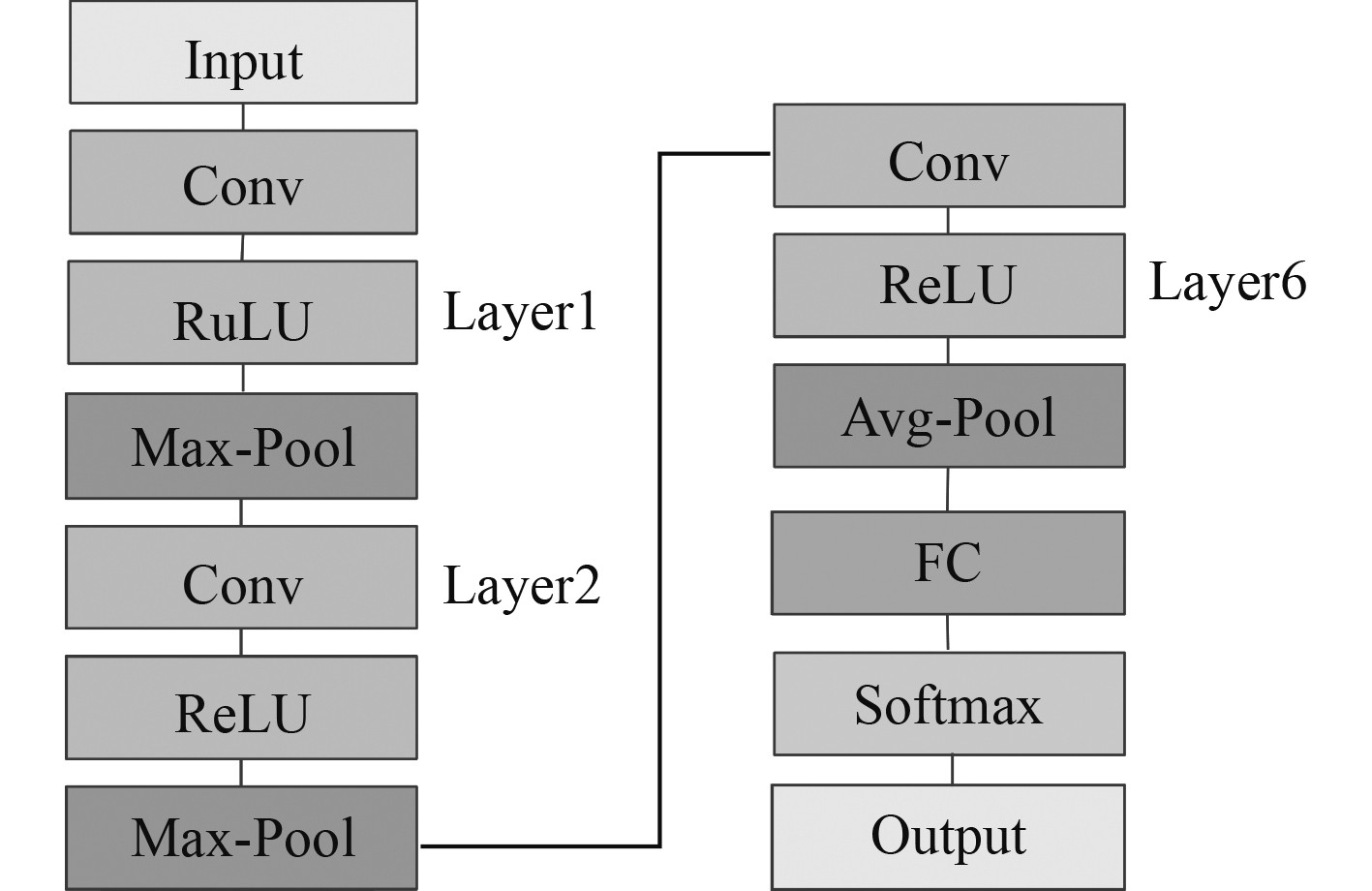
使用的卷积神经网络(CNN)由6个卷积层和1个全连接层组成(见图6)。除最后一个卷积层外,每个卷积层后都有一个批量归一化层、修正线性单元(ReLU)激活层和最大池化层。在第6个卷积层中,利用平均池化而不是最大池化。输出采用softmax激活,它将输出数据转换为概率分布。
|
图 6 CNN网络结构 Fig. 6 CNN network structure |
卷积层对输入信号进行特征提取,具有局部感知机制和权值共享的特性。其中,卷积核的channel数与输入特征层的channel相同,输出的特征矩阵channel 与卷积核的个数相同。经卷积后的尺寸计算由输入大小、卷积核大小、步长以及补零数决定。
批量归一化层用于规范化输入数据,以防止过拟合。批量归一化层将输入数据归一化到具有均值为0和方差为1的均匀分布。
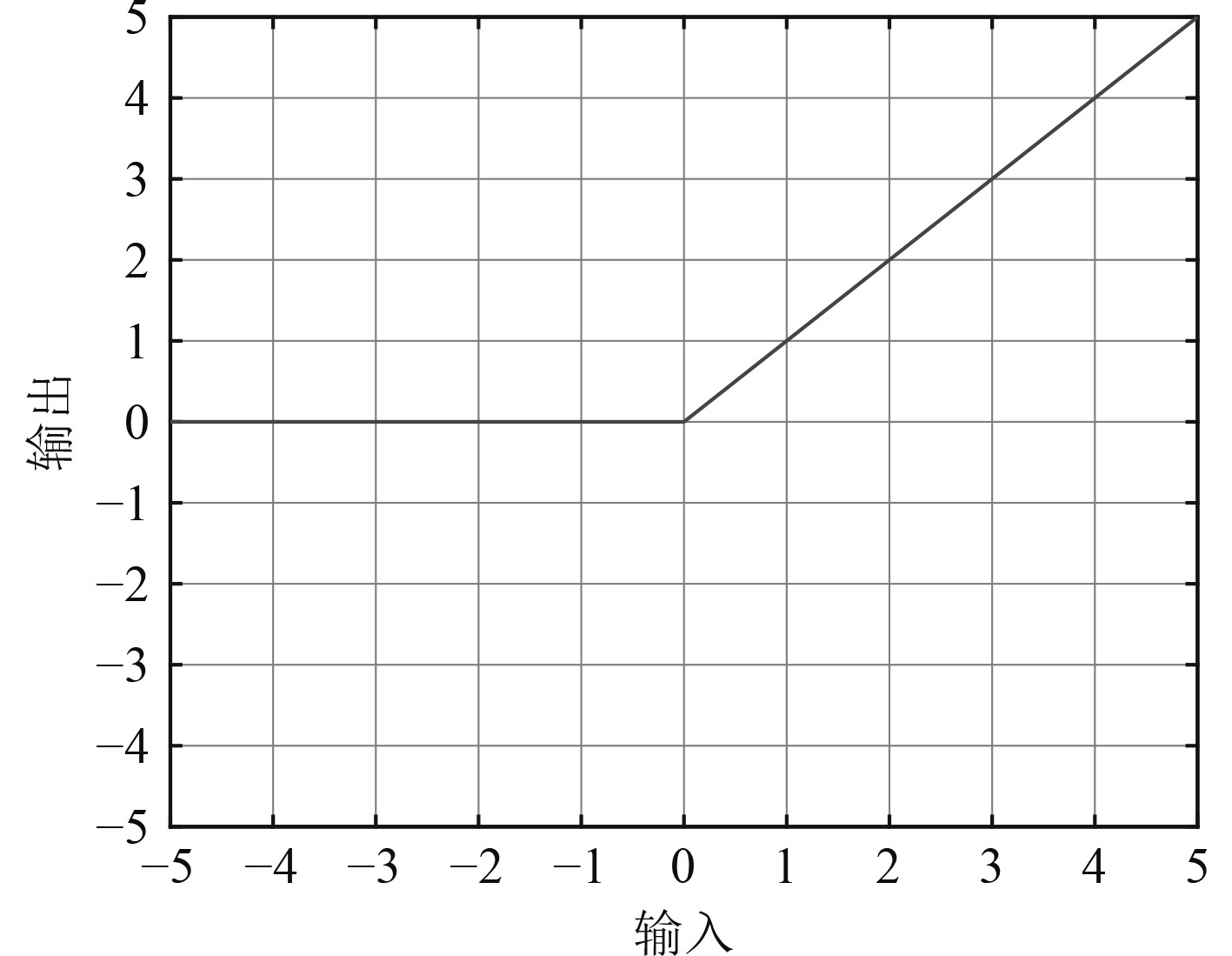
Relu激活函数图像如图7所示,函数表达式为:
|
图 7 Relu函数 Fig. 7 Relu function |
| $ \sigma (x) = \left\{ {\begin{array}{*{20}{l}} {\max (0,x)},&{x \geqslant 0} ,\\ 0。&{x < 0} 。\end{array}} \right.$ | (8) |
Relu激活函数具有以下优点:
1)使网络训练更快。反向传播是不断更新参数的过程,而Relu函数的导数简单好求。
2)增加网络的非线性。Relu函数本身为非线性函数,可拟合非线性映射。
3)防止梯度消失。Relu函数为非饱和激活函数。
4)使网络具有稀疏性。Relu函数会使一部分神经元的输出为0,同时减少了参数的相互依存关系,缓解了过拟合问题的发生。
最大池化层用于降低输入数据的维数,同时保留重要特征。最大池化层将输入数据的每个区域中的最大值保留为输出。平均池化层与最大池化层类似,但它将输入数据的每个区域中平均值保留为输出。池化层没有训练参数,其目的是对数据进行稀疏处理,减少数据运算量。
Softmax层通常作为输出层使用,对于分类识别任务,使用Softmax层来对输出进行概率化处理,将神经网络的输出转换为一个概率分布,每个类别对应一个概率值,并且归一化保证所有概率值的和为1,并使用交叉熵损失函数进行模型训练。
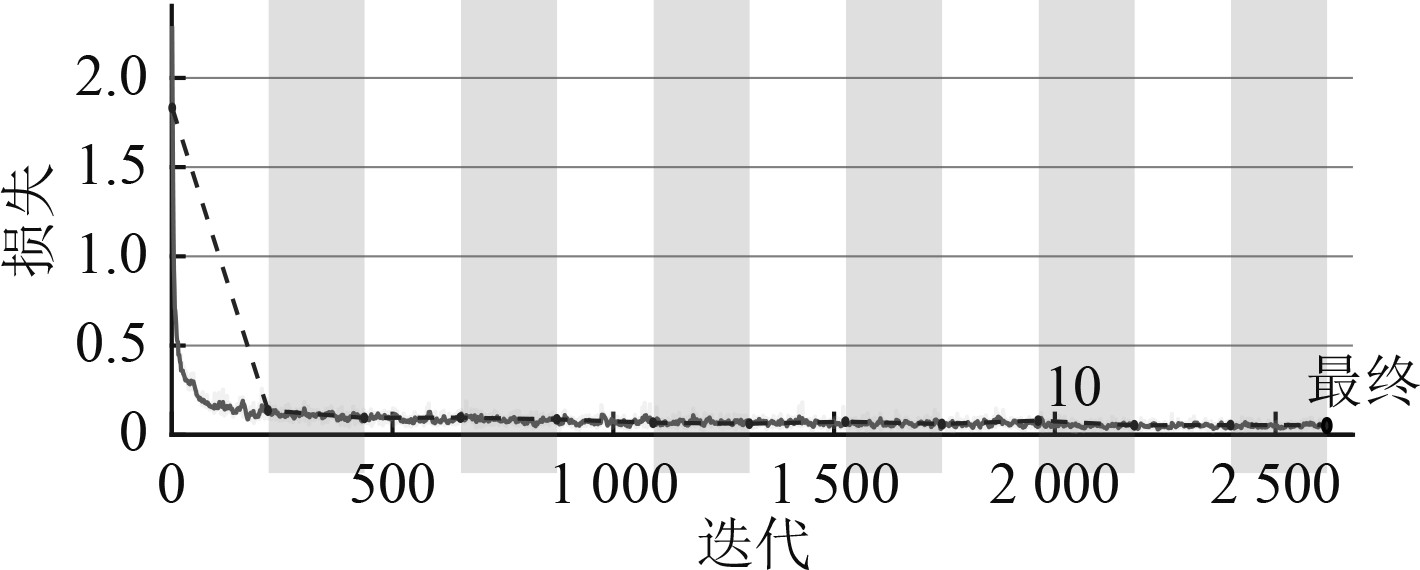
对上述网络进行训练,利用GPU对网络进行训练,训练轮数最大设置为12,刚开始的学习率设为0.02。之后对轮数的增加训练优势不会有更多提升,同时学习率在之后降为原来的1/10。训练的损失函数随迭代次数的变化如图8所示。
|
图 8 训练进度图 Fig. 8 Training progress chart |
本文所采用信号的参数如下:载波频率为16 kHz,采样频率为100 kHz,码元速率为5000 bit/s。信号类别有2ASK、4ASK、2FSK、4FSK、BPSK、QPSK、OFDM等7种数字调制。仿真信噪比为−6~10 dB。使用仿真软件随机多次抽样生成训练集和测试集,然后取平均值。
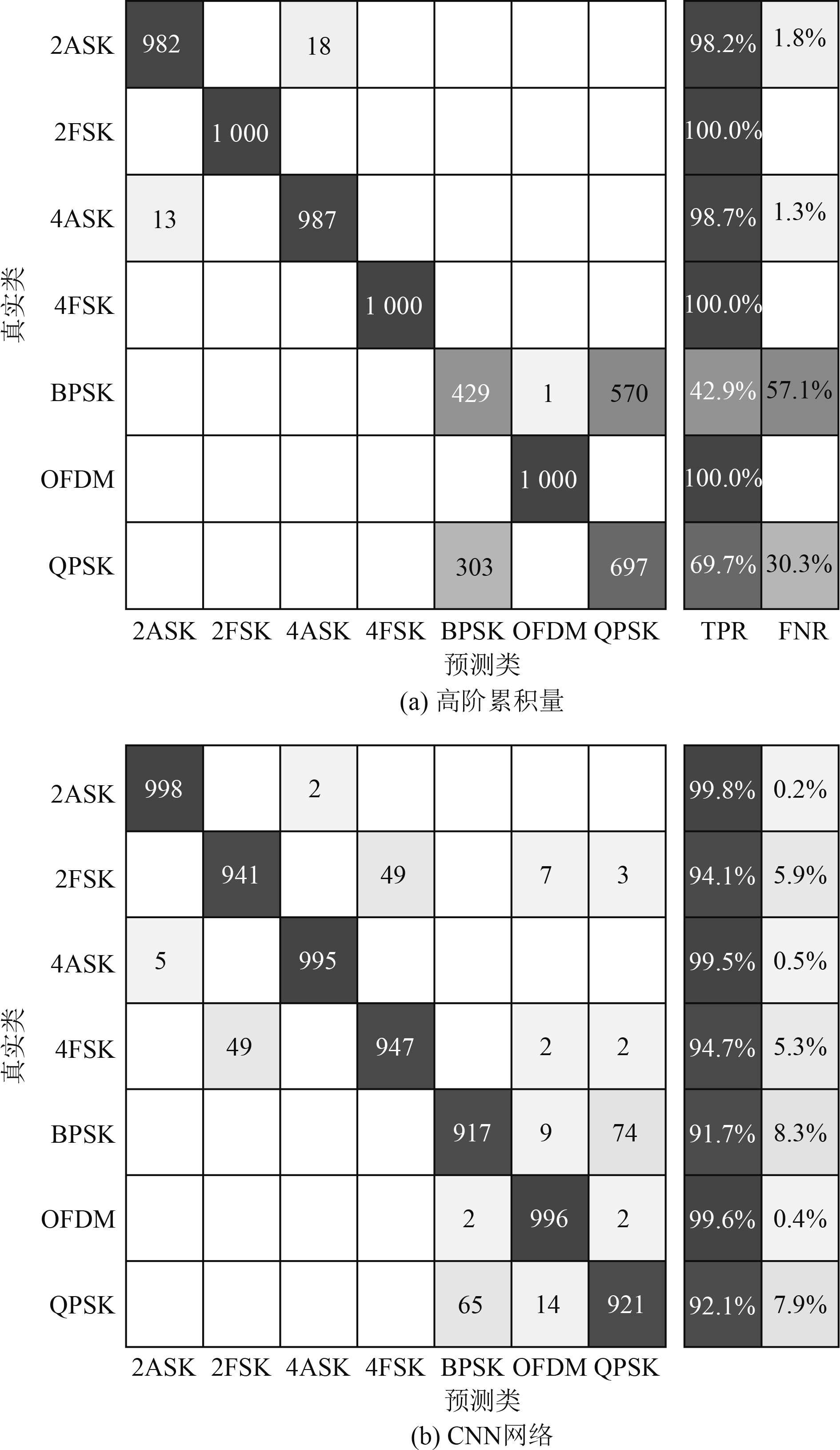
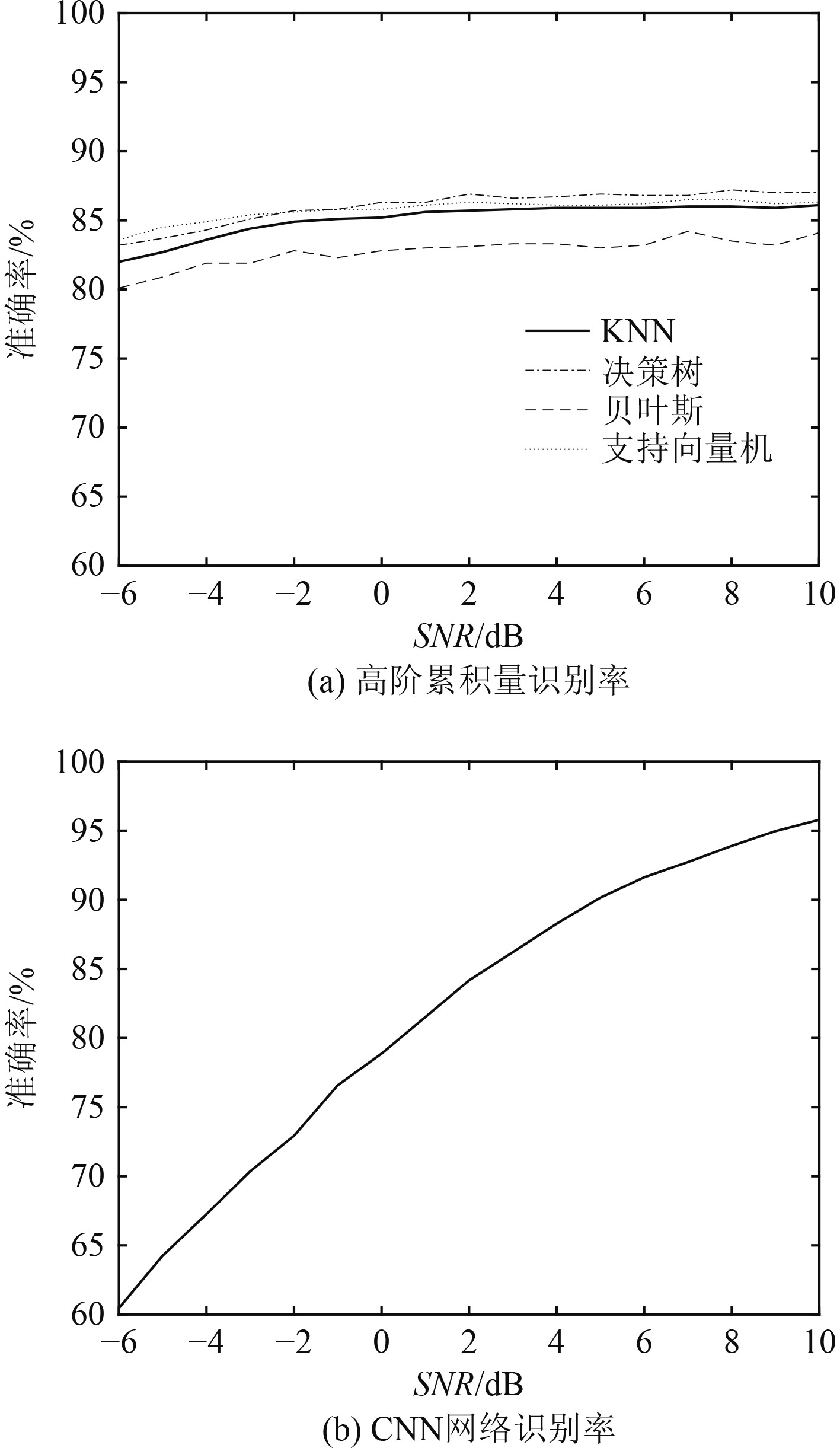
SNR=10 dB时,分类的识别结果绘制混淆矩阵如图9所示。基于高阶累积量的模式识别方法,由图9(a)可知,对于BPSK和QPSK的识别效果不太理想;由图9(b)可知,基于CNN的深度学习方法对每种信号的识别能力都能达到90%以上。改变信噪比,由图10可知,对于4种不同的机器学习分类算法,基于高阶累积量的识别方法,其准确率都维持在80%~87%;而深度学习方法随着信噪比的增大而增大,在SNR>0的条件下,对信号的识别率最高能达到95%。
|
图 9 测试集混淆矩阵 Fig. 9 Test set confusion matrix |
|
图 10 不同信噪比下的识别性能 Fig. 10 Recognition performance under different SNR |
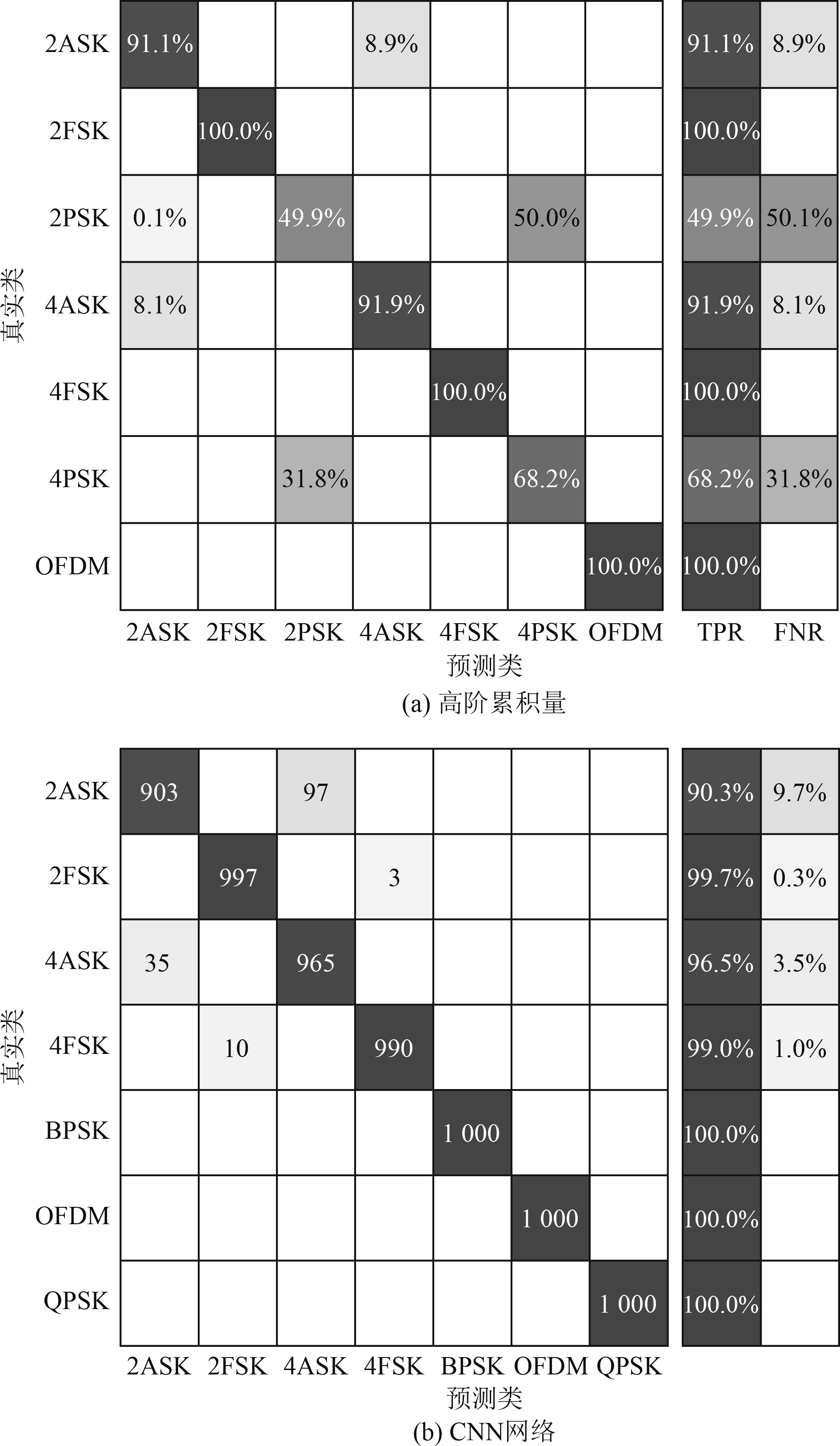
为了进一步对比2种算法在实际工程中的识别性能,本文使用实际的试验数据来测试。试验地点为厦门五缘湾,试验时收发换能器布放深度约10 m,收发距离约500 m。首先采集2ASK、4ASK、BPSK、QPSK、2FSK、4FSK和OFDM等7种信号,信号参数与仿真时一致,再用2种识别方式分别进行分类识别,得到的识别结果如图11所示。
|
图 11 试验数据混淆矩阵(SNR=5 dB) Fig. 11 Experimental data confusion matrix (SNR=5 dB) |
基于CNN方法的7种信号识别率均在90%以上,平均识别率达到97.9%,2种方法对OFDM信号的识别率达到了100%。试验数据处理结果进一步表明,2种算法适用于水下信道。同时,对于2PSK和4PSK来说,本文提出的基于CNN方法优于基于高阶累积量方法。
5 结 语本文利用信号的I/Q分量,结合卷积神经网络完成对2ASK、4ASK、BPSK、QPSK、2FSK、4FSK以及OFDM等7种调制信号的识别。相较于基于高阶累积量的模式识别方法,基于深度学习的方法在对特征提取与类型识别的过程均由网络自动进行,学习的特征有助于提高最终算法模型的性能并具有较好泛化能力。在SNR=5 dB时,利用仿真数据训练的网络对7种仿真信号的识别率都能达到90%以上;该网络对7种湖上试验的通信信号类型平均识别率达到97.9%,证明了算法的良好宽容性。
| [1] |
叶礼邦, 洪丽娜, 崔建岭, 等. 一种适合通信侦察能力试验的电磁环境复杂度定量评估方法[J]. 中国电子科学研究院学报,2014, 9(5): 531−537. YE L B, HONG L N ,CUI J L, et al. A quantitative evaluation method of electromagnetic environment complexity suitable for communication reconnaissance capability test[J]. Journal of China Institute of Electronic Science, 2014, 9(5): 531−537. |
| [2] |
KIM. K, Polydoros. A. Digital modulation classification: The BPSK and QPSK case[C]// Processing MILCOM, 1988, 87: 431−436.
|
| [3] |
BIJAN G M. Digital modulation classification using constellation shape[J]. Signal Processing. 2000, 80(2): 251−277.
|
| [4] |
SANDERSON J, LI X, LIU Z, et al. Hierarchical blind modulation classification for underwater acoustic communication signal via cyclostationary and maximal likelihood analysis[C]// IEEE Military Communications Conference, San Diego, CA, USA, 2013.
|
| [5] |
ZENG C Z, JIA X. Modulation recognition method of communication signals based on correlation characteristics[C]// 2015 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Ningbo, Zhejiang, China, 2015.
|
| [6] |
史文娟, 冯全源. 一种改进的基于支持向量机的 OFDM 识别算法[J]. 微电子学与计算机, 2014, 31(10): 98−102. SHI Wen-juan, FENG Quan-yuan. An improved ofdm recognition algorithm based on support vector machine[J]. Microelectronics and Computers, 2014, 31(10): 98−102. |
| [7] |
沈连腾, 巩克现 , 范磊. 利用局部密度与距离特征的MFSK识别方法[J]. 信号处 理, 2016(12): 1478−1488. SHEN Lian-teng, GONG Ke-xian, FAN Lei. MFSK recognition method using local density and distance features[J]. Signal Processing, 2016(12): 1478−1488. |
| [8] |
周青, 孙海信, 周明章. 一种水声通信信号调制模式识别方法[J]. 通信对抗, 2017, 2: 16-21. ZHOU Qing, SUN Hai-xin, ZHOU Ming-zhang. A modulation pattern recognition method for underwater acoustic communication signals[J]. Communication Countermeasures, 2017, 2: 16-21. |
| [9] |
LU Na. Study of modulation identification and signals feature extraction [D]. Xi’an. Xidian University. 2008.
|
| [10] |
张贤达. 现代信号处理第2版[M]. 北京: 清华大学出版社, 2002.
|
 2024, Vol. 46
2024, Vol. 46
