0 引　言

随着海洋经济的大力开发和水下潜航器电气化程度的提高，作为潜航器的动力部分，电力推进器已成为未来水下动力的发展趋势。相较于传统燃油推进器，电力推进器有以下优势：1）电力推进器的效率高；2）电力推进器可省去变速器的中间环节，使得结构更加简单；3）电力推进器更容易控制；4）电力推进器的振动噪声更小；5）电力推进器对环境更加友好等^[1]。

而水下轮缘推进器因其结构简单、运行稳定、下潜海域深等特点，并且作为电力推进器的重要组成部分，越来越被受到重视。水下轮缘推进器在结构上由壳体、定子、转子、导流罩、螺旋桨、水润滑轴承、水密接插件、密封圈、推力轴承等零部件组成。当三相正弦电流通入定子后，定子会产生一个交变的旋转磁场，与转子上的磁场产生旋转吸力，从而带动转子通过水润滑轴承做出旋转运动，最终实现螺旋桨旋转，旋转的螺旋桨将海水产生局部的压力差，进而产生推力给潜航器提供动力^[2]。

在水下或深海的极端环境下，水下轮缘推进器将会承受来自高压力、高腐蚀以及绝缘等方面的考验，那么水下轮缘推进器的可靠性也是科研人员的工作重点^[3]。为了能计算出水下轮缘推进器的可靠性，本文提出了基于FMECA与RPN的融合策略，将其结果作为加权因子再复合到水下轮缘推进器的可靠性计算中，最终得出水下轮缘推进器的复合可靠性计算值，为工程设计人员提供具有实际意义的可靠性帮助。

1 水下轮缘推进器的FMECA分析 1.1 水下轮缘推进器FMECA方法

FMECA是对于产品失效的全面分析，可确定每种故障对于产品失效影响的程度。通过逐一分析每种故障对于系统的影响程度，可定量给出产品可靠性评价的影响和危害性。由于水下轮缘推进器工作在极端的环境下，需对其进行严格的FMECA分析。

使水下轮缘推进器失效的因素非常复杂，大体可分为内部因素和外部因素。内部因素是指水下轮缘推进器设计生产时就导入的影响因素，包括材料、设计、结构以及生产工艺等。外部因素则是指水下轮缘推进器在运行时的人为因素、关机存放的环境因素以及运行环境因素等。水下轮缘推进器长期运行在水下或深海环境下，长时间高负荷运行会对轴承造成损害；密封部件也会在高压力下减小寿命；绝缘损坏会导致定子绕组故障，轻者会导致推进器输出转矩和平均输出功率下降，严重会造成接地失效，烧毁推进器。所以水下轮缘推进器的绝缘、水润滑轴承、永磁体、密封等因素会成为产生故障的主要原因，这些零部件将会是可靠性分析的重点。

本文采用风险优先数法进行产品故障模式的评价，评价指标主要包括严重度、频度以及检测度，计算公式如下^[5]：

$ RPN = S \times O \times D。$

(1)

式中：S为严重度，表示该失效发生对引起水下轮缘推进器影响的严重程度；O为频度，表示水下轮缘推进器在规定时间内该种失效发生的频率；D为探测度，表示水下轮缘推进器在该失效发生时的检测难度，制定评分标准，如表1～表3所示，RPN数值越大，表示水下轮缘推进器失效模式就越大，失效发生的零部件就越存在薄弱之处。

1.2 水下轮缘推进器FMECA整体分析

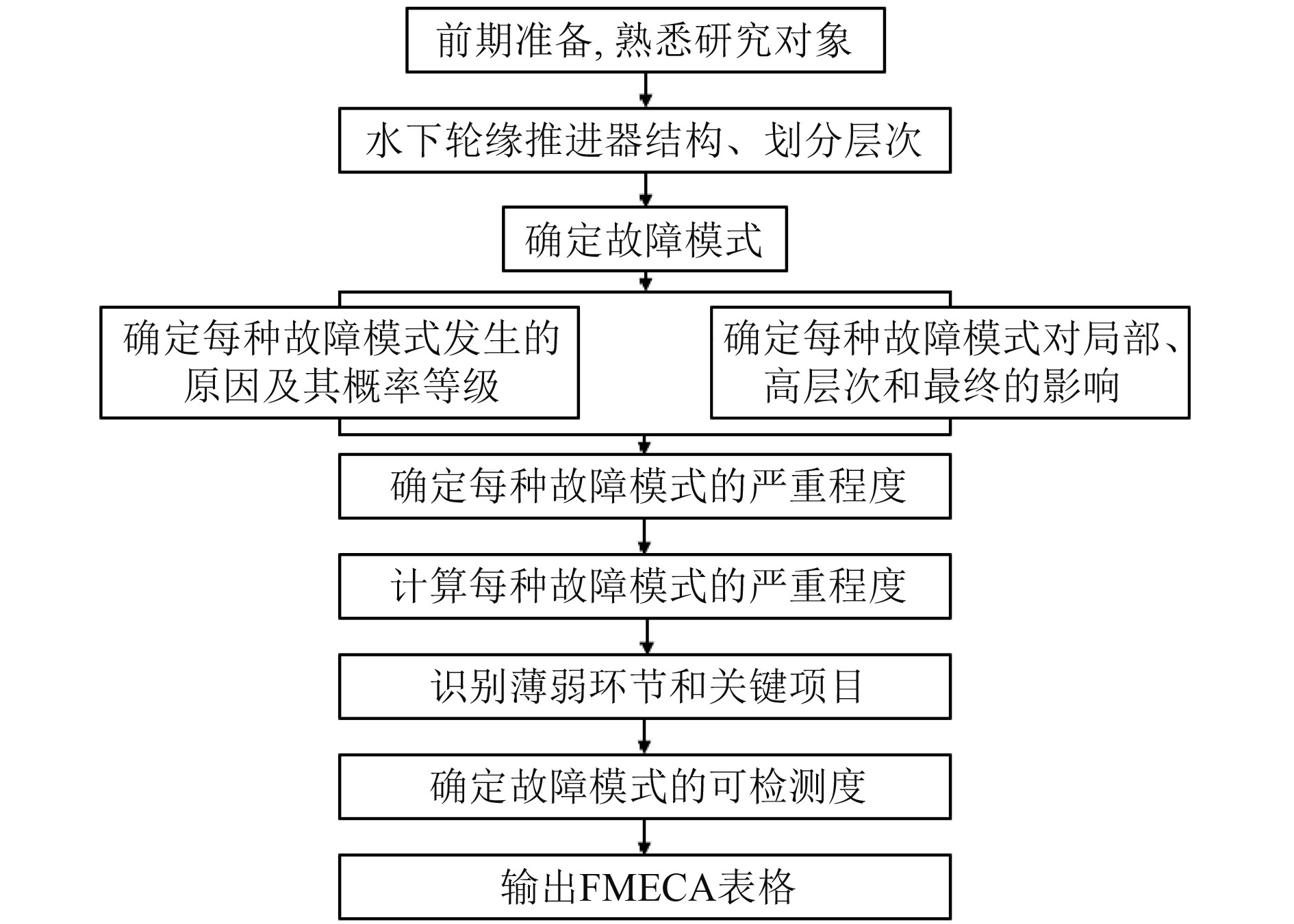
水下轮缘推进器在水下或深海运行时，会出现电气故障和机械故障的情况，水下轮缘推进器电气故障主要体现在定子绕组断路、短路以及绝缘等部位，其机械故障出现在密封、轴承以及受海水压力出现强度薄弱的环节，通过对水下轮缘推进器单元分解，按照FMECA流程图（见图1）进行整体分析（见表4）。

2 水下轮缘推进器本体的可靠性分析 2.1 水下轮缘推进器可靠性模型

水下轮缘推进器主要由定子和转子组成，其中定子包括定子铁芯、绝缘材料、定子绕组、壳体、环氧树脂、水密接插件、前法兰、后法兰、定子护套等；转子包括转子铁芯、磁钢、转子护套、水润滑轴承等。

水下轮缘推进器的可靠性模型为一个串联模型，任何单元的零部件损坏，整个推进器就失去原有的功能。

水下轮缘推进器由各个基本单元串联而成，其故障率为：

$ \lambda_{T}=\sum_{i=1}^{M} N_{\bar{i}} \cdot \lambda_{p} , \;i=1,2,3,...,M。$

(2)

式中：${\lambda _p}$为第i种基本单元的应用失效率；${N_i}$为第i种基本单元数量；$ M $为基本单元种类数。

2.2 水下轮缘推进器可靠性分配 2.2.1 水下轮缘推进器可靠性分配方法

可靠性指标分配原则如下：

1）对水下轮缘推进器的关键部位，可适当提高可靠性指标；

2）对比较复杂的分单元，可适当降低可靠性指标；

3）对便于维修的单元，可适当降低可靠性指标；

4）对于水下轮缘推进器较成熟的分单元，可适当提高可靠性指标；

5）分配结果应使水下轮缘推进器的可靠度满足规定指标。

2.2.2 水下轮缘推进器可靠性分配

水下轮缘推进器可靠性指标可按失效率进行分配，根据《电子设备可靠性预计手册》的可靠性预计方法，对水下轮缘推进器各单元进行计算预计：

$ {\lambda _p} = {\lambda _b}\prod {\pi _i}i=1,2,…,n。$

(3)

式中：${\lambda _p}$为前述所讲的基本单元应用失效率，10⁻⁶/h; ${\lambda _b}$为单元基本失效率；${\pi _i}$为与基本单元失效率有关的失效系数，一般常用的失效系数有温度应力系数${\pi _T}$、结构系数${\pi _E}$、电应力系数${\pi _S}$、质量系数电应力系数${\pi _Q}$、环境系数${\pi _E}$等。基于此，水下轮缘推进器可靠性失效分配如表5。

3 水下轮缘推进器的复合可靠性分析

水下轮缘推进器运行在水下或深海环境下，在进行可靠性分析时，应将推进器本体的结构特点和运行环境复合在一起进行综合分析，本文将水下轮缘推进器的FEMCA风险优先数（RPN）作为可靠性计算的加权因子，水下轮缘推进器系统的复合可靠性计算如下：

$ {p_i} = \frac{{{k_i}}}{{\min ({k_i})}}，$

(4)

$ {\lambda _s} = \sum\limits_{i = 1}^n {{p_i}} \cdot{\lambda _i}。$

(5)

式中：$ {k_i} $为水下轮缘推进器每一单元的RPN；$ {p_i} $为水下轮缘推进器每一单元的加权因子；$ {\lambda _i} $为水下轮缘推进器每一单元的失效率；$ {\lambda _s} $为水下轮缘推进器系统的失效率。

水下轮缘推进器系统可靠性预计以系统的故障率（又称失效率）统计值为基础。系统平均无故障工作时间与系统故障率的关系为：

$ MTBF = 1/{\lambda _s}，$

(6)

根据系统可靠度计算公式：

$ R(t) = {e^{ - (t/MTBF)}} 。$

(7)

式中，t为一次性连续最低工作时间。

通过以上公式计算，水下轮缘推进器系统的可靠度计算数据如表6所示。

4 试　验

为了验证水下轮缘推进器的可靠性，在3 m×10 m×2 m的水池中进行水中试验。水下轮缘推进器潜入水中1 m，接入驱动器，给定额定电压、额定频率，使其达到推进器的额定设计值，保持状态。

水下轮缘推进器测试过程数据如表7所示。

水下轮缘推进器在水池中稳定运行在1000 r/min转速的额定点，电压稳定于区间256～258 V，电流稳定于区间16.8～17.2 A，连续运行1350 h。依据测试数据，水下轮缘推进器运行期间各项参数稳定，其可靠性可达到预定的设计值。

5 结　语

本文对水下轮缘推进器系统进行了FMECA分析，并细化了每一个单元的风险优先数（RPN）。根据水下轮缘推进器组成结构，建立了可靠性模型，并以水下轮缘推进器FEMCA的风险优先数（RPN）作为可靠性计算的加权因子，对水下轮缘推进器系统进行了复合可靠性计算，此方法可综合考虑装备的各种因素，对现实的水下轮缘推进器具有指导意义。