2. 中船重工船舶设计研究中心有限公司,北京 100081;
3. 大连理工大学 能源与动力学院,辽宁 大连116024
2. CSIC Ship Design and Research Center Co., Ltd., Beijing 100081, China;
3. School of Energy and Power, Dalian University of Technology, Dalian 116024, China
在海洋强国的时代背景下,国家大力引导发展海洋旅游业的经济,作业于近远海的超大型浮式综合旅游体应运而生,而海上不比陆地,其情况复杂多变,结构要承受的环境载荷更加突出,浮体长期主要承受波浪造成的交变载荷,浮体结构极易因疲劳而产生破坏,因此对大型浮体结构疲劳特性的研究具有十分广阔的应用前景 [1]。疲劳估价法主要包括时域疲劳估价法和频域疲劳估价法两大类。在实际项目中,主要根据所获得的结构应力形式和难易程度来选择什么样的疲劳评估方法。当结构应力的时间过程较容易得到时,通常采用时域的疲劳评估方法评估结构疲劳 [1 − 4]。当结构受力的功率谱密度函数容易算出时,通常采用频域的疲劳评估方法评估结构的疲劳[5 − 7]。对于一些需要考虑复杂的非线性因素结构,在疲劳分析过程中可用时域疲劳分析方法进行计算,分析精度很高,但计算量却很大。频域疲劳分析方法基于线性化假定,忽略非线性因素以及平均应力的影响,可执行程度高,计算量小。
目前,对于船舶这样的浮式结构来说,其应力反应的时间过程很难获得,因此对其疲劳损伤的评估通常采用频域谱分析方法。张朝阳[8]等运用热应力谱分析方法,计算得出深水半潜式平台薄弱节点处的疲劳寿命,对不同浪向及各短程海况对节点总疲劳损伤度的贡献进行了进一步分析。马网扣等 [9]运用程序对某新型深水半潜式钻井平台典型节点疲劳寿命进行了分析。谢文会等[10]采用疲劳谱分析方法,基于Miner准则,计算了薄弱节点的热点应力传递函数,并对平台典型节点的疲劳寿命进行了评估。
常规的海洋工程结构物的疲劳研究,行业内有丰富的经验,常规海洋工程结构物的疲劳节点位置都位于主体受力框架结构上[11]。随着浮体结构形式的改变,结构受力分析更加困难,如何准确分析结构的疲劳成为一大难点。在对结构疲劳分析中,疲劳位置传递函数的计算对疲劳分析的准确度起着至关重要的作用。一般有4种传递函数的计算方法:1)理论评估法;2)实部虚部合成法;3)简化理论分析法;4)规则波数值模拟试验法。其中,规则波试验法的计算原理最接近真实海况。故本文以某海上大尺度异型镂空浮体为对象,采用规则波数值模拟试验法计算了浮体疲劳点位的传递函数,分别采用名义应力和热点应力谱分析方法对异形体结构进行计算,对比2种计算结果的差异性,并给出合理的工程设计建议。
1 结构疲劳分析的基本原理 1.1 频谱分析法的基本原理频谱分析法是研究船舶结构荷载和响应的一种常用方法,其理论是将随机理论中的线性系统做变换[11]。而船舶结构又是动力系统的一种,系统的输入部分
| $ X(t) = L\left[ {\eta (t)} \right]。$ | (1) |
式中:
根据线性理论,在线性系统条件下,便可计算船舶结构在波浪载荷下的疲劳寿命,不妨假设波浪是一个平稳随机过程,则转化后的响应亦是一个平稳的随机过程。由随机理论,2个平稳随机过程的功率谱密度函数关系为[12]:
| $ {G_X}(\omega ) = {\left| {H(\omega )} \right|^2}\cdot{S_\eta }(\omega )。$ | (2) |
式中:
传递函数为频谱分析法中的最关键要素,传递函数的物理意义是在线性动力系统中做简谐振动其圆频率为
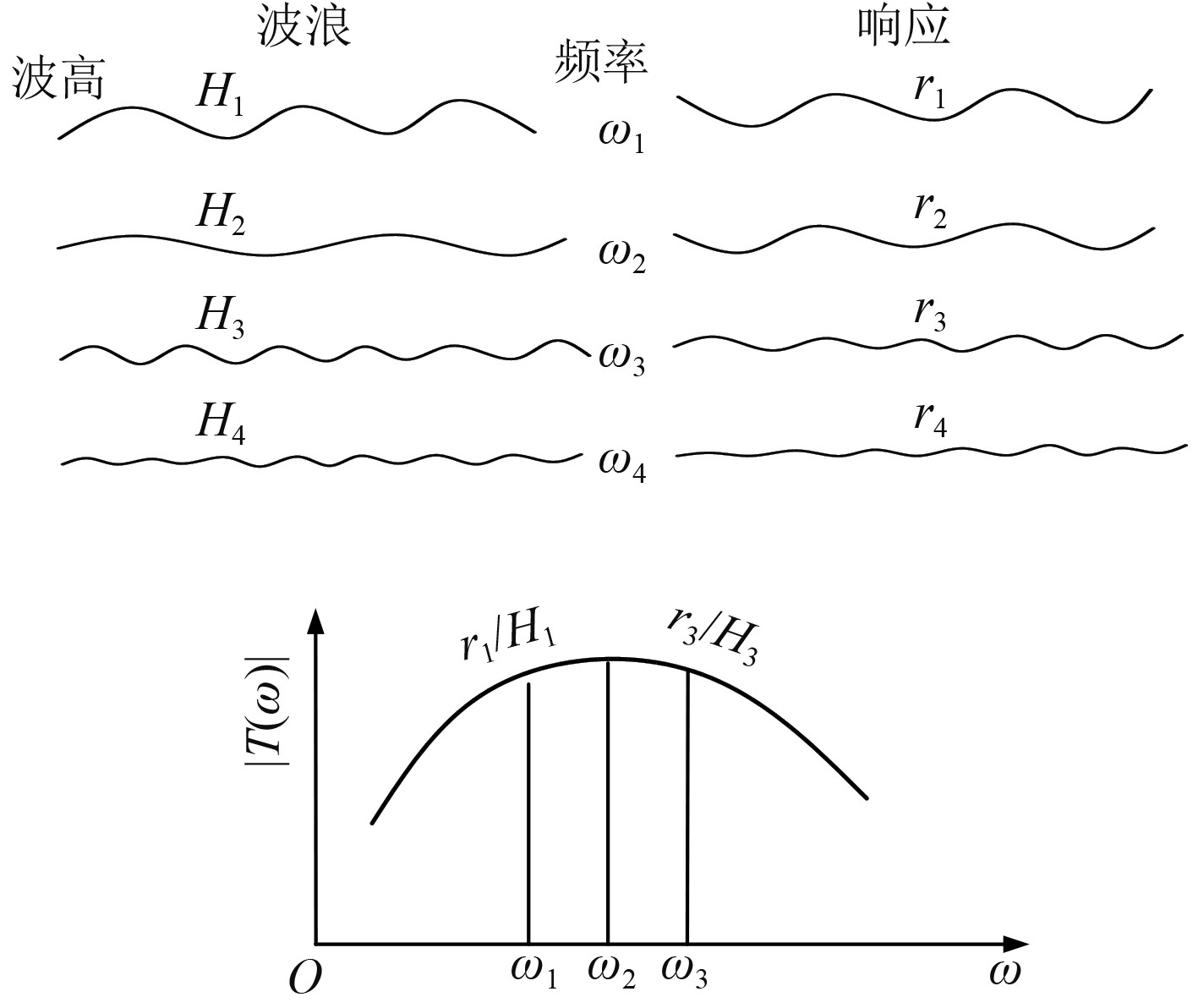
|
图 1 规则波试验法计算传递函数 Fig. 1 Calculation of transfer function by the regular wave test method |
本项目浮体作业位置离岸较近,水深较浅,可采用改进的JONSWAP谱进行计算[13]。其表达形式如下:
| $ S(f)=\beta_{J} H_{\frac{1}{3}}^{2} T_{P}^{-4} f^{-5} \exp \left[-\frac{5}{4}\left(T_{P} f\right)^{-4}\right] \gamma^{\left.\operatorname{expl}-\left(\frac{f}{f_{F}}-1\right)^{2} / 2 \sigma^{x}\right]}。$ | (3) |
式中:
根据公式
| $ \begin{split}S(\omega)= & \frac{1}{2{\text{π}}}\beta_JH_{\frac{1}{3}}^2T_P^{-4}\left(\frac{\omega}{2{\text{π}}}\right)^{-5}\times \\ &\exp\left[-\frac{5}{4}\left(\frac{T_P\omega}{2{\text{π}}}\right)^{-4}\right]\gamma^{\exp\left[\left.-\left(\frac{\omega}{2{\text{π}} f_P}-1\right)^2\right/2\sigma^2\right]}。\end{split} $ | (4) |
再由式(2)即可求得疲劳位置的应力响应谱。
1.4 异形浮体疲劳累计损伤度的计算在获得结构应力的响应谱后, 即可计算出:
| $ {G_{XX}}\left( {{\omega _{\text{e}}}} \right) = {\int\limits}_{ - {\text{π}} /2}^{{\text{π}} /2} {f\left( \beta \right)} {\left[ {H\left( {{\omega _e},\theta - \beta } \right)} \right]^2} \cdot {G_{x}}\left( \omega \right){\text d}\beta 。$ | (5) |
式中:
| $ f\left( \beta \right) = k{\cos ^n}\left( \beta \right) 。$ | (6) |
式中:k和n的取值要满足使
在计算中,根据ITTC的推荐,取
| $ f\left( \beta \right) = \frac{2}{{\text{π}}}{\cos ^2}\left( \beta \right) 。$ | (7) |
交变载荷过程的跨零率
| $ {\nu _0}{\text{ = }}\frac{1}{{2{\text{π}} }}\sqrt {\frac{{{m_2}}}{{{m_0}}}}。$ | (8) |
式中:
| $ {m_n} = {\int\limits}_0^{ + \infty } {\omega _e^n} \cdot {G_{XX}}({\omega _e}){\text d}{\omega _e}。$ | (9) |
在实际使用时,将窄带平稳随机过程认定为某海况给定航向下的交变应力过程,其均值为0,由随机理论可知,结构的应力峰值服从Rayleigh分布,其概率密度函数如下[12]:
| $ f(x) = \frac{x}{{{\sigma ^2}}}\exp \left( { - \frac{{{x^2}}}{{2{\sigma ^2}}}} \right),{0 \leqslant x < + \infty } 。$ | (10) |
式中:
| $ S = 2x 。$ | (11) |
最终得到其在应力范围下的概率密度函数:
| $ {f_S}(S) = \frac{S}{{4{\sigma ^2}}}\exp \left( { - \frac{{{S^2}}}{{8{\sigma ^2}}}} \right),0 \leqslant S < + \infty 。$ | (12) |
假设船舶航行时间为
| $ {D_{ij}} = \frac{{{T_{ij}}.{\nu _{0ij}}}}{A}\int_0^{ + \infty } {{S^m}{f_{Sij}}(S)} {\text d}S 。$ | (13) |
式中:
应力范围S和循环次数N的关系可表示为:
| $ N \cdot {S^m} = A 。$ | (14) |
式中:A、m均为S-N曲线的参数。具体可参照《海洋工程结构物疲劳强度评估技术指南》,根据疲劳点位置的不同选取对应的不同参数[14]。
将相应的短期应力范围分布
| $ \begin{split} {D_{ij}} = & \frac{{{T_{ij}}\cdot{\nu _{0ij}}}}{A}\cdot{(2\sqrt 2 {\sigma _{Xij}})^m}\cdot\Gamma \left(1 + \frac{m}{2}\right) = \\ & \frac{{{T_{ij}}\cdot{\nu _{0ij}}}}{A}\cdot{(2\sqrt {2{m_{0ij}}} )^m}\cdot\Gamma \left(1 + \frac{m}{2}\right)。\end{split}$ | (15) |
对于服役时间为
| $ {T_{ij}} = T\cdot{p_i}\cdot{p_j}。$ | (16) |
期间总损伤应为:
| $\begin{split} D = & \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {{D_{ij}}} } = \frac{T}{A}\cdot\varGamma (1 + \frac{m}{2})\cdot\sum\limits_{i = 1}^m {\mathop \sum \limits_{j = 1}^n } \\ & {p_i}\cdot{p_j}\cdot{\nu _{0ij}}\cdot{(2\sqrt {2{m_{0ij}}} )^m}。\end{split} $ | (17) |
本文采用通用建模软件Ansys-APDL建立异形浮体的有限元模型。其中,板材和T型材采用shell单元,扶墙材和角钢采均用beam单元模拟建立。浮体的有限元模型如图2所示。
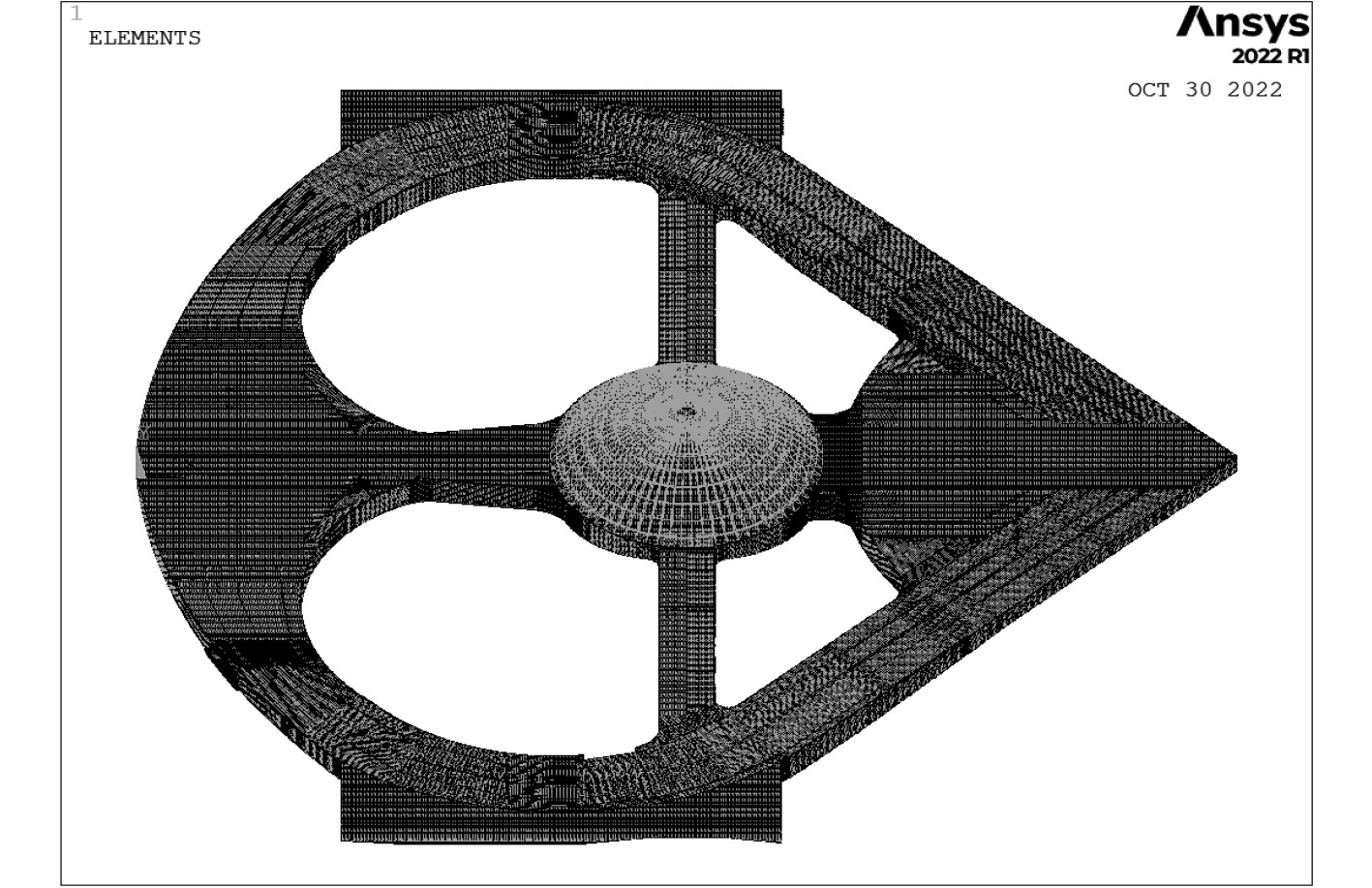
|
图 2 浮体有限元模型 Fig. 2 Floating body finite element model |
此异形浮体整体呈“心”型,中间有4个镂空部分,尺寸偏大(400 m×400 m),该结构尺寸超过了一般船用规范计算标准,属于超大型海上综合式浮体,并且宽度方向上存在2个宽度较窄的长条型连接结构。此部分结构会受到巨大的扭矩和弯矩,强度偏弱,在复杂多变的海洋环境中作业极易产生疲劳破坏。
2.2 异形浮体的水动力分析从浮体有限元模型提取湿表面生成水动力计算模型,将湿表面模型导入到专业从事水动力计算的软件AQWA中进行水动力计算的前处理,结构的重心坐标及转动惯量均从模型的静力分析计算得出。图3为浮体湿表面模型,共包括26542个单元。将处理好的浮体质量模型导入水动力计算软件AQWA中进行求解,求解完成后即可得到浮体任意剖面内的剪力和弯矩,即为传递函数。传递函数为单位波高产生的浮体响应函数,它和浮体外形、遭遇频率、浪向角等紧密相关。图4为计算工况下浮体中部垂向弯矩的传递函数。

|
图 3 异形浮体水动力模型 Fig. 3 Hydrodynamic model of a shaped buoyant body |
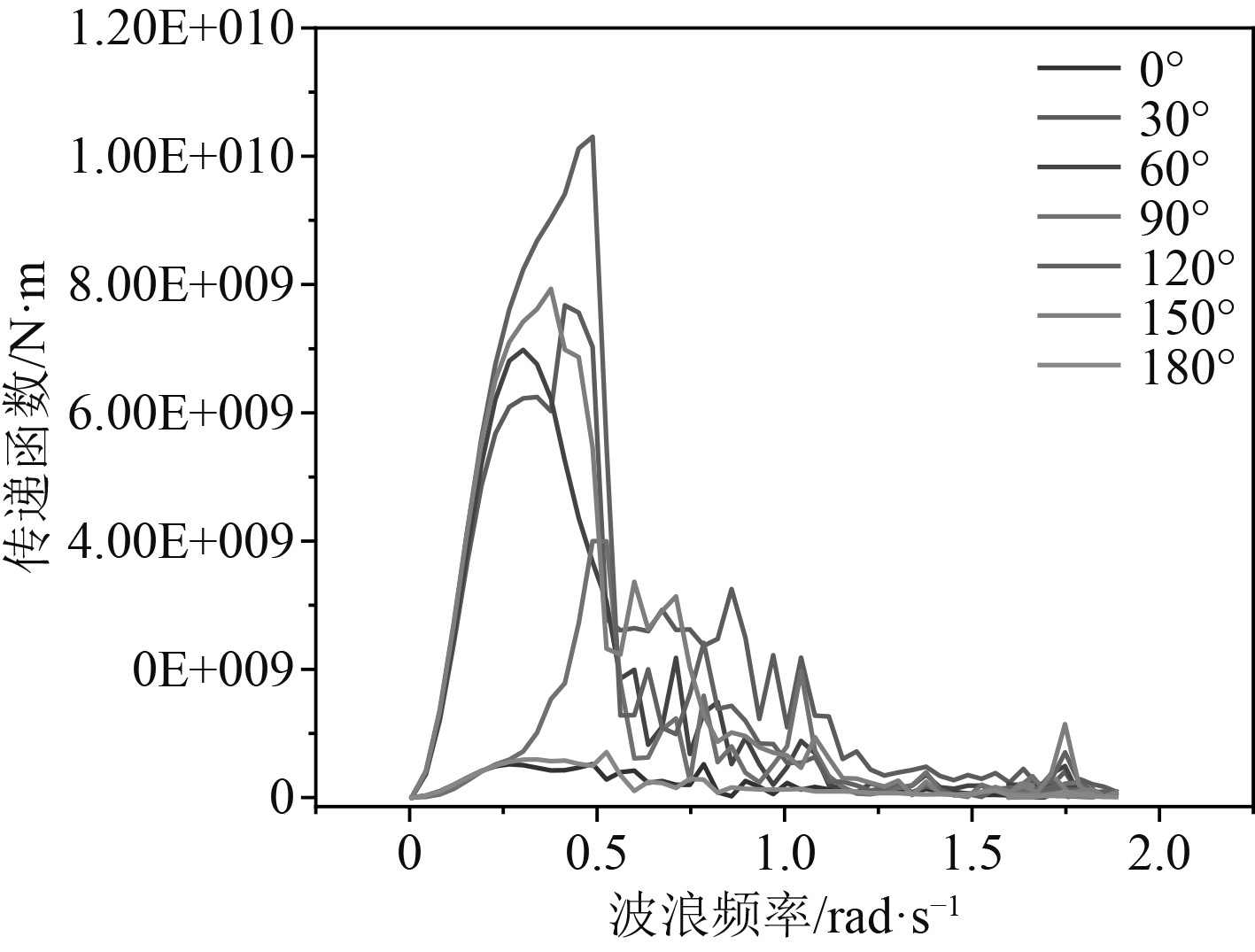
|
图 4 异形浮体中部垂向弯矩的传递函数 Fig. 4 Transfer function of vertical bending moment in the middle of shaped floating body |
根据水动力计算结果,从AQWA中提取0°浪向0.07767 Hz、30°浪向 0.06 588 Hz、60°浪向 0.04818 Hz、90°浪向 0.08357 Hz、120°浪向 0.07178 Hz、150°浪向 0.06588 Hz、180°浪向 0.6588 Hz的波浪载荷文件。将波浪载荷加载到不含静水压的浮式综合体有限元模型上,并计算得到结果。
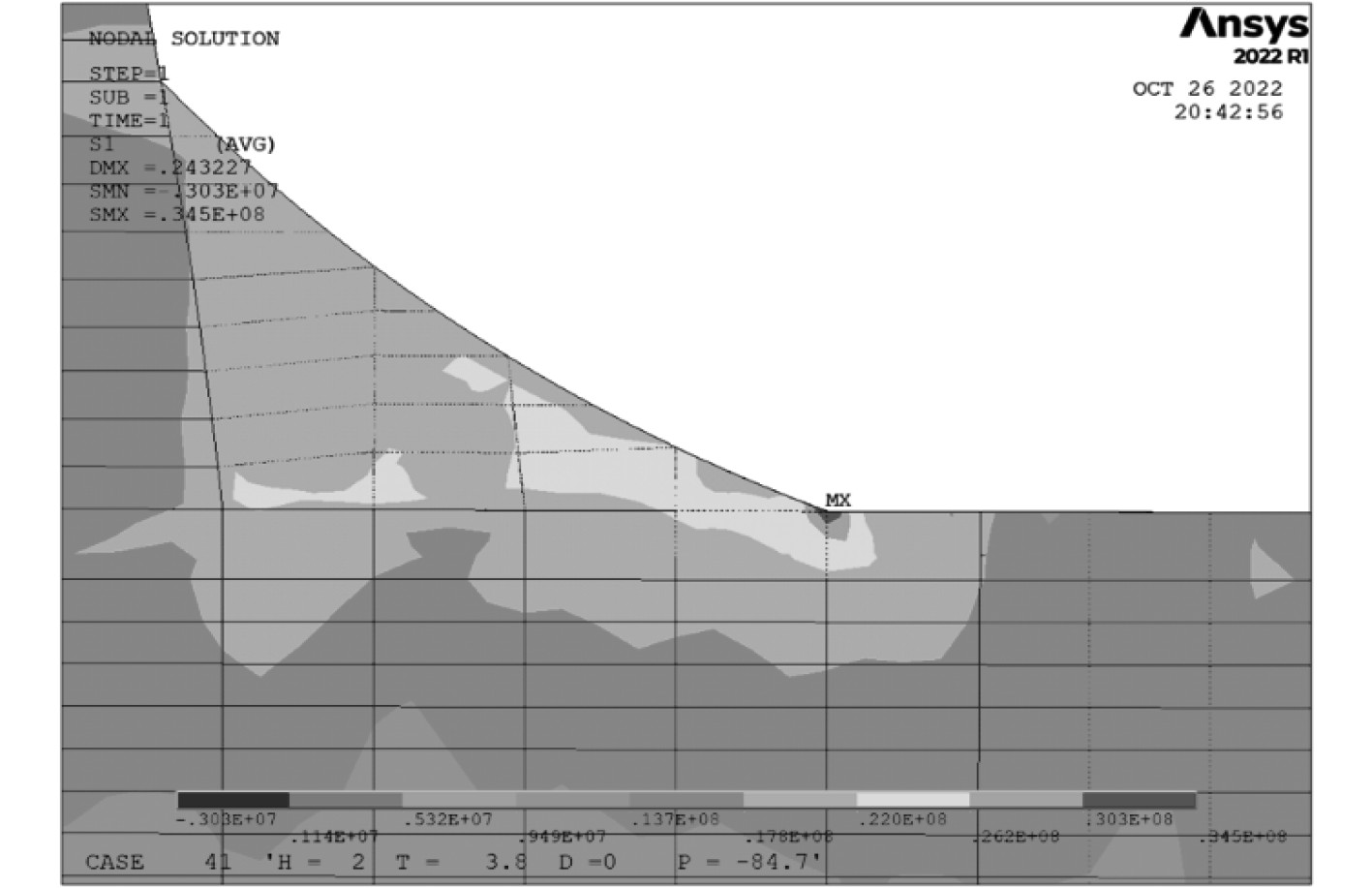
以0°浪向 0.07767 Hz浮体为例,其应力云图和应力最大位置如图5和图6所示。
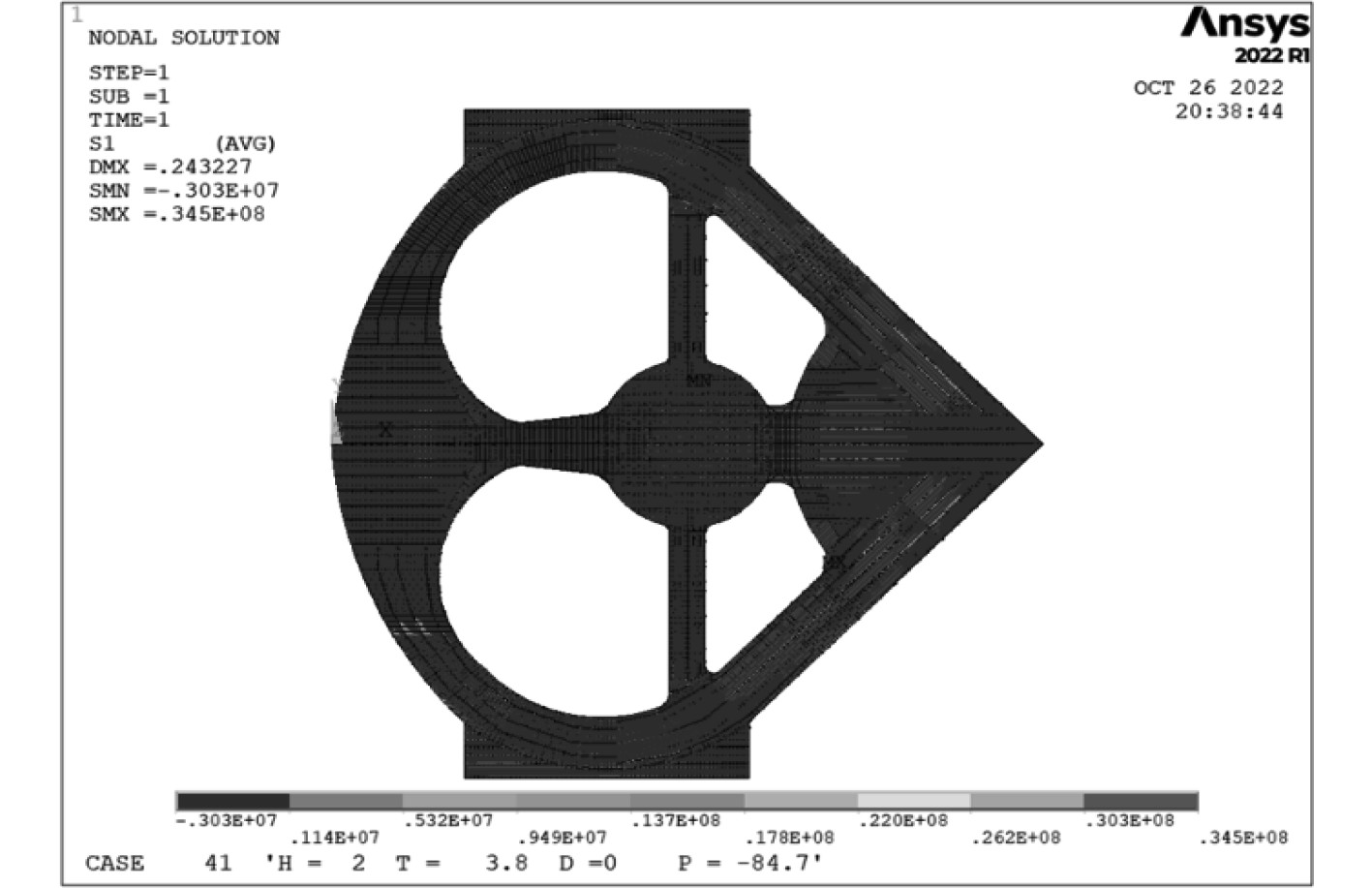
|
图 5 波浪荷载下浮体应力云图 Fig. 5 Stress cloud of floating body under wave loading |
|
图 6 应力最大位置 Fig. 6 Position of maximum stress |
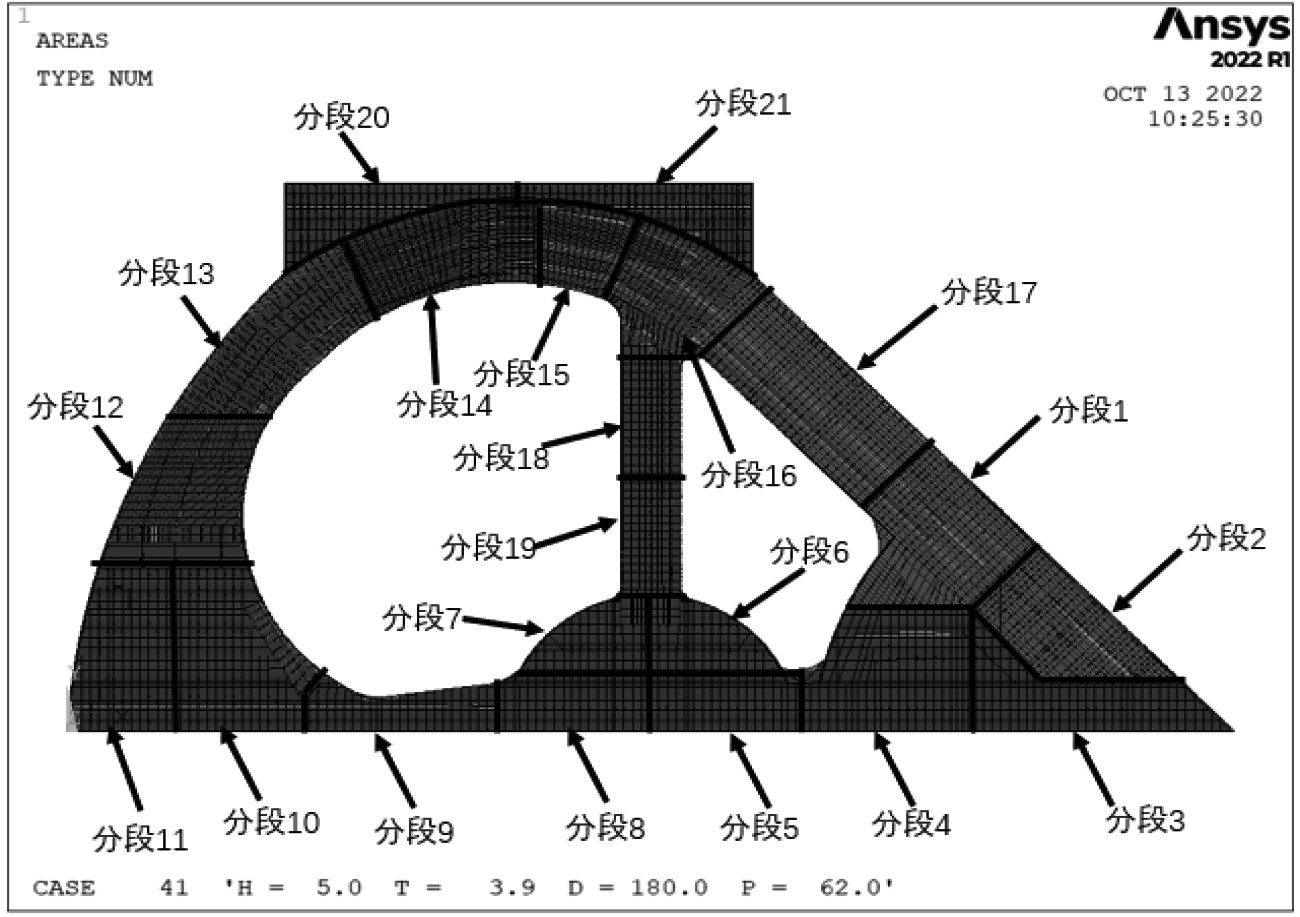
浮体结构分段如图7所示。经过计算从各个浪向的应力响应计算结果中选出了7个应力较大的位置作为疲劳分析的关注点,7个点的单元编号及位置如表1所示。
|
|
表 1 浮体疲劳点编号及位置 Tab.1 Float Fatigue Point Numbers and Locations |
|
图 7 浮体结构分段 Fig. 7 Floating body structure segmentation |
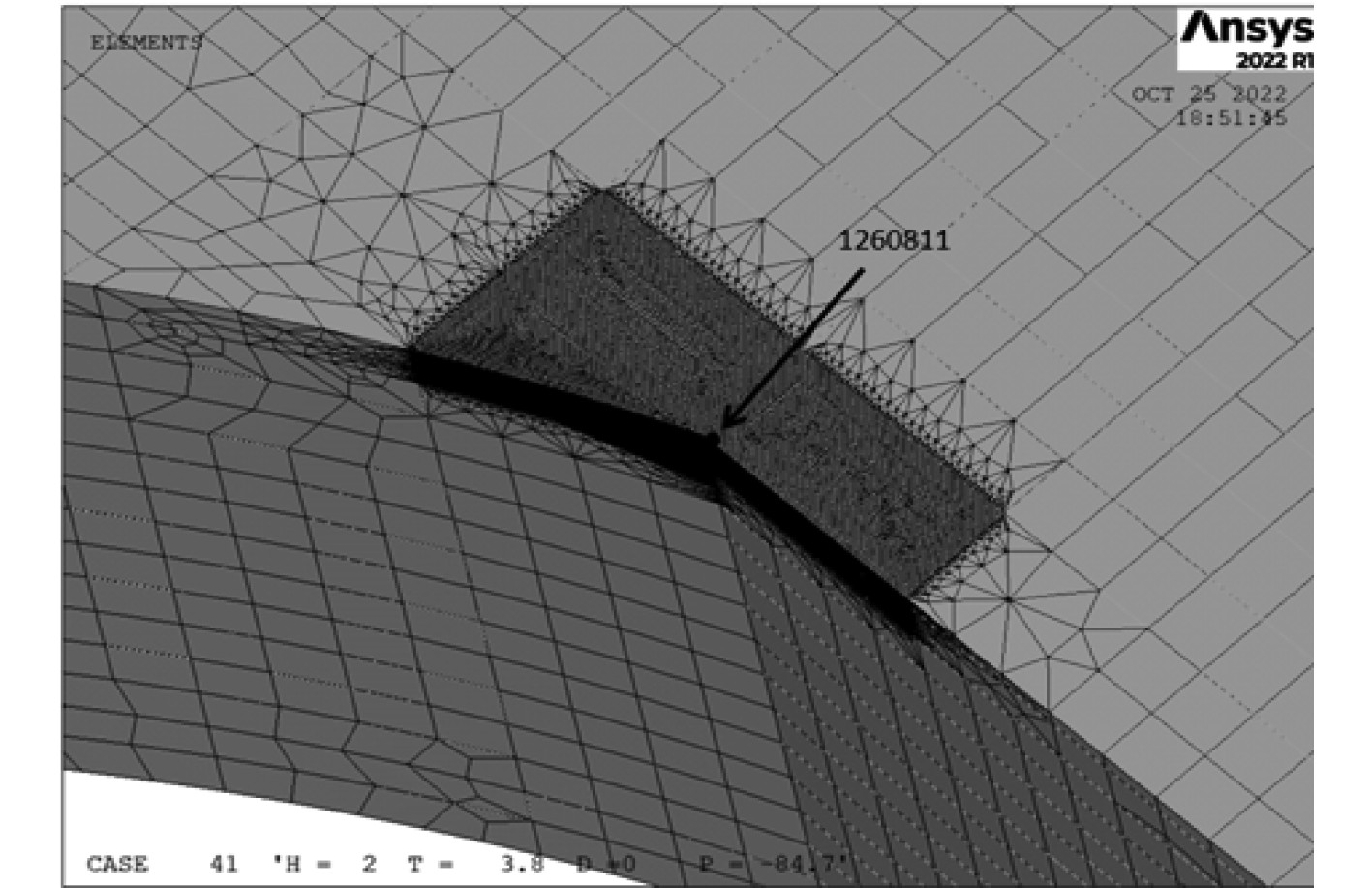
根据《海洋工程结构物疲劳强度评估技术指南》(2022)[14]规范所述,疲劳点位置的有限元模型网格需细化。以2号疲劳点位置为例,网格细化如图8所示。
|
图 8 网格细化 Fig. 8 Mesh refinement |
以0°浪向计算疲劳点的应力响应为例,说明规则波数值模拟计算方法。
利用AQWA软件,计算得到0°浪向角圆频率为0.001 Hz的单位波幅按一定的初相位间隔排列一系列规则波的浮体运动以及外部水动压力的响应,相位取为0°~360°,间隔45°,每个浪向频率下8个规则波,提取波浪载荷文件。分别加载到结构的有限元模型上,得到不同应力响应,再分别采取名义应力法和热点应力法计算疲劳位置的应力。最后通过正弦拟合得到疲劳点位在同一频率下所有相位的应力响应。
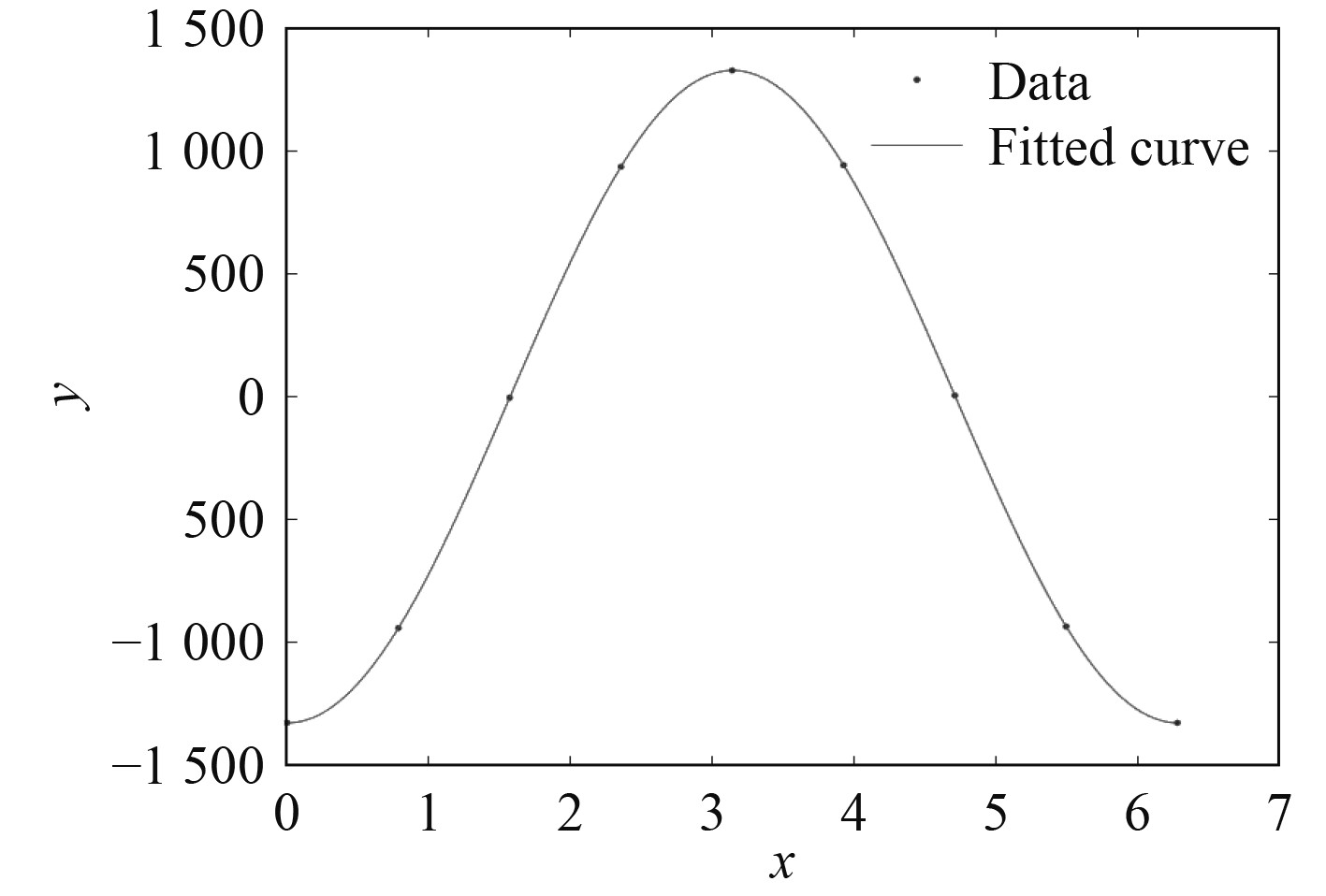
1)名义应力法。名义应力可由提取疲劳点计算得到的应力乘以应力集中系数SCF(Stress Concentration Factor)得到,针对不同位置有不同系数计算公式,具体的应力集中系数可查阅CCS《海洋工程结构物疲劳强度评估技术指南》3.2-3.4节得到[14]。采用名义应力法得到的响应曲线,如图9所示。
|
图 9 名义应力法计算应力的响应拟合曲线 Fig. 9 Response fitting curves for stresses calculated by the nominal stress method |
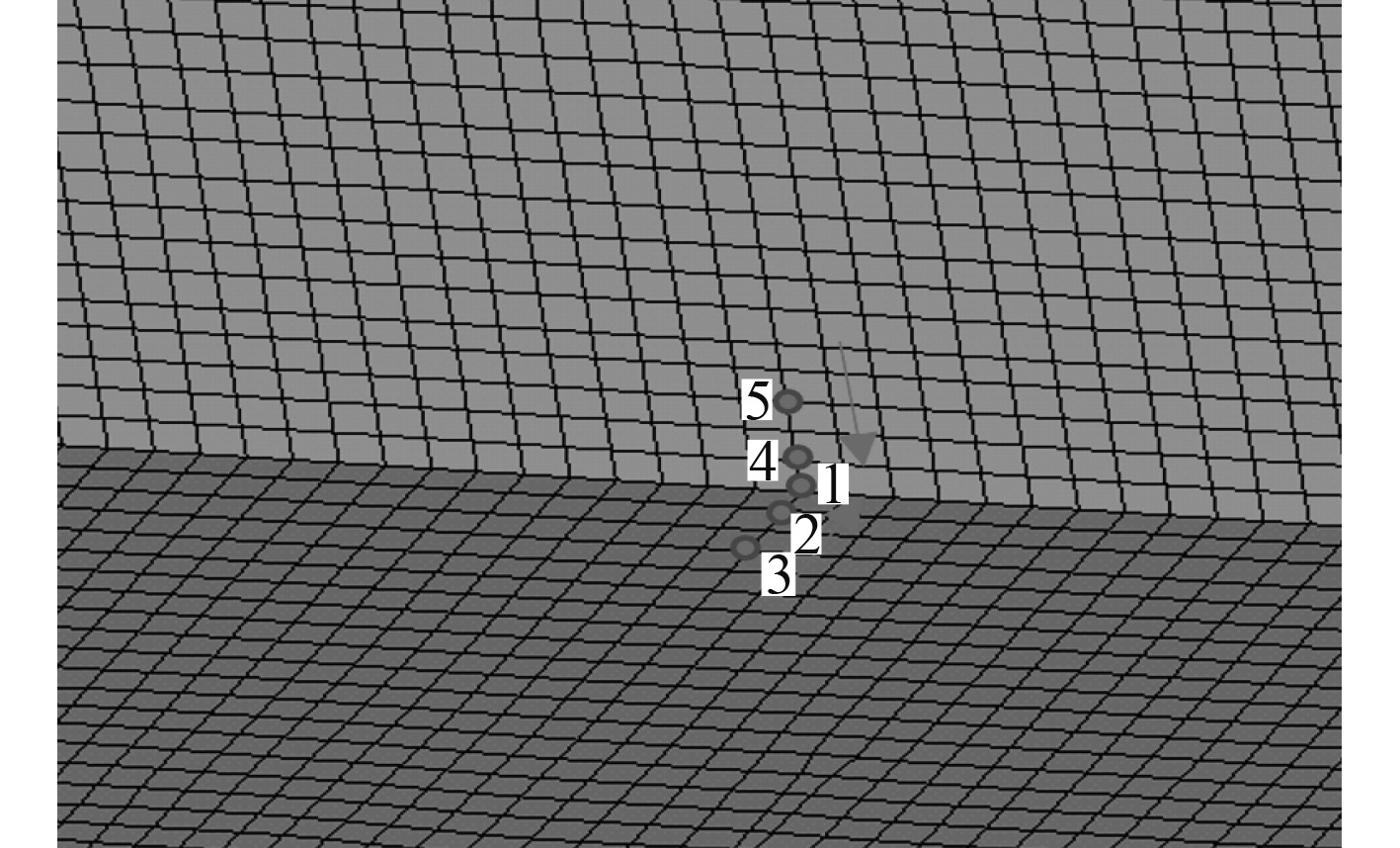
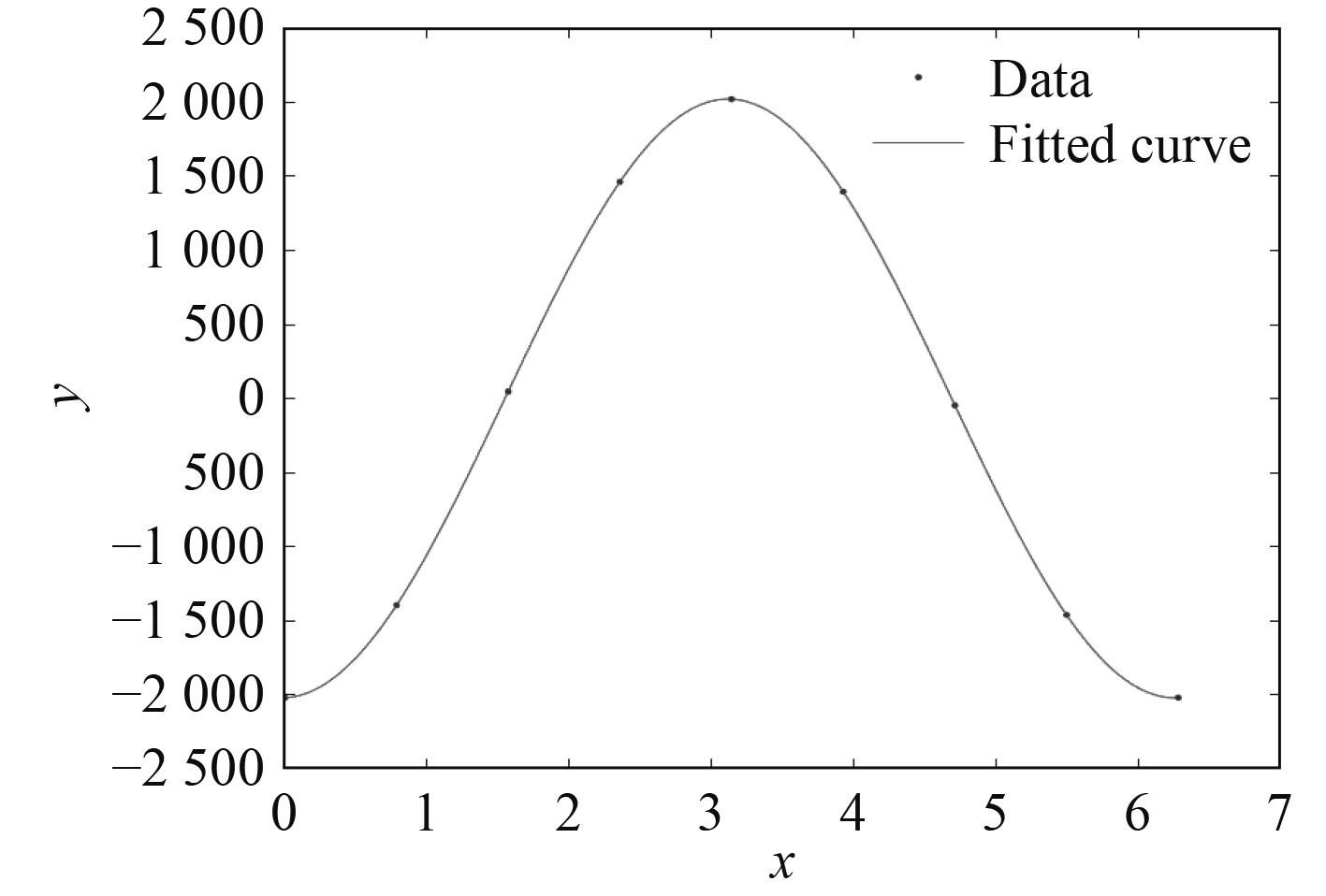
2)热点应力法。焊缝处的热点应力值是通过插值的方法求出,具体方法如图10所示,求得焊缝1号点的热点应力,不能直接读取1号点的应力,需分别计算2条路径(由3到2到1或由5到4到1)的线性插值,取其中较大值为1号点的热点应力。采用热点应力法得到的响应曲线如图11所示具体可由式(18)求得。
|
图 10 疲劳位置热点应力求解路径 Fig. 10 Fatigue location hotspot stress solution paths |
|
图 11 热点应力法计算应力的响应拟合曲线 Fig. 11 Response fitting curve of stress calculated by hot spot stress method |
| $ {\sigma _1} = \max \left\{ \begin{gathered} 1.5{\sigma _2} - 0.5{\sigma _3},\\ 1.5{\sigma _4} - 0.5{\sigma _5}。\\ \end{gathered} \right. $ | (18) |
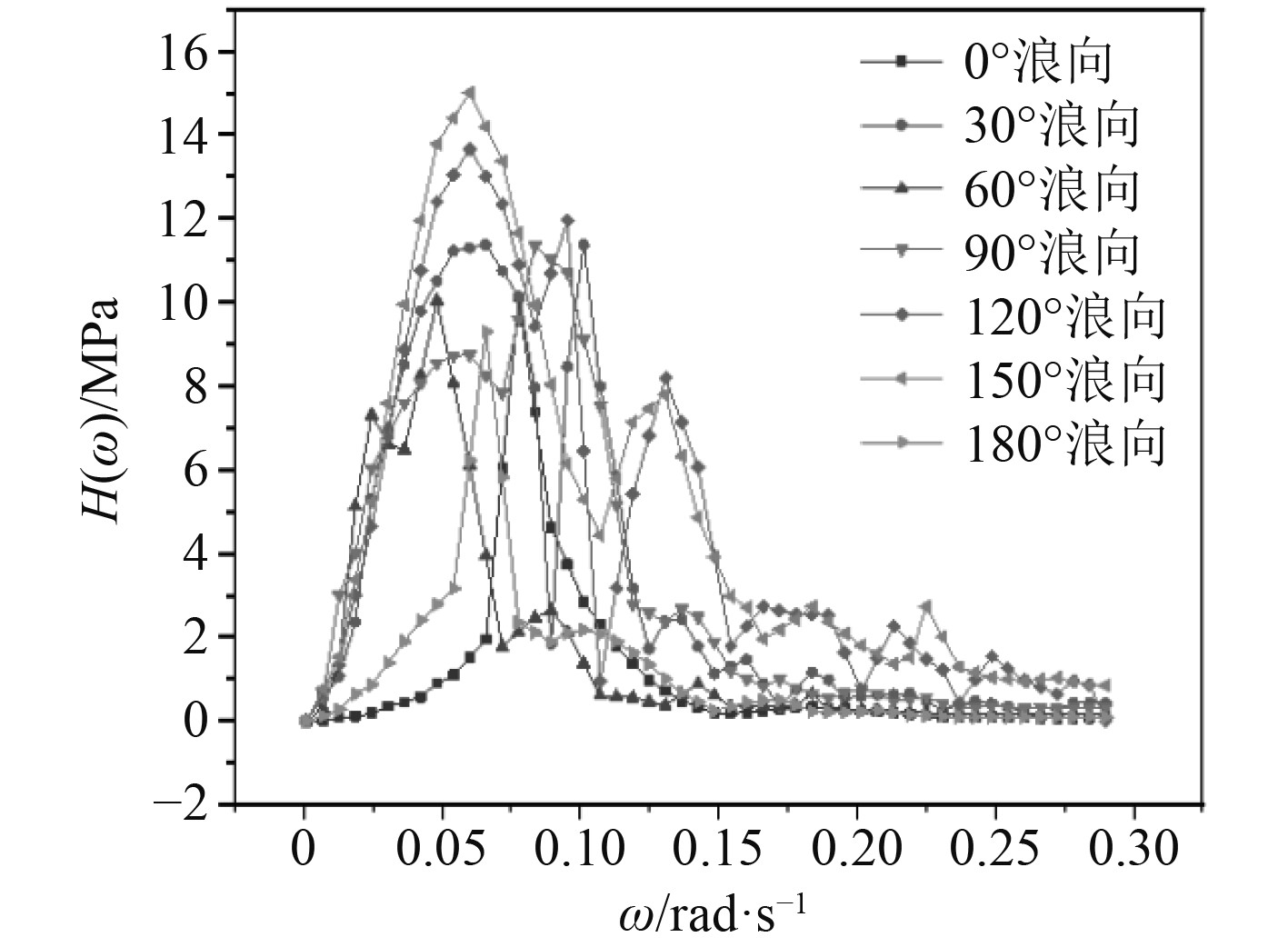
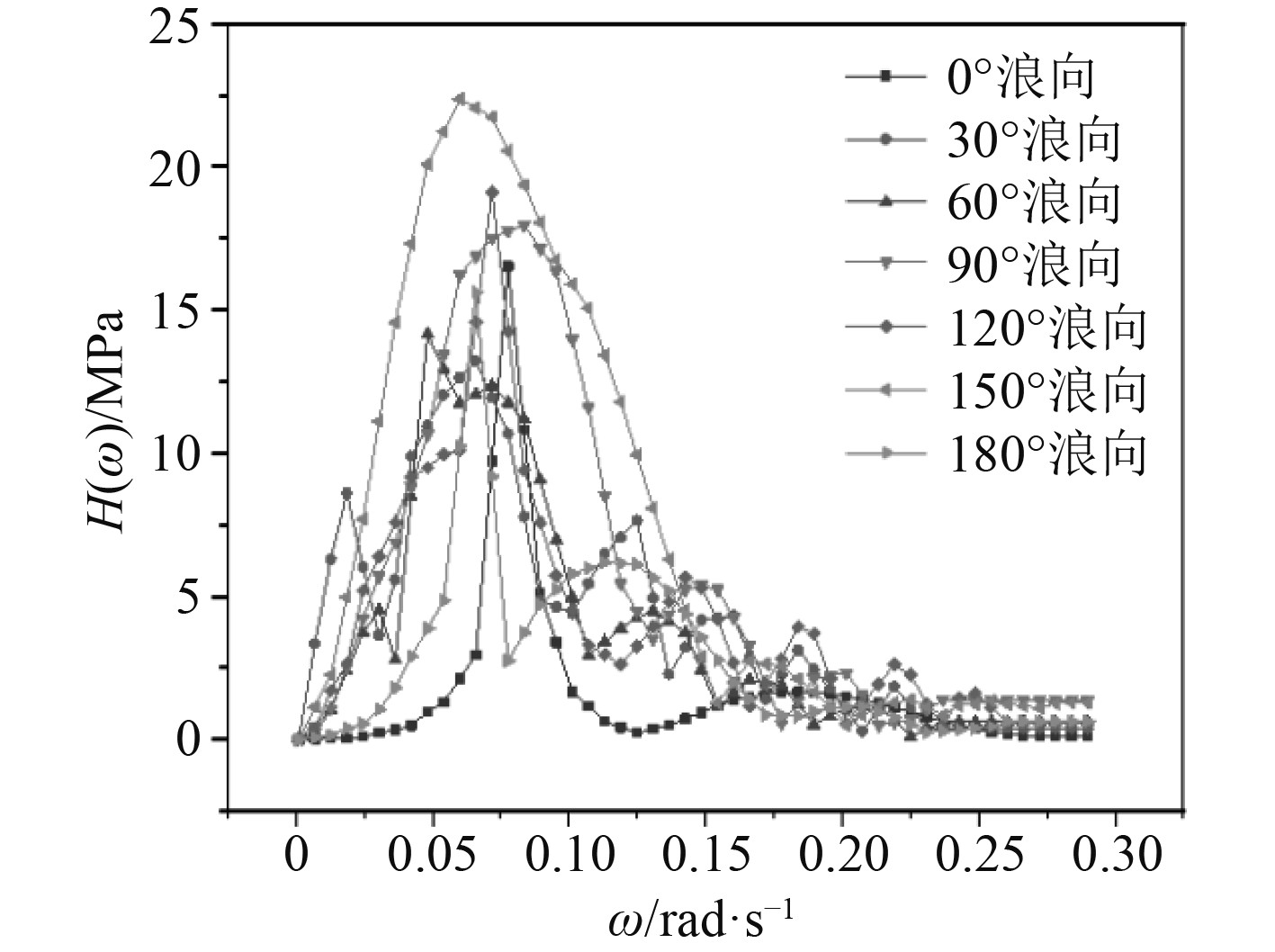
分别计算每个浪向所对应的50个频率点,并提取前节所述的7个疲劳关注点处的应力值计算出名义应力,最终标定的传递函数结果如图12~图15所示(因篇幅有限,这里仅给出4个点的传递函数)。
|
图 12 异形浮体结构1号疲劳点的传递函数 Fig. 12 Transfer function for fatigue point 1 of shaped floating body structure |
|
图 13 异形浮体结构2号疲劳点的传递函数 Fig. 13 Transfer function for fatigue point 2 of the shaped floating body structure |
|
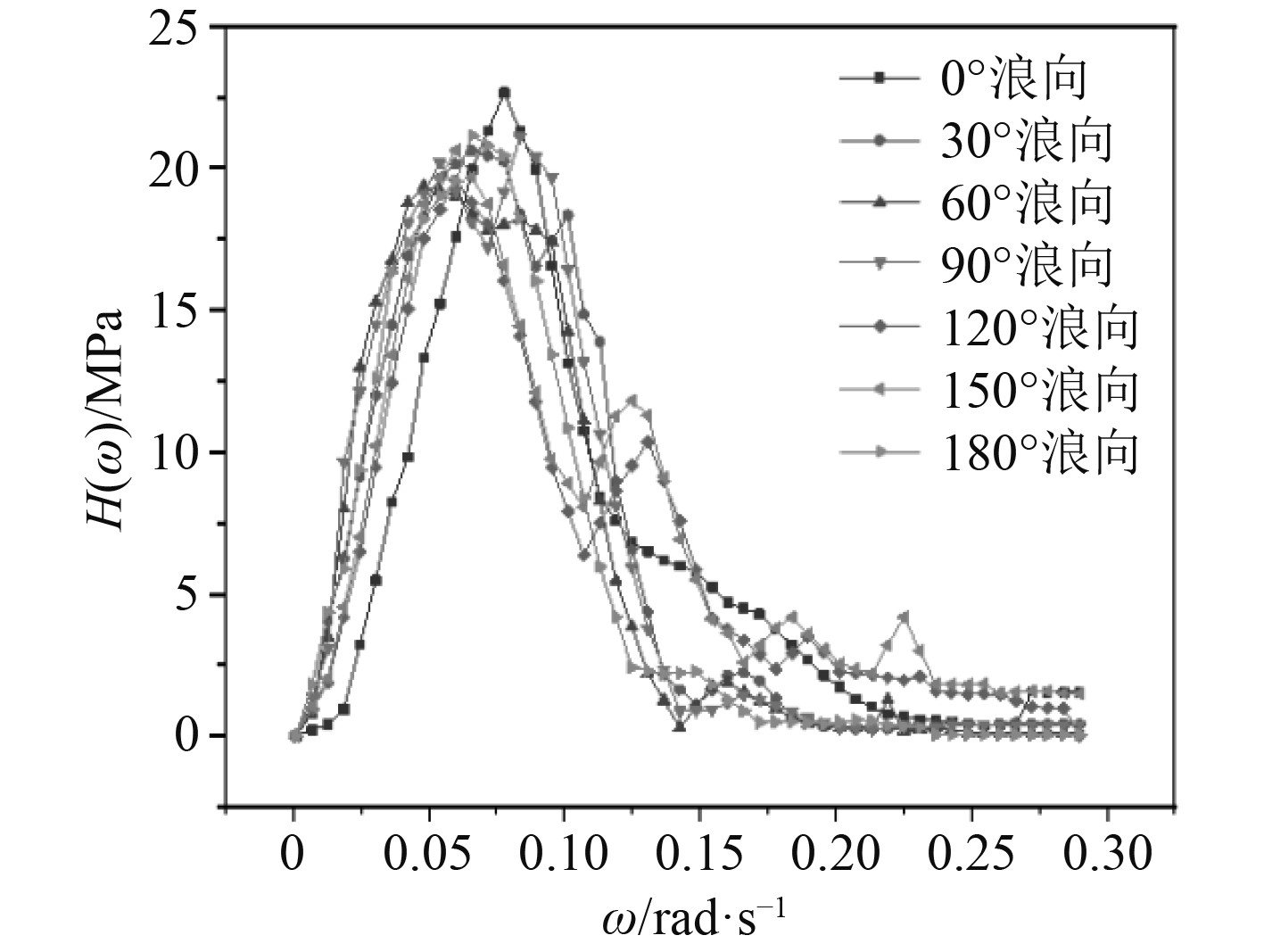
图 14 异形浮体结构3号疲劳点的传递函数 Fig. 14 Transfer function for fatigue point 3 of the shaped floating body structure |
|
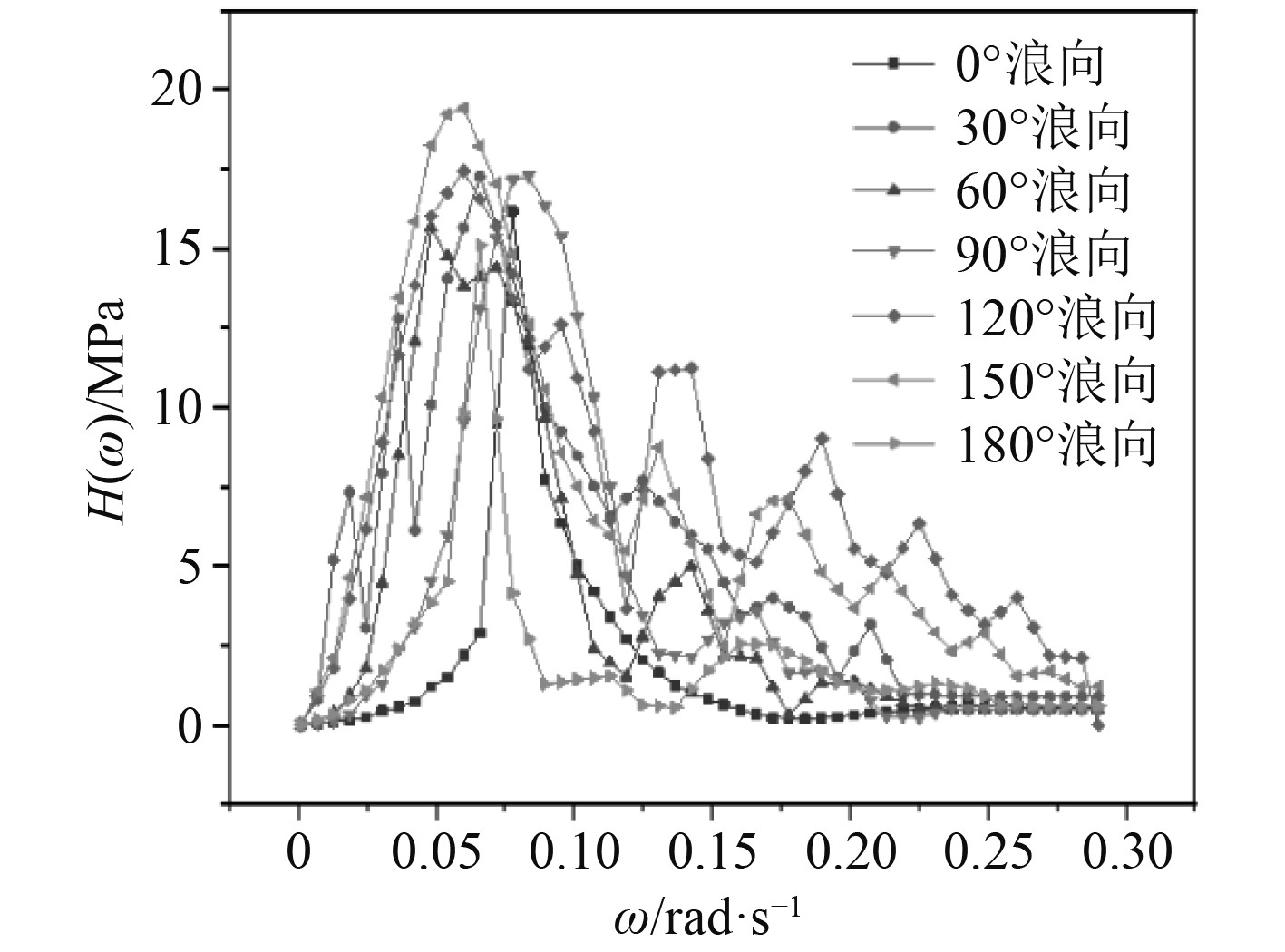
图 15 异形浮体结构4号疲劳点的传递函数 Fig. 15 Transfer function for fatigue point 4 of the shaped floating body structure |
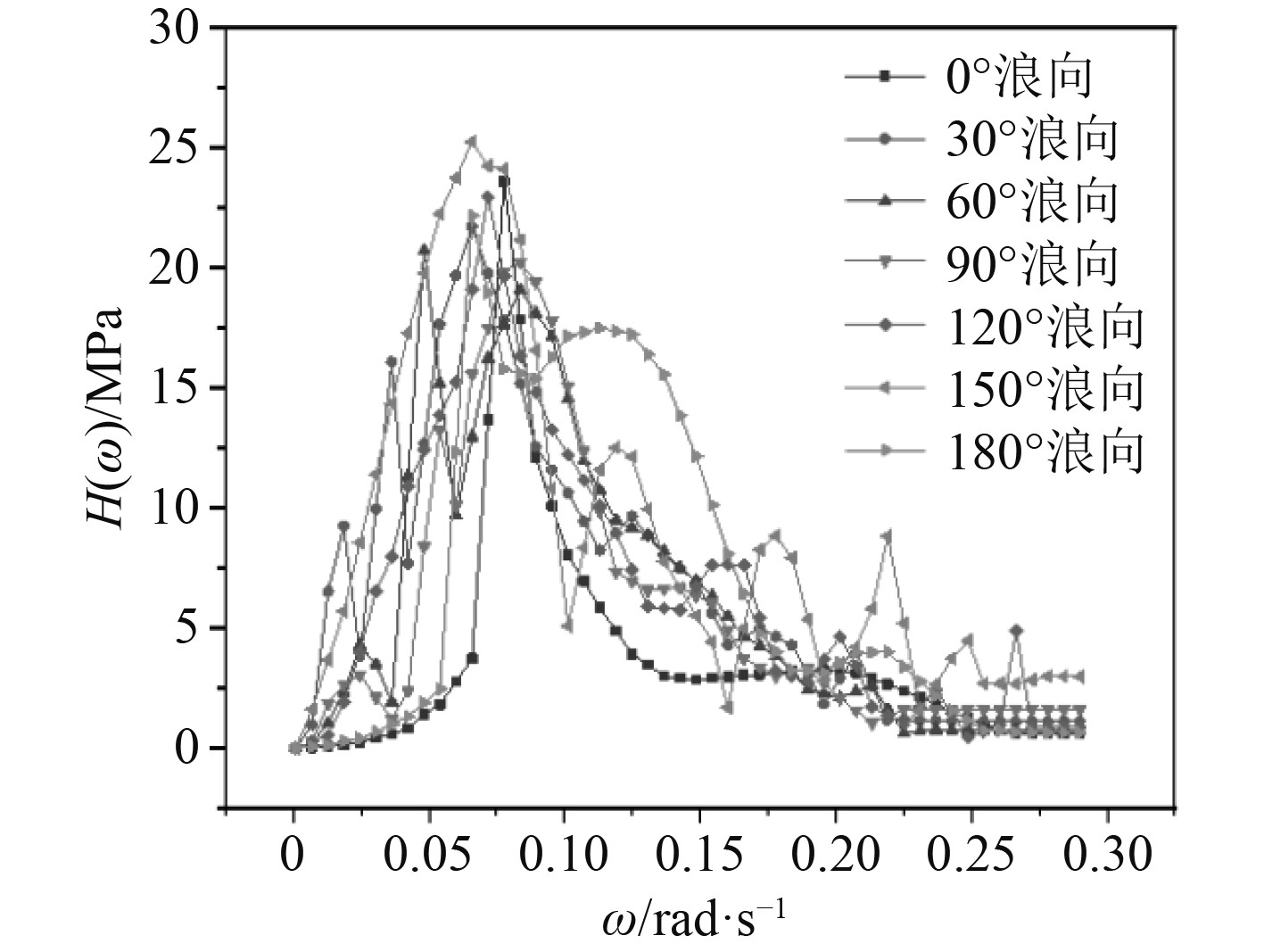
采用热点应力法线性外插的方法计算出各个疲劳关注点的热点应力值,得到异形浮体结构的传递函数如图16~图19所示。
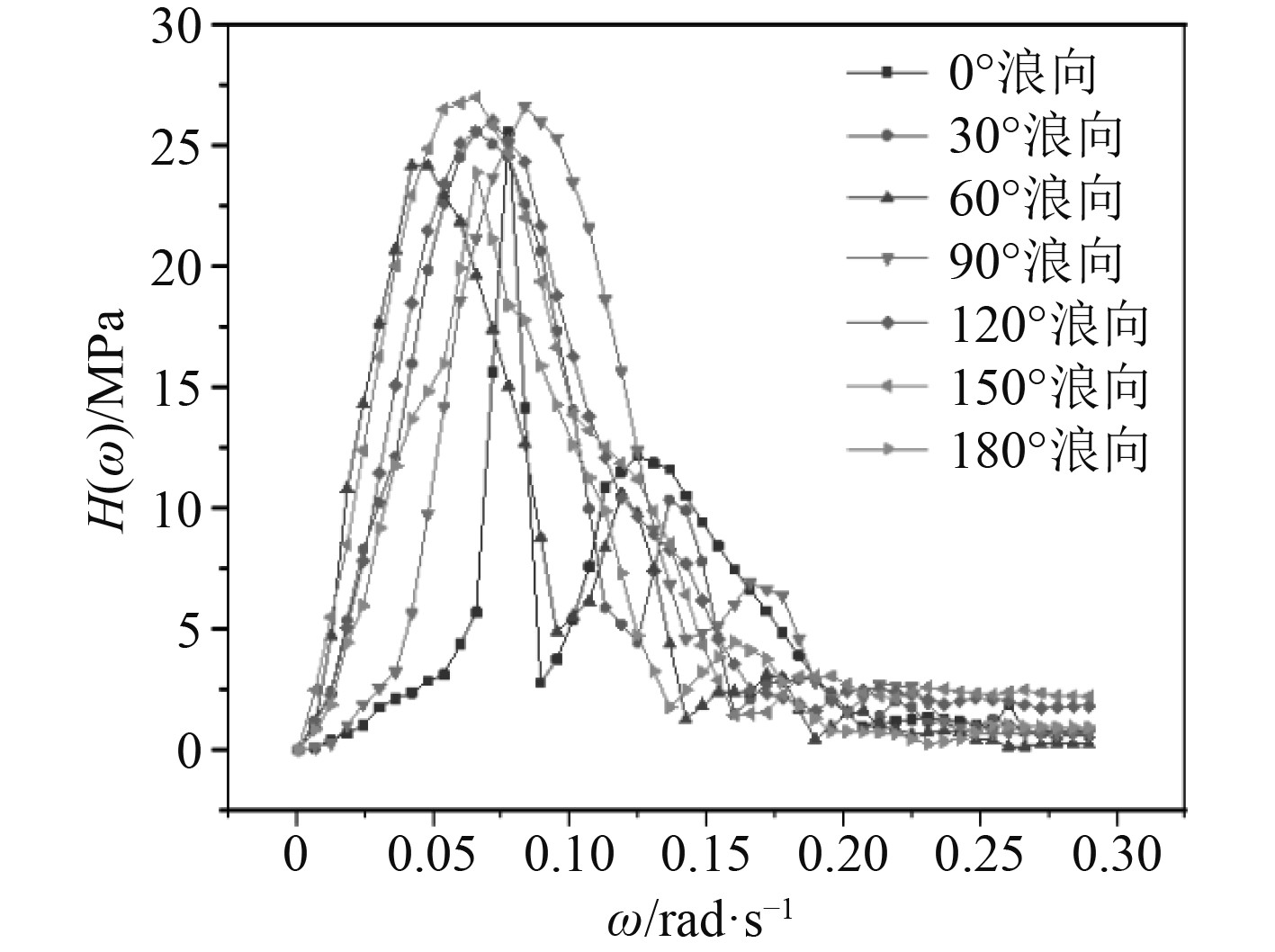
|
图 16 异形浮体结构1号疲劳点的传递函数 Fig. 16 Transfer function for fatigue point 1 of the shaped floating body structure |
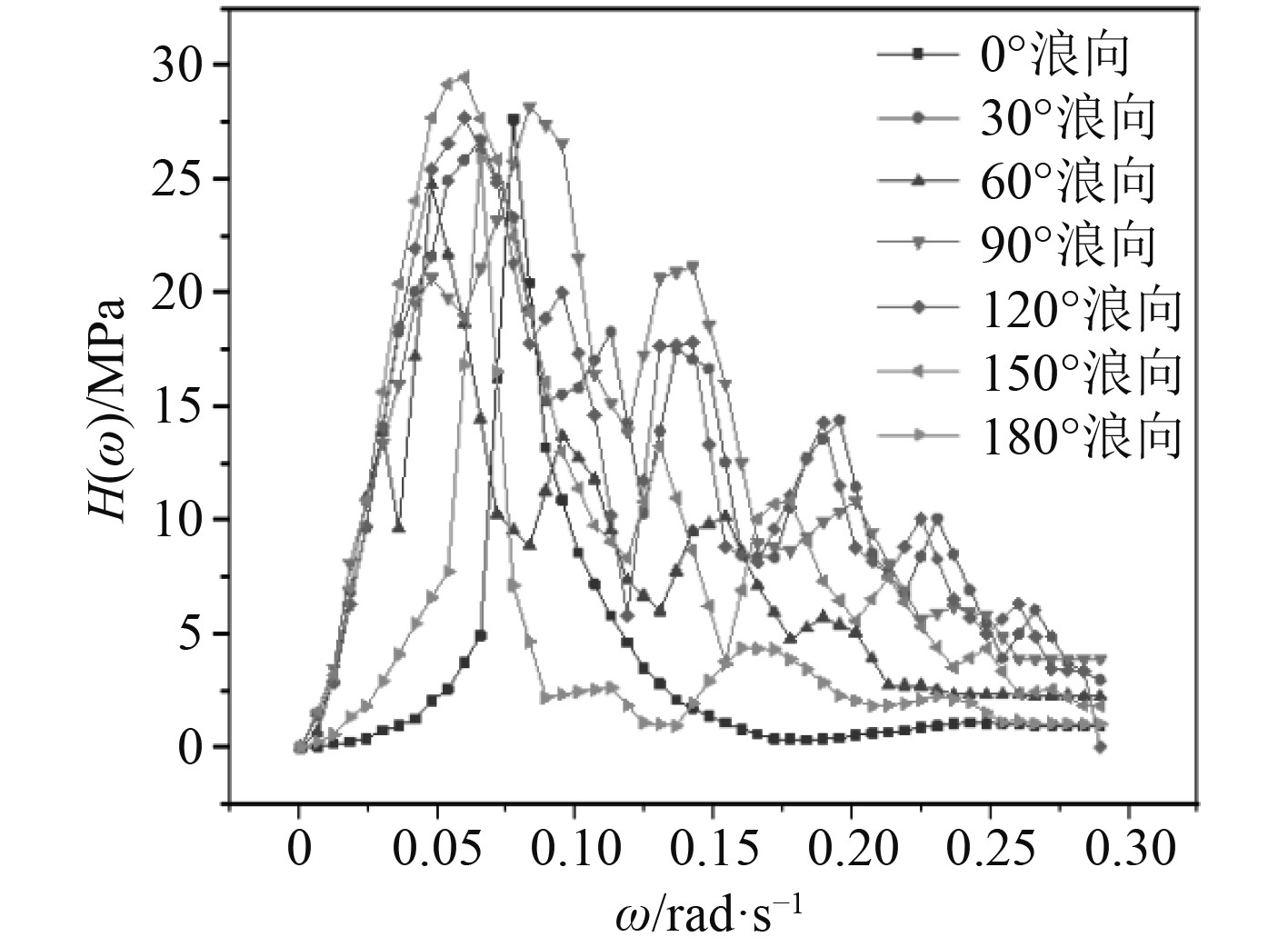
|
图 17 异形浮体结构2号疲劳点的传递函数 Fig. 17 Transfer function for fatigue point 2 of the shaped floating body structure |
|
图 18 异形浮体结构3号疲劳点的传递函数 Fig. 18 Transfer function for fatigue point 3 of the shaped floating body structure |
|
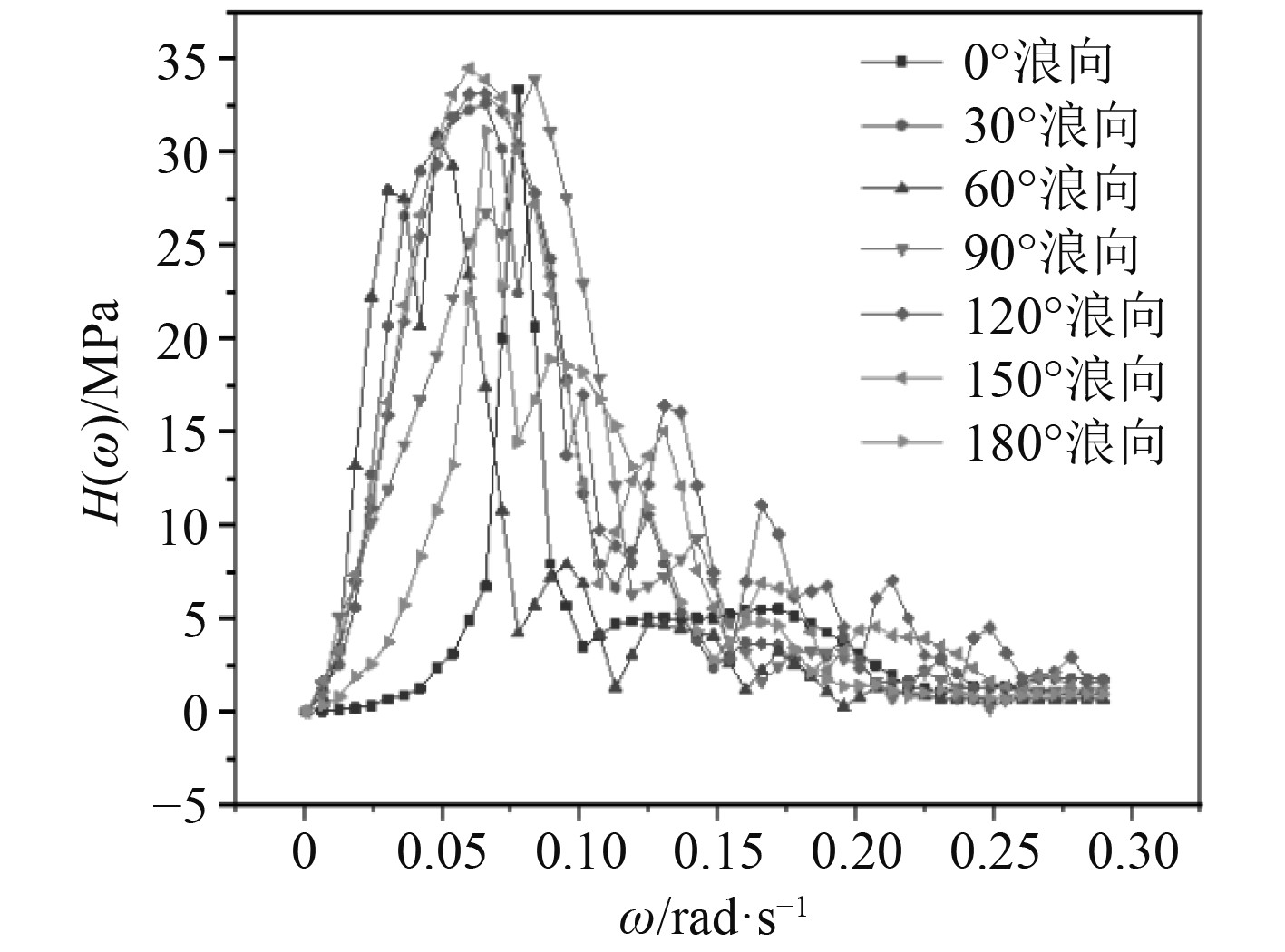
图 19 异形浮体结构4号疲劳点的传递函数 Fig. 19 Transfer function for fatigue point 4 of the shaped floating body structure |
在得到疲劳点的传递函数后,选取式(4)给出的JONSWAP谱,按照式(2)即可求出应力的响应谱,将响应谱按照式(5)进行积分可得到结构交变载荷响应的功率谱密度,为了获得给定时间内的应力循环次数,要用到交变载荷过程的跨零率
|
|
表 2 异形浮体结构的疲劳寿命评估结果 Tab.2 Fatigue life assessment results of shaped floating body structures |
本文运用规则波数值模拟试验法计算得到海上大尺度异型镂空浮体,在波浪载荷下的应力响应后,分别应用热点应力法和名义应力法对该大型异形浮体结构进行疲劳损伤及疲劳寿命评估计算,得到以下结论:
1)浮体的疲劳位置基本都产生在焊缝位置,提高焊接技术有利用提高结构的疲劳寿命。
2)当浮体受到150°方向的波浪荷载时,结构的应力值最大,可基于此对结构进行针对性的加强。
3)采用热点应力法计算的结构疲劳寿命要小于采用名义应力法所计算的结构疲劳寿命,结果偏于保守。在未能准确对焊缝进行建模时,建议采取热点应力法计算结构的疲劳寿命。
| [1] |
MATSUISHI M, ENDO T. Fatigue of metals subjected to varying stress[C]//Fukuoka, Japan: Japan Society of Mechanical Engineers, 1968.
|
| [2] |
RYCHLIK I. A new definition of the rainflow cycle counting method[J]. International Journal of Fatigue 1987, 9(2): 119–121.
|
| [3] |
DOWLING NE. Fatigue-failure predictions for complicated stress–strain histories[J]. Journal of American Society for Testing and Materials, 1972, 7(1): 71–87.
|
| [4] |
WATSON P, DABELL BJ. Cycle counting and fatigue damage: symposium on statistical aspects of fatigue testing[J]. Warwick University, 1975.
|
| [5] |
BRACCESI C, CIANETTI F, LORI G, et al. A frequency method for fatigue life estimation of mechanical components under bimodal random stress process[J]. SDHM structural Durability and Health Monitoring, 2005, 1(4): 277–290.
|
| [6] |
MRŠNIK M, SLAVIC J, BOLTEZAR M. Frequency-domain methods for a vibration-fatigue-life estimation. Application to real data[J]. International Journal of Fatigue, 2013, 4(7): 8–17.
|
| [7] |
WANG M, YAO W. Frequency domain method for fatigue life analysis on notched specimens under random vibration loading[J]. Jounal of NanJing University of Aeronautics and Astronautics, 2008, 40(4): 489–531.
|
| [8] |
张朝阳, 刘俊, 白艳彬, 等. 基于谱分析法的深水半潜式平台疲劳强度分析[J]. 海洋工程, 2012(1): 53-59. |
| [9] |
马网扣, 王志青, 张海彬, 等. 深水半潜式钻井平台节点疲劳寿命谱分析研究[J]. 海洋工程, 2008(3): 1-8. |
| [10] |
谢文会, 谢彬, 王世圣, 等. 深水半潜式钻井平台典型节点谱疲劳分析[J]. 中国海洋平台, 2009(5): 28-33. |
| [11] |
冯国庆. 船舶结构疲劳评估方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2003.
|
| [12] |
冯国庆. 船舶结构疲劳强度评估方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2006.
|
| [13] |
周蕊. 近海海浪的建模仿真研究[D]. 昆明: 昆明理工大学, 2015.
|
| [14] |
中国船级社. 海洋工程结构物疲劳强度评估技术指南[S]. 2022.
|
| [15] |
中国船级社. 基于谱分析的船体结构疲劳强度评估指南[S]. 2018.
|
 2024, Vol. 46
2024, Vol. 46
