随着社会经济的快速发展,能源消耗日益增长,传统石化能源的使用逐渐引发了一系列环境问题[1]。为了适应社会发展的环保主题,各种清洁能源逐步得到重视,风能作为清洁能源之一,其发挥的作用也越来越显著,风电技术也应运而生。随着风电技术的不断发展,海上风电向深水化发展,风机单机容量朝着大规模化前进[2]。风电平台的深水化也就意味着建造坐底式平台的成本和难度越来越高,半潜式平台较低的建造难度和较强的抗风浪能力[3]逐渐显现出来。
由于半潜式平台在恶劣的环境载荷作用下,会产生波频摇荡运动和低频漂移运动,因此半潜式平台副浮筒结构的设计和水动力特性的分析具有重要意义[4]。陈鹏等[5]运用AQWA软件考虑系泊缆的非线性动态特性和平台与系泊缆之间的相互影响,研究了不同环境力方向对平台系泊性能的影响。罗红星[6]研究了半潜式平台优化设计的影响因素,讨论了重心位置、吃水深度、垂荡板这几个因素对平台运动性能的影响。Dey 等[7]提出了将浮式海上风力发电机和波浪能转换器结合在一个平台上的可能性,通过分析得出波浪和风对系统的稳定性具有同步效应。该研究主要针对单个平台的设计因素进行讨论,但并没有对不同参数的平台进行横向对比。
本文基于启东中远海运海洋工程有限公司的奥特宝风电安装平台,设计建立多种副浮筒结构的半潜式海洋平台,对其进行水动力分析,对副浮筒高度参数进行设计和优化,得出一种水动力性能较佳的副浮筒结构参数,为后续的深入研究奠定了基础。
1 半潜式海洋平台建模及边界条件 1.1 多种副浮筒结构设计及计算模型建立本文基于奥特宝风电安装平台所建立的多种副浮筒结构的半潜式海洋平台,平台设计吃水为53 m,主浮筒间距为60 m,主要由4个主浮筒、8个副浮筒、1个底座和1个上甲板组成,平台参数如表1所示,水动力计算模型如图1所示。其中,底座为正八边形结构。本文设计的多种副浮筒结构是指同时改变8个副浮筒的高度参数,设立7组对比模型,8个副浮筒的高度依次为5 m、10 m、15 m、20 m、25 m、30 m和35 m,平台的其他结构参数保持一致。
|
|
表 1 海洋平台主要参数 Tab.1 Main parameters of offshore platform |
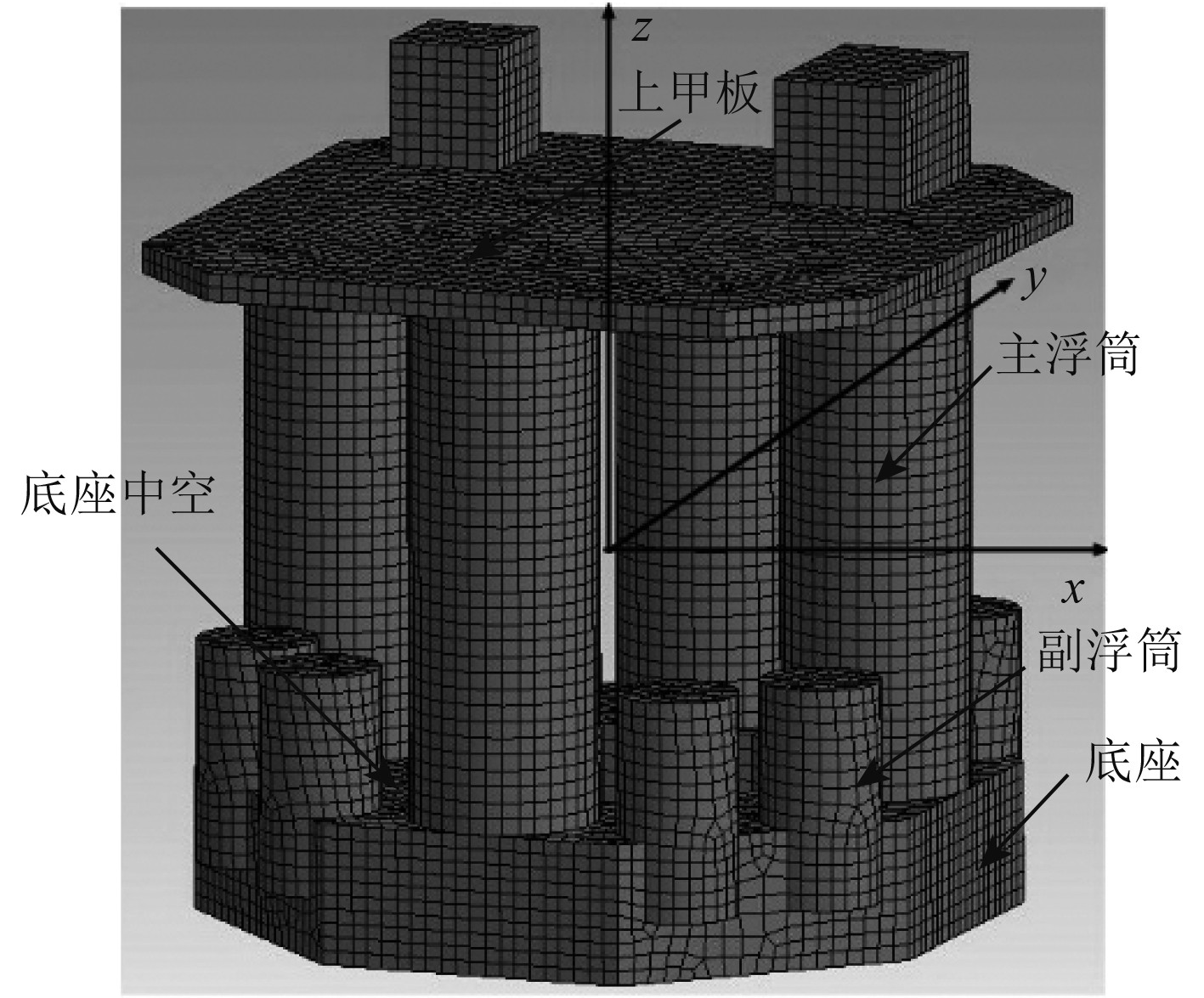
|
图 1 半潜式海洋平台模型 Fig. 1 Hydrodynamic model of semi-submersible offshore platform |
如图2所示,选取该样式的参考坐标系,其坐标原点为海洋平台中轴线与水线面的交点,坐标平面是与水线面重合的平面xoy,z轴垂直于水平面向上,且与平台的中轴线处于同一直线;当波浪沿x轴的正方向传播时,浪向角为0°,当波浪沿y轴的正方向传播时,浪向角为90°,并随着波浪的逆时针方向变化,使浪向角增大。
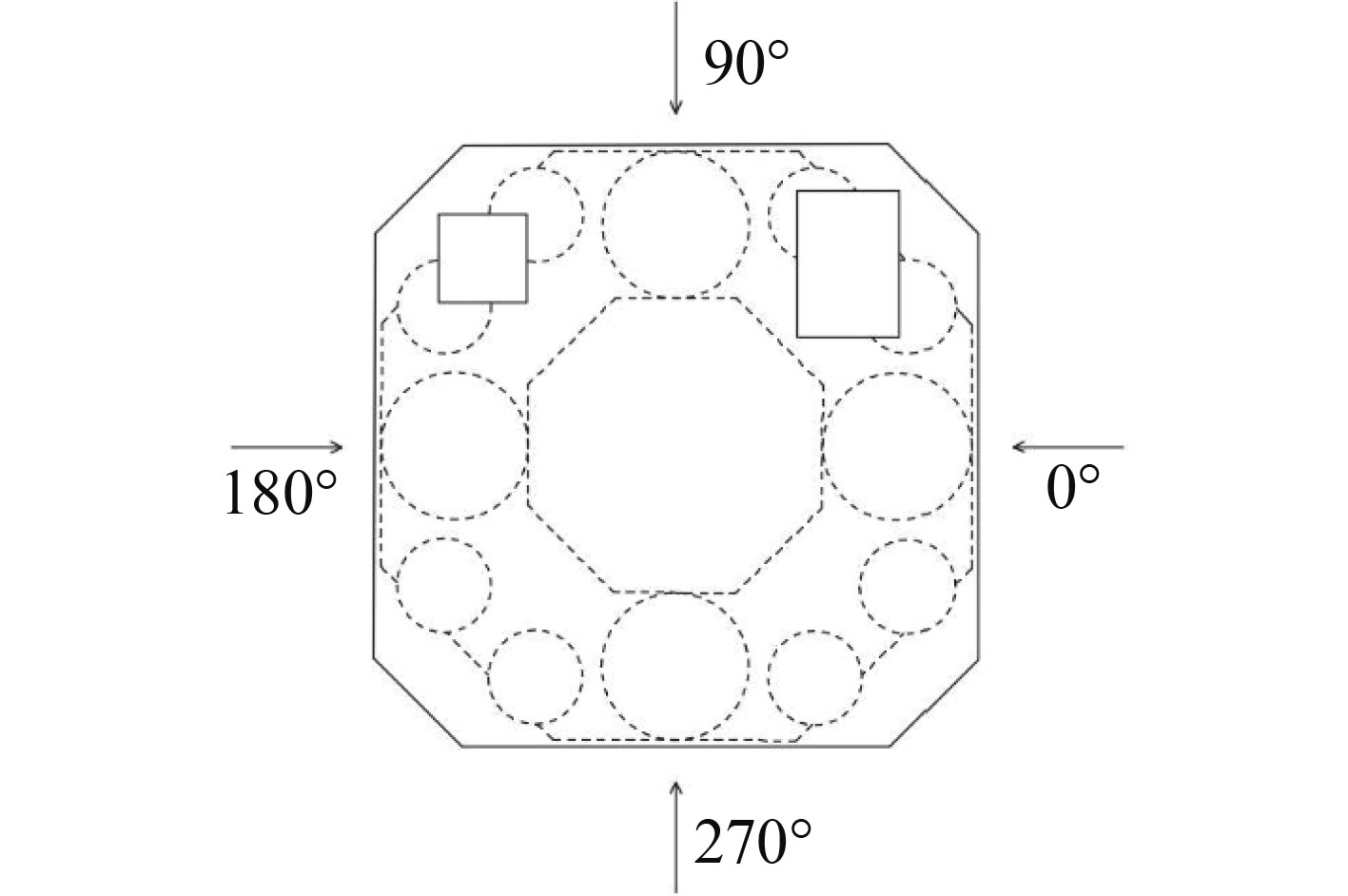
|
图 2 半潜式海洋平台坐标系 Fig. 2 Coordinate system of semi-submersible offshore platform |
本平台没有设置系泊系统,在进行平台的频域分析时,只需考虑海洋平台在波浪作用下的波频运动。设定环境参数的海水深度为 1000 m,波浪频率范围为0.1~2.1 rad/s,计算步频为23,浪向角范围为0~90°,间隔30°,浪向角数为4。波浪载荷的计算方法采用谱分析法,选择不规则波JONSWAP谱作为波浪载荷频谱。
2 水动力特性的数值结果分析运用AQWA水动力分析模块对多种不同副浮筒结构的海洋平台纵荡、横荡、垂荡、横摇、纵摇、首摇6个自由度方向的附加质量系数、附加阻尼系数、一阶波浪力和运动幅值响应算子等重要的水动力参数进行计算,并对计算结果进行后处理分析。由于整个海洋平台只有副浮筒的高度参数发生变化,而其他参数不发生改变,因此对海洋平台的附加质量系数、附加阻尼系数、一阶波浪力仅以副浮筒高15 m的模型水动力参数进行分析,该分析结果可以给其他尺寸的模型提供参考,最终的运动幅值响应算子将7种不同副浮筒高度的模型一起对比分析,对副浮筒高度参数进行设计和优化,研究出一种水动力性能较佳的副浮筒结构参数,为后续的深入研究做基础。
2.1 附加质量系数浮体在规则波中做稳态运动时,由于运动会产生附加质量和附加阻尼,二者不是一个定值,其大小与浮体的形状、航速、海洋开阔度和水深等有关。
由图3分析可知,在纵荡和横荡方向上,海洋平台的附加质量A11与A22呈现基本相同的变化趋势。随着波浪频率的逐渐变大,附加质量总体上是2次增大2次减小最后趋于稳定,第一次达到最大峰值是在波浪频率为0.35 rad/s时,随后迅速下降,并在波浪频率为0.75 rad/s时达到波谷,再次上升后,第二次达到峰值是在波浪频率为1 rad/s时,最后下降并在高频区间小幅波动后趋于稳定,最终稳定在7.5×107 kg;在横摇和纵摇方向上,海洋平台的附加质量A44和A55也呈现基本相同的变化趋势,在波浪频率低于0.8 rad/s时附加质量较为稳定,之后上升并在波浪频率为1 rad/s时达到峰值,随后开始下降并在1.35 rad/s时开始小幅波动后趋于稳定,最终稳定在7×108 kg;在垂荡方向上,海洋平台的附加质量A33变化趋势是在低频区间下降,在高频区间趋于稳定,在0.1~0.5 rad/s的区间缓慢上升,在0.5~0.7 rad/s的区间呈下降趋势,之后在高频区间缓慢上升并趋于稳定,最终稳定在8×107 kg附近;在首摇方向上海洋平台的附加质量A66的变化趋势和横摇与纵摇方向上大概相同,但是首摇方向总体的附加质量比横摇和纵摇方向少3×108 kg,其最终在高频区稳定在4×108 kg。
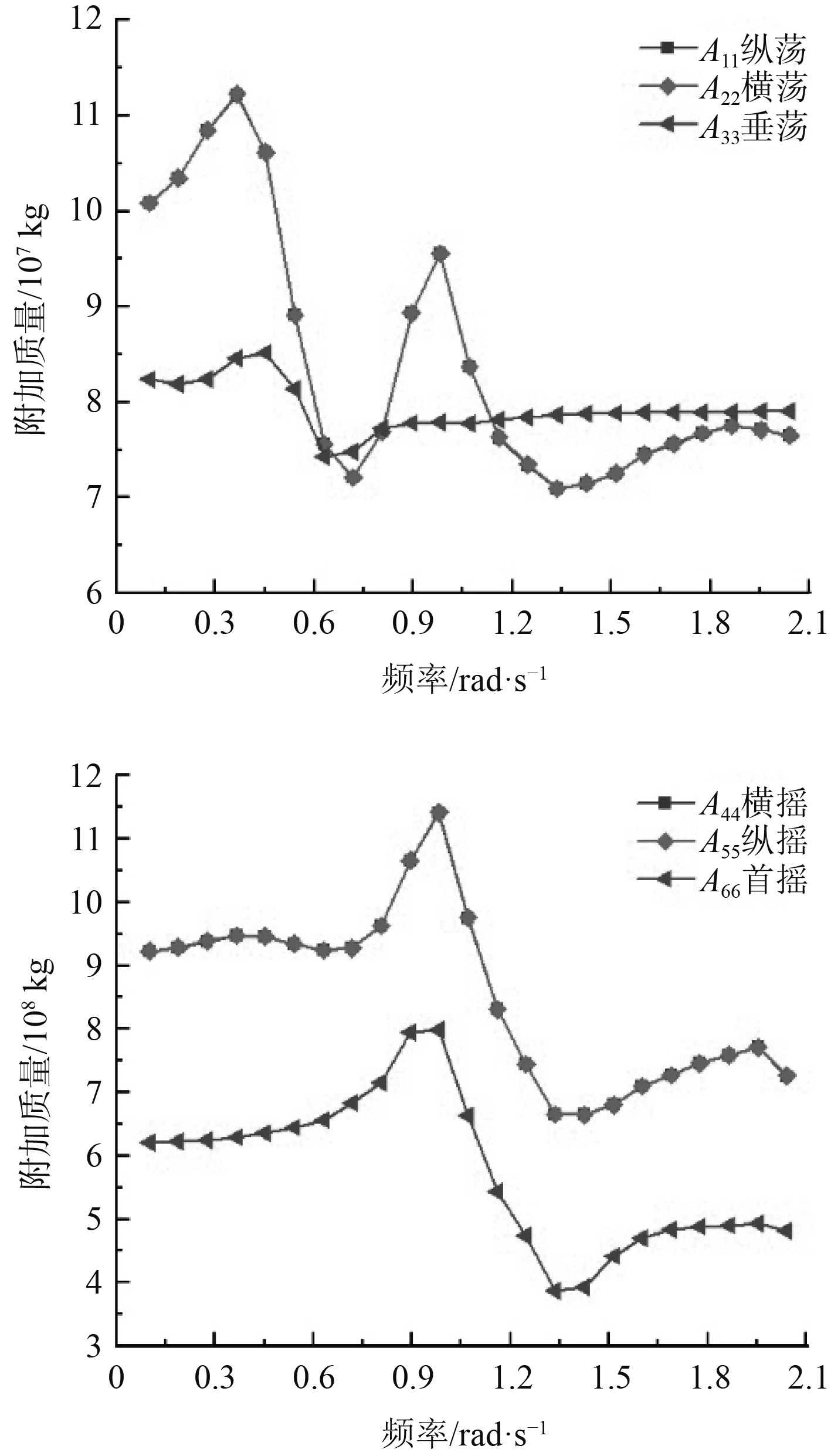
|
图 3 附加质量系数 Fig. 3 Additional mass factor |
由图4分析可知,在纵荡和横荡方向上,海洋平台的附加阻尼系数B11和B22呈现大致相同的变化趋势,总体变化趋势为先增大后减小、再增大后稳定。在第一个波浪频率区间0.1~0.3 rad/s内较为稳定,量级较小,之后在波浪频率为0.6 rad/s时达到第一个峰值,随后在波浪频率0.9 rad/s时处于2个波峰之间的波谷,量级同样较小,之后在波浪频率为1.2 rad/s时附加阻尼系数达到最大峰值2.5×107 N·s/m,最后在高频区间略微波动后稳定在3×106 N·s/m左右;在垂荡方向上,附加阻尼B33在低频区间出现小幅增减,并在高频区间稳定在较低值;在横摇和纵摇方向上,附加阻尼B44和B55变化基本相同,在低频区间变化不明显,但在0.9 rad/s时迅速上升,并在1.1 rad/s时达到峰值4×108 N·s/m,随后减小并出现波动,最后在高频区间稳定在1×108 N·s/m左右;在首摇方向上,附加阻尼B66的变化趋势和横摇、纵摇方向上较为相似,是在低频区间变化不明显,在波频0.9 rad/s开始迅速上升并在1.1 rad/s时达到峰值3.3×108 N·s/m,随后减小并出现波动,最后在高频区间稳定在0.7×108 N·s/m左右。

|
图 4 附加阻尼系数 Fig. 4 Additional damping coefficient |
综合来看,海洋平台的附加质量系数和附加阻尼系数在纵、横荡和纵、横摇方向上大概相同,说明该海洋平台结构对称性良好。
2.3 一阶波浪力海洋平台在海上会受到波浪力的作用,一般情况下包括入射势产生的入射波浪力和绕射产生的绕射波浪力[8]。一阶波浪力考虑了波浪绕射对浮体的影响,因海洋平台结构具有对称性,因此仅考虑波浪入射角为0°、30°、60°和90°时,海洋平台在6个自由度上的一阶波浪力响应曲线。
由图5分析可得,在纵荡、横荡、横摇和纵摇这4个自由度上一阶波浪力对波浪入射角的变化比较敏感,在垂荡自由度上的一阶波浪力对波浪入射角的变化最不敏感。在纵荡和横荡自由度上,一阶波浪力在低频区间迅速增大并在0.5 rad/s时达到最大峰值,随后迅速降低,之后随着频率的增大出现明显波动,但在高频区间趋于较小的平稳值。在纵荡和横荡自由度上的变化趋势是纵荡自由度上0°入射角呈先增大后波动降低趋势,90°入射角始终为接近0的值,而横荡自由度上的一阶波浪力变化趋势与之刚好相反,90°入射角呈先增大后波动降低趋势,0°入射角始终为接近0的值。在垂荡自由度上,一阶波浪力在低频区间呈先降低和增大的趋势,且在0.1 rad/s的起始频率为最大峰值,随后在0.3~0.8 rad/s波频区间内先升高后降低,之后在高频区间保持小范围波动并处于较小的数量级。
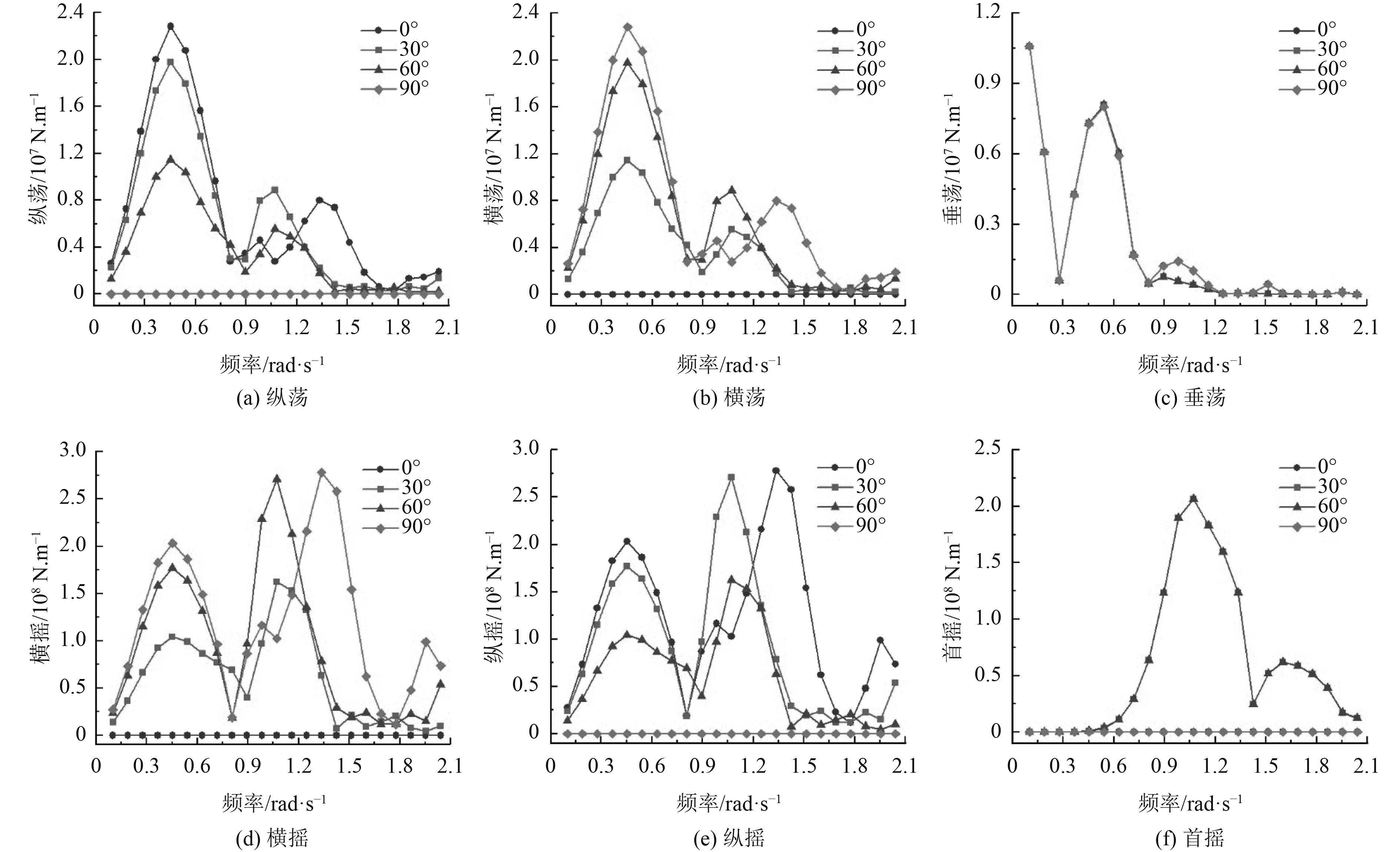
|
图 5 海洋平台一阶波浪力响应曲线 Fig. 5 First order wave force response curve of offshore platform |
在横摇与纵摇自由度上,一阶波浪力总体变化趋势相同,但入射角对一阶波浪力的影响正好相反,在横摇自由度上,入射角0°的一阶波浪力始终接近0,入射角30°、60°和90°的一阶波浪力变化趋势相似,都是在低频区间先增大后减小,在高频区间也先增大后减小,在入射角90°的波频1.4 rad/s时达到最大峰值,而在纵摇自由度上,入射角90°的一阶波浪力始终接近0,入射角0°、30°和60°的一阶波浪力变化趋势相似,都是在低频区间先增大后减小,在高频区间也先增大后减小,在入射角0°的波频1.4 rad/s时达到最大峰值。在首摇自由度上,入射角0°和90°的一阶波浪力始终接近0,入射角30°和60°的一阶波浪力随着波频的增大呈先增大后减小的趋势,并在波频为1 rad/s时达到最大峰值。
3 7组平台的运动响应幅值算子运动响应分析是指浮体在单位入射波下的运动响应结果,运动响应幅值(RAO)与入射波的幅值成线性比例,是浮体自身系统的动态特性[9]。
由图6分析可知,当波浪入射角为0°时的纵荡RAO中,副浮筒高25 m的海洋平台在0.5 rad/s时最高,副浮筒高30 m的海洋平台在0.5 rad/s时也较高,副浮筒高15 m的海洋平台在0.5 rad/s时虽比35 m的略高,但在0.7 rad/s时比35 m的更低,也就是15 m的在低频区间波动略低于35 m。总体来说,副浮筒高15 m的海洋平台在纵荡RAO上要略好于其他高度的海洋平台。在垂荡RAO中,在低频区间0.3~0.6 rad/s内,副浮筒25 m高的海洋平台虽然在0.3 rad/s时垂荡RAO最低,但之后迅速上升并超过5 m、10 m和15 m的平台,相比之下副浮筒15 m高的海洋平台虽在0.3 rad/s时,垂荡RAO略高于25 m和30 m的,但在之后的波频区间表现更好,因此在垂荡RAO中副浮筒15 m高的海洋平台也要略好于其他高度的海洋平台。在纵摇自由度上,副浮筒高15m的海洋平台在低频区间的RAO表现和5 m、10 m、35 m的差不多,但明显比20 m、25 m、30 m的海洋平台表现更好。在横荡、横摇和首摇自由度上的RAO值都是很小的数量级,因此可不用考虑。综合来看,当波浪入射角为0°时,副浮筒高15 m的海洋平台RAO表现要优于其他高度的海洋平台。
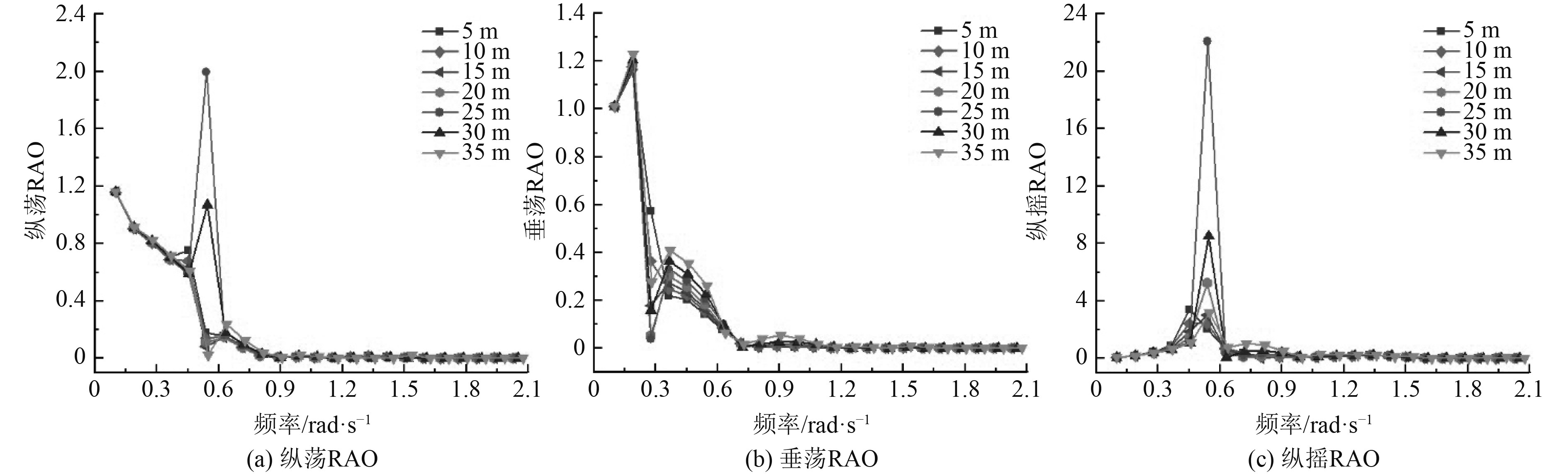
|
图 6 波浪入射角0°的RAO Fig. 6 The RAO of wave incidence is 0° |
由图7分析可知,副浮筒高15 m的海洋平台在纵荡和横荡自由度上的RAO,在全波频区间始终保持最低值,在垂荡自由度上副浮筒高15 m的海洋平台总体趋势和入射角0°的相似,因30°入射角是波浪对平台的偏射,总体量级要比入射角0°的小,因此副浮筒高15 m的海洋平台在垂荡自由度上的RAO表现也较好。副浮筒高15 m的海洋平台在横摇和纵摇自由度上的RAO在低频区间的值要远好于25 m、30 m、35 m和20 m的,也比5 m的略好,和10 m的保持相当。在首摇自由度上副浮筒7个高度的海洋平台都处于较小的量级,差距较小。综合来看,当波浪入射角为30°时,副浮筒高15 m的海洋平台RAO表现要优于其他高度的海洋平台。
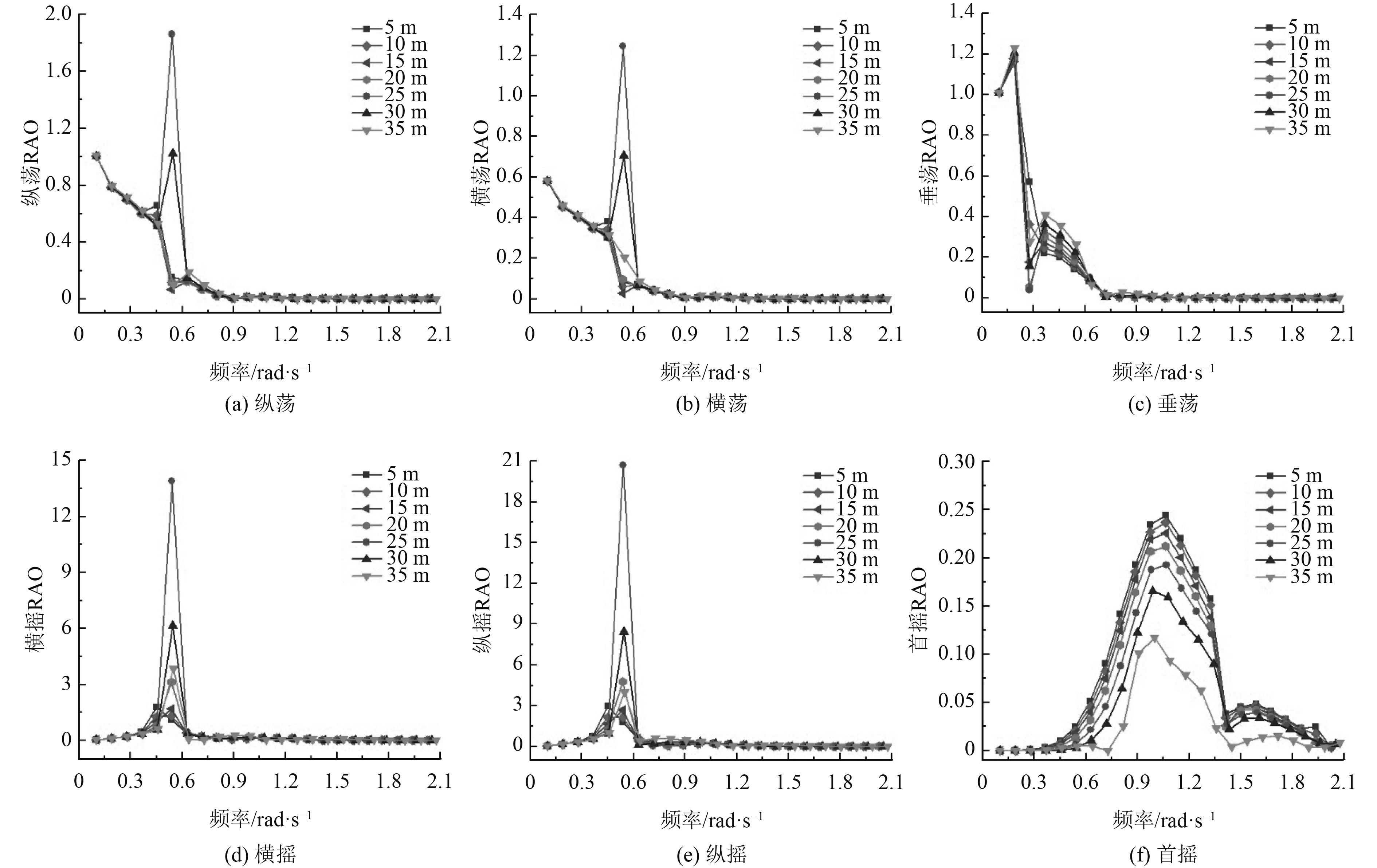
|
图 7 波浪入射角30°的RAO Fig. 7 The RAO of wave incidence is 30° |
由于海洋平台具有良好的对称性,入射角0°时的纵荡RAO和入射角90°时的横荡RAO结果相近,入射角30°时的横摇RAO和入射角60°时的纵摇RAO结果相近,依次类推,波浪入射角为90°时的RAO结果与波浪入射角为0°时的结果相近,波浪入射角为60°时的RAO结果与波浪入射角为30°时的结果相近。综上所述,7组平台中在6个自由度上综合性能最好的是副浮筒高15 m的海洋平台。
4 结 语本文基于启东中远海运海洋工程有限公司的奥特宝风电安装平台设计建立多种副浮筒结构的半潜式海洋平台,通过AQWA软件对半潜式海洋平台的水动力性能进行分析计算,得到了海洋平台在频域内的附加质量、附加阻尼、一阶波浪力和六自由度运动响应幅值算子,之后通过对比分析7组不同副浮筒高度参数的海洋平台频域计算结果,结果表明:
1)海洋平台在纵荡和横荡、横摇和纵摇上的附加质量、附加阻尼基本相同,表明海洋平台具有良好的对称性。
2)海洋平台在频域计算区间内,低频区间和高频区间数值结果差别明显,低频区间运动响应较为明显,高频区间运动响应较小,表明海洋平台在选定海况下具有较好的水动力性能。
3)副浮筒高为15 m的海洋平台综合水动力性能要优于副浮筒高为5 m、10 m、20 m、25 m、30 m和35 m的海洋平台,可为以后的半潜式海洋平台设计提供参考。
| [1] |
张轲. 浮式风机半潜式平台水动力及其运动响应分析[D]. 大连: 大连理工大学, 2021.
|
| [2] |
孔令海, 容学苹, 窦培林, 等. 海上风机四浮筒基础运动响应分析[J]. 舰船科学技术, 2022, 44(17): 90-95. KONG Ling-hai, RONG Xue-ping, DOU Pei-lin, et al. Motion response analysis of four pontoon foundation of offshore wind turbine[J]. Ship Science and Technology, 2022, 44(17): 90-95. DOI:10.3404/j.issn.1672-7649.2022.17.018 |
| [3] |
吴澜, 吴宝山, 匡晓峰, 等. 基于AQWA的半潜式平台水动力特性研究[J]. 中国海洋平台, 2014, 29(5): 29-33. WU Lan, WU Bao-shan, KUANG Xiao-feng, et al. Astudy on the hydrodynamic characteristics of semi-submersible based on AQWA[J]. China Offshore Platform, 2014, 29(5): 29-33. DOI:10.3969/j.issn.1001-4500.2014.05.006 |
| [4] |
唐文献, 高泽, 张建, 等. 基于AQWA的2种副浮筒结构的半潜式海洋平台水动力特性研究[J]. 舰船科学技术, 2017, 39(9): 82-87. TANG Wen-xian, GAO Ze, ZHANG Jian, et al. A study on the hydrodynamic characteristics of semi-submersible offshore platform withtwo column structures based on AQWA[J]. Ship Science and Technology, 2017, 39(9): 82-87. |
| [5] |
陈鹏, 马骏, 黄进浩, 等. 基于AQWA的半潜式平台水动力分析及系泊性能计算分析[J]. 船海工程, 2013, 42(3): 44-47. CHEN Peng, MA Jun, HUANG Jin-hao, et al. Hydrodynamic analysis and mooring system calculation for semi-submersible platform[J]. Ship and Ocean Engineering, 2013, 42(3): 44-47. DOI:10.3963/j.issn.1671-7953.2013.03.011 |
| [6] |
罗红星. 半潜式平台的水动力及系泊系统性能研究[D]. 武汉: 华中科技大学, 2017.
|
| [7] |
DEY, BANIK K. Stability and performance analysis of hybrid braceless semisubmersible platform installed in real seas[J]. Wind Engineering, 2023, 47(1):19−24.
|
| [8] |
陈晨. 海上打桩船水动力性能及系泊系统研究[D]. 镇江: 江苏科技大学, 2021.
|
| [9] |
梁冠辉, 孙宝楠, 薛宇欢, 等. 应用于海洋物性监测仪的小型浮标水动力分析[J]. 海洋科学进展, 2021, 39(1): 136−145. LIANG Guan-hui, SUN Bao-nan, XUE Yu-huan, et al. Hydrodynamic analysis of small buoy applied to marine physical parameters monitor[J]. Advances in Marine Science, 2021, 39(1): 136−145. |
 2024, Vol. 46
2024, Vol. 46
