运用跨介质无人机系统可以延长水下载具的信息探测触角,基于这一需求,各国在跨介质无人机军用化上投入大量研究,以黑翼无人机(Blackwing)为代表的潜射无人机陆续崭露头角,潜射无人机的出现极大地拓展了潜艇的水面感知能力,同时又能够让潜艇保持自身的隐蔽性优势。
目前美国等军事发达国家主流的潜射无人机系统,更多采用无动力水下运载器方案,国内现有的研究集中于无动力运载器,叶衍权等[1-2]通过对运载器出管过程建立数学模型进行分析,设计了一种无动力运载器并通过Isight优化了运载器的外形结构设计,赖坤等[3]总结了目前潜射无人机水下发射技术,并对国内外相关技术作了总结。当采用无动力潜射无人机发射方案时,该类发射技术适合潜艇在较浅的深度发射无人机,对于潜射无人机的姿态控制和无人机携带挂载重量具有严格要求,对姿态控制和挂载重量有一定要求和限制。
在有动力运载器方面,孙希勋[4]设计了一种装配有矢量推进器的潜射无人机水下运载器,并设计了一种自适应模糊滑膜控制器对运载器出水后的首向进行控制。使用有动力运载器时,其优点是具备自主动力,运动更加灵活,可根据实际水下情况进行及时调整,同时由于驱动力的存在,运载器可适应更加多样复杂的水下环境。
本文首先设计了一种具有动力的潜射无人机水下运载器,然后基于运载器外形和运动特点进行动力学建模,进行仿真并利用Star-CCM+测定了运载器的水动力系数,最后设计了一种串级控制器并利用isight进行参数优化设计。本文研究可对潜射无人机水下运载器设计提供一定参考。
1 水下运载器的初步设计 1.1 结构方案本设计外形壳体参考传统AUV(Autonomous Underwater Vehicle)的设计思路,整体外形选择回转体外形设计,将水下运载器的中部设置为负载舱,用于携带无人机,此种设计在外形阻力、壳体内部装配空间、加工难易程度和成本等方面相较于其他外形设计(如多体形、扁平形等)都具有一定优势。
1.2 推进及部分附体配置方案目前主流水下潜航器的推进器方案大致分为2种,一种为大部分AUV采用的“推进螺旋桨+控制舵”模式,此种模式脱胎于潜艇驱动控制模式,有丰富的设计经验作为借鉴,但是该模式在水中实现姿态控制或静态姿态保持有一定困难,不适于作为潜射无人机的水中运载器以及发射平台。另一种为大部分ROV采用的“多推进螺旋桨”模式,该方案可以在运载器3个主轴方向进行位移,同时也可在静态模式下调整姿态并保持,基于灵活性和姿态保持能力方面的考虑,本文选择第2种推进器方案。
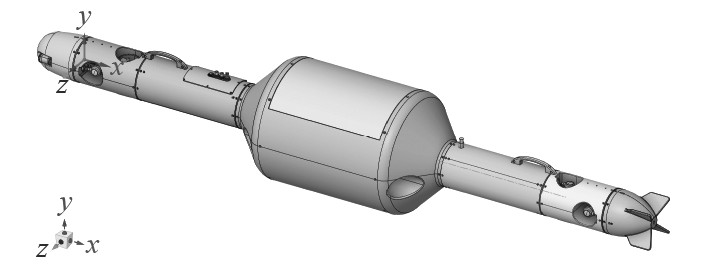
在运载器附体及内部配置的选择方面,同样参照一般ROV的设计选配,如光学系统(摄像机)、定位信标、P360声呐以及外壳搬运把手等,图1为经初步设计后的3D建模图。
|
图 1 运载器初步设计三维模型 Fig. 1 Preliminary design of the underwater vehicle |
通过Star-CCM+软件对水下运载器进行约束模型试验,包括斜航试验(ORT)、回转臂试验(RAT)和平面运动机构试验(PMM),通过对仿真数据进行分析,最终得到水下运载器的无因次水动力系数。最终计算结果如表1所示。
|
|
表 1 基于Star-CCM+的约束模型试验结果 Tab.1 Experimental results of constrained model based on Star-CCM+ |
本文参考相关文献[5-9]对潜航器进行建模,潜航器的动力学方程如下:
| $ \boldsymbol{F}_h=\boldsymbol{MA}+\boldsymbol{CV}-F_I\boldsymbol{A}-\boldsymbol{F}_V-G+B,$ | (1) |
| $ \begin{split} \boldsymbol{F}_V= & F_uu+F_vv+F_ww+F_{uu}u^2+F_{vv}v^2+F_{ww}w^2+ \\ &F_{uv}uv+F_{uw}uw+F_pp+F_qq+F_rr。\end{split} $ | (2) |
与一般ROV不同,本文设计运载器在3个主轴方向均为对称设计,运载器以大小相等方向相反的速度分别在纵向、横向以及垂向运动时受到的阻力数值大小可认为近似相等,所以在建模过程中可对部分运载器粘性水动力方程做进一步简化:
| $ X_V=X_{uu}u^2+X_{ww}w^2,$ | (3) |
| $ Y_V=Y_{vv}v^2+Y_{uv}uv+Y_pp+Y_rr,$ | (4) |
| $ Z_V = Z_{uu}u\left|u\right| + Z_{uu}u^2 + Z_{vv}v\left|v\right| + Z_{ww}w\left|w\right| + 2Z_{uw}uw + Z_qq。$ | (5) |
潜航器线速度所在固连坐标系与地面坐标系之间的转换关系以及角速度与姿态角之间的转换关系为:
| $\begin{split} & \left[ {\begin{array}{*{20}{c}} {\dot x} \\ {\dot y} \\ {\dot z} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \theta \cos \psi }&{ - \cos \varphi \sin \psi + \sin \varphi \sin \theta \cos \psi }\\ {\cos \theta \sin \psi }&{\cos \varphi \cos \psi + \sin \varphi \sin \theta \sin \psi } \\ { - \sin \theta }&{\sin \varphi \cos \theta } \end{array}}\right.\\ & \left.{\begin{array}{*{20}{c}} {\sin \varphi \sin \psi + \cos \varphi \sin \theta \cos \psi } \\ { - \sin \varphi \cos \psi + \cos \varphi \sin \theta \sin \psi } \\ {\cos \varphi \cos \theta } \end{array}} \right] \left[ {\begin{array}{*{20}{c}} u \\ v \\ w \end{array}} \right],\end{split} $ | (6) |
| $ \left[\begin{array}{*{20}{c}}\dot{\varphi} \\ \dot{\theta} \\ \dot{\psi}\end{array}\right]=\left[\begin{array}{*{20}{c}}1 & \sin\varphi\tan\theta & \cos\varphi\tan\theta \\ 0 & \cos\varphi & -\sin\varphi \\ 0 & \sin\varphi/\cos\theta & \cos\varphi/\cos\theta\end{array}\right]\left[\begin{array}{*{20}{c}}p \\ q \\ r\end{array}\right]。$ | (7) |
式中:
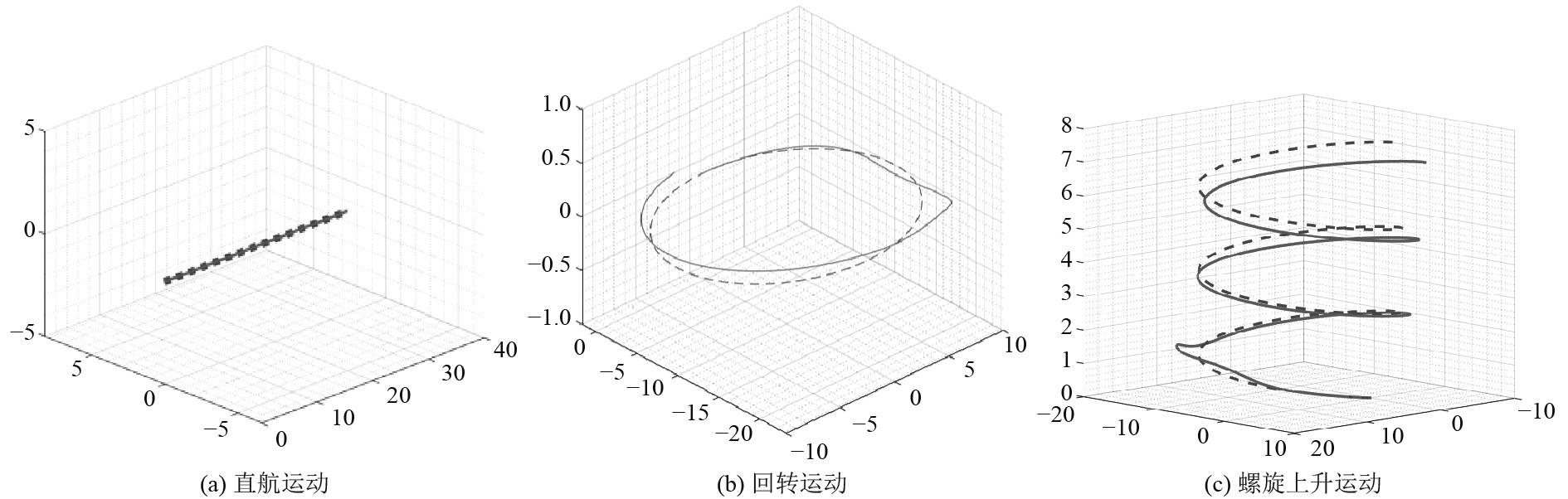
模型构建完成后首先使用简单PID控制器对水动力模型进行仿真,分别控制潜航器进行直航运动、回转运动和螺旋上升运动,仿真效果如图2所示,图中虚线为目标轨迹,实线为运行轨迹。可知,潜航器均具有较好的跟踪性,说明该模型具有有效性,也为后续优化控制打好了基础。
|
图 2 运动模型仿真效果图 Fig. 2 Motion simulation rendering |
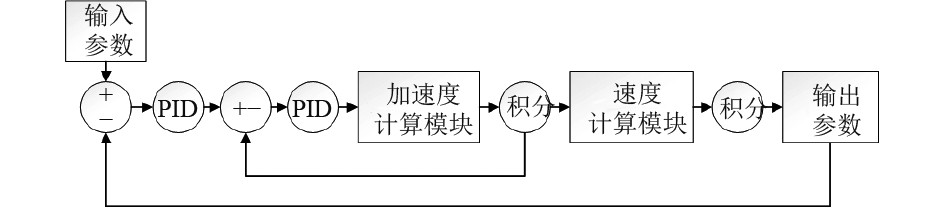
本文运载器运动模型框图如图3所示。运载器运动方程首先输入设定的六自由度运动参数,经过与实际输出规律作差后由PID控制器输出控制量,由加速度计算模块输出模型加速度,再由速度计算模块计算后经积分,最终输出模型实际运动参数,在仿真过程中,此种单PID控制方法时常出现超调或跟踪效果不良的情况,鲁棒性较差,同时在运载器实际运动过程中,由于航行环境复杂,单PID控制器很难胜任本文运载器的操纵性等特性要求,基于此点,相关领域学者在针对水下航行器的非线性特点所设计的自适应控制、模糊控制和自抗干扰控制等方面都取得了进展[10-13]。下面将通过相对简易可行的串级PID控制器设计思路来设计水下运载器的运动控制器。

|
图 3 运载器运动仿真模型框图 Fig. 3 Vehicle motion simulation model block diagram |
运载器的仿真模型主体由加速度运算模块和速度运算模块组成,所以在设计串级PID控制器时,由内环控制器控制速度运算模块,再由外环控制器控制加速度运算模块。由于采用ROV的推进模式,潜航器的深度变化与自身俯仰角度并非完全耦合,若仅对深度以及俯仰角度采用单PID控制,经常会出现潜航器失控的情况,所以需在速度计算模块前加入微分环节来抑制潜航器姿态的变化速率,即内环PID的目的是对各自由度的速度扰动进行反应。同时为了增加运载器3个方向主轴位移的调节效果,选择在其加入比例控制比重。综合上述分析,在内环控制中,深度控制等位移参数方面使用以比例控制为主的控制方法,在俯仰角度等姿态参数控制方面选择增加微分项的比重以抑制姿态的波动。经过调整后的运载器仿真如图4所示。
|
图 4 增加串级控制后的系统图 Fig. 4 System block diagram after adding cascade control |
为了与单级PID控制做对比,在串级PID实验中让外环PID参数与单级控制器PID参数保持一致,内环PID参数设置初始值如表2所示。
|
|
表 2 外环PID参数 Tab.2 Outer ring PD parameters |
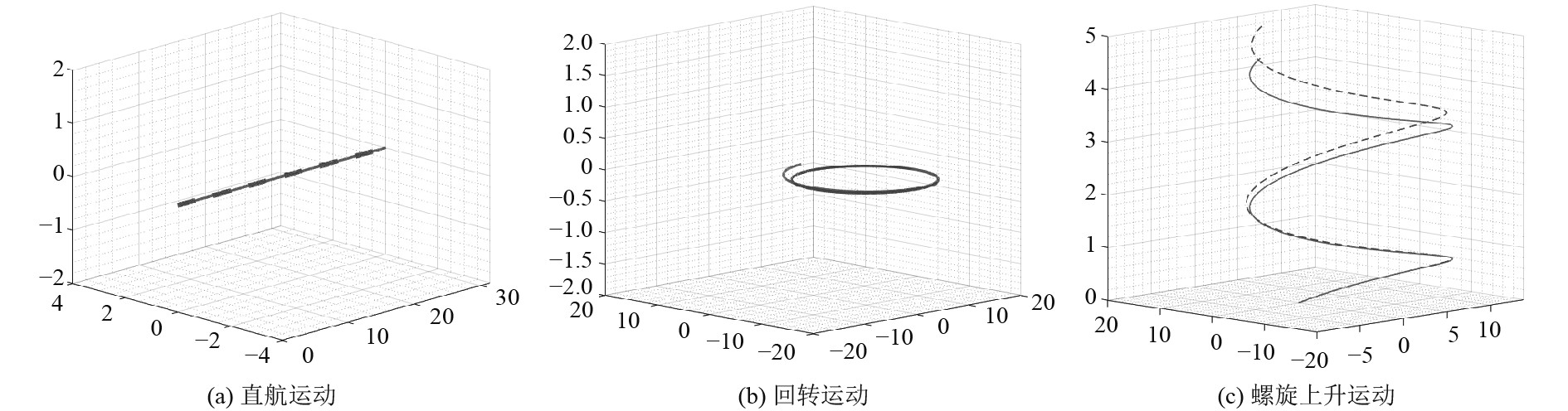
在目标轨迹设置上使用相同轨迹,以便于单级PID控制方法与串级PID控制方法作对比,同样分别选用直线轨迹、圆轨迹和螺旋上升轨迹,串级PID控制效果如图5所示,并以螺旋上升运动为例,比较2种控制方法在六自由度上的平均误差。
|
图 5 串级控制方法仿真实验效果图 Fig. 5 Effect chart of cascade control method simulation experiment |
通过仿真效果图以及误差(见表3)对比可看出,普通PID控制方法在3个主轴方向误差较串级PID控制方法分别高出3.4%、103.4%和25.5%,姿态角误差数据中,除俯仰角误差较串级PID控制低外,其余误差分别高出16.6%和18.6%,综合来看,本模型使用的串级控制方法的控制效果优于最初设计的单级控制方法的控制效果,在控制稳定性上串级控制模式明显优于单级控制,说明在控制方法上串级控制较单级控制更好。
|
|
表 3 2种控制方式的平均误差 Tab.3 Average error of two control methods |
首先在串级控制器参数的评估方面设置具体的量化标准,即为控制器6个自由度的轨迹误差:
| $ E_{mpara}=\frac{\sum_{ }^{ }|P-dP|}{k},$ | (8) |
| $ k=\frac{T}{t}。$ | (9) |
其中:
首先输入参数选择串级控制器前后两级的PID控制器参数,共36个,输出参数选择模型运行后六自由度的目标轨迹与实际轨迹差值,同时在Isight工作流中将Task替换为Optimization即可进行优化计算,分别选择Evol优化算法以及自适应DOE优化法分别进行优化计算。考虑到实际控制器情况,需对控制器参数取值做出限制,暂定控制器中所有P值取值范围为0~20,D值取值范围为0~30。
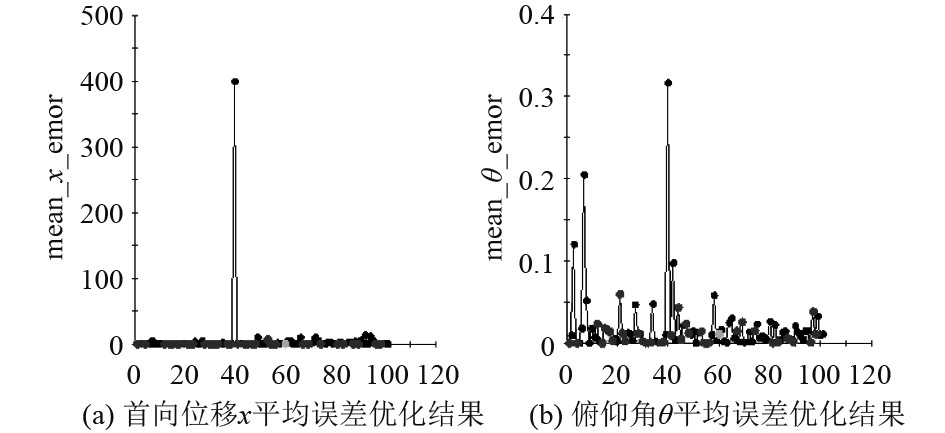
参数以及流程设置完毕后即可进行优化计算,2种优化方法分别经过101以及909次迭代计算,计算结果如图6和图7所示,由于计算参数多,产生图表数量较大,以首向位移
|
图 6 Evol 优化计算结果 Fig. 6 Evol optimization results |
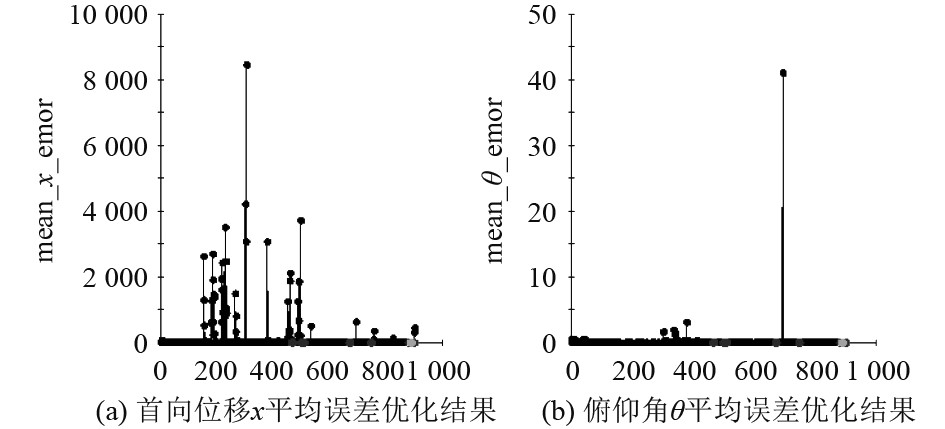
|
图 7 自适应DOE优化计算结果 Fig. 7 Adaptive DOE optimization calculation results |
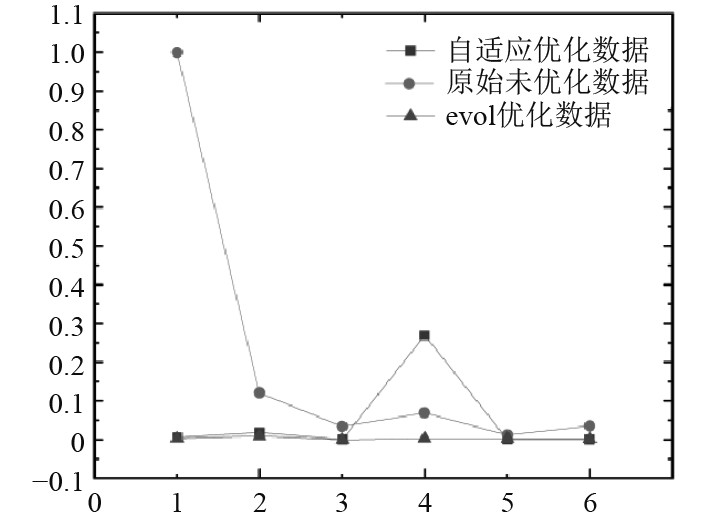
分别将2组优化结果以及初始参数组合代入模型运行,分别得到各自的运行结果,通过将3组数据与目标轨迹取差值比较不同方法的优化效果,由于运算结果单位以及尺度各不相同,在作比较前将3组数据进行归一化处理,得到的结果如图8所示。
|
图 8 优化参数与原始参数运行效果对比 Fig. 8 Comparison between optimized parameters and original parameters |
图中横坐标1~6代表参数依次为x方向位移误差、y方向位移误差、z方向位移误差、横滚角误差、俯仰角误差以及偏航角误差,可知,2种优化方法均有较好的优化效果。自适应DOE优化方法与Evol优化方法相比较,前者在横滚角误差方面较后者大0.298,产生误差远大于后者,Evol优化算法效果更好,同时自适应DOE优化共执行909组迭代计算,而Evol优化共执行102组迭代计算,自适应DOE优化法计算成本相对更高。
5 结 语1)初步设计了一种具有动力的潜射无人机水下运载器,结合AUV外形与ROV驱动方式,为无人机跨介质机动的改进提供了基础。
2)对水下运载器进行了动力学建模,结合运载器的外形特点对动力学方程进行了一定简化,并运用Matlab/Simulink工具进行了仿真试验,并根基串级控制模式为该运载器设计了一种串级PID控制器。由于控制器参数较多,本文在控制器选择上仅选择了较为简单的单级PID控制器,后续研究可选择控制效果较好的模糊PID控制器或MPC模型预测控制器。
3)通过基于Matlab/Simulink与Isight联合的优化方法不需要进行复杂建模和算法设计,较易操作,优化效率高,可为水下运载器控制器设计提供一定的参考。
| [1] |
叶衍权, 马宇. 潜射无人机运载器发射出管过程安全性仿真[C]//北京力学会. 北京力学会第二十五届学术年会会议论文集, 2019.
|
| [2] |
叶衍权, 马宇. 潜射无人机运载器的水弹道仿真[J]. 计算机仿真, 2020, 37(6): 322-327. |
| [3] |
赖坤, 魏建峰, 苑华林. 潜射无人机鱼雷管水下发射技术研究[J]. 飞航导弹, 2018(4): 22-24. |
| [4] |
孙希勋. 近海面发射UAV的特种运载器运动控制方法[D]. 哈尔滨: 哈尔滨工程大学, 2017.
|
| [5] |
昝英飞, 袁利毫, 郭睿男, 等. 一种五自由度ROV非线性运动学建模方法[P]. 黑龙江省: CN110083941A, 2019-08-02.
|
| [6] |
陈营营. 水下运载器鲁棒控制策略与弹道特性研究[D]. 哈尔滨: 哈尔滨工程大学, 2016.
|
| [7] |
张润博. 基于液压驱动的ROV水下作业仿真研究[D]. 哈尔滨: 哈尔滨工程大学, 2016.
|
| [8] |
施生达. 潜艇操纵性[M]. 北京:国防工业出版社,1995.
|
| [9] |
徐诗婧. 开架式ROV水动力特性与运动仿真研究[D]. 哈尔滨: 哈尔滨工程大学, 2018.
|
| [10] |
张明臣. 载荷布放强扰下UUV自适应控制方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2015.
|
| [11] |
钱缘. 基于T-S模糊模型的UUV鲁棒运动控制[D]. 上海:上海交通大学, 2020.
|
| [12] |
张宇哲. 布放载荷强扰条件下UUV快速镇定控制方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2020.
|
| [13] |
SHEN C, SHI Y, BUCKHAM B. Trajectory tracking control of an autonomous underwater vehicle using Lyapunov-based model predictive control[J]. IEEE Transactions on Industrial Electronics, 2017, 65(7): 5796-5805. |
 2024, Vol. 46
2024, Vol. 46
