0 引　言

对潜搜索是反潜作战的重要组成部分，是海军兵力实施对潜攻击的前提和保证^[1]。传统的对潜搜索兵力主要包括水面舰艇、潜艇和航空兵^[2]。随着无人装备的快速发展，美军将反潜战、情报监视与侦察作为UUV的重要使命任务^[3]，因此UUV已成为重要的无人对潜搜索装备。

在对潜搜索问题中，吴芳等^[4]在研究多机吊放声呐应召搜潜建模中，对目标的运动模型归为三类，分别是已知潜艇初始位置、航向，已知潜艇初始位置、航向未知，已知潜艇所在区域、位置航向未知，潜艇的机动策略是定期在一定范围内随机转向。丛红日等^[5]建立了一种基于蒙特卡洛法的声呐浮标搜索概率通用仿真模型，通过该模可计算各种阵型声呐浮标的搜索概率，但该模型假定敌潜艇定速直航，且在航行过程中航行状态不改变。鞠建波等^[6-7]提出双机使用吊放声呐和声呐浮标的多基地搜潜模式，考虑潜艇初始位置航向和航速散布，计算了不同搜索阵型的对潜发现概率，说明了多基地较单基地探测的优越性，但未考虑潜艇的机动规避；同时还提出了采用拖曳声呐和反潜直升机布放浮标联合的多基地搜潜方式，采用蒙特卡洛法计算了几种浮标阵型下多基地声呐的对潜发现概率，仿真中认为目标初始位置满足正态分布，航速满足瑞利分布，航向为均匀分布。在UUV对潜搜索的研究中，陈盼等^[8-10]给出了UUV搜索静止目标的准最优方法，验证了该方法的搜索效果优于最优搜索效果，实际上，该文中给出了UUV的搜索点，但搜索点之间并不连通，这就意味着UUV在运动向新的搜索点时要浪费航程；同时基于改进粒子群算法采用UUV编队协同最优扩方应召搜索水下匀速直线运动目标，该方法主要是用改进的粒子群算法计算了扩方搜索中的最优转向角；并研究了无人水下航行器编队，根据目标后验概率分布采用贪婪算法应召搜索马尔科夫运动的问题，对搜索区域进行了划分，UUV在接到任务后要赶赴到区域内，目标分布概率最高的点之后再开始进行搜索，这样是否恰当，值得商榷。高永琪等^[11]提出一种利用改进型头脑风暴优化算法优化基于目标存在概率、环境不确定度、协调信息素目标函数的AUV协同搜索静态目标方法。综上可知，在对潜搜索问题中，结合目标运动模型、目标分布概率更新等问题的搜索路径优化有待进一步研究。

本文将搜索区域栅格化，考虑目标在特定任务背景下的运动规律，引入隐马尔科夫模型，同时考虑探测结果对目标分布概率的更新，采用改进的遗传算法对UUV搜索路径进行规划，并进行了仿真验证。

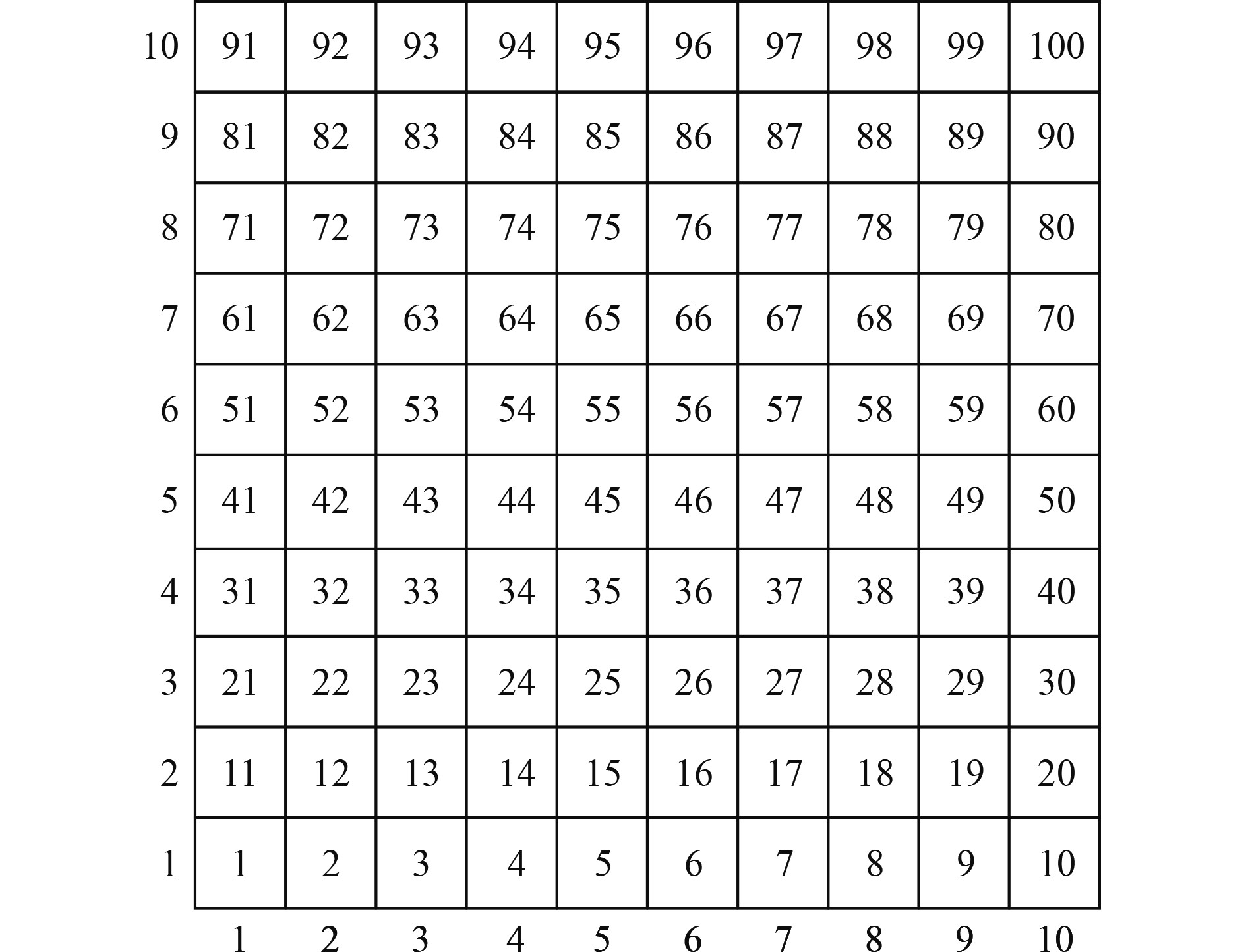
1 搜索区域栅格化模型

路径规划要进行适当的环境建模，本文采用栅格法将UUV的搜索区域分解成若干个规格相同的单元。假设搜潜区域为二维平面内的一矩形区域，将区域的左下角作为坐标原点，以横向为$x$轴，纵向为y轴，建立直角坐标系，搜索区域在$x$ 、$y$方向的最大值分别为${x_{\max }}$和${y_{\max }}$。定义UUV一次有效观察时间为$\Delta T$，对应航行步长为$\delta $，以$\delta $为步长对搜索区域进行划分，则每行对应栅格数为${N_x} ={x_{\max }}/\delta$，每列的栅格数为${N_y} = y_{\max }/\delta$。本文不考虑搜索区域内存在不可到达栅格的情况，因此所有栅格均为自由栅格。如图1所示，以10$ \times $10的栅格搜索空间为例，对每个栅格进行编号，则搜索路径可用一系列的栅格编号来描述。

栅格坐标$({x_p},{y_p})$和栅格序号之间的映射关系可表示为：

$ \left\{ \begin{gathered} {x_p} = \text{mod} ((p - 1),{N_x}) + 1 ，\\ {y_p} = \mathrm {int} ((p - 1)/{N_x}) + 1 。\\ \end{gathered} \right. $

(1)

其中：mod为求余运算；int为舍余取整运算；$p = 1, 2, \cdots ,{N_x}{N_y}$。

潜艇目标和UUV只能向其相邻的上下左右4个栅格运动，将栅格$i$的相邻栅格记为集合${C_i}$。

2 目标运动模型

对运动目标搜索问题建立隐马尔科夫模型，则目标的运动轨迹即为模型的隐状态，用$x(k)$表示$k$时刻的目标位置，则位置集合$\{ x(1),x(2), \cdots x(K)\} $为目标的位置状态序列，其中，$K$表示总的搜潜时间。隐状态集合$ {\boldsymbol{Q}}=1,2,3,\cdots {N}_{x}{N}_{y}$，隐状态个数为${N_x}{N_y}$。UUV可在搜索区域内每个栅格进行观测，观测状态用$o(k)$表示，则$o(k) \in \{ 0,1\} $，UUV的一次观测有2种可能结果，即探测到目标或未探测到目标。

隐马尔科夫模型用$\lambda {\text{ = (}}{\boldsymbol{A}}{\text{,}}{\boldsymbol{B}}{\text{,}}{\boldsymbol{\pi}} {\text{)}}$表示。其中，${\boldsymbol{A}} = \{ {a_{ij}}\} $为隐状态的状态转移矩阵，如下：

$ {a_{ij}} = P(\left. {x(k) = j \in {{\boldsymbol{C}}_i}} \right|x(k - 1) = i) 。$

(2)

式中：$x(k)$为目标在$k$时刻所处的栅格序号；${{\boldsymbol{C}}_i}$为栅格$i$的邻域。

${\boldsymbol{B}} = \{ b_{o(k)i}^p\} $为观测状态生成矩阵，其中，$b_{o(k)i}^p = P(\left. {o(k)} \right|x(k) = i,u(k) = p)$即$b_{o(k)i}^p$为UUV位于栅格$p$，探测位于栅格$i$的目标，探测结果为$ o(k) $。$b_{o(k)i}^p$可表示为：

$ b_{o(k)i}^p=\left\{\begin{gathered}p_{_d},o(k)=1,i\in R_p(k)，\\ 1-p_{_d},o(k)=0,i\in R_p(k) ，\\ p_{_f},o(k)=1,i\notin R_p(k)，\\ 1-p_{_f},o(k)=0,i\notin R_p(k)。\\ \end{gathered}\right. $

(3)

式中：${R_p}(k)$为UUV在栅格$p$时的探测范围；$ p_{_d} $为UUV的探测概率；$ p_{_f} $为虚警概率。

$\pi {\text{ = \{ }}{\pi _i}{\text{\} }}$为目标的初始状态，即目标的初始概率分布，其中，${\pi _i} = P(x(0) = i)$，$i = 1,2, \cdots ,{N_x}{N_y}$。

在隐马尔科夫模型中，目标的运动服从其次马尔科夫假设，目标当前时刻状态至于前一时刻状态有关，与其他时刻的状态和观测无关，因此目标的前验概率分布为:

$ \pi (\left. k \right|k - 1) = \boldsymbol{A}\pi (\left. {k - 1} \right|k - 1)。$

(4)

根据观测独立性假设，即任意时刻的观测只依赖于该时刻的状态与其他时刻的状态和观测无关。采用贝叶斯准则，当UUV在栅格$p$中搜索目标，且探测概率为$ p_{_d} $，虚警概率为${p_{_f}}$，假设UUV一次探测覆盖的栅格数为$M$，目标的后验概率分布为：

${ {\pi }_{i}(k|k)=\left\{\begin{array}{l}\dfrac{(1-{\overline{p}}_{d}{\overline{p}}_{f}^{M-1}){\pi }_{i}(k|k-1)}{{\displaystyle \sum _{\upsilon \in {R}_{p}(k)}(1-{\overline{p}}_{d}{\overline{p}}_{f}^{M-1}){\pi }_{\upsilon }(k|k-1)}+{\displaystyle \sum _{\upsilon \notin {R}_{p}(k)}(1-{\overline{p}}_{f}^{M}){\pi }_{\upsilon }(k|k-1)}},i\in {R}_{p}(k)且o(k)=1，\\ \dfrac{(1-{\overline{p}}_{f}^{M}){\pi }_{i}(k|k-1)}{{\displaystyle \sum _{\upsilon \in {R}_{p}(k)}(1-{\overline{p}}_{d}{\overline{p}}_{f}^{M-1}){\pi }_{\upsilon }(k|k-1)}+{\displaystyle \sum _{\upsilon \notin {R}_{p}(k)}(1-{\overline{p}}_{f}^{M}){\pi }_{\upsilon }(k|k-1)}},i\notin {R}_{p}(k)且o(k)=1，\\ \dfrac{{\overline{p}}_{d}{\overline{p}}_{f}^{M-1}{\pi }_{i}(k|k-1)}{{\displaystyle \sum _{\upsilon \in {R}_{p}(k)}{\overline{p}}_{d}{\overline{p}}_{f}^{M-1}{\pi }_{\upsilon }(k|k-1)}+{\displaystyle \sum _{\upsilon \notin {R}_{p}(k)}{\overline{p}}_{f}^{M}{\pi }_{\upsilon }(k|k-1)}},i\in {R}_{p}(k)且o(k)=0，\\ \dfrac{{\overline{p}}_{f}^{M}{\pi }_{i}(k|k-1)}{{\displaystyle \sum _{\upsilon \in {R}_{p}(k)}{\overline{p}}_{d}{\overline{p}}_{f}^{M-1}{\pi }_{\upsilon }(k|k-1)}+{\displaystyle \sum _{\upsilon \notin {R}_{p}(k)}{\overline{p}}_{f}^{M}{\pi }_{\upsilon }(k|k-1)}},i\notin {R}_{p}(k)且o(k)=0。\end{array}\right.} $

(5)

式中，$ \overline{p}_{_d}=1-p_{_d} $，$ \overline{p}_{_f}=1-p_{_f} $，$ \upsilon \text{=}1,2，\cdots ，{N}_{x}{N}_{y} $。

特别地，当$M = 1$时：

$ { {\pi }_{i}(k|k)=\left\{\begin{array}{l}\dfrac{{p}_{d}{\pi }_{i}(k|k-1)}{{\displaystyle \sum _{\upsilon \in {R}_{p}(k)}{p}_{d}{\pi }_{\upsilon }(k|k-1)}+{\displaystyle \sum _{\upsilon \notin {R}_{p}(k)}{p}_{f}{\pi }_{\upsilon }(k|k-1)}}\text{，}i\in {R}_{p}(k)且o(k)=1，\\ \dfrac{{p}_{f}{\pi }_{i}(k|k-1)}{{\displaystyle \sum _{\upsilon \in {R}_{p}(k)}{p}_{d}{\pi }_{\upsilon }(k|k-1)}+{\displaystyle \sum _{\upsilon \notin {R}_{p}(k)}{p}_{f}{\pi }_{\upsilon }(k|k-1)}},i\notin {R}_{p}(k)且o(k)=1，\\ \dfrac{(1-{p}_{d}){\pi }_{i}(k|k-1)}{{\displaystyle \sum _{\upsilon \in {R}_{p}(k)}(1-{p}_{d}){\pi }_{\upsilon }(k|k-1)}+{\displaystyle \sum _{\upsilon \notin {R}_{p}(k)}(1-{p}_{f}){\pi }_{\upsilon }(k|k-1)}},i\in {R}_{p}(k)且o(k)=0，\\ \dfrac{(1-{p}_{f}){\pi }_{i}(k|k-1)}{{\displaystyle \sum _{\upsilon \in {R}_{p}(k)}(1-{p}_{d}){\pi }_{\upsilon }(k|k-1)}+{\displaystyle \sum _{\upsilon \notin {R}_{p}(k)}(1-{p}_{f}){\pi }_{\upsilon }(k|k-1)}},i\notin {R}_{p}(k)且o(k)=0。\end{array}\right. }$

(6)

3 探测概率模型

搜潜路径规划的根本目的是规划一条能最大可能发现目标的路径。UUV的搜索路径为一系列相邻栅格序列。假定UUV在每个栅格内进行一次有效探测，由于各次探测之间相互独立，K步的累积探测概率为：

$ P = 1 - \prod\limits_{k = 1}^K {\left(1 - \sum\limits_p {\sum\limits_i {{\pi _i}(\left. k \right|k - 1)b_{1i}^p{\psi _i}(k)} } \right)} 。$

(7)

式中：$ {\psi }_{i}(k)\text{=}\left\{\begin{array}{l}1，\text{UUV}在k时刻位于栅格i，\\ 0，\text{UUV}在k时刻不位于栅格i，\end{array}\right. $$i = 1, 2, \cdots ,{N_x}{N_y}$；$i \in {R_p}(k)$，即这里去除了虚警对目标函数的影响，即目标函数仅考虑正确探测到目标的概率；${\pi _i}(\left. k \right|k - 1)$为$k$时刻目标在栅格$i$的先验概率；$b_{1i}^p$为目标位于栅格$i$，UUV位置栅格$p$，观测结果$o(k) = 1$的概率。

这一规划问题可表示为：

$ \mathop {\max }\limits_\psi P (8) {\mathrm{s}}.{\mathrm{t}}. \sum \limits_{i = 1}^{{N_x}{N_y}} {{\psi _i}(k)} = 1 \sum\limits_{i \in A} {{\psi _i}(k)} - \sum \limits_{{C_i} \in A} {{\psi _{{C_i}}}(k + 1)} = 0。$

(8)

式中，$k = 1,2, \cdots K$，$ {\psi _i}(k) \in {\text{\{ 0,1\} }} 。$

4 基于遗传算法的路径规划算法

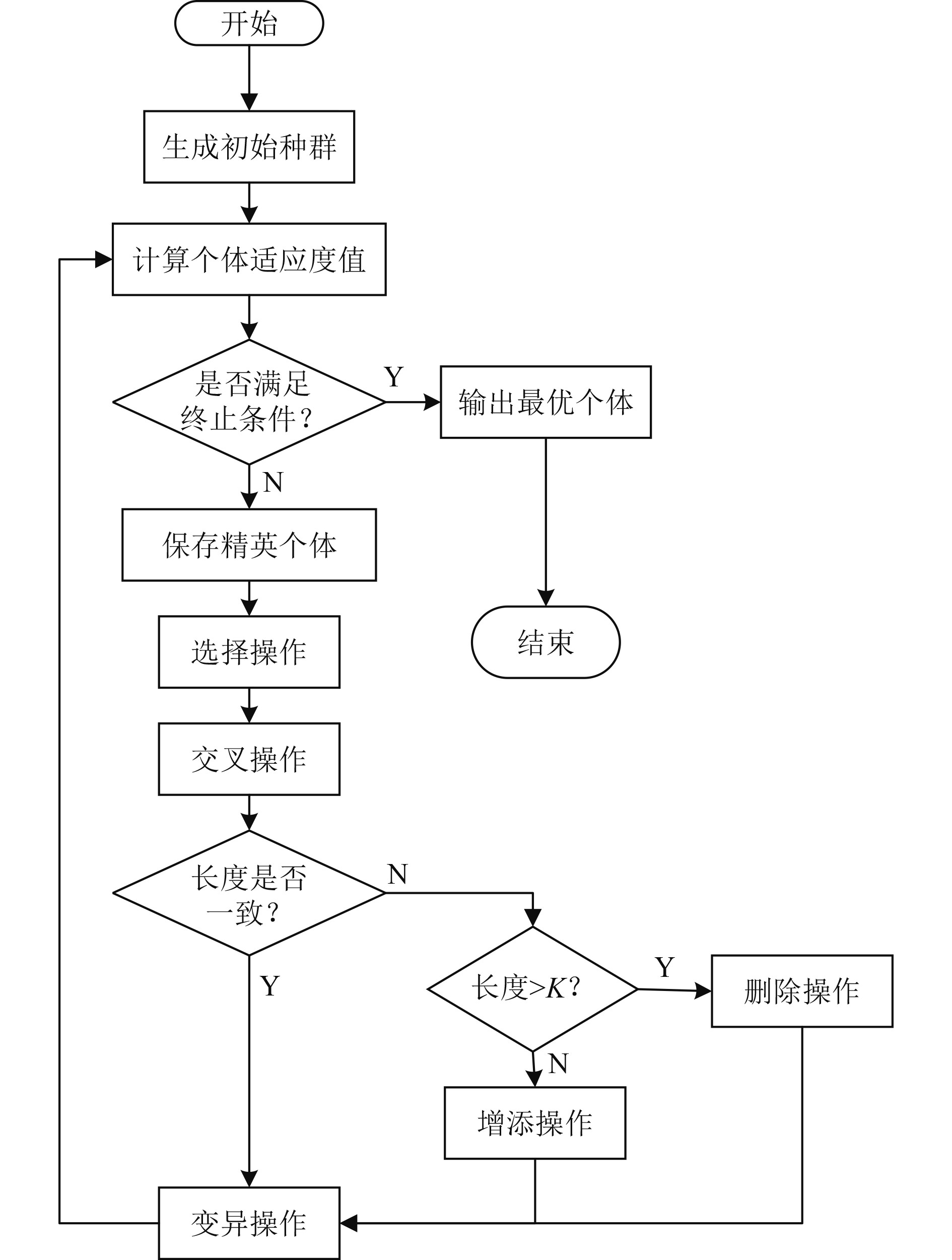
遗传算法共一种通过模拟自然进化过程搜索最优解的方法^[12]。与常规遗传算法不同，为保证搜索路径的连通性，本文在常规遗传算法的基础上加入了删除、增添等操作。同时，由于路径交叉易造成优秀个体丢失，导致算法难以收敛，本文在选择操作中保存精英个体使算法快速收敛。算法具体过程如图2所示。

4.1 染色体编码

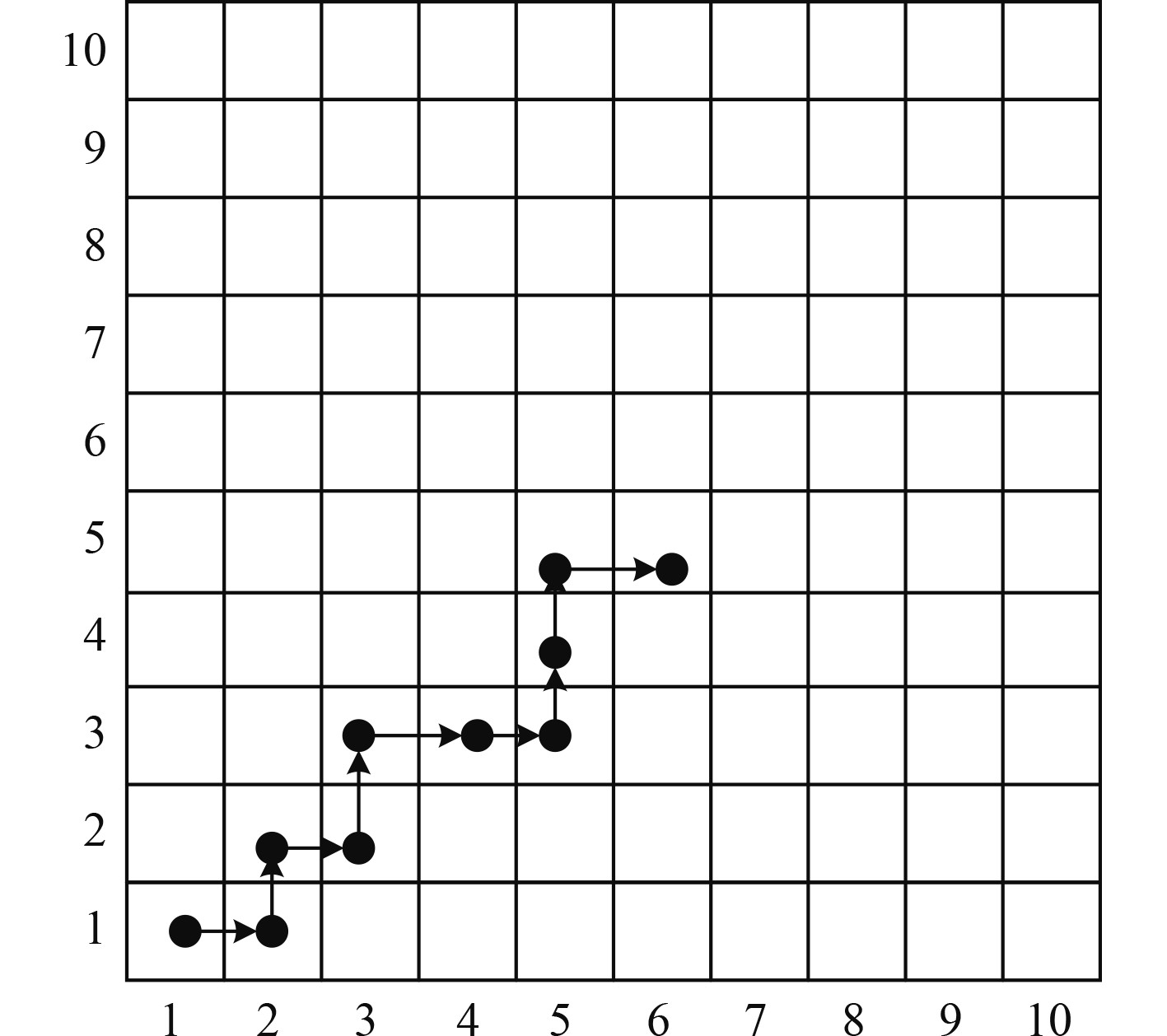
将UUV经过的单个栅格定义为基因，则一条搜索路径构成一条染色体，假定种群中每个个体只包含一条染色体。栅格序号较栅格坐标形式更加简单，采用栅格序号对染色体进行编码。如图3所示，[1, 2, 12, 13, 23, 24, 25, 35, 45, 46]构成一条搜索路径。

4.2 种群初始化

种群初始化生成一系列连通路径，本文采用邻接矩阵，生成随机搜索路径。对于搜索区域为${N_x}{N_y}$的栅格区域，其邻接矩阵可表示为：

$ D(i,j) = \left\{ \begin{gathered} 1,j \in {C_i} ，\\ 0,j \notin {C_i}。\\ \end{gathered} \right. $

(9)

给定搜索路径的起点和搜索步数，可生成随机路径，完成种群初始化。

4.3 改进遗传算子

1）改进选择算子

与传统的避障型最短路径规划不同，以搜索效果为个体适应度值的搜索路径规划，单独采用轮盘赌方法随机性较大，易丢失优秀个体，产生适应度值难以收敛的问题。本文将精英个体进行保留，替代父代种群中适应度值较差的个体，保证适应度值高的个体不会因为选择误差被淘汰，也不会一次交叉变异操作完全丢失。

2）改进交叉算子

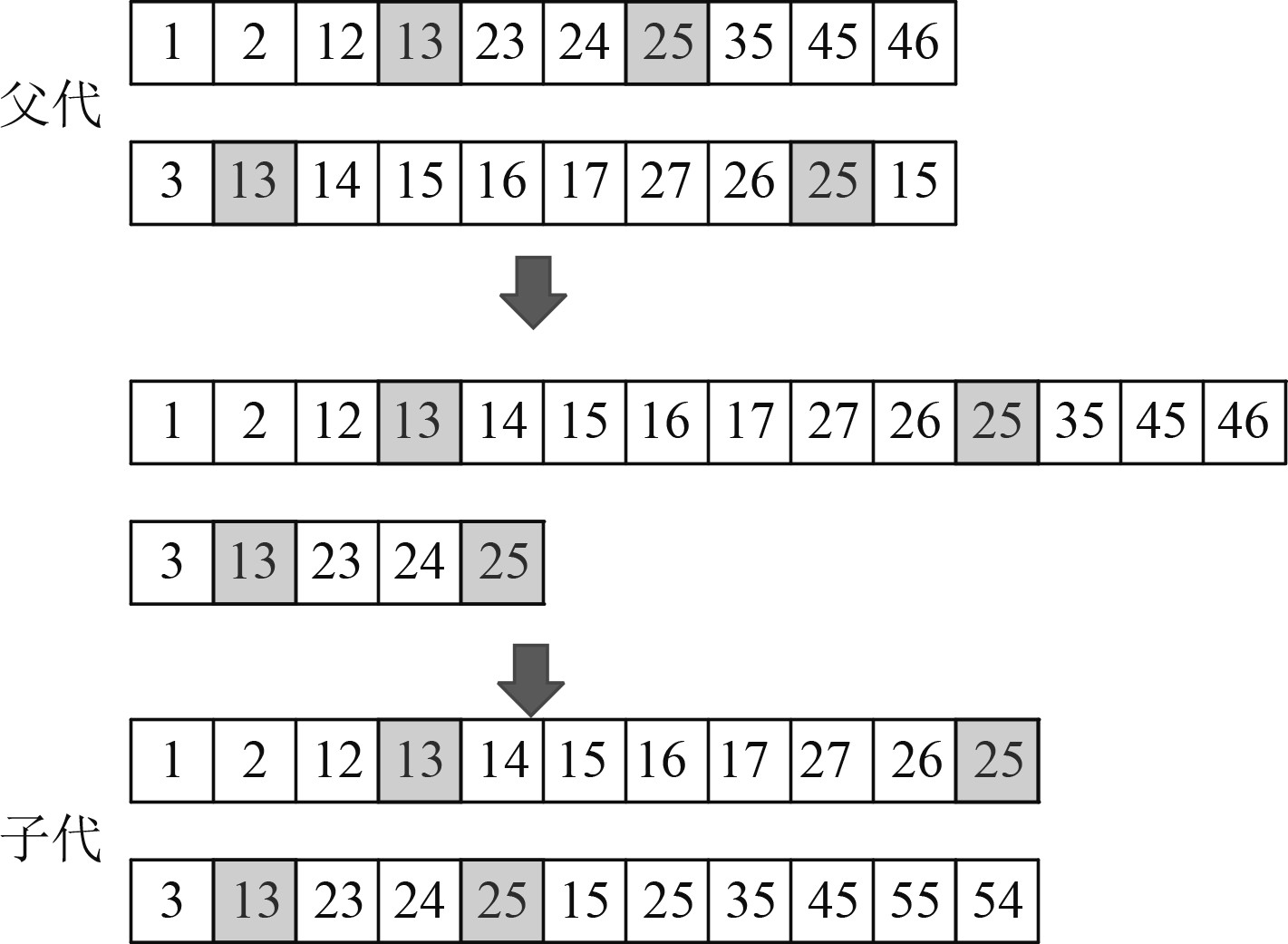
为了保证搜索路径的连通性，不能采用传统的交叉方式。在交叉时，双亲的某些对应基因位点必须有相同值，此时，2条染色体对应的基因片段才能进行交叉。交叉后，为了保证子代与父代染色体长度相同，需进行删除和增添操作，如图4所示。

3）改进变异算子

常规的变异方法是随机选择一个路径点替代原路径点，容易破坏路径的连通性。随机选定一基因进行变异操作，包括删除和移动。删除和移动操作同样可能导致搜索路径的连通性被破坏，需进行增添操作，增添后还需通过删除操作，使子代的染色体长度与父代保持一致。

5 仿真实验 5.1 已知目标初始位置的路径规划

假设搜索平台只能在其上、下、左、右4个相邻栅格内移动，考虑一种较为简单的情形，即搜索只能探测到处于当前栅格内的目标，即${R_p}(k) = p$。设定总的搜索时间$K = 10$，每个时间间隔被定义为搜索平台从一个栅格移动到相邻栅格的时间，搜索区域为3 km$ \times $3 km的方形区域，将该区域划分为9个栅格，即UUV的探测范围为1 km$ \times $1 km的方形区域。

假定潜艇目标留在原地的概率是0.4，向其他相邻栅格转移的概率之和是0.6，且向每个栅格转移的概率相同。初始时刻目标位于栅格9。

假设遗传算法的种群大小为20，迭代次数为100，交叉概率为0.8，变异概率为0.2。

在设定条件相同时，表1列出了本文的计算结果和文献[13]的计算结果，二者计算结果完全一致，验证了本文算法的正确性。

5.2 已知目标位置分布概率的路径规划

实际中，通常只知道目标的散布，而难以准确掌握目标的位置。假设目标在区域内均匀分布，为10×10栅格，搜索可以覆盖9个栅格，探测概率0.9，虚警概率为0。遗传算法的种群个体数为80，迭代次数为1000，交叉概率为0.8，变异概率为0.2。目标停留在原栅格的概率设置为0.1，向相邻栅格运动的概率相同。

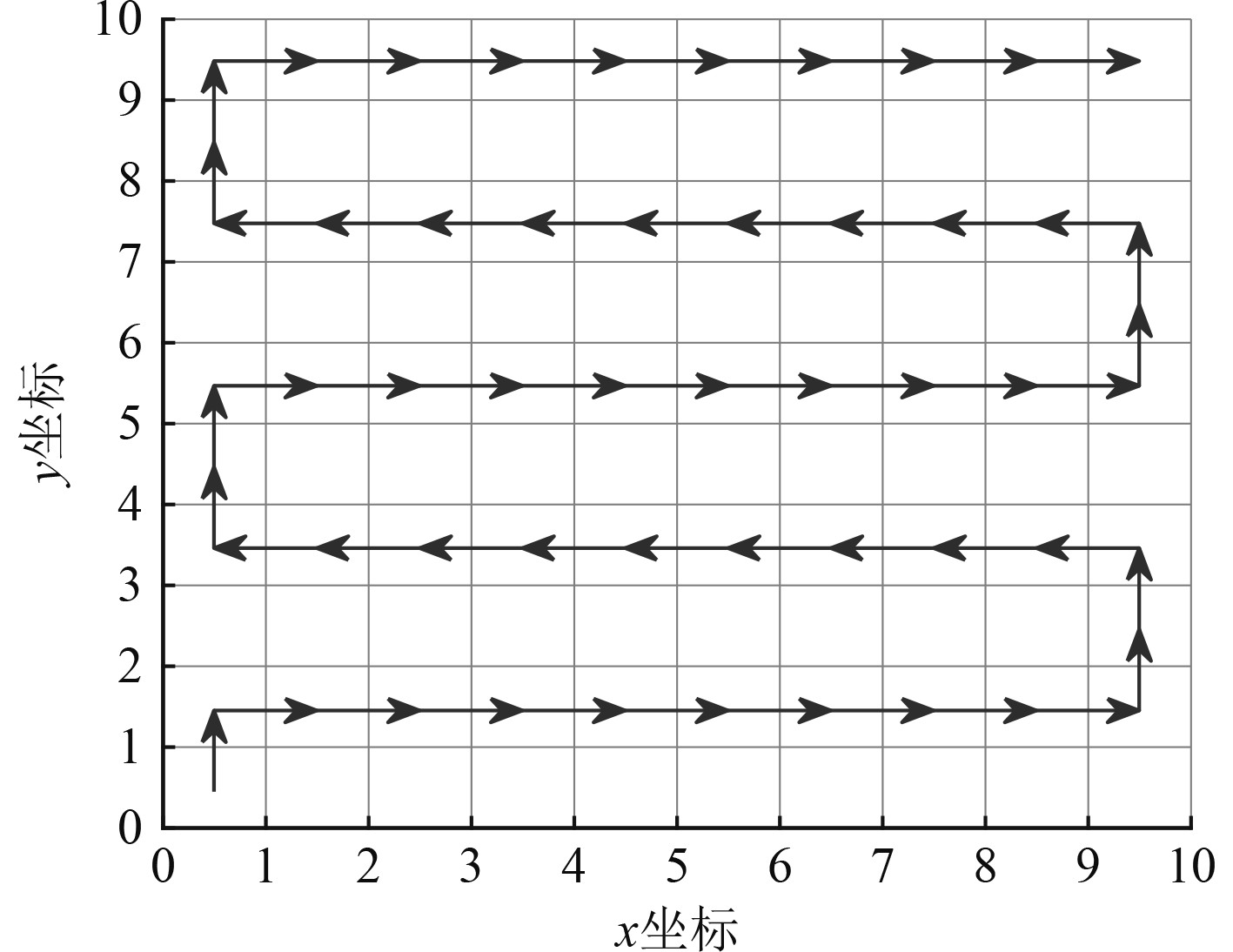
设置搜索步数设置为5、10、20、30时，分别采用本文优化算法、矩形搜索、随机搜索3种方法计算搜潜期望。假设UUV初始时刻位于栅格1。其中，矩形搜索^[14]是一种常见的搜潜方式，本文中矩形搜索的路径宽度为2个栅格宽度，搜索路径长度为9个栅格宽度，矩形搜索路径如图5所示。

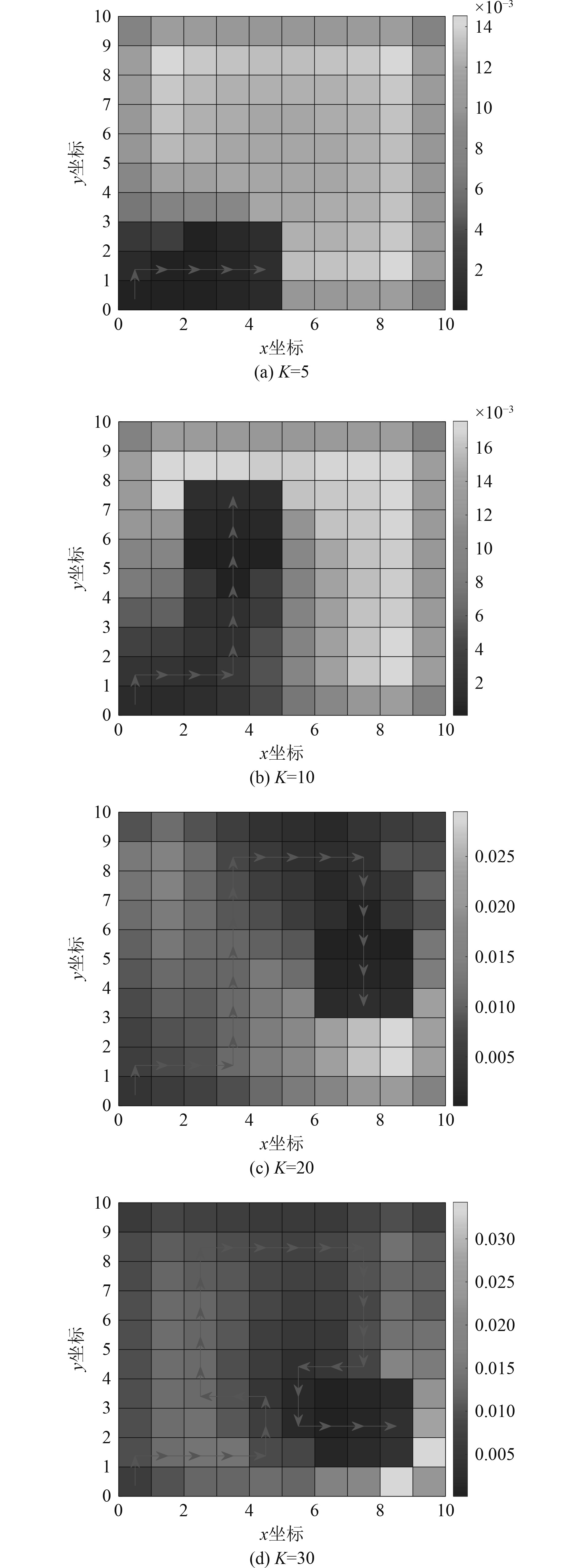
由图6可知，在目标初始分布为均匀分布的情况下，UUV搜索路径较为平直。随着搜索步数的增加，搜索逐渐呈合围趋势。

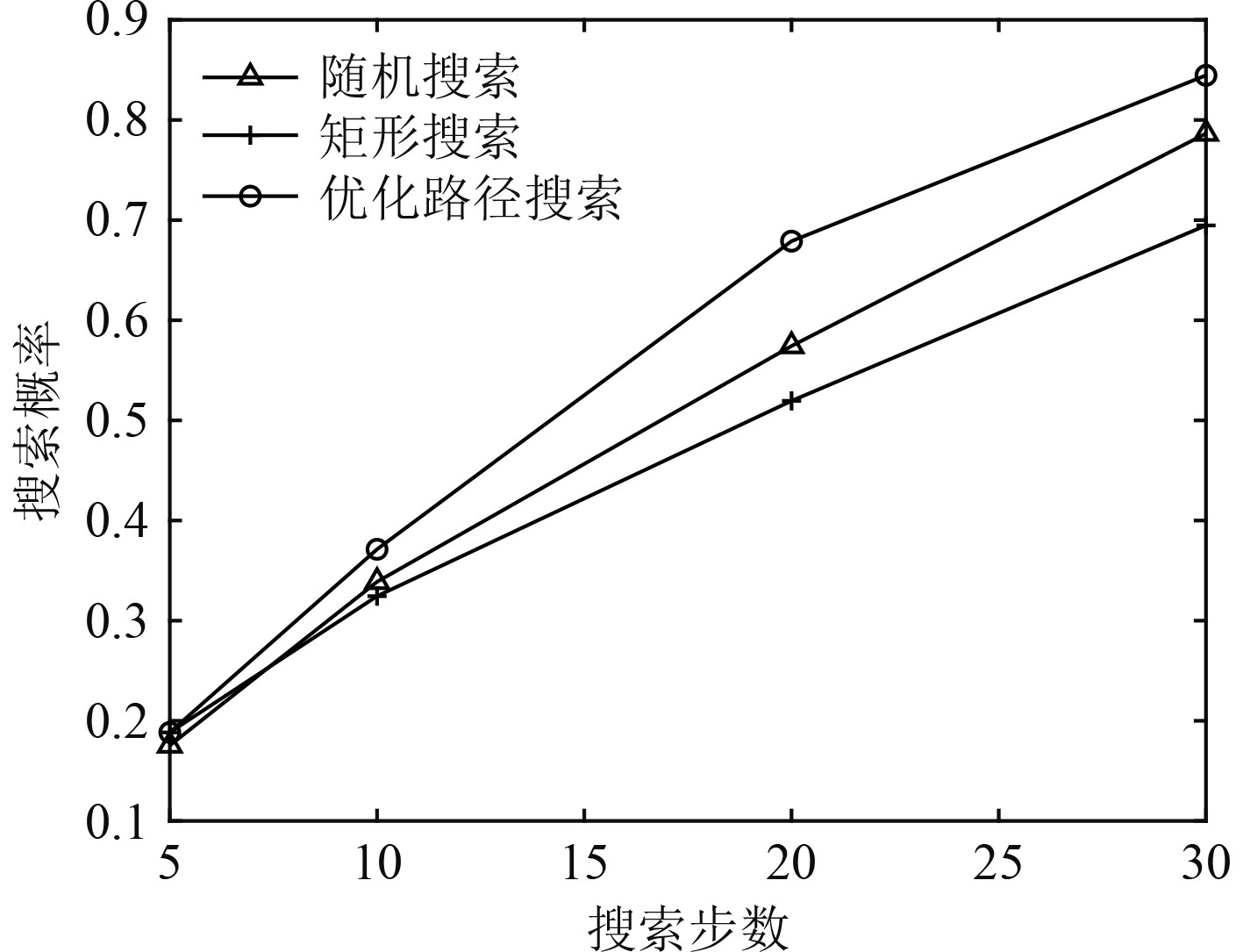
由图7可见优化后的搜索路径对潜发现概率均高于矩形搜索和随机搜索，而且随着搜索步数的增加，优势更加明显，证明了该算法的有效性。

6 结　语

本文基于隐马尔科夫模型建立了目标运动模型，以探测概率最大为目标函数，采用改进遗传算法，对UUV搜潜路径进行规划。在仿真实验中，通过与矩形搜索、随机搜索2种常用搜索方法进行对比，说明了该方法的有效性。下一步，将基于该算法将进行多平台搜潜研究。