2. 中国船舶工业贸易有限公司,北京 100037
2. China Shipbuilding Trading Co. , Ltd. , Beijing 100037, China
近年来,世界各国都在加大对海洋资源投入和利用的力度,各种无人化海军装备正逐步显示其影响力和展现出改变未来作战方式的巨大潜力[1]。水面无人艇(Unmanned Surface Vehicle,USV)作为监测海洋环境、维护海洋权益的现代化智能运载平台,能够在复杂海洋环境中航行并完成各种任务,已成为国内外智能化海洋装备的研究热点[2]。
水面无人艇的路径规划是保障船舶安全航行和执行任务的前提。路径规划的核心是路径规划算法[3]。Fox等[4]将路径规划分为全局路径规划和局部路径规划。Sedighi等[5]将混合A*算法与可见图算法相结合,在混合A*算法中引入改进的代价函数,改进后的算法计算速度比混合A*算法提高了40%。Kozynchenko等[6]针对动态障碍物状态的不确定性,将人工智能算法应用于无人艇的路径规划问题,实现了对无人艇的实时路径优化。Kumar等[7]提出一种混合优化算法—谷鸟搜索优化算法(WCSOA),增大了搜索空间,提高了全局搜索能力并加快了收敛速度,该方法降低了总搜索时间和能量消耗。Tsou等[8]基于海面环境信息与COLREGS规则,利用蚁群算法进行了船舶动态避障与路径选择,同时考虑了对态目标和静态目标的避碰。Yu等[9]为了解决复杂环境下无人巡航船的水质采样问题,提出了一种基于A*算法和改进APF方法的混合路径规划算法。
现有的路径规划算法,主要考虑全局路径规划,多为无人艇的静态运动路径,规划得到的路径为折线,未考虑无人艇航行过程中自身的操纵特性,如回转半径、应舵时间等。当无人艇在开阔水域航行时,在路径规划中通过对障碍物留有足够的余量以保障航行的安全性。当无人艇在狭窄航道航行时,则会出现两类问题:一是余量的设置问题,如果余量太大则会导致找不到可行解,余量太小则会因为实际轨迹与规划轨迹不完全一致增加碰撞风险,无法保障航行时的安全性;二是在无人艇因避障等原因偏离航线返回路线过程中,通常需要将路径中某点作为目标点并重新规划路径,此时无人艇到达目标点时的航向应当与路径中对应点处的航向一致,以避免到达目标点进行多余的转舵操作。故将类似于上述两类问题定义为局部路径规划问题。本文以无人艇路径局部规划为研究目标,提出一种考虑运动特性的水面无人艇局部路径规划方法,该方法从无人艇的运动特性出发,根据无人艇的运动模型事先仿真无人艇的操纵运动,尽可能地减少打舵次数,不仅考虑规划的局部路径距离最短,还能够保障无人艇按照指定的航向到达目的点。该方法的输出结果是舵角与时间的拟合,最终从无人艇实际的仿真运动轨迹中选出最佳规划方案。
1 无人艇响应型数学模型船舶运动数学模型是船舶运动仿真与控制问题的核心[10]。其中,响应型模型是目前船舶运动控制领域应用最广泛的数学模型。本文采用二阶非线性响应模型[11],如下式:
| $ T_1T_2\ddot{r}+(T_1+T_2)\dot{r}+r+\alpha r^3=K(\delta_r+\delta)+KT_3\dot{\delta}。$ | (1) |
式中:
考虑到船舶操舵的延时特性,舵机伺服模型的特性方程为[12]:
| $ \dot{\delta}\text{ = }-\frac{1}{T_r}\delta+\frac{1}{T_r}\delta_E。$ | (2) |
式中:
在已知无人艇的出发点、目的点、初始航向和到达目的点的航向约束情况下,考虑无人艇的运动特性,基于无人艇的二阶非线性响应模型事先仿真无人艇的运动轨迹,尽可能地减少打舵次数,如何确定打舵、回正舵时间以及选取打舵舵角成为了解决这一问题的关键。考虑到无人艇的实际操纵情况,本文选取典型的舵角进行研究,选取的舵角为:−30°、−25°、−20°、−15°…15°、20°、25°、30°。
假设第1次打舵都是从出发点开始,在1次打舵和1次回正舵不能同时满足到目的点的距离精度和航向精度要求的情况时,均默认是2次打舵和1次回正舵,即从出发点开始第1次打舵,然后在t1时刻第2次打舵,在t2时刻回正舵,然后正舵航行到目的点。
为了便于研究,首先确定某一航向且经过目的点的目标参考直线,通过对无人艇运动仿真试验的分析和总结,不断的改变t1和t2值,进而得出结论,即在图1情况下寻找满足要求的方案。
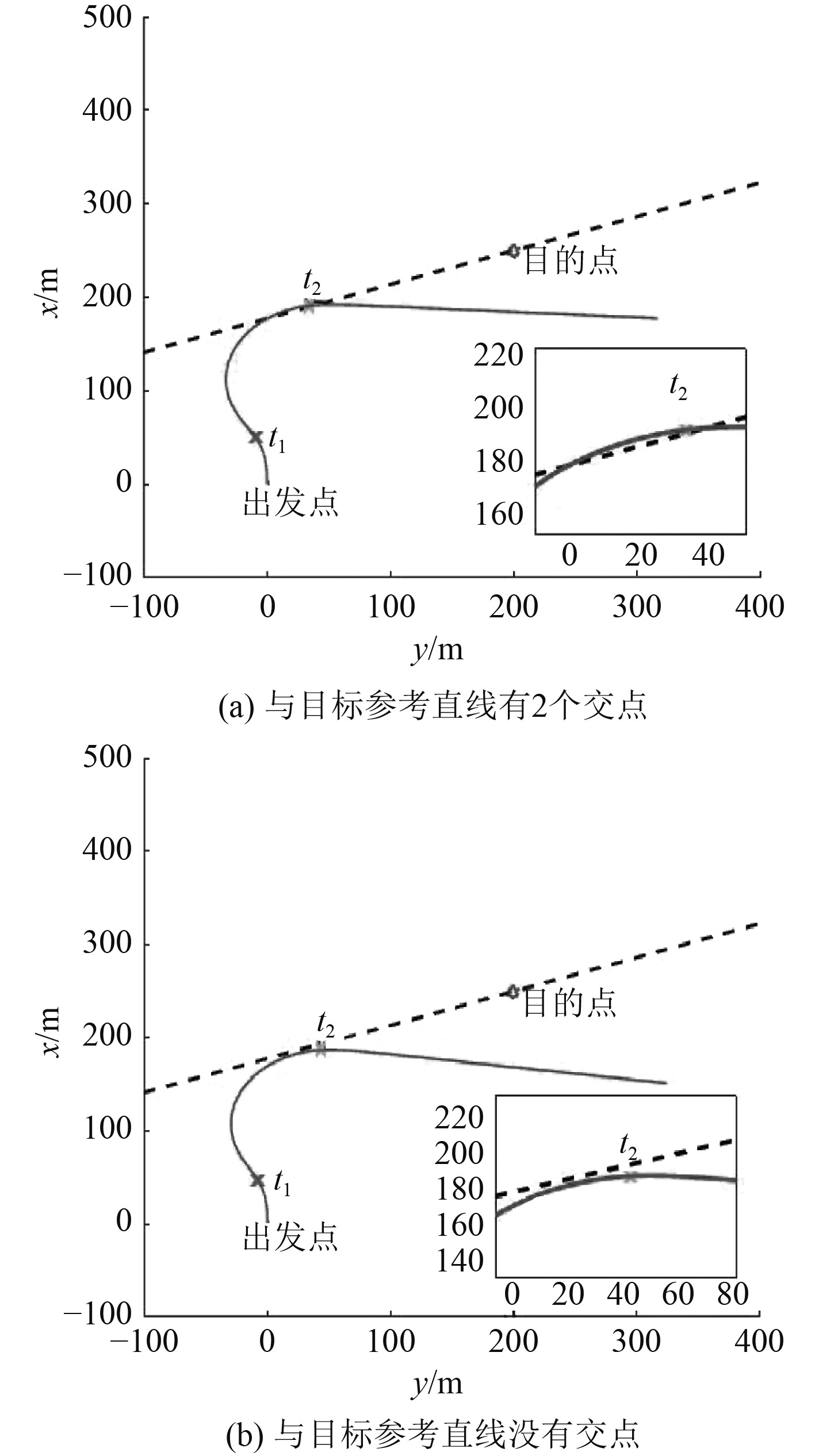
|
图 1 可能满足方案要求的运动情形 Fig. 1 Motion situation that may meet the requirements of the scheme |
通过不断改变t1和t2的值,寻找能够同时满足距离和航向要求的最优路径,常用的方法有二分法(Bisection method)[13]、牛顿迭代法(Newton’s method)[14]等。其中二分法适用于数据量较大且需要对处理的时间复杂度进行优化的情况,是一种较为高效的搜索算法,因而本文采用二分法。由于方案的不唯一性,本文按照图1(a)中的情形展开搜索。具体原理流程如图2所示。
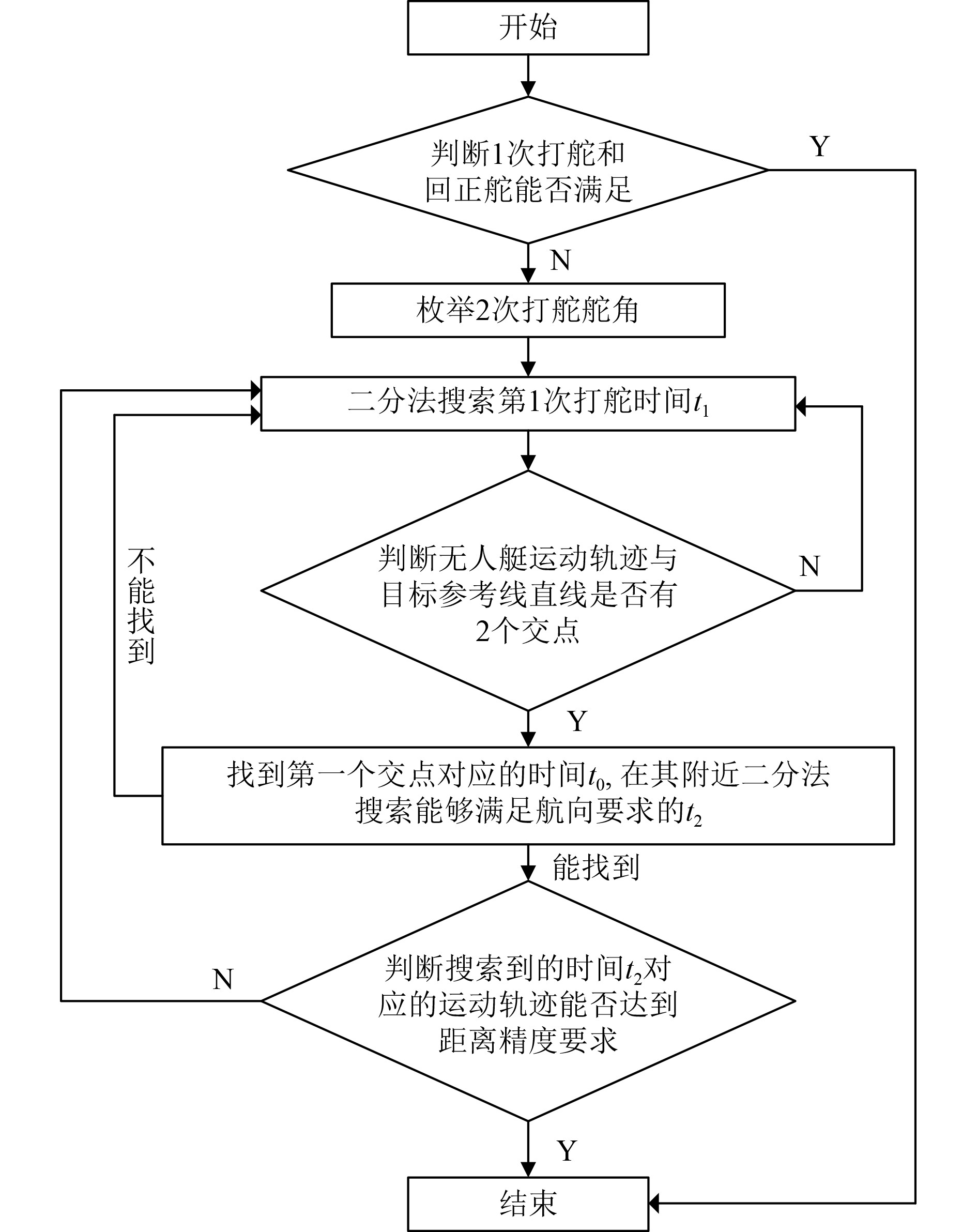
|
图 2 融合算法原理流程 Fig. 2 Fusion algorithm principle flow |
具体实现流程如下:
步骤1 采用枚举法从典型舵角中选取2次打舵舵角,根据无人艇的初始航向和目标航向的关系,初步判断,减小搜索范围。
步骤2 在确定2次打舵舵角后,t1选取一个较小的值t1L,为t1搜索区间的下限,t2选取一个较大的值,使其满足无人艇的运动轨迹与目标参考直线没有交点;然后t1再选取一个较大的值t1D,t2选取与上一步相同的值,使其满足无人艇的运动轨迹与目标参考直线有一个交点。
步骤3 取t1L和t1D的中间时间t1中,t2取值与步骤2相同,再仿真无人艇的运动,判断无人艇的运动轨迹与目标参考直线是否有2个交点;若有2个交点,则执行步骤4;若无交点,则取t1中和t1D这个时间半区,返回继续执行步骤3;若有一个交点,则取t1L和t1中时间半区,返回继续执行步骤3。
步骤4 计算出无人艇运动轨迹与目标参考直线2个交点中的第1个交点坐标和时间t0,根据无人艇的运动特性,在取该t1值情况下,假如存在同时满足到目的点的距离和航向要求的路径,那么t2的取值必定在t0附近,采用二分法对确切的t2值展开搜索,搜索区间的下限和上限分别为t0-N和t0+N,N的取值不宜过大。将t2分别取t0-N和t0+N,比较2种情况下无人艇正舵航向时的轨迹,若均分布在目标参考直线的一侧,则直接返回步骤3,继续搜索t1值;若分步在目标参考直线的两侧,以回正舵稳定航行后的航向与目标航向是否相同为参照,采用二分法不断搜索到确切的t2值,然后再判断无人艇的运动是否满足距离要求。若同时满足要求,则搜索结束,输出t1和t2以及到达目的点的时间和航向;若不能同时满足要求,返回步骤3继续搜索t1值。
2.2 几何数学模型分析2.1节中并未给出t1搜索区间的具体范围,如果搜索范围过大,一方面会增加计算量,另一方面搜索具有一定的盲目性。为了解决这一问题,在上述研究的基础上,对无人艇运动轨迹的几何分析。
图3为无人艇运动轨迹几何分析。为了求解t1、t2和t3,需对无人艇的运动作出如下假设:1)将无人艇在打舵期间的运动轨迹看成圆周运动;2)t1时刻进行第2次打舵,无人艇能够迅速响应,t1~t2期间的运动轨迹同样看成圆弧;3)t2时刻回正舵能够迅速响应,将t2~t3期间的运动看成直线。在这种理想情况下求解出的t1和t2存在一定的误差,但这将为2.1中t1的选取提供重要参考,极大减小了对t1的搜索范围,提高了计算效率和降低了搜索的盲目性。
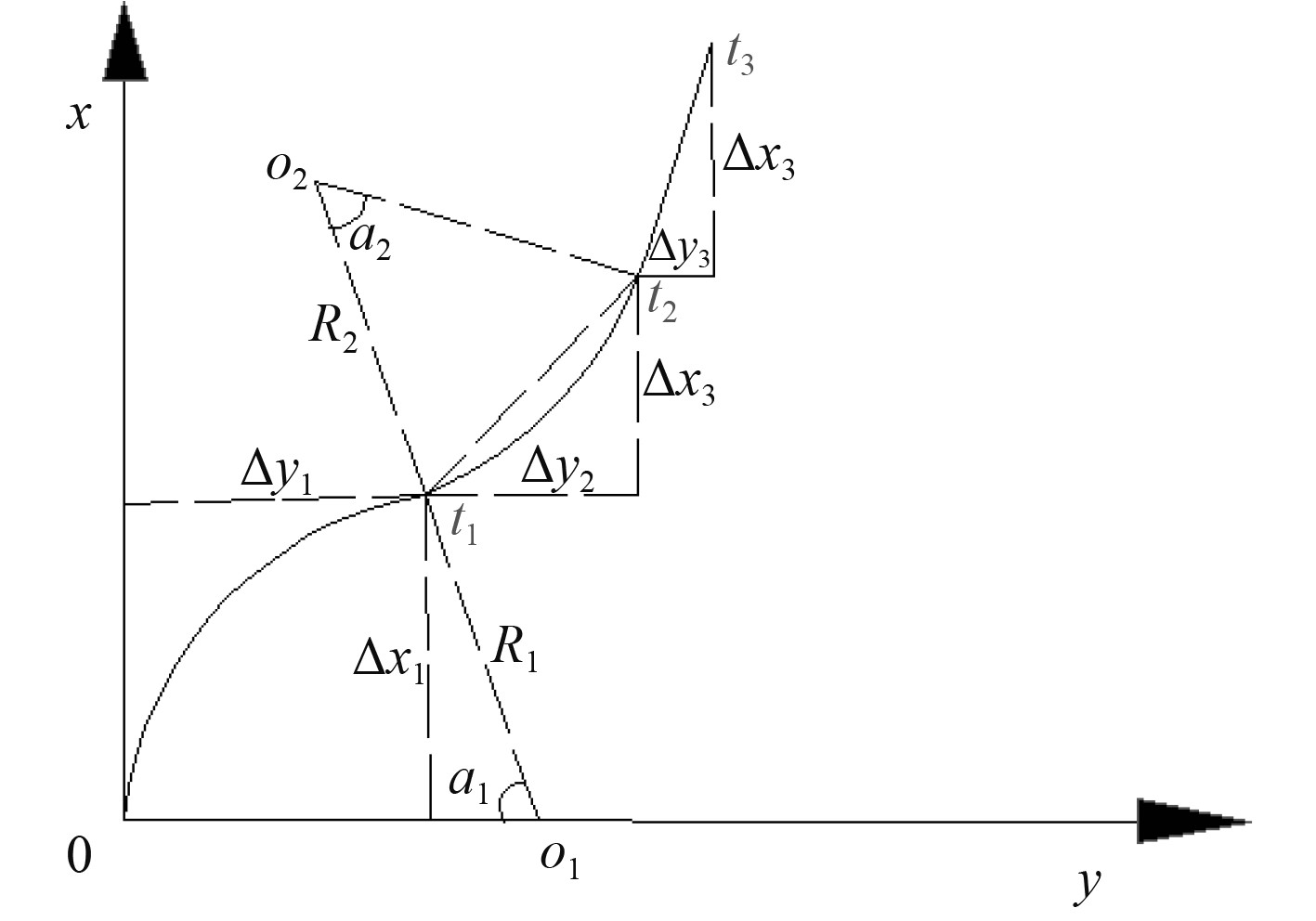
|
图 3 无人艇运动轨迹几何分析 Fig. 3 Geometric analysis of unmanned boat trajectory |
基于无人艇的二阶非线性响应模型和舵机伺服模型,运用工程上广泛采用的四阶龙格库塔法预报无人艇的操纵运动,初始化模型中各个参数,如表1所示。同时,设定航速为10 kn,无人艇的初始航向和首向角均为0°,设定到达目的点的航向要求为70°。判断是否到达目的点的距离精度大小为0.5 m,航向精度大小为0.3°。通过上述设定,得到部分局部路径规划结果如图4所示。表2为规划方案的具体结果。
|
|
表 1 参数初始化 Tab.1 Initialization of Parameters |
|
|
表 2 局部路径规划的具体方案 Tab.2 Specific scheme of local path planning |
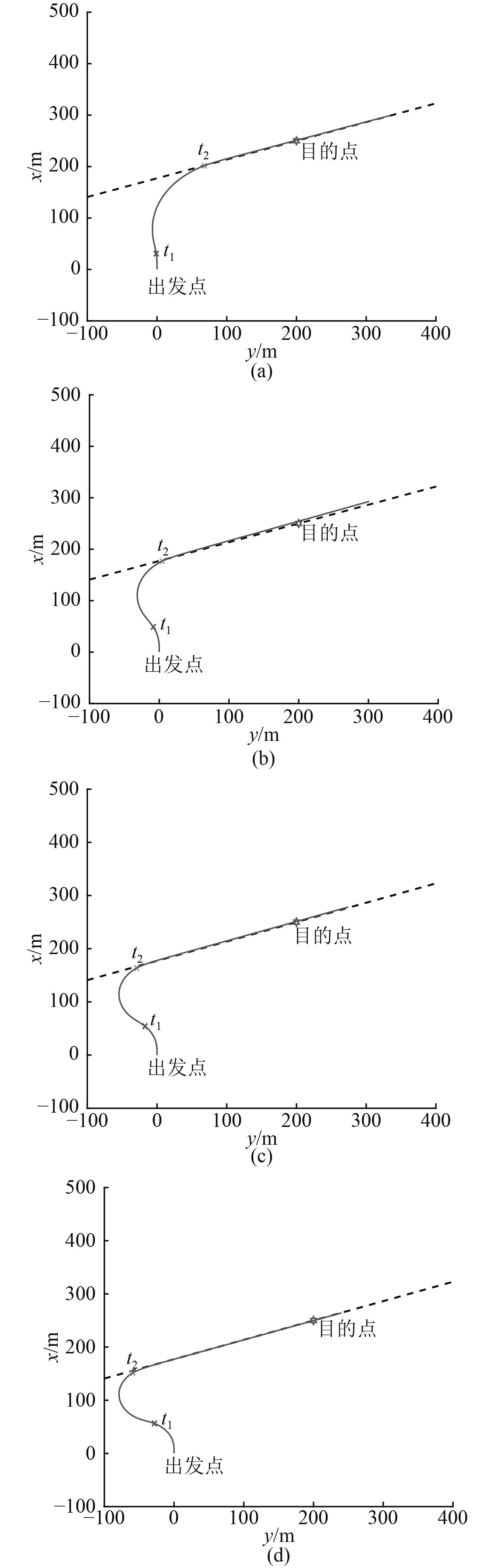
|
图 4 局部路径规划的轨迹显示 Fig. 4 Trajectory display of local path planning |
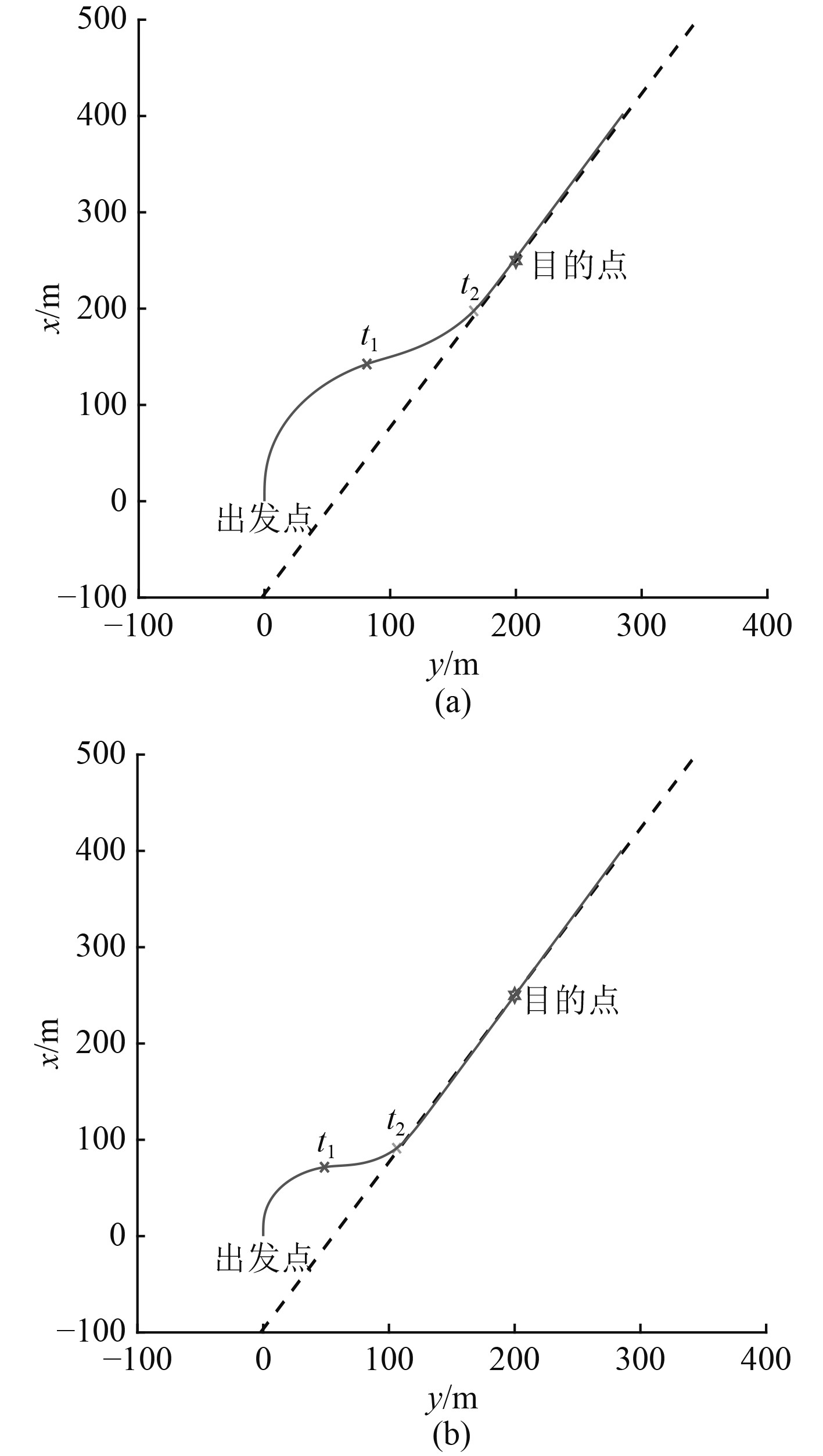
在上述实例中,将到达目的点的航向要求改为30°,其他条件不变,得到的部分规划方案如图5所示。
|
图 5 局部路径规划的轨迹显示 Fig. 5 Local path planning trajectory display |
通过2个具体实例仿真了无人艇在无障碍物环境下的局部路径规划,综合运用融合算法和几何数学模型分析,并考虑了无人艇的实际运动特性,在打舵次数尽可能少的情况下,可以得到多种能够使无人艇既能满足距离精度要求也能满足航向精度要求的局部路径规划方案,证明了该方法的可靠性和有效性。
3 结 语现有的路径规划算法只考虑了障碍物和航程大小等因素,并未考虑无人艇实际的运动特性,不符合无人艇实际航行的需要。因此,本文基于无人艇的运动数学模型,考虑无人艇的运动特性,枚举典型打舵舵角并结合二分法搜索打舵和回正舵时间,事先仿真得到无人艇的运动轨迹,尽可能地减少打舵次数,不仅能够使无人艇到达目的点,而且按照指定的航向约束到达。此外,该局部路径规划方案的输出结果是舵角与时间的拟合关系,这为之后的路径跟踪也带来了极大的便利,具有重要的工程应用价值。文中船舶运动模型采用二阶非线性响应模型,实际上文中的方法也适用于其他运动模型。当模型参数变化或者运动模型改变时,无人艇的运动轨迹会有所不同,但是采用文中方法总能找到准确的控制参数。
| [1] |
陈映彬. 无人艇发展现状及其关键技术综述[J]. 科学技术创新, 2019(2): 60−61. CHEN Ying-bin. Overview of development status and key technologies of unmanned boats[J]. Scientific and Technological Innovation, 2019(2): 60−61. |
| [2] |
杨鑫. 无人艇操纵运动模型参数辨识研究[D]. 武汉:武汉理工大学, 2019.
|
| [3] |
玄世龙, 许志远, 孙帅, 等.基于禁忌搜索算法的无人艇路径规划研究[J]. 船舶工程: 1−8. [2022-05-24]. XUAN Shi-Long, XU Zhi-Yuan, SUN Shuai, et al. Path planning of unmanned ship based on tabu search algorithm[J]. Ship Engineering: 1−8[2022-05-24]. |
| [4] |
FOX D, BURGARD W, THRUN S. The dynamic window approach to collision avoidance[J]. IEEE Robotics &Automation Magazine. 1997, 4(1): 23−33.
|
| [5] |
SEDIGHI S, NGUYEN D V, KUHNERT K D. Guided hybrid A-star path planning algorithm for valet parking applications[C]//2019 5th international conference on control, automation and robotics (ICCAR). IEEE, 2019: 570−575.
|
| [6] |
KOZYNCHENKOA I. A, KOZYNCHENKOA AS. Applying the dynamic predictive guidance to ship collision avoidance: Crossing case study simulation[J]. Ocean Engineering, 2018, 164: 640-649. DOI:10.1016/j.oceaneng.2018.07.012 |
| [7] |
KUMAR S V, JAYAPARVATHY R, PRIYANKA B N. Efficient path planning of AUVs for container ship oil spill detection in coastal areas[J]. Ocean Engineering, 2020, 217: 107932. DOI:10.1016/j.oceaneng.2020.107932 |
| [8] |
TSOU M C. Multi-target collision avoidance route planning under an ECDIS framework[J]. Ocean Engineering, 2016, 121(15): 268-278. |
| [9] |
YU Jiabin, DENG Wei, ZHAO Zhiyao, et, al. A hybrid path planning method for an unmanned cruise ship in water quality sampling[J]. IEEE ACESS, 2019, 2925894.
|
| [10] |
张国庆. 超恶劣海况下船舶运动简捷鲁棒自适应控制[D]. 大连: 大连海事大学, 2015.
|
| [11] |
XIE Shuo, CHU Xiumin, LIU Chenguang, et, al. Parameter identification of ship motion model based on multi-innovation methods[J]. Journal of Marine Science and Technology, 2020(25): 162-184.
|
| [12] |
张显库, 金一丞. 控制系统建模与数字仿真[M]. 大连: 大连海事大学出版社. 2013.
|
| [13] |
ELGHANDOUR AESHA N, SALAH AHMED M, ELMASRY YASSER A, et al. An image encryption algorithm based on bisection method and one-dimensional piecewise chaotic map[J]. IEEE ACESS,2021(9): 43411−43421.
|
| [14] |
ONANAYE, ADENIYI SAMSON. Nonlinear programming: theories and algorithms of some unconstrained optimization methods(Steepest descent and Newton’s method)[J]. International Journal of Engineering and Management Research. 2020(10): 1−12.
|
 2024, Vol. 46
2024, Vol. 46
