0 引　言

随着无人艇（Unmanned Surface Vehicle, USV）单艇自主化程度的提高，越来越多研究人员参与USV集群作业任务的研究，如集群破障、协同反潜、反水雷等^[1-4]。在集群作业过程中，群体成员之间会遇到避碰问题，群体成员和外部动、静目标也存在碰撞风险，因此研究集群避障问题十分重要。全局规划和局部规划是USV导航和路径规划系统中非常重要的2个部分，两者在避碰行为中都发挥重要的作用。全局规划算法侧重在已知环境中进行全局最优无碰路径的搜索，如A*、RRT (Rapidly-exploring Random Tree)算法^[5]等，局部规划算法更适合对近距离运动目标的避障，如APF (Artificial Potential Field)、VO (Velocity Obstacle)、DWA (Dynamic Window Algorithm)、DDPG (Deep Deterministic Policy Gradient)等^{[6 − 7]}。

USV实艇应用中通常将全局规划和局部规划结合，根据高精度的电子海图、河道地图进行全局规划，得到无碰路径。局部规划算法基于障碍物位置等信息进行反应式避障^[8]。一些局部规划算法将障碍物当作绝对静止或是定常运动的动态目标，通过实时重规划应对环境的动态变化，这种处理方式对于速度远低于本船或完全静止的稀疏障碍很有效^[9]。但在出现速度接近或超过本船的运动目标时，这种避障方式往往因为缺乏对速度信息的引入，导致USV避障行为滞后，USV避障方向和障碍目标运动方向接近，发生平行运动或碰撞问题^[10]。VO算法是局部规划中的一种避障算法，综合考虑了障碍速度和位置，并衍生了RVO (Reciprocal Velocity Obstacles)^[11]、HRVO (Hybrid Reciprocal Velocity Obstacle)^[12]、GVO (Generalized reciprocal collision avoidance)^[13]等算法，这些算法在无人车和无人机领域有较多应用。VO算法由于同时考虑了障碍位置、速度、会遇位置等信息，对动态目标避障场景具有较好的鲁棒性和实时性。

本文提出一种针对无人艇集群海上避碰场景的局部规划算法。该算法在VO算法基础上进行优化，引入了COLREGs (International Regulations for Preventing Collisions at Sea)定义无人艇避障方向，后文将用CVO (COLREGs based Velocity Obstacle)命名该算法。CVO考虑了时间窗口中可能发生碰撞的所有水面目标，通过排除二维平面上可能的会遇区域，得到安全的可行区域。考虑到有人和无人艇混合航行的场景，使用COLREGs来限定会遇时本船的避障方向，进一步约束可行区域。最后在所有可行区域的交集上进行寻优，得出合理的期望航向及速度。为了验证算法效果，本文进行了仿真，数十个USV被分为多组，在场景中互相避障。仿真结果验证了算法的可靠性。

1 无人艇集群避障问题

在无人艇集群航行场景下，无人艇不仅要注意避让本队中的其他无人艇，还要避开地形障碍、漂浮障碍以及其他船舶。其中地形障碍可视为静态障碍，漂浮障碍、船舶可视为动态障碍，单个无人艇通过在障碍区域内实时寻找最优可行速度，便能引导自身脱离障碍区域或避免发生碰撞。

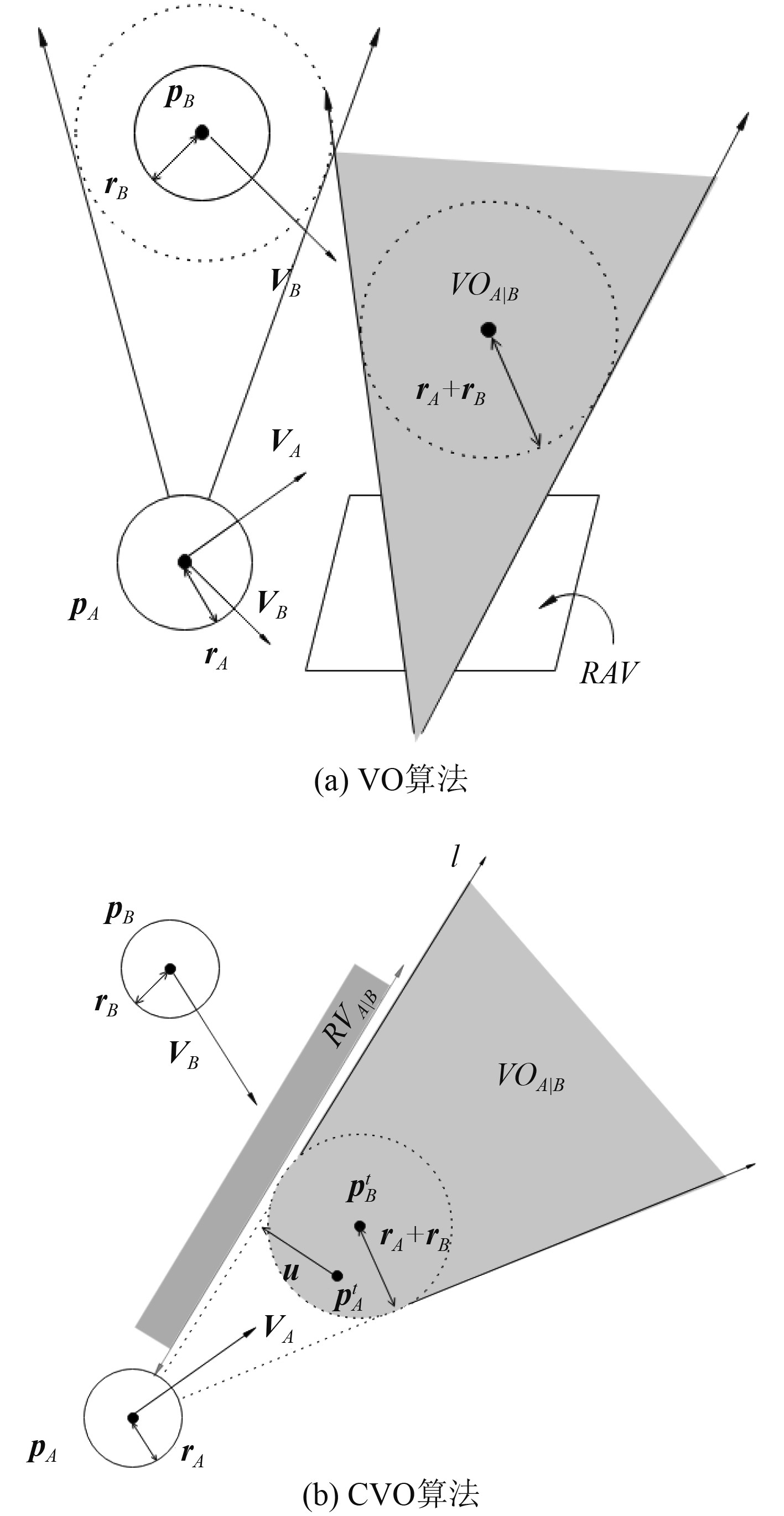
1.1 VO算法

图1为VO算法和CVO算法的图形化描述。

图1(a)中，定义圆$D({\boldsymbol{p}},r)$，${\boldsymbol{p}}$为圆心，$r$是安全半径。如果动态障碍物中心进入安全半径，则认为发生碰撞。无人艇A为圆$D({{\boldsymbol{p}}_A},{r_A})$，动态障碍物为$ D({{\boldsymbol{p}}_B},{r_B}) $。定义$\lambda ({\boldsymbol{p}},{\boldsymbol{v}}) = \{ {\boldsymbol{p}} + t{\boldsymbol{v}}|t > 0\} $，${\boldsymbol{v}}$为速度矢量。当无人艇A以速度${{\boldsymbol{v}}_A}$、障碍B以速度${{\boldsymbol{v}}_B}$运动时，在t时刻，A相对B的位置矢量为$\lambda ({{\boldsymbol{p}}_A},{{\boldsymbol{v}}_A} - {{\boldsymbol{v}}_B})$，如果该矢量与$ D({{\boldsymbol{p}}_B},{r_A} + {r_B}) $有交集，那么，A相对B存在一个危险速度的矢量集合$C{C_{A|B}}$，有：

$ C{C_{A|B}} = \{ {\boldsymbol{v}}|\lambda ({{\boldsymbol{p}}_A},{{\boldsymbol{v}}_A} - {{\boldsymbol{v}}_B}) \cap D({{\boldsymbol{p}}_B},{r_A} + {r_B}) \ne \emptyset \}。$

(1)

由于B存在速度${{\boldsymbol{v}}_B}$，因此危险速度集合修正为$V{O_{A|B}} = C{C_{A|B}} \oplus {{\boldsymbol{v}}_B}$，$ \oplus $为明可夫斯基和。$V{O_{A|B}}$之外，A的速度矢量是安全的无碰撞速度。通常，无人艇具有速度、加速度限制，则该可取速度集合中不属于$V{O_{A|B}}$的速度矢量便是无人艇的可行速度。

1.2 CVO算法

图1(b)为CVO算法。CVO对传统VO算法进行了修改，修改后的$V{O_{A|B}}$、$C{C_{A|B}}$定义如下：

$ \begin{split} & V{O_{A|B}} = C{C_{A|B}} = \{ {\boldsymbol{v}}|\lambda ({{\boldsymbol{p}}_A},{\boldsymbol{v}}_A^{opt} - {v_B}) \cap D\\ & ({{\boldsymbol{p}}_B} + t{{\boldsymbol{v}}_B},{r_A} + {r_B}) \ne \emptyset {\text{\} }}。\end{split} $

(2)

其中，$D\left( {{{\boldsymbol{p}}_B} + t{{\boldsymbol{v}}_B},{r_A} + {r_B}} \right)$为t时刻的障碍圆B，安全半径为$ {r_A} + {r_B} $。用于计算$V{O_{A|B}}$的速度${\boldsymbol{v}}_A^{opt}$为：

$ \boldsymbol{v}_A^{opt}=\boldsymbol{v}_A^{{perfer}}= \left\| \boldsymbol{v}_A^{\max} \right\| \frac{\boldsymbol{p}_A^{\mathrm{target}}-\boldsymbol{p}_A}{ \left\| \boldsymbol{p}_A^{\mathrm{target}}-\boldsymbol{p}_A \right\| }。$

(3)

式中：$ \boldsymbol{v}_A^{{perfer}} $为当前时刻无人艇A朝向人为设定目标位置$ \boldsymbol{p}_A^{\mathrm{target}} $的最大可行速度。$V{O_{A|B}}$之外的区域为可行区域。为了明确无人艇A的避让方向，引入COLREGs进一步约束可行区域。

1972海事避碰规则包括了38条规则，分成常规、转向和航行、灯光和外形、声音和灯光信号，以及豁免，并进行了多次修订。无人艇面临和有人船混合航行的场景，因此无人艇遵守有人船航行规则可以降低与有人船碰撞的风险，且便于界定责任。规则中提及了3种避障情形：第十三条追越、第十四条对遇和第十五、十七条交叉相遇^[14]。

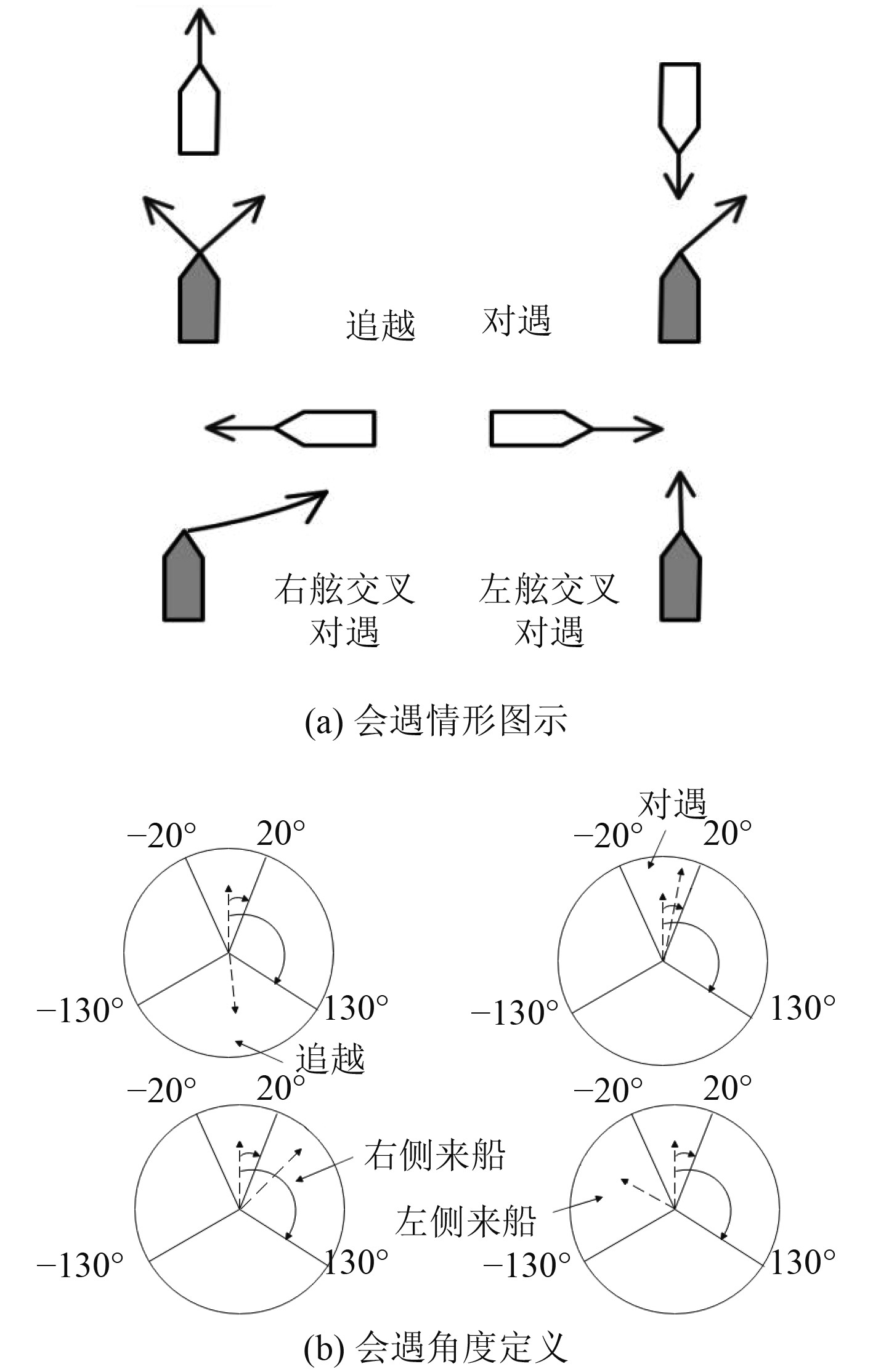
本文参考规则制定的绘制的避障方法如图2(a)所示。

对于左舷来船本船不需要主动避障的情况，本文规定无人艇应向右转向绕开左侧来船，而不是不做避障动作。无人艇向右避障也可以避开遵守COLREGs向右绕行的对方船舶。

由于计算$V{O_{A|B}}$时已经对无人艇A和障碍B是否碰撞进行了判断。若满足碰撞条件，进而使用COLREGs给出避让方向。由于COLREGs没有明确各种会遇情形的判定方法，为方便程序处理，本文按图2(b)根据相对速度${{\boldsymbol{v}}_A} - {{\boldsymbol{v}}_B}$和${{\boldsymbol{v}}_A}$的夹角来判断障碍B相对本船A的运动情形。

定义$R{V_{A|B}}$为COLREGs约束避让方向后的无碰航行区域，如图1(b)所示，该半平面$R{V_{A|B}}$约束区域为$V{O_{A|B}}$截锥一条边沿法线向外的区域，${\boldsymbol{p}}_A^t$为t时刻无人艇A的位置，${\boldsymbol{u}}$为半平面$R{V_{A|B}}$的法线矢量，有

$ R{V_{A|B}} = \left\{ {{\boldsymbol{v}}\left| {\cos \left\langle {{\boldsymbol{v}},{\boldsymbol{n}}} \right\rangle < 1} \right.} \right\}。$

(4)

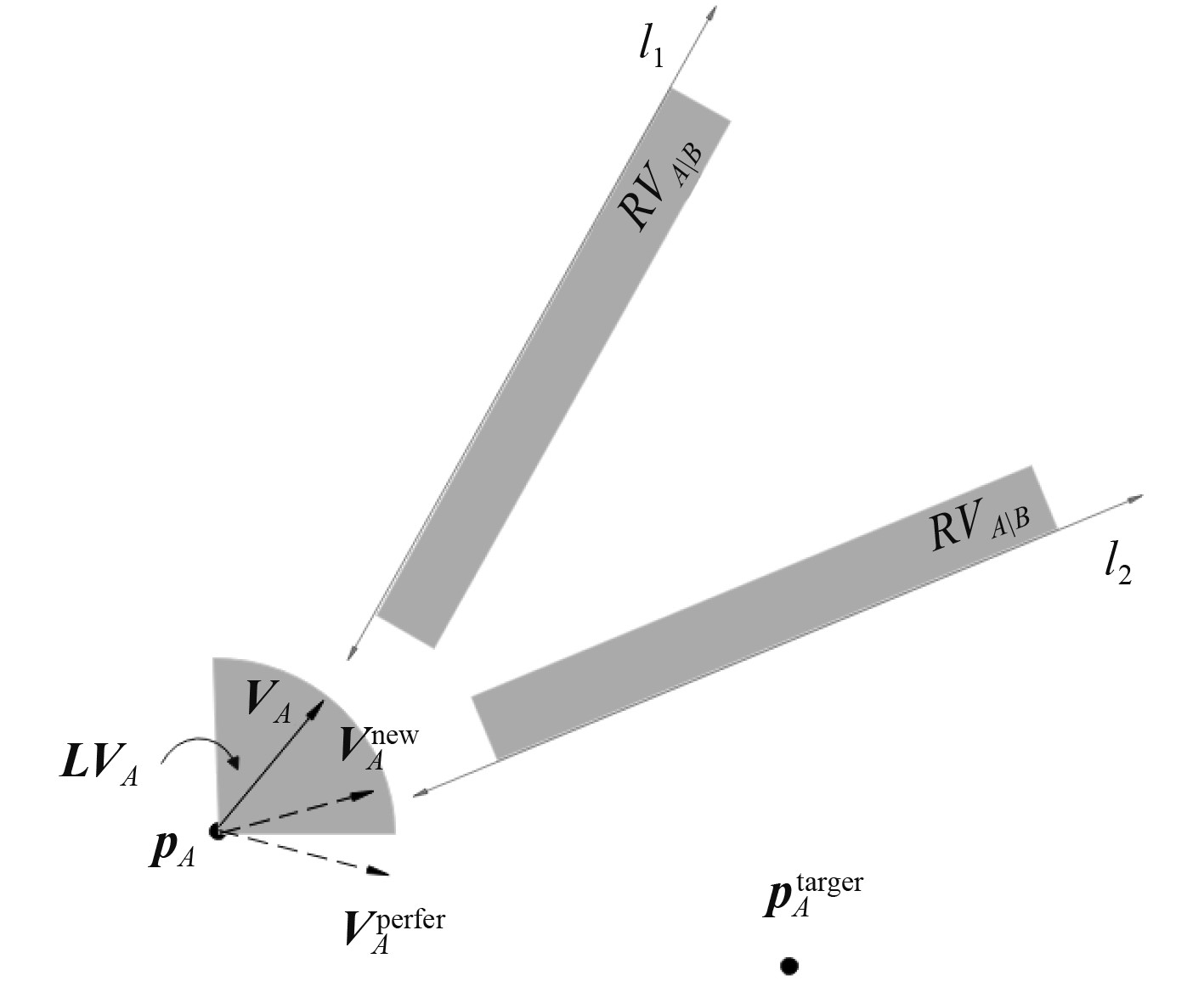
通常，无人艇依靠舵转向，且速度存在上下限，定义图3中扇形区域$L{V_A}$为无人艇A可取速度集合。那么，$L{V_A}$和$R{V_{A|B}}$的交集中最接近$ v_A^{{perfer}} $的速度矢量便是无人艇A下一时刻的期望速度$ \boldsymbol{v}_A^{\mathrm{new}} $，如式(5)。

$ {\boldsymbol{v}}_A^{{\mathrm{new}}} = \mathop {\arg \min }\limits_{{\boldsymbol{v}} \in \{ {\boldsymbol{v}}|L{V_A} \cap R{V_{A|B}} \ne \emptyset \} } \left\| {{\boldsymbol{v}} - {\boldsymbol{v}}_A^{{{perfer}}}} \right\|。$

(5)

计算出当前时刻的$ \boldsymbol{v}_A^{\mathrm{new}} $之后，无人艇将$ \boldsymbol{v}_A^{\mathrm{new}} $作为下一时刻的${{\boldsymbol{v}}_A}$，通过不断迭代计算，最终避开障碍物抵达目标点$ \boldsymbol{p}_A^{\mathrm{target}} $。

2 仿真验证

通过仿真方法验证CVO集群算法。仿真虚拟无人艇使用一阶非线性K-T模型，该公式可以较好模拟小扰动下的无人艇水平面运动特性。一阶非线性K-T运动方程如下：

$ \left\{ {\begin{array}{*{20}{l}} {T\dot r = K({\delta _m} + \delta ) - r - \alpha {r^3}}，\\ {\dot \psi = r} 。\end{array}} \right. $

(6)

式中：$r$为回转角速度；$\psi $为首向角；K为回转性指数；T为应舵指数；${\delta _m}$为压舵角；$\delta $为操舵舵角；$\alpha $为非线性项系数。仿真中参数取值如表1所示。在CVO算法计算出$ \boldsymbol{v}_A^{\mathrm{new}} $后，将该矢量方向作为期望航向方向，矢量的模作为仿真艇下一时刻航行速度。使用PD（Proportion Differentiation）控制器对舵角进行调节，控制虚拟无人艇按期望航向航行，如下式：

$ \left\{\begin{array}{*{20}{c}} e=\psi-\psi\mathrm{^{desire}}，\\ \delta=k_pe+k_d\dot{e}。\end{array}\right. $

(7)

式中：${k_p}$为比例系数；${k_d}$为微分系数；$e$为首向误差；${\psi ^{{\mathrm{desire}}}}$为期望首向角。

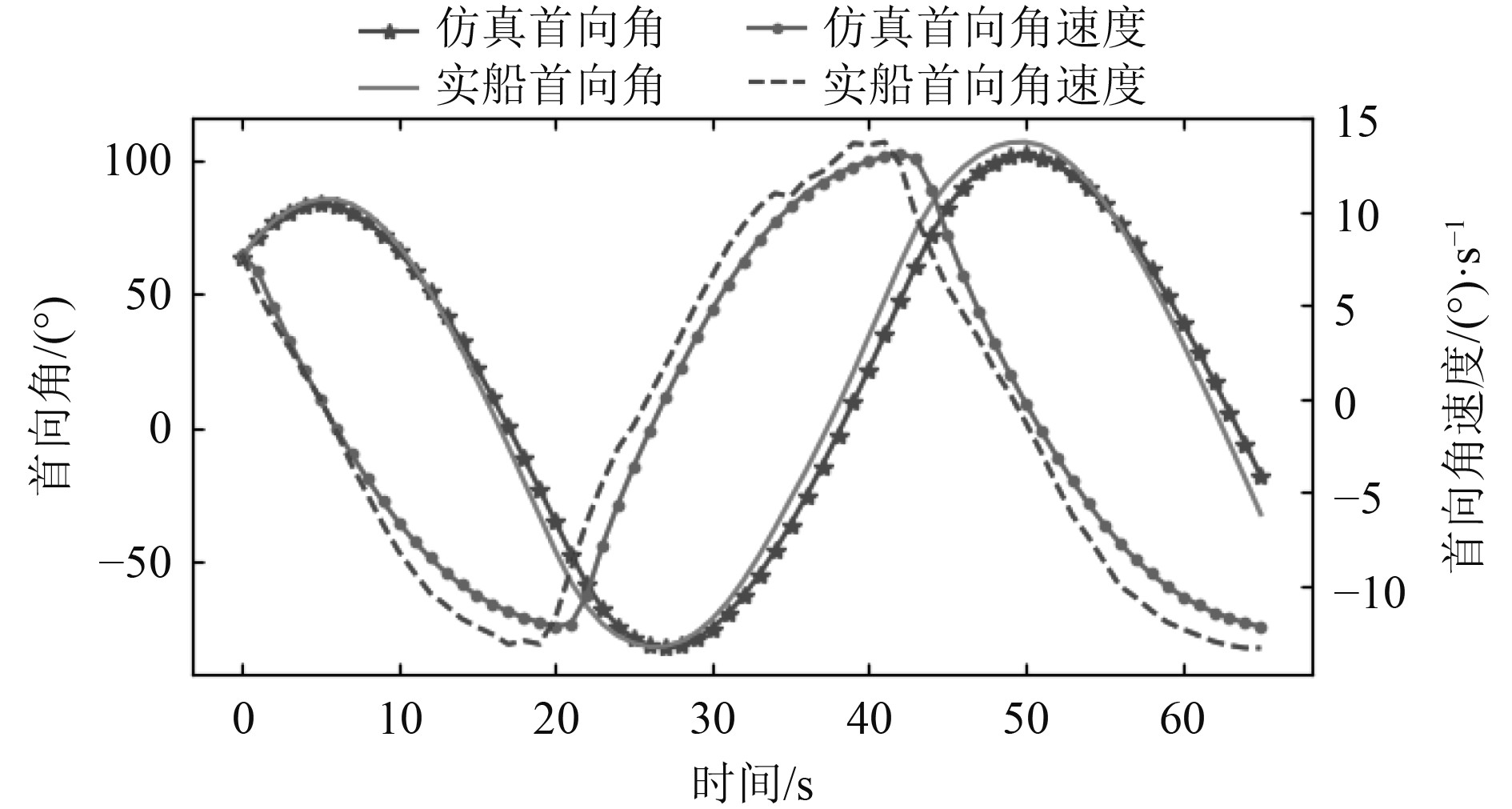
虚拟无人艇的Z型运动数据和对应实艇实测Z型运动数据对比如图4所示，仿真和实船数据均为连续时间下以1 s为间隔进行采样的数据，实艇数据来自某2 m小型无人艇^[15]。在相同初始首向角和角速度，以及时变操舵角输入下，仿真艇首向角、角速度与实船首向角、角速度的MSE（Mean Square Error）偏差为15.58，MSE误差公式如下：

$ loss\left( {{{\hat{\boldsymbol y}}},{\boldsymbol{y}}} \right) = \frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{{\widehat {\boldsymbol{y}}}_i} - {{\boldsymbol{y}}_i}} \right)}^2}}，$

(8)

$ {\boldsymbol{y}} = \left[ {\begin{array}{*{20}{c}} r \\ \psi \end{array}} \right] 。$

(9)

式中：$loss\left( {{{\hat {\boldsymbol{y}}}},{\boldsymbol{y}}} \right)$为首向角、角速度的MSE偏差。${{{\hat {\boldsymbol{y}}}}_i}$为第$i$组仿真数据的首向角和角速度；${{\boldsymbol{y}}_i}$为第$i$组实艇数据的首向角和角速度。通过实船数据和仿真数据对比，可以说明仿真模型能够准确模拟真实无人艇的操纵特性，便于后续开展无人艇集群的避障仿真。

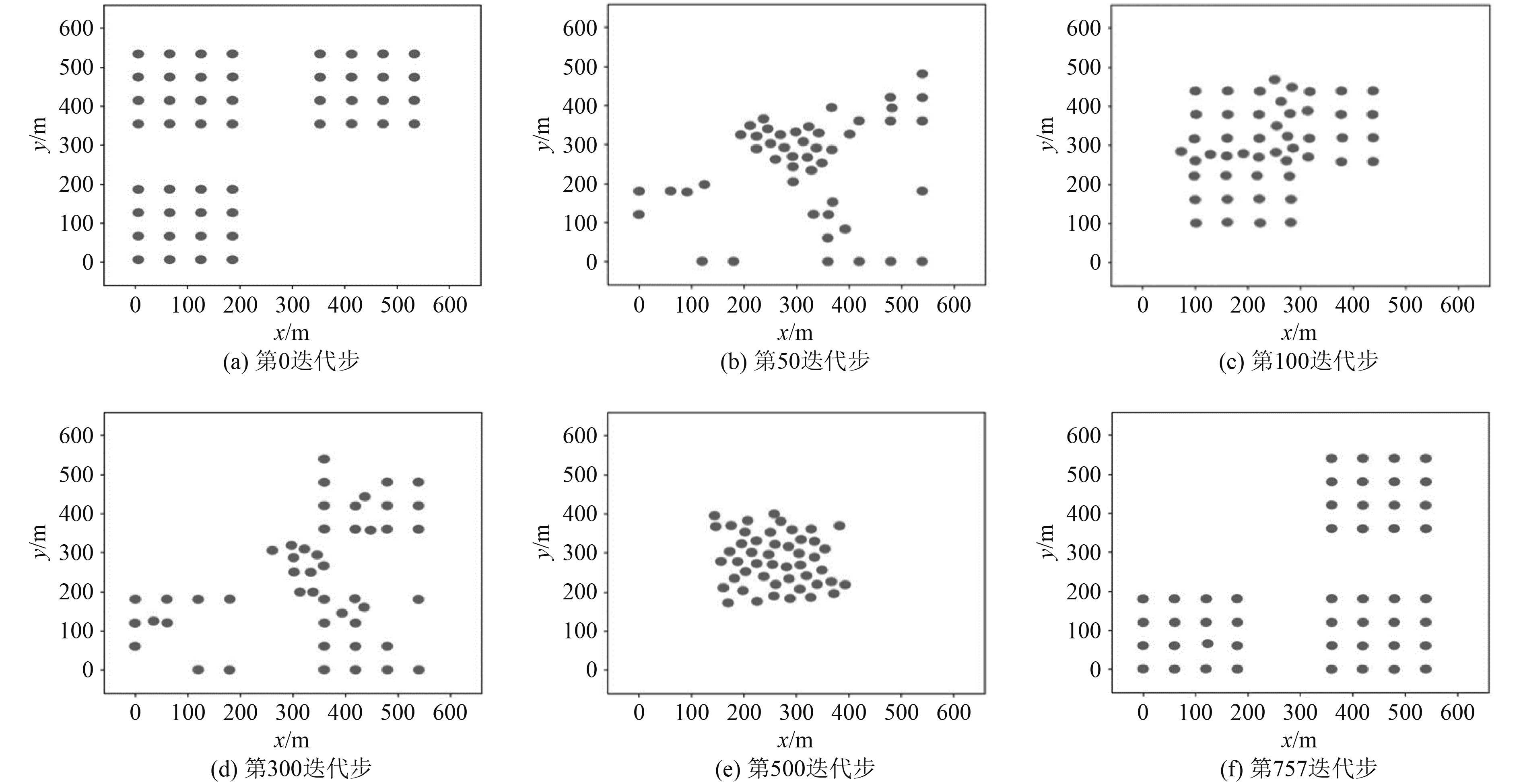
图5为3个无人艇集群互相避障并抵达各自目的地的仿真过程，每组16个虚拟无人艇，共48个无人艇。图中的黑色圆为单艇的安全范围，安全半径为15 m，即黑色圆直径为15 m，若2个黑色圆有重叠部分，则认为两艇相互避障失败，发生了碰撞。

图5(a)为第0个迭代步，3组无人艇从各自的起始区域出发，朝向目标区域直线航行。图5(b)为第50个迭代步，3个无人艇集群相遇，并因为相互避障，阵型发生破坏。图5(c)为第100个迭代步，3组无人艇相遇，阵型完全消失。图5(d)为第300个仿真步，部分无人艇开始脱离相遇区，并朝各自的目标位置航行。图5(e)为第500个仿真步，3个集群均脱离相遇区，并在各自目标区域进行集群内相互避障。图5(f)为第757个仿真步，3个集群在各自的目标区域完成了集群内避障，每个无人艇都抵达了对应的目标点位，阵型恢复。图5(a)~图5(f)为一个完整的集群避障流程。在一个完整集群避障中，没有发生虚拟无人艇碰撞，即黑色圆相互侵入。仿真结果展示出CVO集群避障算法的鲁棒性较强，在动态障碍物密集的环境下仍能够完成避障和恢复队形的工作。

仿真电脑配置为i5-11400 H 2.70 GHz，16 G内存，Windows 11系统，使用单线程运行CVO集群避障算法。算法计算时间随虚拟无人艇数量变化情况如表2所示。随着无人艇数量递增，单个迭代步的总计算时间也显著上升。平均到单个艇的计算时间也发生了递增，这是由于单艇纳入计算的障碍物数量显著增加了。从表2展示出的单艇单步计算时间来看，CVO算法的计算时间和障碍物数量正相关，实时性并不是很高，但足够用于无人艇实艇的实时避障。

3 结　语

本文提出一种基于海事避碰规则的速度障碍算法CVO。该算法是一种局部规划算法，可实现无人艇集群在密集离散的动态障碍环境下进行实时避障，主要针对艇群相遇的避障问题。本文通过48个2 m尺度的小型虚拟无人艇的避障仿真测试了该算法的避让效果和实时性。仿真结果表明，该算法针对动态障碍有较好的避障效果，且不因集群规模的增加而发生避障失败，可用于更大规模无人艇集群航行。

在实际工程应用中，该算法受传感器设备测量精度的影响很大，若海事雷达、毫米波雷达、激光雷达以及光电设备等传感器测量的动态障碍位置、速度误差较小，CVO算法将具有较好的避障效果。由于该算法实现简单、实时性高，后续将部署在中小型无人艇上，用于编队航行、集群避障等作业场景，进一步测试该算法的实际应用价值。