2. 哈尔滨工程大学 烟台研究院,山东 烟台 264000
2. Yantai Research Institute, Harbin Engineering Unirersity, Yantai 264000, China
船舶在海上航行时会不断地受到海浪、气流等恶劣的环境因素的冲击和干扰,而产生强烈地摇荡运动,对船舶安全性造成严峻的考验,而导致船舶受损甚至倾覆沉没的惨剧也常有发生[1],因此准确的对船舶在大幅波浪中的运动进行预报显得尤为重要。
本文主要研究不同海浪谱对船舶在极限海况下运动统计特征值的影响,故基于线性假设,采用三维势流理论计算某船型在波浪中的运动响应,根据St. Denis等在1953年提出的预报海上航行船舶响应的数值统计方法,计算极限海况下船舶运动的统计特征值,该方法将船舶看作一个线性系统,海水表面看作是各态经历的零均高斯随机过程,很多学者基于此方法对船舶的运动进行了预报[2]。李积德等[3]针对单体复合型船舶,提出了一种应用STF切片法和二维半理论,考虑粘性影响的预报方法,并对该船型在规则波中的纵向运动响应进行预报,提高了预报精度。李海波等[4]基于线性频域势流理论,预报了浮式储油平台在三维短峰波中的运动响应有义值。
双峰谱波浪大部分是基于单峰谱波浪频谱进行叠加演化而来,Strekalov等[5]将双峰谱分解成低频谱和高频谱,使用渐进Gauss分布模拟低频部分谱型,Phillips谱[6]平衡域关系表示高频部分谱型,将两部分相加来表示整个双峰谱谱型,Ochi等[7]在这种方法的基础上,提出了一个包含6个参数的双峰谱谱型公式,低频和高频部分皆使用变形的P-M谱表示,每个分谱包含3个参数,最后将两部分相加组合形成六参数双峰谱,具有较强的适用性。
史宪莹等[8]采用物理模型试验方法,对波浪总能量相同、不同低频能量比例的双峰谱波浪与单峰谱波浪横向作用下的系泊船舶运动进行了对比分析,得出双峰谱波浪低频能量的比例对系泊船舶的运动起着关键作用,且混合浪作用下系泊船舶的运动量要比纯风浪的作用下大的多,因此双峰谱混合浪对船舶运动有着巨大影响。靳丰富[9]利用自研CFD求解器,对各个海况下的混合浪进行模拟分析,并使用标准船模DTMB5512对6级、8级海况下的迎浪运动进行模拟,得出在双峰谱混合浪中高频部分能量对船舶垂荡、纵摇运动响应的影响比普通不规则波更大。根据以上预报方法及对双峰谱波浪的研究,本文使用不同海浪谱对船舶在极限海况下的运动统计特征值进行预报,分析不同海浪谱对极限海况下船舶运动的影响。
1 基于不同海浪谱的运动预报方法 1.1 运动预报船型本文研究船型主尺度如表1所示。
|
|
表 1 计算模型主尺度 Tab.1 The main scale of the calculation model |
在进行极值预报过程中,单峰谱波浪采用ITTC单参数谱,表达式为:
| $ {S_\zeta }(\omega ) = \frac{A}{{{\omega ^5}}}{e^{ - \frac{B}{{{\omega ^4}}}}}。$ | (1) |
式中:
双峰谱波浪采用奥启等[7]提出的六参数谱,其表达式为:
| $\begin{aligned} {S}_{\zeta }(\omega )=& \frac{1}{4}{\displaystyle \sum _{j}\frac{\frac{4{\lambda }_{j}+1}{4}{({\omega }_{mj}^{4})}^{{\lambda }_{j}}}{\Gamma ({\lambda }_{j})}}\frac{{H}_{j}^{2}}{{\omega }^{4{\lambda }_{j}+1}}\\ &\mathrm{exp}\left[-\frac{4{\lambda }_{j}+1}{4}{\left(\frac{{\omega }_{mj}}{\omega }\right)}^{4}\right]。\end{aligned} $ | (2) |
式中:
根据Rice理论可以求得双峰谱波浪的有效波高
| $ H = \sqrt {H_1^2 + H_2^2}。$ | (3) |
式中:
| $ E=\frac{1}{4}\rho\mathit{\mathit{g}}H^2=\frac{1}{4}\rho\mathit{\mathit{g}}(H_1^2+H_2^2)。$ | (4) |
式中:
| $ \begin{gathered} {\omega _{mj}} = {a_j}\exp ( - {b_j}H),{\lambda _j} = {c_j}\exp ( - {d_j}H)。\end{gathered} $ | (5) |
式中,
|
|
表 2 Ochi-Hubble谱参数取值 Tab.2 Ochi-Hubble spectrum parameter value |
根据三维势流软件计算出的运动响应,应用谱分析方法研究船舶在不规则波中的运动特性。
计算船舶在不规则波中的升沉与纵摇、横摇运动,依据下式:
| $ \begin{gathered} {S_z}\left( {{\omega _{\mathit{e}}}} \right) = {W_z}^2\left( {{\omega _{\mathit{e}}}} \right){S_\zeta }\left( {{\omega _{\mathit{e}}}} \right),\\ {S_\theta }\left( {{\omega _{\mathit{e}}}} \right) = {W_\theta }^2\left( {{\omega _{\mathit{e}}}} \right){S_\zeta }\left( {{\omega _{\mathit{e}}}} \right),\\ {S_\varphi }\left( {{\omega _{\mathit{e}}}} \right) = {W_\varphi }^2\left( {{\omega _{\mathit{e}}}} \right){S_\zeta }\left( {{\omega _{\mathit{e}}}} \right)。\\ \end{gathered} $ | (6) |
式中:
由于波能谱
| $ \begin{gathered} {\text{ }}{\omega _e} = \omega + \dfrac{{{\omega ^2}}}{g}V\cos \beta,\\ {S_\zeta }\left( {{\omega _e}} \right) = \dfrac{{{S_\zeta }\left( \omega \right)}}{{1 + \dfrac{{2\omega V}}{g}\cos \beta }}。\\ \end{gathered} $ | (7) |
式中:
根据遭遇波浪谱,可以根据式(8)计算各运动参数运动幅值的有义值
| $ \begin{aligned}&{m}_{0z}={\displaystyle \int_0^{\infty}S_z}\left({\omega }_{e}\right){\mathrm{d}}{\omega }_{e}\text{,}\\ &{m}_{0\theta }={\displaystyle \int_0^{\infty}S_{\theta}}\left({\omega }_{e}\right){\mathrm{d}}{\omega }_{e}\text{,}\\ &{m}_{0\phi }={\displaystyle \int_0^{\infty}S_{\phi}}\left({\omega }_{e}\right){\mathrm{d}}{\omega }_{e}。\end{aligned}$ | (8) |
根据三维势流软件计算得到的运动响应,分别使用ITTC单参数谱、双峰谱波浪对14 m有义波高下船舶的运动进行预报,探究不同航速、浪向角及低频能量所占比例对预报结果的影响。
其中双峰谱波浪可以根据低频能量占比的不同划分为风浪为主(低频占30%)、风涌相当(低频占50%)和涌浪为主(低频占70%)三种形式。
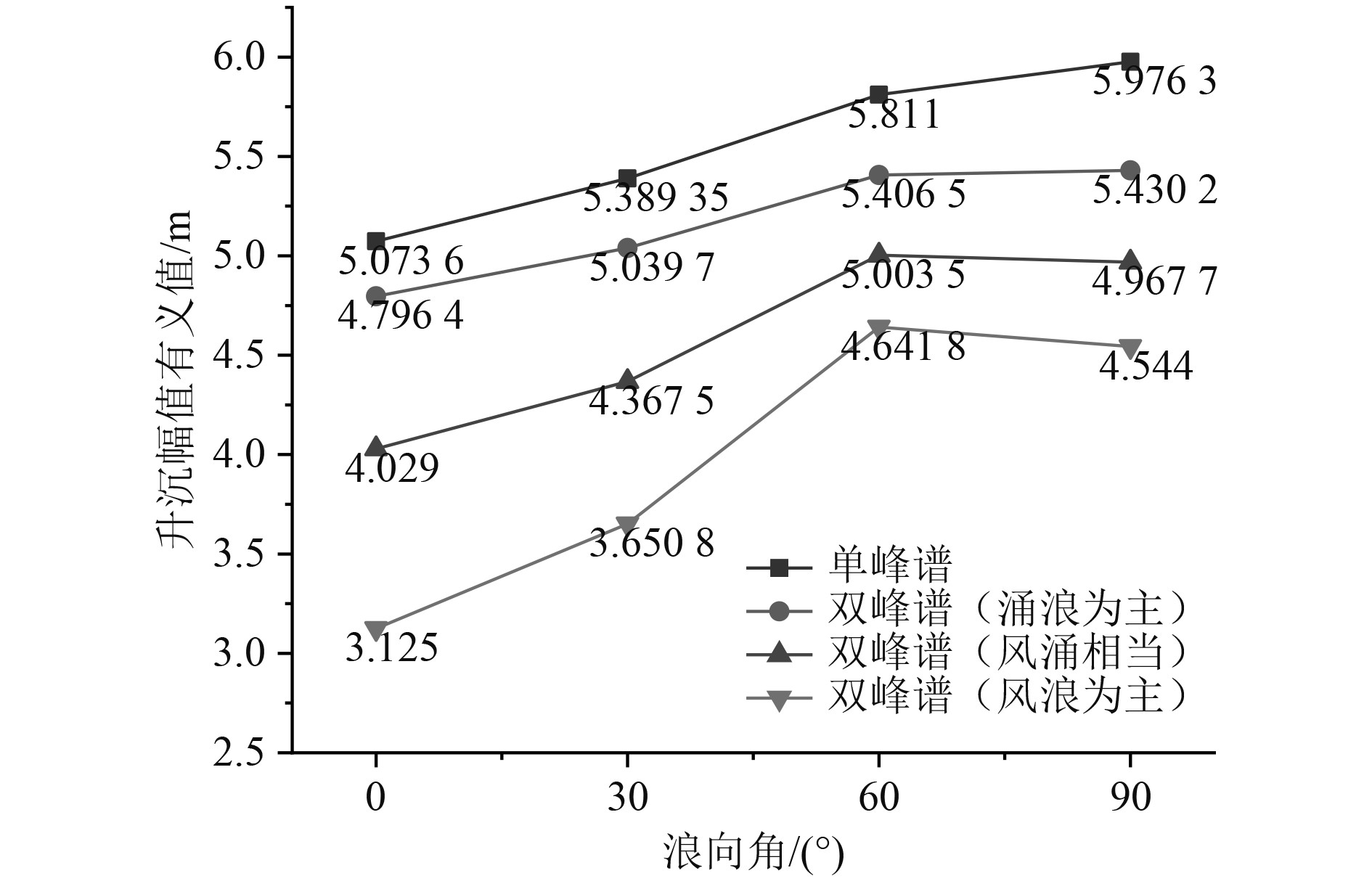
|
图 2 航速24 kn升沉幅值有义值结果比对 Fig. 2 Comparison of amplitude significant value of heave at 24 kn |
由图1~图3可知,当航速在18 kn和24 kn,不同海浪谱预报得到的升沉幅值有义值随浪向角从0°到90°的变化随之增大,在横浪90°时达到最大;单峰谱预报得到的结果与双峰谱波浪比较相对更大一些,双峰谱波浪中低频能量占比越低,预报出的升沉幅值有义值也越小;当航速在30 kn,使用双峰谱波浪预报得到的升沉幅值有义值先增大再减小,在顶斜浪60°时最大,随双峰谱波浪低频能量占比的降低,预报得到的升沉幅值有义值随之增加,在低频能量占比为30 %时达到最大。
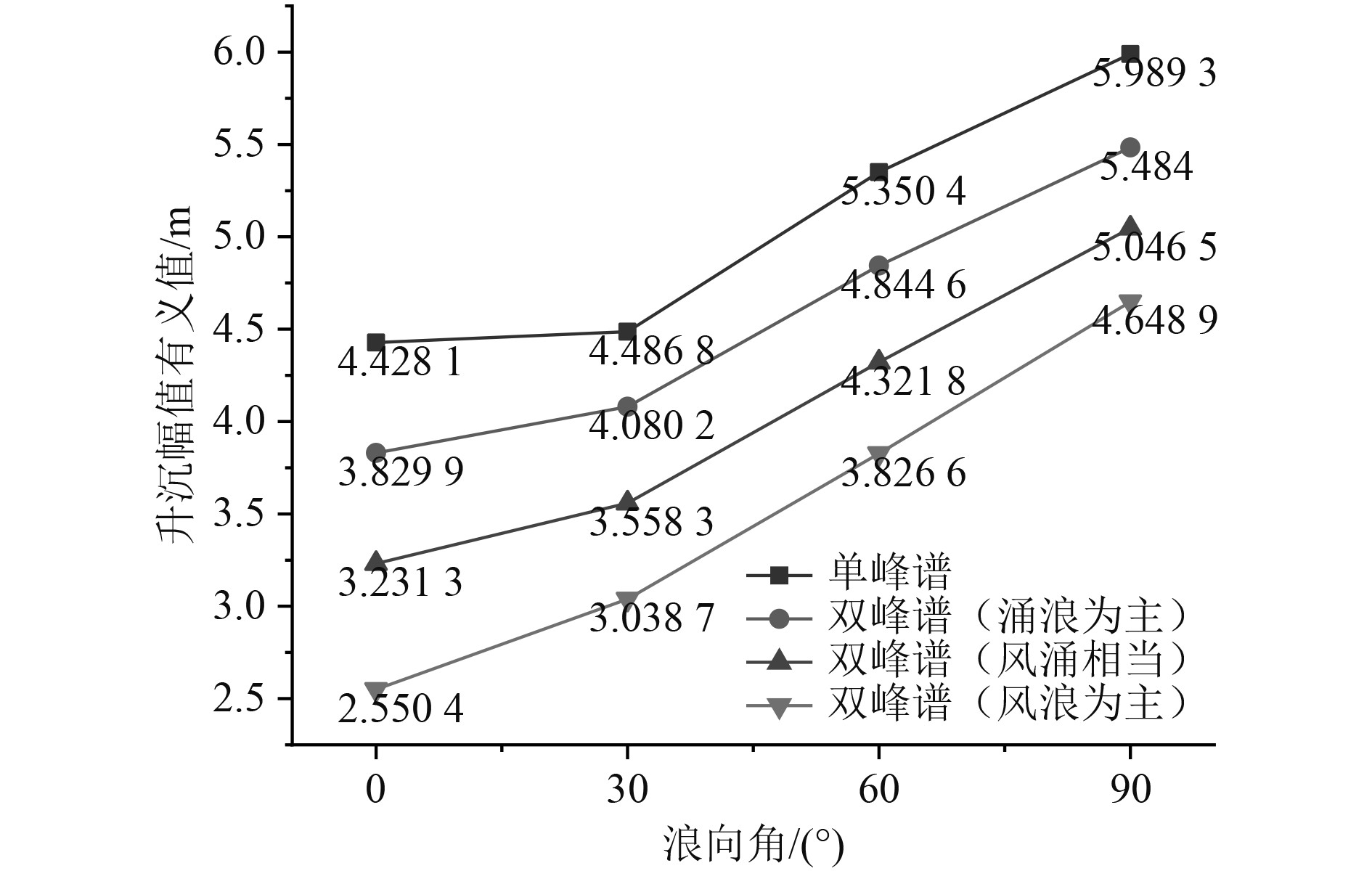
|
图 1 航速18 kn升沉幅值有义值结果比对 Fig. 1 Comparison of amplitude significant value of heave at 18 kn |
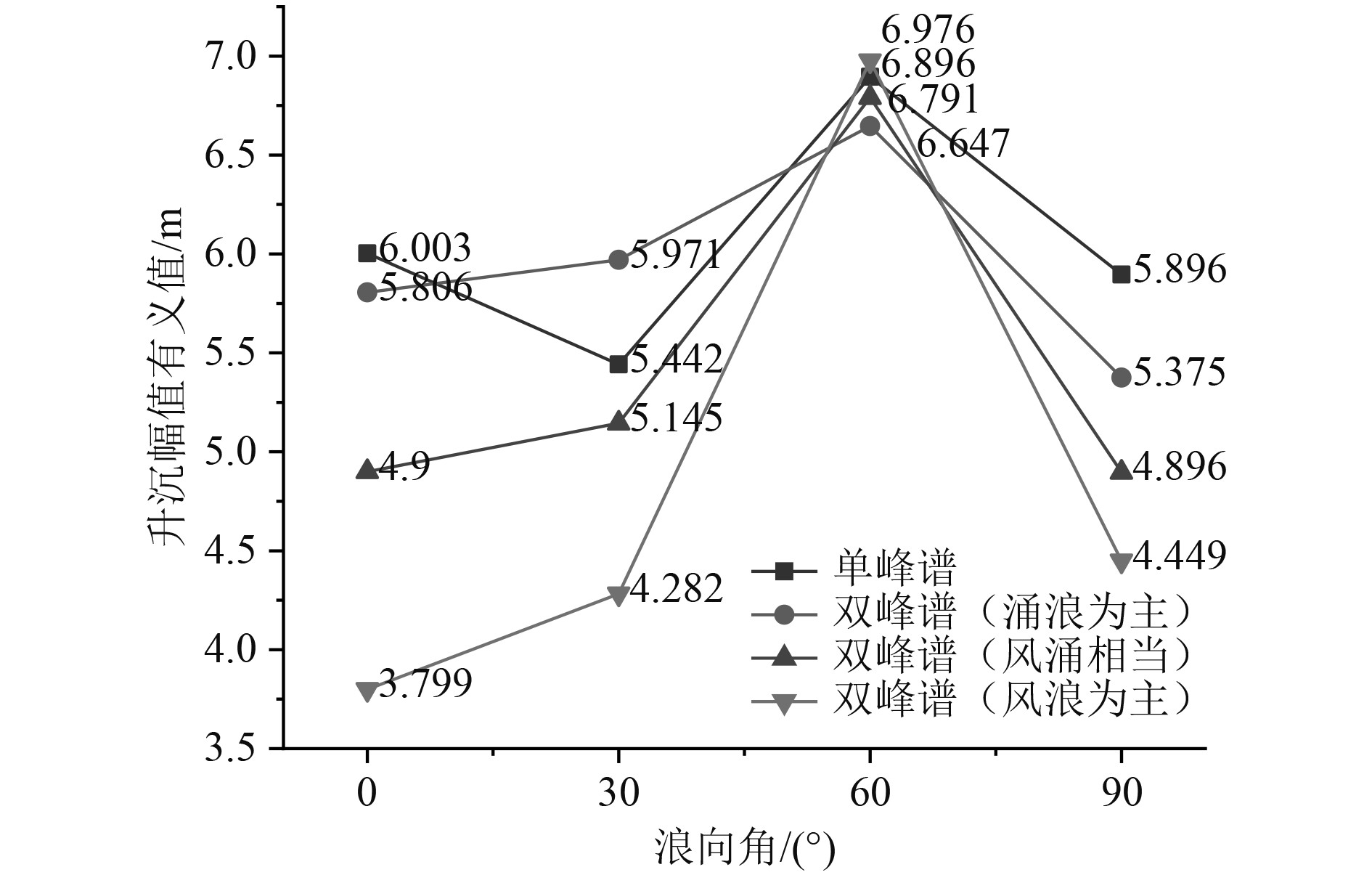
|
图 3 航速30 kn升沉幅值有义值结果比对 Fig. 3 Comparison of amplitude significant value of heave at 30 kn |
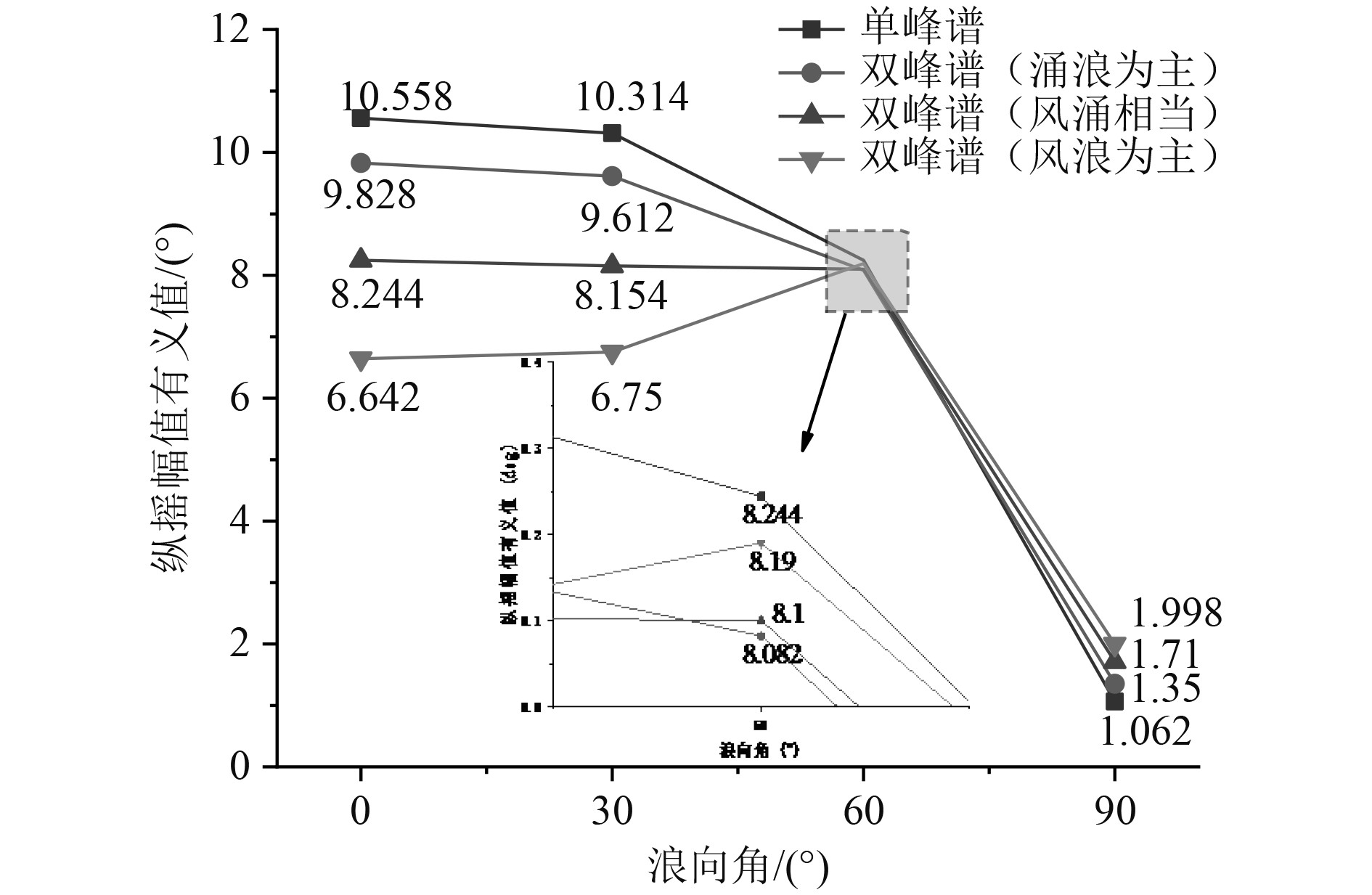
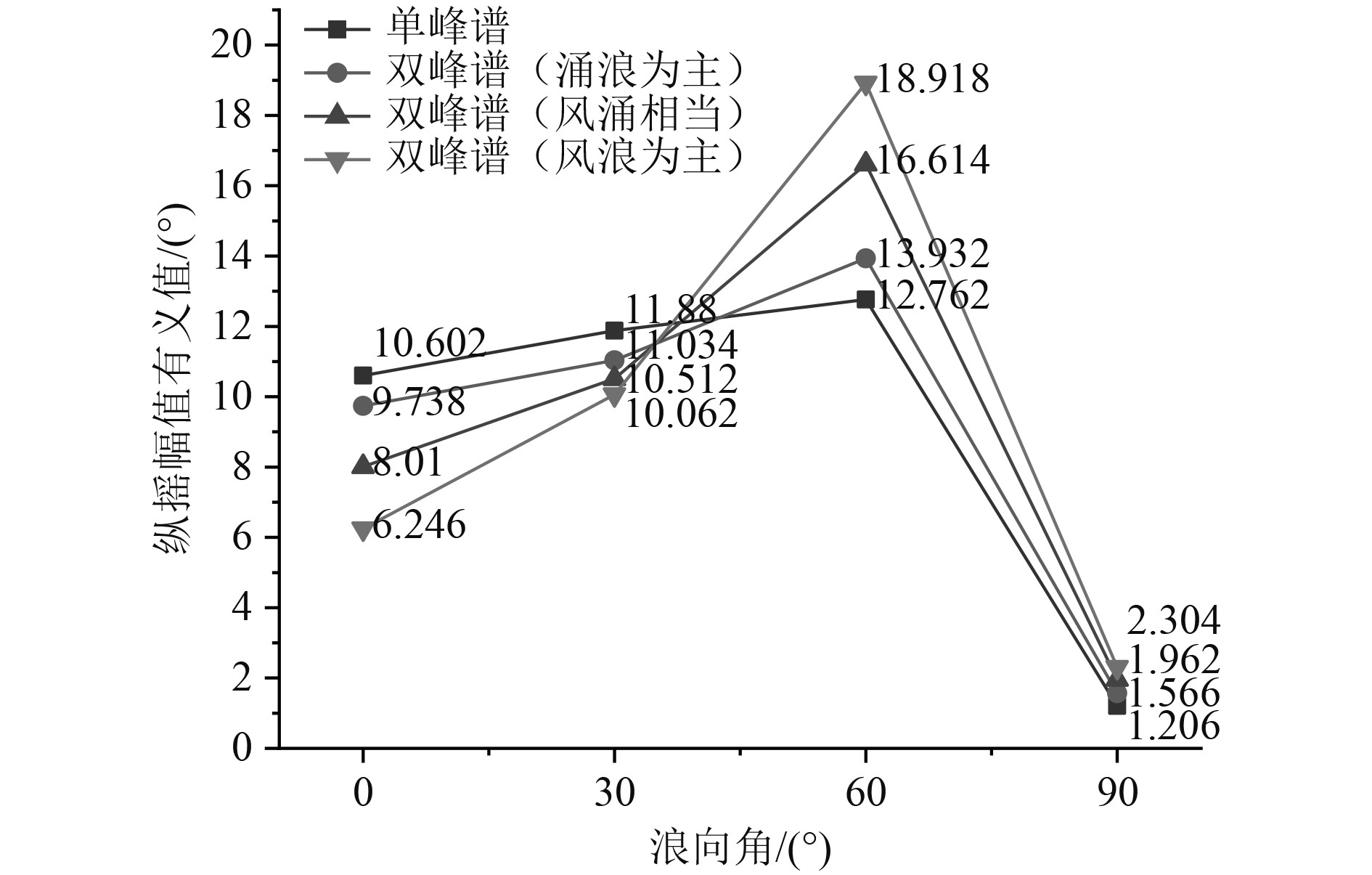
通过图4~图6可知,当航速在18 kn和24 kn,使用单峰谱波浪与双峰谱波浪中低频能量占比为70 %预报时,纵摇幅值有义值在迎浪0°达到最大,随浪向角变化到横浪90°,纵摇幅值有义值随之减小;当双峰谱波浪中低频能量占比在50 %和30 %时,纵摇幅值有义值呈先增大再减小的趋势,并在顶斜浪60°时达到最大;当航速在30 kn,不同海浪谱预报得到的纵摇幅值有义值呈先增大再减小的趋势,在顶斜浪60°时达到最大;航速在24 kn和30 kn,浪向角大于60°时,随双峰谱波浪低频能量占比的降低,预报得到的纵摇幅值有义值随之增加,在低频能量占比为30 %时达到最大。
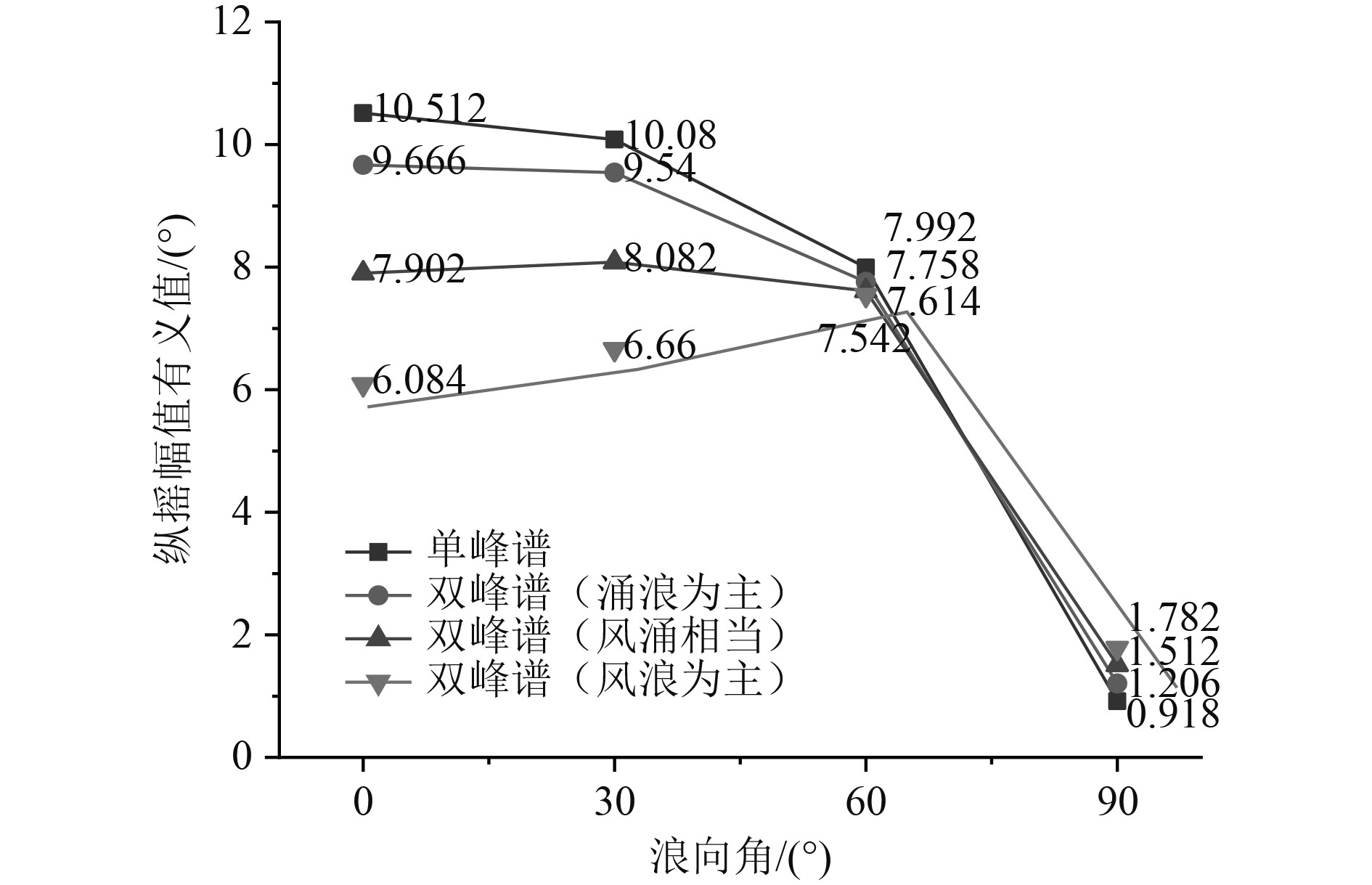
|
图 4 航速18 kn纵摇幅值有义值结果比对 Fig. 4 Comparison results of amplitude significant value of pitch at 18 kn |
|
图 5 航速24 kn纵摇幅值有义值结果比对 Fig. 5 Comparison results of amplitude significant value of pitch at 24 kn |
|
图 6 航速30 kn纵摇幅值有义值结果比对 Fig. 6 Comparison results of amplitude significant value of pitch at 30 kn |
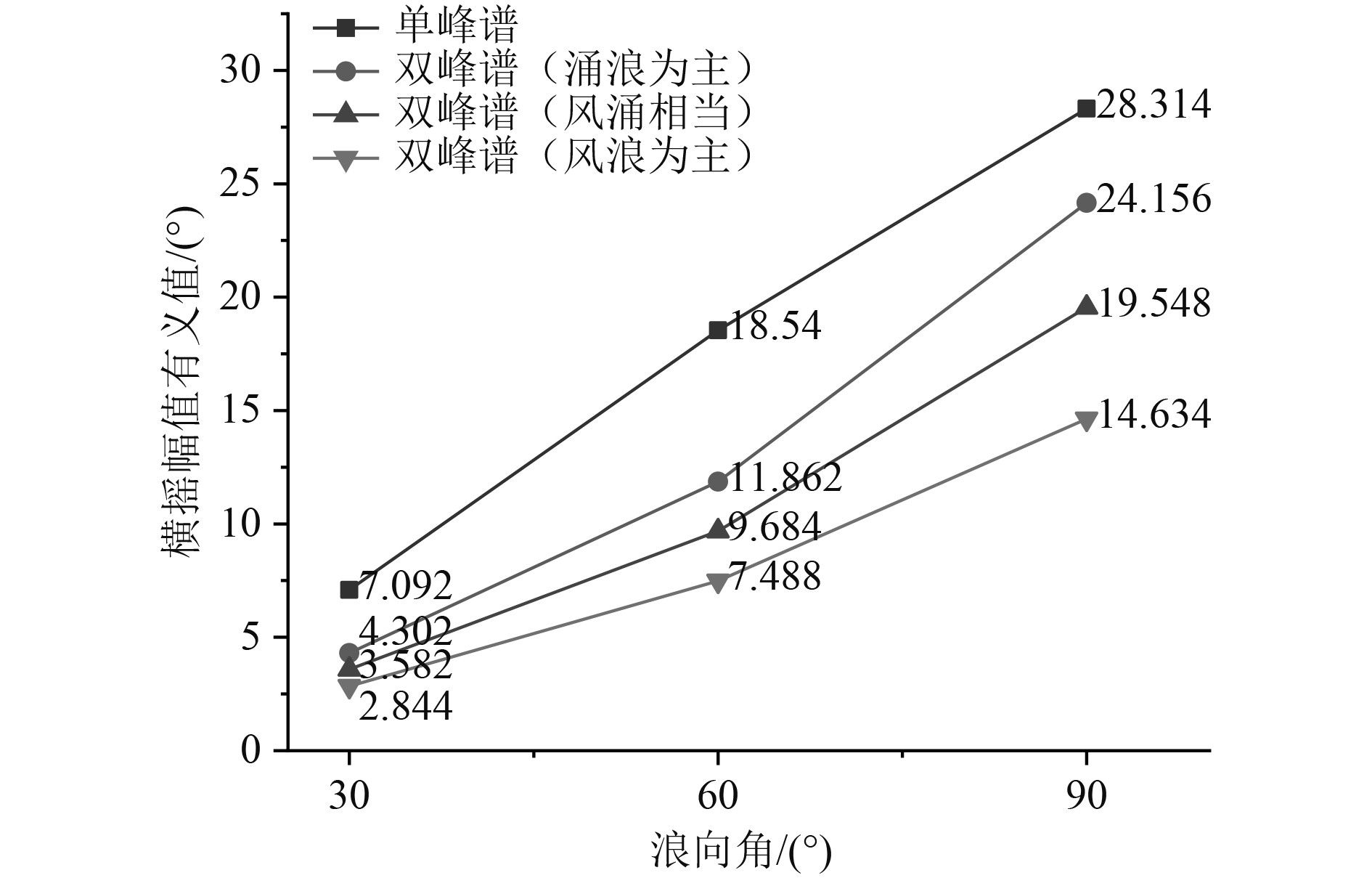
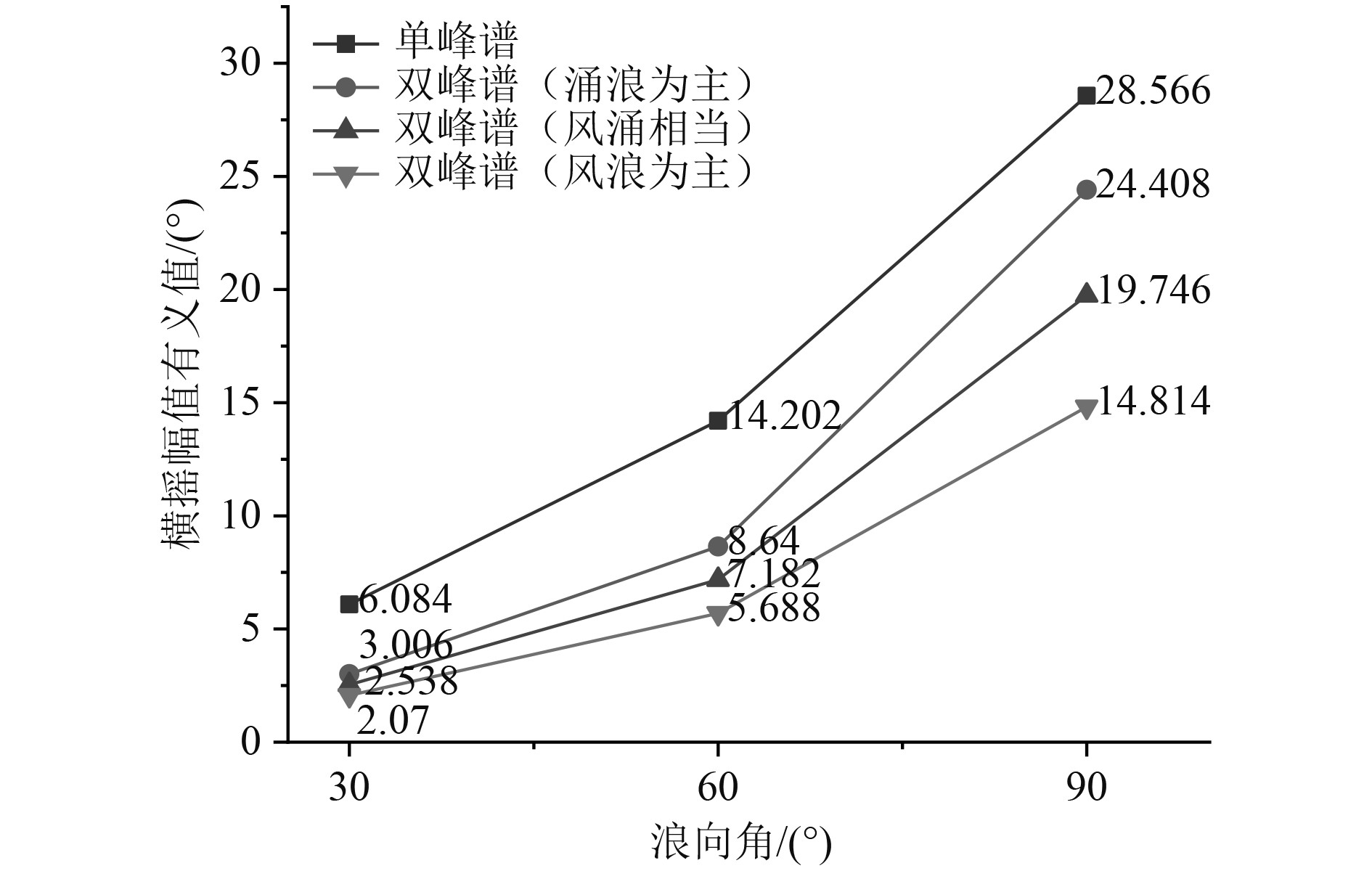
通过图7~图9可知,在各个航速下,随浪向角从30°增加到90°,横摇幅值有义值随之增大,并在30 kn达到最大;当考虑波浪成分时可以看出,单峰谱波浪预报出的结果与双峰谱波浪比较相对更大一些,双峰谱波浪中低频能量占比越低,预报出的横摇幅值有义值也越小。
|
图 7 航速18 kn横摇幅值有义值结果比对 Fig. 7 Comparison results of amplitude significant value of roll at 18 kn |
|
图 8 航速24 kn横摇幅值有义值结果比对 Fig. 8 Comparison results of amplitude significant value of roll at 24 kn |
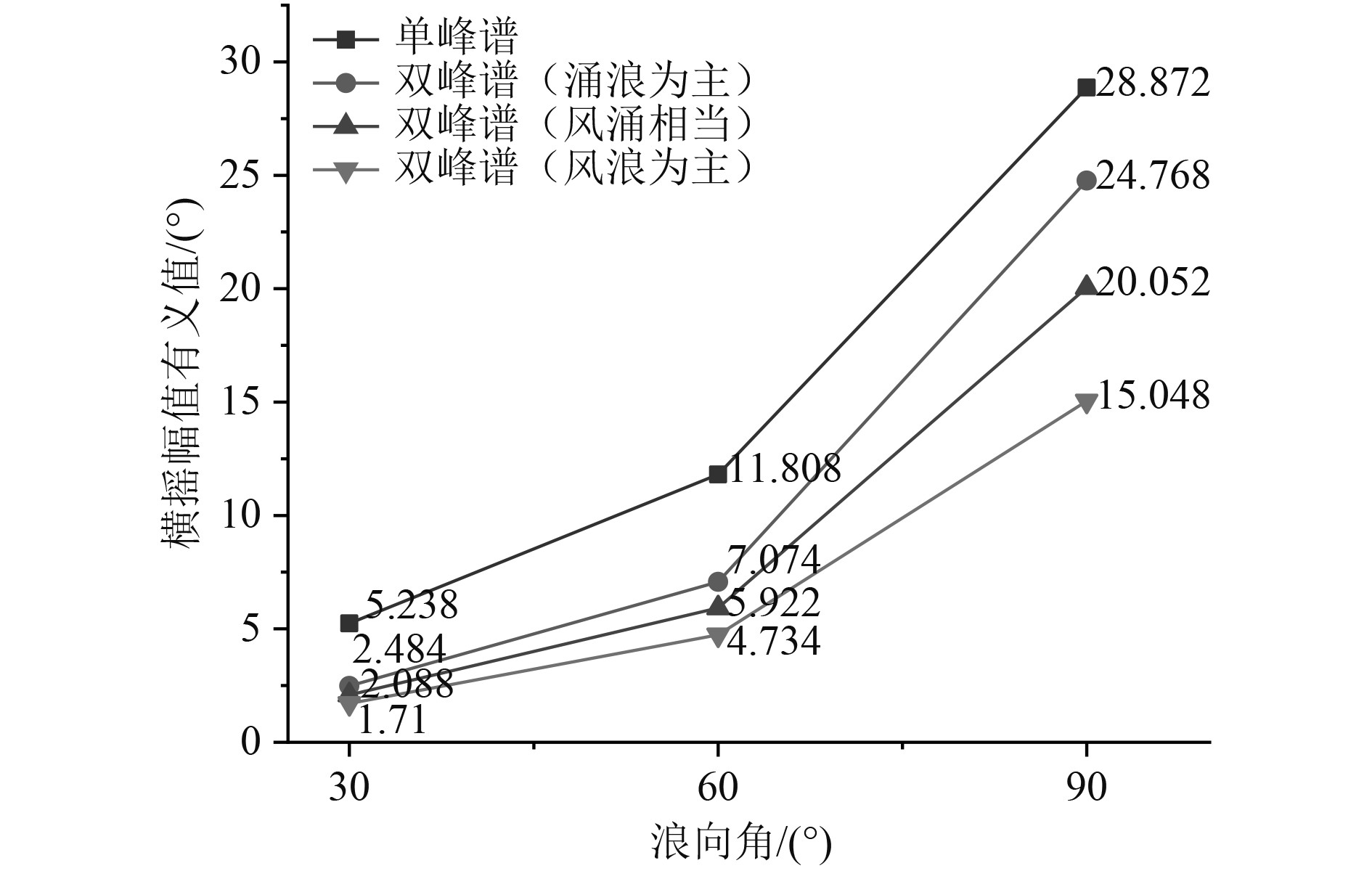
|
图 9 航速30 kn纵摇幅值有义值结果比对 Fig. 9 Comparison results of amplitude significant value of roll at 30 kn |
根据相同航速,不同浪向角预报的结果,选择横浪90°时的横摇、升沉运动,顶浪0°与顶斜浪60°时的升沉和纵摇运动进一步比较航速对预报结果的影响。
由图10可知,升沉幅值有义值随航速提高而减小,横摇幅值有义值随航速提高而增加,可以得出在横浪90°时,随航速变化,升沉和横摇运动变化并不明显。
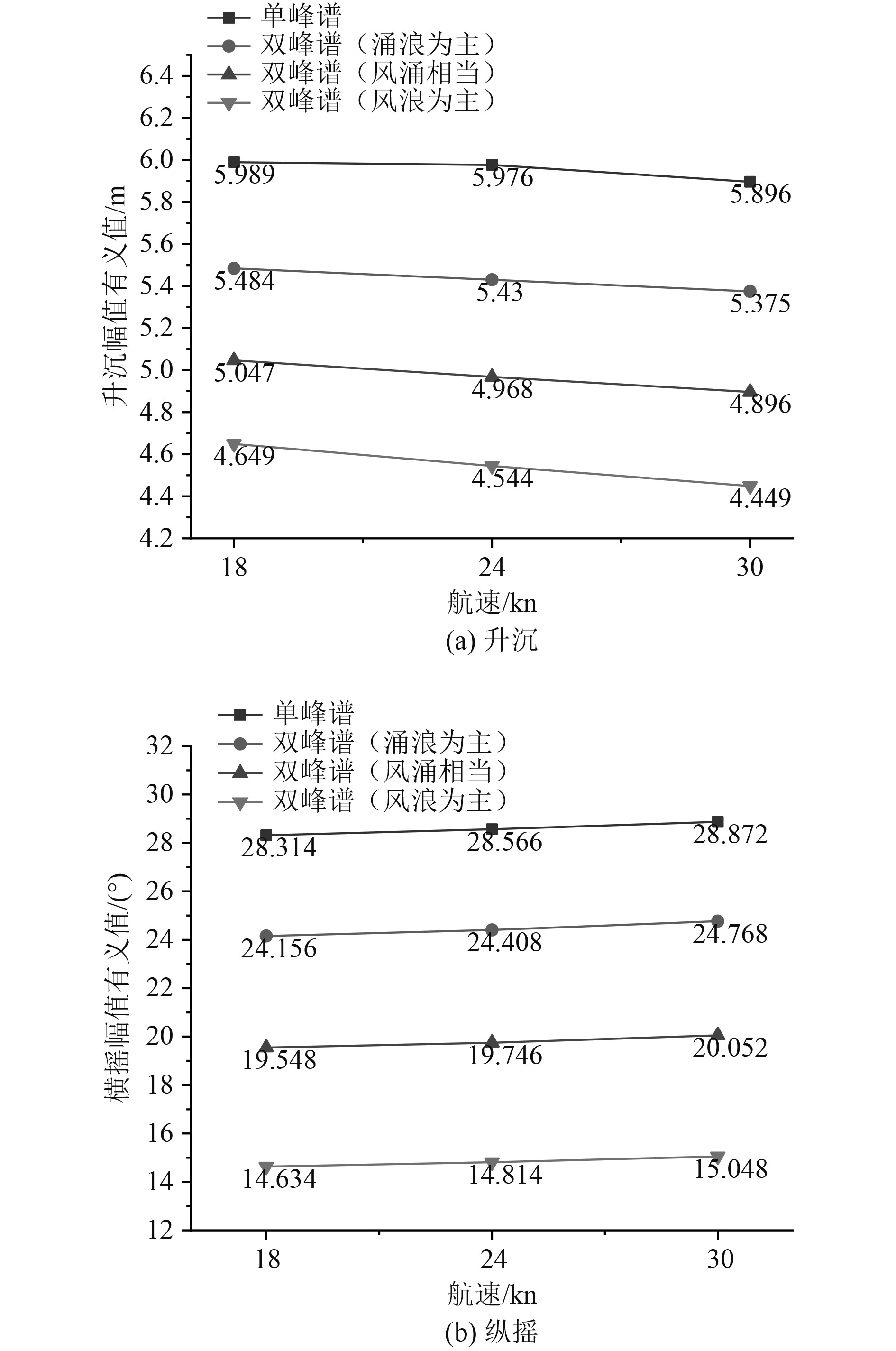
|
图 10 横浪90°升沉、横摇幅值有义值结果比对 Fig. 10 Comparison results of amplitude significant value of heave and roll under 90° |
由图11可知,升沉与纵摇的幅值有义值随航速的提高而增加,且随双峰谱波浪中低频能量占比的降低,变化更加剧烈,在航速30 kn,低频能量占比30 %时达到最大。
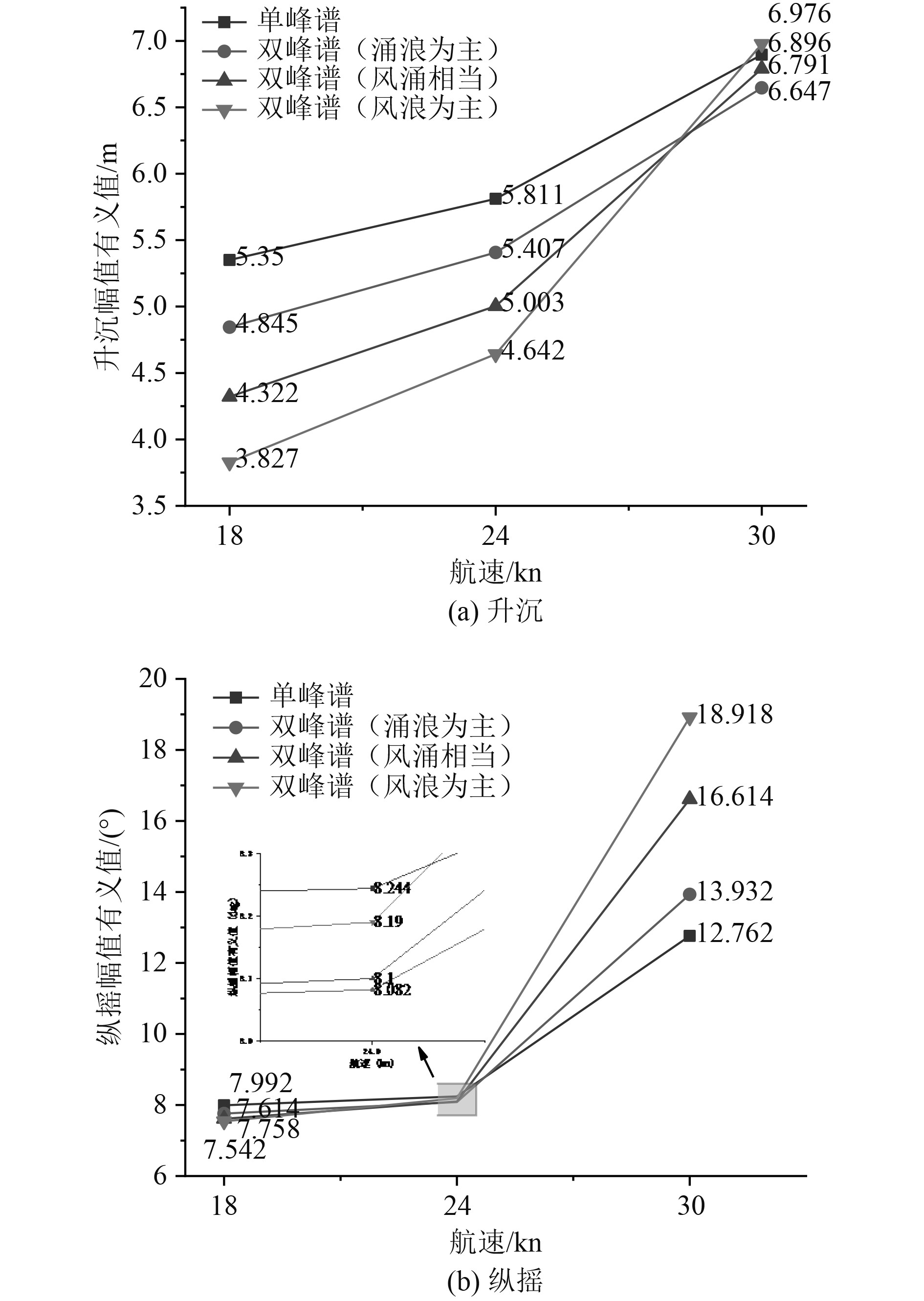
|
图 11 顶斜浪60°升沉、纵摇幅值有义值结果比对 Fig. 11 Comparison results of amplitude significant value of heave and pitch under 60° |
由图12可知,升沉有义值幅值随航速提高而增加,纵摇幅值有义值在不考虑低频能量影响时,随航速的提高而增加;考虑低频能量的影响时,纵摇幅值有义值在航速为24 kn时达到最大,在30 kn航速时有所降低
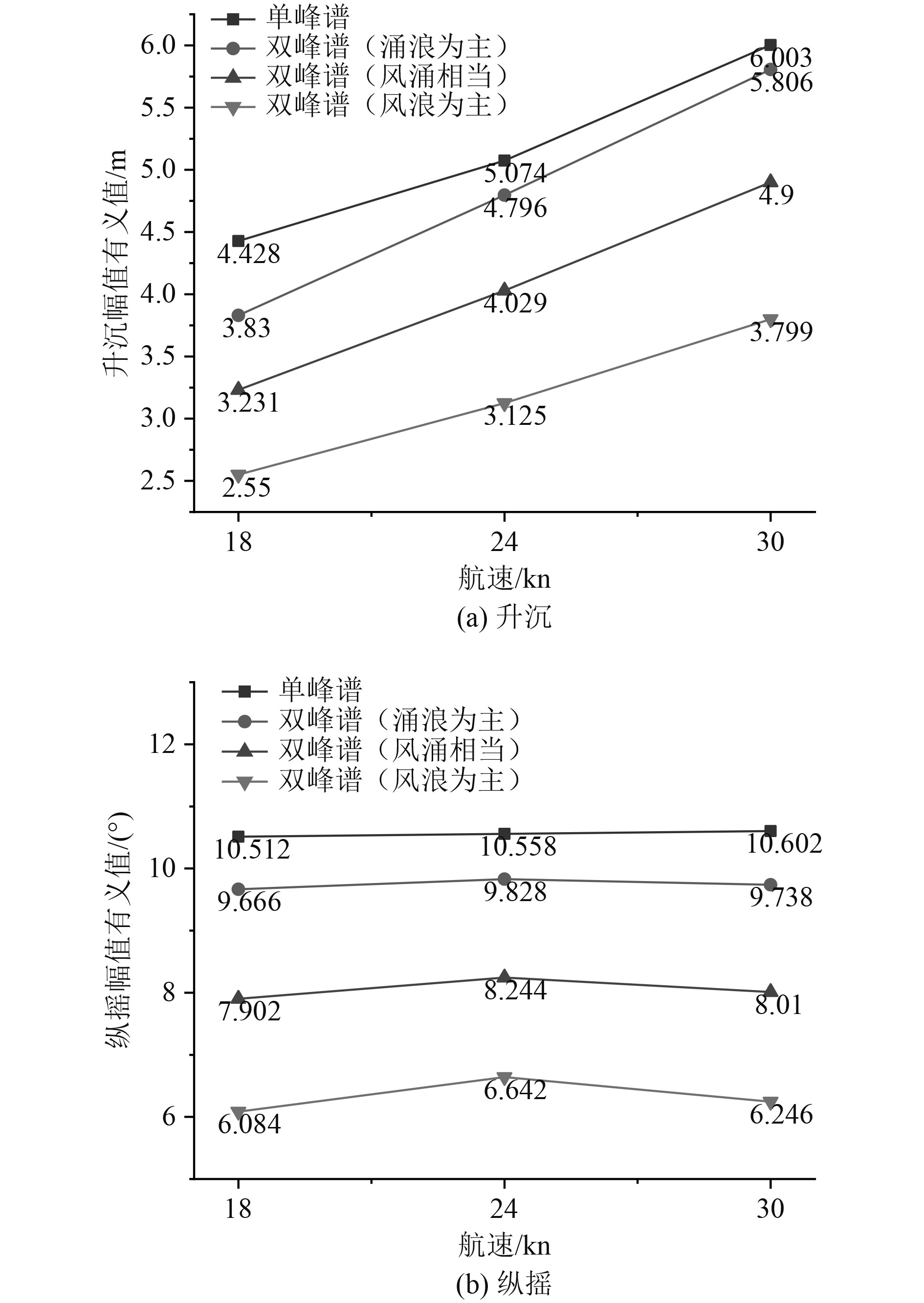
|
图 12 顶浪0°升沉、纵摇幅值有义值结果比对 Fig. 12 Comparison results of amplitude significant value of heave and pitch motion under 0° |
本文对极限海况下,使用不同海浪谱预报得到的。不同航速、不同浪向角运动幅值有义值进行比较分析得出如下结论:
1)基于相同航速不同浪向角预报结果比较得出,在高航速30 kn时,顶斜浪60°航行会对极限海况下船舶的升沉和纵摇运动产生较大影响,在较低航速18 kn和24 kn时,顶浪0°会发生剧烈的纵摇运动,横浪90°会发生剧烈的升沉运动;而横摇运动的极值发生在横浪90°。
2)基于相同浪向角不同航速预报结果比较得出,航速对于升沉、纵摇和横摇运动有不同的影响,在产生较大运动幅值的工况下,横摇运动受航速的影响不大,升沉与纵摇运动会随航速的增加产生较大的变化,尤其在航速30 kn。
3)依据不同海浪谱预报得到的结果得出,在较低航速与运动幅值较小的浪向下,单峰谱波浪预报的运动单幅有义值要高于双峰谱波浪预报结果,而在高航速及运动剧烈的浪向下,如顶斜浪60°时的升沉与横摇,运动幅值有义值随双峰谱波浪中低频能量占比的降低而升高,皆高于单峰谱波浪预报得到的结果。
根据以上结论,本文对船舶在极限海况的运动预报提出以下建议:
1)使用单峰谱波浪预报18 kn与24 kn航速下迎浪航行的升沉与纵摇运动更能为恶劣海况船舶的安全评估提供参考,而在30 kn航速下需充分考虑双峰谱波浪中低频能量占比及顶斜浪60°对预报结果的影响。
2)使用单峰谱波浪预报高航速下,横浪90°的横摇运动更能为极限海况下的横摇预报提供参考。
| [1] |
李积德. 船舶耐波性[M]. 北京: 北京国防工业出版社, 1981.
|
| [2] |
李积德, 张恒. 考虑粘性影响的单体复合船型的运动预报[J]. 船舶力学, 2008, 12(2): 180-187. LI Ji- de, ZHANG Heng. Motion prediction of hybrid monohull considering viscous effect[J]. Journal of Ship Mechanics, 2008, 12(2): 180-187. |
| [3] |
李海波, 温宝贵. 用短峰波理论预报南海浮式生产储油装置运动响应[J]. 中国海上油气, 2007(5): 346−349. LI Haibo, WEN Baogui.. Predicting movement behavior of Nanhai FPSO by short-crested wave theory[J]. China Offshore Oil and Gas, 2007(5): 346−349. |
| [4] |
DINIS. M , PIERSON JWJ . On the motions of ships in confused seas[J]. Japanese Journal of Phytopathology, 1953, 57(4): 573-576. |
| [5] |
STREKALOV S S, TSYPLOUKHIN V P, MASSEL S T. Structure of sea wave frequency spectrum[M]//Coastal Engineering 1972. 1973: 307−314.
|
| [6] |
PHILLIPS O M. The equilibrium range in the spectrum of wind-generated waves[J]. Journal of Fluid Mechanics, 1958, 4(4): 426-434. DOI:10.1017/S0022112058000550 |
| [7] |
OCHI M K, HUBBLE E N. Six-Parameter wave spectra[C]// Coastal Engineering , 1976.
|
| [8] |
史宪莹, 陈昌平, 郑艳娜, 等. 双峰谱与单峰谱波浪作用下系泊船舶运动对比研究[C]// 第十八届中国海洋(岸)工程学术讨论会, 2017.
|
| [9] |
靳丰富. 基于双峰海浪谱的混合浪数值仿真及应用[D]. 武汉:华中科技大学, 2021.
|
 2024, Vol. 46
2024, Vol. 46
