0 引　言

在全球范围内，为了满足节约能源、降低排放和减少污染等方面的需求，LNG燃料正逐步被广泛应用。目前，以LNG燃料为主要原料的双燃料发动机船舶已建成并投入运行，同时也在进行单种LNG燃料船的设计。国内外众多研究人员对LNG运输船的加注方式进行了研究和改进。朱永凯等^[1]对比现有LNG运输船加注方式，综合分析了LNG运输船加注的各个环节，对原来的加注方案进行简化改进，使操作流程简单，节约了作业时间和LNG用量。因为这类船要绕着海上平台航行，对机动性有很高的要求，所以一般都会在船首和尾部安装一台侧推器装置，以达到作业操作的要求。韦晓强等^[2]针对国内对海上LNG加注船的需求，将海洋石油301船在原LNG运输船功能的基础上新增LNG加注作业所需设备，改造原船系统，使原船具有LNG加注船功能。Ahn等^[3]为了评估液化LNG运输船的长期晃动载荷，使用六自由度不规则晃动模型检验进行了一系列联合工业实验，根据指南区分的短期和长期方法的比较，提供了对晃动载荷的评估，并提出了可能的参考值。Pak等^[4]为SLBV前体和后体船体形状的最佳LCB位置和设计方向提供最有用的方法，由于SLBV的这些特殊性，最佳LCB位置与传统LNG运输船非常不同，并应用各种方法来确定最佳的前体和后体船体形状。通过数值模拟，将最佳船体形态的设计方向评估为总阻力的最小化，包括兴波阻力和形状阻力。李高强等^[5]为了揭示船舶无轴轮缘侧推器的水动力性能，分析侧推器结构参数的影响规律，采用计算流体力学对无轴侧推器水动力参数进行数值计算，研究船首位置的无轴侧推器水动力性能，周围流场的分布规律及其水动力性能变化的影响参数，获得不同螺距比、盘面比及毂径比对无轴侧推器水动力特性的影响规律。肖智俊等^[6]对槽道式侧推器的水动力性能预报方法、螺旋桨设计、槽道口减阻降噪设计、做功能力影响因素、空化噪声和脉动压力、减摇作用以及操纵效能等方面的研究进展进行回顾。YAN等^[7]介绍了无轴轮缘驱动推进器（RDT）的最新研究重点、进展和应用，讨论了RDT的设计、性能分析和控制的理论和实验研究，包括电动机、轴承结构、流体动力学优化以及RDT与船体的耦合设计。

在侧推器推力性能上，大多都以侧推器供应商提供的推力数据为准，但在实船建造中不同的船型存在船身线型以及侧推器隧道长度的差异，侧推器推力往往与理想值有一定出入^[8]，并且船舶航速也会对侧推器推力造成较大影响^[9]。采用水池实验对此类问题进行研究投入较大，采用CFD数值模拟技术不失为一种可行的方法。目前对以侧推进装置为基础的船舶操纵问题的数值研究很少，大部分侧推器的研究通过螺旋桨的一些基本参数，比较侧推器的效率与翼形状、形式导管以及出入流口之间的关系，部分数值研究只建立单纯的船首或是船尾流场，以模拟舰船行进时侧推器打开后的推进效率^[10]，和整船流场及整船受力实际状况相差很大。除实船试验和水池试验能较逼真地模拟出船身流场之外，其余少数研究途径大多是基于势流理论分离建模，利用自行编写的程序进行数学建模，侧推器产生的推力作为外力单独施加在主船体之上，忽略船舶操纵过程中船舶和侧推器之间以流场作为介质并由于流体粘性所引起的互相干扰^[11]。

本文基于以粘性流理论为基础的Fluent求解器，利用混合网格技术对一条装配有首尾侧推器的LNG运输及加注船进行船体与侧推器整体流场进行网格划分，利用MRF模型模拟侧推器螺旋桨旋转绕流场，计算了14组低航速范围内的首尾侧推器推力性能，侧推器螺旋桨的扭矩与推力系数，同时对船舶的侧向力与转首力矩进行分析，对比首尾侧推器推力性能的差异及其受航速的影响。

1 问题描述及数值方法 1.1 研究对象

本文以船长159.70 m的LNG运输及加注船模型为研究对象。船模缩尺比$ \lambda = 1:30 $，船模与实船主尺度参数见表1。

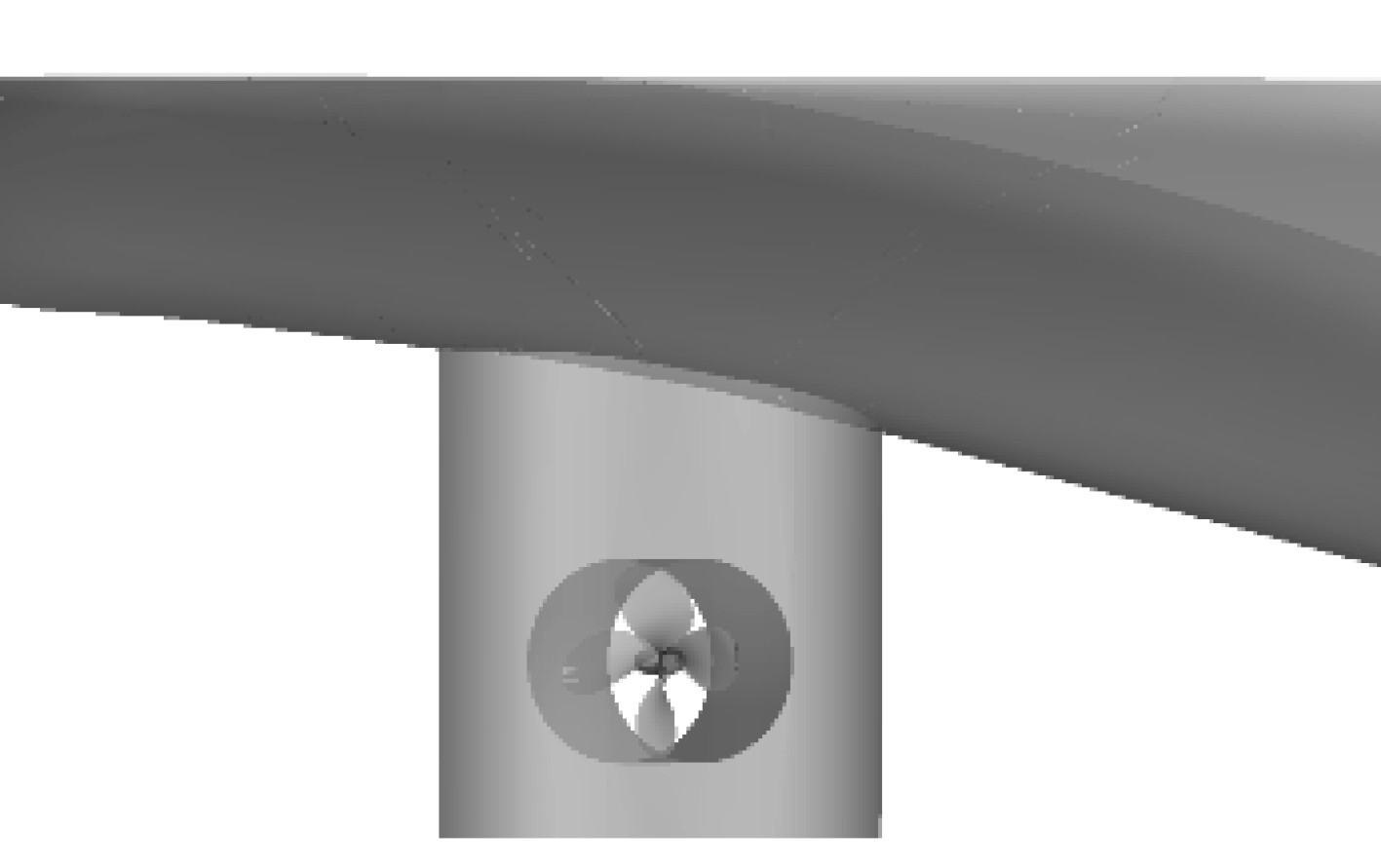
侧推器采用Rolls-Royce TT1650 DPN CP型侧推器，船首部和船尾部各1个，桨型采用可调螺距桨，转速为313 r/min，首侧推的安装位置距首柱14.62 m、距船底2.93 m。侧推器选择了和船模一样缩尺比的侧推器数值模型，螺旋桨直径1.65 m、桨叶4片。按实船总平面图确定首尾侧推器装置的安装点，首侧推距离首柱为14.62 m，尾侧推与尾柱之间的距离为15.38 m。首尾侧推按照相同缩尺比进行缩放并结合某LNG运输和加注船同步构建几何模型。图1和图2分别为首尾侧推器附近区域几何模型示意图。

1.2 航速工况

在采用侧推器的情况下，船舶的速度以中低速为主。大多数的水池试验、实船试验和数值仿真的结果都显示在4～6 kn的速度下首侧推进器将会发生推力的失效^[12]，而尾侧推器推力可能出现不变甚至增加的情况^[13]。本文针对某LNG运输及加注船在中低速范围（v = 0.5 ~7.0 kn） 受到旋转侧推器推力作用运动时的船体周围粘性流场进行数值模拟，并计算粘性水动力和螺旋桨扭矩。本文对14种不同航速情况下船舶流场进行模拟计算，实船航速及对应的模型速度如表2所示。

1.3 粘性流动控制方程和湍流模型

在对计及船体干扰后首尾侧推器水动力这一不可压流体流动进行研究时，流体流动需满足质量守恒和动量守恒，其控制方程如下^[14]：

$ \frac{\mathrm{\mathrm{\partial}}u_{\overline{i}}}{\mathrm{\partial}x_i}=0，$

(1)

$ \frac{\mathrm{\partial}u_{\overline{i}}}{\mathrm{\partial}t}+\frac{\mathrm{\partial}}{\mathrm{\partial}x_j}\left(u_iu_j\right)=-\frac{1}{\rho}\frac{\mathrm{\partial}p}{\mathrm{\partial}x_{\overline{i}}}+v\frac{\mathrm{\partial}}{\mathrm{\partial}x_j}\left[\frac{\mathrm{\partial}u_{\overline{i}}}{\mathrm{\partial}x_j}+\frac{\mathrm{\partial}u_j}{\mathrm{\partial}x_{\overline{j}}}\right]。$

(2)

其中：$ {u_i}、{u_j} $，$ {x_i}、{x_j} $分别为3个维度上的速度分量与坐标分量，$ i,j = 1,2,3 $；$ p $为流场压强，Pa；$ \rho $为流体密度，$ \mathrm{{\rm kg}/{\rm m}}^3 $；$ \nu $为流体的运动粘度，m²/s；t为时间，$ {\mathrm{s}} $。

本文开展侧推器水动力性能数值模研究时选用配合标准壁面函数的$ \mathrm{SST} \;k - \omega $模型，相较其他湍流模型，其在收敛性与精度上均有较好表现。$ {\mathrm{SST}} \;k - \omega $模型中考虑基本湍动剪切应力之后，使用修正湍动粘度定义式对近壁区域及远场均具有良好预测结果^[15]。

2 边界条件与网格划分 2.1 计算域与边界条件

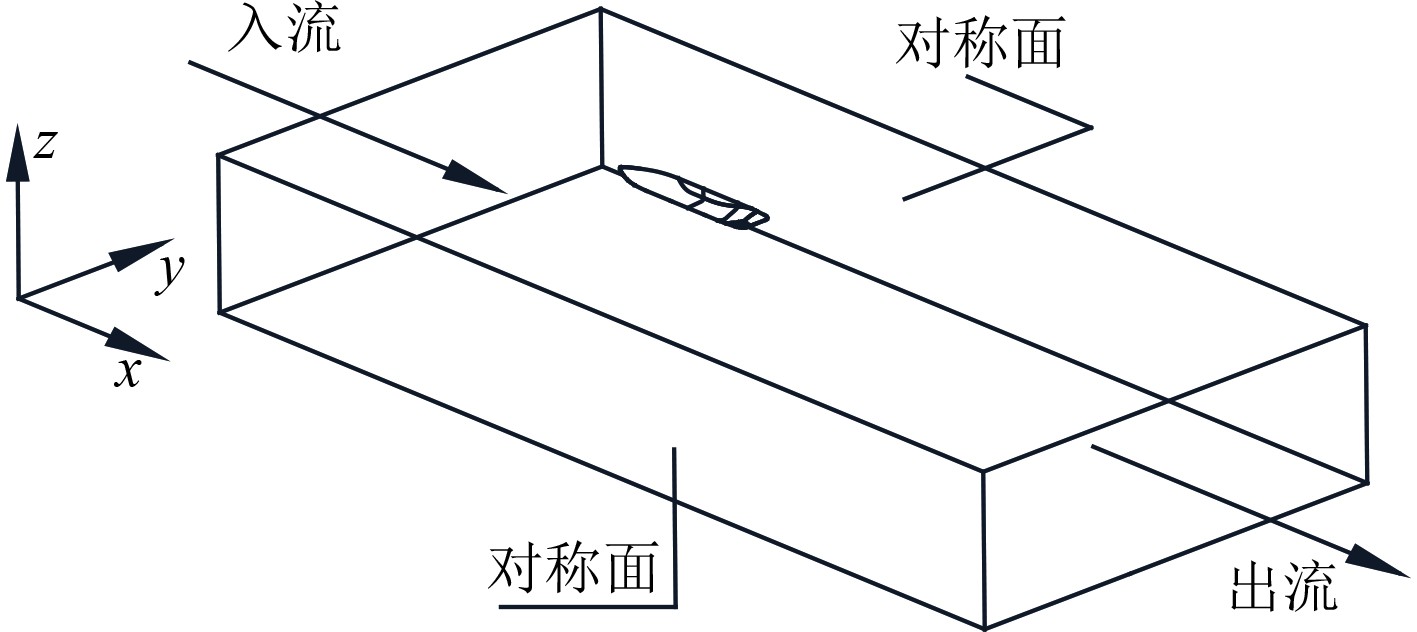
在计算中需要分别对船舶首端和尾端侧推器的推力特性进行数值仿真，在仿真船首侧推器的螺旋桨转动时，船尾侧推器的螺旋桨必须设置在一个没有滑移的固定壁面上；在尾侧推螺旋桨旋转的仿真中，船首侧推器设置在相同的无滑移静壁上。图3为整体外流场计算域及边界条件。本文研究深水情况，在计算区域中来流区以及船体底部以下，计算域边界距离船体1倍船长；尾流区计算域边界距离船尾4倍船长；左右两侧的计算域边界距离船体左右舷侧1倍船长。水流入口设置为速度入流，速度参考见表2。所述出水口设置成出流；底部和顶部计算区域的边界面设置为对称面边界条件；船体表面为无滑移固体壁面边界条件。多重参考系（Multiple Reference Frame，MRF）模型相较滑移网格、动网格方法在计算时间上有很大优势，并且可以得到良好的结果^[16]，因此利用MRF模型模拟螺旋桨旋转，螺旋桨桨叶以及其他部位均设置为滑移壁面，螺旋桨旋转区域和外部区域之间设置为interface交界面来进行数据交换。

2.2 网格划分与求解参数

因为结构性网格在计算速度和精度方面比非结构性网格有更好的表现，因此将结构性网格应用于船体和外部流域，同时对网格的质量进行控制，对船首和船尾进行了Y型网格划分，以解决曲面的过渡问题。在船首和尾部侧推器开口区附近，以适应侧推器出流计算数据交换，还进行了从密集到稀疏的网格过渡。在尾侧推器舱底部的处理中，采取了2种C型网格切分法。

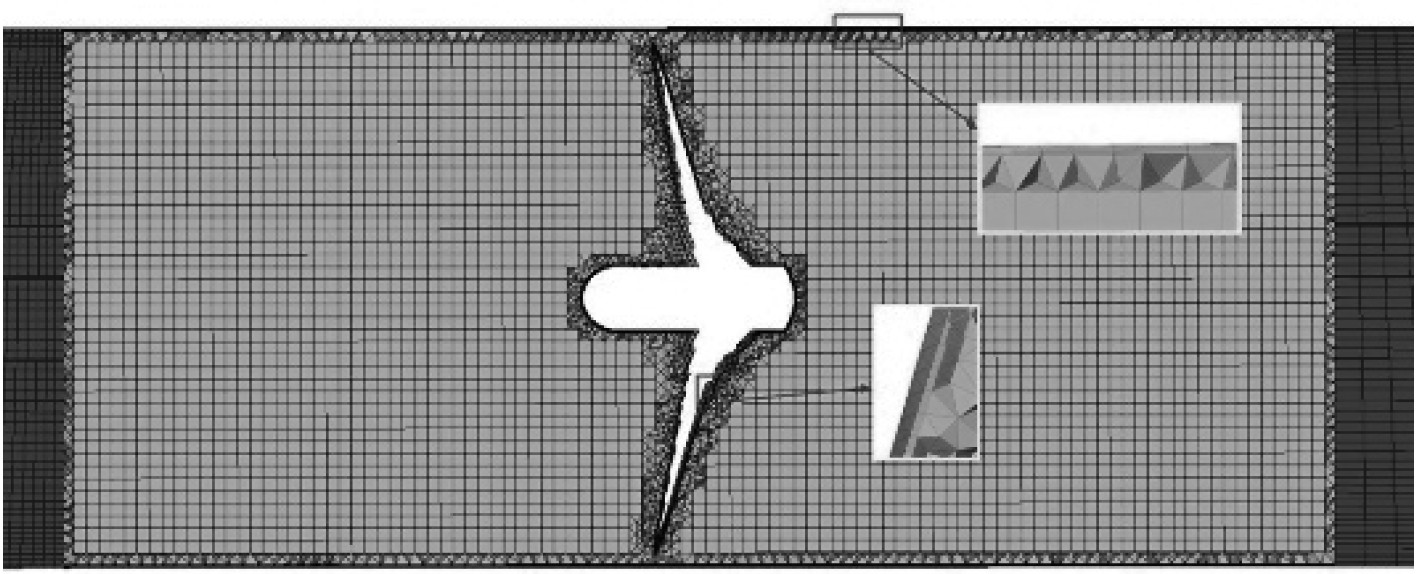
图4为外部流域结构化网格，从图中可以看到密集的边界层网格被布置在靠近船体的位置，把网格布置成由密到疏以提高计算精度并降低计算的工作量。外部区域采用六面体网格，网格数量300万。在艏侧推器内部，在螺旋桨中心的左右两侧分别取侧推器隧道管壁1倍桨径D，此处划分非结构化网格。如图5所示，为让计算更加精准，对隧道管壁、螺旋桨叶表面、桨毂等处设置成三棱柱边界层网格，并通过四面体非结构化网格转换生成首侧推器螺旋桨左右两部分1倍桨径D内流域内六面体内核网格，计算准确度随网格数增加而增加，船首侧推器内包括三棱柱、四面体和六面体三类网格，网格总数为80万。

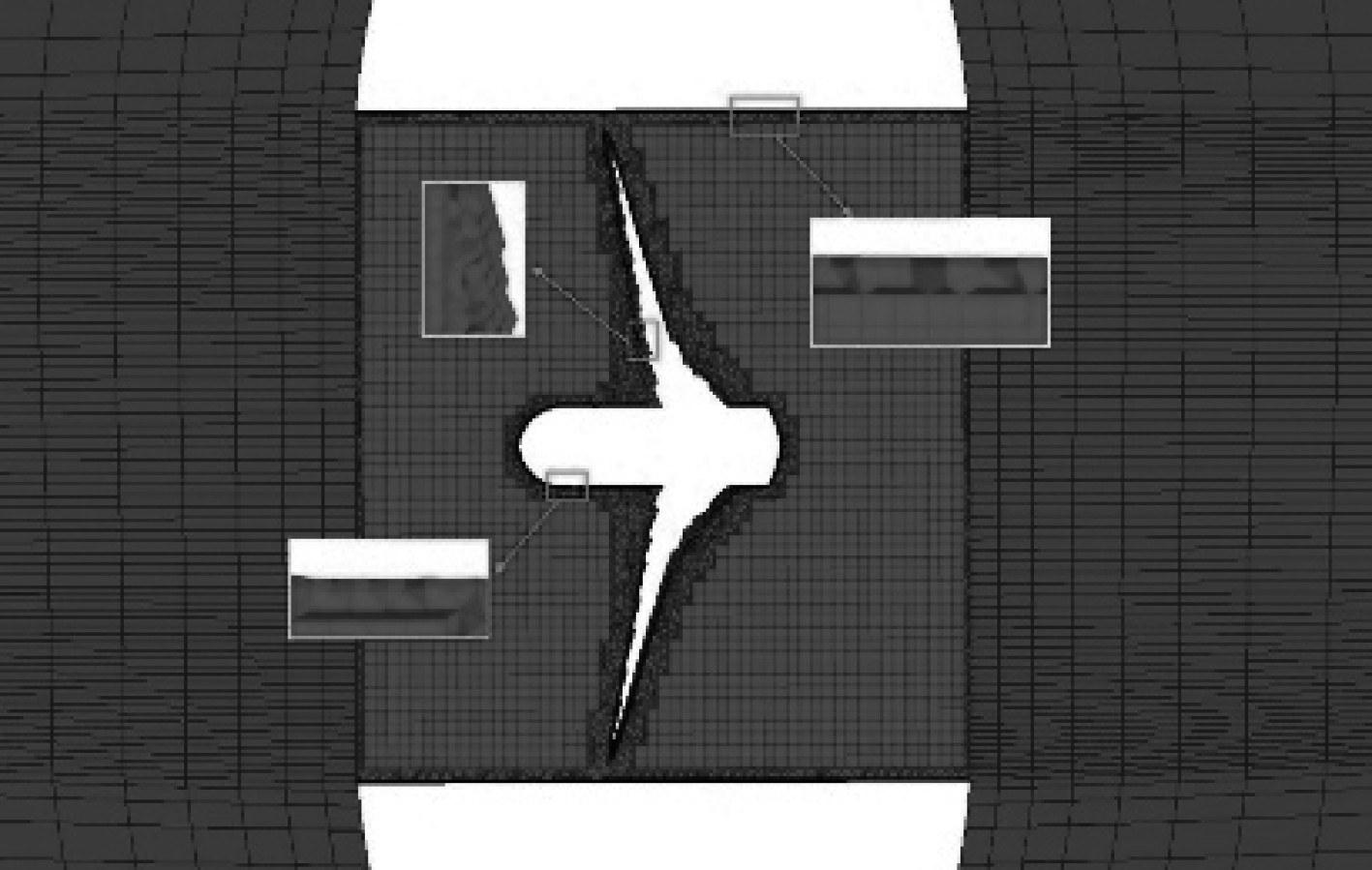
在侧推器隧道的1D外的范围内，采用结构化和非结构化混合网格对计算域进行划分，交界面和界面上采用O型网格，船尾侧推器设备的出口处依然用O型网格，这种混合网格的划分方式便于在数值计算中使用MRF旋转模型。因为尾侧推器隧道是一种标准的圆柱形结构，所以为了满足后期的旋转坐标系计算，不需要利用外部流场的延伸来构造一个内部圆柱形结构，所以螺旋桨叶面和桨毂表面之间，同首侧推器相同，还设有三棱柱边界层网格，如图6所示。尾侧推流域三棱柱、四面体和六面体网格共86万，船首侧推器和船尾侧推器的内部流域以及船舶的外部流域的网格数共450万。

本文采用SIMPLE算法进行压力速度耦合求解，压力离散采用PRESTO！控制方程采用二阶上风格式进行求解。由于研究对象船舶速度范围较小，首尾侧推器浸水深距水线相当远，自由液面在计算中的作用可忽略不计，可使计算时间显著缩短。

3 数值结果分析

侧推器产生的推力应等于船体所受的侧向阻力Y，它包括螺旋桨推力T和诱导侧向力F，除了侧推器机构外船舶所受的侧向力也就是诱导侧向力F。根据下式确定T和F的无量纲系数：

$ C_T=\frac{T}{\rho\mathit{{n}}^2D^4}，$

(3)

$ C_F=\frac{F}{\rho\mathit{{n}}^2D^4}。$

(4)

其中，$ {C_T} $为桨无量纲化推力系数。螺旋桨转矩系数的表达式为：

$ C_Q=\frac{Q}{\rho n^2D^5}。$

(5)

无量纲化的船体侧向阻力系数、转首力矩系数为：

$ C_Y=\frac{Y}{\rho{n}^2D^4}，$

(6)

$ C_M=\frac{M}{\rho{n}^2D^4L}。$

(7)

式中：$ \rho $为流体密度；$ {{n}} $为转速；$ {{D}} $为桨直径；$ {{L}} $为船长；$ Q $为扭矩。

相比于船后螺旋桨进速较大，侧推器运行过程中进速较小，船舶首尾侧推器运转时船体所受的侧向力系数$ \mathit{\mathit{C_Y}} $和转首力矩系数$ {C_M} $更能反映侧推器的作用效果^[17]。

3.1 首尾侧推器推力性能对比

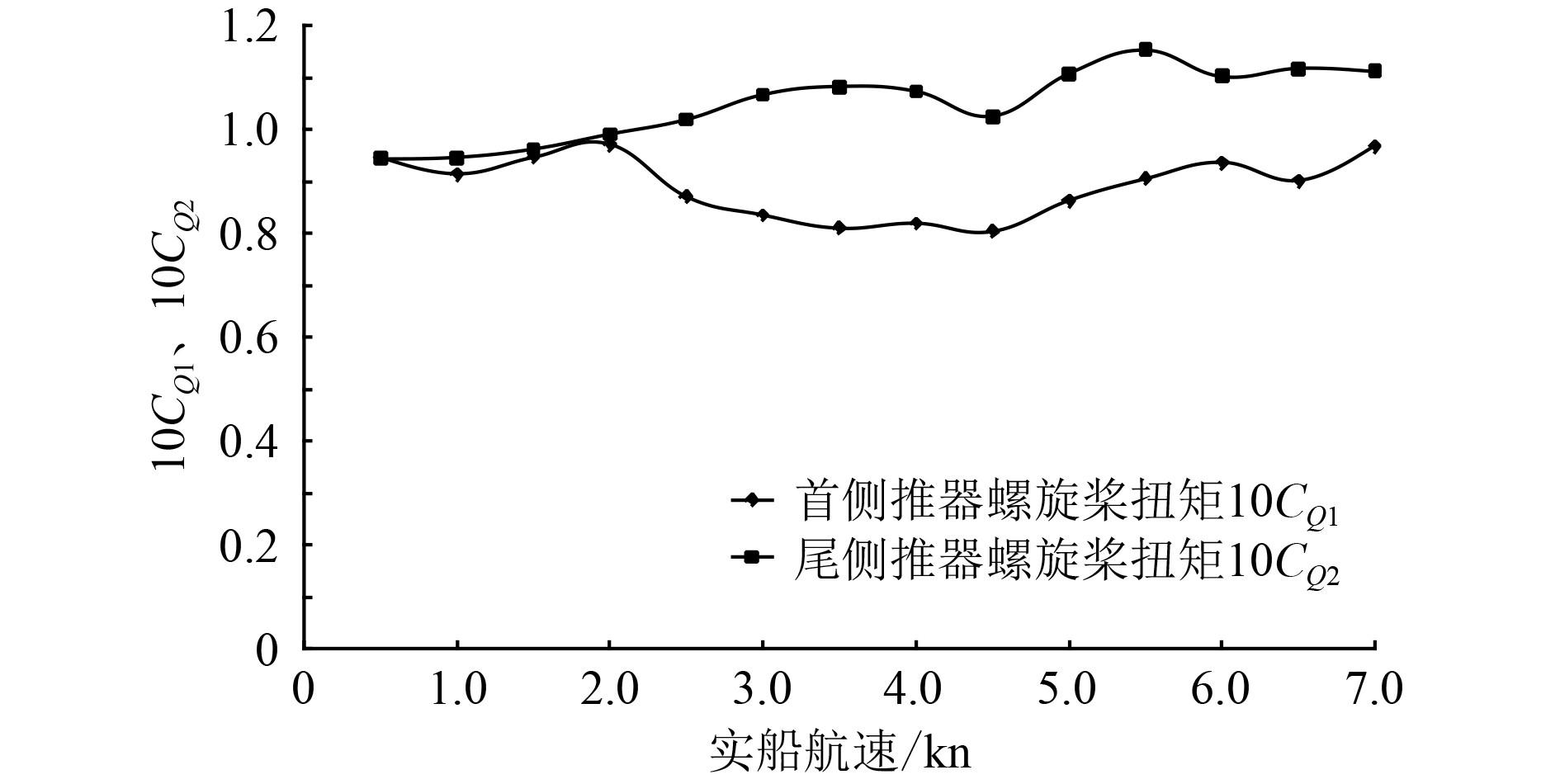
图7为14种航速下首尾侧推器螺旋桨扭矩系数$ {C_{Q1}} $、$ {C_{Q1}} $曲线图。可以看出，2个指标都存在着显著的波动。$ {C_{Q2}} $随航速有一点点的增加，整体上高于$ {C_{Q1}} $，这是因为在面对船体的时候，首侧推器隧道开口会有很大的迎流面积，这就使得它能够在一定程度上产生随螺旋桨进行敞水试验时的来流速度，因此$ {C_{Q1}} $较$ {C_{Q2}} $要小。

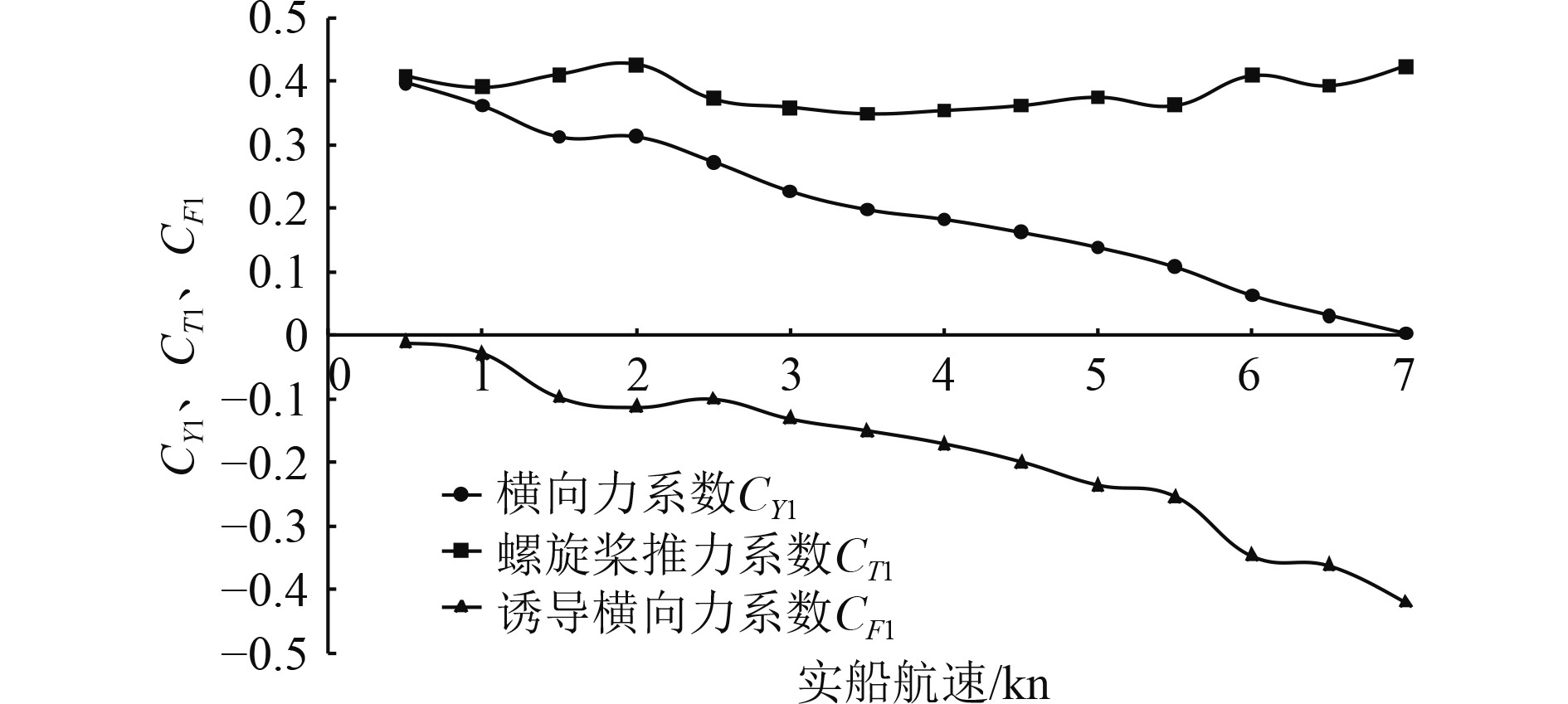
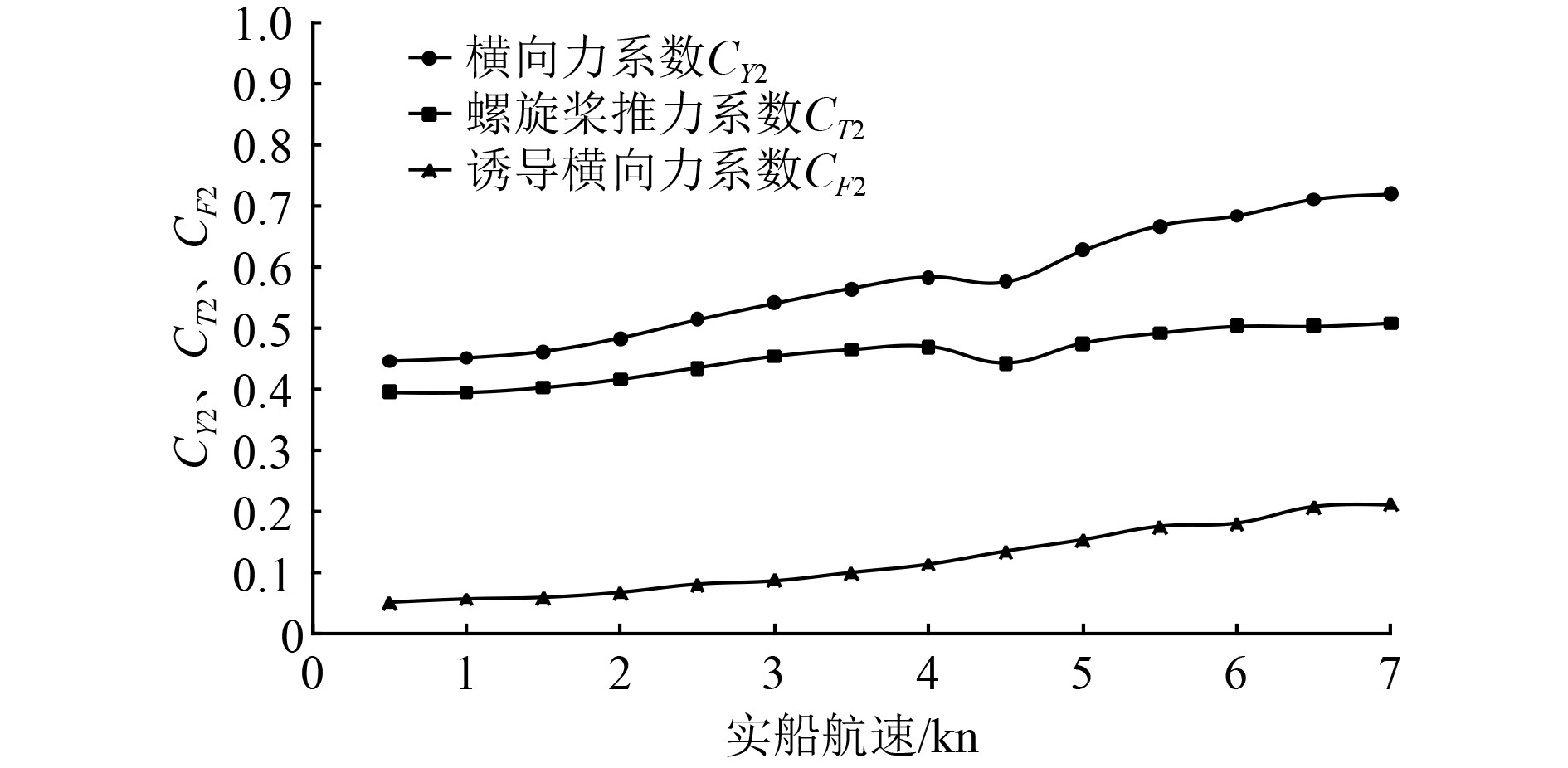
图8和图9分别为船舶在不同航速下，首尾侧推器独立运转时的船体所受侧向力系数$ {C_Y} $、侧推器推力系数$ {C_T} $以及诱导产生的侧向力系数$ {C_F} $。侧推器产生的推力系数$ {C_{T1}} $不同航速状态下总体维持在0.4左右，航速范围在3.0~5.5 kn之间时，$ {C_M} $的值相对较小。在整个航速范围，$ {C_{F1}} $均小于0，因此侧推器射流在船体两侧均产生了较强的反作用力，两侧压力与推进器推力相反，且该反作用力随转速增加较大。首侧推器开启时，侧向力系数$ {C_{Y1}} $在0.5 kn时最大，在7.0 kn左右接近于0。而$ {C_{T2}} $的变化很稳定，随着航行速度的略微提高，其数值在计算的速度之内要高于$ {C_{T1}} $，并且$ {C_{F2}} $一直为正值，据此可推断出其原因是船尾侧推器有单独的舱室，和船首侧推器有区别，船首侧推器是连通安装在首侧推器上的，而船尾侧推器隧道很短，进出流口两侧的流场相互连通，因此由于主船体运动产生伴流效应，船尾侧推器产生的射流将与之发生显著的相互作用，舱内流场区域将形成一个循环流动，从而导致$ {C_{Y2}} $总体维持在较高的水平。通过对比两图可以看出，$ {C_{Y1}} $比$ {C_{Y2}} $小。

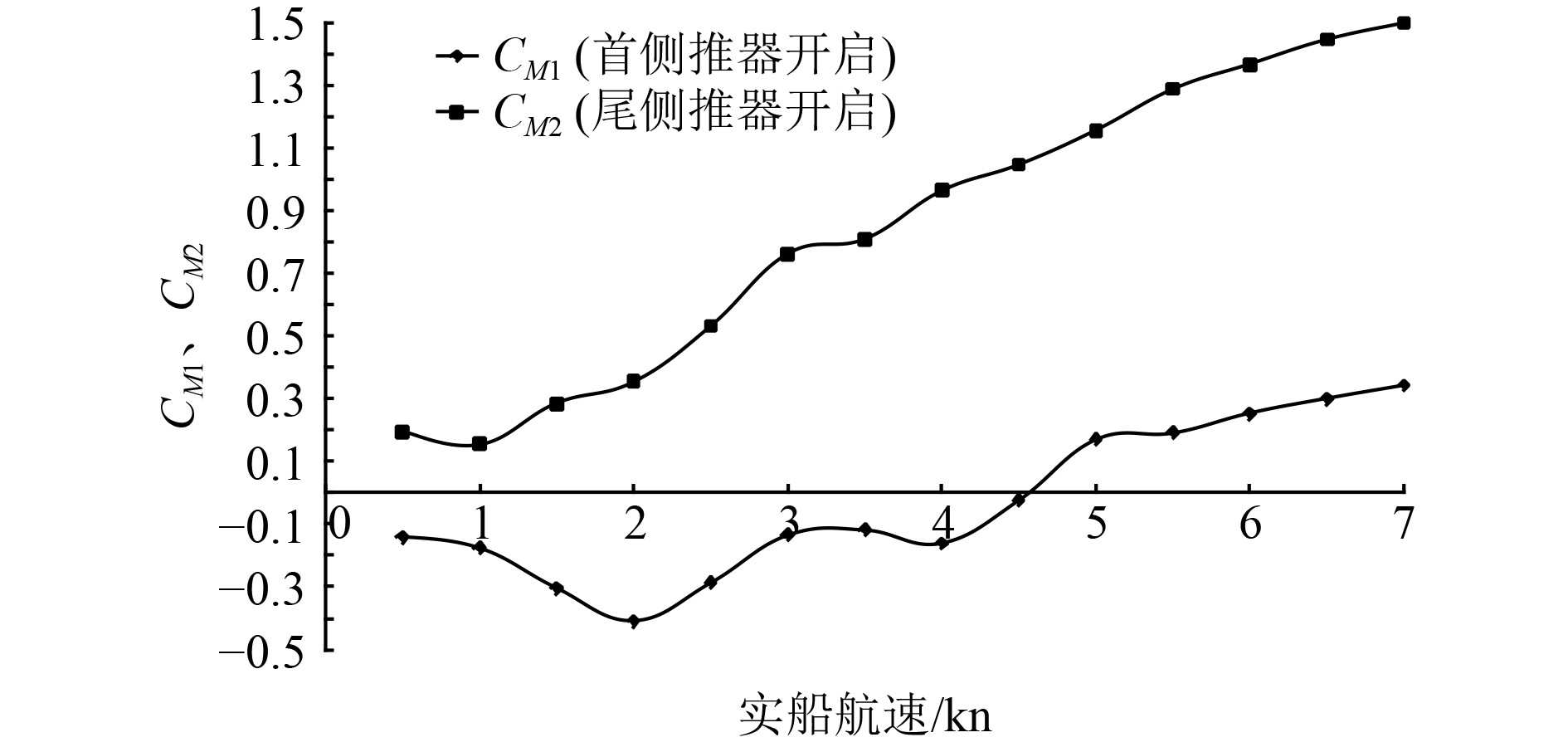
图10为船舶在不同航速下首尾侧推器分别运行时船体所受的转首力矩系数变化曲线。可知，当船尾侧推器打开的时候同时产生反向转首力矩，$ {C_{M2}} $的绝对值比$ {C_{M1}} $大。$ {C_{M2}} $始终保持相同的变化趋势，当航速增大的时候也随之增加。在速度较低时$ {C_{M1}} $为负值，随着航速的增加其大小总体来说逐渐减小。当航速达到4.5 kn左右时，其方向发生改变与之前相反，并随着航速的增加其大小也逐渐增加，此时若使用首侧推器进行船舶回转操纵将存在较大的风险。

3.2 压力场分析

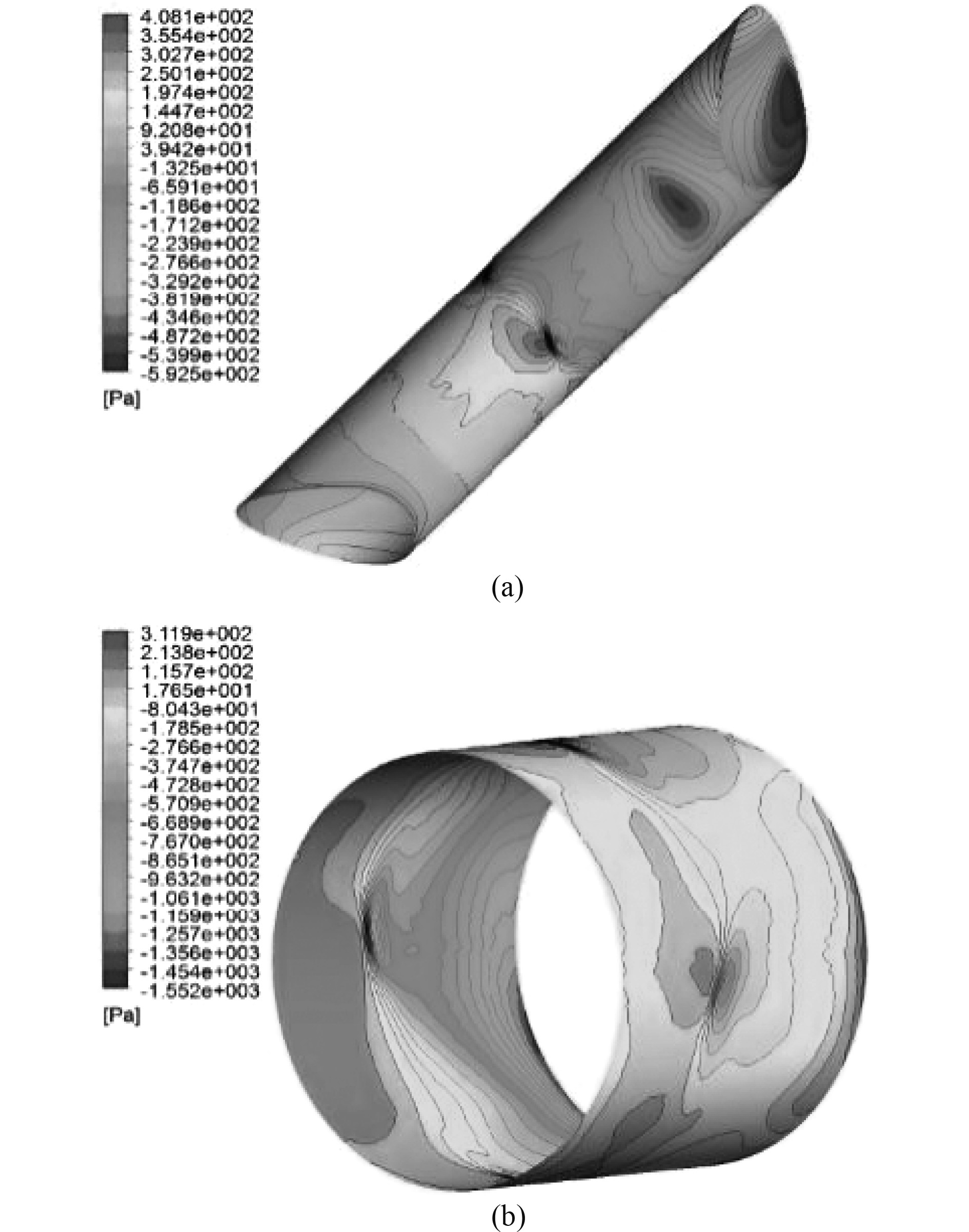
图11为v = 0.730 m/s时船舶首尾侧推器管壁上的压力分布。图中螺旋桨叶梢附近压力变化明显，图11(a)中靠近入口处存在明显的低压区域，表明此区域流场涡流很大，而图11(b)中无此现象，故可推断由于首侧推器开口端的管壁不平齐，还会存在一定程度的偏斜，侧推器进入隧道端口面存在非常显著的入流吸力差从而形成非常显著的涡形。图中在入口处产生的低压区在尾侧推器上更为显着，这表明隧道管壁上的压强大小与隧道长短有关。

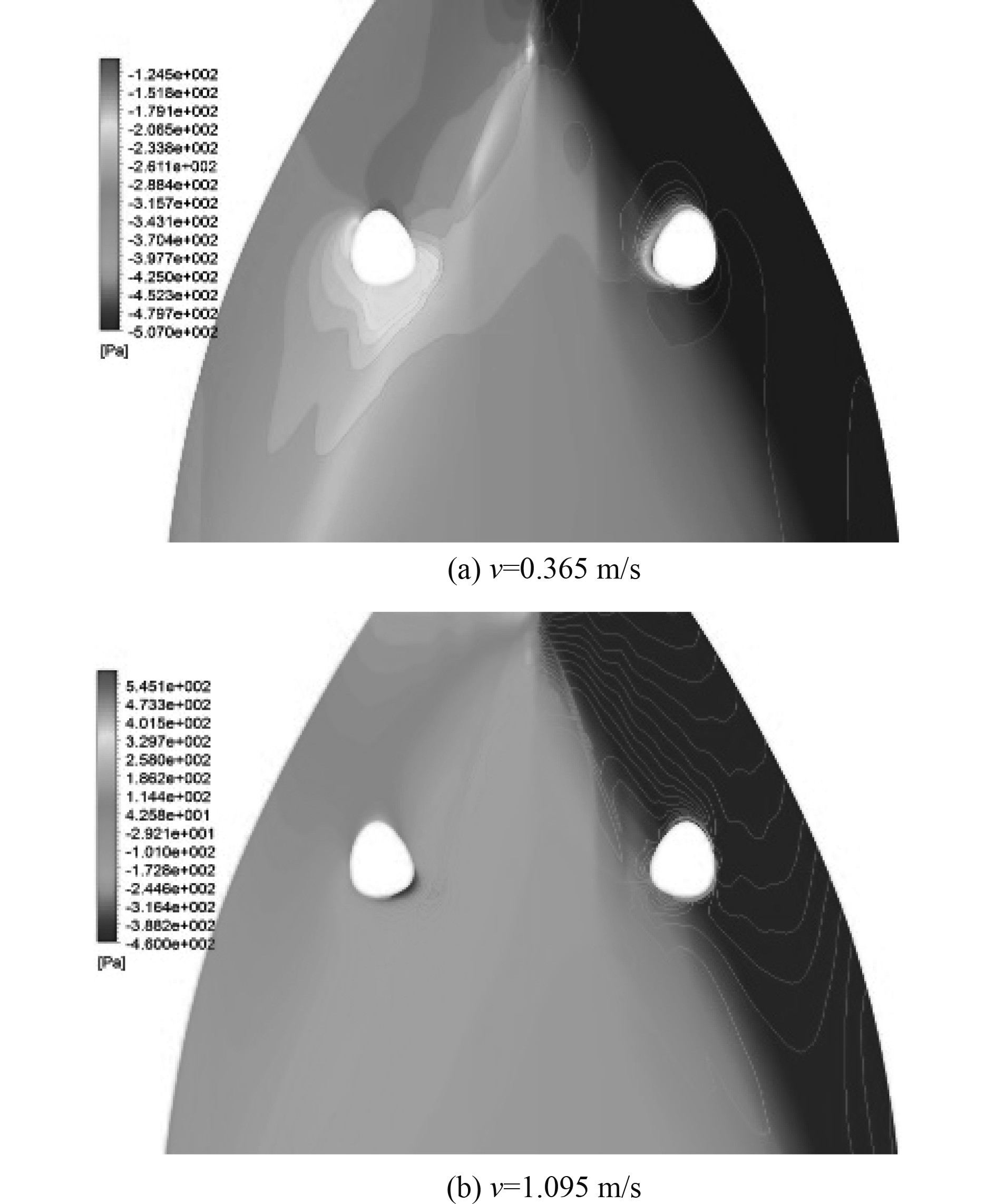
图12为不同速度首侧推器出口和入口附近船体表面压强分布。从图中右端的入流口和左端的出流口均可看出在出流口下游船身表面有明显低压区且在出流口附近低压部位很显著，流速增大后该区域明显增大而压强减小。因为船身的来流和侧推器的射流互相作用，在出流口形成低压区，但船首两侧流场相互独立从而形成较大压差使$ {C_{F1}} $下降，航速越高其下降越显著。

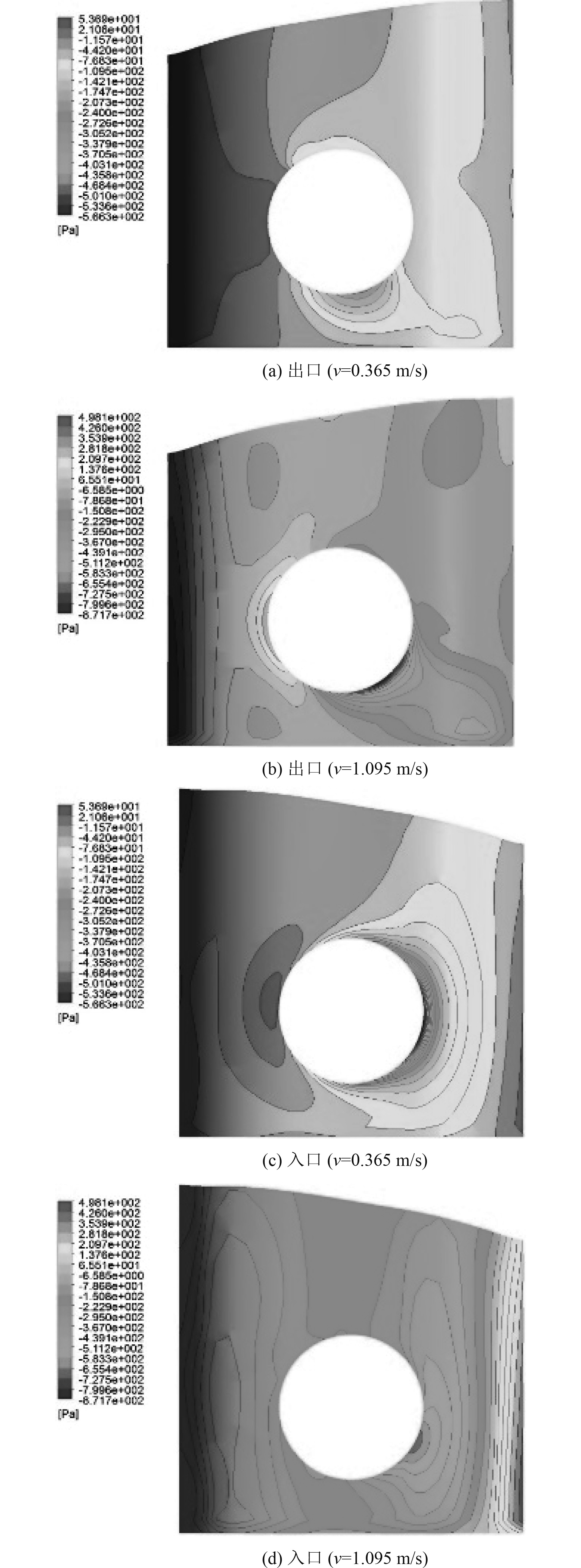
图13为不同速度尾侧推器出口和入口附近船体表面压强分布。与首侧推器情况相似，在其出口附近靠近船体尾部区域存在明显的低压区，当船速增加的时候低压现象更加明显，而且在出口处上游也出现低压。不过由于船体产生的伴流和侧推器的射流互相干扰，部分区域压强较高，入口附近由于抽吸的作用会产生低压区。侧推进器舱的出入流面总压力也不同，一般为出流面高于入流面，其根本原因可能是因为隧道流场的贯通性。

4 结　语

本文采用混合网格技术对全船外流域和侧推器内流域进行网格划分，并基于粘性流体数值求解方法运用MRF模型对船体绕流场和侧推器出入流的互相干扰进行研究，数值模拟首尾侧推器在14种航速下的运转情况，得到以下结论：

1）在首尾侧推器独立运转时，尾侧推器产生的扭矩总体来看大于首侧推器上的扭矩，转速对其扭矩值影响较小。

2）尾侧推器产生的推力大于首侧推器产生的推力，当首侧推器分别以较高转速和较低转速运转时，将产生方向相反的诱导侧向力，在航速较高时诱导侧向力几乎把侧推器产生的推力抵消掉，而尾侧推器产生的推力及诱导侧向力均随螺旋桨转速增加而变大。

3）首侧推器产生的转首力矩在航速较低时方向随其转速发生改变；而尾侧推器产生的转首力矩方向不随其转速改变，其大小随转速增加不断变大。

通过本文数值计算结果发现，采用独立舱室排列且隧道长度较短的尾侧推器具有较好的推力性能，且能在中低速时达到较佳的转首效果。在船舶其他性能满足相关规定的情况下，首侧推器的设计思路可借鉴尾侧推器布局设计以提高其侧推效果。