潜艇是“三位一体”核打击中的重要组成部分,确保其隐身性能是航行的关键,而潜艇航行产生的湍流尾流是雷达探测的重要目标[1]。潜艇围壳与艇身连接处产生的马蹄涡结构对尾流(桨盘面)影响较大,因推进螺旋桨工作于潜艇的尾流区域,此处的入流均匀性和螺旋桨产生的噪声直接相关,故研究围壳前缘马蹄涡形态特征、控制方法及其对潜艇尾流的影响,对降低潜艇航行时的噪声并提高其隐身性能具有重要意义。
SUBOFF全附体潜艇模型是美国大卫泰勒研究中心的DARPA SUBOFF研究小组于1989年提出,并给出了阻力、压力、摩擦阻力以及桨盘面位置处的轴向无量纲速度等实验数据[2 − 3]。随着计算流体力学(Computational Fluid Dynamics, CFD)技术的发展,其逐渐成为研究潜艇绕流场的重要工具之一[4 − 6]。QU等[7]基于大涡模拟(Large Eddy Simulation,LES)计算了SUBOFF全附体模型流场,并采用Q准则和Liutex方法分析了围壳与艇体交接处的马蹄涡形态特征,发现此处马蹄涡呈现高强度的U形结构且围壳前缘有横向涡流产生。刘志华等[8]采用分离涡模拟(Detached Eddy Simulation,DES)对在围壳前缘两侧加装消涡整流片的SUBOFF潜艇进行研究,发现消涡整流片既能有效控制马蹄涡强度,又降低了潜艇尾部的伴流影响。LIU等[9 − 10]则采用LES方法对SUBOFF模型的绕流流场进行计算,研究发现布置在距围壳前缘1.64 m处并与来流方向呈30°角的三角形机械涡流发生器,可抑制围壳前缘马蹄涡的形成,围壳前缘锯齿则可降低马蹄涡强度。
根据公开文献报道,在围壳与艇体结合部加装填角,亦能达到调控围壳底部区域马蹄涡的效果。张楠等[11]对加装了前缘填角的直立型围壳及不同流线型围壳的潜艇模型进行数值模拟,结果表明该措施改善了围壳附近的流动品质,围壳下游马蹄涡涡腿明显弱化。TOXOPEUS等[12]基于全附体BB1艇体,采用CFD方法研究围壳填角对马蹄涡的影响,研究表明合适的填角可很好地抑制马蹄涡的形成及尾流的耗散。WANG等[13]对SUBOFF全附体模型进行数值模拟计算,对围壳前缘填角参数化分析,发现加装当高度和长度尺寸合适的抛物线填角时,能有效降低围壳处马蹄涡强度。此外,李孟捷等[14 − 15]研究尾翼加装填角时,潜艇尾流场变化,发现可抑制艇尾马蹄涡强度并改善尾部伴流场。
综上可知,改变围壳几何外形、增加附属消涡结构及尾翼处加装填角均可控制近潜艇附体区域的马蹄涡强度,进而影响潜艇尾流场。而前人对围壳填角几何外形研究大多在同一类型填角的参数变化。基于此,本文在围壳根部前缘加装凸线型、平线型和凹线型的平滑过渡围壳填角,采用数值模拟方法,研究填角几何型线对马蹄涡的产生、强度以及潜艇尾部伴流场的影响。
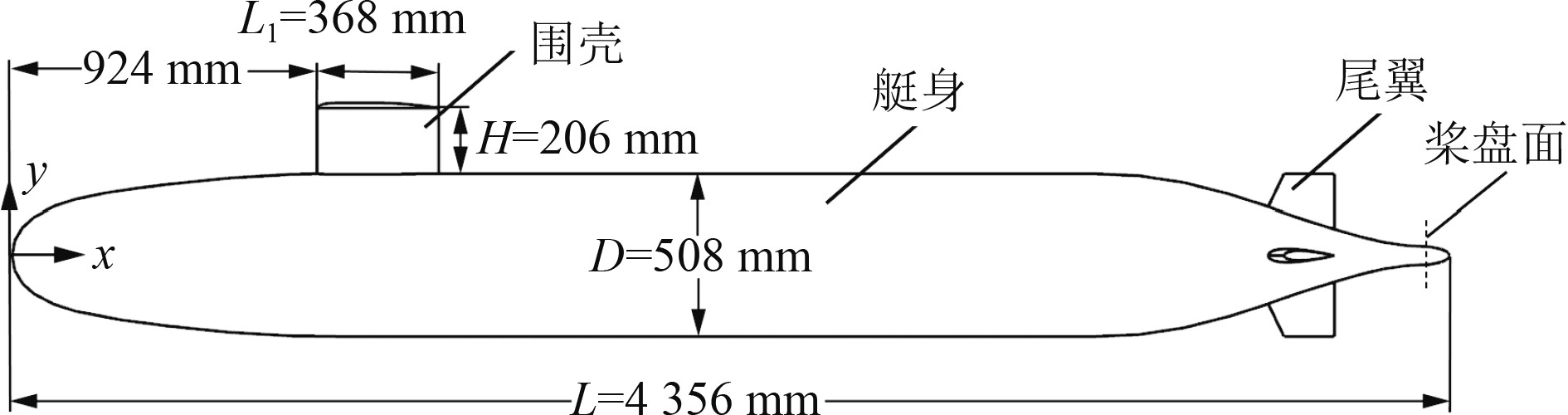
1 数值研究方法 1.1 计算模型本文以SUBOFF模型为基础模型。由图1可知,该模型主要由轴对称的艇身、围壳和尾翼3部分组成。艇首顶部为坐标原点,x轴与艇身轴线重合,总长L=4356 mm,艇身最大回转直径D=508 m,即R=254 mm,围壳前缘位于x=924 mm处,围壳长和高分别为L1=368 mm、H=206 mm。推进螺旋桨安装在桨盘面,即x/L为0.978处。
|
图 1 SUBOFF潜艇模型几何尺寸 Fig. 1 Geometric data of SUBOFF model |
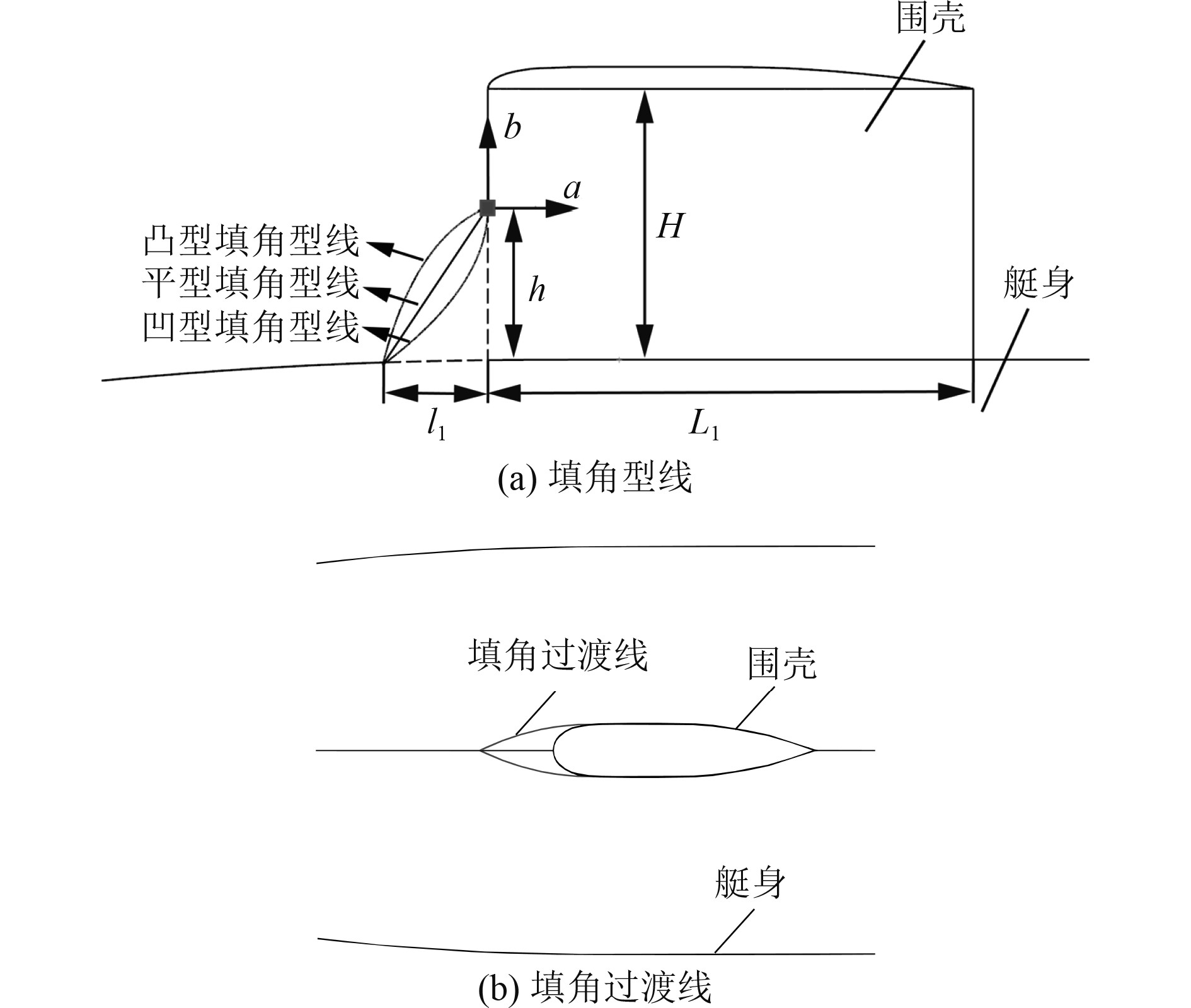
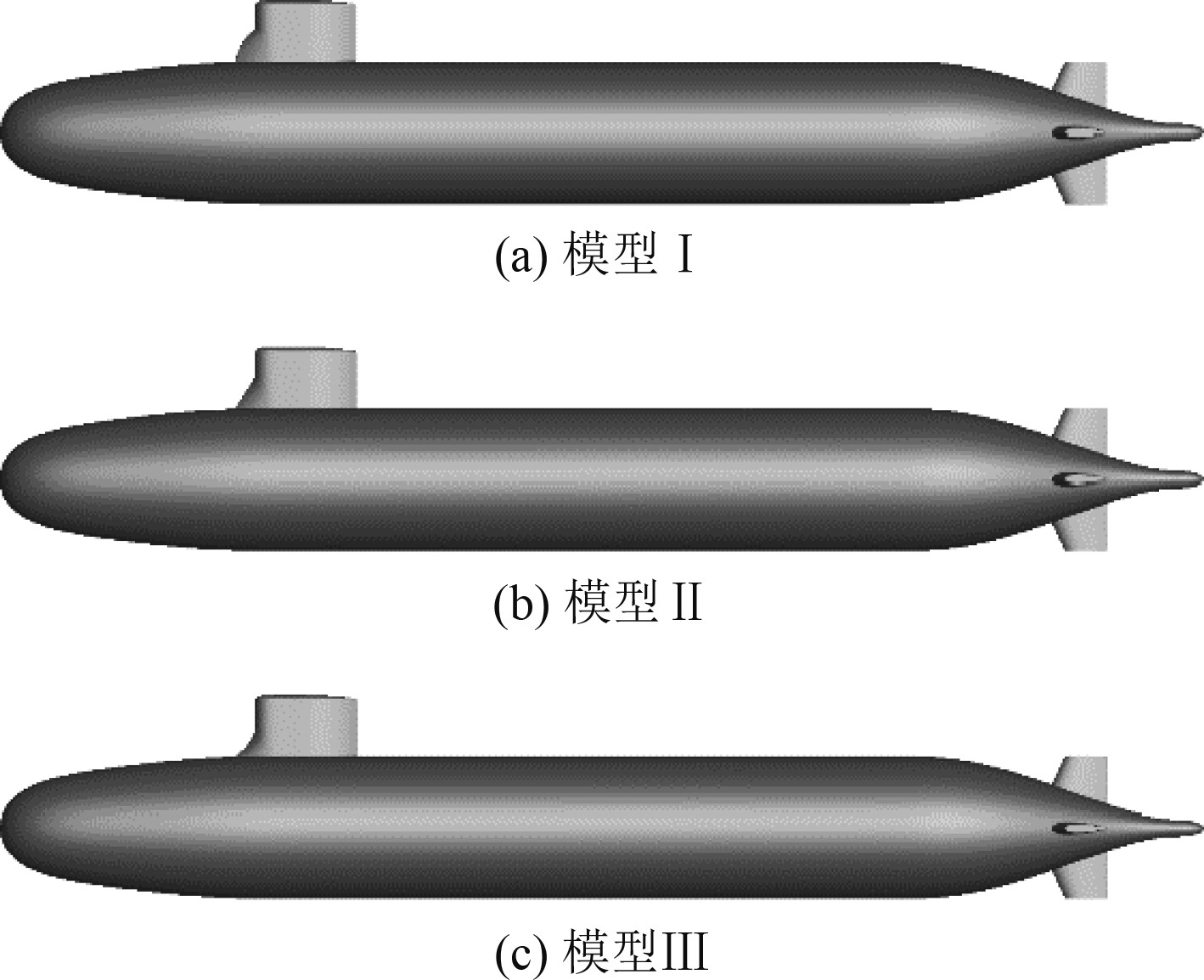
为表达填角型线,本文参考文献[12]建立了如图2所示的局部坐标系,图中h和l1分别为填角的高度和长度,研究时选取h/H=0.58,l1/L1=0.22。为保持围壳与艇体过渡区域形状流畅,保证型线在围壳最大厚度处相切的前提下,以弧形作为围壳前缘的填角过渡线。凸型、平型和凹型3种围壳填角型线表达式如表1所示。为方便起见,加装了填角Ⅰ、Ⅱ、Ⅲ的潜艇模型分别命名为模型Ⅰ、模型Ⅱ、模型Ⅲ,如图3所示。
|
图 2 填角型线与填角过渡线 Fig. 2 Fairwater fillet curve and fillet transition line |
|
|
表 1 填角型线函数 Tab.1 Fillet curve function |
|
图 3 含围壳填角潜艇模型 Fig. 3 Model of submarine with fairwater fillet |
数值模拟时潜艇航速取3.05 m/s,此为低马赫数流动问题。在笛卡尔坐标系下,不可压流体雷诺时均Navier-Stokes方程(简称N-S方程)为:
| $ \frac{{\partial {U_i}}}{{\partial {x_i}}} = 0 ,$ | (1) |
| $ \frac{{\partial {U_i}}}{{\partial t}} + \frac{{\partial \left( {{U_i}{U_j}} \right)}}{{\partial {x_j}}} = - \frac{1}{\rho }\frac{{\partial P}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left[ {\nu \left( {\frac{{\partial {U_i}}}{{\partial {x_j}}} + \frac{{\partial {U_j}}}{{\partial {x_i}}}} \right)} \right ] - \frac{{\partial \overline {{{u'}_i}{{u'}_j}} }}{{\partial {x_j}}}。$ | (2) |
式中:
本文流场计算采用RNG
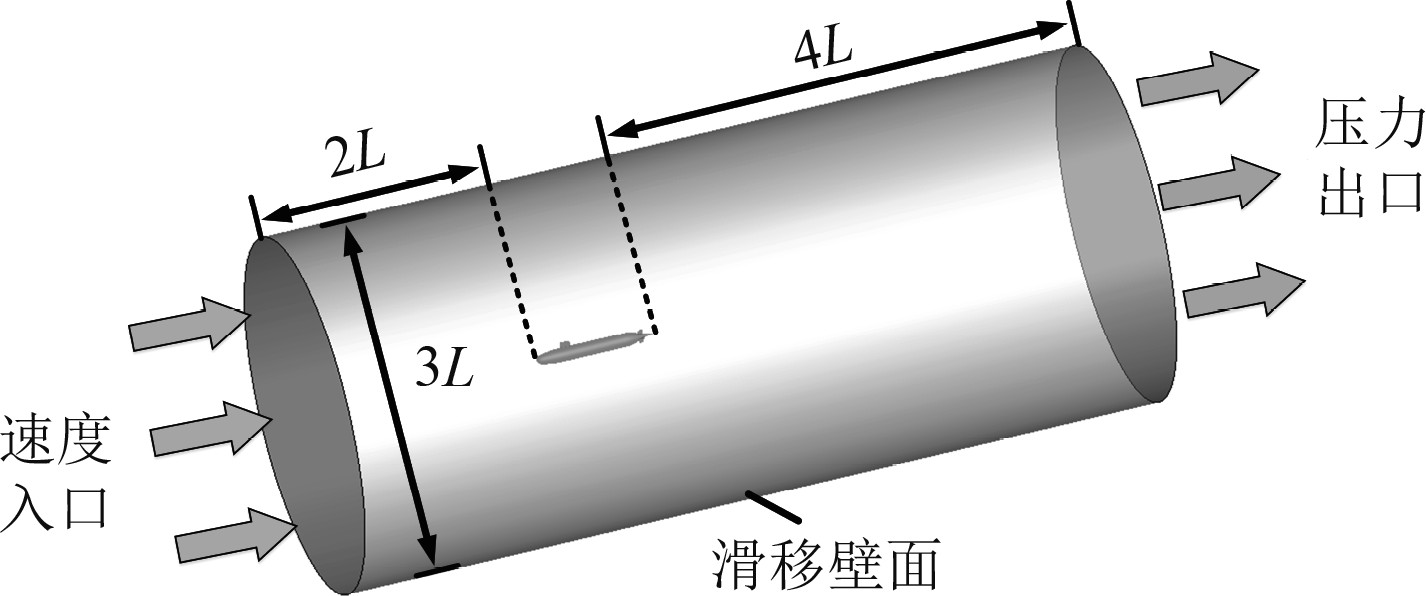
数值模拟的计算域为圆柱域,如图4所示。计算域进口至艇首的距离为2L,艇尾至计算域出口取4L,柱体直径为3L,其中L为潜艇艇长。给定速度进口,压力出口边界条件,侧面为零剪切光滑壁面,潜艇表面则采用无滑移壁面。
|
图 4 流场计算域 Fig. 4 Flow field computing domain |
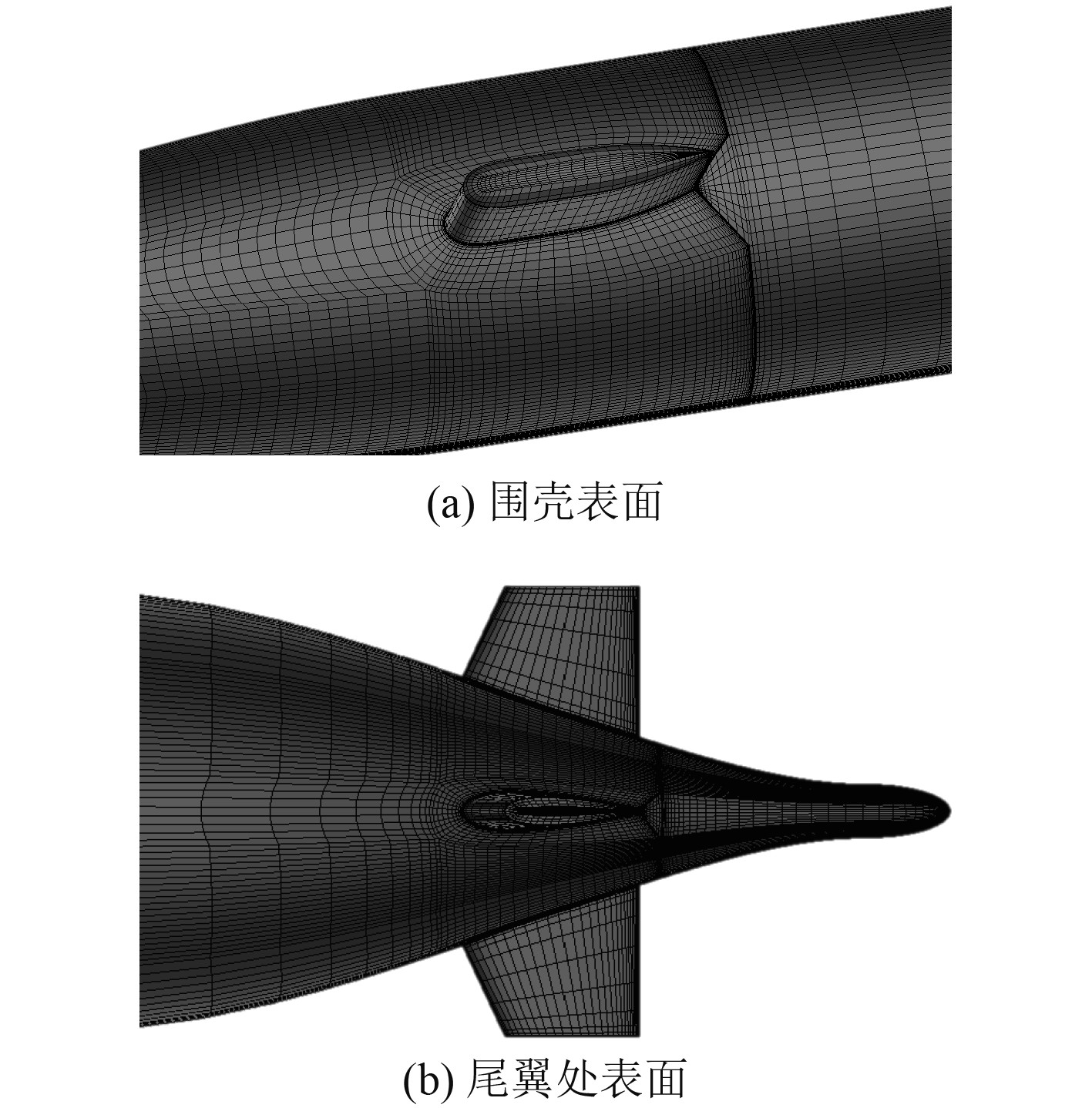
为确保计算域网格质量,采用分区域结构化网格对计算域进行离散,对潜艇表面、近流场及尾流场区域的网格进行加密,网格量为615万,网格质量在0.3以上。图5为围壳以及尾翼附近的局部网格示意图。
|
图 5 网格示意图 Fig. 5 Grid diagram |
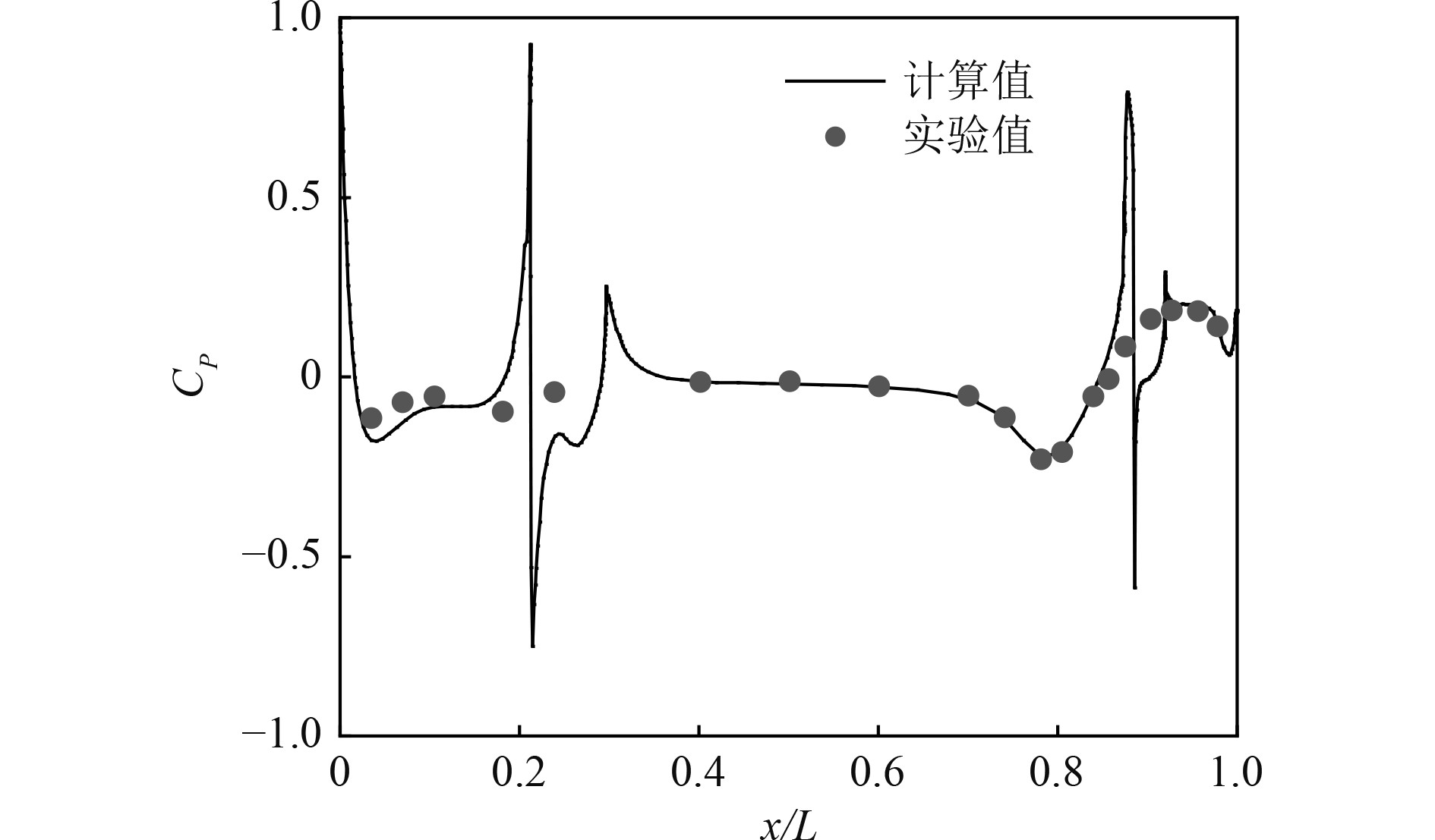
在来流速度为3.05 m/s条件下,对SUBOFF模型进行定常计算,计算得到阻力值为100.8 N,与实验中的102.3 N误差为1.4%。图6为潜艇中纵剖面上半缘线上的压力系数
|
图 6
|
| $ {C_P} = \frac{{P - {P_{ref}}}}{{0.5{\rho _{ref}}v_{ref}^2}} 。$ | (3) |
式中:
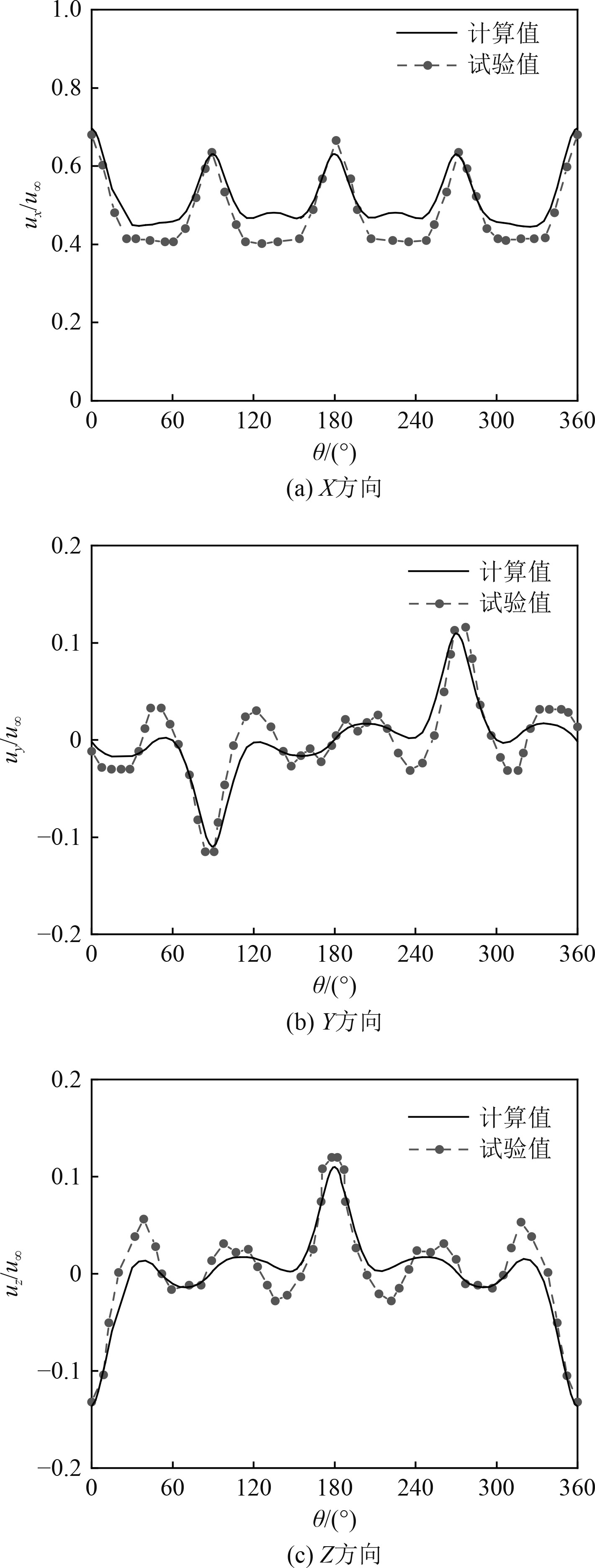
图7为桨盘面上r/R=0.25处流体在X、Y、Z这3个方向的伴流分数沿周向的分布,图中
|
图 7 r/R=0.25桨盘面处各方向伴流分数[3] Fig. 7 The wake fraction in each direction at the r/R=0.25 propeller plane[3] |
|
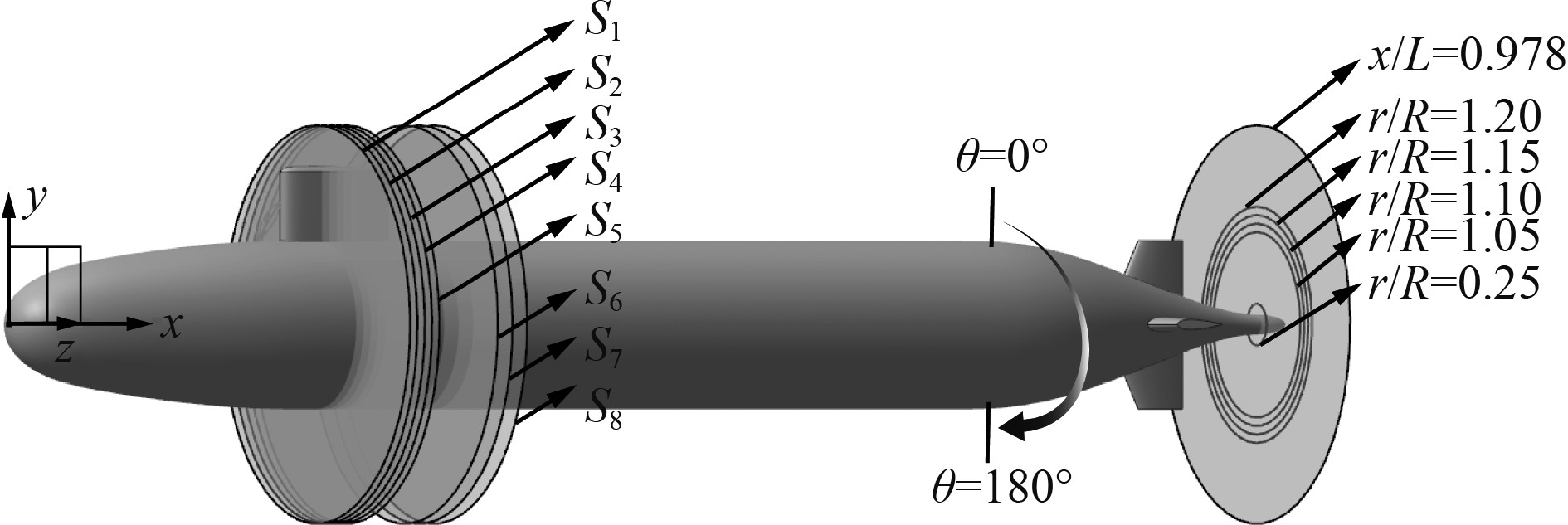
图 8 观测截面与尾部桨盘面处圆观测线位置示意图 Fig. 8 Position of sections and lines of circle at propeller plane |
通过图6和图7中实验值与计算值的对比,验证了计算方法的可行性。
2 结果与讨论 2.1 围壳填角形状对马蹄涡强度的影响图8为围壳处沿流向布置的S1~S8这8个流场观测截面,以及潜艇尾部桨盘面处不同半径位置上的圆观测线示意图。图中截面S1为x/L=0.240,沿来流方向间隔x/L=0.005取5个截面,而S6为x/L=0.310,沿来流方向间隔x/L=0.010取3个截面。
图9为SUBOFF模型与模型Ⅰ、模型Ⅱ、模型Ⅲ近围壳区域对称面及y=R的XZ平面上X方向速度云图与流线分布。

|
图 9 各模型围壳处速度云图与截面流线 Fig. 9 Velocity and streamline of each model in the fairwater |
由图9(a)SUBOFF模型围壳前缘根部处流线与X方向速度分布可知,由于围壳本身的阻滞作用,使得围壳前缘端壁区域的低能量流体逆向流动,与前方来流在围壳根部前缘位置相遇,形成马蹄涡的鞍点。观测图9(a)围壳处S1~S5截面上的流线,可见在围壳与艇体交接的壁角处,存在二次涡结构,且涡的范围沿来流方向先增大后减小,由文献[7, 12]对马蹄涡发展的论述,该5处截面产生的二次涡结构实为微小纵向涡进一步被拉伸而成的马蹄涡涡腿,加之围壳形状与水翼类似,此结构使得流体沿来流方向先收缩后扩张,故马蹄涡涡腿强度先增强后减弱;观测图9(a)围壳侧面近流场速度云图及S5截面流线,围壳侧流流体被加速后与围壳表面产生压力差,使得截面流体往围壳侧面流动,两侧方向的压差促使流体在围壳尾缘处汇合,从而使截面S6~S8处马蹄涡涡腿强度沿来流方向逐渐增强。
由图9(b)~图9(d)可知,模型Ⅰ、模型Ⅱ、模型Ⅲ围壳前缘根部处的流线无局部回流和微小纵向涡,且在围壳侧面处截面S1~S5流动正常向下游传播,即平滑过度填角起到了导流效果,来流流体沿着填角表面往后流动,有效抑制了马蹄涡的产生;由观测截面S5~S8处流线可得,因含围壳填角模型Ⅰ、模型Ⅱ、模型Ⅲ的围壳侧面结构较SUBOFF模型的改变仅在围壳侧面前端,故模型Ⅰ、模型Ⅱ、模型Ⅲ与SUBOFF模型在截面S5~S8处流体流向成因相同。此外,在围壳尾缘处截面S6~S8形成了沿来流方向逐渐增强的涡结构,根据流体力学定义,该涡结构为涡管[16],且此处涡管强度较SUBOFF模型马蹄涡涡腿低。
通过对图9的分析,平滑过度填角对围壳前缘根部处消除纵向涡有显著效果,且抑制了马蹄涡的产生,且模型Ⅰ、模型Ⅱ、模型Ⅲ在围壳前缘根部处对来流有很好地导流效果,这也间接说明了马蹄涡在围壳前缘根部与侧面处起源与发展,围壳前缘根部形状对马蹄涡的产生与强度有重要影响。
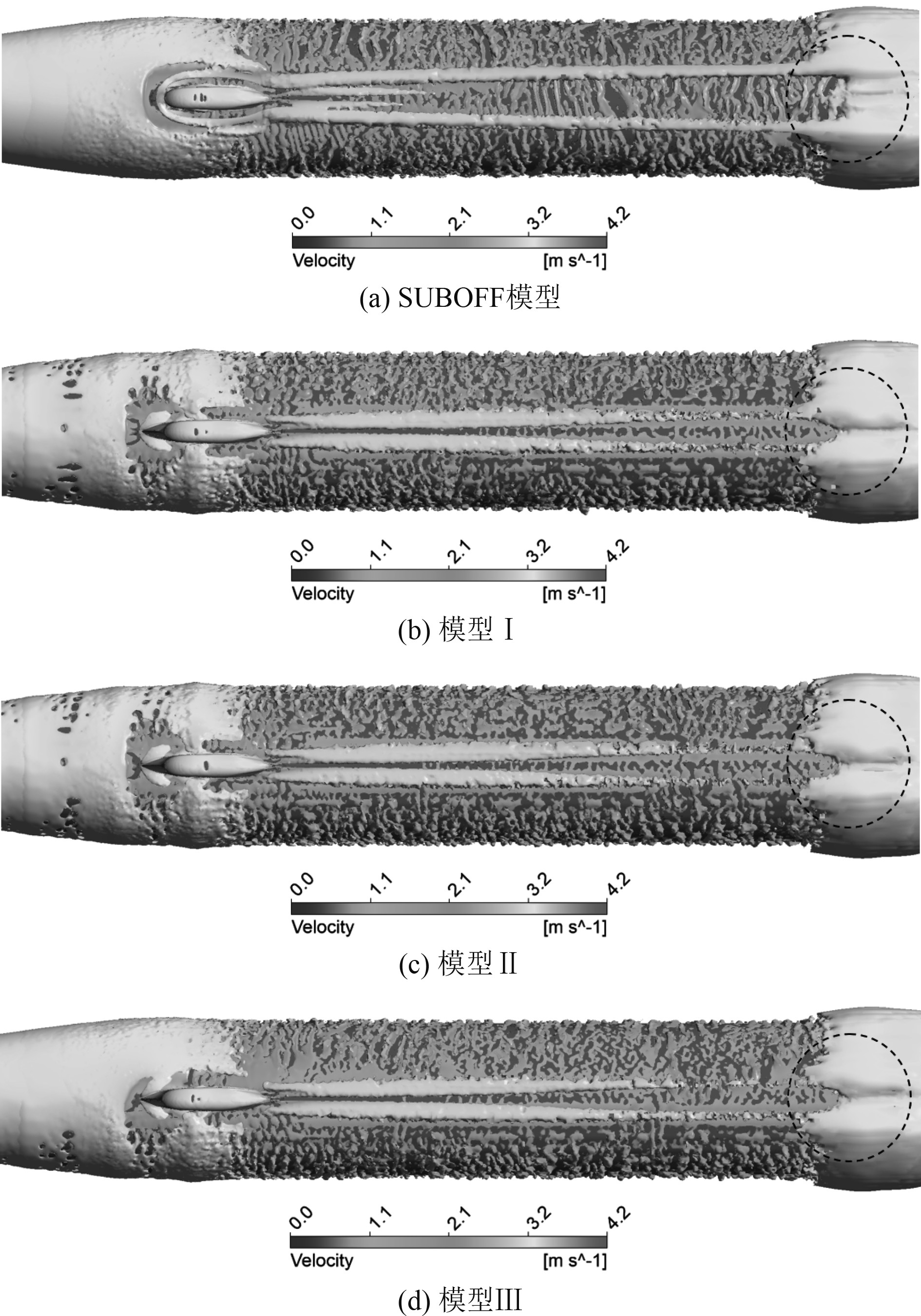
为更加直观地观测模型Ⅰ、模型Ⅱ、模型Ⅲ围壳附近的马蹄涡结构区别,图10为采用Q准则的瞬时等值面图。图10(a)中U形结构的马蹄涡过围壳后沿下游一段距离内逐渐增强并趋于稳定,围壳附近的马蹄涡涡腿强度呈先增强后减弱趋势,与图9(a)描述一致。从图10(b)~图10(d)中明显看出,围壳加装填角后有效阻碍了马蹄涡的产生,进而抑制了马蹄涡强度。当马蹄涡沿艇身发展时,由于涡能量耗散,在艇尾部会形成一个明显的凹陷,较原模型相比,3种不同围壳填角模型的凹陷宽度变窄,这正是填角削弱围壳马蹄涡强度的表现。
|
图 10 Q准则的瞬时等值面(Q=1.5 s−2) Fig. 10 Instantaneous isosurface of Q criterion (Q= 1.5 s−2) |
上节对围壳附近马蹄涡产生及其强度进行分析,发现模型Ⅰ、模型Ⅱ、模型Ⅲ都可抑制马蹄涡产生,为深入探究何种围壳填角对潜艇尾部伴流场的入流均匀性影响较大,提取潜艇桨盘面处流场信息进行研究。
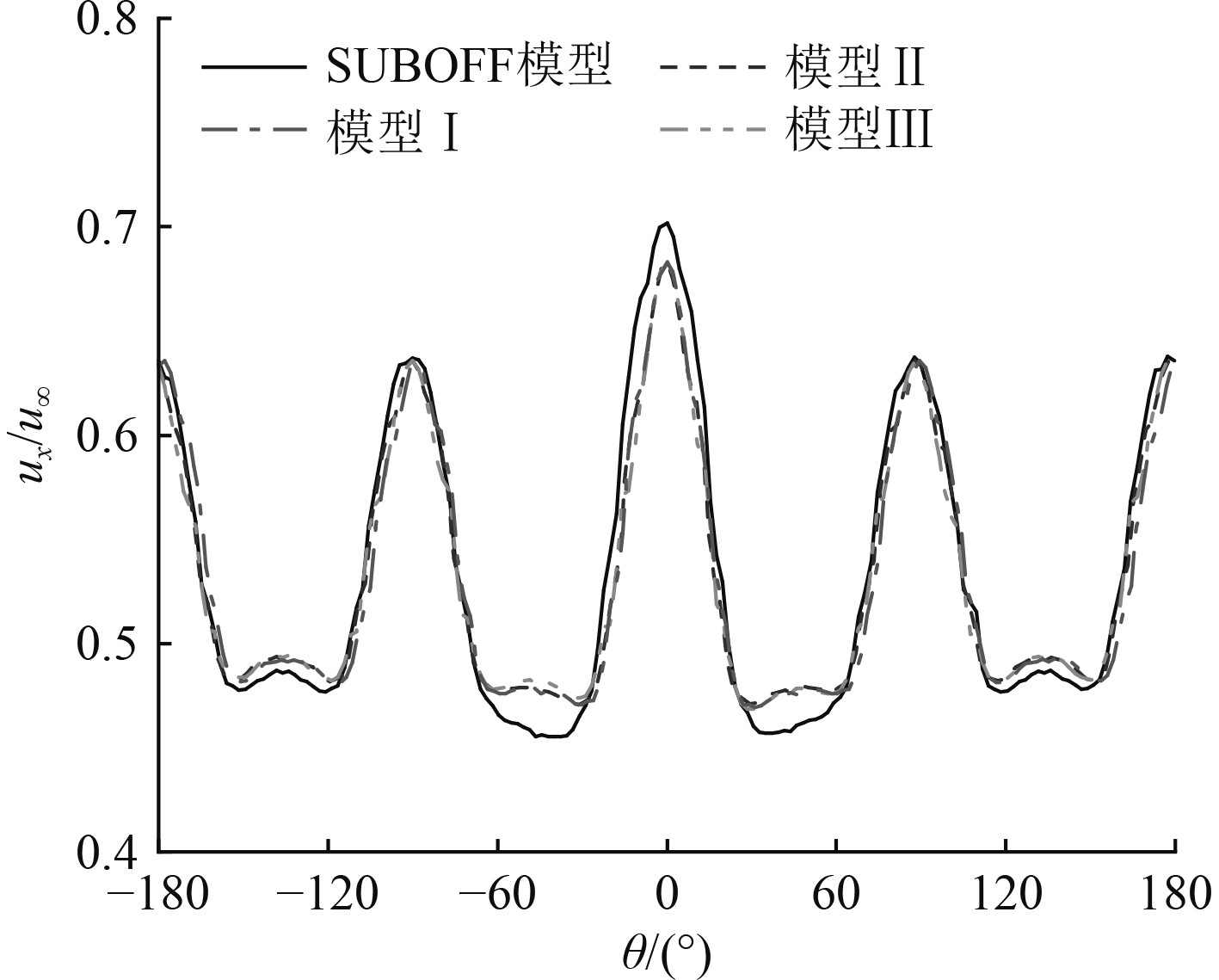
图11为桨盘面上r/R=0.25处,不同模型的
|
图 11 r/R=0.25桨盘面处X方向速度分量 Fig. 11 Velocity component of X direction in r/R=0.25 propeller plane |
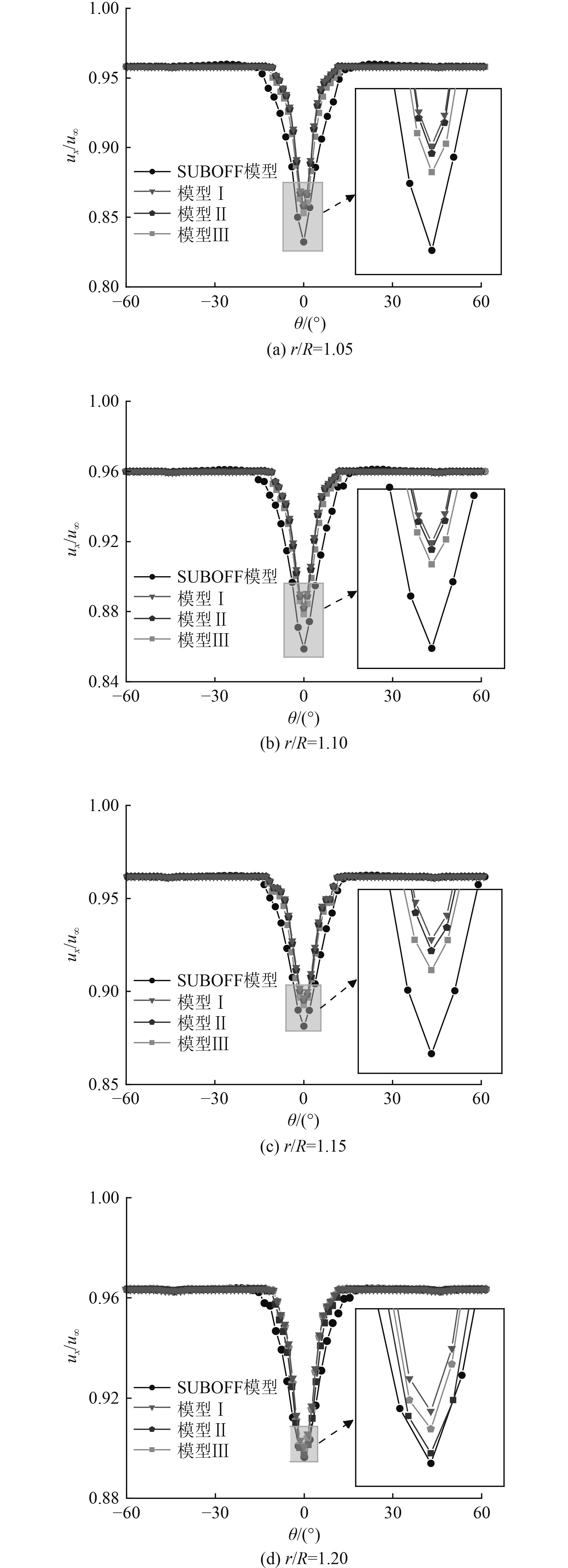
为涵盖不同围壳填角几何外形对潜艇尾流影响的区域,给出各潜艇模型桨盘面处r/R为1.05、1.10、1.15、1.20处,X方向速度分量在桨盘面处沿周向角的变化曲线,如图12所示。潜艇围壳对潜艇尾流的影响主要在周向角
|
图 12 桨盘面处各圆半径X方向速度分量 Fig. 12 Velocity component of X direction in the radius of each circle of propeller plane |
对桨盘面处X方向速度分量周向不均匀性下降效果进行定量分析,流场速度分量的周向不均匀度系数的表达式为:
| $ {u_{x\Delta }} = ({u_{x\max }} - {u_{x\min }})/{u_\infty } 。$ | (4) |
式中:
|
|
表 2 各潜艇模型桨盘面处 |
可知,在桨盘面处圆半径r/R为1.05、1.10、1.15时,模型Ⅰ、模型Ⅱ、模型Ⅲ较SUBOFF模型桨盘面处
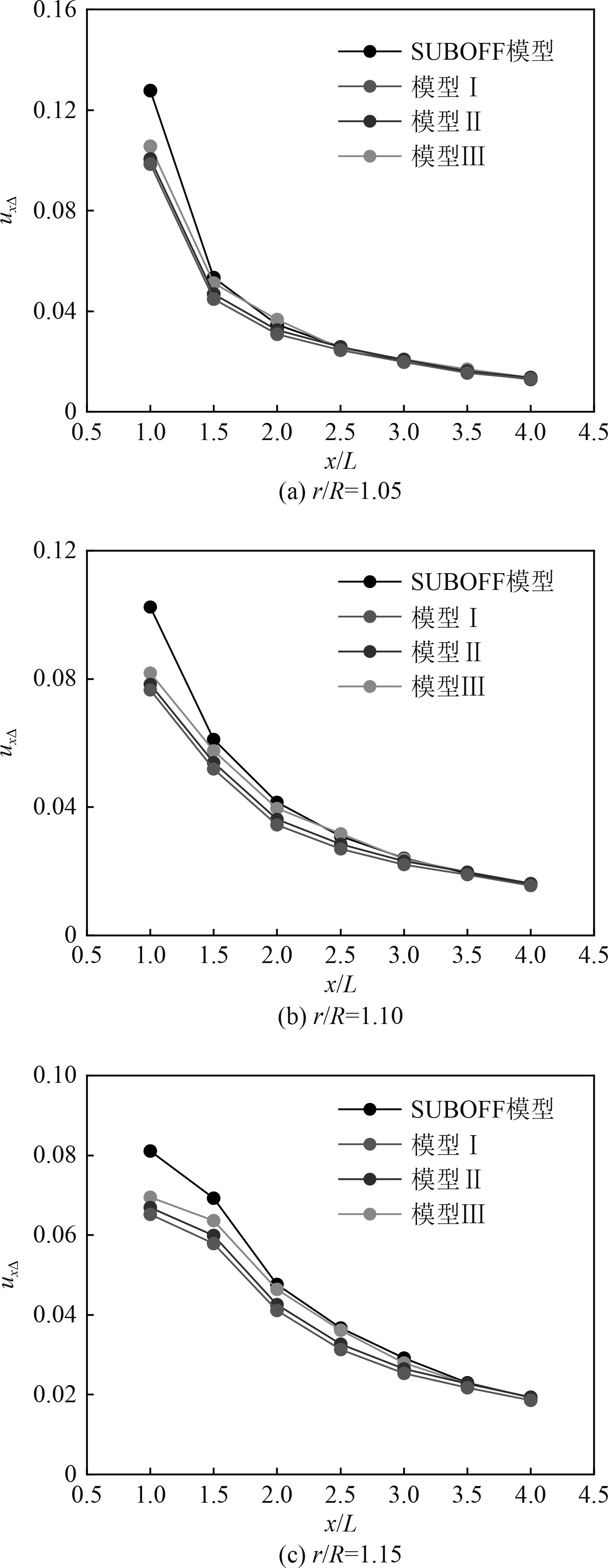
图13是圆半径r/R为1.05、1.10、1.15下
|
图 13
沿来流方向 |
本文对SUBOFF模型进行数值模拟,将计算结果与实验值对比以验证数值方法的可行性,在此基础上,探讨3种不同围壳填角模型与SUBOFF模型的尾部伴流场对比分析。主要结论如下:
1)潜艇围壳处马蹄涡在围壳前缘根部与侧面处起源与发展,含平滑过度围壳填角潜艇模型Ⅰ、模型Ⅱ、模型Ⅲ在围壳前缘根部处对来流形成导流效果,阻碍了围壳前缘根部处纵向涡被进一步拉伸,从而抑制马蹄涡的产生。
2)围壳填角可降低潜艇模型桨盘面处,沿来流方向速度分量不均匀度并加快潜艇尾部伴流的耗散,含凸型围壳填角的模型Ⅰ效果最优,其桨盘面处沿来流方向速度分量不均匀度最高下降幅度为24.5%。
| [1] |
王兴茹. 潜艇尾流空间演化及流场特性仿真分析[D]. 哈尔滨:哈尔滨工业大学, 2019.
|
| [2] |
GROVES N C, HUANG T T, CHANG M. S. Geometric characteristics of DARPA SUBOFF models[R]. David Taylor Research Center, 1989.
|
| [3] |
HUANG T, LIU H L. Measurement of flows over an axisymmetric body with various appendages in a wind tunnel; the DARPA SUBOFF experimental program[J]. Fluid Dynamics, 1994.
|
| [4] |
涂海文, 孙江龙. 基于CFD的潜艇阻力及流场数值计算[J]. 舰船科学技术, 2012, 34(3): 19-25. TU Hai-wen, SUN Jiang-long. Numerical calculation of submarine drag and flow field based on CFD[J]. Ship Science and Technology, 2012, 34(3): 19-25. |
| [5] |
吕晓军, 周其斗, 段嘉希. 网格参数与离散格式对潜艇阻力预报精度的影响[J]. 海军工程大学学报, 2014, 26(2): 40-44. LV Xiao-jun, ZHOU Qi-dou, DUAN Jia-xi. Grid parameter and discrete scheme for predicting submarine resistance[J] Journal of Naval University of Engineering, 2014, 26(2): 40−44. |
| [6] |
吴方良, 吴晓光, 马运义, 等. 潜艇指挥台围壳对阻力和伴流场影响数值研究[J]. 海洋工程, 2009, 27(3): 91-99. WU Fang-liang, WU Xiao-guang, MA Yun-yi, et al. The effect of submarine sail on the resistance and wake field[J]. Ocean Engineering, 2009, 27(3): 91-99. |
| [7] |
QU Y, WU Q, ZHAO X, et al. Numerical investigation of flow structures around the DARPA SUBOFF model[J]. Ocean Engineering, 2015, 32(9): 200−242.
|
| [8] |
刘志华, 熊鹰. 消涡整流片对潜艇马蹄涡的控制及其与辅翼效果的比较[J]. 船舶力学, 2011, 15(10): 1102-1109. LIU Zhi-hua, XIONG Ying. Comparison on the submarine horseshoe vortex control effects by vortex control bafflers and fillets[J]. Journal of Ship Mechanics, 2011, 15(10): 1102-1109. |
| [9] |
LIU Y W, JIANG H X, LI Y L, et al. Suppression of the hydrodynamic noise induced by the horseshoe vortex through mechanical vortex generators[J]. Applied Sciences, 2019, 9(4): 737.
|
| [10] |
LIU Y W, LI Y L, SHANG D J. The hydrodynamic noise suppression of a scaled submarine model by leading-edge serrations[C]// OES China Ocean Acoustics Conference, 2021.
|
| [11] |
张楠, 吕世金, 沈泓萃, 等. 潜艇围壳线型优化抑制脉动压力与流激噪声的数值模拟研究[J]. 船舶力学, 2014, 18(4): 448-458. ZHANG Nan, LU Shi-jin, SHEN Hong-cui, et al. Suppression of the hydrodynamic noise induced by the horseshoe vortex through mechanical vortex generators[J]. Journal of Ship Mechanics, 2014, 18(4): 448-458. |
| [12] |
TOXOPEUS S, KUIN R, KERKVLIET M, et al. Improvement of resistance and wake field of an underwater vehicle by optimising the fin-body junction flow with CFD[J]. American Society of Mechanical Engineers, 2014(2): 8−13.
|
| [13] |
WANG X, HUANG Q, PAN G. Numerical research on the influence of sail leading edge shapes on the hydrodynamic noise of a submarine[J]. Applied Ocean Research. DOI:10.1016/j.apor.2021.102935 |
| [14] |
李孟捷, 王梦璇, 王力, 等. 水下航行体降噪艉翼填角的数值模拟与试验研究[J]. 船舶力学, 2016, 20(10): 1345-1354. LI Meng-jie, WANG Meng-xuan, WANG Li, et al. Experiment and numerical simulation of denoising fillets of stern appendages on underwater vehicle[J]. Journal of Ship Mechanics, 2016, 20(10): 1345-1354. |
| [15] |
JIN Z, WANG P, XIA H, et al. Validation of numerical simulation on the flow field of submarine with various types of stern appendages[C]// MTS/IEEE Charleston OCEANS Conference 2007(3): 341−350.
|
| [16] |
李文科. 工程流体力学[M]. 合肥: 中国科学技术大学出版社, 2007.
|
 2024, Vol. 46
2024, Vol. 46
