0 引　言

用以输送各种流体工质的管路系统广泛应用在船舶动力、海洋工程和航空航天等领域。管路系统工作过程中受到液体的压力波脉动、管壁振动以及2种振动的相互耦合，不可避免地产生振动和噪声。当振动频率与管路系统的固有频率相重合时，由于出现共振现象会产生较大危害^{[1 − 2]}。现阶段常用的管路减振措施主要包括粘贴阻尼材料、安装减振器、添加阻振质量、安装消声器、串接挠性接管等^{[3 − 6]}。这些控制措施虽然取得了一定进展，但也存在诸多不足。周期结构特有的带隙特性能对对应频段内的弹性波传播进行抑制，为工程结构减振降噪提供了新契机^{[7 − 8]}。基于声子晶体理论，设计周期管路结构，可实现低频振动控制，推进管路结构减振降噪由“治理技术”向“设计技术”的管路系统一体化设计^{[9 − 10]}。

在管路振动传递控制应用研究方面，国内外学者从周期管路结构的设计、带隙特性计算、减振特性分析和试验分析等多个方面进行研究。Sorokin等^{[11 − 12]}将充液管路设计成沿轴向交替分布的复合材料周期结构和弯管沿轴向阵列分布的几何周期结构，并计算了周期管路中振动能量的传递特性。汤璐嘉等^[13]分析了局域共振型声子晶体梁的长度和晶格常数对带隙的影响。Park等^[14]通过结构设计和参数调节证明了声子晶体梁可在相当低的频率范围内，实现超宽低频带隙。Shen 等^[15]研究了三维周期复合材料管路在不同振动激励下的振动传输特性，在三维空间内周期管路仍能保持原有的带隙。Fang 等^[16]研究了管中周期附加亚波长 Helmholtz结构的声波带隙特性，指出该周期管内流体介质，在声压带隙对应频段具有等效的负材料特性。已有周期结构设计研究多针对梁结构，大多为单一带隙特性的分析。对于结合2种带隙特性的周期管路结构设计，并详细分析结构参数对减振特性影响规律的研究还不深入。

本文将布拉格声子晶体和局域共振声子晶体引入周期管路系统的设计，结合传递矩阵方法和有限元方法，揭示布拉格周期结构的带隙特性。并借助有限元技术，建立周期管路系统的数值模型，分析周期结构参数对管路减振效果的影响。设计局域共振单元添加到布拉格结构中，进一步提升低频减振效果，数值研究局域共振单元对减振效果的影响，与普通管路对比验证了周期结构可实现更好的管路声振控制。

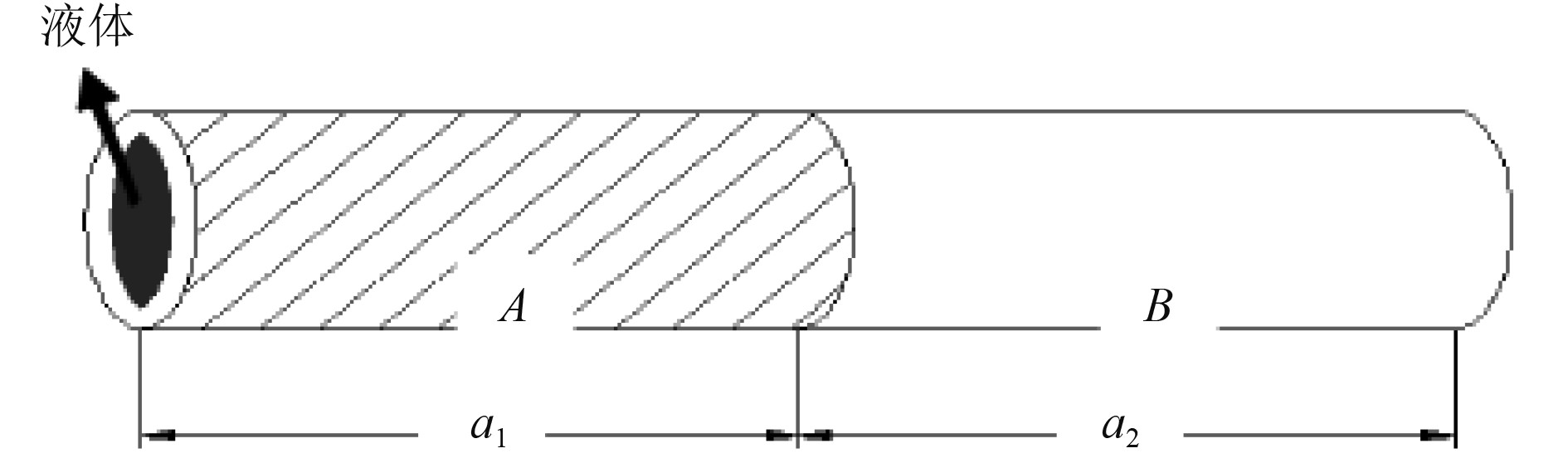
1 周期管路结构带隙特性计算 1.1 管路振动传递矩阵

基于布拉格带隙机理将周期管路系统的管壁设计成材料或几何周期结构，如图1所示。管路A和B沿管路中心轴交替排列形成，可使用不同材料，也可使用不同几何参数，其长度分别为$ {a}_{1} $、$ {a}_{2} $，单个周期管路晶格常数为$ a $，$ a={a}_{1}+{a}_{2} $。传递矩阵法基于一维波动方程，根据质点位移连续和应力连续推导周期管路的传递矩阵，可用于求解周期结构的带隙特征。

对于周期管路，相邻原胞界面处的位移$ w $、转角$ {w}' $、弯矩$ EI{w}'' $、剪切力$ EI{w}''' $均为连续函数，在$ x= na $处，根据力学分析，可得

$\left\{ \begin{aligned} & {w_{n,A}}\left( 0 \right) = {w_{n - 1,B}}\left( {{a_2}} \right)，\\ & {w'_{n,A}}\left( 0 \right) = {w'_{n - 1,B}}\left( {{a_2}} \right)，\\ & {E_A}{I_A}{w''_{n,A}}(0) = {E_B}{I_B}{w''_{n - 1,B}}({a_2})，\\ & {E_A}{I_A}{w'''_{n,A}}(0) = {E_B}{I_B}{w'''_{n - 1,B}}({a_2})。\end{aligned}\right. $

(1)

将式(1)写成矩阵，即：

$ {\boldsymbol{k}}{{\boldsymbol{W}}_{n,A}} = {\boldsymbol{H}}{{\boldsymbol{W}}_{n - 1,B}}，$

(2)

$ {\boldsymbol{K}} = \left[ {\begin{array}{*{20}{c}} 1&1&1&1 \\ {{k_{A1}}}&{{k_{A2}}}&{{k_{A3}}}&{{k_{A4}}} \\ {{E_A}{I_A}{k^{}}{{_{A1}}^2}}&{{E_A}{I_A}{k^{}}{{_{A2}}^2}}&{{E_A}{I_A}{k^{}}{{_{A3}}^2}}&{{E_A}{I_A}{k^{}}{{_{A4}}^2}} \\ {{E_A}{I_A}{k^{}}{{_{A1}}^3}}&{{E_A}{I_A}{k^{}}{{_{A2}}^3}}&{{E_A}{I_A}{k^{}}{{_{A3}}^3}}&{{E_A}{I_A}{k^{}}{{_{A4}}^3}} \end{array}} \right]，$

(3)

$\begin{split} {{\boldsymbol{H}}} = & \left[{ {\begin{array}{*{20}{c}} {{e^{{k_{B1}}{a_2}}}}& {{e^{{k_{B2}}{a_2}}}} \\ {{k_{B1}}{e^{{k_{B1}}{a_2}}}}& {{k_{B2}}{e^{{k_{B2}}{a_2}}}} \\ {{E_B}{I_B}{k_{B1}}^2{e^{{k_{B1}}{a_2}}}}& {{E_B}{I_B}{k_{B2}}^2{e^{{k_{B2}}{a_2}}}} \\ {{E_B}{I_B}{k_{B1}}^3{e^{{k_{B1}}{a_2}}}}& {{E_B}{I_B}{k_{B2}}^3{e^{{k_{B2}}{a_2}}}} \end{array}}}\right.\; \left.{ {\begin{array}{*{20}{c}} {{e^{{k_{B3}}{a_2}}}}& {{e^{{k_{B4}}{a_2}}}} \\ {{k_{B3}}{e^{{k_{B3}}{a_2}}}}& {{k_{B4}}{e^{{k_{B4}}{a_2}}}} \\ {{E_B}{I_B}{k_{B3}}^2{e^{{k_{B3}}{a_2}}}}& {{E_B}{I_B}{k_{B4}}^2{e^{{k_{B4}}{a_2}}}} \\ {{E_B}{I_B}{k_{B3}}^3{e^{{k_{B3}}{a_2}}}}& {{E_B}{I_B}{k_{B4}}^3{e^{{k_{B4}}{a_2}}}} \end{array}}} \right]，\end{split} $

(4)

$\left\{\begin{split} &{{\boldsymbol{W}}_{n,A}} = {\left[ {{{\boldsymbol{W}}_{A1}},{{\boldsymbol{W}}_{A2}},{{\boldsymbol{W}}_{A3}},{{\boldsymbol{W}}_{A4}}} \right]^{\mathrm{T}}}，\\ & {{\boldsymbol{W}}_{n - 1,B}} = {\left[ {{{\boldsymbol{W}}_{B1}},{{\boldsymbol{W}}_{B2}},{{\boldsymbol{W}}_{B3}},{{\boldsymbol{W}}_{B4}}} \right]^{\mathrm{T}}}。\end{split}\right.$

(5)

同理，由管路在$ x=\left(n-1\right)a+{a}_{1} $处的位移、转角、弯矩和剪切力的连续性得到：

$ {{\boldsymbol{K}}_1}{{\boldsymbol{W}}_{n,A}} = {{\boldsymbol{H}}_1}{{\boldsymbol{W}}_{n,B}} 。$

(6)

由式(2)和式(6)，可得第n个和第（n-1）个原胞之间的传递关系：

$ {{\boldsymbol{W}}_{n,B}} = {\boldsymbol{T}}{{\boldsymbol{W}}_{n - 1,B}}。$

(7)

式中，$ {\boldsymbol{T}}={{\boldsymbol{H}}}_{1}^{-1}{{\boldsymbol{K}}}_{1}{{\boldsymbol{K}}}^{-1}{\boldsymbol{H}} $为传递矩阵。

根据管路的周期性，利用Bloch定理可得到：

$ {{\boldsymbol{W}}_n} = {e^{iqa}}{{\boldsymbol{W}}_{n - 1}}。$

(8)

式中，q为一维Bloch波矢。

联立求解式(7)和式(8)，即可得到标准的矩阵特征值问题：

$ \left| {{\boldsymbol{T}} - {e^{iqa}}I} \right| = 0 。$

(9)

式中：$ {\boldsymbol{I}} $为四阶的单位矩阵。通过求解传递矩阵$ {\boldsymbol{T}} $的本征值，便可得出波矢$ q $和频率$ \mathrm{\omega } $之间的频散关系，获得无限周期管路结构的能带结构图。

1.2 无限管路结构带隙特性分析

选取一维周期结构组成材料为硅酮橡胶和金属钢，$ {a}_{1}={a}_{2}=0.06\;{\mathrm{m}} $，材料参数如表1所示。

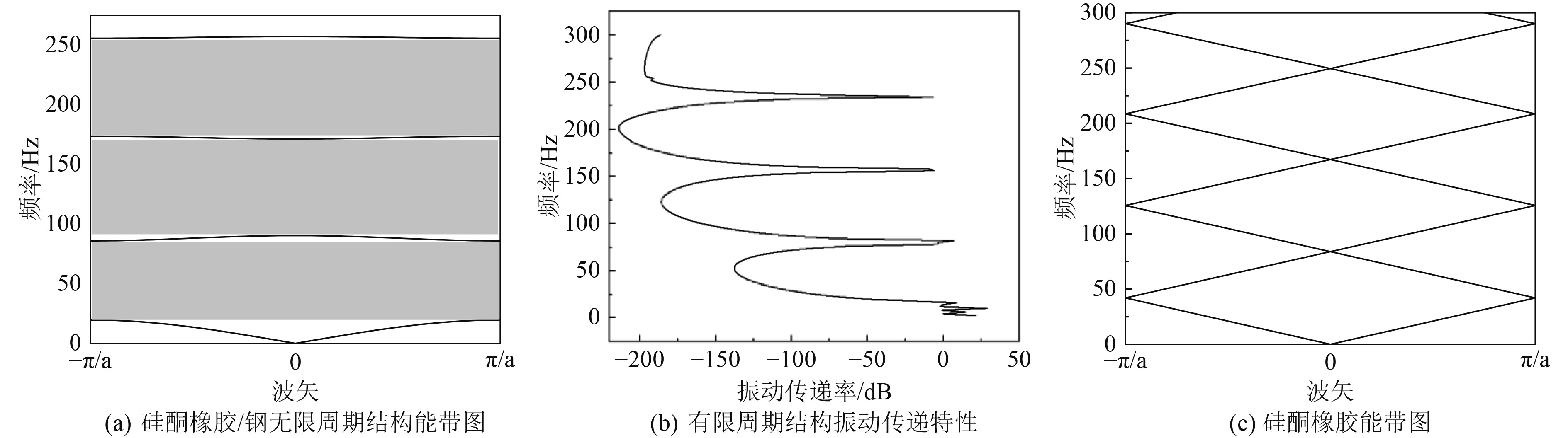
基于式(9)使用Matlab编程计算得到一维无限管路系统的能带结构，如图2(a)所示，0～300 Hz内，出现了３条禁带，使用有限元方法对有限周期结构进行振动传递特性仿真，计算结果如图2(b)所示。

通过对比能带和振动传递特性可发现：传递矩阵法计算得到的3条禁带与振动特性计算得到的3个较大振动衰减频段基本一致，表明能带结果和振动特性结果吻合良好。因此，对于布拉格有限周期管路及引入局域共振结构的有限周期管路系统，可使用有限元法计算振动传递特性来表征其带隙特性。如果管路结构使用同一种材料，其能带图如图2(c)所示，可见单一材料的结构没有带隙出现，表明周期性材料排布才能产生带隙。

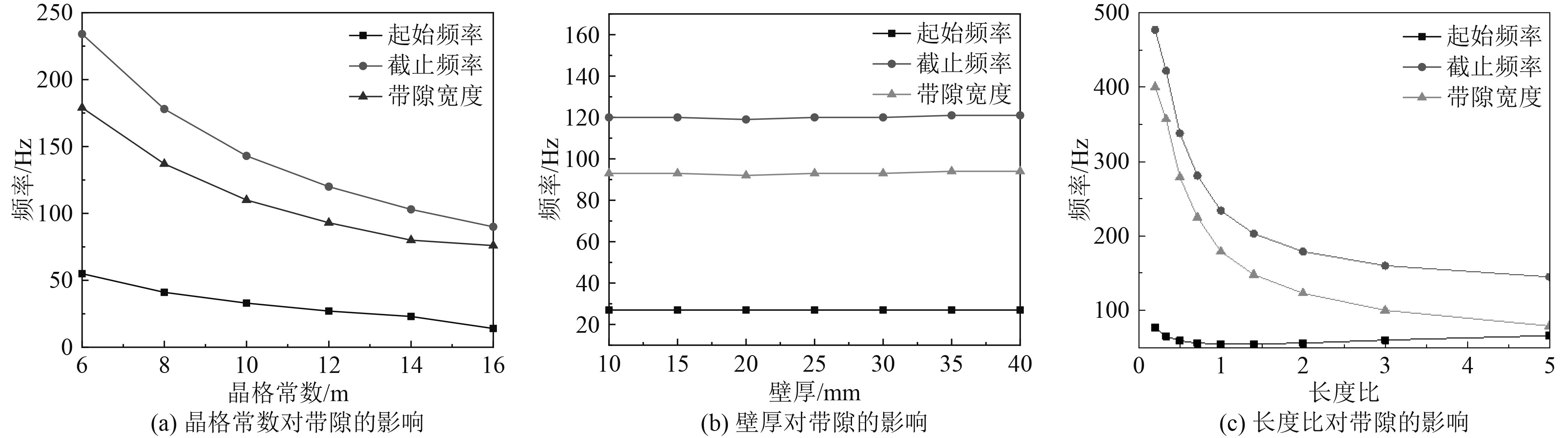
将图1所示单个周期管路进行延拓，管路内、外径分别为1.2 m和1.3 m，采用控制变量法对环氧树脂-钢复合材料周期管路结构进行分析，可得到周期管路系统的结构参数对带隙特性的影响规律，如图3所示。

可知，带隙的起始频率和截止频率均随着晶格常数的增大而减小，但截止频率下降更迅速，因此，晶格常数增大不利于拓宽带隙区间；管路壁厚改变，无论起始频率曲线还是截止频率曲线，基本没有变化，所以无法通过改变周期管路结构的壁厚来对其带隙特性进行优化设计；改变管路A和B的长度比，当长度比小于1时，起始频率逐渐减小；当长度比等于1时，取得最小值，长度比继续增大，起始频率缓慢增加，但整个取值区间内起始频率的数值变化很小，而截止频率随长度比增加迅速减小，带隙宽度也是越来越窄。因此，二者的长度比越小，有减振效果的频率区间越宽。

2 布拉格管路结构的减振性能

在一维周期管路带隙特性研究的基础上，进一步分析布拉格周期管路结构晶格长度、管路半径对减振性能的影响规律。初始选取管路A、B内径相同均为1.2 m，壁厚为0.03 m，有限周期管路总长度为60 m。

使用有限元软件对周期管路系统进行振动传递特性分析，管路结构一端施加轴向简谐激励力，另一端作为输出响应端，频响计算可得到输出端的振动响应。选取加速度振动传递率评价周期管路的减振效果，定义如下：

$ {L_D} = 20\lg \frac{{{a_0}}}{a} 。$

(10)

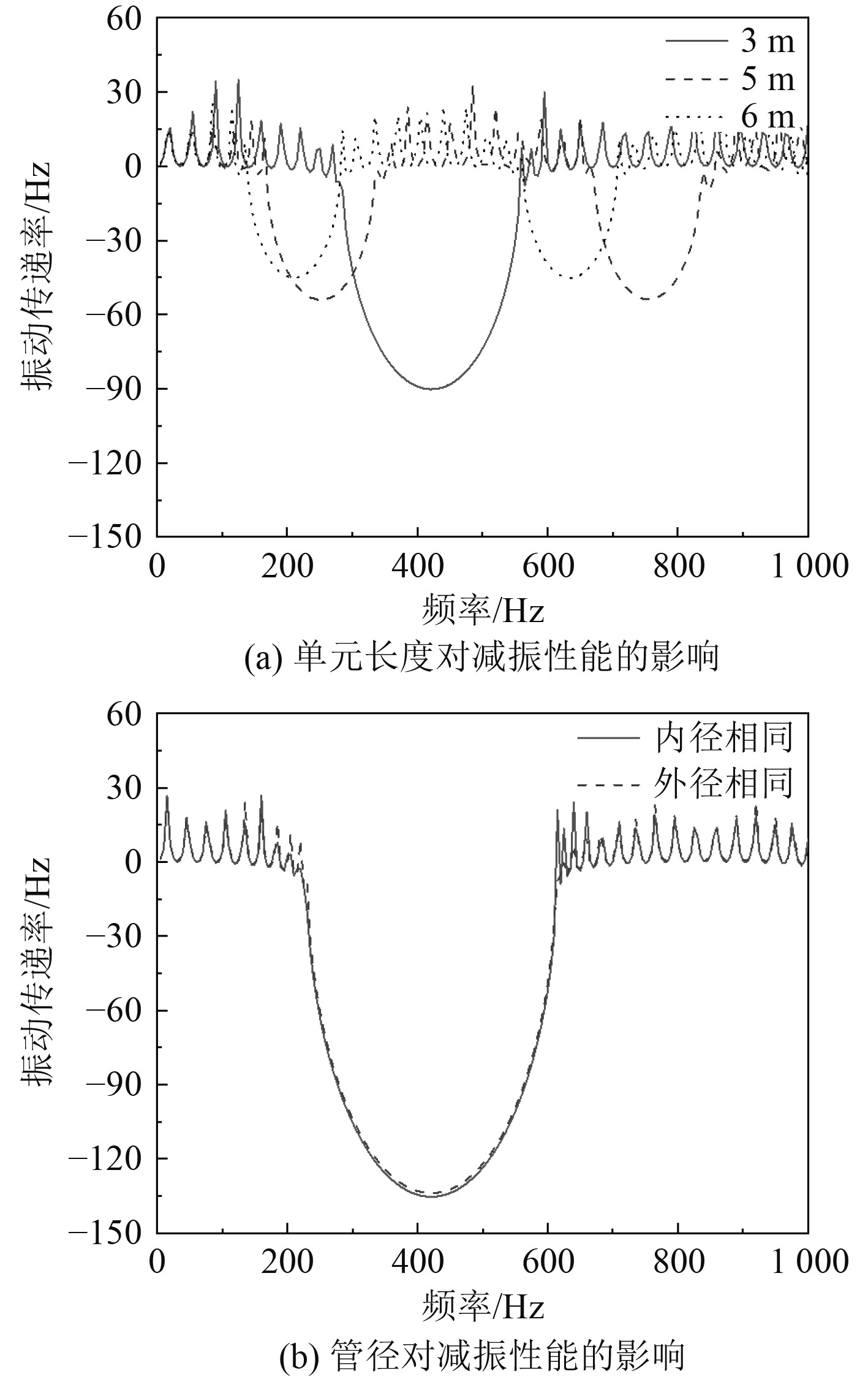
式中：a₀为输出端的加速度响应，a为激励端的加速度响应。根据控制变量法，可得到不同周期结构参数变化在轴向激励下的振动传递率，如图4所示。

由图4(a)可知，管路单元长度增加，带隙的数量增多，带隙的中心频率向低频移动，且带隙的宽度由61 Hz减小至30 Hz，计算频率段内减振效果减少了9 dB，这与带隙计算中，晶格常数对带隙特性的影响规律是一致的。

选取管路的单元长度为3 m，管A材料为铝，壁厚为0.03 m，管B材料为钢，壁厚为0.05 m。二者交替排列，分别研究2段管路内径相同、外径不同和外径相同、内径不同2种情况下的减振性能，可发现带隙的起始频率相同，带隙宽度也基本一致，计算频率段内前者的减振效果比后者高0.6 dB。可见在壁厚确定的情况下，管径对带隙特性和减振特性影响不大，若周期结构选择不同壁厚排布，为便于加工，可选取管路保持内径相同。

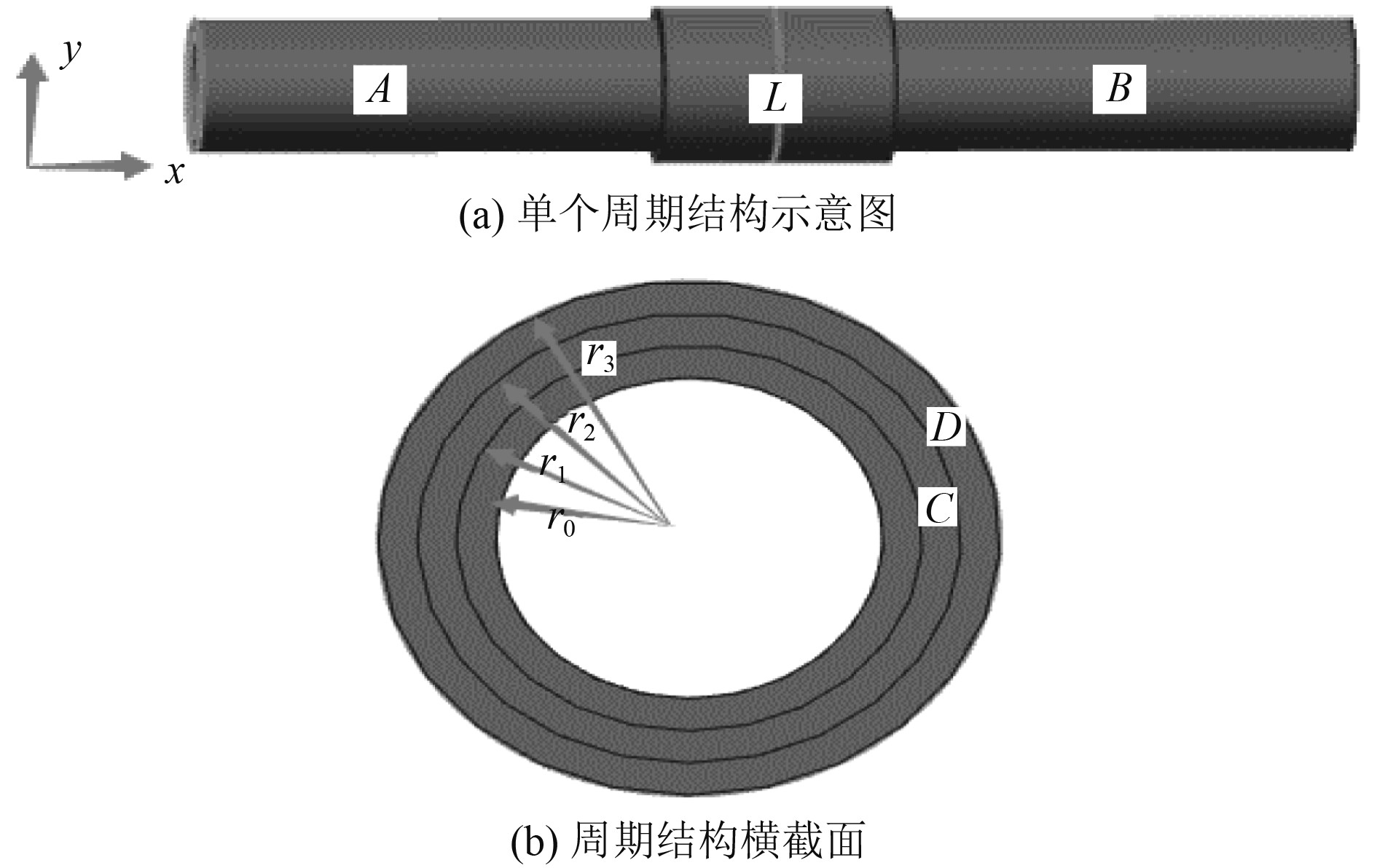
3 局域共振型周期结构的减振性能

将局域共振结构引入到布拉格周期管路结构中，复合型周期管路模型如图5所示。

管路结构由内、外两层组成，内管布拉格周期结构由管段A、B组成，晶格常数为$ a $，内径为$ {r}_{0} $，外径为$ {r}_{1} $。外管局域共振单元分为管段C、D两部分，由2种不同的材料组成，宽度分别为$ {L}_{1} $和$ {L}_{2} $，且外管可分区域设置为多层。本文中选取C为单层，外径为$ {r}_{2} $，D为双层，外径由内至外分别为$ {r}_{2} $、$ {r}_{3} $，且内层材料与C相同。第一层局域共振结构的高度为$ {h}_{1}={r}_{2}- {r}_{1} $，第二层局域共振结构的高度为$ {h}_{2}={r}_{3}-{r}_{2} $，局域共振型周期管路的结构参数如表2所示。

3.1 局域共振结构的带隙特性分析

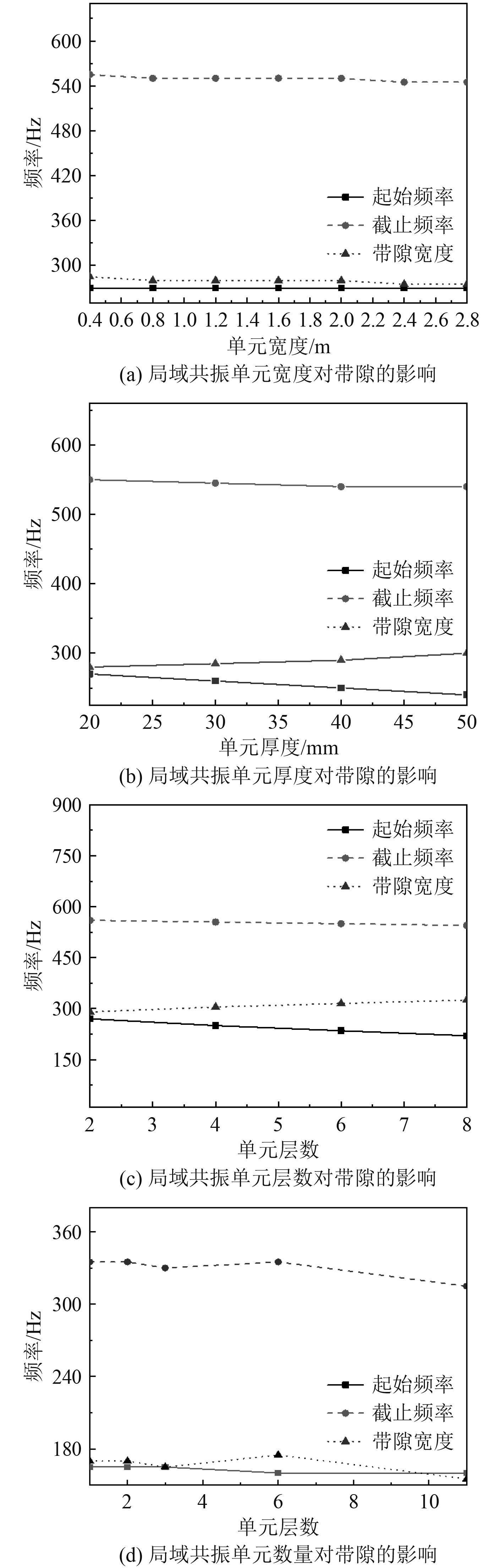
带隙取决于起始频率和截止频率，管路低频减振要求设计人员应尽量降低带隙的起始频率，同时拓宽带隙的宽度范围。因此，通过分析局域共振单元的结构参数对第一带隙的影响规律，指导管路结构的局域共振单元设计。局域共振单元尺寸对带隙影响规律的计算结果，如图6所示。

可知，局域共振单元的宽度增加不影响带隙的起始频率，截止频率略有下降，带隙的宽度随局域共振宽度的变化也不大；局域共振管路的管壁厚度增加可降低带隙的起始频率，对截止频率影响小于起始频率，带隙宽度增加；改变局域共振单元D的层数，带隙的起始频率从270 Hz减小至220 Hz，且起始频率的减低速度小于截止频率。因此，带隙宽度增加，减振区间拓宽。

保持管路长度和布拉格周期结构不变，改变局域共振单元的数量，并将这些单元沿长度均布排列，可发现，当共振单元数量增加时，带隙的起始频率先降低后升高，在取值为6时得到最小的带隙起始频率，带隙的截止频率则是先减小后变大，当共振单元数量为6时取得最大值。因此，计算范围内存在带隙宽度的极值，可见局域共振单元数量有最优值。工程设计中，可通过增加局域共振的壁厚和层数降低带隙起始频率，拓宽带隙频率范围，但共振单元数量的取值需通过优化方法得到最佳值。

3.2 局域共振结构的减振性能分析

布拉格型周期管路A、B的材料选用铝和钢，局域共振结构C为一层环氧树脂，D分两层，内层为环氧树脂，其外侧又采用了一层钢环固定约束。通过改变局域共振型单元的高度和宽度等结构参数，可调控管路的减振性能。

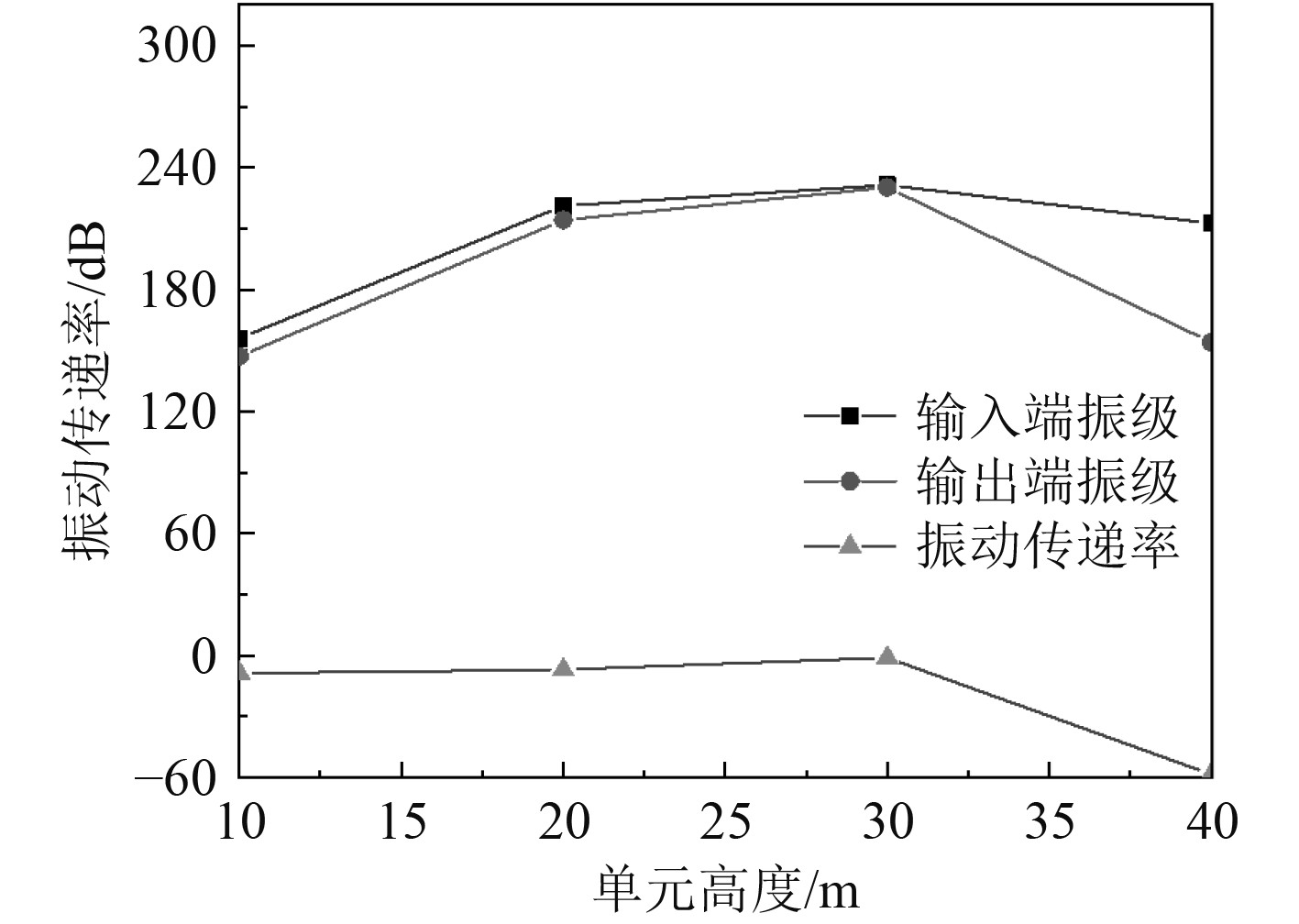
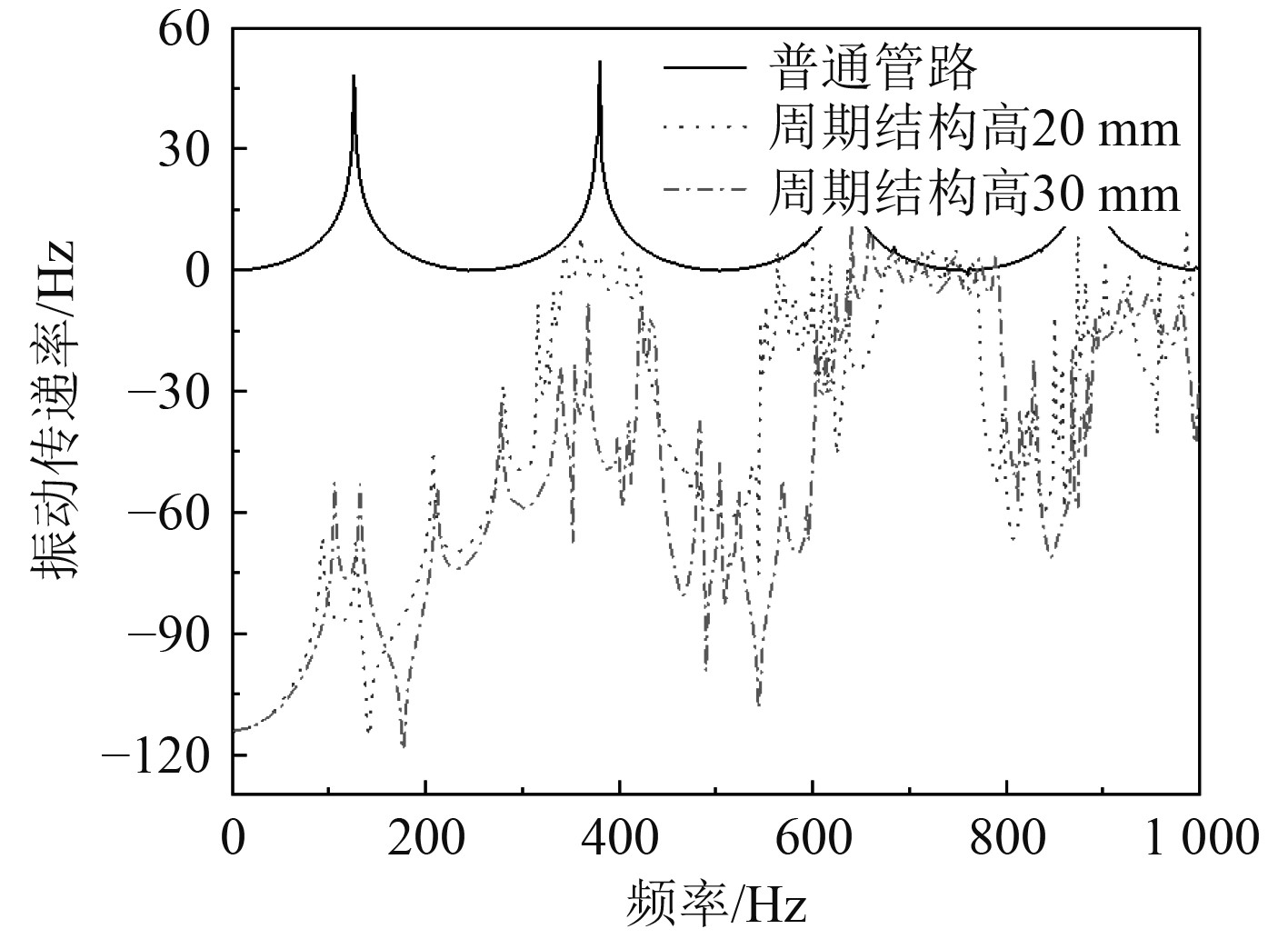
设置局域共振单元的宽度为60 mm，分析局域共振单元高度变化对管路减振效果的影响。此时，管路结构的激励输入端加速度振级、响应输出端加速度振级和振动传递率，如图7所示。可知，保持宽度不变，增大局域共振单元高度，管路输出端和输入端的加速度振级先变大后减小，振动传递率随单元高度增加而增大。图8给出了局域共振单元高度变化对管路减振效果的影响，并与单一材料非周期结构的普通管路进行对比。可发现：普通管路没有带隙特性，周期结构排布的管路系统出现了带隙特性，振动隔离效果明显提升，且管路的振动传递率随着周期结构高度的增加而减小。

接下来，改变共振单元的宽度，研究宽度对减振效果的影响。本文未详细列出单元宽度取值不同时的振动传递率曲线，部分尺寸下的减振效果值如表3所示。不同宽度下的振动传递率特性表明单元宽度改变会改变带隙的起始频率，但并非随宽度单调变化。局域共振单元高度相同时，振动传递率随宽度的增加而减少，减振效果得到了改进。且各种结构组合计算得到的减振效果均明显优于普通管路系统。

4 结　语

管路振动容易导致管路疲劳断裂或设备损坏，对管路进行有效的振动控制具有广泛的工程应用价值。周期结构产生的带隙能抑制弹性波在结构中的传播，将其引入管路系统设计中，结合传递矩阵法与有限元法计算周期管路的带隙特性和减振效果，结果表明：

1） 基于传递矩阵法计算的能带结构与有限元法得到的振动传递特性具有一致性，验证了周期结构仿真方法的可行性。

2） 根据布拉格散射机理将管路结构设计为不同材料排布的周期结构形式，管路的减振效果优于单一材料管路。

3） 改变布拉格结构的参数可优化管路带隙的起始频率、截止频率和带隙宽度，有效提高减振效果。

4） 基于布拉格散射型和局域共振型2种带隙机理设计的周期管路系统比普通管路的振动传递率进一步降低，减振效果明显提升。为管路系统的振动控制提供了一条新的技术途径。