2. 上海船舶设备研究所,上海 200031;
3. 船舶数据技术与支撑软件湖北省工程研究中心,湖北 武汉 430074;
4. 船舶和海洋水动力湖北省重点实验室,湖北 武汉 430074
2. Shanghai Marine Equipment Research Institute, Shanghai 200031, China;
3. Ship Data Technology and Support Software Hubei Engineering Research Center, Wuhan 430074, China;
4. Hubei Key Laboratory of Ship and Marine Hydrodynamics, Wuhan 430074, China
船舶螺旋桨“过重”是一个普遍存在的问题。新船下水后推进器受到的流体阻力大于设计水平,致使主机储备功率无法满足工况需求;旧船因长时间航行导致螺旋桨锈蚀、破损断裂等这些因素都会导致船机桨无法正常匹配,螺旋桨转速降低,造成船速下降[1 − 2]。实际生产生活中,一般通过螺旋桨削边的方法减少推进器负荷,使船机桨重新匹配。
螺旋桨的削边方法一般分为随边削边法与直径削边法,相较于随边削边法,直径削边法对工艺的要求较低、切割次数少、易于操作,且在桨叶断裂的极端情况下一般只能采取直径削边法进行修削。
对于螺旋桨直径削边的问题,已有大量相关人员展开研究。欧礼坚等[3]通过对亚龙X轮案例分析,发现螺旋桨削边技术不但可以优化船机桨的匹配,而且可以减小因螺旋桨脉动压力偏大而引起的局部振动。赵阳等[4]发现直径削边技术对改善老旧船的船-机-桨匹配具有重要作用,通过数十艘船的实验表明,削边技术可以使主机负荷减轻、工况改善,从而延长船舶的寿命。杨佑宗等[5]研究分析了折断后的螺旋桨对船舶推进性能的影响,获得了直径削边后螺旋桨主机转速、功率及航速的关系。熊鹰等[6]提出通过切割性能系列图谱来确定螺旋桨直径削边的切割量。杨帅等[7]通过理论计算方法和经验公式法与实测轴功率数据的对比,总结得出适用于确定高速艇螺旋桨切割量的计算方法。张济猛[8]给出了确定桨叶直径切割和随边切割前后桨叶几何要素的计算方法。张松鹤[9]根据螺旋桨盘面比的变化给出了桨叶直径切割的适用船型。欧礼坚等[10]提出采用CFD方法进行桨叶切割能更准确地确定螺旋桨切割量与转速提高之间的定量关系。杨波[11]结合实际工作提出螺旋桨削边技术能提高螺旋桨转速、节省能源,具有重要现实意义。
综上所述,当前文献大多集中于研究直径切割对螺旋桨水动力性能方面的影响,以及如何进行直径切割以改善螺旋桨水动力性能,对直径削边后螺旋桨的振动特性机理关注并不多。由于直径切割使螺旋桨几何形状改变,必然会使螺旋桨桨叶振动特性相应改变,若削边后螺旋桨的固有频率与其叶频及其倍频相近,则会造成桨叶共振,产生较大变形与噪声,严重时甚至再次发生桨叶折断事故,因此有必要开展直径切割量等相关参数对螺旋桨桨叶振动特性的研究。
本文以无侧斜及有侧斜螺旋桨为研究对象,基于有限元法,融合Matlab编程技术、Ansys二次开发技术,开展不同直径切割量下螺旋桨的振动特性研究,揭示关键参数对切割前后螺旋桨振动规律的影响机理。
1 直径削边螺旋桨振动分析理论 1.1 直径削边螺旋桨几何数学表达螺旋桨的几何参数可由剖面半径(比)、螺距比、导边至参考线距离、初始纵倾、内弦弦长、拱度分布和厚度分布共同决定。由以上参数可推导出螺旋桨桨叶表面的数学表达[12],由剖面几何分布可计算剖面侧斜角分布如下:
| $ \delta_f(r) = \delta_m(r) + h\left(r\right)\left(a - \frac{1}{2}\right) \frac{\cos\phi(r)}{r} - \left(f\pm t\right)\frac{\sin\phi(r)}{r} + \varepsilon。$ | (1) |
式中:
可得桨叶各点三维坐标:
| $ \left\{ \begin{array}{l} x(r) = r\sin {\delta _f}(r) ,\\ y(r) = r\cos {\delta _f}(r) ,\\ z(r) = {z_m}(r) + h\left( r \right)\left( {a - 1/2} \right)\sin \phi (r) - \left( {f \pm t} \right)\cos \phi (r)。\end{array} \right. $ | (2) |
式中:x、y和z分别为各点笛卡尔坐标;
直径削边前后剖面形状未发生改变,故仍可参照式(1)和式(2)求得削边后桨叶各点坐标。
1.2 直径削边螺旋桨结构动力学模型求解螺旋桨等结构的弹性动力学问题,就是在初边值给定的条件下求解其动力学方程。然而由于螺旋桨几何形状不规则,直接求解十分困难,只能设法寻求其数值解。有限元理论是常用的结构振动分析方法,本文采用其对直径削边螺旋桨振动进行分析。经过推导,有限元离散后的考虑直径削边效应的螺旋桨振动控制方程如下:
| $ \boldsymbol{M\ddot{\delta}}+\boldsymbol{C\dot{\delta}}+\boldsymbol{K\delta}=\boldsymbol{F}。$ | (3) |
式中,由于螺旋桨转速较低,忽略了科氏力和离心力的影响。
2 直径削边螺旋桨参数化建模方法 2.1 直径削边螺旋桨几何建模程序实现由于直径削边技术涉及到对螺旋桨几何参数的大量修改,需要对螺旋桨重复性建模,若手动操作十分繁琐。为提高效率,本文利用参数化建模技术(APDL),编写程序实现削边螺旋桨几何建模及振动分析自动化。基于有限元软件Ansys,采用Matlab编程语言,开发直径削边螺旋桨几何的参数化创建、批量修改等功能;并在此基础上,探讨针对直径削边螺旋桨建模模块及振动分析模块进行二次开发的主要流程和若干技术细节。
根据螺旋桨桨叶拱弧面的数学表达式(1),桨叶面上每一点的三维坐标对应6个原始参数(半径
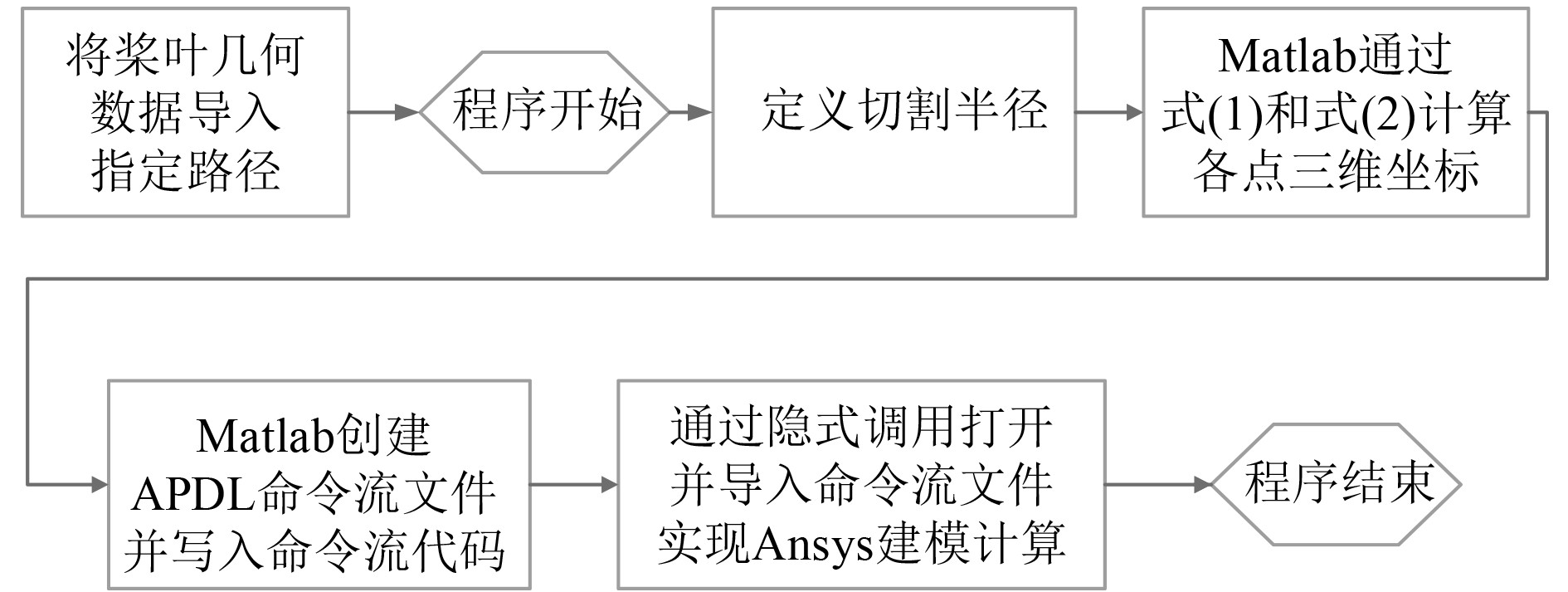
由于直径削边只是将切割处半径以外的桨叶部分直接去掉,因此只需插值出直径切割处剖面的各项几何参数,得到切割处剖面的桨叶三维坐标,之后取切割处剖面以内的坐标值进行建模计算即可。在这里,结合Matlab程序与APDL程序来实现建模过程。利用Matlab软件的编程计算能力得到切割半径处以内剖面的桨叶三维坐标,之后再由Matlab循环命令得到APDL命令流,程序流程图见图1。通过该程序代码,可快捷高效地建立直径切割后螺旋桨模型。
|
图 1 直径削边参数化建模程序流程图 Fig. 1 Flow chart of parametric modeling program for diameter trimming |
在Matlab中计算出指定半径处叶切面所有三维点坐标,接着采用三维绘图命令mesh即可在Matlab绘制出螺旋桨桨叶三维网格图,见图2。由此可以检查计算得到的桨叶三维坐标值是否正确。

|
图 2 Matlab中螺旋桨桨叶三维网格面 Fig. 2 3D mesh surface of propeller blade in Matlab |
本文提出上述方法,在Matlab中编写源程序,产生上述操作的APDL命令流文件,将文件导入Ansys命令行,由程序完成自动建模,很大程度上提高了工作效率。
2.2 直径削边螺旋桨振动分析程序实现在建模完成后,采用Ansys软件对螺旋桨进行振动分析步骤为赋材料属性,选取单元类型,网格划分,设置边界条件,选择模态求解方法进行螺旋桨模态求解。
材料属性包括弹性模量、泊松比、密度。本文模型的材料弹性模量为72 GPa、泊松比为0.3、密度为2 800 kg/m3。
选取单元类型为四面体10节点solid187单元。对于大型三维实体结构需要选择实体单元进行有限元计算。常用的实体单元类型有solid45、solid92、solid185及solid187。其中,solid45与solid185是六面体单元,solid92与solid187为带中间节点的四面体单元。对于螺旋桨这种复杂实体结构,很难划分出效果较好的六面体单元,若选用六面体单元对螺旋桨进行网格划分也很容易退化为四面体单元。虽然单元的主要功能相同,但退化后六面体单元计算精度很差。因此,选择四面体单元对螺旋桨进行网格划分,并且优选四面体单元中目前性能最好的solid187单元。
网格划分时,选择由面分割尺寸定义网格大小,网格尺寸为4.5 mm,最终将模型划分为229164个单元,共354381个节点。边界条件设为桨毂处固定。
模态求解方法选择分块兰索斯算法。兰索斯算法是用一组特征向量实现Lanczos迭代计算。在已知需求解的频率范围时,这种方法可高效率地求解结构模态。在一般方法中高频部分的求解比低频部分慢很多,而用此方法求解,两者的求解速度几乎一样快。该法多用于求解大型壳单元或实体单元模型的多阶模态。此外,这种方法还可以较好地求解刚体模态。因此,本文采用兰索斯法求解模态。
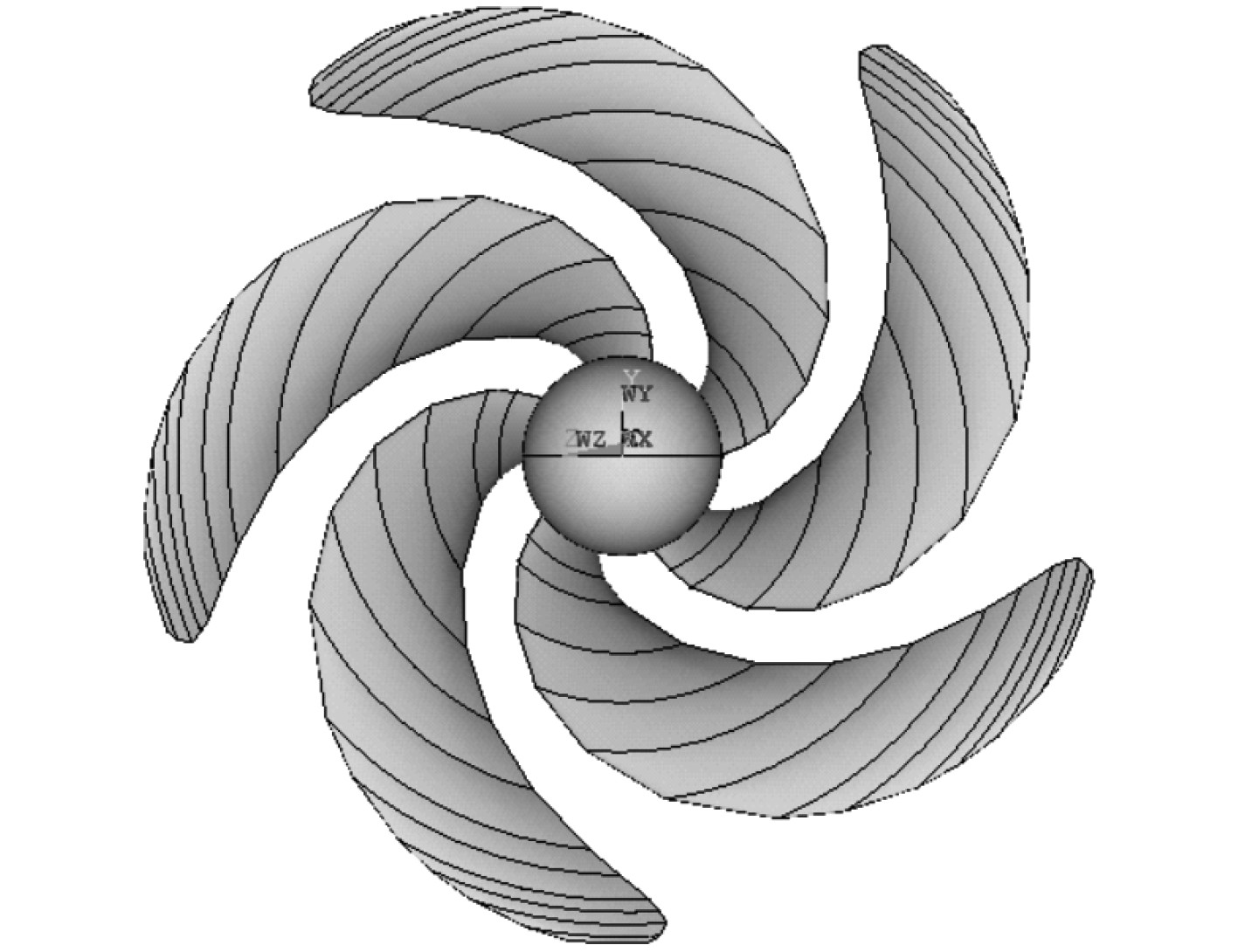
3 直径削边对螺旋桨振动特性的影响 3.1 程序预报结果验证以4384螺旋桨为例,对本文的计算方法进行验证,该桨几何见图3,主要参数见表1。本文方法得到的螺旋桨前五阶固有频率与文献[11]的计算结果对比如表2所示。
|
图 3 4384螺旋桨几何图形 Fig. 3 4384 propeller geometry |
|
|
表 1 4381桨~4384桨主要参数(4381、4382、4383、4384桨侧斜角分别为0°、36°、72°、108°) Tab.1 Main parameters of 4381-4384 propellers (the side slope angles of 4381, 4382, 4383 and 4384 propellers are 0°, 36°, 72° and 108° respectively) |
|
|
表 2 固有频率比较 Tab.2 Comparison of natural frequencies |
可知,本文研发计算程序的计算所得结果与Young[13]文献中结果的前五阶接近,各阶数据的相对误差均在5.1%以内。这说明本文有限元计算模型的建立、有限元网格的划分、边界条件的设置和计算理论方法的选择是合理的,而计算程序的功能性和准确性也得到了证实。
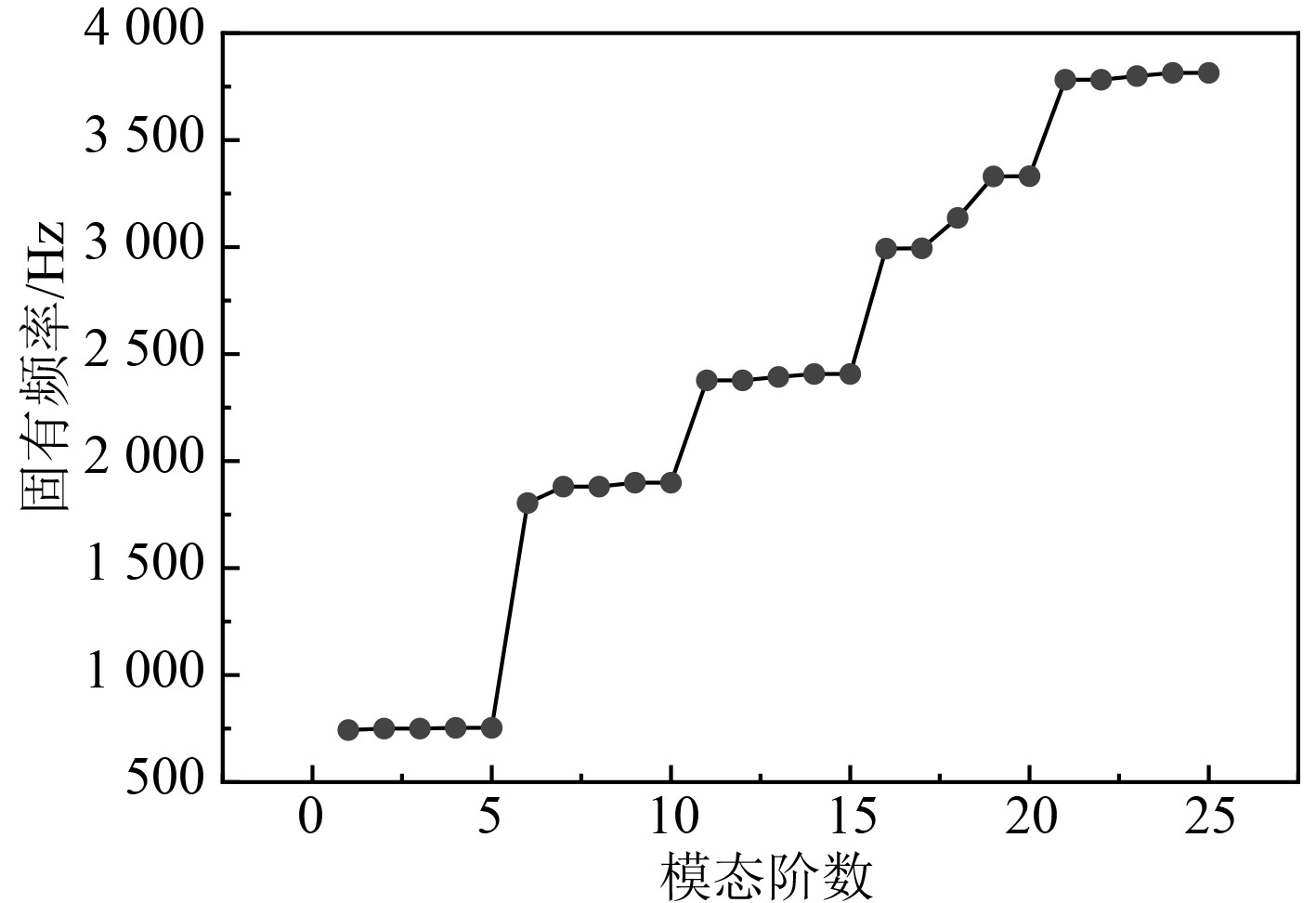
3.2 无侧斜桨直径削边振动特性使用计算程序对无侧斜4381桨进行前25阶的模态计算。4381桨的几何与材料参数见表1。各阶模态的固有频率变化如图4所示。
|
图 4 4381桨各阶模态固有频率的变化曲线 Fig. 4 Variation curve of modal natural frequency of 4381 propeller |
可知,计算结果具有以下特点:前25阶模态分成5组,每组包含5个固有频率相近及单桨叶振型相似的桨叶模态。固有频率随分组阶数的增加而跳跃式增长。振动形式随分组阶数的增加而变得越来越复杂。
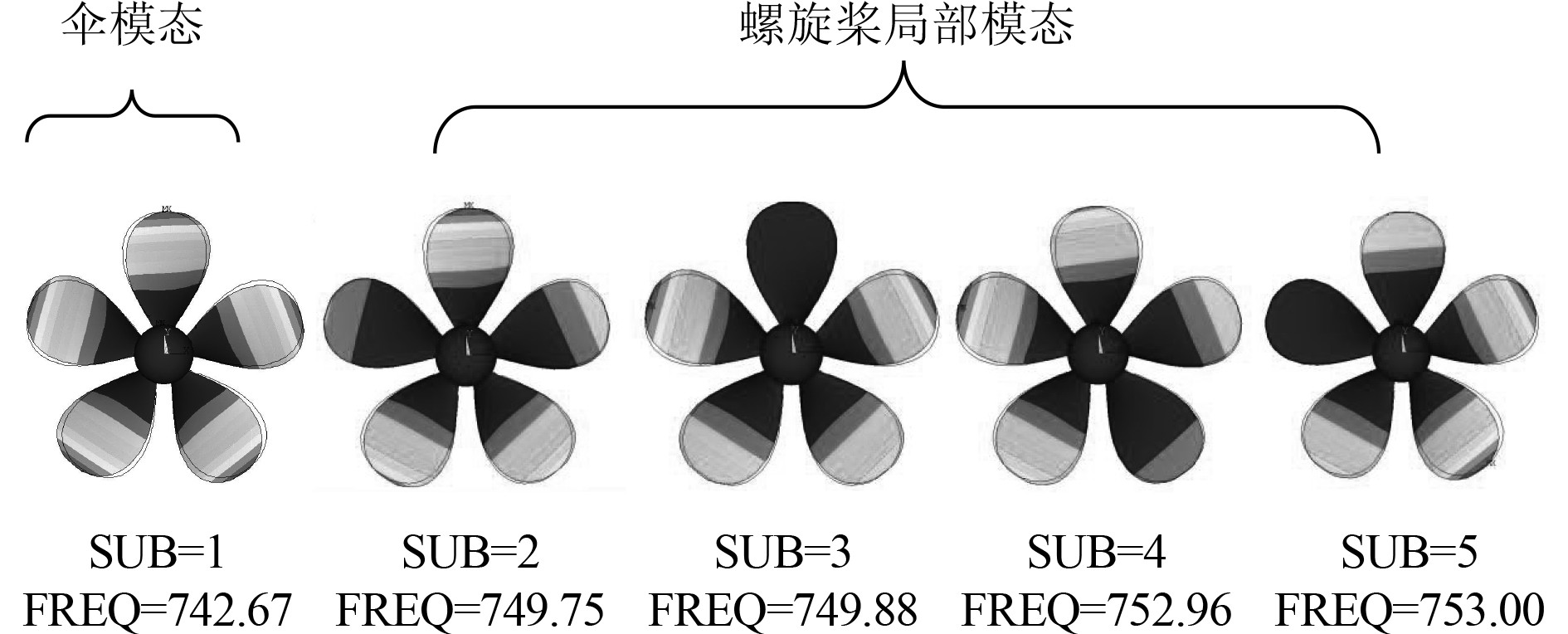
为了进一步研究同组螺旋桨模态规律,提取第1组螺旋桨模态振型和固有频率如图5所示,研究表明,对每一组模态而言,均分为伞模态和局部模态。其中,伞模态表现为5个桨叶同时振动,且幅值相近,其频率为同组5个频率数值中某一单值;局部模态表现为若干桨叶振动较大,剩余桨叶振动较小,其频率近似成对出现。
|
图 5 螺旋桨第一组振型图 Fig. 5 Vibration mode diagram of the first group of propellers |
由于伞模态状态下更容易将力传递到轴系,因此伞模态是结构振动中更为重要的模态类型。后文均研究直径削边对螺旋桨伞模态振型和频率的影响。
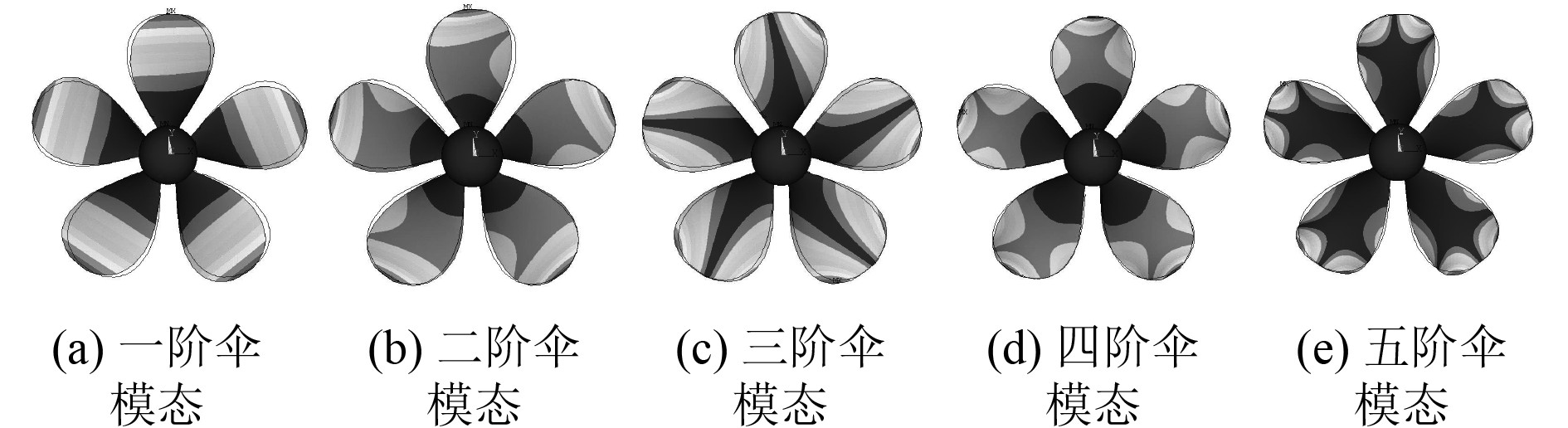
提取前5组模态中伞模态振型图,如图6所示。一阶伞模态是桨叶的悬臂振动,为基础振型;二阶伞模态表现为叶梢的悬臂振动与一侧的扭转振动,振动形态更为复杂;三阶伞模态是桨叶两侧局部弯曲振动,可以将叶梢到叶根的中间部分看作挠度为0的节线;四阶伞模态表现为叶梢的悬臂振动与叶面两侧的扭转振动;随着频率的增大,五阶伞模态呈现出更为复杂的弯扭振动模态。
|
图 6 4381桨前5阶伞模态振型图 Fig. 6 Vibration mode diagram of the first five order parachute modes of 4381 propeller |
从实际情况出发,要使得直径切割对船舶航速的影响较小,直径切割量宜控制在4%以内。然而,船舶实际航行时,螺旋桨桨叶可能出现折断,为保持桨叶受力平衡,会对直径进行较大量切割。综上考虑,选择0%、10%、20%的直径切割量进行研究。
首先对4381桨进行4种大小的直径切割计算3种切割量下的螺旋桨模态频率与振型,并与切割前进行对比,结果如表3及图7所示。
|
|
表 3 不同直径切割量下4381桨固有频率(Hz) Tab.3 Natural frequency of 4381 propeller under different diameter cutting amount (Hz) |
|
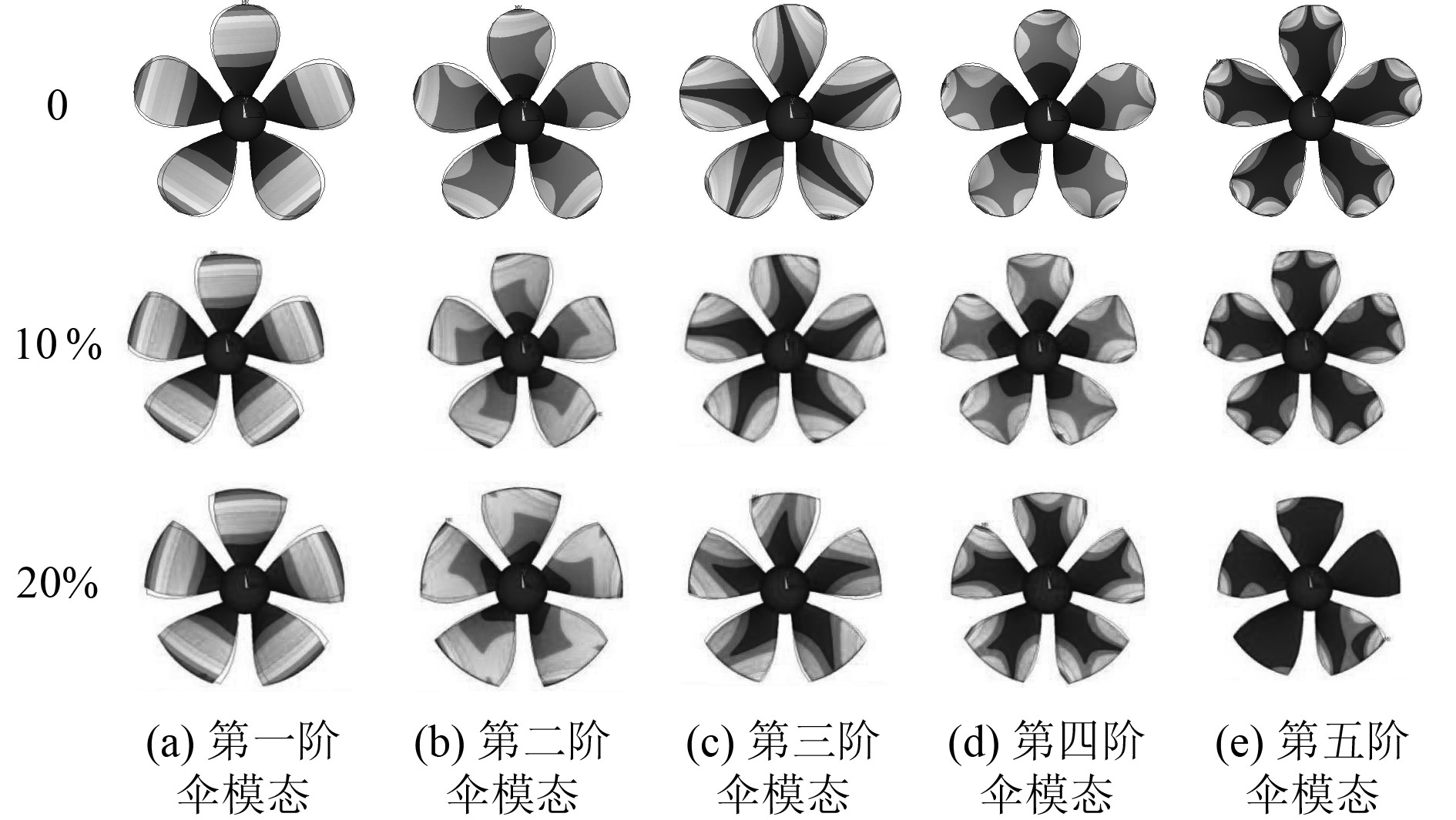
图 7 不同直径切割量下4381桨伞模态振型图 Fig. 7 Modal vibration mode diagram of 4381 propeller umbrella under different diameter cutting amount |
由表3可以看出,切割量P越大,螺旋桨切割后直径越小,桨叶越“短”,其对应组数固有频率越高。
对于螺旋桨振型,当直径切割量较小的时候,各阶数伞模态变化较小。随着切割量的增大,螺旋桨直径变小,桨叶的振动范围逐渐变大,直到延伸至整个桨叶。其部分伞模态由扭转变为悬臂振动,这是由于桨叶长度的减小,悬臂振动形式比扭转振动形式更易出现。
3.3 有侧斜桨直径削边振动特性选取0%、10%、20%的切割量对有侧斜的4382桨、4383桨及4384桨进行切割,计算4种切割量下三类桨的模态频率,并与切割前进行对比,固有频率值如表4~表6所示。
|
|
表 4 不同直径切割量下4382桨固有频率(Hz) Tab.4 Natural frequency of 4382 propeller under different diameter cutting amount (Hz) |
|
|
表 5 不同直径切割量下4383桨固有频率(Hz) Tab.5 Natural frequency of 4383 propeller under different diameter cutting amount (Hz) |
|
|
表 6 不同直径切割量下4384桨固有频率(Hz) Tab.6 Natural frequency of 4384 propeller under different diameter cutting amount (Hz) |
与4381桨直径切割模态结果对比可以看出,有侧斜4382桨、4383桨及4384桨直径切割后具有相似的振动特性:切割量P越大,螺旋桨切割后直径越小,桨叶越“短”,其相应阶数固有频率越高。不同的是,相较于4381桨,不同切割量下相应固有频率值偏低,切割量越大,伞模态阶数越高,频率差值越大。这也是由于4382桨、4383桨及4384桨有侧斜的原因。
与图7相似,当切割量较小的时候,4382桨、4383桨及4384桨各阶伞模态变化不大。随着切割量的增大,螺旋桨直径变小,桨叶的振动范围逐渐变大,直到延伸至整个桨叶,高阶伞模态由局部扭转变为整个桨叶的扭转振动,振动形态更为复杂。但相较于4381桨,4382桨、4383桨及4384桨没有出现部分伞模态由扭转变为悬臂振动的现象,这是由于4382桨、4383桨及4384桨各个剖面有侧斜角的原因,侧斜角越大,扭转振动比悬臂振动越容易出现。
4 结 语本文以有/无侧斜螺旋桨为研究对象,围绕直径切割量对螺旋桨振动特性影响这一关键问题,开展了使用参数化建模方法的螺旋桨直径削边振动分析研究,揭示了直径切割量对螺旋桨振动的影响规律。通过设计程序对4384桨进行模态计算,并与文献结果对比,说明程序和计算结果可信。
在此基础上,利用自研程序计算了无侧斜桨4381及有侧斜桨4382桨、4383桨、4384桨在不同直径切割量下的振动模态,对比分析得到以下结论:
对于无侧斜4381桨,桨叶的直径切割量越大,其相应阶数固有频率越高。由于桨叶长度减小,悬臂振动形式比扭转振动形式更易出现,其部分伞模态由扭转变为悬臂振动;而在直径切割方式下,对4381桨桨叶直径进行切削后,螺旋桨的固有频率及伞模态振型变化不大,即其振动形态大致相同。
对于有侧斜4382桨、4383桨及4384桨,其固有频率随直径及直径切割量的变化规律与无侧斜4381桨基本相同。侧斜不会改变螺旋桨在直径切割方式下的振动特性规律。
研究人员可依据本文发现的规律,寻求船-机-桨匹配下振动特性最优的直径削边方案。
| [1] |
邱嗣镐. "浙水院-3"船改装中螺旋桨的修改设计[J]. 浙江水产学院学报, 1990(1): 66+73-76. QIU S H. Modified design of propeller in refitting "zheshui institute-3" ship [J] Journal of Zhejiang Fisheries University, 1990 (1): 66 + 73-76. |
| [2] |
金咸定, 夏利娟. 船体振动学[J]. 海洋工程装备与技术, 2015, 2(2): 127. JIN X D, XIA L J. Hull vibration [J]. Offshore Engineering Equipment and Technology, 2015, 2(2): 127. |
| [3] |
欧礼坚, 李德玉, 欧家铭, 等. 螺旋桨削边技术减振的分析及应用[J]. 广东造船, 2016, 35(3): 31-32+45. OU L J, LI D Y, OU J M, et al. Analysis and application of vibration damping of propeller trimming technology[J]. Guangdong Shipbuilding, 2016, 35(3): 31-32+45. |
| [4] |
赵阳, 欧礼坚. 应用螺旋桨削边技术减轻老旧船的主机负荷[J]. 珠江水运, 2010(7): 76-77. ZHAO Y, OU L J. Application of propeller trimming technology to reduce the main engine load of old ships[J]. Pearl River Water Transport, 2010(7): 76-77. DOI:10.3969/j.issn.1672-8912.2010.07.035 |
| [5] |
杨佑宗, 许晶, 占金锋. 螺旋桨切割法在突发事件中的实际应用[J]. 上海造船, 2008(1): 36-37+50. YANG Y Z, XU J, ZHAN J F. Practical application of propeller cutting method in emergencies [J] Shanghai Shipbuilding, 2008 (1): 36-37 + 50. |
| [6] |
熊鹰, 瞿守恒. 确定螺旋桨直径切割量的图谱和方法[J]. 海军工程学院学报, 1995(1): 1−6. XIONG Y, QU S H. Atlas and method for determining the cutting amount of propeller diameter [J] Journal of Naval Engineering College, 1995(1): 1−6. |
| [7] |
杨帅, 许晟, 朱志洁, 等. 螺旋桨切割直径法在高速艇中的应用[J]. 中国舰船研究, 2011, 6(4): 61−63. YANG S, XU S, ZHU Z J, et al. Application of propeller cutting diameter method in high speed boat [J]. China Ship Research, 2011, 6 (4): 61−63. |
| [8] |
张济猛. 切割螺旋桨叶片边缘来调整负荷的方法[J]. 船舶工程, 1981(3): 6−12. ZHANG J M. Method of cutting the edge of propeller blade to adjust the load [J]. Ship Engineering, 1981(3): 6−12. |
| [9] |
张松鹤. 漫话船舶螺旋桨的切割方法[J]. 航海技术, 1996(1): 64−66. ZHANG S H. Random talk on cutting method of ship propeller [J] Navigation technology, 1996 (1): 64−66. |
| [10] |
欧礼坚, 安源, 叶家玮, 等. 基于CFD计算的螺旋桨削边研究及应用[J]. 科学技术与工程, 2010, 10(19): 4699-4703. OU L J, AN Y, YE J W, et al. Research and application of propeller trimming based on CFD calculation[J]. Science, technology and engineering, 2010, 10(19): 4699-4703. |
| [11] |
杨波. 修改随边提高螺旋桨转速技术的应用[J]. 交通节能与环保, 2006(1): 46+48. YANG B. Application of the technology of improving propeller speed with modification [J]. Transportation Energy Conservation and Environmental Protection, 2006 (1): 46+48. |
| [12] |
王国强, 董世汤. 船舶螺旋桨理论与应用[M]. 哈尔滨:哈尔滨工程大学出版社, 2007.
|
| [13] |
YOUNG Y L. Time-dependent hydroelastic analysis of cavitating propulsors[J]. Journal of Fluids & Structures, 2007, 23(2): 269-295. |
 2024, Vol. 46
2024, Vol. 46
