钻井船在船级社审图归类为移动平台,相较海船规范而言,平台规范要求相对较高,且更注重疲劳强度校核。疲劳强度分析分为全概率谱分析方法和简化分析方法;谱疲劳分析法精度高,能够反映船舶的真实状态,但计算过程复杂工作量大,同时对硬件要求高;简化法疲劳分析方法通过选取典型装载工况模拟设计波进行校核,能够有效地把控设计载荷,但结果偏保守不利于结构优化设计[1],2种方法均普遍应用于船舶与海洋工程领域。近年来随着有限元软件的大力开发,船级社针对结构强度校核的关注程度也不断增加;但国际油价持续低迷,近5年新造钻井船数量在国内范围更是屈指可数,原本就不完善的规范体系加上有限的学习资料,是制约我国海洋工程装备整体设计水平的因素之一。
钻井船月池区及钻台区为高应力区,该区域的结构设计思路与校核方法是结构设计的核心技术之一,掌握该核心技术便能够攻破此类船型的设计难点。通过借助某型深海钻井船项目设计经验对月池角隅、钻台及钻台支腿结构典型疲劳节点的简化法疲劳强度评估方法进行阐述,从各项载荷的选取、设计工况及校核流程进行阐述;同时提供该船设计载荷与关键区域构件信息供参考;最后,针对疲劳载荷敏感性进行分析,提出影响该区域结构疲劳设计寿命的重要因素。
1 简化法疲劳强度校核按船级社规范[2-3],对简化法疲劳节点的计算校核流程进行阐述,分别从装载工况选取、疲劳载荷选取、制定设计波工况、疲劳节点差值方法进行描述。
1.1 概述该船总长179.8 m,宽32.8 m,型深15.5 m,结构设计吃水9.5 m,设计排水量约42500 t,最大作业水深约2500 m,最大钻深约11000 m。入中国船级社(CCS)及挪威船级社(DNV-GL)双船级,结构设计校核需满足双船级社规范要求。船体中部为月池区及钻探区域,为降低钻台及井架重心高度,月池开孔为大小月池相连形式,小月池供采油树移运至井口重心位置,月池开孔长24.5 m,宽9.8 m。
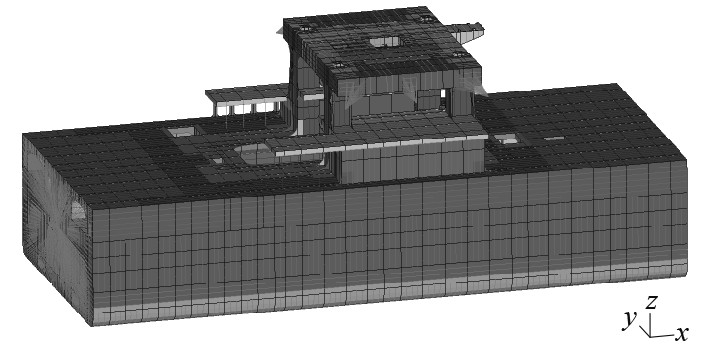
采用简化分析方法对月池角隅及钻台各位置进行疲劳强度评估,利用MSC. Patran建立三舱段有限元模型模拟钻台月池区及前后相邻舱段,如图1所示。模型中的骨材、桁材面板及支柱采用beam单元模拟,其余结构均采用shell单元模拟;疲劳校核区域采用txt细化网格,保证网格精度且延伸至少10个单元以上;并逐渐过渡至粗网格sxs粗网格。
|
图 1 舱段有限元模型 Fig. 1 FE-model of hull vessel |
对月池角隅、钻台与支腿及钻台与井架连接处的典型疲劳节点进行疲劳寿命评估,包含月池角隅自由边、过渡肘板圆弧自由边及肘板趾端处的焊缝疲劳,模型细化区域如图2所示,肘板趾端焊缝处的疲劳又细分为焊缝前侧、左右两侧及甲板以下焊缝。

|
图 2 疲劳节点示意图 Fig. 2 Fatigue hot-spot plot |
疲劳强度评估时,装载工况按以下方式选取,原则上应选取服役期内存在周期最长的装载工况进行计算分析[6],但假定各疲劳载荷在该装载状态下达到极值。
1)航行工况:航行出港工况(100 %装载)及航行到港工况(10 %装载)。
2)作业工况:钻杆钻进工况及下套管工况。
对于疲劳载荷概率水平的选取,由于疲劳损伤往往源于较小的应力循环,故该船疲劳校核设计载荷均取10−2概率水平下的数值作为设计输入进行计算。疲劳校核工况的时间占比按照业主需求取作业工况占80 %,航行工况占20 %;其中作业工况下在南海北部海域作业时间占48 %,全球海域占32 %。
波浪载荷预报中分别针对上述要求选取相应波浪散布图,同时配合最大垂向弯矩、垂向剪力和扭矩装载工况进行波浪载荷预报,得出相应设计载荷包络值分别为:作业工况包络线1(南海北部)、作业工况包络线2(全球海域)和航行工况包络值(全球海域)。作业工况按各自海域散布图进行长期预报,以PM谱模拟,浪向按规范[2]有动力定位的船舶,取迎浪占60%,±15°角占30%,±30°角占10%,考虑cos2扩散函数;航行工况取全球散布图,以PM谱模拟,各浪向角等概率分布,考虑cos2扩散函数。各载荷设计值如表1所示。
|
|
表 1 波浪载荷设计包络值 Tab.1 Design envelop of wave load |
加速度预报值也按此要求分海域提供,所有载荷均基于10−2概率水平。航行工况进行疲劳计算时,因有限元模型模拟到钻台面,井架及相应钻台面设备以质量点型式施加,为保守考虑,该工况下的加速度位置取井架及相应设备重心处所对应值;作业工况下取钻台面井口中心位置处的加速度值,井架及液压顶升油缸处的疲劳载荷按支反力形式加载与模型中。该船疲劳计算加速度数值如表2所示。
|
|
表 2 全船各位值加速度值 Tab.2 Design acceleration of hull spot |
井架及顶升液压油缸支反力由设备商提供,该载荷是基于10−8概率水平下的支反力,通过换算得到10−2概率水平下对应值,换算过程见以下说明:
1) 疲劳寿命评估的前提是总的疲劳累计损伤与载荷选取的超越概率水平无关,意味着无论设计载荷取10−2、10−4或10−8,累计损伤值均应相等。
2) 根据规范DNV-RP-C203,假设威布尔分布加速度及应力下的损伤表达式为:
| $ D=\frac{n}{\bar{a}}\cdot {q}^{m}\cdot \Gamma \left(1+\frac{m}{h}\right)。$ | (1) |
式中:D为累计损伤;n为循环次数;
| $ q=\frac{\Delta {\sigma }_{0}}{{\left(\mathrm{ln}{n}_{0}\right)}^{1/h}}。$ | (2) |
式中:
| $ \Delta\sigma_4=\Delta\sigma_8\cdot\left(\frac{\left(\mathrm{ln}10^4\right)}{\left(\mathrm{ln}10^8\right)}\right)^{1/h} 。$ | (3) |
式中:h为威布尔形状系数,保守考虑取1.1[4]。即可得到10−2概率水平下的用于疲劳计算的支反力数值,按下式所得:
| $ R_{-4}=R_{-8}\cdot\left(\frac{\mathrm{ln}10^4}{\mathrm{ln}10^8}\right)^{1/1.1},$ | (4) |
| $ R_{-2}=R_{-8}\cdot\left(\frac{\mathrm{ln}10^2}{\mathrm{ln}10^8}\right)^{1/1.1}。$ | (5) |
式中:R为支反力。按此推算,所得支反力如表3所示,假定井架4条支腿承受各项载荷均为最大值。计算时,对于一组循环工况,支反力取值大小相同,符号相反。
|
|
表 3 设备支反力(基于波频) Tab.3 Reaction force of derrick (wave frequency) |
简化法疲劳强度评估是通过模拟多种等效设计波工况进行计算校核,双船级社规范中提供了5种设计波工况,分别为:
1)(HSM)迎浪工况,船中处大垂向弯矩;
2)(FSM)随浪工况,船中处大垂向弯矩;
3)(BSR)横浪工况,最大横摇运动;
4)(BSP)横浪工况,水线处最大海水动压力;
5)(OST)斜浪工况,最大扭矩。
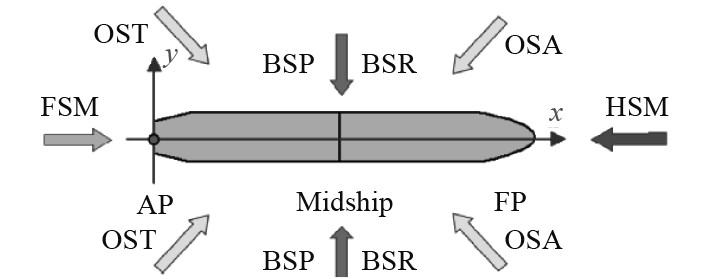
OSA同为斜浪工况,最大纵摇运动,但此设计波工况仅用于屈服、屈曲强度校核,不用于疲劳强度校核。各设计波模拟如图3所示。
|
图 3 设计波工况示意图 Fig. 3 Equivalent design wave (EDW) |
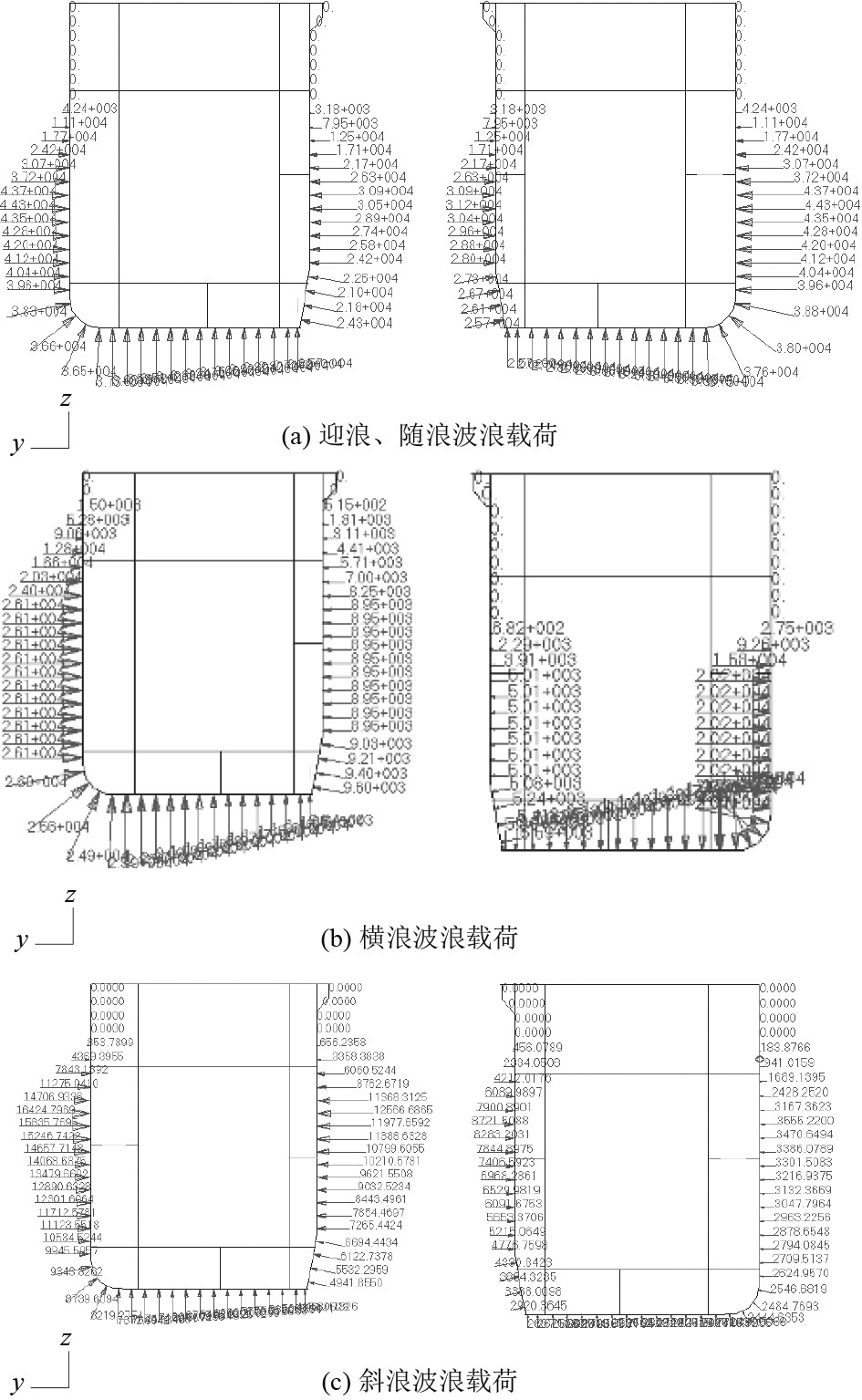
在设计波工况中,除施加波浪载荷、加速度外,还需模拟舷外水压力。根据规范公式对各设计波工况所对应的舷外水压力进行计算并得出各位置处的压力值,在Patran中建立以Y-Z双向的二维场进行模型加载,施加于船体外板与月池围壁处,模型压力场如图4所示。
|
图 4 舷外水压力示意图 Fig. 4 Outboard wave pressure spot |
建立各项设计波工况,对应不同工况,波浪载荷可进行折减;各设计波工况对加速度方向要求也有明确规定,该船计算后的设计波工况参数如表4所示,针对不同船型尺度、计算校核位置,各项参数略有不同。
|
|
表 4 设计波工况载荷系数选取 Tab.4 Load factor of EDW |
按照规范进行热点应力插值。热点应力范围应为垂直于焊趾方向左右45°范围内的热点主应力。
1)焊接型节点热点应力计算
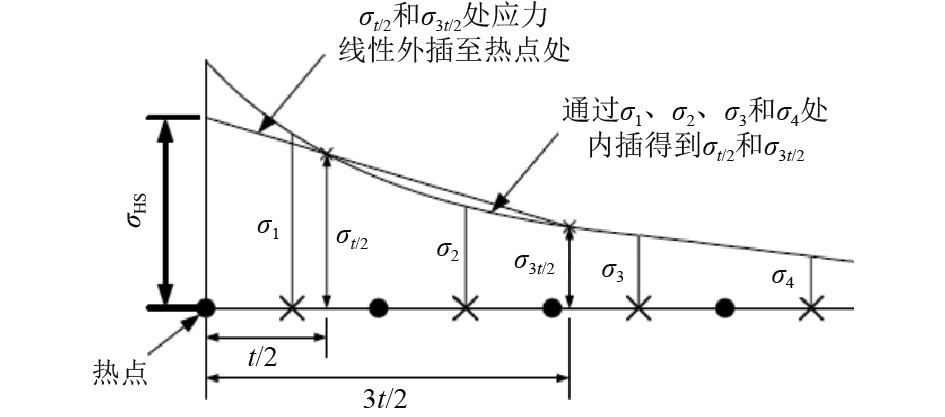
对于一般焊接型节点(如肘板趾端等),热点应力计算式为:
| ${\sigma }_{ij\left(k\right)}=\frac{3{\sigma }_{ij\left(k\right),t/2}-{\sigma }_{ij\left(k\right),3t/2}}{2},\left(j=\mathrm{1,2}\right),{{\mathrm{N/mm}}}^{2}。$ | (6) |
式中:
|
图 5 一般焊接型节点热点应力插值 Fig. 5 Stress interpolation of general welding joint spot |
2)板材自由边热点应力计算
对于板材自由边的疲劳评估,需使用梁单元(横截面积极小)来获取疲劳寿命,应力范围考虑梁单元的轴向力和弯曲应力,梁单元的高度与所考虑板材的厚度相同,宽度方向近似忽略[7]。
1.5 疲劳损伤计算该船设计寿命30年,根据各海域波浪散布图及航行-作业时间占比(20%~80%)推算出航行状态下载荷共循环2.21E+07次,作业状态下载荷循环1.33E+08次。
疲劳节点的总损伤表达式为:
| $ {D}_{\text{总}}={D}_{\text{航行}}+{D}_{\text{作业}}。$ | (7) |
式中,D作业又分为D南海和D全球,通过南海散布图预报出来的加速度和波浪载荷计算所得到的损伤为D南海,全球散布图预报出来的加速度和波浪载荷计算所得到的损伤为D全球,则按作业海域时间占比系数得到作业状态下总损伤D作业:
| $ {D}_{\text{作业}}=60{\text{%}} \cdot {D}_{\text{南海}}+40{\text{%}}\cdot {D}_{\text{全球}} 。$ | (8) |
航行工况下的损伤D航行按航行船规范考虑,取所有等效设计波工况中的最大值工况,即假定航行期间全概率承受该设计波影响;作业工况下的累计损伤D作业按平台规范取浪向等概率分布,即迎浪、随浪占12.5 %,横浪占25 %,斜浪占50 %。
对于各疲劳节点的安全系数取值,需结合规范及业主需求,经业主认可该船能够满足5年内进坞检查维修,计算中选用的疲劳安全系数如表5所示。
|
|
表 5 疲劳安全系数取值 Tab.5 Design safety factor |
各疲劳校核节点所选用的S-N曲线如表6所示。
|
|
表 6 S-N曲线选取及参数 Tab.6 S-N curve |
对于板厚修正系数ft=(t/22)n,其中系数n=0.1(圆弧自由边),n=0.25(焊接节点)。
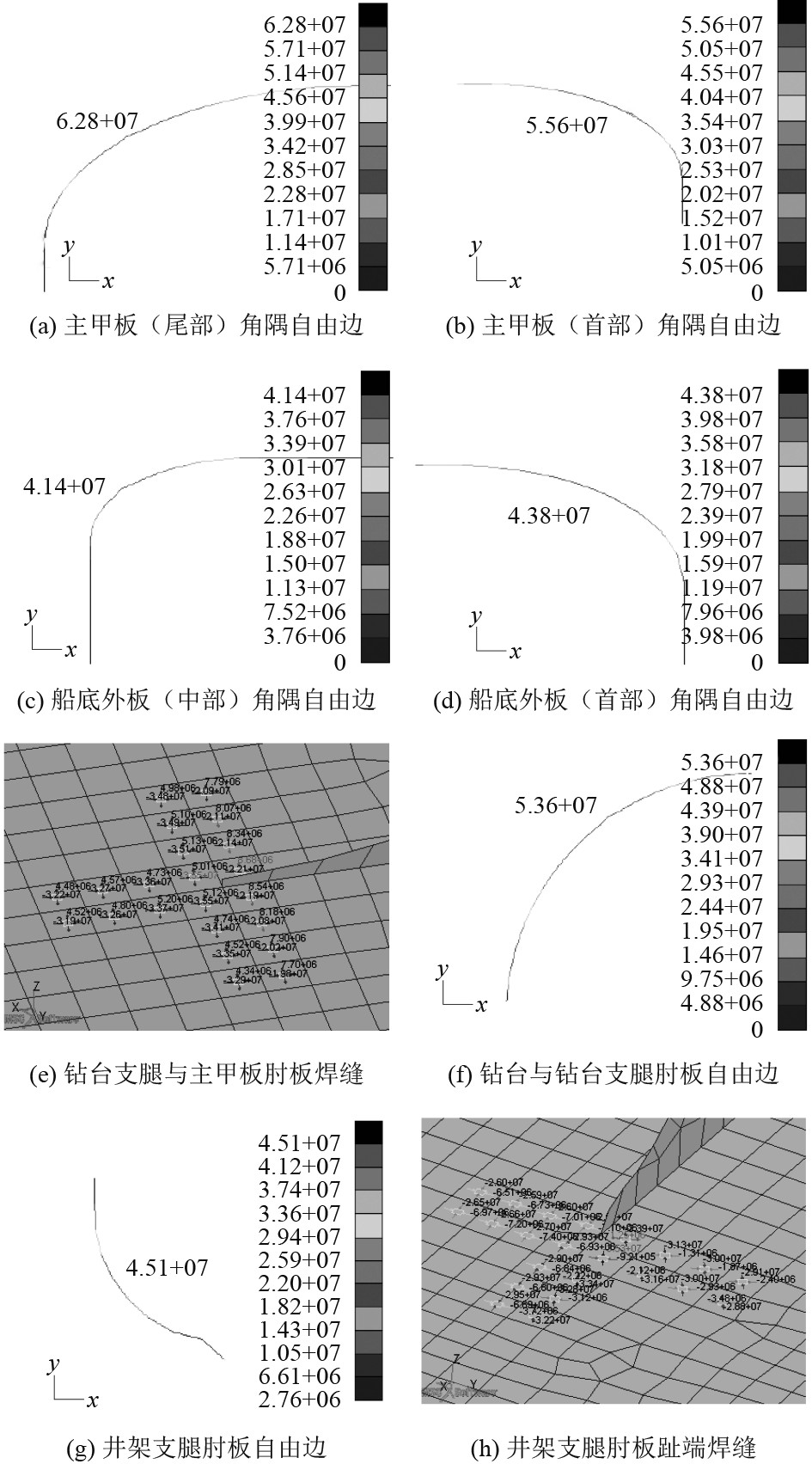
1.6 计算结果通过模拟设计波工况,对月池角隅及钻台支腿、井架支腿等疲劳热点区域进行校核,得出累计损伤换算得到设计寿命如表7所示,该船疲劳设计寿命30年,计算结果均满足设计要求。通过计算所得:主甲板月池角隅取50 mm(FH36)、中间甲板15 mm(AH36)、双层底25/30 mm(DH36)及船底外板50/60 mm(FH36);井架支腿面板取80 mm(FH36),腹板60 mm(FH36),钻台与支腿角隅板35/50 mm(EH36/FH36),钻台支腿与主甲板连接处肘板35/50 mm(EH36/FH36)。各区域应力云图如图6所示。
|
|
表 7 月池角隅各区域疲劳寿命列表 Tab.7 Design fatigue life of moonpool corners |
|
图 6 各区域应力云图 Fig. 6 Stress plot of each hot-spot |
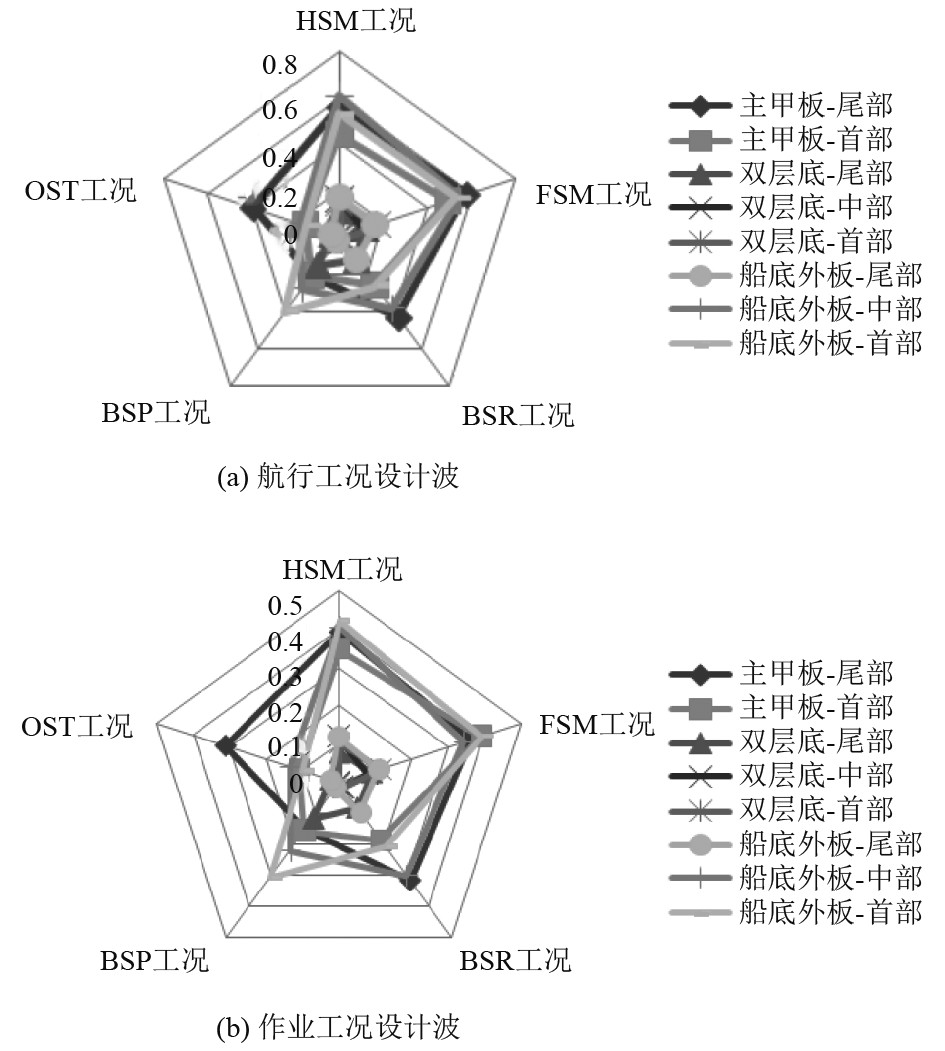
针对月池角隅区域,各设计波工况计算所得的损伤见表8,敏感性分析见图7。经过对比分析得到:以航行工况为例,设计波工况HSM与FSM对月池角隅的疲劳损伤较高,BSP与BSR工况敏感度适中,斜浪OST工况的敏感度最低。
|
|
表 8 设计波工况敏感性分析结果 Tab.8 EDW sensitivity analysis |
|
图 7 各工况设计波敏感性分析 Fig. 7 Load condition sensitivity analysis |
对波浪载荷进行敏感性分析,简化法疲劳强度评估计算的加载流程是建立设计波工况,针对典型装载工况施加加速度、舷外水压力及井架疲劳载荷(仅存在于作业工况)后,运算并得到该状态下的波浪载荷数值;再通过对比波浪载荷目标值进行模型调载,使得模型月池中心位置处横剖面达到各项载荷目标值。
敏感性分析是通过调整波浪载荷时,额外增加5 %及10 %进行第2次、第3次运算并得到损伤值,进而通过对比3次运算的损伤得到敏感性分析结论。调载时,仅调整波浪载荷中的单一数值。例如,调整弯矩增加5%时,剪力和扭矩维持原有设计值,进行对比分析。该文对航行工况进行波浪载荷敏感性进行分析,得出的相应结论对作业工况同样适用,分析结果见表9及图8。
|
|
表 9 波浪载荷敏感性分析结果(航行工况) Tab.9 Wave load sensitivity analysis |

|
图 8 载荷敏感性分析 Fig. 8 Wave load sensitivity analysis |
可知,垂向弯矩和扭矩对月池角隅的影响较大,剪力对其影响较小;其中弯矩占据主要地位,弯矩与疲劳损伤的几乎呈1∶1线性关系,可见降低设计弯矩与扭矩对提高月池角隅的疲劳寿命有极大的影响。
2.3 加速度敏感性分析对加速度进行载荷敏感性分析,计算流程如上节所述,但改变加速度数值后需重新调整波浪载荷使其达到原有目标值。同时保证除加速度外的其他各项载荷维持不变进行对比分析,结果见表10及图9。
|
|
表 10 加速度敏感性分析结果(航行工况) Tab.10 Acceleration sensitivity analysis |

|
图 9 加速度敏感性分析 Fig. 9 Acceleration sensitivity analysis |
可知,横、纵向加速度敏感度不及垂向加速度对月池角隅的影响。
3 结 语该文基于对钻井船关键区域进行简化法疲劳强度评估流程的阐述与结果分析,结合载荷敏感性分析得出如下结论:
1)该文列出简化法疲劳强度评估的详细流程与载荷选取思路,并得出相应关键区域的构件尺寸信息供参考。
2)对于大小月池开口型式,小月池剖面由于模数高于大月池剖面,相应角隅处的疲劳寿命略高于大月池位置处的角隅。
3)该船月池在主甲板位置为大开孔,在中间甲板及以下设置大小月池,对于主甲板位置的月池角隅,小月池剖面位置的疲劳寿命低于大月池剖面处。
4)设计波工况HSM及FSM对月池角隅的敏感度较高,OST工况敏感度最低;垂向弯矩及扭矩对月池角隅的敏感度较高,垂向剪力对其敏感度较低;垂向加速度对月池角隅的敏感度略大于水平加速度。
5)通过降低设计垂向弯矩及扭矩,是提高月池角隅的疲劳寿命的重要因素。
| [1] |
刘玉超, 任慧龙, 冯国庆,等. 船体结构疲劳评估直接计算的简化方法[J]. 华中科技大学学报(自然科学版), 2021, 49(12): 40-45. DOI:10.13245/j.hust.211208 |
| [2] |
挪威船级社. Guide for fatigue assessment of ship structures[S]. 2018.
|
| [3] |
中国船级社. 钢制海船入级规范[M]. 北京: 人民交通出版社, 2021.
|
| [4] |
挪威船级社. Standard for drilling plant[S]. 2013.
|
| [5] |
王斯虎, 薛鸿祥, 唐文勇. 超深水钻井船月池角隅区域疲劳强度及载荷敏感性分析[J]. 船海工程, 2020, 49(1): 56-60. |
| [6] |
迟少艳, 杨青, 钟晨. “TIGER”钻井船结构设计[J]. 船舶与海洋工程, 2016, 32(1): 7-12. DOI:10.14056/j.cnki.naoe.2016.01.002 |
| [7] |
王醍, 王璞, 林瞳,等. 3000 m深水钻井船月池角隅疲劳强度研究[J]. 船舶, 2018, 29(4): 38-44. DOI:10.19423/j.cnki.31-1561/u.2018.04.038 |
 2024, Vol. 46
2024, Vol. 46
