0 引　言

极地船舶在平整冰中破冰航行性能优劣的重要评价指标是破冰能力，破冰能力由冰厚与速度曲线（h-v曲线）来描述，h-v曲线表征了船舶使用满额功率在特定冰厚下所能达到的航速。现阶段极地船舶破冰能力的评估主要依赖于冰水池模型试验结果到实船的换算，我国大型冰水池试验设施及试验能力建设处于起步阶段，不能有效支撑极地船舶破冰能力评估和船型研发，故开发具有一定数值精度且高效的破冰能力数值评估方法具有重要的现实意义。

极地船舶连续破冰过程就是船体遭遇的破冰阻力与螺旋桨净推力动态平衡的过程，因此连续破冰阻力和净推力的精确计算是破冰能力评估的关键。在极地船舶初始设计阶段，船舶的推力、推力减额甚至静水阻力很难精确获取，Riska等^[1]提出一种简化的净推力计算公式，主要是通过船舶的系柱拉力乘以速度二次方关系函数获得，其中系柱拉力可由芬兰-瑞典冰级规则^[2]及Juva等^[3]的研究成果获得。关于连续破冰阻力的计算，近年来国内外学者将研究重点放在了对连续破冰进程的物理建模，意识到掌握破冰机理可以提高数值方法的可靠性。Riska ^[4]率先分析了船舶与大块浮冰的相互作用机理，提出一种求解船舶冰阻力和运动响应的理论模型。Valanto^[5]开发了一种模拟平整冰中船体水线处连续破冰过程的三维数值模型，该模型用于计算船体遭遇的冰阻力和船体局部冰载荷，船体水下部分遭遇冰阻力采用Lindqvist^[6]提出的经验公式。Liu等^[7]开发了一种船-冰相互作用数值模型，该模型中船-冰接触面积基于一种时域理论进行计算，下一阶段的船-冰接触面积计算基于当前的碎冰航道和船舶运动。Sawamura等^[8]提出一种模拟船舶在层冰中航行连续破冰过程及计算冰阻力的数值模型，应用有限元思想采用不同种类冰缘形状来离散层冰计算船-冰相互作用产生的动力响应。Zhou等^[9]基于一系列船-冰相互作用模型试验，开发了系泊结构物在层冰中的冰阻力数值模拟方法，该方法考虑了碎冰堆积效应对冰阻力的影响。国内方面，曹成杰^[10]基于RBF神经网络理论开展了极地船舶连续破冰能力评估方法研究，其中船体冰阻力采用键型近场动力学方法对连续破冰过程进行数值模拟，并结合Lindqvist ^[6]提出的经验公式对水下冰阻力进行计算。为了开发工程适用的连续破冰阻力数值预报方法，刁峰等^[11]开发了一种基于预设冰网格技术的连续破冰阻力数值模拟理论，预先对船体水线附近的线型进行分层离散及对冰场进行方形网格离散，通过几何计算和受力分析在时域内数值模拟连续破冰进程及产生的破冰阻力分量，获得了与模型试验结果相吻合的数值模拟结果。

本文在一种基于预设冰网格技术的连续破冰阻力数值模拟理论的基础上，开发了静态和动态2种破冰能力数值评估方法，应用于某极地双向破冰油船破冰能力评估，并与冰水池模型试验结果进行对比分析，为极地船舶性能评估提供了有效工具。

1 极地船舶破冰能力数值评估方法 1.1 基于预设冰网格技术的连续破冰阻力数值模拟理论

基于预设冰网格技术的连续破冰阻力数值模拟理论的核心是将船舶连续破冰视为接触-挤压-破碎的循环过程，通过对冰层进行合理的方形冰网格离散、对船体水线附近线型采用分层离散的技术手段，在时域内动态求解船舶六自由度运动微分方程，建立考虑运动与阻力耦合效应的连续破冰数学模型。基于预设冰网格技术的连续破冰阻力数值模拟理论详见文献[11]。

船体六自由度运动方程在随船坐标系中向量表达形式：

$ \left( {{\boldsymbol{M}} + {\boldsymbol{A}}} \right)\ddot {\boldsymbol{r}}\left( t \right) + {\boldsymbol{B}}\dot {\boldsymbol{r}}\left( t \right) + {\boldsymbol{C}}{\boldsymbol{r}}\left( t \right) = {\boldsymbol{F}}\left( t \right)。$

(1)

式中：M为质量矩阵；A为附加质量矩阵；B为阻尼矩阵；C为静水恢复力矩阵；F为对应于随船坐标系的外力和外力矩。外力和外力矩可表示为：

$ F = {F_{H}} + {F_{P}} + {F_{R}} + {F_{E}} 。$

(2)

式中：$ {F_{H}} $、$ {F_{P}} $和$ {F_{R}} $分别为作用于船体、螺旋桨和舵的水动力；$ {F_{E}} $为包括风、浪、流及海冰在内的环境力，连续破冰阻力$ {F_{{\text{ice}}}} $是航行于层冰覆盖水域船舶所受的主要环境力，因此式（2）可表示为：

$ F = {F_{H}} + {F_{P}} + {F_{R}} + {F_{\text{ice}}}。$

(3)

连续破冰阻力$ {F_{{\text{ice}}}} $由破冰阻力$ {F_{{{br}}}} $、冰浮力$ {F_{b}} $和除冰力$ {F_{cl}} $组成，冰浮力和除冰力可统称为浸没冰阻力$ {F_s} $。

$ {F_{{\text{ice}}}} = {F_{{{br}}}} + {F_{{b}}} + {F_{{{cl}}}} = {F_{{{br}}}} + {F_{{s}}}。$

(4)

破冰阻力$ {F_{br}} $采用文献[11]中提出的基于预设冰网格技术的连续破冰时域理论进行计算。破冰阻力数值计算流程主要包括：将连续破冰过程离散为连续的时间步长，在每个时间步内建立船舶六自由度运动方程，根据船舶当前状态变量（位置、速度和加速度）、当前冰缘形状和船-冰接触几何状况，计算冰阻力和其他外部环境力；求解运动方程得到相应的状态增量，考虑冰阻力与船舶运动相耦合，在每个时间步长内进行迭代以达到动态平衡；更新船舶状态变量及船-冰接触几何状况，判定冰层是否发生弯曲失效，如果冰层失效，删除冰网格，更新冰缘形状，重复下一时间步长的破冰过程。

浸没冰阻力$ {F_{s}} $采用改进后的Lindqvist浸没冰阻力经验公式^[11]：

$\begin{split} {F_{s}} = & ( {\rho _{{\Delta}}}g{h_i}( {BT( {B + T} )/( {B + 2T} )} ) +\\ & \mu {A_{f}} )( {1 + 9.4{v /{\sqrt {g{L_{\text{WL}}}} }}})。\end{split}$

(5)

式中：$ {\rho _{{\Delta }}} $为海水和海冰密度差；g为重力加速度；$ {h_i} $为冰厚；B为船体型宽；T为船体吃水；$ \mu $为摩擦系数；$ {A_{f}} $为船首湿表面积；v为航速；$ {L_{\text{WL}}} $为船体水线长。

作用于螺旋桨水动力$ {F_{{P}}} $可由Bertram^[12]提出的简化公式获取，Bertram提出的由螺旋桨和舵诱导的船体受力在水平面内有如下简化计算公式：

$ \left\{ \begin{gathered} {F_{XP}}{\text{ + }}{F_{XR}} = {T_{\text{net}}} - \frac{1}{2}{C_D}{\rho _w}V_f^2{A_r}，\\ {F_{YP}}{\text{ + }}{F_{YR}} = \frac{1}{2}{C_L}{\rho _w}V_f^2{A_r}，\\ {F_{NP}}{\text{ + }}{F_{NR}} = \frac{1}{2}{C_L}{\rho _w}V_f^2{A_r}{x_r}。\\ \end{gathered} \right. $

(6)

式中：$ {T_{\text{net}}} $为螺旋桨净推力；$ {C_L} $和$ {C_D} $为舵的升力和阻力系数；$ {V_f} $为流体速度；$ {A_r} $为舵面积；$ {x_r} $为舵纵向位置坐标。

螺旋桨净推力$ {T_{\text{net}}} $可通过Riska等^[1]提出的简化估算公式计算获取：

$ {T_{\text{net}}} = f\left( v \right) \cdot {T_{\text{pull}}}，$

(7)

$ f\left( v \right){\text{ = }}1 - \frac{1}{3}\frac{v}{{{v_{ow}}}} - \frac{2}{3}{\left( {\frac{v}{{{v_{ow}}}}} \right)^2} ，$

(8)

$ {T_{\text{pull}}} = {K_e} \cdot {\left( {{P_D} \cdot {D_P}} \right)^{{2 \mathord{\left/ {\vphantom {2 3}} \right. } 3}}}。$

(9)

式中：${T_{\text{pull}}}$为系柱拉力；${v_{ow}}$为敞水速度；$v$为破冰航速；${P_D}$为推进功率；${D_P}$为螺旋桨桨径；${K_e}$为系柱拉力经验系数，根据芬兰-瑞典冰级规则^[2]，对于调距桨、电力或液压推进系统，单桨船${K_e}$可取为0.78，双桨船${K_e}$可取为0.96，三桨船${K_e}$可取为1.12，对于定距桨建议再乘以系数0.9。

1.2 破冰能力静态评估方法

在极地船舶工程设计中，表征破冰能力的h-v曲线最终是通过冰水池模型试验获取的，在初始设计阶段可借助数值手段按照以下步骤获得：首先，基于数值方法计算获得不同冰厚下的连续破冰阻力和航速曲线；其次，计及冰区推力减额计算获得不同航速下用于克服连续破冰阻力的净推力曲线；最后，将上述2条曲线的交点连起来即可获得h-v曲线。为了衡量船舶的破冰能力水平，可采用1 kn航速对应的破冰厚度来考核其破冰能力，冰厚越大破冰能力越强。

基于上述分析，可以建立一种船舶破冰能力静态评估方法：首先，采用基于预设冰网格技术的连续破冰阻力数值模拟方法计算获得不同冰厚下的连续破冰阻力和航速曲线；其次，采用规范和经验估算方法获得净推力和航速曲线；最后，提取2条曲线的交点即可获得表征破冰能力的h-v曲线。

1.3 破冰能力动态评估方法

船体六自由度运动方程（1）可以表达为：

$ \left( {{\boldsymbol{M}} + {\boldsymbol{A}}} \right)\ddot {\boldsymbol{r}}\left( t \right) + {\boldsymbol{B}}\dot {\boldsymbol{r}}\left( t \right) + {\boldsymbol{Cr}}\left( t \right) = {F_{br}}\left( t \right) + {F_{s}}\left( t \right) + {T_{\text{net}}}\left( t \right)。$

(10)

由此可以建立一种船舶破冰能力动态评估方法：通过求解船舶在不同冰厚下连续破冰的六自由度运动微分方程（10），在每个时间步长内动态更新连续破冰阻力和净推力，当连续破冰阻力和净推力达到平衡时，获得特定冰厚下的稳定航速，从而获得h-v曲线。

2 双向破冰油船破冰能力验证分析 2.1 研究对象及冰水池模型试验

本文研究对象为一艘航行于北极地区具有双向破冰能力、主要从事原油运输任务的油船，破冰能力可达PC3级。双向破冰船舶首、尾均具有破冰能力，当遭遇较厚的层冰或冰脊导致首向无法破冰时，利用其配备的全回转吊舱推进器在冰区将船舶灵活的掉过头来，船尾变成船首，吊舱推进器旋转180°为尾向破冰提供动力，同时吊舱推进器螺旋桨的加强型叶片快速旋转将厚冰层或冰脊根部切碎从而实现尾向破冰。极地油船主尺度及用于估算净推力的输入参数见表1。

极地油船在俄罗斯克雷洛夫研究院冰水池开展了一系列连续破冰快速性模型试验。极地油船具有典型的双向破冰型船型特点，首部线型具有典型的有利于破冰的前倾型首柱，首部底端设有楔形前踵防止骑上冰面发生搁浅事故，尾部采用双吊舱推进系统。

极地油船对应于实船状态的连续破冰快速性模型试验工况见表2，试验在设计吃水状态下进行。试验主要分为首向和尾向连续破冰，其中首向连续破冰模型试验开展了2种不同冰厚、4种不同航速下的冰阻力测量；尾向连续破冰模型试验中电机驱动螺旋桨运行，同样开展了2种不同冰厚、4种不同航速下的冰阻力和螺旋桨推力测量试验。极地油船双向破冰模型试验照片见图1。

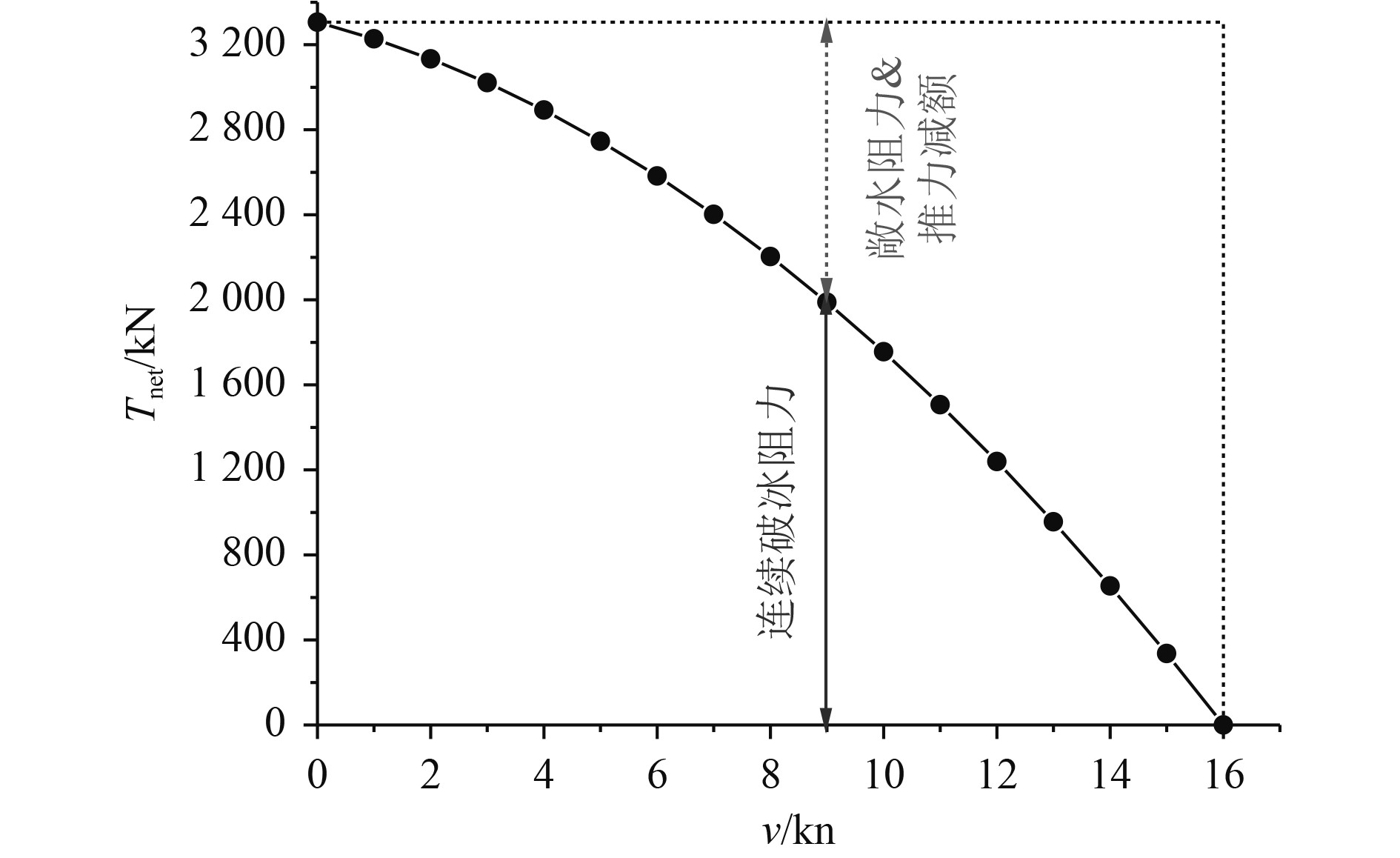
根据式（7）～式（9）可以估算获得极地油船净推力与航速关系曲线，极地油船首向破冰模式下的净推力与航速关系曲线如图2所示。考虑到尾向破冰状态的系柱拉力及对应的净推力是小于首向破冰状态的，本文参考极地油船模型试验结果对首向破冰系柱拉力进行相应折减获得尾向破冰模式下的净推力与航速关系曲线。

2.2 破冰能力静态评估方法验证分析

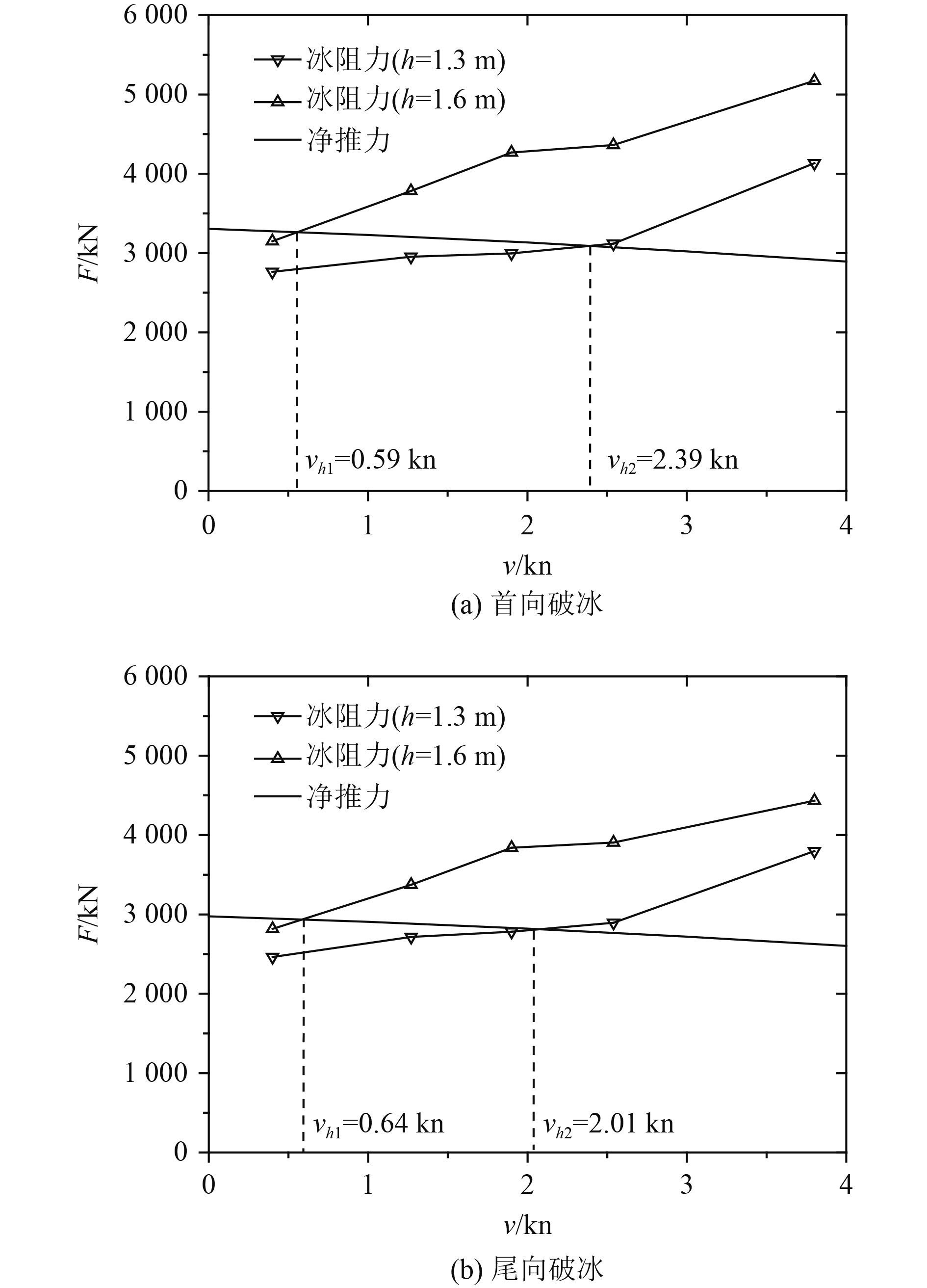
根据破冰能力静态评估方法，将极地油船不同冰厚下的连续破冰阻力和航速曲线与对应模式下的净推力和航速曲线相结合即可获得特定冰厚下的航速值，以此获得h-v曲线，由静态评估方法获得的极地油船2种破冰模式下的破冰能力评估结果见图3。可知：基于螺旋桨净推力与连续破冰阻力的平衡，首向破冰模式，极地油船在1.3 m冰厚能达到的最大航速为2.39 kn，1.6 m冰厚能达到的最大航速为0.59 kn；尾向破冰模式，极地油船在1.3 m冰厚能达到的最大航速为2.01 kn，1.6 m冰厚能达到的最大航速为0.64 kn。

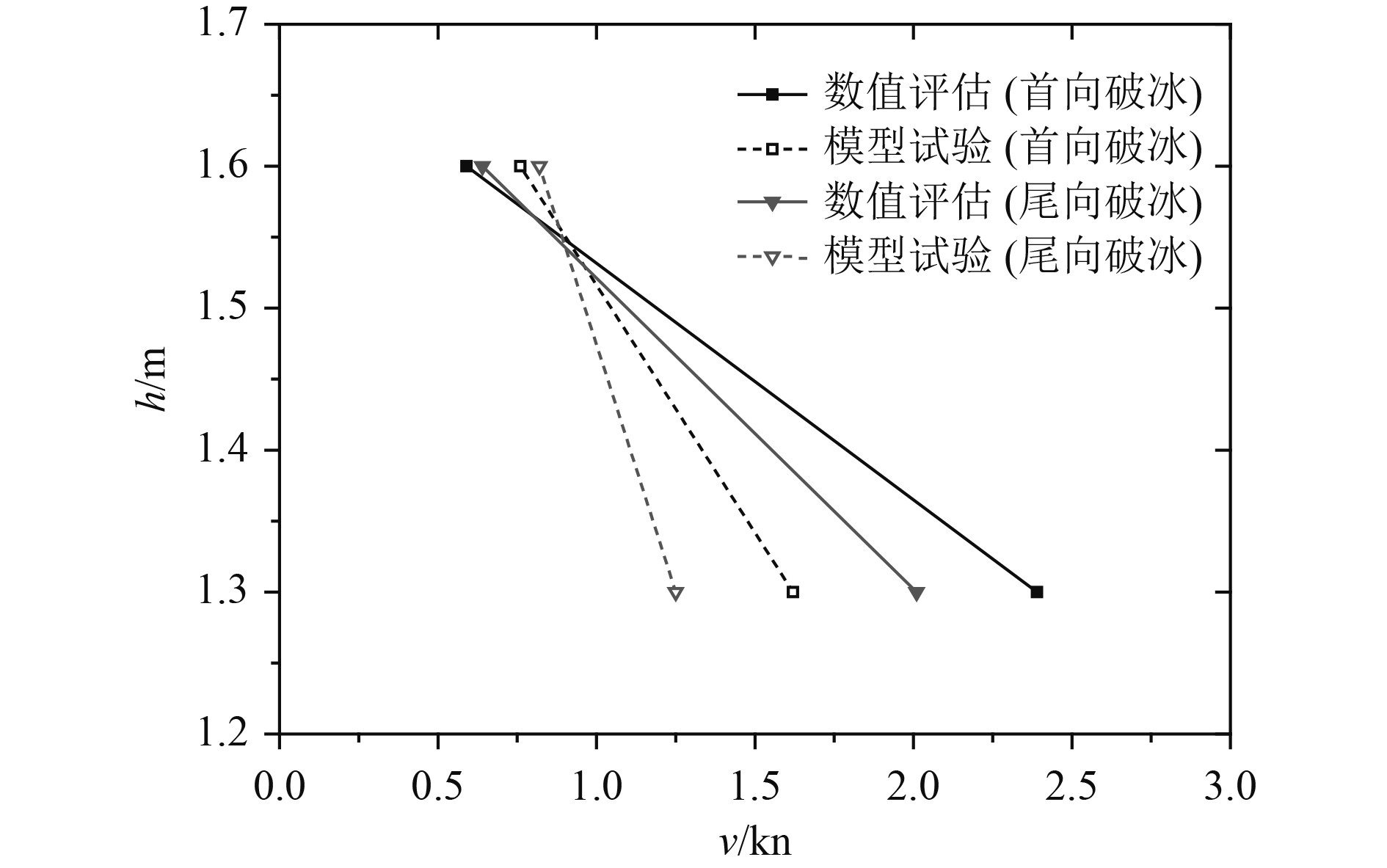
上述冰厚及对应的最大航速即是由静态评估方法获得的极地油船h-v曲线，与由模型试验获得的h-v曲线对比见图4。可知：2种破冰模式下，静态评估方法获得的h-v曲线不管是自身变化规律还是与模型试验之间的相对变化趋势均较为接近。首先，静态评估方法获得的首向破冰和尾向破冰h-v曲线斜率相近且靠的很近，两者的差别在于尾向破冰h-v曲线大部分位于首向破冰h-v曲线下方，两者在航速0.8 kn左右存在交点。v>0.8 kn，极地油船首向破冰能力大于尾向破冰能力；v<0.8 kn，极地油船尾向破冰能力则大于首向破冰能力。2种破冰模式下，模型试验获得的h-v曲线也具有上述相似规律，差别在于模型试验h-v曲线交点在v=0.9 kn左右，且模型试验结果显示出的首向破冰能力与尾向破冰能力的差距明显大于静态评估方法获得的结果；其次，静态评估结果与模型试验结果相比，模型试验获得的h-v曲线的基本位于静态评估方法获得的h-v曲线下方，2种破冰模式下数值与试验的h-v曲线交点均在v=0.9 kn左右。总体而言，静态评估方法计算得到的破冰能力大于模型试验测得的破冰能力，首向破冰能力大于尾向破冰能力。

2.3 破冰能力动态评估方法验证分析

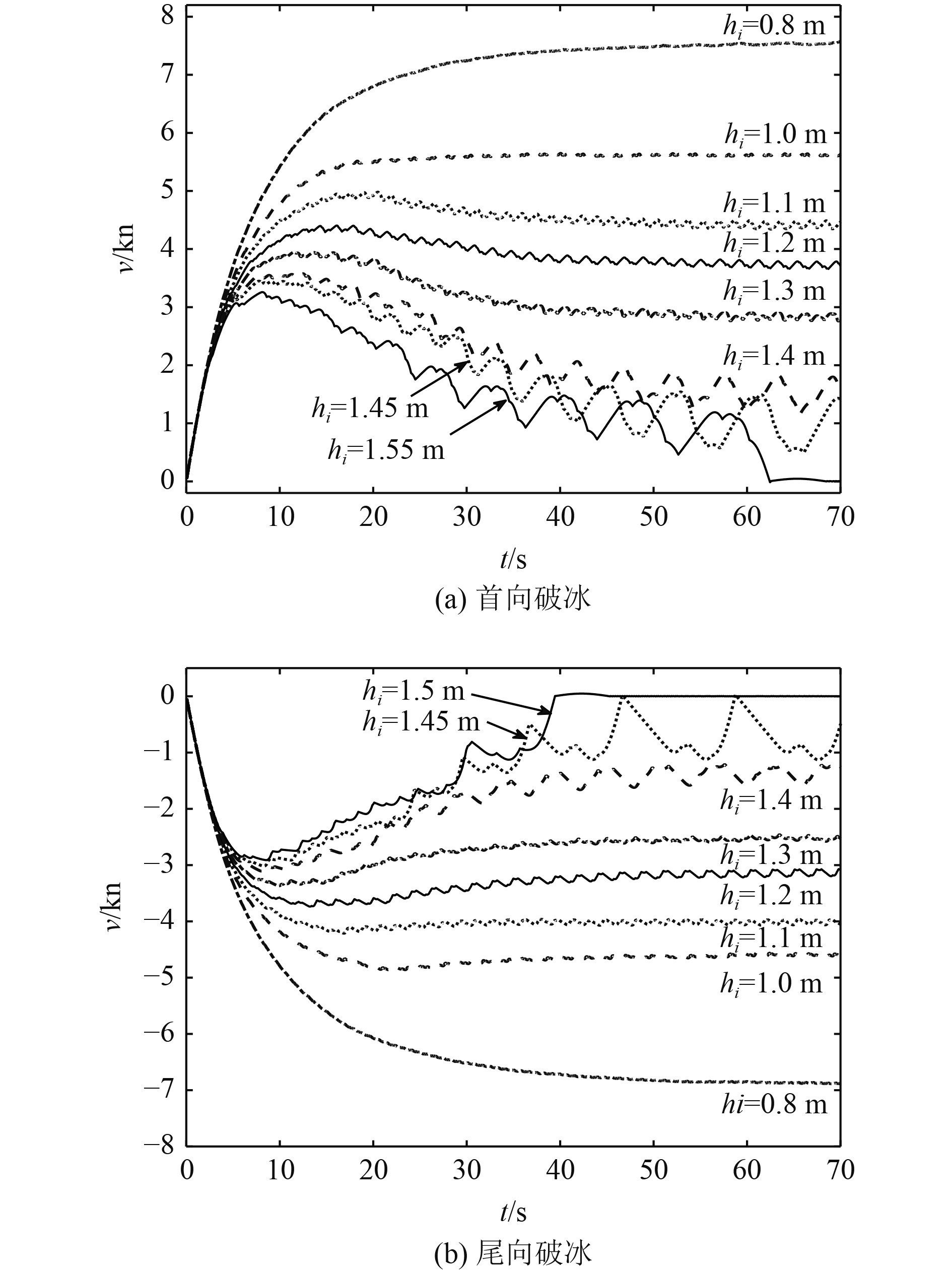
根据破冰能力动态评估方法，数值模拟t=0 s时刻，净推力为最大值即为系柱拉力，连续破冰阻力和速度则为0；随着数值模拟时间推进，船舶在净推力作用下速度增大，相应的连续破冰阻力增大、净推力降低，在某一时刻航速达到稳定值数值模拟即停止。首向连续破冰模式下，在0.8～1.55 m范围内选取8个冰厚，破冰能力动态评估方法获得了不同冰厚下的航速随时间变化规律，结果如图5（a）所示。可知：在数值模拟时间段内，不同冰厚下的速度均达到稳定值，冰厚越大，获得的速度稳定值越小，在冰厚1.55 m工况，最终航速接近于0，表现为船舶在冰层中“困住”了，这是由于螺旋桨最大净推力也不足以克服连续破冰阻力；当冰厚较小时，如冰厚0.8 m和1.0 m工况，随着时间推进航速逐渐增大，直至达到峰值并在后续时间段内保持稳定状态，说明在达到稳定航速时净推力大于连续破冰阻力；随着冰厚不断增加，如冰厚大于1.0 m的所有工况，航速先随着时间不断增大，达到峰值后会缓慢回落，在之后的时间段内围绕某一固定航速值上下震荡变化，且冰厚越大，振荡越剧烈，说明当航速达到峰值时连续破冰阻力大于净推力。图5（b）为尾向连续破冰模式下，由破冰能力动态评估方法获得的不同冰厚下的航速随时间变化规律，相关结论与首向连续破冰模式基本一致。不同的是，极地油船在1.5 m冰厚工况下尾向破冰时稳定航速就已经趋为0，说明了首向破冰能力大于尾向破冰能力。

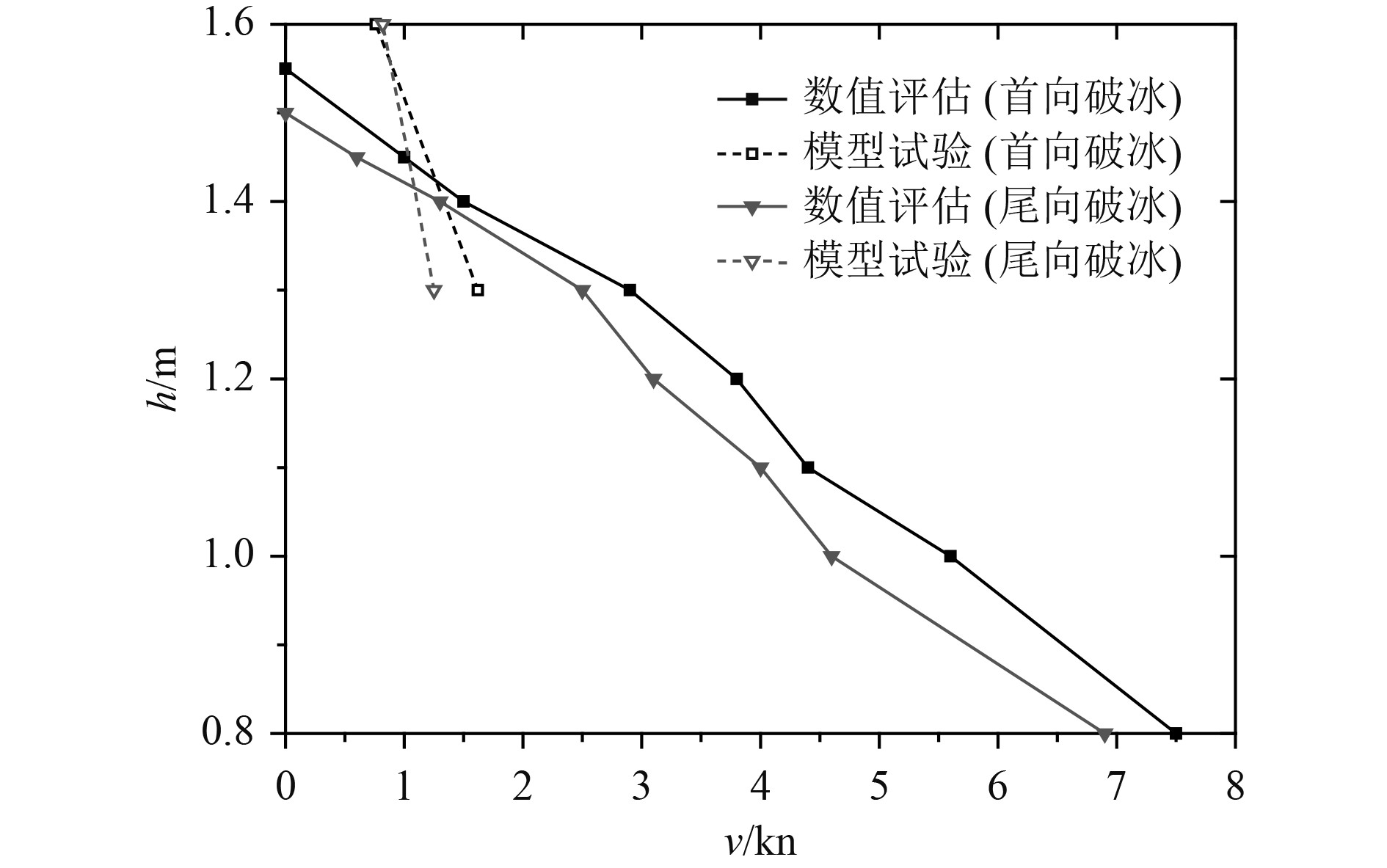
将图5对应的冰厚和稳定航速提取出来即可获得由动态评估方法对应的h-v曲线，并与模型试验结果进行比较，结果如图6所示。可知：由动态评估方法获得的首向破冰h-v曲线位于尾向破冰h-v曲线上方，说明首向破冰能力大于尾向破冰能力，这与模型试验的结果趋于一致；动态评估方法获得的h-v曲线与模型试验对应的结果相比，斜率存在较大差异，动态评估与模型试验曲线存在交点，在交点右侧动态评估计算得到的破冰能力大于模型试验测得结果，交点左侧动态评估计算得到的破冰能力则小于模型试验测得结果。

由静态评估方法、动态评估方法及模型试验获得的1 kn航速对应的最大破冰厚度结果见表3。结合图4、图6和表3可知：静态评估方法和动态评估方法获得的1 kn航速对应的最大破冰厚度与模型试验结果较为接近，可以满足对极地油船破冰能力的考核要求；不管采用何种手段进行破冰能力评估，极地油船首向破冰能力均大于尾向破冰能力；静态评估方法获得的破冰能力大于模型试验结果，动态评估方法获得的破冰能力则小于模型试验结果，动态评估方法偏于保守；除了1 kn航速附近，不管静态评估方法还是动态评估方法获得的h-v曲线与模型试验对应的结果相比存在一定差异，究其原因，除了连续破冰阻力数值模拟与模型试验存在误差外，连续破冰过程中的船舶的推进性能及净推力也是极其重要的影响因素，数值模拟采用的净推力是基于经验公式，并不具有普适性，而模型试验净推力则是通过自航试验获得的，具有较高的可靠性。

3 结　语

本文在一种基于预设冰网格技术的船舶连续破冰数值模拟理论基础上提出2种破冰能力评估方法：静态评估方法和动态评估方法。以某极地双向破冰油船为研究对象，将2种破冰能力评估方法数值评估结果与模型试验结果进行对比分析，得到以下结论：

1）2种破冰能力评估方法获得的极地油船首向和尾向破冰模式下1 kn航速对应的破冰厚度与模型试验结果吻合较好，验证了2种破冰能力评估方法的可行性；

2）除了1 kn航速附近，2种破冰能力评估方法获得的h-v曲线与模型试验结果相比存在一定差异，破冰能力数值评估涉及的连续破冰阻力和净推力数值计算方法存在改进空间；

3）2种破冰能力评估方法结果均显示极地油船首向破冰能力均大于尾向破冰能力，与实际情况相符；

4）静态评估方法获得的破冰能力大于模型试验结果，动态评估方法获得的破冰能力则小于模型试验结果，动态评估方法偏于保守，动态评估方法在极地船舶初始设计阶段适用性更强。