舰船作为水上交通工具,其航行安全性至关重要。航行姿态的稳定控制对于保持船舶的平稳航行、减小倾覆和碰撞风险具有重要意义[1]。随着现代海战和海洋探测技术的发展,舰船航行姿态控制技术的地位愈发重要。从军事角度来看,舰船航行姿态控制能够有效地控制舰船的姿态,提高其机动性和稳定性,从而提高舰队的快速反应能力和作战效能;从民用角度来看,在海上运输中,通过精确的航行姿态控制,可以减少船舶摇晃,提高货物的安全性和运输效率[2]。但由于现代航行环境复杂多变,包括不同的海况、风浪、潮流等外部干扰因素,在这些不确定性因素下姿态控制的正确性较低。
针对舰船航行的姿态控制技术,有许多学者进行了充分的研究。刘国海等[3]提出的利用滑模控制器完成的姿态控制算法,对需要控制的舰船建模,并将控制模型进行调节后,获取反馈置信标准;对控制波形线性扩展以及扰动补偿,结合补偿后的控制律,采用滑模控制器完成最终的姿态控制。该算法虽然可以控制船舶的姿态,但是对于海面复杂情况考虑不全面,因此在后续使用滑模控制器进行控制时无法达到最佳的控制结果。刘佳仑等[4]提出的船舶航行的姿态控制算法,构建并分析变稳船系统架构,建立舰船三自由度运动模型,定义位置变稳误差由船舶三自由度的变稳目标得出,采用滑模控制器完成舰船的姿态控制。由于滑模控制存在着“抖振”现象以及对初始条件和参数变化敏感的问题,会导致最终的控制效果变差。Liu等[5]提出的船舶三自由度稳定控制算法,建立船舶的运动学解和动力学模型,补偿了船舶造成的姿态偏差,利用层极限学习机(Multilayer Extreme Learning Machine,ML-KELM)对三自由度进行解耦,得到每一自由度上的控制结果,完成船舶的姿态控制。由于极限学习机存在着可能无法寻找全局最优解、泛化能力有限、对大数据处理能力较差的问题,在这种情况下对于船舶的三自由度解耦可能存在误差,导致最终的控制结果产生偏差。Xiao等[6]提出的基于固定时间收敛的自适应容错姿态跟踪控制,利用对数映射将跟踪问题转化为其相关李代数上的镇定问题。设计了一种新的基于固定时间的非奇异滑模,既避免了奇异性,又保证了跟踪误差沿滑动面的收敛时间与状态值无关。构造了一个自适应容错控制律,引入在线自适应控制律来估计集总不确定性的上界。通过自适应控制率达到控制船舶航行姿态的目的。该方法中奇异滑模控制器复杂,参数调节时可能导致出现控制准确率下降的问题,无法满足高精度的舰船姿态控制。
随着传感器技术、通信技术和数据处理技术的不断发展,未来的舰船航行姿态控制系统将更加集成化和模块化。通过将各种传感器、执行器、控制器和通信设备集成在一个模块或节点上,可以实现快速、灵活的系统集成和升级维护。同时,数据处理技术的进步也将为航行姿态控制提供更加精准和实时的数据处理和分析能力,有助于提高系统的智能化水平和响应速度,而以上方法无法精确控制航行姿态。因此,为了解决以上问题,提出考虑多约束条件的舰船航行姿态自适应控制算法。将多约束条件作为达成最终目标过程中需要满足的多种限制条件,RBF网络具有十分强大的逼近性能和全局收敛能力,能够准确求解出多约束条件的目标函数。实验表明,该算法能够十分精确的控制舰船在航行时的姿态,达到最佳的控制效果。
1 舰船航行姿态自适应控制 1.1 舰船运动分析对于海面航行的舰船,由于环境原因一般会产生2种主要的影响船舶航行姿态的因素,一是由海面的波浪和风以及二阶波浪力产生的低频运动,低频运动会使船漂离当前位置,该过程时间较为漫长;二是高频运动,即一阶波浪力产生的频率较高的往复运动,高频运动会使舰船的动力系统产生磨损,控制时的能量产生损耗,同时高频运动还会影响舰船中高精度传感器的精度[7]。在这种情况下,若要实现船舶航行的姿态控制,既要保证有效提出船舶的高频运动带来的噪声和运动分量,同时还要减少低频运动带来的微量影响。基于此,对船舶海面航行时的低频以及高频运动分别建模,以分析舰船的运动情况。
1.1.1 舰船低频运动分析一般对于大型的舰船来说,低海况下,海水对纵摇、横摇以及起伏运动影响很小,几乎可以忽略,在这种情况下,简化舰船处于海面中的运动情况,对于船舶的运动模型,建立
|
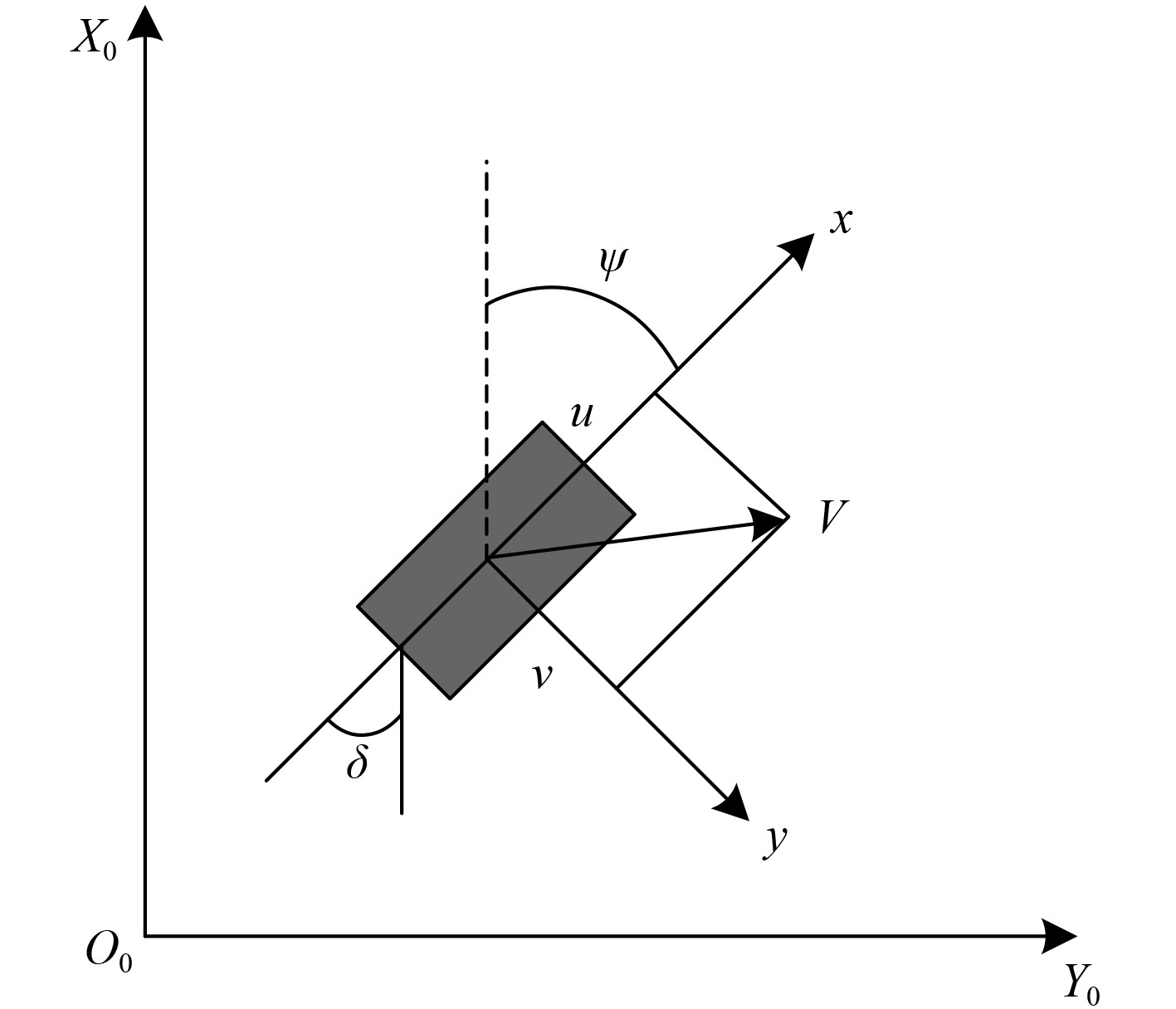
图 1 船舶平面附体坐标系与惯性坐标系 Fig. 1 Ship plane attachment coordinate system and inertial coordinate system |
在图1中,
| $ \begin{split} {Q_1} =\,& m\left( {u - vr} \right) + \left( {{m_x}u - {m_y}vr} \right) = \\ \,& {X_S} + \left( {1 - {t_p}} \right)\rho {n^2}D_p^4{K_T}\left( J \right) + {t_R}{F_N}\sin \delta + {X_{ENV}} ,\end{split} $ | (1) |
| $ \begin{split} {Q_2} =\,& m\left( {\dot v - ur} \right) + \left( {{m_y}\dot v - {m_y}ur} \right)= \\ \,&{Y_S} + \left( {1 - {a_H}} \right){F_N}\cos \delta + {Y_{ENV}},\\ \end{split} $ | (2) |
| $ \gamma = {I_Z}{N_X}{Q_1} + \left( {{x_R} + {a_H}{x_H}} \right){F_N}\cos \delta + {Z_{ENV}}{J_Z}/{Q_2} 。$ | (3) |
式中:
根据获取的三自由度运动的非线性动力学模型,构建船舶的运动学和动力学模型,以分析舰船低频运动。表达式为:
| $ \delta = \frac{{\gamma \left( {m + {m_y}} \right)vr + {X_s} + {t_p}\rho {n^2}D_p^4{K_T}\left( J \right) + {t_R}{F_N}\sin \delta + {X_{ENV}}}}{{\left( {m + {m_x}} \right)}}。$ | (4) |
舰船的运动可以分为低频和高频分量。低频运动主要涉及整体船体的姿态、偏航等大幅度运动,而高频运动则包括更小尺度的细微振动和摆动。舰船的低频和高频运动受到不同的激励因素影响。低频运动主要受到外部环境因素如风浪、潮流等的影响,而高频运动则通常与船舶本身的结构特性、推进系统、航行速度以及加载情况等相关。因此,分析舰船的高频运动可以更加深入地研究和评估这些特定因素对船舶运动的影响。在高频运动模型中引入海面波浪模型,公式为:
| $ h\left( s \right) = \frac{{{K_\omega }s}}{{{s^2} + 2\lambda {\omega _0}s + \omega _0^2}} 。$ | (5) |
式中:
考虑海面波浪模型,获取舰船高频运动模型公式为:
| $ \left\{ \begin{gathered} {\xi _h} = {\partial _h}{\xi _h} + {E_h}{\omega _h},\\ {\eta _h} = h\left( s \right){\Im _h}{\xi _h} 。\\ \end{gathered} \right. $ | (6) |
式中,行波运动
为保证舰船行航行姿态控制时不能与障碍物碰撞,因此需要进行避障约束,将舰船简单视为一个顶点为ABCD的长方形,舰船的4个顶点需要不能接触障碍物,则公式表达为:
| $ \left\{ \begin{gathered} {x_i} = x + L\cos r - \sin r,\\ {y_j} = y + L\sin r - \cos r。\\ \end{gathered} \right. $ | (7) |
式中,
舰船的最小转弯半径要求规划路径的曲率必须小于舰船转弯运动轨迹的曲率,即规划路径的最大曲率
| $ {R_{path\max }} < \frac{1}{{{R_{\min }}}}。$ | (8) |
式中,
在海面航行时,舰船会受到控制输入限制,传感器限制等约束,因此形成了控制输入饱和约束:
| $ {q_i}\left( t \right) \leqslant {q_{\max }},t \in \left[ {{t_0},{t_f}} \right]。$ | (9) |
式中:
以舰船航行姿态控制的能量消耗最低作为目标,公式表达为:
| $ f(x) = {E_h}{\eta _h}\left( {q_1^2 + q_2^2 + q_3^2} \right)/\delta \cdot {\xi _h}。$ | (10) |
式中,
RBF是一种基于核函数的神经网络模型,具有良好的逼近能力和灵活性。通过使用RBF网络对目标函数进行逼近,可以将船舶航行姿态控制问题转化为一个优化问题,以实现对船舶运动的精确控制和适应性调整。因此,采用RBF对航行姿态自适应控制模型的目标函数
| $ \hat f\left( x \right) = {\hat \theta ^{\mathrm{T}}}\phi \left( x \right) ,$ | (11) |
| $ u\left( t \right) = b \cdot \left[ {\hat f\left( x \right) - {\xi _h} + h\left( s \right)} \right] 。$ | (12) |
式中:
为了保证网络能够最大程度逼近
| $ L = - \varepsilon \frac{{{\Im _h}^{\rm{T}}P}}{{\left\| {{\Im _h}^{\rm{T}}P} \right\| \cdot u\left( t \right)}} 。$ | (13) |
式中:
为了验证本文的舰船在多约束条件下的航行姿态控制算法,选择位于某沿海城市码头中的1艘大型船舶进行实验,该舰船的具体参数如表1所示。
|
|
表 1 舰船参数 Tab.1 Ship parameters |
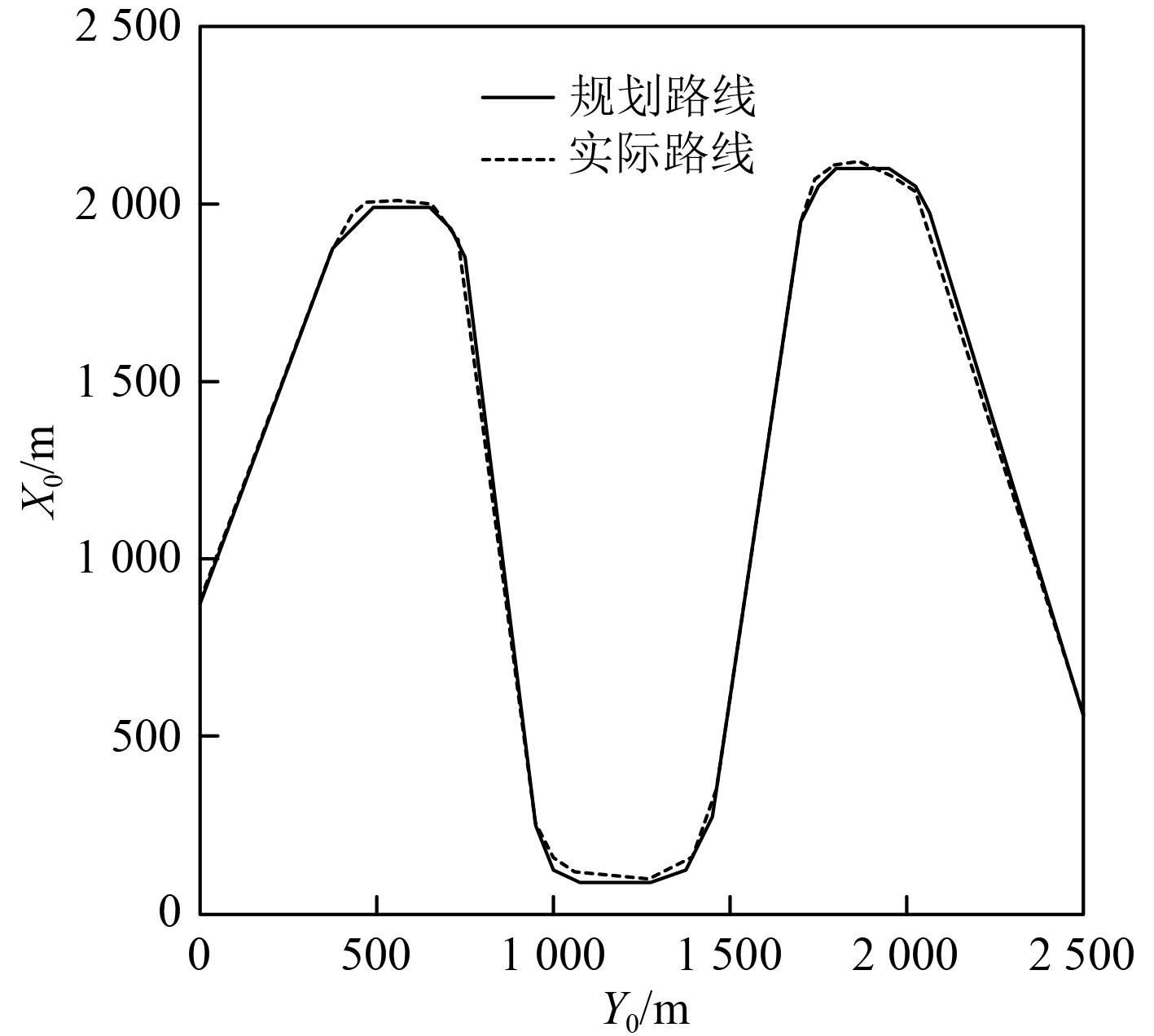
为验证本文的舰船航行姿态控制算法的效果,在一开阔航道规划航行路线,并使用本文方法进行航行姿态控制,结果如图2所示。
|
图 2 规划路线与实际航行路线对比 Fig. 2 Comparison between planned route and actual navigation route |
可以清晰地看到,规划的航行路线呈现出较为规整的情况,其转弯的曲率相对较小。在实际情况中,舰船在直线航行阶段与规划路线保持一致。然而,在转弯过程中,路线存在微小的偏差。尽管如此,这种偏差非常小,显示出本文的航行姿态控制方法具有出色的控制能力。这为舰船的安全、稳定航行提供了强有力的支持。
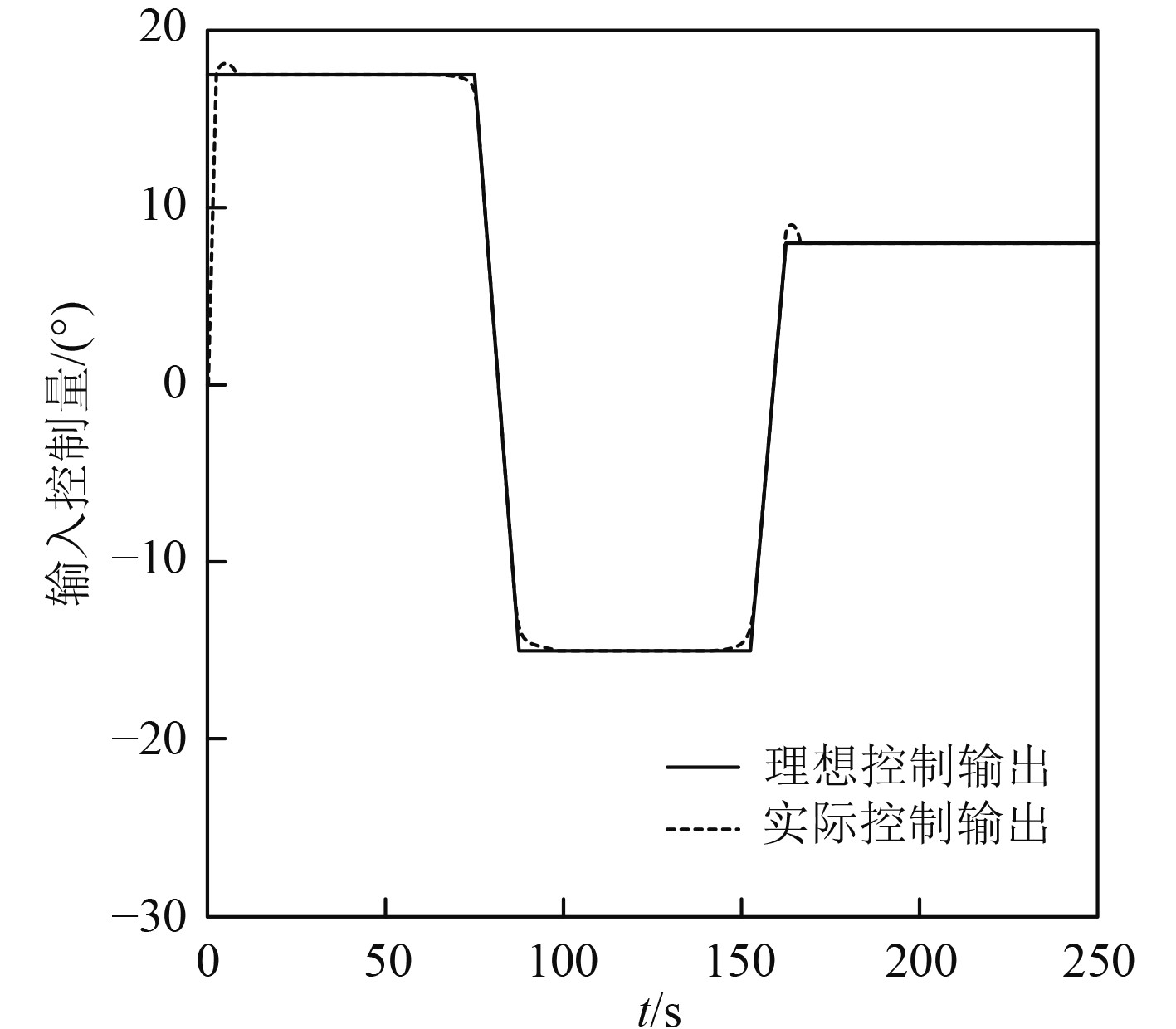
在进行船舶航行控制时,规划路线的航行输入控制量与本文方法在进行姿态控制时的输入控制量的对比如图3所示。
|
图 3 控制量对比 Fig. 3 Comparison of control quantities |
可以清晰地看到,规划路线的控制量呈现笔直的线段,意味着在直线航行阶段控制量保持稳定。相比之下,本文算法的控制结果展现了出色的性能。其控制指令的发出速度快,且非常接近理想控制水平。在转弯过程中,控制命令的超调量极小,进一步突显了本文算法在舰船航行姿态控制中的强大能力。这为舰船在实际航行中的稳定性和安全性提供了坚实的保障。
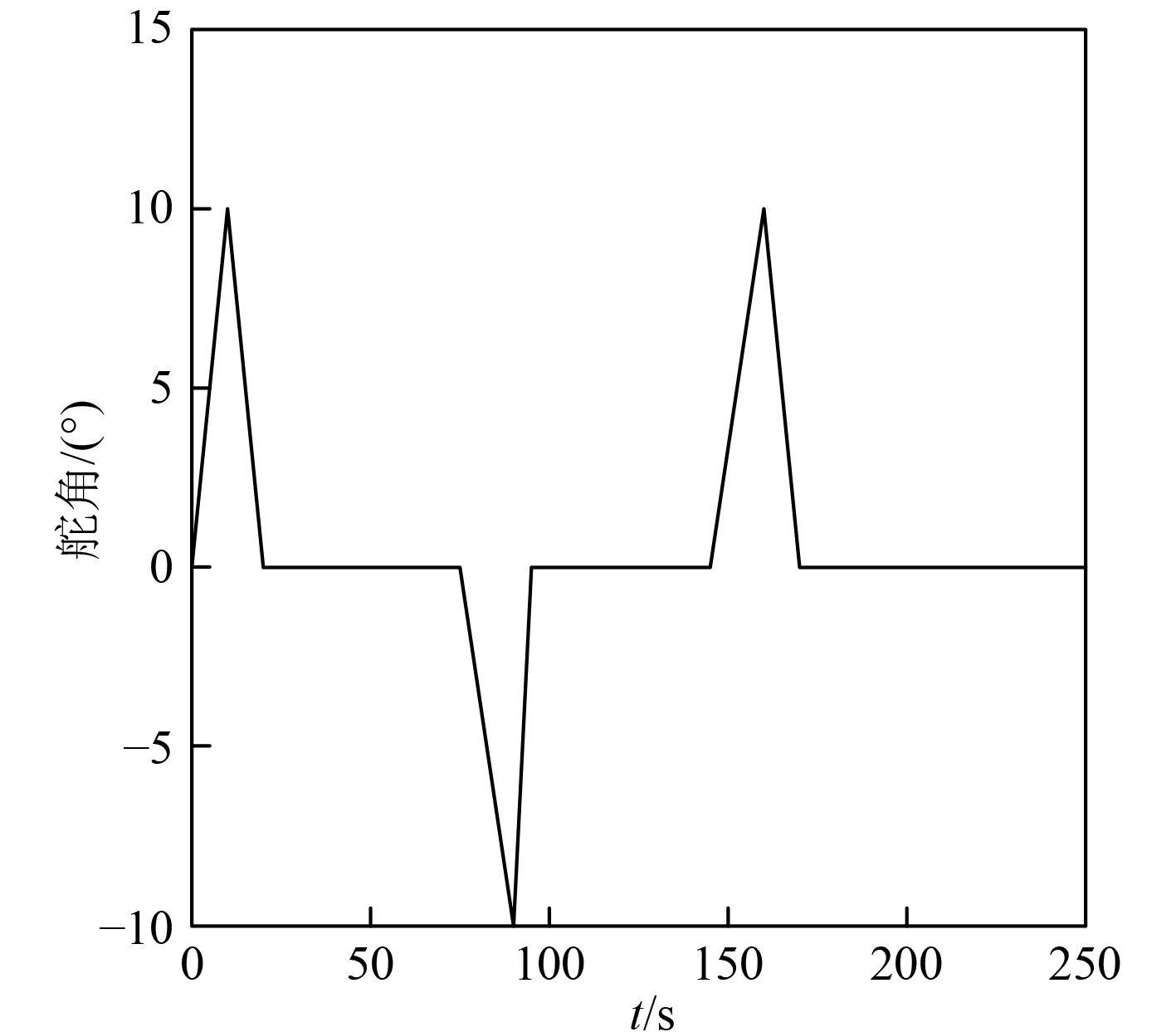
在按照规划路线航行时,本文航行姿态控制算法发出控制信号,舰船舵角变化情况如图4所示。
|
图 4 发出控制信号后舵角变化情况 Fig. 4 Changes in rudder angle after sending control signals |
可知,在发出控制信号后,舵角会经历减小、归零和增加的过程。这一变化规律与规划路线的航行要求相匹配,确保了舰船在航行过程中的稳定性。由于规划的路线相对一致,因此在每次转弯过程中,舵角的最大角度保持相同。这一特点进一步突显了本文提出的舰船航行姿态控制算法具有极高的稳定性。这为船舶在航行过程中精确控制航行姿态提供了强有力的支持,确保了航行的安全性和可靠性。
为保证本文算法的适用性,选择真实航道进行航行姿态控制实验。在本次实验中,共选择10条航道,每条航道测试10次,统计10条航道中姿态控制时的稳态误差、调整时间、超调量以及操舵次数的平均值,结果如表2所示。
|
|
表 2 不同航道引用本文方法结果 Tab.2 Results of different waterways using the method proposed in this paper |
可以看到,在不同的航道环境下,控制结果存在一定的差异。然而,从10条航道完成航行姿态控制的数据中,可以得出结论:即使在最差的环境中,本文算法的姿态控制表现依然出色。稳态误差最大值为0.15°,调整时间最长为127 s,超调量最多为4.8%,操舵次数最多为167次。这些数据表明,本文算法在最差情况下依然能够保持优秀的控制性能,确保船舶航行的高安全水平。这为实际应用中的航行安全提供了坚实的保障,进一步证明了本文算法在复杂航道环境下的稳定性和可靠性。
3 结 语本文研究了一种应用于舰船航行时多约束条件下的姿态控制算法。通过实验验证,该算法在预设航道中实现了控制后舰船航行路径与提前设定路线的几乎一致性。然而,由于预设航线的控制量过于理想化,本文算法只能接近该理想状态。尽管如此,本文算法在控制速度、超调量以及反应速度方面表现出色,确保了舰船航行时的安全性。在多种不同航道环境下,本文算法依然能够保持优秀的控制结果。无论是稳态误差、调整时间、超调量还是操舵次数,都能保持在较低的水平。这充分证明了本文算法的有效性和实用性,为舰船在实际航行中的安全性和稳定性提供了坚实的保障。在实际应用中,本文算法能够根据多约束条件进行姿态控制,确保舰船在复杂航道环境中安全、稳定地航行。这一研究成果不仅对舰船航行控制领域具有重要意义,还可应用于其他需要精确姿态控制的领域。
| [1] |
罗春艳, 李元, 殷飞, 等. 考虑最优路径的水面清漂船自主导航算法设计[J]. 计算机仿真, 2022, 39(3): 253-257. LUO Chun Yan, LI Yuan, YIN Fei, et al. Design of autonomous navigation algorithm for surface drifting ship considering optimal path[J]. Computer Simulation, 2022, 39(3): 253-257. DOI:10.3969/j.issn.1006-9348.2022.03.050 |
| [2] |
仲伟波, 杨忠凯, 温景松, 等. 基于自抗扰的双桨单舵水面无人艇航行控制[J]. 中国造船, 2020, 61(1): 167-176. ZHONG Weibo, YANG Zhongkai, WEN Jingsong, et al. A motion control system based on auto disturbances rejection controller for unmanned surface vessel with double propellers and single rudder [J]. Shipbuilding of China, 2020, 61(1): 167-176. |
| [3] |
刘国海, 李持衡, 沈跃, 等. 基于滑模自抗扰的同步转向高地隙喷雾机姿态控制[J]. 农业机械学报, 2023, 54(3): 180-189+300. LIU Guo hai, LI Chi heng, SHEN Yue, et al. Attitude control of synchronous steering high gap sprayer based on sliding mode active disturbance rejection[J]. Transactions of Agricultural Machinery, 2023, 54(3): 180-189+300. DOI:10.6041/j.issn.1000-1298.2023.03.018 |
| [4] |
刘佳仑, 谢玲利, 李诗杰, 等. 面向船舶智能航行测试的变稳船控制系统设计[J]. 中国舰船研究, 2023, 18(3): 38-47+74. LIU Jialun, XIE Lingli, LI Shijie, et al. Design of variable stability ship control system for ship intelligent navigation test[J]. Chinese Journal of Ship Research, 2023, 18(3): 38-47+74. |
| [5] |
LIU S , SONG J , ZHANG L. Research on 3-DOF stabilized control system of ship propulsion-assisting sail[J]. Ocean Engineering, 2023, 278(6): 114370.1−114370.18.
|
| [6] |
XIAO Ning shi, ZHI Gang zhou, ZHOU D. Adaptive fault-tolerant attitude tracking control of rigid spacecraft on lie group with fixed-time convergence[J]. Asian Journal of Control, 2020, 22(1): 423-435. DOI:10.1002/asjc.1888 |
| [7] |
何建慧. 输入扰动对波动鳍推进性能影响的研究[J]. 船舶力学, 2020, 24(1): 18-30. HE Jian hui. Research on the effect of input perturbation on the propulsion performance of an undulating fin[J]. Journal of Ship Mechanics, 2020, 24(1): 18-30. DOI:10.3969/j.issn.1007-7294.2020.01.003 |
| [8] |
刘浩, 赵文涛, 孙朝阳, 等. 无人帆船四自由度运动建模与试验分析[J]. 船舶工程, 2023, 45(7): 9-16. LIU Hao, ZHAO Wen tao, SUN Chao yang, et al. Four-degree-of-freedom motion modeling and experimental analysis of unmanned sailboat[J]. Marine Engineering, 2023, 45(7): 9-16. |
 2024, Vol. 46
2024, Vol. 46
