随着水声技术的不断发展,基于多波束测深技术的不断完善[1 − 4],使得地形辅助导航得到广泛应用,利用地形辅助导航校正舰船的导航误差,可有效抑制惯导系统随时间累积的定位误差,实现高精度导航[5 − 7]。由于海洋环境的复杂性,海底地形测量不同于陆地测量,在测量过程中资源消耗量较大,目前海底地图的数据分辨率不能完全满足高精度导航的需求。利用海底地形数据进行地形匹配导航时,由于不同区域具有不同地貌特征[8 − 10],辅助导航系统有不一样的工作能力[11 − 16]。因此,研究地形匹配区域的适配性,掌握地形匹配区域的选择准则,具有非常重要的实际意义。
目前,地形辅助导航中匹配区域的选择方式主要是根据地形的统计特征对相关匹配性能的影响。朱华勇等[17]基于地形差分矩设计地形匹配区与选择准则,改善地形匹配过程的时间性能。刘鹰等[18]在地形信息的分析上提出对地形类型进行初判,再根据地形的起伏度与相关度分析,为航迹规划提供可信参考。郑彤等[19]基于多波束测深数据,给出了利用地形标准差和地形相关系数的适配区选择方案,提升地形匹配效果。徐振烊等[20]基于灰色模糊理论,提出多个地形特征参数融合的适配区选择准则,解决了靠单一参数判断的不稳定问题。以上文献是通过研究地形的起伏特征对地形匹配适配区进行划分,由于海洋环境的复杂性,不同海底底质对于地形匹配精度也会产生影响。
针对海底底质反向散射强度差异、海洋噪声影响反射信号、对匹配区域特征分析不完全以及单一特征参数无法全面准确评价区域适配性的问题,本文提出融合地形统计特征参数、海底底质和海洋噪声的适配区选择准则,基于多波束测深数据,利用ICCP(Iterative Closest Contour Point)算法进行地形匹配,在适配区内进行地形匹配可有效提升地形匹配的精度。
1 海底底质分析传统适配区选择方法仅考虑海底地形特征参数,但在利用多波束测深设备进行海洋深度测量时,不同的海底底质对于声线的反射能力不同,对测深结果产生影响,进而影响地形辅助导航的精度。多波束测深过程的声能变化如式(1)所示:
| $ EL=SL-2TL+BS-NL+DI_R。$ | (1) |
式中:
| $ BS=BS_B+10{\mathrm{lg}}A。$ | (2) |
式中:
通常情况下,海底底质可分为“硬质”海底与“软质”海底,2种海底底质的
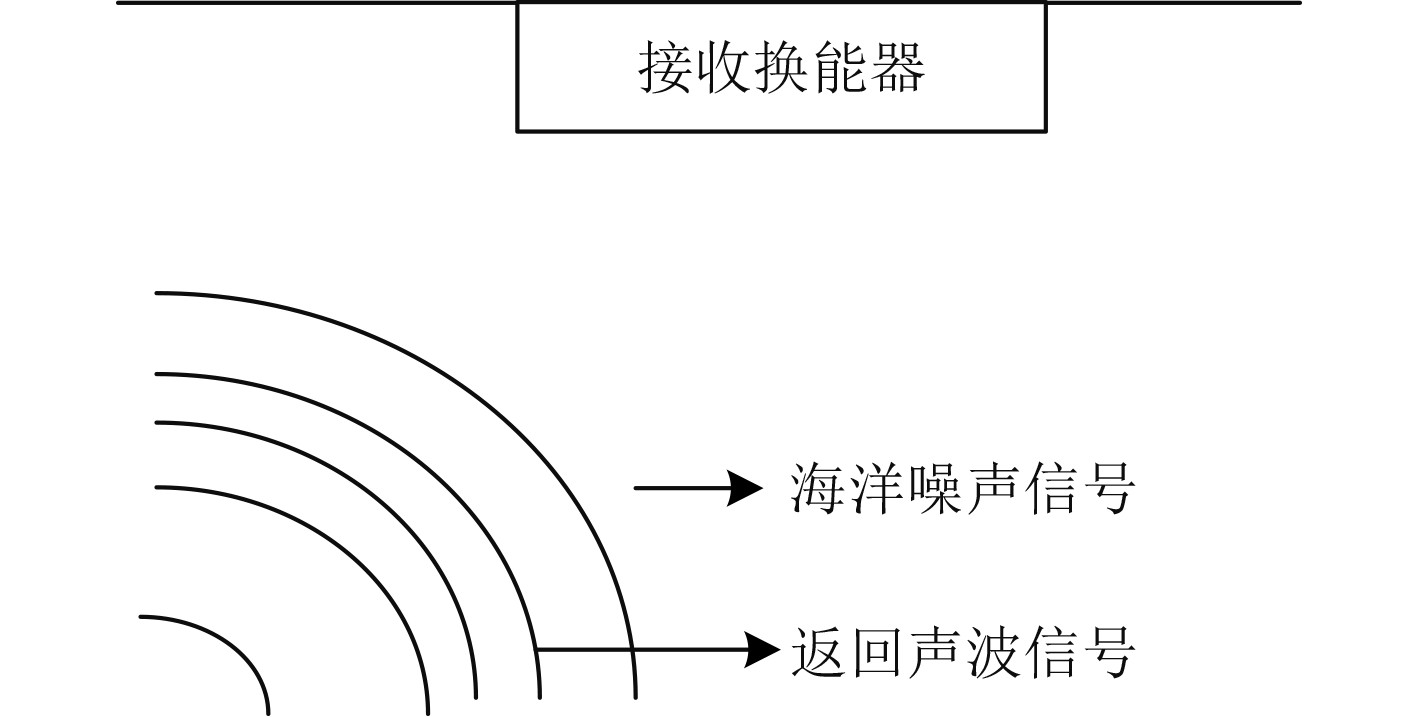
海洋环境噪声的频率在1 ~200 kHz之间,多波束探测仪的声波频率在100 ~750 kHz之间可调。当对不同的海底底质进行测量时,不同底质对声波的反向散射能力存在差异,测量散射强度弱的黏土底质时,海洋噪声与声波信号到达声波接收器的时间相近,导致深度测量存在误差 ,误差计算如式(3)所示,根据滤波原则难以将其去除。因此会对测深声波信号的接收造成较明显干扰,如图1所示。
|
图 1 海洋噪声干扰示意图 Fig. 1 Schematic diagram of marine noise interference |
| $ \Delta x={c} \times \Delta t 。$ | (3) |
式中:
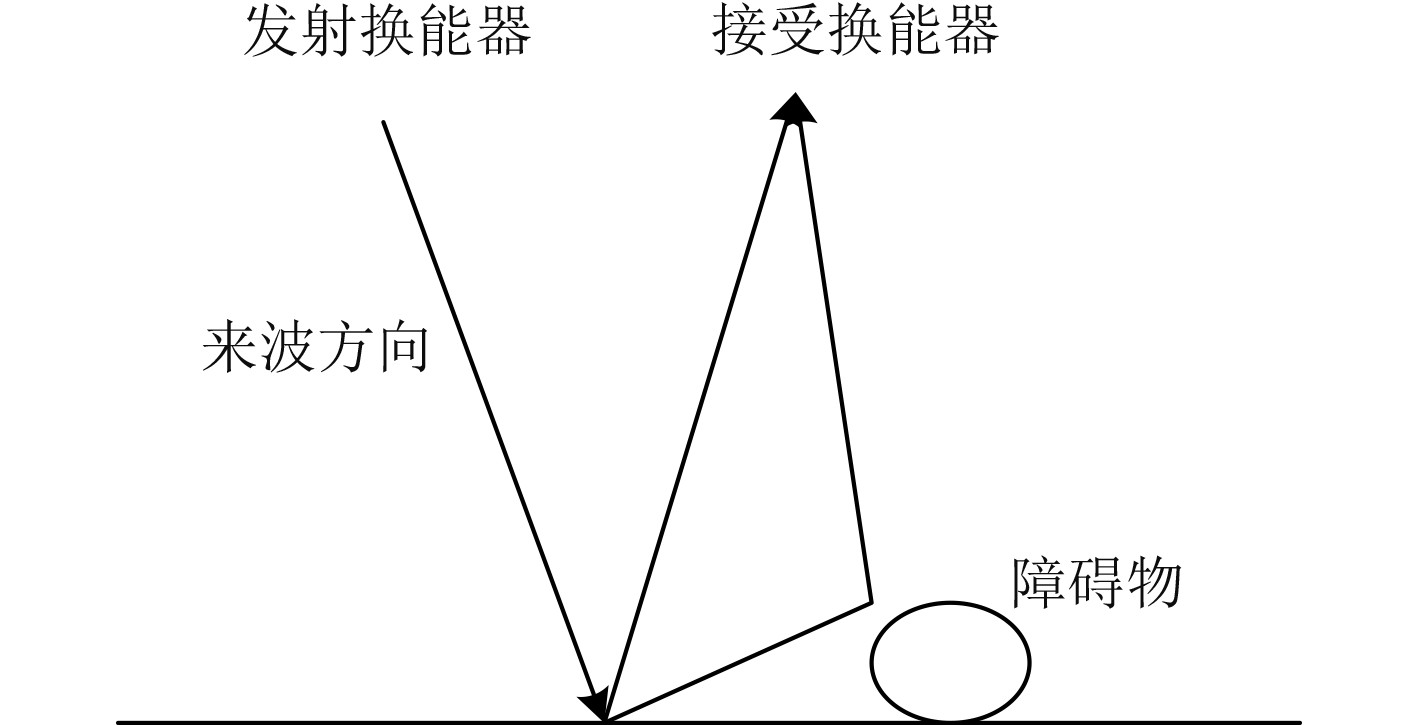
当测量基岩底质时,由于基岩底质具有较强反向散射能力,存在区域内多次反射的“多径效应”问题,如图2所示。“多径效应”会导致声波到达接受换能器的时间不同,相互叠加产生干扰,导致接收到的声信号产生错误。以上这2种情况都会对多波束测深数据产生影响,进而造成地形匹配误差,因此在选择地形适配区时应将海底底质作为重要参考因素。
|
图 2 测深多径效应示意图 Fig. 2 Diagram of multipath effect of sounding |
传统衡量地形适配性的因素通常为地形标准差、地形相关系数等地形特征参数,而由于不同海底底质反向散射能力存在差别,不同深度下的同一地形特征参数反映的海底起伏也有差别,融合海底底质、地形特征参数与深度等因素并构建地形适配区选择准则函数。
2.1 区域地形特征参数计算地形特征参数用来表示区域内地形起伏情况以及地形信息的复杂度,依据地形高程数据,判断区域内地形变换平缓或起伏明显。
海底地形数据相对于陆地高程数据获取难度更大,精度更低。通常首先对海底地形数据格网化处理,区域跨度为A×B时,(i,j)格网坐标处的深度值表示为h(i,j)。计算区域特征参数时,局部计算窗口大小为a×b。
1)地形标准差。地形标准差反映的是地形的高程与区域平均高程之间的关系,可判断出整体地形的变换是否明显。
| $ \sigma=\sqrt{\frac{1}{{a}(b-1)} \sum_{i=1}^{a} \sum_{j=1}^{b}[h(i, j)-\bar{h}]^{2}} ,$ | (4) |
| $ \bar{h}=\frac{1}{a b} \sum_{i=1}^{a} \sum_{j=1}^{b} h(i, j) 。$ | (5) |
2)粗糙度。粗糙度反映单位平面上地形表面积大小。其值越大,地形的起伏越明显;经度方向的绝对粗糙度
| $ r_{\lambda}=\frac{1}{b(a-1)} \sum_{i=1}^{a-1} \sum_{j=1}^{b}|h(i, j)-h(i+1, j)|,$ | (6) |
| $ r_{\lambda}=\frac{1}{a(b-1)} \sum_{i=1}^{a} \sum_{j=1}^{b-1}|h(i, j)-h(i, j+1)|。$ | (7) |
3)经度局部地形相关系数
| $ R_{\lambda}=\frac{1}{b(a-1) \sigma^{2}} \sum_{i=1}^{a-1} \sum_{j=1}^{b}[h(\bar{i}, j)-\bar{h}][h(\bar{i}+1, j)-\bar{h}] ,$ | (8) |
| $ R_{\phi}=\frac{1}{a(b-1) \sigma^{2}} \sum_{i=1}^{a} \sum_{j=1}^{b-1}\left[h\left(i_{i}, j\right)-\bar{h}\right][h(i, j+1)-\bar{h}] 。$ | (9) |
4)局部地形坡度S由地形区域在经度方向和纬度方向的变化率
| $ S_{\lambda}=\frac{1}{6}\left[\begin{array}{l} h(i+1, j+1)+h(i+1, j)+ \\ h(i+1, j-1)-h(i-1, j-1) \\ -h(i-1, j)-h(i-1, j+1) \end{array}\right],$ | (10) |
| $ S_{\phi}=\frac{1}{6}\left[\begin{array}{l} h(i-1, j+1)+h(i, j+1)+ \\ h(\bar{i}-1, j+1)-h(i-1, j-1) \\ -h(i, j-1)-h(i+1, j-1) \end{array}\right],$ | (11) |
| $ S=\arctan \left(\sqrt{S_{\lambda}^{2}+S_{\phi}^{2}}\right)。$ | (12) |
其中,粗糙度与相关系数呈现相反趋势,在深度水平大于200 m的情况下,坡度大于23且地形标准差大于100时,地形为复杂地形;坡度小于23且标准差小于100时,地形为平坦地形。
2.2 海底散射误差分析根据实际测量发现,“黏土泥质”地区对声波的反向散射能力较弱;而“基岩”地区,对声波的反射能力较强,且深度数据变化较为明显。因此,基于海底底质数据和多波束模拟测深过程,模拟弱反射和强反射过程。
通过量化平均水深
|
|
表 1 测区海底地貌分类标准 Tab.1 Standard for classification of seafloor landforms in survey area |
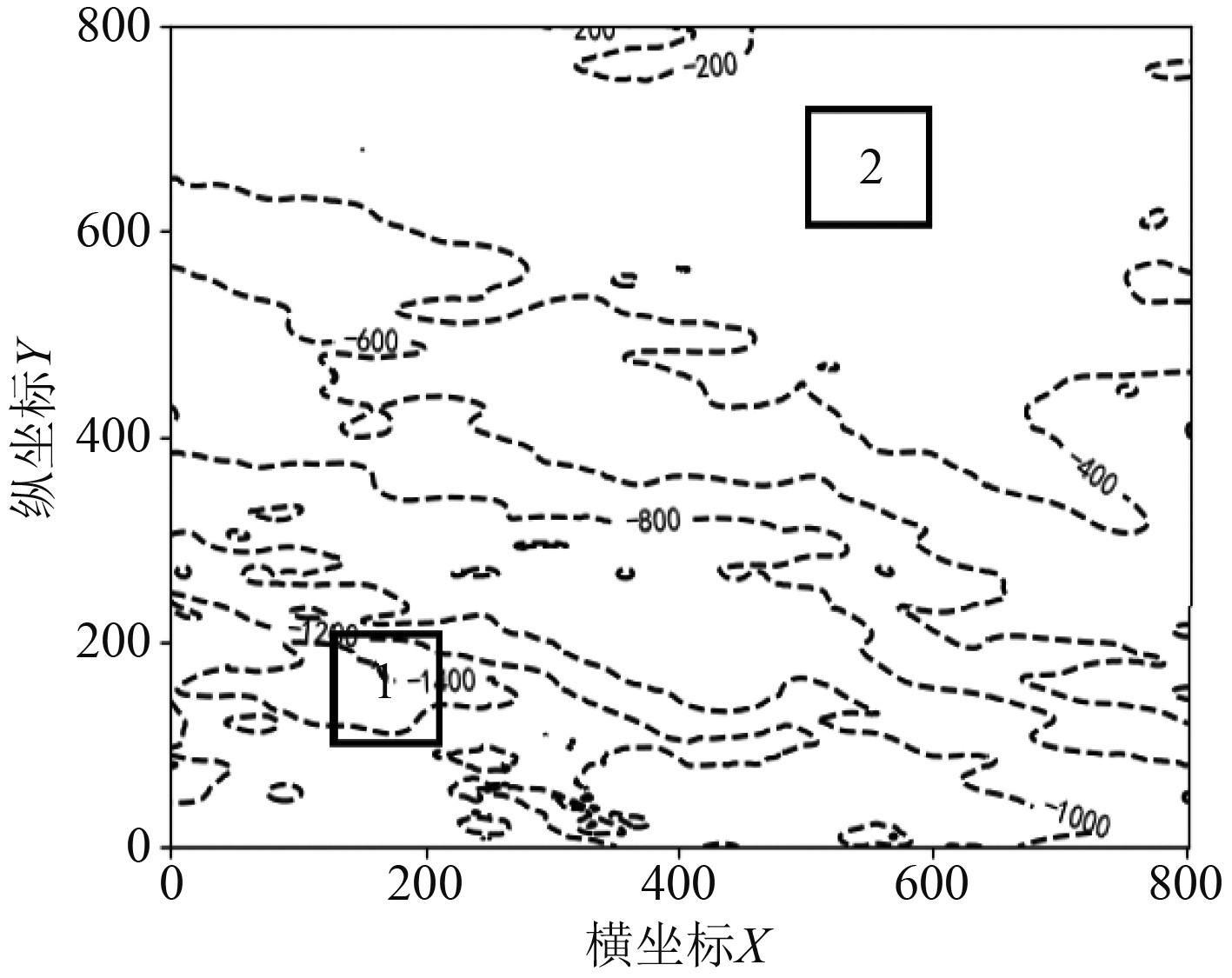
图3中,1区域为底质强反射区域,2区域为底质弱反射区域,其中强反射区域的地形特征复杂,起伏明显,地形标准差为111.08,而弱反射区域属于一般平坦地形,起伏变化较小,地形标准差为32.51。
|
图 3 地形深度图 Fig. 3 Topographic depth map |
设定脉冲响应时间为40 ms,海洋噪声造成的信号提前作用时间为4 ms时,对2个反射区域进行多次反射模拟,得出强反射和弱反射的误差均值,如表2所示。
|
|
表 2 反射测量深度误差 Tab.2 Reflection measurement depth error |
根据IHO海道测量规范测量最低标准,反射区域内的测量精度应按照二等测量计算,测深误差最大在30 m左右,对比强弱反射的模拟过程发现,不同海底底质造成的深度测量误差较大,需在区域选择时将底质问题作为一个重要项考虑。
2.3 构建地形适配区选择函数基于地形适配区选择的多个参考项,采用层次分析法对如何确定适配区进行判定。为了量化节点间的优劣先后,将用到判断矩阵标度定义,如表3所示。
|
|
表 3 判断矩阵标度定义表 Tab.3 Judgment matrix scale definition table |
此时,需构建准则层、目标层与方案层之间的判断矩阵,并进行一致性检验。其中,
步骤1 计算一致性指标CI
| $ {CI}=\frac{\lambda_{\max }-{n}}{{n}-1}。$ | (13) |
步骤2 根据已有表格查找对应的平均随机一致性指标RI,如表4所示。
|
|
表 4 平均一致性指标表 Tab.4 Average consistency indicator table |
步骤3 计算一致性比例CR:
| $ {CR}=\frac{{CI}}{{RI}} 。$ | (14) |
CR<0.1时,认为判断矩阵合理,否则需对矩阵重新修改。
步骤4 通过特征值法求权重并得出结果。其中,以匹配误差小为例,其权重矩阵为表5所示。
|
|
表 5 匹配误差小权重矩阵表 Tab.5 Match error small weight matrix table |
得出各项参数的指标权重如表6所示,根据指标权重对各项参数按比例融合,得出适配区选择准则函数RES。
|
|
表 6 权重矩阵表 Tab.6 Weight matrix table |
| $ { RES }= 0.33 \times { index } _1 + 0.59 \times { index }_ 2 + 0.07 \times { index }_ 3 。$ | (15) |
其中:index1为底质非强散射;index2为地形特征参数;index3为海洋噪声。RES0.625时,结果为非适配区;反之为适配区。
3 试验分析根据层次分析法得到区域适配性选择准则函数后,通过ICCP算法及蒙特卡洛仿真实验对该函数进行验证。
基于载多波束设备测得区域海洋深度数据,对试验区域格网化,格网长度为10 m,格网数为1000×1000,水深量程为−1 600 ~0 m,导航初始误差为(400 m, 200 m),仿真初始位置分别为(5 000 m,5 000 m)、(2 000 m,2 000 m)、(3 000 m,3 000 m),航向角度为0°~15°、45°~60°,航行速度2 m/s。
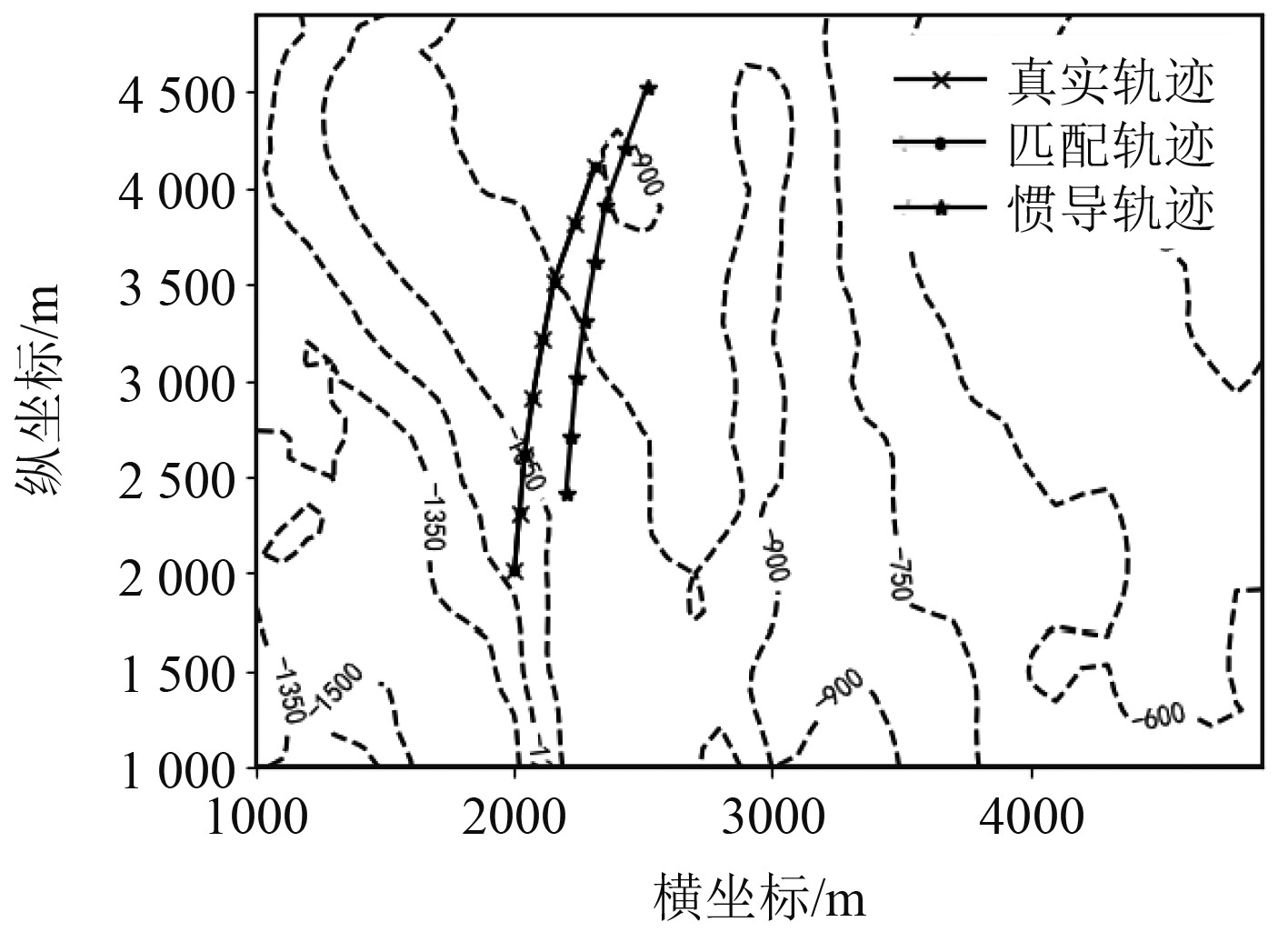
首先,根据匹配区域选择准则判断匹配区域的适配性,在适配区与非适配区内分别进行蒙特卡洛仿真实验,实验次数为50次,利用ICCP匹配算法进行地形匹配仿真。图4和图5为在非适配区a和适配区b的仿真模拟路径图,图6为匹配误差对比图。
|
图 4 非适配区a轨迹位置图 Fig. 4 Trajectory location map of non-adaptive region a |
|
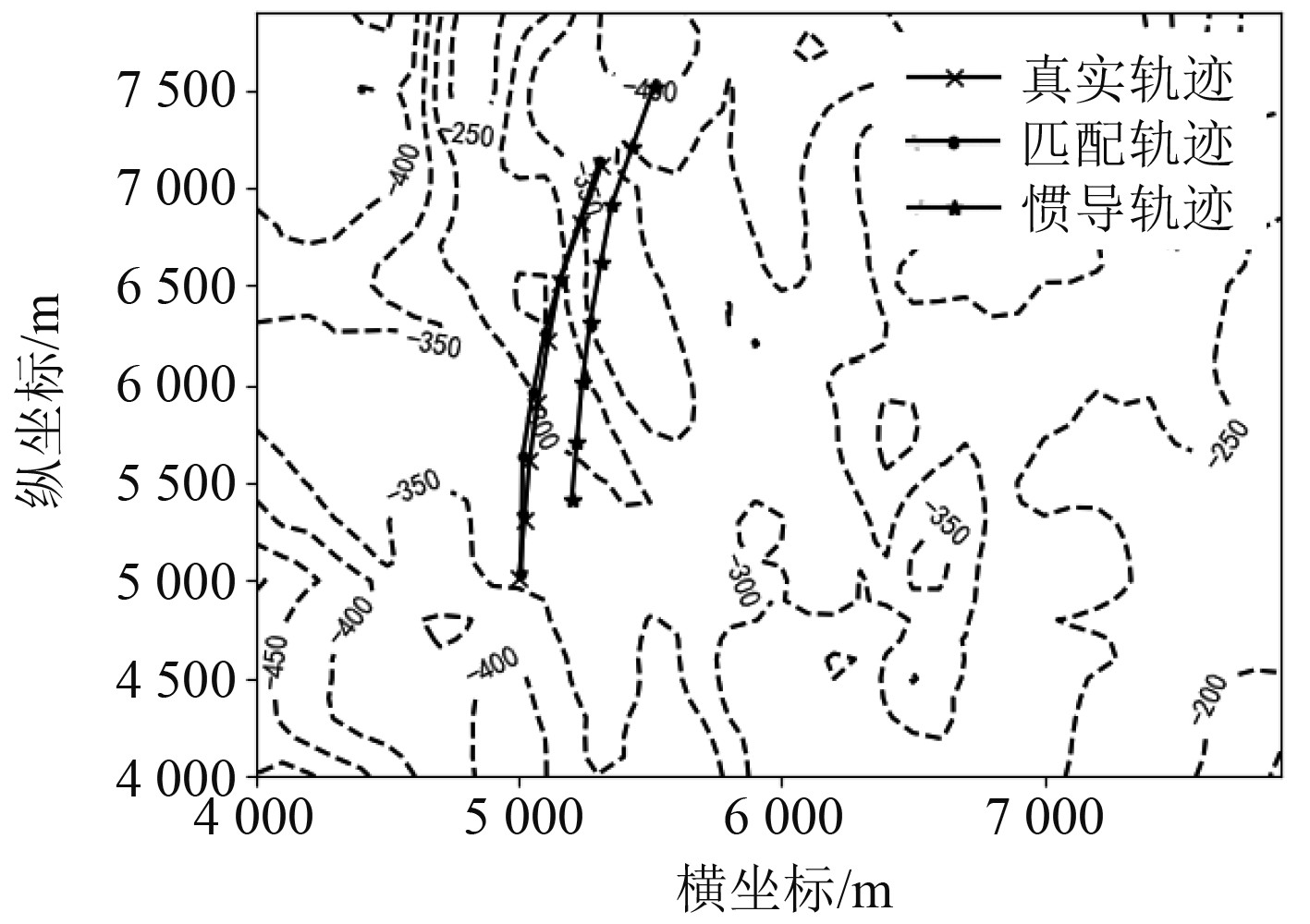
图 5 适配区b轨迹位置图 Fig. 5 Trajectory location map of adaptation area b |
|
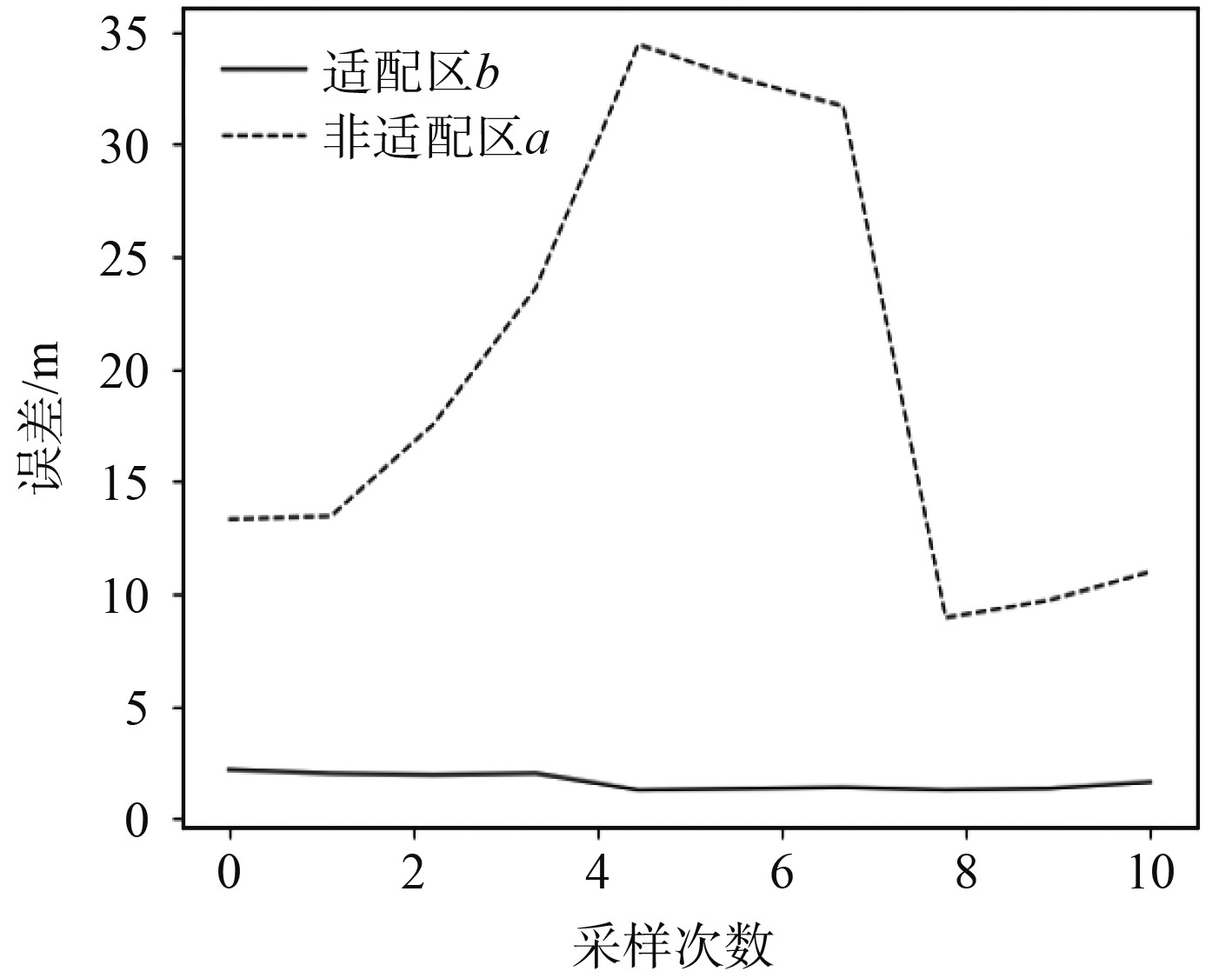
图 6 匹配误差对比图 Fig. 6 Matching error comparison graph |
在起点为(5 000 m,5 000 m)的航迹区域内,水深均值大于200 m,水深差值小于200 m,水深统计标准差小于100 m,地形平坦,海底底质不会造成声波强散射,对深度测量影响小,RES值为0.625,此处区域属于非适配区。区域内匹配误差平均值在25 m左右,最大值为39 m。起点为(2 000 m,2 000 m)的航迹区域内水深均值大于200 m,水深差值大于200 m,水深统计标准差小于100 m,海底地形复杂,海底底质不会造成声波强散射,RES值为0.92,此处区域属于适配区。区域内匹配误差平均值在3.8 m左右,最大值为4.7 m。根据仿真实验结果统计,适配区b内的地形匹配误差小于非适配区a。图7和图8为非适配区b内的仿真模拟路径图及匹配误差图。
|
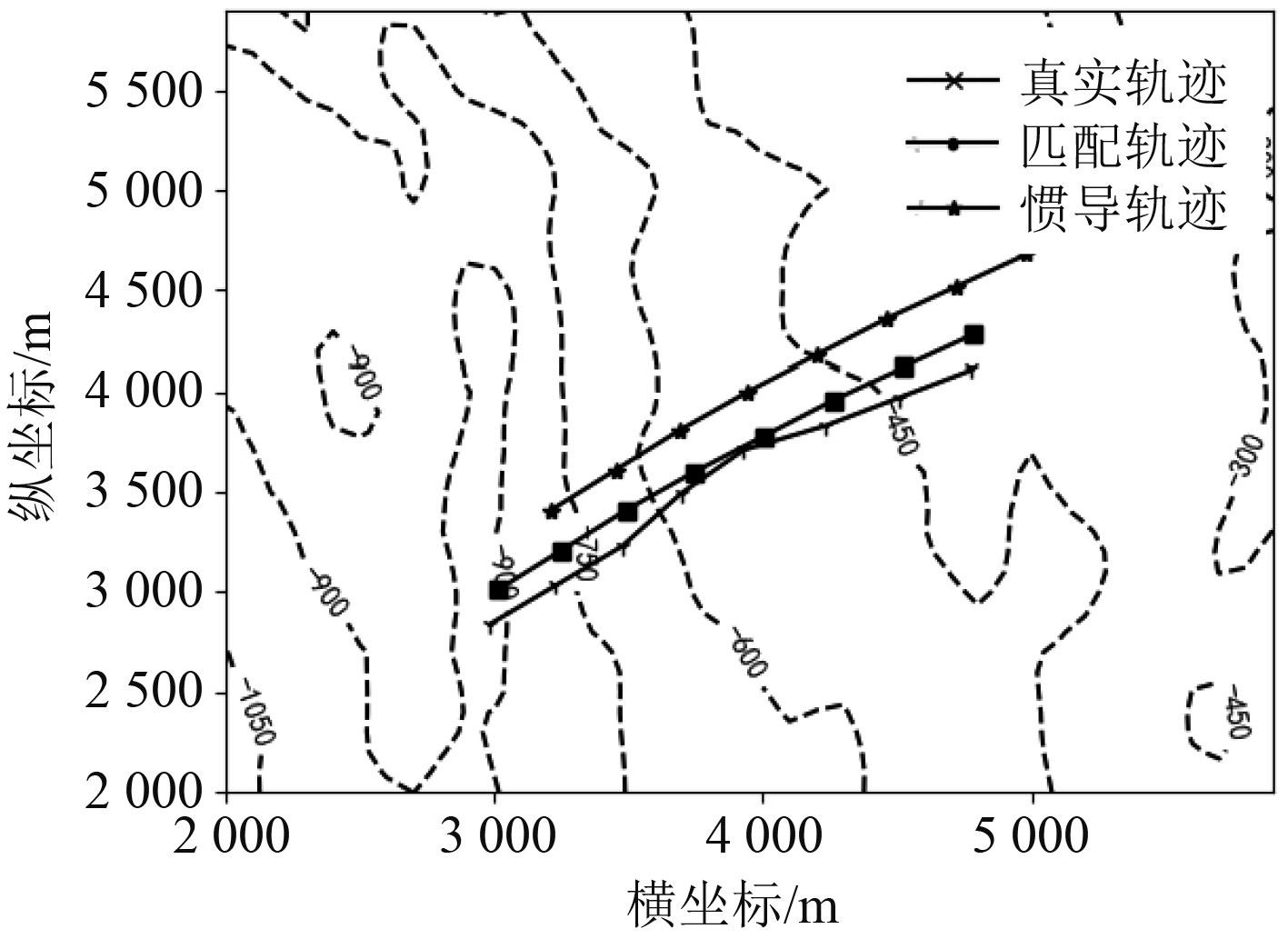
图 7 非适配区b轨迹位置图 Fig. 7 Trajectory location map of non-adaptive area b |
|
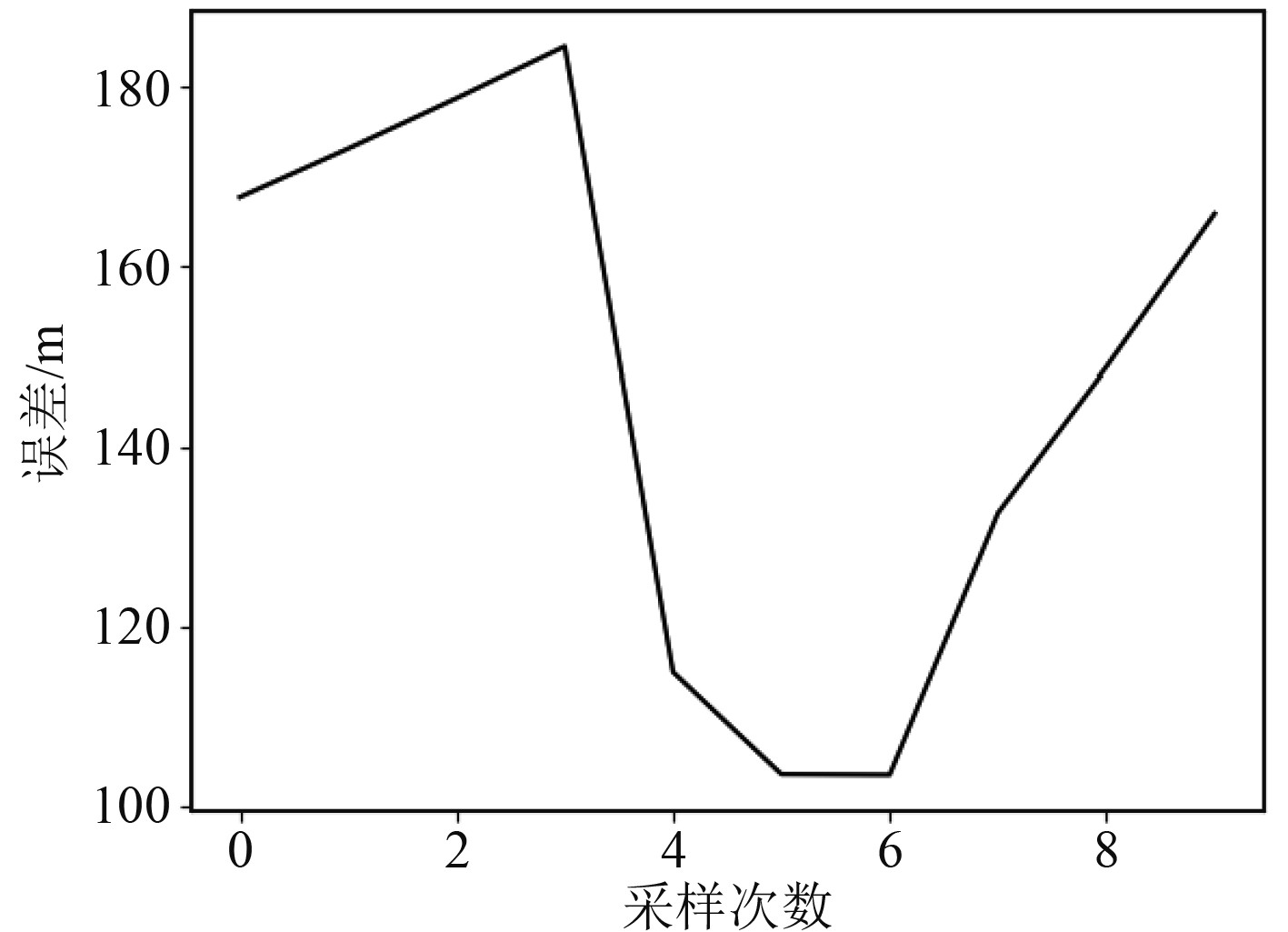
图 8 非适配区b匹配误差图 Fig. 8 Matching error diagram for non-adaptive area b |
在起点为(3 000 m,3 000 m)的航迹区域内,水深均值大于200 m,水深差值小于200 m,水深统计标准差大于100 m,海底地形复杂,但海底底质的反射能力强,传统适配区选择方法认为该区域为适配区。但实验结果表明区域内匹配误差平均值为142.9 m,最大值为179.2 m。由于深度测量过程中,海底底质的强反射产生多径效应并造成较大深度误差,因此在地形匹配时导致了匹配误差过大的问题。
|
|
表 7 实验结果误差统计表 Tab.7 Statistical table of experimental results error |
根据实验结果误差统计表可得,地形适配区选择准则可有效筛选出地形匹配的适配区域,提升地形匹配的精度,同时有效避免因仅考虑地形特征参数而导致的误匹配问题。
4 结 语针对海底数据精度低不能完全满足高精度导航以及传统适配区判定方法不准确的问题,本文基于不同深度条件下的海底地形特征参数,结合海洋噪声和海底底质反射特性,模拟不同海底底质的反射误差。根据层次分析法得出各项评价指标的权重向量,构建适配区选择准则函数,利用ICCP算法基于实际数据进行仿真研究。仿真结果表明,海底底质、地形特征参数以及海洋噪声可作为适配区选择的参考因素,融合多因素的地形适配区选择准则相较于传统判断方式可更准确判断出地形匹配区域的适配性,在适配区使用相关算法可提升匹配精度,减少误匹配,对实现水下高精度导航具有重要意义。
| [1] |
赵建虎, 陆振波, 王爱学. 海洋测绘技术发展现状[J]. 测绘地理信息, 2017, 42(6): 1-10. ZHAO J H, LU Z B, WANG A X. Development status of marine surveying and mapping technology[J]. Journal of Geomatics, 2017, 42(6): 1-10. |
| [2] |
赵建虎, 欧阳永忠, 王爱学. 海底地形测量技术现状及发展趋势[J]. 测绘学报, 2017, 46(10): 1786-1794. ZHAO J H, OUYANG Y Z, WANG A X. Status and development tendency for seafloor terrain measurement technology[J]. Journal of Geodesy and Geoinformation Science, 2017, 46(10): 1786-1794. |
| [3] |
陆秀平, 黄谟涛, 翟国君, 等. 多波束测深数据处理关键技术研究进展与展望[J]. 海洋测绘, 2016, 36(04): 1−6. LU X P, HUANG M T, ZHAI G J, et. Research progress and prospect of key technologies of multibeam sounding data processing[J]. Hydrographic Surveying and Charting, 2016, 36(04): 1−6. |
| [4] |
WANG H, XU X, ZHANG T. Multipath parallel ICCP underwater terrain matching algorithm based on multibeam bathymetric data[J]. IEEE Access, 2018, 6.
|
| [5] |
Y M Y, W H L, S M L, et al. Improvement of TERCOM aided inertial navigation system by velocity correction: Proceedings of the 2012 IEEE/ION Position, Location and Navigation Symposium[C]//2012.
|
| [6] |
CHEN P Y, CHANG J L, HAN Y J, et al. Underwater terrain-aided navigation method based on improved Gaussian sum particle filtering[J]. International Journal of Advanced Robotic Systems, 2019, 16(1).
|
| [7] |
A E J, J F M. Overview of terrain relative navigation approaches for precise lunar landing: 2008 IEEE Aerospace Conference[C]//2008.
|
| [8] |
郭发滨, 杜德文. 不同海底底质类型水深数据特征分析[J]. 海洋科学进展, 2003(3): 349-354. GUO F B, DU D W. Analysis of bathymetric data characteristics of different submarine sediment types[J]. Advances in Marine Science, 2003(3): 349-354. |
| [9] |
纪雪. 基于多波束数据的海底底质及地形复杂度分类研究[D]. 北京: 国家海洋局第一海洋研究所, 2017.
|
| [10] |
高靖萱, 杜昊翰, 张亚. UUV海底地形匹配导航的适配性高效分析方法[J]. 舰船科学技术, 2022, 44(24): 114-118. GAO J X, DU H H, ZAHNG Y. Adaptive and efficient analysis method for UUV submarine terrain matching navigation[J]. Ship Science and Technology, 2022, 44(24): 114-118. |
| [11] |
LI Y, MA T, CHEN P Y, et al. Autonomous underwater vehicle optimal path planning method for seabed terrain matching navigation[J]. Ocean Engineering, 2017, 133: 107-115. DOI:10.1016/j.oceaneng.2017.01.026 |
| [12] |
LI Z W, ZHENG W, WU F. Geodesic-based method for improving matching efficiency of underwater terrain matching navigation[J]. SENSORS, 2019, 19(12).
|
| [13] |
JIAN S, JING S, LU X. Modeling of underwater terrain aided navigation and terrain matching algorithm simulation[M]. Photorerctronic technology committee, 2016: 424−432.
|
| [14] |
HE Y P, LIU X X, CAI Y P, et al. Research on aided navigation based on terrain elevation matching and simulation[C]. Photoelectronic Technology Committee, 2016.
|
| [15] |
乔淼. 基于高差与标准差法的中国地形起伏度研究[J]. 绿色科技, 2020(6): 31-33. |
| [16] |
金绍华, 翟京生, 刘雁春, 等. Simrad EM多波束反向散射强度数据精处理研究[J]. 测绘科学, 2010, 35(2): 106-108. |
| [17] |
朱华勇, 沈林成, 常文森. 基于地形差分矩的TERCOM地图性能估计[J]. 国防科技大学学报, 2000(4): 98-101. |
| [18] |
刘鹰, 张继贤, 柳健. 面向地形辅助导航的地形信息分析[J]. 遥感信息, 2000(2): 21-23. |
| [19] |
郑彤, 蔡龙飞, 王志刚, 等. 地形匹配辅助导航中匹配区域的选择[J]. 中国惯性技术学报, 2009, 17(2): 191-196. |
| [20] |
徐振烊, 张静远, 王鹏. 水下地形辅助导航中匹配航路的选取[J]. 系统工程与电子技术, 2019, 41(11): 2588-2596. |
 2024, Vol. 46
2024, Vol. 46
