2. 辽宁省航海安全保障重点实验室,辽宁 大连 116026
2. Key Laboratory of Navigation Safety Guarantee of Liaoning Province, Dalian 116026, China
随着船舶的大型化和高速化发展,海上交通运输任务日益繁重,船舶航行安全受到人们的关注。为了保障人命财产和船舶航行的安全,每艘船周围需要一个安全缓冲区域—船舶领域[1]。作为研究海上交通安全的重要指标,船舶领域在船舶碰撞风险评估、船舶危险驶过检测等方面有广泛的应用。
近年来,许多学者对船舶领域进行了研究。WANG等[2]假设船舶领域尺寸是船长和速度的函数,并使用遗传算法和船舶自动识别系统(Automatic Identification System, AIS)数据对该函数进行校准。Dinh等[3]考虑到本船航速、他船船长等因素的影响,提出了四边形船舶领域。Pietrzykowski等[4]考虑船长和船舶类型等因素的影响,基于波罗的海AIS数据,研究了通航分道的船舶领域模型。文元桥等[5]以最近船舶的位置分布为样本,构造出不同船长的船舶领域。周田瑞等[6]利用螺头水道的AIS数据,构造出不同长度的船舶以不同航速航行时的船舶领域模型。Zhang等[7]基于新加坡海峡AIS数据,通过计算船舶间相对方位、临界船舶安全距离,构造出具有模糊边界的概率船舶领域。LIU等[8]基于大沽沙航道AIS数据,构建了不同船长区间的船舶领域模型。DU等[9]通过识别船舶转向点和估计船舶意图,检测船舶的第一次避险行为,再结合驾驶员感知碰撞风险对船舶领域的影响,根据船舶会遇样本对船舶领域的进行构建。Pietrzykowski等[10]使用电子海图显示与信息系统模拟器,分析本船船长、航速对船舶领域的影响。Pan等[11]考虑到操限船的航行特点以及船间效应的影响,提出一种繁忙水域中操限船的领域模型。Fan等[12]考虑船长、旱季和雨季的影响,计算他船在本船周围每个网格的密度,确定了不同类型的船舶领域模型。Silveira等[13]通过AIS数据挖掘出船舶在不同长度区间和不同船舶类型时四元船舶领域。
目前,船舶领域大多具有单一边界,而能够表征船舶航行风险级别的船舶领域模型研究较少。AIS数据可提供详细的船舶动态信息,反映出船舶在水域中的分布情况。因此,本文基于椭圆领域模型,使用AIS数据,构建一种具有风险级别的船舶领域模型,利用老铁山水道AIS数据对所提模型进行实验,并分析船舶风险领域特征。
1 船舶风险领域模型的构建方法 1.1 AIS数据预处理在传输过程中,受设备、天气、海况等因素限制,AIS数据会缺失及出现错误[14]。因此,船舶位置、航向等数据异常,应从AIS数据中剔除,而对于缺失的数据,则将该缺失数据所在时刻的所有数据删除。
AIS数据的动态信息更新频率随着船舶航行状态的变化而改变,而船舶相对位置的计算需两船的轨迹数据具有同步的时间,所以需对轨迹数据同步线性内插处理。但在此之前,需先根据水上移动通信业务标识码确定2艘不同的船在同一时间段内航行。预处理后的数据集合如下式:
| $ \begin{split}{S_{{\text{preprocessing}}}} =& \{ ({t_1},{l_{1 - }}_1,la{t_{1 - 1}},lo{n_{1 - 1}},headin{g_{1 - 1}},\\& {l_{2 - }}_1,la{t_{2 - 1}}, {lo{n_{2 - 1}}} ),...,({t_i},{l_{1 - }}_i, la{t_{1 - i}},\\& lo{n_{1 - i}},headin{g_{1 - i}}, {l_{2 - }}_i,la{t_{2 - i}}, { {lo{n_{2 - i}}} )} \}。\end{split}$ | (1) |
式中:i为数据集中的第i行数据;ti为第i行数据的时刻;l1-i, lat1-i, lon1-i, heading1-i分别为第i行数据的本船船长、纬度、经度、船首向;l2-i, lat2-i, lon2-i分别为第i行数据的他船船长、纬度、经度。
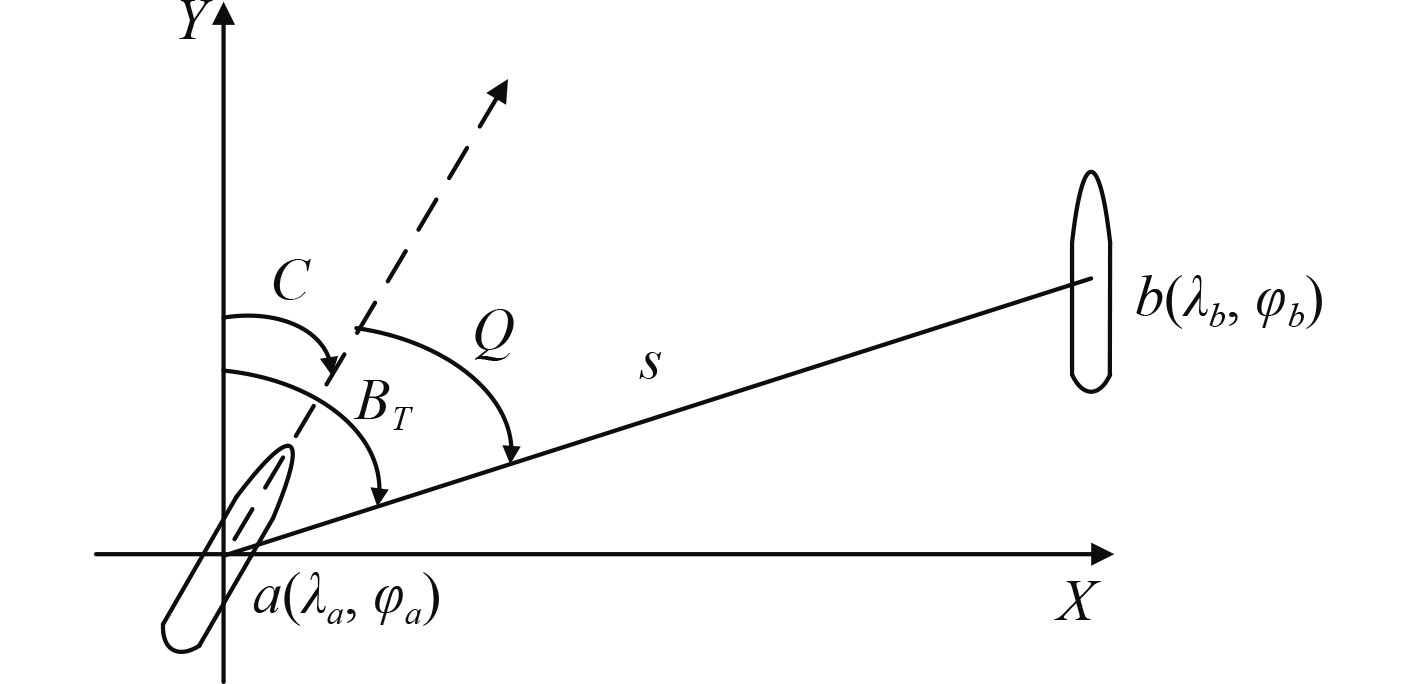
1.2 船舶相对位置计算为了后续船舶位置信息叠加,需计算船舶间相同时刻的相对位置。如图1所示,基于船a的位置,建立船a的随船坐标系。(λa, φa)、(λb, φb)分别为船a、船b的经纬度坐标;C为船a的首向角;BT为用圆周法表示的真方位;Q为船b相对于船a的方位;s为船a与船b之间的距离。
|
图 1 船舶相对位置关系 Fig. 1 Relative position relationship between ships |
| $ \cos {s_0} = \sin {\varphi _{{a}}} \times \sin {\varphi _{{b}}} + \cos {\varphi _{{a}}} \times \cos {\varphi _{{b}}} \times \cos {D_\lambda },$ | (2) |
| $ s = {s_0} \times 60 \times 1852,$ | (3) |
| $ \cos {B_{{{{T}}_0}}} = \frac{{\sin {\varphi _{{b}}} - \sin {\varphi _{{a}}} \times \cos {s_0}}}{{\cos {\varphi _{{a}}} \times \sin {s_0}}},$ | (4) |
| $ \left\{ \begin{gathered} {B_{{T}}} = {B_{{{{T}}_0}}},\;{\rm{if}}\;{\varphi _{{a}}} \geqslant 0,{D_\lambda } \geqslant 0,\\ {B_{{T}}} = 360^\circ - {B_{{{{T}}_0}}},\;{\rm{if}}\;{\varphi _{{a}}} \geqslant 0,{D_\lambda } < 0,\\ {B_{{T}}} = 180^\circ - {B_{{{{T}}_0}}},\;{\rm{if}}\;{\varphi _{{a}}} < 0,{D_\lambda } \geqslant 0,\\ {B_{{T}}} = 180^\circ + {B_{{{{T}}_0}}},\;{\rm{if}}\;{\varphi _{{a}}} < 0,{D_\lambda } < 0。\end{gathered} \right. $ | (5) |
| $ Q = {B_{{T}}} - C,$ | (6) |
| $ \left\{ \begin{gathered} Q = Q,{\text{ }}Q \geqslant 0,\\ Q = Q + 360^\circ ,{\text{ }}Q < 0。\end{gathered} \right. $ | (7) |
式中:Dλ为船a与船b之间的经差;BT0为用半圆周法表示的真方位。
根据式(1)代表的数据集,计算同一时刻他船相对本船的位置。然后存储“距离”、“相对方位”2种字段的信息。数据集如下式:
| $ S = \left\{ {\left( {{t_1},{l_{1 - }}_1,{s_1},\left. {{Q_1}} \right)} \right.} \right.,...,\left( {{t_i},{l_{1 - }}_i,} \right.{s_i},\left. {\left. {{Q_i}} \right)} \right\} 。$ | (8) |
式中,si、Qi分别为第i行数据的他船相对于本船的距离、方位。
1.3 船舶风险领域模型由于一艘船周围的船舶数量有限,不能有效地反映出船舶领域的形状和大小,因此,本文采用多船位置信息叠加的方法对船舶领域进行统计[18]。
步骤1 船舶相对位置坐标计算
由于船舶的航行状态并不是维持不变的,为便于统计他船在本船周围的分布情况,将每一艘本船的船首向统一为0°,位置统一为坐标原点(0, 0)。在对他船分布统计之前,他船相对于本船的位置坐标(xi, yi)为:
| $ \left\{ \begin{gathered} {x_i} = {s_i} \times \sin {Q_i},\\ {y_i} = {s_i} \times \cos {Q_i} 。\end{gathered} \right. $ | (9) |
最终获得以下数据集合:
| $ {S_{{\text{new}}}} = \left\{ {\left( {{t_1},{l_{1 - }}_1,{s_1},{Q_1},{x_1},\left. {{y_1}} \right)} \right.} \right.,...,\left( {{t_i},{l_{1 - }}_i,} \right.{s_i},{Q_i},{x_i},\left. {\left. {{y_i}} \right)} \right\} 。$ | (10) |
步骤2 筛选数据
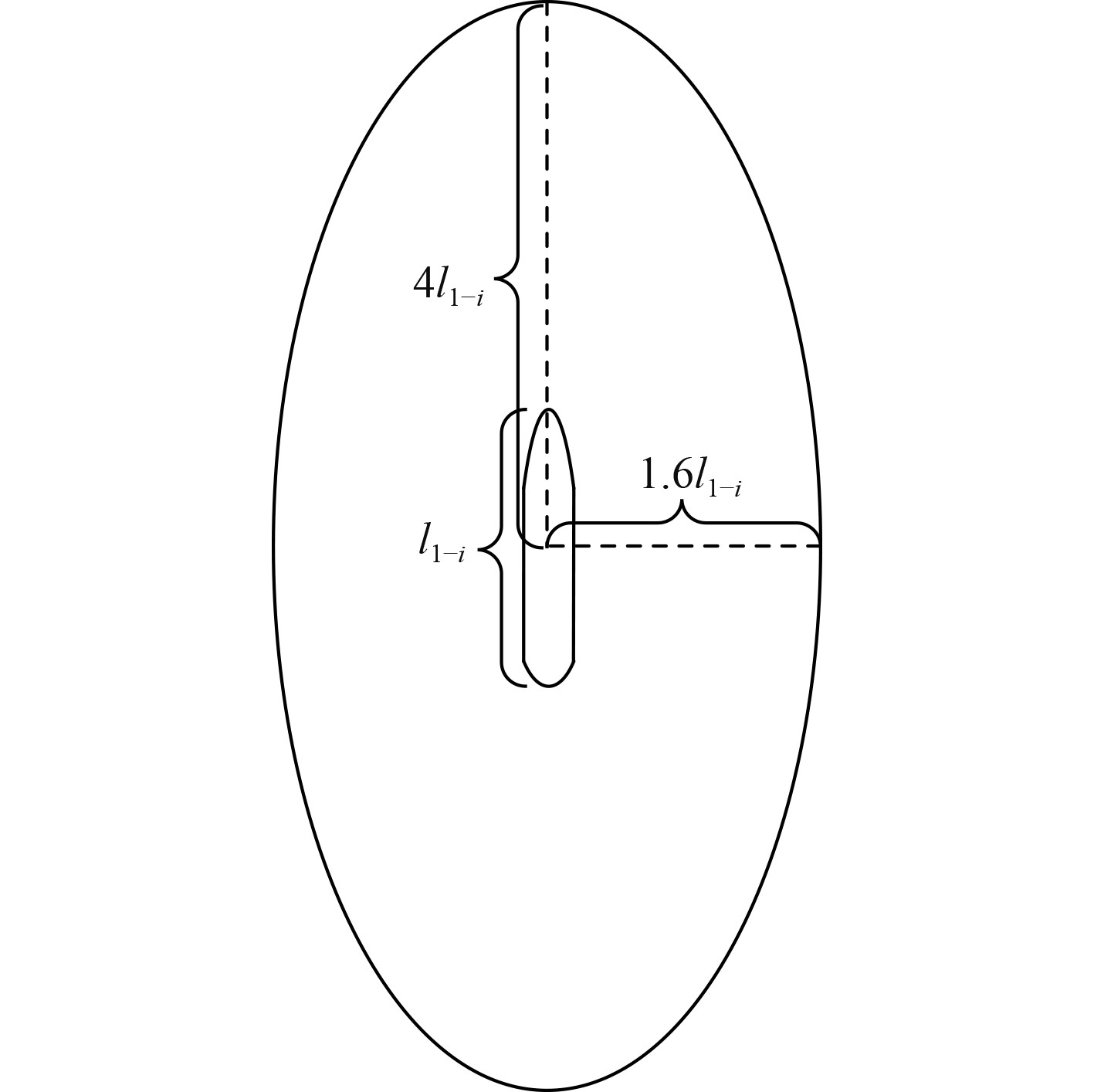
船舶领域常被用作判断是否存在航行风险,如果他船在本船的船舶领域之外,则不存在风险,反之则存在[17]。藤井模型是基于日本海域所构造的领域模型,并被推广为椭圆领域模型。后来学者对船舶领域进行研究,LIU等[8]构造出不同船长船舶的椭圆模型,其长轴为7.82~8.34倍船长,短轴为3.05~3.42倍船长。Hansen等[16]得到了长轴为8倍船长、短轴为3.2倍船长的椭圆领域模型。Pan等[11]、周洋宇等[14]在研究时,采用了该尺寸的椭圆领域模型。因此,本文采用长轴为8倍船长、短轴为3.2倍船长的椭圆领域模型构造船舶风险领域。如图2所示,本船船长为l1-i,以本船为中心,构建椭圆领域。根据式(11)筛选出侵入本船椭圆领域的他船。
|
图 2 椭圆领域 Fig. 2 Elliptic domain |
| $ \frac{{{y_i}^2}}{{{{\left( {4 \times {l_{1 - i}}} \right)}^2}}} + \frac{{{x_i}^2}}{{{{\left( {1.6 \times {l_{1 - i}}} \right)}^2}}} \leqslant 1。$ | (11) |
步骤3 多船位置数据叠加
在构造船舶领域时,可将同种类型(如船长、航速相同等)的船舶作为样本进行研究[5]。本文将相同船长的船舶作为研究对象。在确定本船船长后,遍历步骤2获得的每一行数据,将符合本船条件的船舶相对位置数据进行存储,从而得到多船位置信息数据。
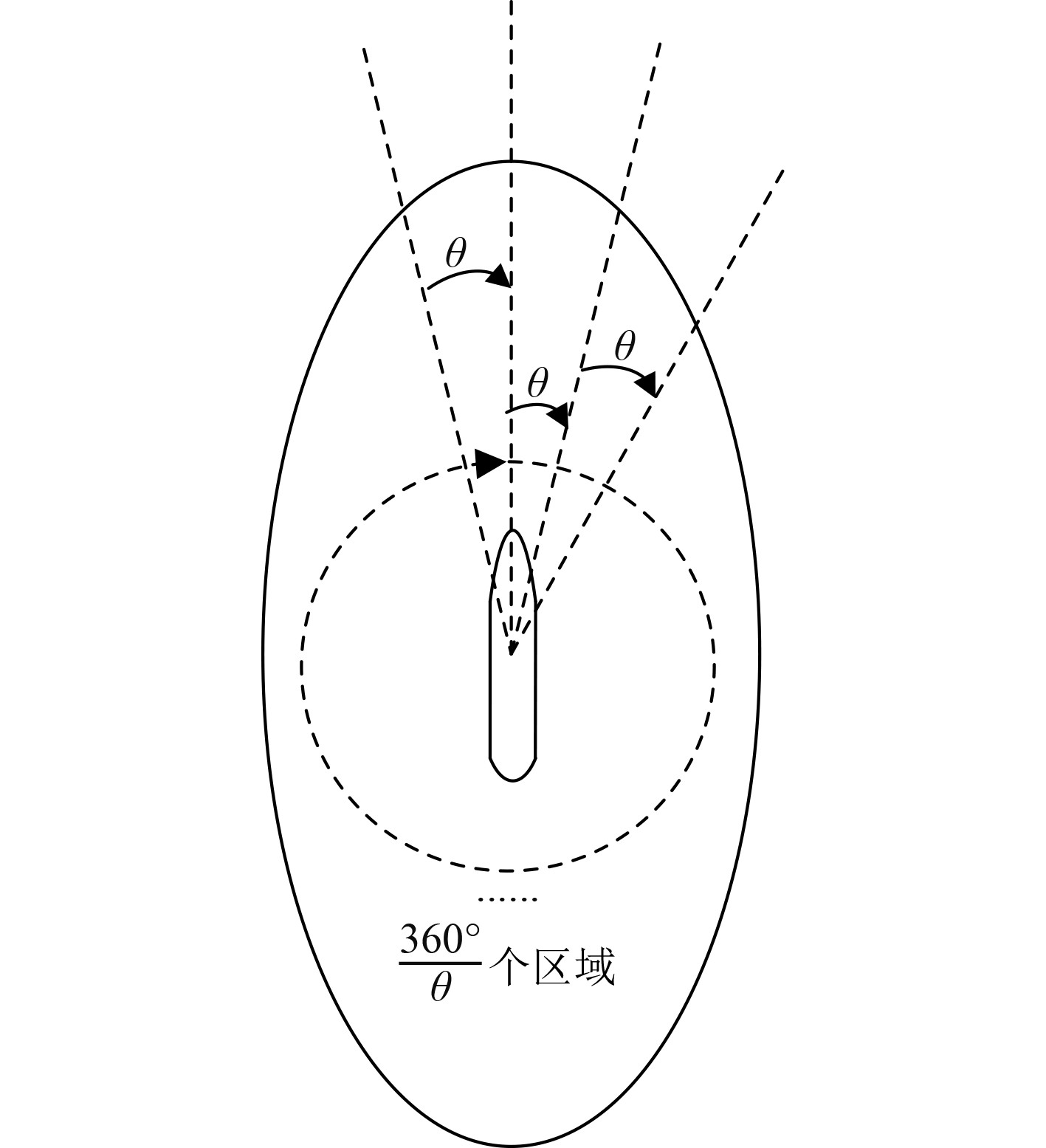
为了展现他船在本船周围的空间分布,本文以一定角度θ为步长,按顺时针将椭圆领域划分为360°/θ个小区域,如图3所示。
|
图 3 椭圆领域划分 Fig. 3 Elliptic domain division |
根据文献[7,17],椭圆领域边界作为风险级别为0的船舶领域。对于椭圆领域内风险级别的构建,本文通过计算在每个小区域中他船在离本船一定距离内出现的概率来衡量船舶航行风险,如下式:
| $ \left\{ \begin{gathered} P({r_j}) = \frac{{{n_{{r_j}}}}}{{{n_j}}},\\ R({r_j}) = 1 - P({r_j}) 。\end{gathered} \right. $ | (12) |
式中:j为以本船船首向为起始,顺时针划分的第j个区域;rj为第j个区域中他船与本船的距离,取值范围为0≤rj≤dj-max。其中,dj-max为在第j个区域中他船离本船的最大距离;nrj为他船船舶点在rj内的数量;nj为第j个区域他船船舶点的数量;P(rj)为他船船舶点在rj内的概率;R(rj)为他船和本船的距离在rj时的风险级别。
本文的风险级别是指在离本船周围一定距离与椭圆领域边界间的区域中,他船出现的概率。因此,式(12)所代表的含义是,他船在距离本船rj内出现的概率越大,航行风险越低。在与船舶最近的距离内,船舶出现概率降低到0,航行风险增加到最大值1。
首先根据“相对方位”对他船所属的区域进行分配并利用“距离”信息以由近及远的原则对他船数据进行排序。其次,通过设定风险级别和统计区域内的他船数据,根据式(12)可求解出每个区域在预设风险级别时的他船船舶点数量以及达到该数量值所需的距离。然后,求出在该距离时的他船位置坐标,并将该坐标点作为该风险级别的临界点,将各点连接起来便可得到该风险等级的船舶领域,但其形状复杂,不利于应用到实践中。本文采用最小二乘法对各点进行椭圆拟合,即可得到船舶风险领域边界。
风险级别为1的船舶领域是不容他船侵犯的区域,为拟合的边界尽可能不包含船舶点,在构建风险级别为1的船舶领域时,本文将椭圆领域划分为8个区域[5];而在构建风险级别小于1的船舶领域时,为了拟合的椭圆边界可以较好地反映风险级别,则是将椭圆领域划分为72个区域[18]。
2 实例分析 2.1 船舶风险领域计算老铁山水道是船舶进出环渤海各港口的重要航路,船舶交通流量巨大。本文将其作为研究水域,边界点坐标分别为A(38°36′.70N, 120°57′.60E),B(38°32′.20N, 121°07′.60E),C(38°27′.50N, 121°04′.10E),D(38°31′.90N,120°54′.10E)。本文采用了研究水域2021年7月的AIS数据,在剔除不完整、错误的数据后,获取了204582条AIS数据;在对AIS数据进行时间段重叠判断和同步内插后,获得了34445378条AIS数据。最终经筛选,本文获取了3088艘船舶的数据,共计548105条。
为确保本船周围具有足够他船数据,本文将149 m、190 m、229 m、300 m船舶作为研究对象。表1为不同尺度船舶其周围他船船舶点的数量。
|
|
表 1 不同尺度船舶的数量及其周围他船船舶点的数量 Tab.1 The number of ships of different scales and the number of other ship points around them |
为了让驾驶员根据风险级别对航行区域有着清楚的定位,根据文献[19],本文根据风险级别将椭圆领域内的区域划分为5个等级,如表2所示。
|
|
表 2 区域风险等级划分 Tab.2 Risk classification of region |
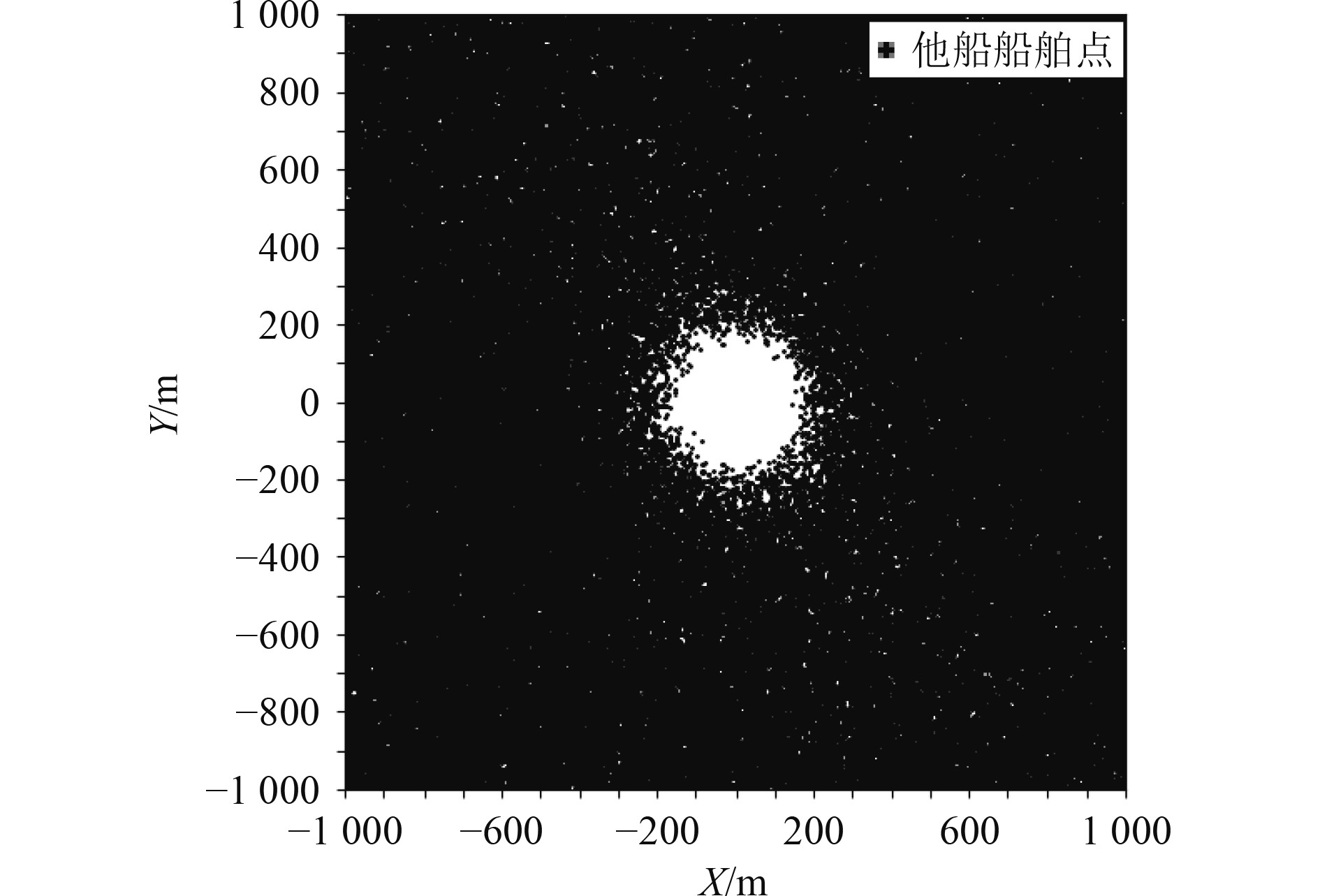
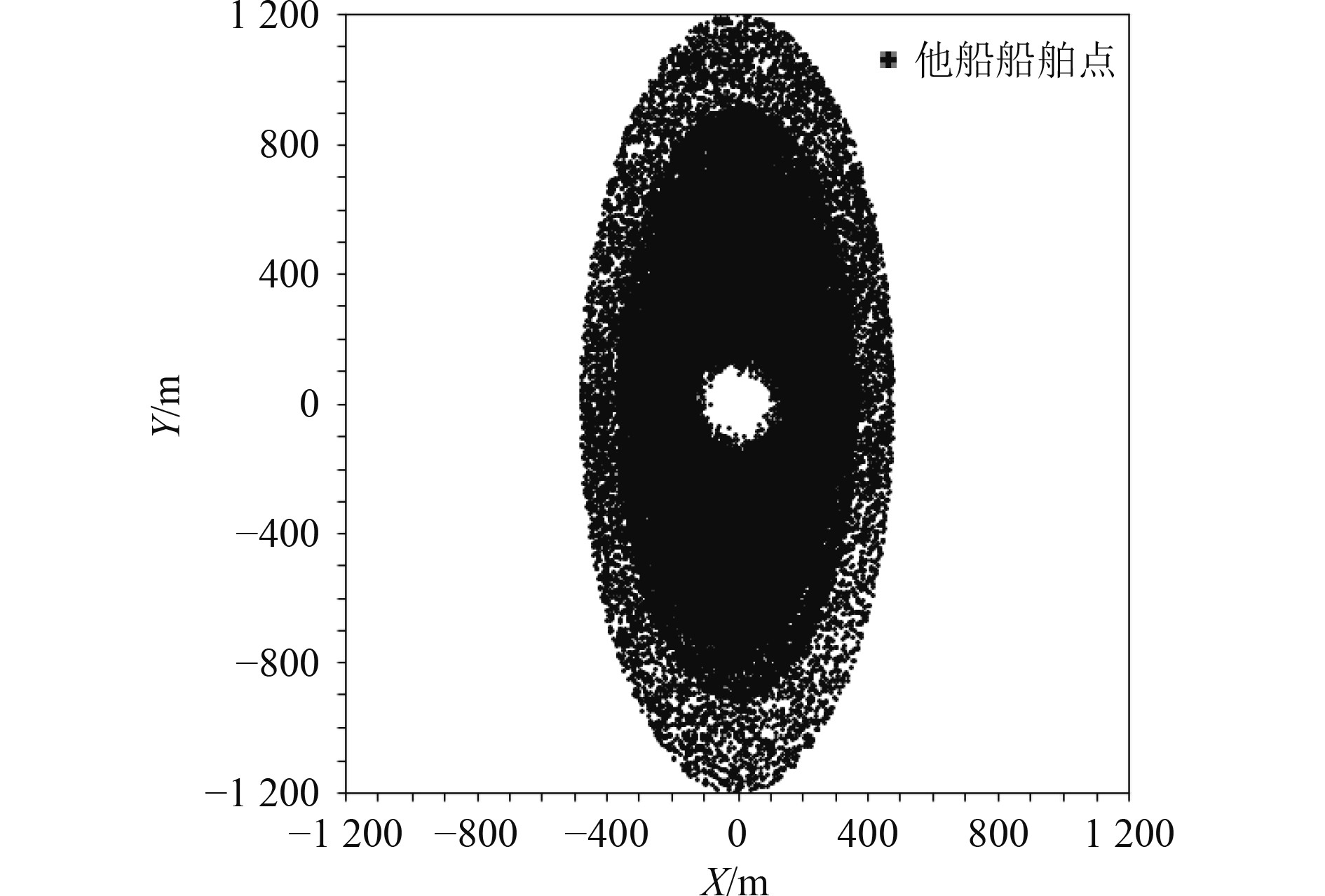
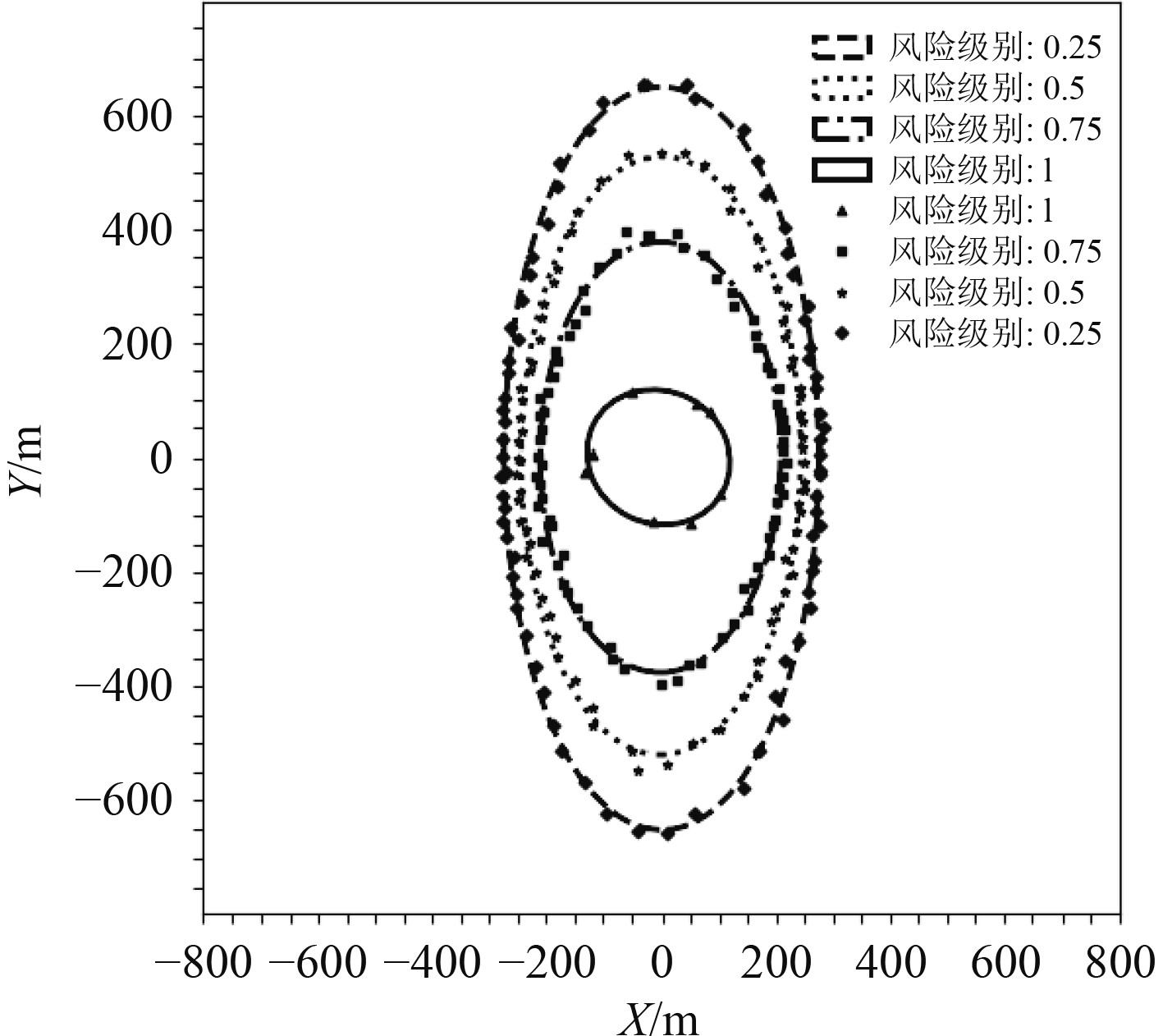
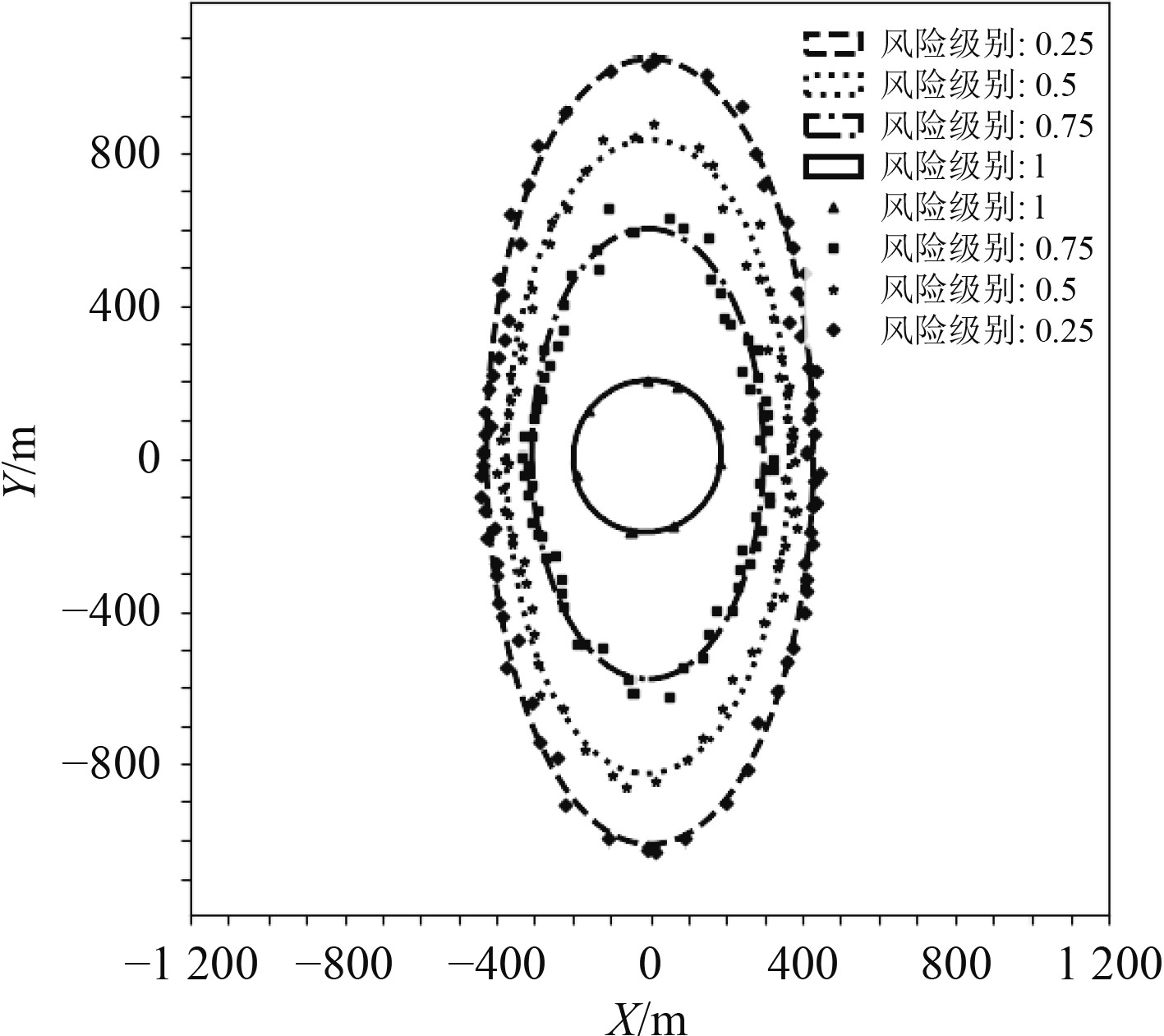
接下来本文构建风险级别为0.25、0.5、0.75、1的船舶领域边界。根据多船位置信息叠加方法的步骤1,本文获取到未经筛选的AIS数据,并提取他船分布图,如图4所示。图中,本船坐标为(0,0),船首向为0°,船首向为Y轴正方向,船舶右舷方向为X轴正方向,圆点为他船。根据步骤2和步骤3筛选数据,本文获取了4种船长船舶的91016条AIS数据,并提取他船分布图,如图5所示。根据风险级别、叠加的数据,通过式(12),可获取到每个区域的临界点坐标,从而构建临界点分布图,并使用最小二乘法对各点拟合,结果如图6~图9所示。
|
图 4 数据未经筛选生成的他船分布图 Fig. 4 Distribution map of other ships generated without data filtering |
|
图 5 数据经筛选生成的他船分布图 Fig. 5 Distribution map of other ships generated through data filtering |

|
图 6 149 m船舶风险领域 Fig. 6 Risk domain of 149 m ship |
|
图 7 190 m船舶风险领域 Fig. 7 Risk domain of 190 m ship |

|
图 8 229 m船舶风险领域 Fig. 8 Risk domain of 229 m ship |
|
图 9 300 m船舶风险领域 Fig. 9 Risk domain of 300 m ship |
|
|
表 3 不同尺度船舶的风险领域长半轴长度(单位:m) Tab.3 The length of the long half axis in the risk domain of ships of different scales (unit: m) |
|
|
表 4 不同尺度船舶的风险领域短半轴长度(单位:m) Tab.4 The length of the short half axis in the risk domain of ships of different scales (unit: m) |
为检验最小二乘法的拟合效果,本文将船舶风险领域包含船舶点的实际数量与理论值进行比较,其中,理论值根据风险级别、式(11)筛选的数据,通过式(12)计算,结果如表5所示。可知,不同尺度船舶的风险领域包含船舶点数量与理论值相差较小。因此,最小二乘法拟合的椭圆边界可以较好地反映船舶的风险级别。
|
|
表 5 不同尺度船舶的风险领域包含船舶点的实际数量及理论值 Tab.5 The actual number of ship points contained by the risk domains of ships of different scales and theoretical values |
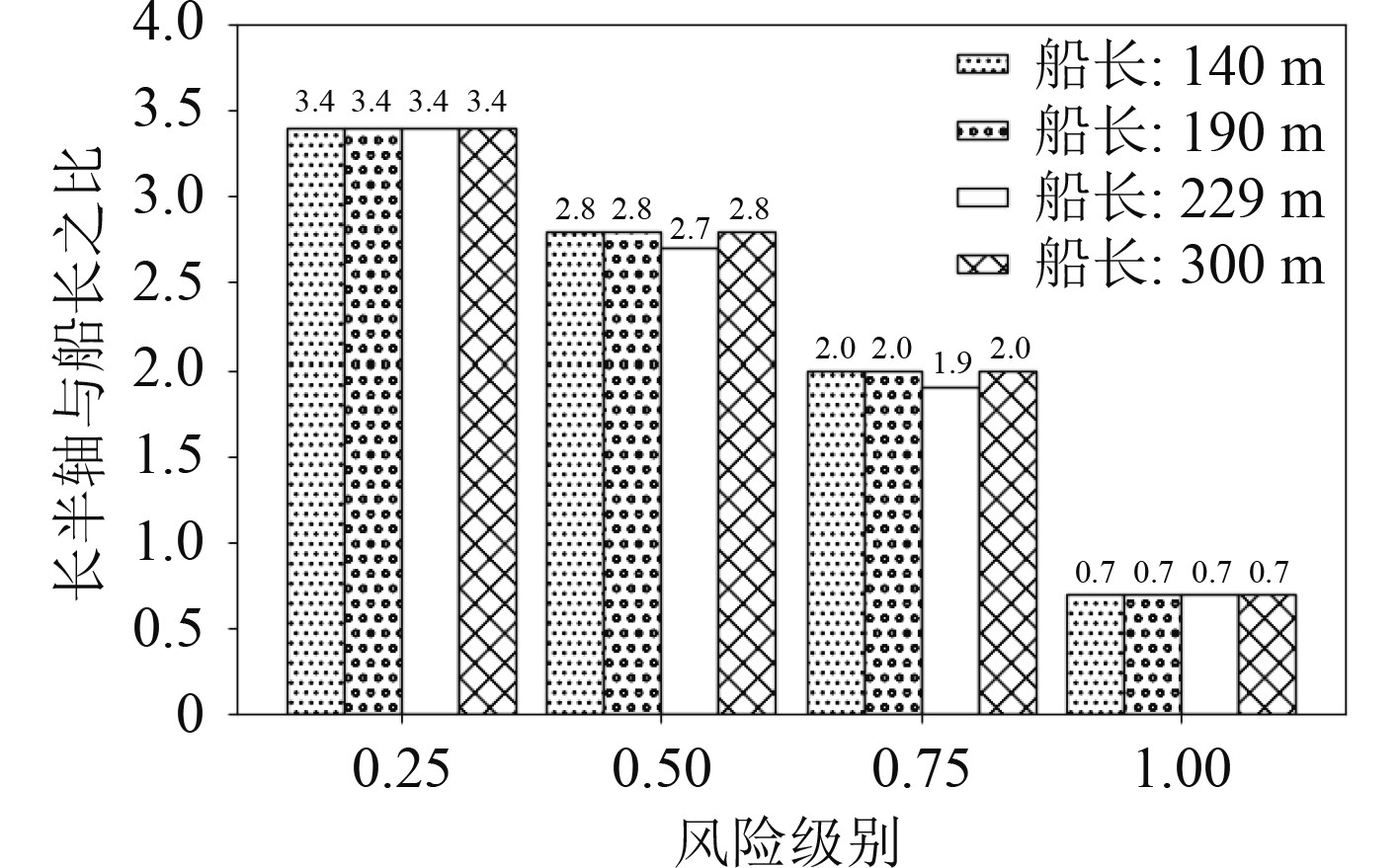
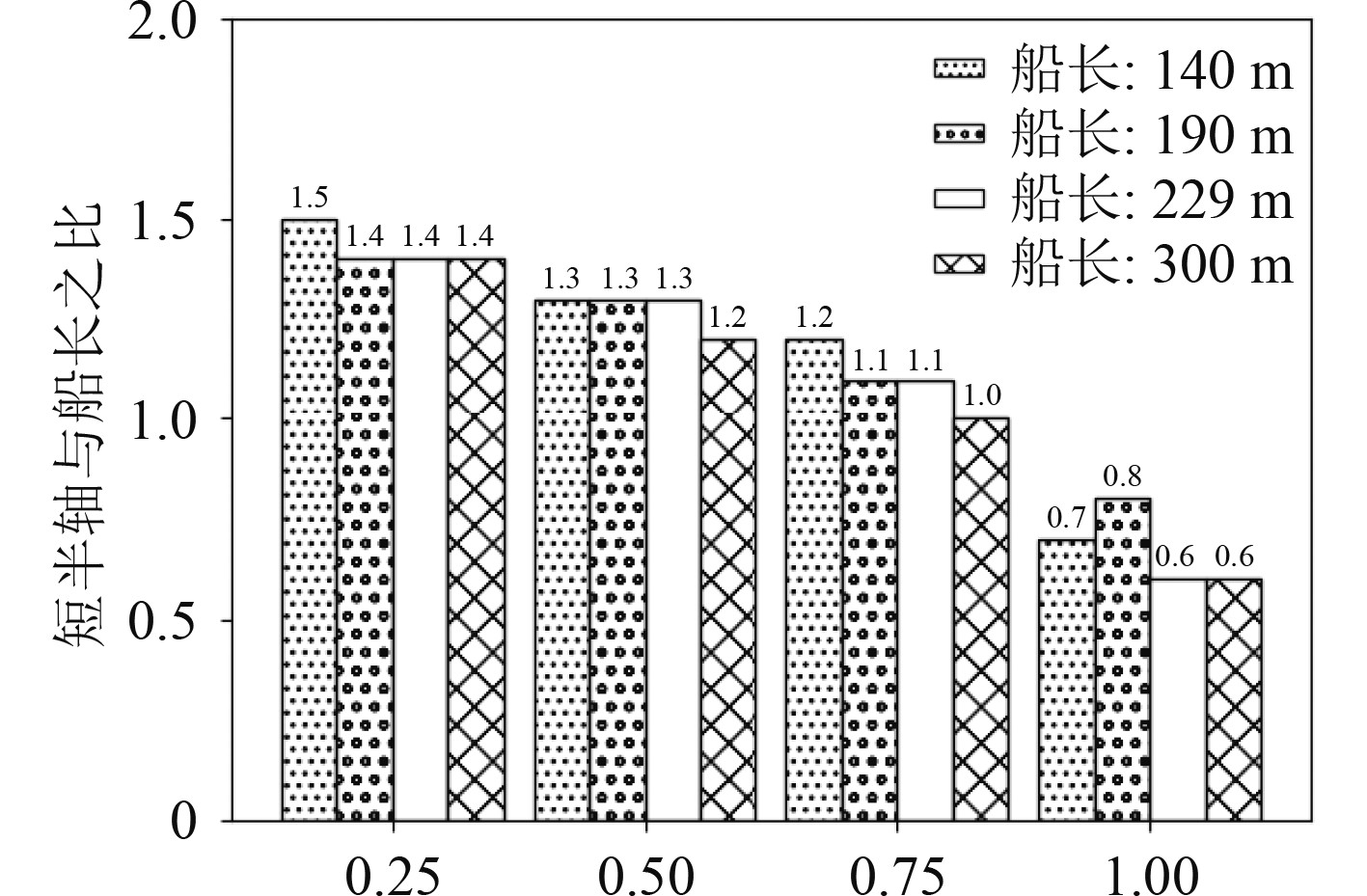
根据表3、表4,可获得不同尺度船舶的风险领域长、短半轴之比,结果如表6所示。可知,风险领域长、短半轴之比随着风险级别的提升而减小,风险级别为1的比值接近1,因此,本船周围禁止他船进入的区域边界接近于圆形,出现这种情况原因可能是,老铁山水道分为东西2条航道,根据老铁山水道船舶定线制的规定,每条航道的船舶主流航向是一致的,因此,船舶间更多处于追越局面,船舶相对速度较小,相比其他会遇局面,船舶纵向所需的安全距离较小,最终导致本船的禁止区域接近圆形。
|
|
表 6 不同尺度船舶的风险领域长、短半轴之比 Tab.6 Ratio of major and minor axes of risk domain for ships of different sizes |
根据表3和表4,可获得不同尺度船舶的风险领域长、短半轴与船长的关系,结果如图10和图11所示。可知,当确定了风险级别,不同尺度船舶间的风险领域长、短半轴与船长之比差异较小。因此,可根据船长和长、短半轴与船长之比大致计算船舶风险领域的尺寸。
|
图 10 船舶风险领域长半轴与船长之比 Fig. 10 Ratio of the semi major axis to the length of ship in ship risk domain |
|
图 11 船舶风险领域短半轴与船长之比 Fig. 11 Ratio of the semi minor axis to the length of ship in ship risk domain |
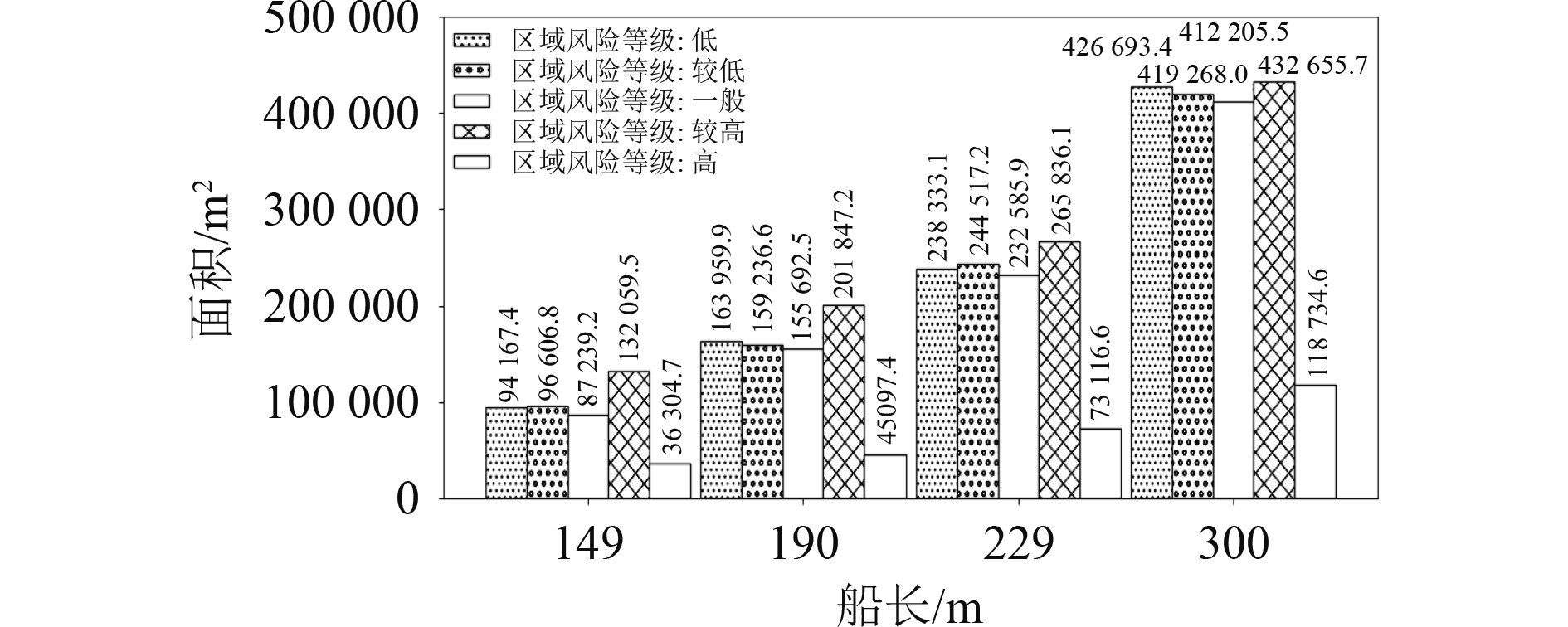
本文的风险级别是由他船在离本船一定距离内出现的概率衡量的,因此,当风险级别以0.25的步长从0提升到1时,他船在风险区域的数量相同。因此,为了展现他船在风险领域内的分布情况,本文计算风险区域的面积,结果如图12所示。
|
图 12 不同尺度船舶风险区域的面积 Fig. 12 Area of risk level areas of different scale ship |
可知,区域风险等级从低升为一般时,面积变化的幅度相对较小,说明他船分布情况大致相同,他船在该区域航行的偏向程度大致相同;区域风险等级从一般变化至较高时,区域面积增幅最大,他船船舶点分布稀疏,这说明他船驾驶员明显意识到了航行风险;与其他风险等级相比,风险等级为高的区域面积最小,是他船不容侵犯的区域。
通过上述分析,当他船在风险等级为低的区域航行时,他船船舶点分布较密集,他船比较偏向于在此处航行,本船应及时关注他船的航行动态,他船应及时驶出本船的船舶领域。当他船在风险等级为较低、一般的区域航行时,随着风险等级的提高,他船分布相对密集,对本船的航行造成了潜在的风险,本船应重点关注在此处航行的他船。当他船在风险等级为较高的区域航行时,由于他船离本船较近且他船船舶点分布稀疏,说明他船认为此处风险等级较高,不愿在此航行,因此,本船或他船应尽早采取措施,避免他船进入本船高风险等级的区域内。
3 结 语本文使用椭圆领域,基于大量的AIS数据,构建了船舶风险领域模型。为了验证该模型的有效性,利用老铁山水道的AIS数据,以149 m、190 m、229 m、300 m船舶为研究对象,分别构建风险级别为0、0.25、0.5、0.75、1的船舶风险领域。
研究发现,拟合的椭圆边界可以较好地反映船舶的风险级别。在同一风险级别时,149 m、190 m、229 m、300 m船舶间的风险领域长、短半轴与船长之比差异较小。风险级别为1的船舶领域边界接近于圆形。另外,当区域风险等级从低升为较高时,他船分布的密集程度不同,风险等级为低、较低、一般时,他船分布相对密集;风险等级为较高时,他船分布稀疏。
所提模型因其具有多层边界,可进一步用于不同风险级别时的船舶风险评估、船舶危险驶过检测和航道通过能力分析。主管部门和船舶驾驶员根据船舶相对位置,获知船舶当前所处于的风险级别,同时本文所提方法可为具有单一边界的船舶领域从数据统计的角度构建不同风险级别的边界提供了思路。
| [1] |
徐周华, 牟军敏, 季永清. 内河水域船舶领域三维模型的研究[J]. 武汉理工大学学报(交通科学与工程版), 2004(3): 380-383. XU Z H, MU J M, JI Y Q. A study of 3D model of ship domain for inland waterway[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2004(3): 380-383. |
| [2] |
WANG Y, CHIN H. An empirically-calibrated ship domain as a safety criterion for navigation in confined waters[J]. Journal of Navigation, 2016, 69(2): 257-276. DOI:10.1017/S0373463315000533 |
| [3] |
DINH G H, IM N. The combination of analytical and statistical method to define polygonal ship domain and reflect human experiences in estimating dangerous area[J]. International Journal of e-Navigation and Maritime Economy, 2016, 4: 97-108. DOI:10.1016/j.enavi.2016.06.009 |
| [4] |
PIETRZYKOWSKI Z, MAGAJ J. Ship domain as a safety criterion in a precautionary area of traffic separation scheme[J]. TransNav, the International Journal on Marine Navigation and Safety of Sea Transportation, 2017, 11(1): 93-98. DOI:10.12716/1001.11.01.10 |
| [5] |
文元桥, 王玉宾, 张帆, 等. 基于AIS数据的船舶领域建模[J]. 中国航海, 2018, 41(4): 1-6. WEN Y Q, WANG Y B, ZHANG F, et al. Ship domain modeling based on AIS data[J]. Navigation of China, 2018, 41(4): 1-6. |
| [6] |
周田瑞, 邵哲平, 潘家财, 等. 基于AIS数据挖掘的受限水域船舶动态领域研究[J]. 集美大学学报(自然科学版), 2018, 23(1): 33-38. ZHOU T R, SHAO Z P, PAN J C, et al. Research on dynamic of ship movements in restricted waters based on massive AIS data[J]. Journal of Jimei University (Natural Science), 2018, 23(1): 33-38. |
| [7] |
ZHANG L, MENG Q. Probabilistic ship domain with applications to ship collision risk assessment[J]. Ocean Engineering, 2019, 186: 106130. DOI:10.1016/j.oceaneng.2019.106130 |
| [8] |
LIU C, LIU J, ZHOU X, et al. AIS data-driven approach to estimate navigable capacity of busy waterways focusing on ships entering and leaving port[J]. Ocean Engineering, 2020, 218: 108215. DOI:10.1016/j.oceaneng.2020.108215 |
| [9] |
DU L, BANDA O A V, HUANG Y, et al. An empirical ship domain based on evasive maneuver and perceived collision risk[J]. Reliability Engineering & System Safety, 2021, 213: 107752. |
| [10] |
PIETRZYKOWSKI Z, WIELGOSZ M. Effective ship domain – Impact of ship size and speed[J]. Ocean Engineering, 2021, 219: 108423. DOI:10.1016/j.oceaneng.2020.108423 |
| [11] |
PAN W, XIE X, BAO T, et al. Ship domain model for ships with restricted maneuverability in busy waters[J]. Journal of Navigation, 2021, 74(3): 673-697. DOI:10.1017/S037346332000065X |
| [12] |
ZHANG F, PENG X, HUANG L, et al. A spatiotemporal statistical method of ship domain in the inland waters driven by trajectory data[J]. Journal of Marine Science and Engineering, 2021, 9(4): 410. DOI:10.3390/jmse9040410 |
| [13] |
SILVEIRA P, TEIXEIRA A P, GUEDES SOARES C. A method to extract the Quaternion Ship Domain parameters from AIS data[J]. Ocean Engineering, 2022, 257: 111568. DOI:10.1016/j.oceaneng.2022.111568 |
| [14] |
杨家轩, 周洋宇, 刘家国. 船间危险驶过持续时间模型及应用分析[J]. 中国舰船研究, 2021, 16(5): 172-180. YANG J X, ZHOU Y Y, LIU J G. Ship near-miss duration model and application analysis[J]. Chinese Journal of Ship Research, 2021, 16(5): 172-180. |
| [15] |
赵健, 王新建, 高飞德, 等. 基于动态水域网格计算的船舶领域研究[J]. 舰船科学技术, 2017, 39(9): 152-156. ZHAO J, WANG X J, GAO F D, et al. Research on grid computing in ship domain based on dynamic water[J]. Ship Science and Technology, 2017, 39(9): 152-156. DOI:10.3404/j.issn.1672-7619.2017.05.031 |
| [16] |
HANSEN M G, JENSEN T K, et al. Empirical ship domain based on AIS data[J]. Journal of Navigation, 2013, 66(6): 931-940. DOI:10.1017/S0373463313000489 |
| [17] |
DEBNATH A K, CHIN H C. Navigational traffic conflict technique: A proactive approach to quantitative measurement of collision risks in port waters[J]. Journal of Navigation, 2010, 63(1): 137-152. DOI:10.1017/S0373463309990233 |
| [18] |
张鹏. 基于AIS数据的船舶领域模型统计平台研究[D]. 大连: 大连海事大学, 2016.
|
| [19] |
刘超凡, 郭国平, 吴兵, 等. 基于FAHP-云模型的CAPE型船舶内河航行安全评估[J]. 武汉理工大学学报, 2021, 43(7): 29-35+47. LIU C F, GUO G P, WU B, et al. CAPE-type ship navigation safety assessment based on FAHP-cloud model[J]. Journal of Wuhan University of Technology, 2021, 43(7): 29-35+47. |
 2024, Vol. 46
2024, Vol. 46
