2. 山东省科学院海洋仪器仪表研究所,山东 青岛 266318;
3. 乌克兰国立技术大学基辅工学院,乌克兰 基辅 03056
2. Institute of Oceanographic Instrumentation, Shandong Academy of Sciences, Qingdao 266318, China;
3. Kyiv Polytechnic Institute, National Technical University of Ukraine, Kyiv 03056, Ukraine
随着对水下资源的探索以及科学研究领域的需求不断增加,水下信息的准确获取与传输等技术成为研究热点[1 − 2]。然而,由于水声通信系统受时变水声信道的影响,多途传播效应较为严重;另外发射机和接收机之间的相对运动会导致信道状态变化剧烈,以上问题的存在使得实现可靠的水声通信具有挑战性[3 − 5]。
水声信道估计的目标是获取信道的特性,为信道的均衡提供可靠信息。针对信道估计问题,国内外多位学者进行了大量研究。Yang等[6]提出一种改进的比例归一化最小均方算法进行迭代信道估计与均衡,该算法具有较高的性能、传输效率和较低的计算复杂度;Li等[7]提出基于时延-多普勒扩展函数的稀疏信道估计方法,改善了信道估计性能;Yong等[8]针对水声(UWA)正交频分复用(OFDM)系统,提出一种基于自适应降噪的信道估计算法,该算法适用于强噪声、恶劣的水声信道;Wu等[9]提出一种基于压缩感知框架下的长时延水声信道估计算法,提高水下浅稀疏信道大时延分布的估计性能;Tong等[10]提出一种新的序贯自适应观测长度正交匹配追踪(SAOLOMP)算法,对快变水声信道进行估计,有效改善了快速时变环境下水声通信系统的性能。
然而以上信道估计算法均采用传统的时分复用方案,即在数据序列中直接插入训练序列,该方案会导致频谱损耗和功率损耗。为了解决以上问题,提高对信道的跟踪能力,Guo等[11 − 14]提出了叠加训练(ST)方案,实现了信道信息的融合。
在此基础上,本文提出了基于虚拟训练序列的双向水声信道精准估计(VT-BCE)算法,实现了时变水声信道的精准估计。采用ST方案,将训练序列与符号序列线性叠加,使得训练序列连续传输,增强了时变水声信道的跟踪能力[15-18]。双向信道估计(BCE)算法将一个数据块分割为多个短块,充分利用信道短块之间的相关性,通过前向递归、反向递归和消息融合获取短块的全局信道估计,以此实现精准的信道估计。将信道估计、频域均衡和译码以迭代的方式相结合,使估计出来的符号序列作为信道估计的虚拟训练(VT)序列,提高信道估计和跟踪性能。最后进行仿真和水池试验,充分验证了所提算法的有效性。
1 BCE算法原理由于水声信道存在一定的变化规律,因此相邻短块的信道具有一定的相关性。基于因子图置信传播,利用信道相关性,BCE算法将水声信道中一个数据块分成多个短块,采用相邻短块间的信道相关系数表征信道相关性,其中所有消息均为高斯消息,用均值和方差进行描述。通过前向递归、反向递归以及双向消息融合获得当前短块的信道估计。BCE算法相当于利用多个短块信息估计当前短块信道,实现对当前短块的全局信道估计。
传输信号结构如图1所示,1帧数据由多个数据块构成,将1个数据块分成多个短块,每个短块附加一个循环前缀(CP)作为保护间隔,避免短块间干扰。同时采用正负调制率的双曲调频(HFM)信号分别作为帧的头部和尾部,同步接收信号。
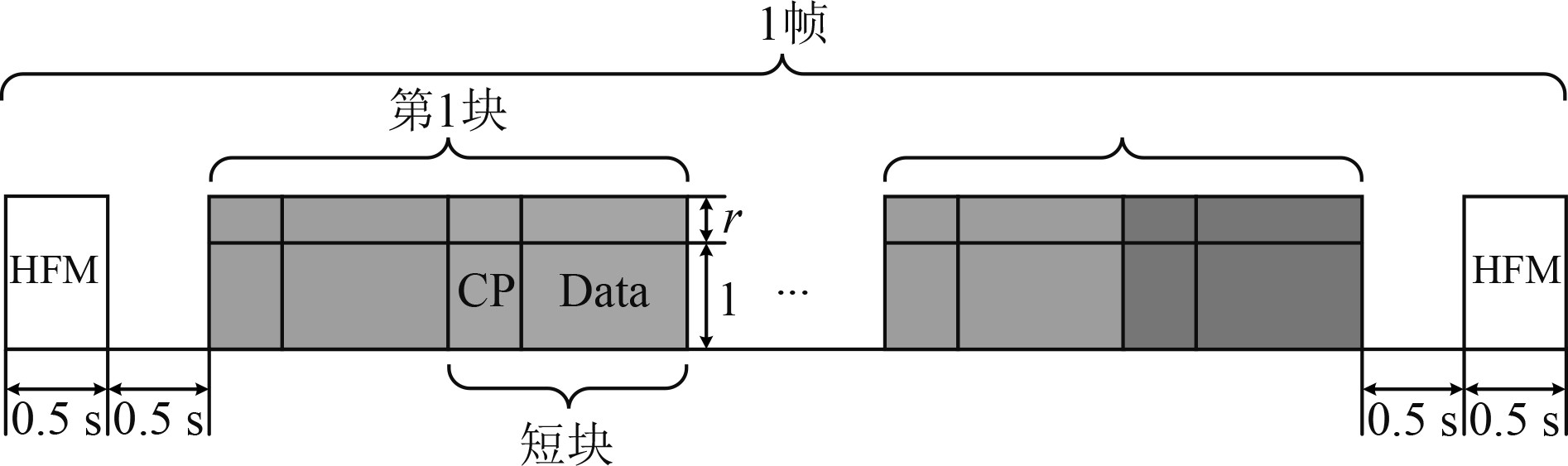
|
图 1 传输信号结构 Fig. 1 Structure of the transmitted signal |
BCE算法实现原理如图2所示,将1个数据块分成

|
图 2
第 |
定义信息比特
| $ {\boldsymbol{s}} = {\boldsymbol{q}} + r{\boldsymbol{t}}。$ | (1) |
将
| $ \begin{split} {{\boldsymbol{y}}_{{n_s}}} = {{\boldsymbol{H}}_{{n_s}}}\left( {{{\boldsymbol{t}}_l} + {{\boldsymbol{s}}_{{n_s}}}} \right) + {{\boldsymbol{w}}_{{n_s}}} = {\text{ }} {{\boldsymbol{H}}_{{n_s}}}{{\boldsymbol{s}}_{{n_s}}} + {{\boldsymbol{H}}_{{n_s}}}{{\boldsymbol{t}}_l} + {{\boldsymbol{w}}_{{n_s}}} 。\end{split} $ | (2) |
若短块长度
定义
| $ {\boldsymbol{A}} = {\left[ \begin{gathered} {\text{ }}{t_0}{\text{ }}{t_{T - 1}}{\text{ }} \ldots {\text{ }}{t_{T - {L_{ch}} + 1}} \\ {\text{ }}{t_1}{\text{ }}{t_0}{\text{ }} \ldots {\text{ }}{t_{T - {L_{ch}} + 2}} \\ {\text{ }} \vdots {\text{ }} \vdots {\text{ }} \cdots {\text{ }} \vdots \\ {t_{T - 1}}{\text{ }}{t_{T - 2}}{\text{ }} \ldots {\text{ }}{t_{T - {L_{ch}}}} \\ \end{gathered} \right]_{T \times {L_{ch}}}}。$ | (3) |
基于最小二乘(Least Square, LS)法,第一个短块的信道估计可表示为:
| $ {\hat {\boldsymbol{h}}_1} = {\left[ {{{\left( {{{\boldsymbol{A}}^{\mathrm{H}}}{\boldsymbol{A}}} \right)}^{ - 1}}{{\boldsymbol{A}}^{\mathrm{H}}}\left( {\frac{1}{p}\sum\limits_{i = 1}^p {{\boldsymbol{y}}_{iT}^{\mathrm{T}}} } \right)} \right]_{{L_{ch}} \times 1}}。$ | (4) |
向
| $ {\hat {\boldsymbol{h}}_{\text{1}}} = {\left[ {{{\hat {\boldsymbol{h}}}_{\text{1}}},{\mathbf{0}}} \right]_{{N_f} \times 1}}。$ | (5) |
则整个发射信号对应的水声信道估计可表示为
基于ST方案的信道估计算法是利用一个短块进行分析,属于局部信道估计算法。考虑到相邻短块之间的信道相关性,局部信道估计无法获取准确的信道信息,因此可以充分利用信道的相关性对当前短块进行估计,以获取每个短块的全局信道估计,进而实现对每个短块信道的精准估计。
定义高斯分布
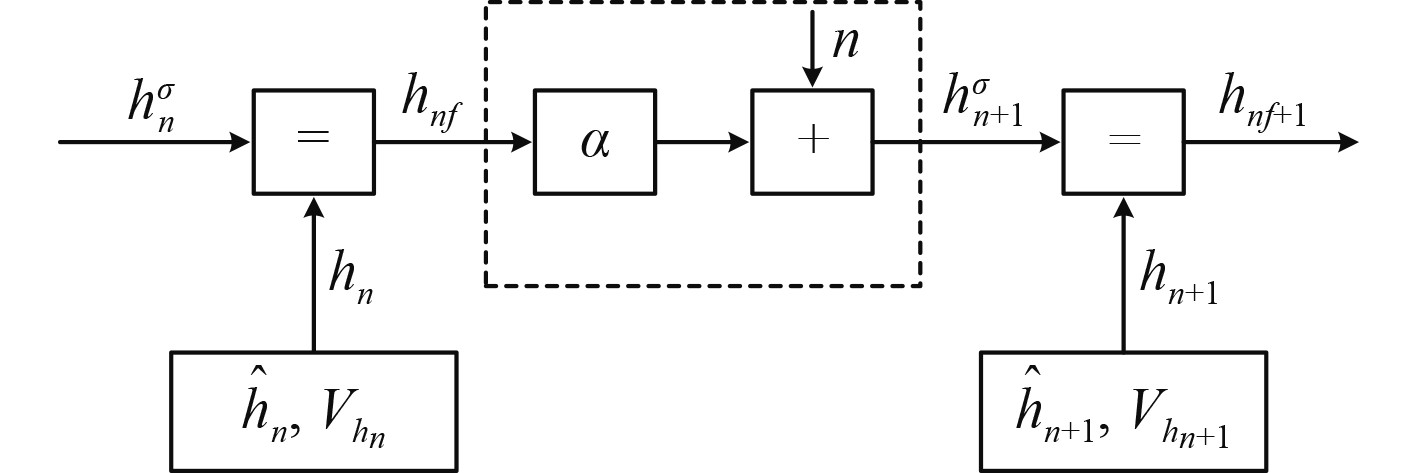
|
图 3 前向递归因子图 Fig. 3 Factor graph representation for the forward recursion |
将上一个短块的信息
| $ \left\{ \begin{aligned} & {\boldsymbol{V}}_{{h_{nf}}}^{{{ - 1}}}{\text{ = }}{\boldsymbol{V}}_{{h_n}}^{{{ - 1}}}{\text{ + }}{\boldsymbol{V}}_{h_n^\sigma }^{{{ - 1}}},\\ & {{\hat {\boldsymbol{h}}}_{nf}}{\text{ = }}{{\boldsymbol{V}}_{{h_{nf}}}}\left( {{\boldsymbol{V}}_{{h_n}}^{{{ - 1}}}{{\hat {\boldsymbol{h}}}_n} + {\boldsymbol{V}}_{h_n^\sigma }^{{{ - 1}}}\hat h_n^\sigma } \right) 。\end{aligned} \right. $ | (6) |
相邻短块之间的信道关系可表示为[13]:
| $ \hat {\boldsymbol{h}}_{n + 1}^\sigma {\text{ = }}\alpha {\hat {\boldsymbol{h}}_{nf}}{\text{ + }}{\boldsymbol{n}}。$ | (7) |
式中:
| $ \left\{ \begin{gathered} \hat h_{n + 1}^\sigma {\text{ = }}\alpha {{\hat h}_{nf}},\\ {V_{h_{n + 1}^\sigma }}{\text{ = }}{\alpha ^2}{V_{{h_{nf}}}} + \beta I 。\end{gathered} \right. $ | (8) |
反向递归的因子图如图4所示,定义

|
图 4 反向递归的因子图 Fig. 4 Factor graph representation for the backward recursion |
反向递归的消息融合可表示为:
| $ \left\{ \begin{gathered} {\boldsymbol{V}}_{{h_{NF{\text{ + 1}}}}}^{{{ - 1}}}{\text{ = }}{\boldsymbol{V}}_{{h_{n{\text{ + 1}}}}}^{{{ - 1}}}{\text{ + }}{\boldsymbol{V}}_{h_{n + 1}^\sigma }^{{{ - 1}}},\\ {{\hat {\boldsymbol{h}}}_{NF + 1}}{\text{ = }}{{\boldsymbol{V}}_{{h_{NF + 1}}}}\left( {{\boldsymbol{V}}_{{h_{n + 1}}}^{{{ - 1}}}{{\hat h}_{n + 1}} + {\boldsymbol{V}}_{h_{n + 1}^\sigma }^{{{ - 1}}}\hat {\boldsymbol{h}}_{n + 1}^\sigma } \right) 。\end{gathered} \right. $ | (9) |
根据相邻信道短块的关系,信道估计的反向递归消息更新可表示为:
| $ \left\{ \begin{gathered} \hat {\boldsymbol{h}}_n^\sigma = {\alpha ^{ - 1}}{{\hat {\boldsymbol{h}}}_{NF + 1}},\\ {{\boldsymbol{V}}_{h_n^\sigma }} = {\alpha ^{ - 2}}\left( {{{\boldsymbol{V}}_{{h_{NF + 1}}}} + \beta I} \right)。\end{gathered} \right. $ | (10) |
将得到的信息进行融合,当前短块双向信息融合的因子如图5所示,可得到当前短块的最终(全局)信道估计,即:
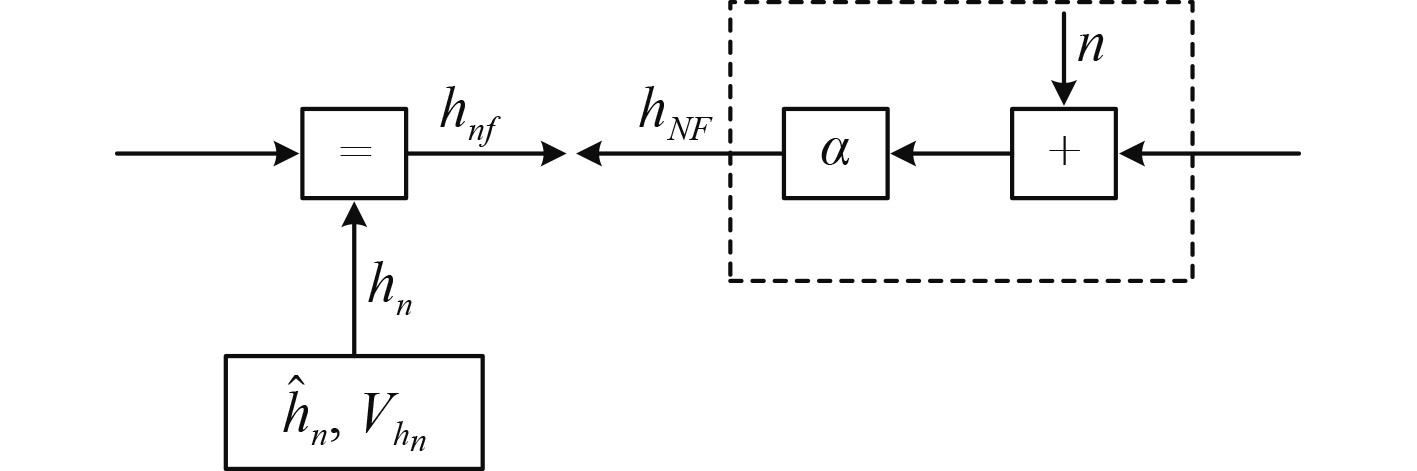
|
图 5 双向消息融合的因子图 Fig. 5 Factor graph representation for bidirectional message fusion |
| $ \left\{ \begin{aligned} & {\boldsymbol{V}}_{{h_{nF}}}^{{{ - 1}}}{\text{ = }}{\boldsymbol{V}}_{{h_{nf}}}^{{{ - 1}}}{\text{ + }}{\boldsymbol{V}}_{{h_{NF}}}^{{{ - 1}}}, \\ & {{\hat {\boldsymbol{h}}}_{nF}}{\text{ = }}{{\boldsymbol{V}}_{{h_{nF}}}}\left( {{\boldsymbol{V}}_{{h_{nf}}}^{{{ - 1}}}{{\hat {\boldsymbol{h}}}_{nf}} + {\boldsymbol{V}}_{{h_{NF}}}^{{{ - 1}}}{{\hat {\boldsymbol{h}}}_{NF}}} \right)。\end{aligned} \right. $ | (11) |
同理,可得到所有短块的全局信道估计,即
定义
| $ {{\boldsymbol{H}}_{{n_s}}} = {{\boldsymbol{F}}^{\mathrm{H}}}{{\boldsymbol{D}}_{{n_s}}}{\boldsymbol{F}}。$ | (12) |
式中:
在频域进行训练序列干扰消除,定义
| $ \begin{split} {{\boldsymbol{z}}_{{n_s}}} =\,& {\boldsymbol{F}}{{\boldsymbol{y}}_{{n_s}}} - {\boldsymbol{F}}{{\hat {\boldsymbol{h}}}_{{n_s}F}}.*{\boldsymbol{F}}{{\boldsymbol{t}}_l}= \\ {\text{ }} \,& {\boldsymbol{F}}{{\boldsymbol{F}}^{\mathrm{H}}}{{\boldsymbol{D}}_{{n_s}}}{\boldsymbol{F}}\left( {{{\boldsymbol{t}}_l} + {{\mathbf{s}}_{{n_s}}}} \right) + {\boldsymbol{F}}{{\boldsymbol{w}}_{{n_s}}} - {\boldsymbol{F}}{{\hat {\boldsymbol{h}}}_{{n_s}{\boldsymbol{F}}}}.*{\boldsymbol{F}}{{\boldsymbol{t}}_l}= \\ {\text{ }} \,& {{\boldsymbol{D}}_{{n_s}}}{\boldsymbol{F}}{{\mathbf{s}}_{{n_s}}} + {{\boldsymbol{D}}_{{n_s}}}{\boldsymbol{F}}{{\boldsymbol{t}}_l} + {\boldsymbol{F}}{{\boldsymbol{w}}_{{n_s}}} - {\boldsymbol{F}}{{\hat {\boldsymbol{h}}}_{{n_s}{\boldsymbol{F}}}}.*{\boldsymbol{F}}{{\boldsymbol{t}}_l}= \\ {\text{ }} \,& {{\boldsymbol{D}}_{{n_s}}}{\boldsymbol{F}}{{\boldsymbol{s}}_{{n_s}}} + \left[ {{{\boldsymbol{D}}_{{n_s}}}\left( {{\boldsymbol{F}}{{\boldsymbol{t}}_l}} \right) - {\boldsymbol{F}}{{\hat {\boldsymbol{h}}}_{{n_s}{\boldsymbol{F}}}}.*{\boldsymbol{F}}{{\boldsymbol{t}}_l} + {\boldsymbol{F}}{{\boldsymbol{w}}_{{n_s}}}} \right]= \\ {\text{ }} \,& {{\boldsymbol{D}}_{{n_s}}}{\boldsymbol{F}}{{\boldsymbol{s}}_{{n_s}}}{\text{ + }}{{w'}_{{n_s}}},\end{split} $ | (13) |
且
| $ \left\{ \begin{aligned} & {{\boldsymbol{D}}_{{n_s}}} = {\boldsymbol{F}}{{\boldsymbol{H}}_{{n_s}}}{{\boldsymbol{F}}^{\mathrm{H}}} = Diag\left\{ {d_{{n_s}}^1,d_{{n_s}}^2, \cdots ,d_{{n_s}}^{{N_f}}} \right\},\\ & \left[ {d_{{n_s}}^1,d_{{n_s}}^2, \cdots ,d_{{n_s}}^{{N_f}}} \right] = \sqrt {{N_f}} {\boldsymbol{F}}{{\boldsymbol{h}}_{{n_s}}} 。\end{aligned} \right. $ | (14) |
所有短块进行训练消除干扰,可得到
当发射符号的功率为1时,每个短块的噪声功率为接收信号的功率与对应信道能量的差值,即:
| $ \hat \sigma _{{n_s}}^2{\text{ = }}{P_{{y_{{n_s}}}}}{\text{ - }}{\left\| {{{\hat h}_{{n_s}F}}} \right\|^2}。$ | (15) |
因此,可得到
根据文献[11-13]计算符号的先验、后验、外均值和方差,分别用
| $ \left\{ \begin{array}{l} m_l^a = \dfrac{1}{{\sqrt 2 }}\tanh \left( {\dfrac{{{L^a}(c_l^1)}}{{\text{2}}}} \right){\text{ + }}j\dfrac{1}{{\sqrt 2 }}\tan h \left( {\dfrac{{{L^a}(c_l^2)}}{{\text{2}}}} \right),\\ \nu _l^a = 1 - {\left| {m_l^a} \right|^2} 。\end{array} \right. $ | (16) |
将
| $ \left\{ \begin{gathered} \nu _1^p = \nu _2^p = \cdots = \nu _{{N_s}}^p = \frac{1}{{{N_s}}}\sum\limits_{k = 1}^{{N_s}} {{{\left( {\frac{1}{{\bar v}} + \frac{{{{\left| {\hat d_{{n_s}}^k} \right|}^2}}}{{\sigma _{{n_s}}^{\text{2}}}}} \right)}^{ - 1}}} ,\\ {{\boldsymbol{m}}^p}{\text{ = }}{{\boldsymbol{m}}^a} + {{\boldsymbol{F}}^{\mathrm{H}}}\hat {\boldsymbol{D}}_{{n_s}}^{\mathrm{H}}{\left( {\frac{{\sigma _{{n_s}}^{\text{2}}}}{{\bar v}}{\boldsymbol{I}} + {{\hat {\boldsymbol{D}}}_{{n_s}}}\hat {\boldsymbol{D}}_{{n_s}}^{\mathrm{H}}} \right)^{ - 1}} \left( {{{\boldsymbol{z}}_{{n_s}}} - {{\hat {\boldsymbol{D}}}_{{n_s}}}F{m^a}} \right) 。\end{gathered} \right. $ | (17) |
其中,
| $ \left\{ \begin{gathered} \nu _l^e = {\left( {\frac{{\text{1}}}{{\nu _l^p}} - \frac{{\text{1}}}{{\nu _l^a}}} \right)^{ - 1}},\\ m_l^e = \nu _l^e\left( {\frac{{m_l^p}}{{\nu _l^p}} - \frac{{m_l^a}}{{\nu _l^a}}} \right) 。\end{gathered} \right. $ | (18) |
采用QPSK映射,交织编码比特
| $ \left\{ \begin{gathered} L_{}^e\left( {c_l^1} \right) = 2\sqrt 2 {\text{Re}}\left[ {m_l^e/v_l^e} \right],\\ L_{}^e\left( {c_l^2} \right) = 2\sqrt 2 {\text{Im}}\left[ {m_l^e/v_l^e} \right] 。\end{gathered} \right. $ | (19) |
其中,得到的估计符号序列
信道均衡的计算复杂度可由式(17)计算得到,其中
基于VT的时变水声信道精准估计迭代过程如图6所示。将先验对数似然比
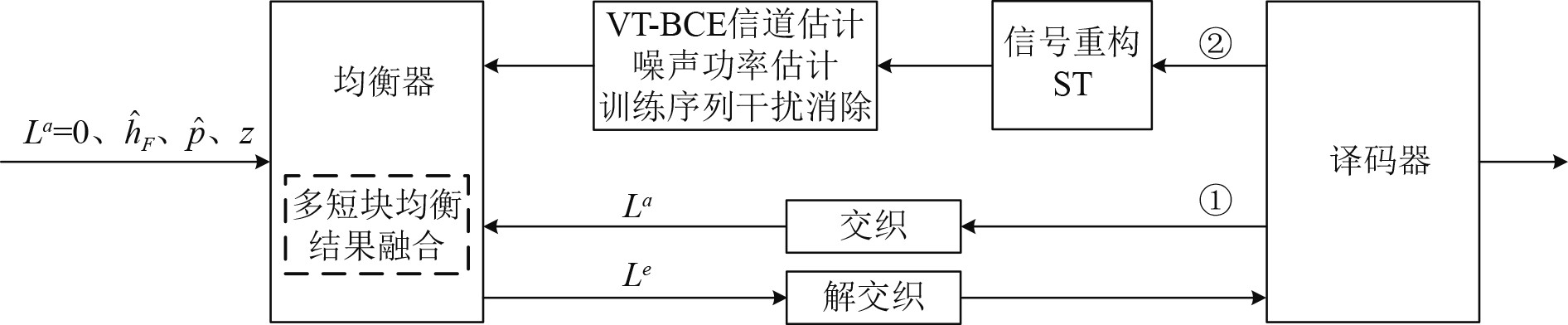
|
图 6 迭代过程 Fig. 6 Iterative process |
仿真采用1/2码率的非系统
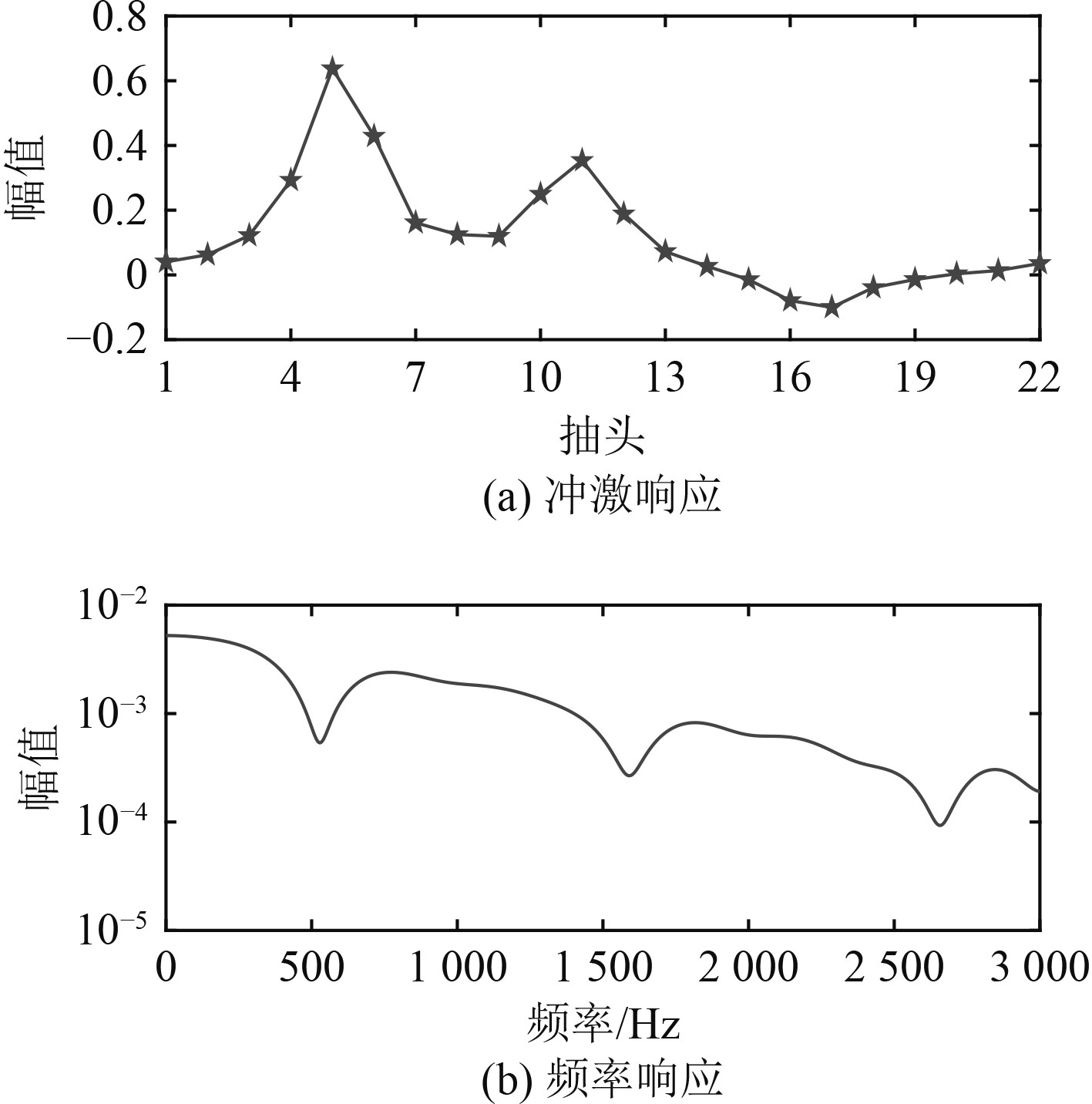
|
图 7 静态信道 Fig. 7 Static channel |
发射100块信息比特,利用图7所示的信道进行信息传输。以S256为例,分析了不同信噪比下迭代次数与均方误差(Mean Square Error, MSE)的关系,结果如表1所示。可看出,随着迭代次数的增加,均方误差随之变小;随着信噪比的不断增大,均方误差不断减小。当信噪比为11 dB时,经过2次迭代后,均方误差为0,系统性能较好。
|
|
表 1 不同信噪比下系统均方误差的比较 Tab.1 The comparison of the MSE of the system with different signal-to-noise ratios |
此外,从误码率(BER)的角度分析VT-BCE算法对系统性能的影响。当信噪比为11 dB时,误码性能如表2所示。可看出,未使用VT-BCE算法进行信道估计时,随着短块长度的增加,系统的误码率随之减小。当采用VT-BCE算法进行信道精准估计时,短块的长度对系统误码率的影响不大,其性能更好。仅经过3次迭代后,信息比特全部正确解码;其中S256经过2次迭代就能获得较好的系统性能。通过对比分析,VT-BCE算法利用虚拟训练序列(估计的符号序列)可以准确获得信道信息,提升信道估计性能,验证了该算法的有效性。
|
|
表 2 当信噪比为11 dB时VT-BCE算法的误码率 Tab.2 The BER of VT-BCE algorithm when signal-to-noise ratios is 11 dB |
采用QPSK映射、1/2码率的
移动通信水池试验部署如图8所示。收发节点水平距离约为9 m,部署深度随机,水听器静态,换能器以水平速度0.5~1 m/s、垂直速度0.2~0.6 m/s移动。
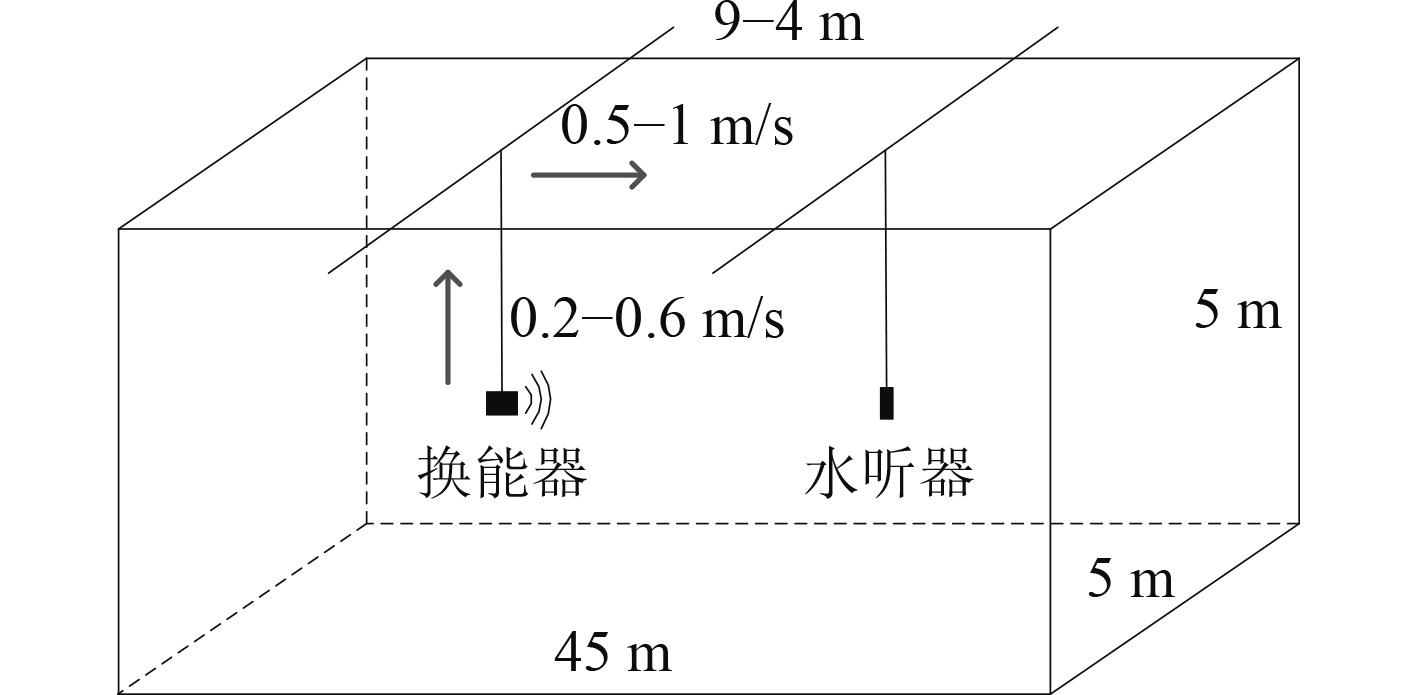
|
图 8 水池试验部署 Fig. 8 Experimental layout in a pool |
试验过程中,对基准turbo系统与VT-BCE turbo系统进行比较,以此验证VT-BCE算法能够实现精准信道估计。当换能器垂直运动时,以第1帧数据为例,分别用#1、#3、#5和#7表示基准turbo系统的第1块、第3块、第5块和第7块,其误码率如图9所示。可以看出,第1帧中第3块和第5块的译码效果不佳,信息未能全部正确解码,这是因为假设一个块的静态信道无效,导致了显著的信道估计误差。定义

|
图 9 水池试验仪器 Fig. 9 Experimental instruments in a pool |
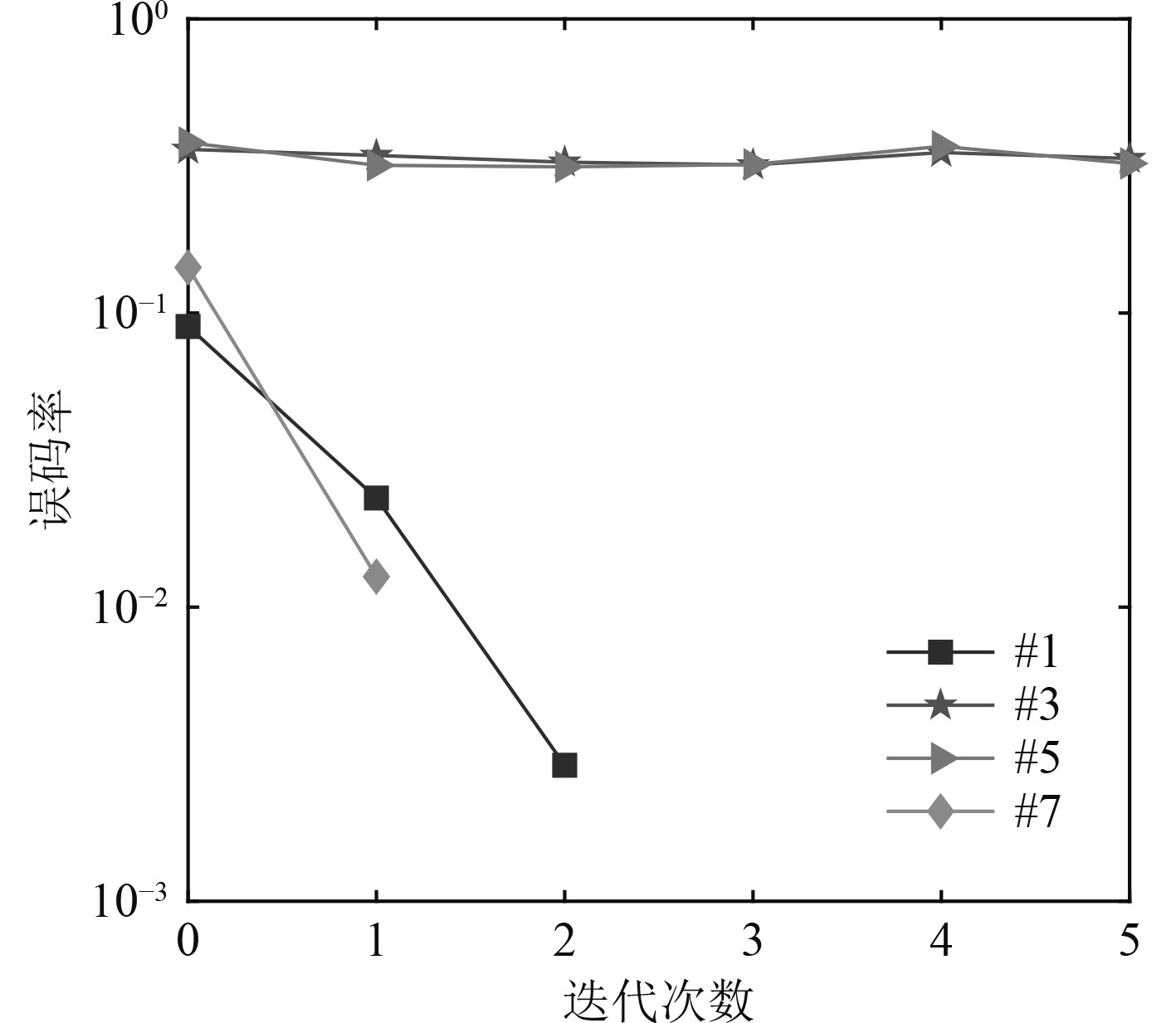
|
图 10 基准turbo系统的误码率 Fig. 10 The BER performance of the baseline turbo system |
当换能器水平运动时,2种不同系统的误码率性能如图11所示。分别用#1、#7和#9表示第1块、第7块和第9块数据。可以看出,在VT-BCE系统中,仅经过1次迭代,误码率最小。因此VT-BCE系统的性能优于基准turbo系统,验证了VT-BCE算法的有效性。

|
图 11 VT-BCE系统的误码率 Fig. 11 The BER performance of the VT-BCE system |

|
图 12 不同系统下误码性能比较的对比 Fig. 12 The comparison of BER performance under different systems |
本文提出了VT-BCE算法,实现了双向水声信道的精准估计。采用ST方案,将训练序列和符号序列线性叠加,使得训练序列持续传输,提升了信道的跟踪能力。基于置信传播,提出了BCE算法,将一个数据块分成多个短块,充分利用相邻短块间的信道相关性,以此得到全局信道估计,从而实现了每个短块的精准信道估计。将信道估计、信道均衡(频域)和译码以迭代的方式相结合,使估计的符号序列作为虚拟训练序列,提升了每个短块的信道估计性能,进而提高了系统的性能增益。最后,仿真和水池试验验证了所提算法的有效性。
| [1] |
BERGER C R, ZHOU S, PREISIG J C, et al. Sparse channel estimation for multicarrier underwater acoustic communication: From subspace methods to compressed sensing[J]. IEEE Transactions on Signal Processing, 2010, 58(3): 1708-1721. DOI:10.1109/TSP.2009.2038424 |
| [2] |
梁仕杰, 王彪, 张岑. 基于gOMP算法的FBMC水声通信信道估计方法[J]. 声学技术, 2021, 40(3): 329-335. |
| [3] |
SONG A, MILIOA S, MANDAR C. Editorial underwater acoustic communications: where we stand and what is next?[J]. IEEE Journal of Oceanic Engineering, 2019, 44(1): 1-6. DOI:10.1109/JOE.2018.2883872 |
| [4] |
邵宗战. 现代水声通信技术发展探讨[J]. 科技创新与应用, 2022, 12(20): 152-155. |
| [5] |
杨斌斌, 鄢社锋, 章绍晨, 等. 基于Kalman滤波的水声混合双向迭代信道均衡算法[J]. 电子与信息学报, 2022, 44(6): 1879-1886. |
| [6] |
YANG Z, ZHENG Y R. Iterative channel estimation and turbo equalization for multiple-input multiple-output underwater acoustic communications[J]. IEEE Journal of Oceanic Engineering, 2016, 41(1): 232-242. DOI:10.1109/JOE.2015.2398731 |
| [7] |
LI W, PREISIG J C. Estimation of rapidly time-varying sparse channels[J]. IEEE Journal of Oceanic Engineering, 2007, 32(4): 927-939. DOI:10.1109/JOE.2007.906409 |
| [8] |
Y CHO, H KO. Channel estimation based on adaptive denoising for underwater acoustic OFDM systems[J]. IEEE Access, 2020, 8: 157197-157210. DOI:10.1109/ACCESS.2020.3018474 |
| [9] |
伍飞云, 周跃海, 童峰, 等. 稀疏长时延水声信道的压缩感知估计[J]. 东南大学学报(英文版), 2014(3): 271-277. |
| [10] |
JIANG W H, TONG F, ZHU Z L. Exploiting rapidly time-varying sparsity for underwater acoustic communication[J]. IEEE Transactions on Vehicular Technology, 2022, 71(9): 9721-9734. |
| [11] |
GUO Q H, HUANG D F, NORDHOLM S, et al. Iterative frequency domain equalization with generalized approximate message passing[J]. IEEE Signal Processing Letters, 2013, 20(6): 559-562. DOI:10.1109/LSP.2013.2256783 |
| [12] |
GUO Q H, HUANG D F. A concise representation for the soft-in soft-out LMMSE detector[J]. IEEE Communications Letters, 2011, 15(5): 566-568. DOI:10.1109/LCOMM.2011.032811.102073 |
| [13] |
GUO Q H, PING L, HUANG D F. A low-complexity iterative channel estimation and detection technique for doubly selective channels[J]. IEEE Transactions on Wireless Communications, 2009, 8(8): 4340-4349. DOI:10.1109/TWC.2009.081448 |
| [14] |
GUO Q H, HUANG D F. EM-based joint channel estimation and detection for frequency selective channels using gaussian message passing[J]. IEEE Transactions on Signal Processing, 2011, 59(8): 4030-4035. DOI:10.1109/TSP.2011.2153201 |
| [15] |
YANG G, LIU T L, DING H X, et al. Joint channel estimation and generalized approximate messaging passing-based equalization for underwater acoustic communications[J]. IEEE Access, 2021, 9: 56757-56764. DOI:10.1109/ACCESS.2021.3065430 |
| [16] |
YANG G, WANG L, QIAO P Y, et al. Joint multiple turbo equalization for harsh time-varying underwater acoustic channels[J]. IEEE Access, 2021, 9: 82364-82372. DOI:10.1109/ACCESS.2021.3087260 |
| [17] |
YANG G, GUO Q H, DING H X, et al. Joint message-passing-based bidirectional channel estimation and equalization with superimposed training for underwater acoustic communications[J]. IEEE Journal of Oceanic Engineering, 2021, 46(4): 1463-1476. DOI:10.1109/JOE.2021.3057916 |
| [18] |
杨光, 丁寒雪, 郭庆华, 等. 基于叠加训练序列和低复杂度频域 Turbo 均衡的时变水声信道估计和均衡[J]. 电子与信息学报, 2021, 43(3): 850-856. |
| [19] |
LOELIGER HA, DAUWELS J, HU J L, et al. The factor graph approach to model-based signal processing[J]. Proceedings of the IEEE, 2007, 95(6): 1295-1322. DOI:10.1109/JPROC.2007.896497 |
 2024, Vol. 46
2024, Vol. 46
