聚焦“双碳”目标的深入推进[1],国务院印发《2030年前碳达峰行动方案》,明确要求航运业应推动运输工具装备低碳转型,到2030年为止当中新增清洁能源动力交通工具比例达到40%。在此背景下,纯电动船舶的研究成为我国内河航运业实现“双碳”战略的重要途径[2]。纯电动船舶电力系统的负荷情况直接影响到整个船舶的运行状态,准确的负荷预测不仅使得船舶的电力系统稳定运行,而且可通过负荷预测情况对不同工况下的发电量进行合理调控,从而有利于电力系统对大规模电动船舶充电的合理调度[3]。因此,对纯电动船舶进行精准的负荷预测十分必要。
对于船舶的负荷预测,早期采用趋势分析法、回归分析法和时间序列分析法等传统的统计学模型方法[4]。近年来,随着人工智能的飞速发展,使用机器学习进行船舶负荷预测取得了很好的效果[5]。侯文君等[6 − 7]利用支持向量机算法,将复杂的船舶负荷值非线性映射回归问题转化为简单线性回归问题,实现对船舶电力系统负荷的预测。刘银波等[8]利用径向基函数神经网络(Radial Basis Function Neural Network,RBF神经网络)算法,由RBF神经元构成的隐藏层对负荷值进行空间变换,将低维非线性不可分数据变换为高维线性可分数据,从而进行船舶负荷预测。阳曾等[9]分别利用反向传播(Back Propagation,BP)、RBF和Elman这3种不同的神经网络模型对纯电动船舶实现负荷预测。上述文献均只利用单一方法进行船舶负荷预测,虽预测精确度较高,但泛化性弱、容错率低,特别是涉及到船舶运行样本数据不够或某些样本数据缺失的情况时,单一方法负荷预测显然具有一定局限性[10]。
纯电动船舶综合电力系统作为一个相对独立系统,其负荷特性与岸电电力系统相比具有明显差异[11]。一是负荷波动大,船舶水上作业的特殊环境和船舶运行时的多种工况导致船舶的负荷波动很大;二是负荷具有连续性,船舶上的往往具备有不间断的电力负荷例如通信负荷、日常生活必需的负荷等[12]。因此,对于此类无规律且变动大的负荷数据而言非常适合使用神经网络算法来预测,但分别使用上述单一网络进负荷预测时会有因为自身网络结构而导致的局限性[13],不可避免的出现个别预测点结果偏差过大的情况,这使得整个预测模型的容错率低,预测效果较差,所以需要泛化能力强,能够进一步提高预测精度的组合预测方法。
针对以上问题,本文提出一种基于BP和RBF神经网络模型[14]的组合预测船舶综合电力系统负荷方法。选用载重量、水流速度、吃水深度和船舶电力负荷四维输入变量,经过数据完善、数据限值[15]和归一化[16]等处理后输入至BP和RBF神经网络预测模型中分别获取预测结果。将2种模型的预测结果进行加权求和,加权系数通过方差倒数法[17]和等比例法确定,加权求和结果反归一化后即为船舶负荷的最终预测值。此方法同时具有BP和RBF神经网络模型的优越性[18],不仅具有更高的预测精度,而且极大地提高了预测模型的泛化能力。
1 复杂工况下纯电动船舶综合电力系统的负荷特性分析以江苏某纯电动船舶为例,其综合电力系统示意图如图1所示。由磷酸铁锂蓄电池组和超级电容蓄电池组向全船供电,直流母线提供614 V直流电压,其上搭载全船的动力系统,包括调速器、推进电机和螺旋桨负载,此外由直流电压逆变至三相380 V交流电压,三相交流负载包括水泵、通风机等各类电机,单相交流负载包括照明负载、生活负载和通信负载。

|
图 1 纯电动船舶综合电力系统示意图 Fig. 1 Schematic diagram of electric power system for pure electric ships |
根据纯电动船舶的不同用途,其电力系统的负荷特性也会有较大差别。由于本文研究对象为民用船舶,不涉及起货机、绞盘机等大型电机设备,故船舶电力系统的主要负荷为动力推进系统。因此,纯电动船舶电力系统的负荷特性主要由动力推进系统决定,特别是推进电机和螺旋桨负载。按照船舶用电设备的使用时间可将船舶综合电力系统负荷分为三类:第一类为不间断工作的恒定负荷,如照明负荷、通信和通风设备等生活所必需的负荷;第二类为短时或短时重复使用的负荷,如推进电机;第三类为偶然极短时使用的负荷,如搜救灯等,船舶综合电力系统负荷表达式如下:
| $ {P}_{\text{ship}}=\underset{一类负荷}{\underbrace{{{k}}_{1}{\displaystyle \sum _{{i=}1}^{{n}}{P}_{1}}}}+\underset{二类负荷}{\underbrace{{{k}}_{2}{\displaystyle \sum _{{i=}1}^{{m}}{P}_{2}+{P}_{{m}}+P\left(\alpha \right)}}}+\underset{三类负荷}{\underbrace{{\displaystyle \sum _{{i=}1}^{{k}}{P}_{3}}}}。$ | (1) |
其中:
由上述公式可知,由于一类负荷为恒定输出的负荷,所以船舶综合电力系统负荷具有连续性性的特征。而在不同工况下运行时,二类负荷一直处于变化状态如表1所示,由于恶劣环境下航行时,螺旋桨的阻力会在大范围下时刻变化,甚至会出现脱落、出水等情形,这都会极大影响推进系统的负荷进而使得船舶综合电力负荷具有随机性的特征。
|
|
表 1 不同运行工况下动力推进系统的负荷特性 Tab.1 Load characteristics of power propulsion systems under different operating conditions |
考虑复杂工况下的纯电动船舶综合电力系统负荷具有随机性和连续性的特点可选择BP和RBF这2种神经网络进行负荷预测。此2种神经网络的结构相对简单且收敛速度很快,理论上可逼近任意的非线性函数[19],有效避免由于船舶负荷数据差异过大而导致的网络不收敛问题,RBF神经网络同时具有全局逼近能力,在预测过程中可以避免可能出现的陷入局部最优解情况[20]。
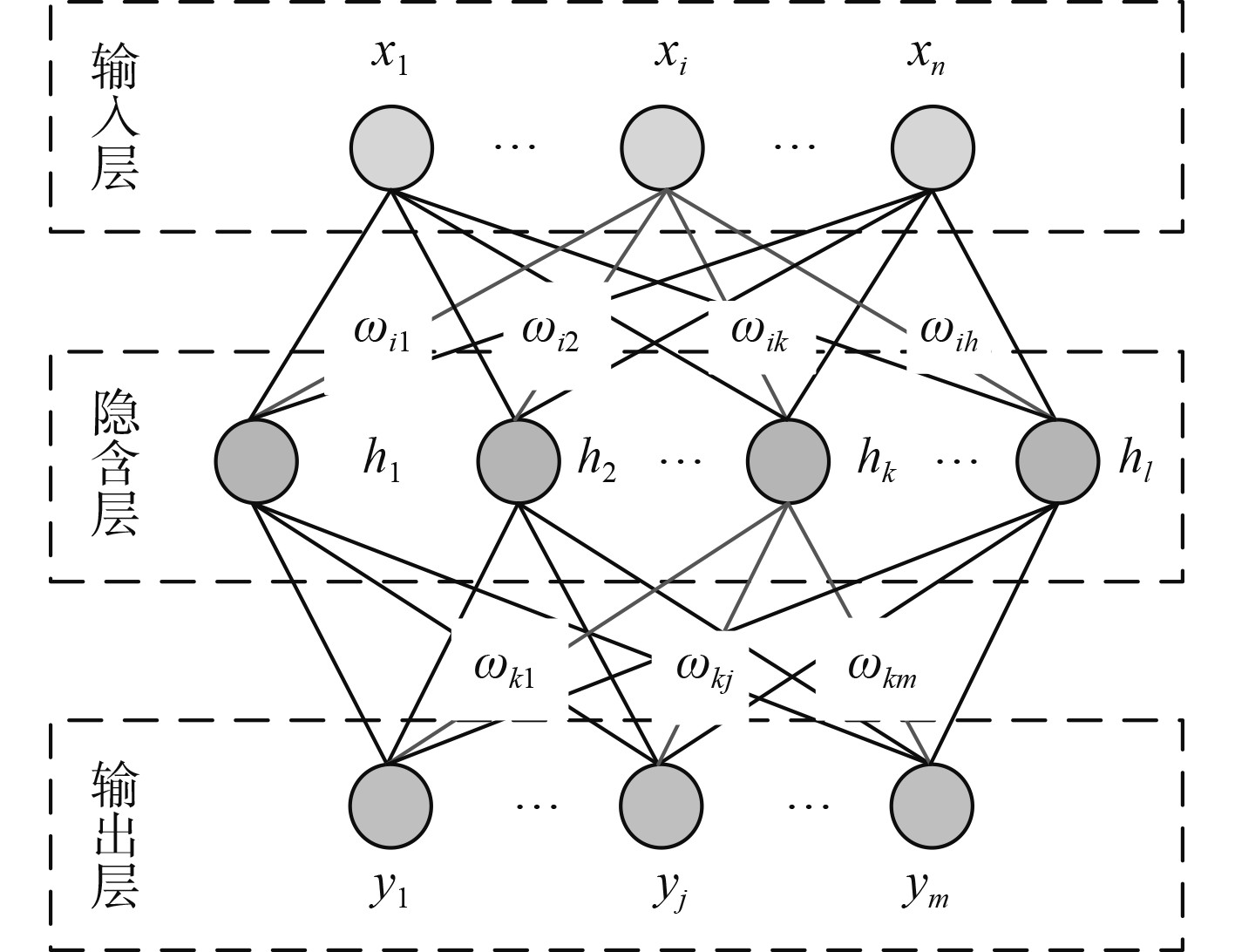
2 基于典型神经网络的船舶综合电力系统负荷预测及局限性 2.1 基于典型神经网络的负荷预测BP神经网络是一种多层的前向神经网络,通常为3层结构,其网络参数学习更新公式,如图2所示。
|
图 2 3层BP神经网络 Fig. 2 Three layer BP neural network |
假定隐含层与输出层的激活函数均为sigmoid函数即:
| $ {{f}}\left( {{x}} \right){{ = {\mathrm{sigmoid}}}}\left( {{x}} \right){{ = }}\frac{1}{{1{{ + }}{{{{{e}}}}^{{{ - x}}}}}}。$ | (2) |
计算第
| $ \left\{ \begin{gathered} {\alpha _{{k}}}{{ = }}\sum\limits_{{{k = }}1}^{\rm{l}} {{\omega _{{{ik}}}}{{{x}}_{i}}},\\ {\beta _{{j}}}{{ = }}\sum\limits_{{{j = }}1}^{{m}} {{\omega _{{{kj}}}}{{{h}}_{{k}}}}。\\ \end{gathered} \right. $ | (3) |
对输入的训练样本
| $ {E_k} = \frac{1}{2}\sum\limits_{j = 1}^m {{{\left( {{{y}}_{{j}}^{{{{\mathrm{st}}}}} - y_j^{\mathrm{s}}} \right)}^2}}。$ | (4) |
由于在BP神经网络误差的反向传播中,误差基于梯度下降策略向负梯度方向进行参数修正,以权值参数
| $ \Delta {\omega _{{{kj}}}} = - \eta \frac{{\partial {E_k}}}{{\partial {\omega _{{{kj}}}}}}{{ = }} - \eta \frac{{\partial {E_k}}}{{\partial {{y}}_{{j}}^{{{{\mathrm{st}}}}}}}\frac{{\partial {{y}}_{{j}}^{{{{\mathrm{st}}}}}}}{{\partial {\beta _j}}}\frac{{\partial {\beta _j}}}{{\partial {\omega _{{{kj}}}}}}。$ | (5) |
定义
| $ \begin{split} {{{g}}_{{j}}}{{ = }}\,&- \frac{{\partial {E_k}}}{{\partial {{y}}_{{j}}^{{{st}}}}}\frac{{\partial {{y}}_{{j}}^{{{st}}}}}{{\partial {\beta _j}}} {{ = }} - \left( {{{y}}_{{j}}^{{{st}}} - y_j^s} \right){{{f}}^{'}}\left( {{\beta _j} - {\theta _j}} \right) = \\ &{{ y}}_{{j}}^{{{st}}}\left( {1 - {{y}}_{{j}}^{{{st}}}} \right)\left( {y_j^s - {{y}}_{{j}}^{{{st}}}} \right)。\end{split} $ | (6) |
由此,得到权值参数
| $ \left\{ \begin{gathered} \Delta {\theta _j} = - \eta {g_j} ,\\ \Delta {\omega _{ik}} = \eta {e_k}{x_i} ,\\ \Delta {\gamma _k} = - \eta {e_k}。\\ \end{gathered} \right. $ | (7) |
式中,定义
对于BP神经网络模型,由于复杂工况下船舶综合电力系统的负荷值随机波动大,所以更容易出现网络陷入局部最小值的问题。设

|
图 3 局部最小值和全局最小值 Fig. 3 Local minimum and global minimum |
虽然目前有许多方法可有效缓解陷入局部最小问题,如增加数据量、优化初始参数等,但都只是尽可能的避免而无法彻底消除局部最小值问题。
对于RBF神经网络模型而言,采用局部激励函数克服了BP神经网络中的陷入局部最小值的问题。但其缺点主要体现在样本数据上,分为:1)RBF网络没有误差反向传播的能力,这就意味着不能对外界的输入数据进行问答,一旦外界输入数据不够充分,其网络训练状态就很糟糕。2)对于复杂工况运行下的纯电动船舶而言,其多种工作环境和状态的特征在RBF网络中均表现为数值,把实际信息变为数值计算,其结果可能会丢失信息。3)RBF神经网络隐含层基函数的中心实际是由输入的样本数据中选取的,大多数情况很难反映出输入输出之间的耦合关系。
3 纯电动船舶综合电力系统负荷的组合预测 3.1 纯电动船舶综合电力系统负荷组合预测数据预处理 3.1.1 历史数据选择与完善选择纯电动船舶电力系统历史负荷数据时,必须考虑样本数据的容量。海量的样本数据显然可增加神经网络的训练效果,进而提高预测精度,但过量的样本数据会导致网络训练过度以至于出现网络过拟合的情况;样本数据太少会出现网络训练未达到期望效果,甚至出现网络预测结果发散的问题。因此,必须根据既定目标合理选择样本数据的容量,本文选择样本数据中训练集和测试集比例为5∶1。
由于船舶工作时的特殊环境限制,不可避免的会出现故障时刻以至于某些时刻的电力系统负荷值丢失记录。对于类似问题,一般采用插值法填补缺失数据,但船舶电力系统负荷值受水流速度等客观因素影响,难以找到多维离散数据对应的连续函数模型,因此插值法不能完全适用。本文采取经验修正法填补缺失的样本数据负荷值,即采用同类型对应相同时刻的正常负荷值的加权平均数代替缺失数据。对应计算公式如下:
| $ {P_{{d}}}{{ = }}\sum\limits_{{{i}} = 1}^{{n}} {{{{k}}_{{i}}}{P_{{i}}}},{{ }}i = 1,2, \cdots \cdots ,n 。$ | (8) |
式中:
纯电动船舶复杂的工况导致其某些时刻的电力系统负荷值出现极值,这些极大值或极小值与正常的样本数据偏差过大,会造成网络训练不收敛的问题,故不能加入样本数据。对此类数据实施横向与纵向的限值处理,同一次航程内连续前后时刻的船舶电力系统负荷值差值不会太大,不同航程内同一航速的船舶电力系统负荷值差值也不会很大。因此,选择合理的负荷阈值,超过阈值的负荷值记为异常数据,对异常数据取边界值加入样本数据,即:
| $ {P_{\min }} \leqslant {P_{{s}}} \leqslant {P_{\max }} 。$ | (9) |
式中:
当所选择的样本数据值满足式(9)时,直接加入样本数据训练网络,而当其样本数据小于
由于神经网络中神经元的饱和特性,对样本数据进行归一化处理,即将数据通过一定计算压缩变换到一定范围内,一般取区间[0,1]。本文采用缩放法归一化样本数据,计算公式如下:
| $ L{\text{ = }}\frac{{{L_o} - {L_{\min }}}}{{{L_{\max }} - {L_{\min }}}}。$ | (10) |
式中:
对载重量、水流速度、吃水深度和船舶电力系统负荷值四维样本数据进行归一化处理作为BP和RBF神经网络的输入变量。对于最终加权求和后的负荷值进行对应的反归一化处理,使其转化为实际负荷预测值,反归一化处理公式如下:
| $ {L_{{\mathrm{real}}}} = \left( {{L_{\max }} - {L_{\min }}} \right){L_\Sigma } + {L_{\min }} 。$ | (11) |
式中:
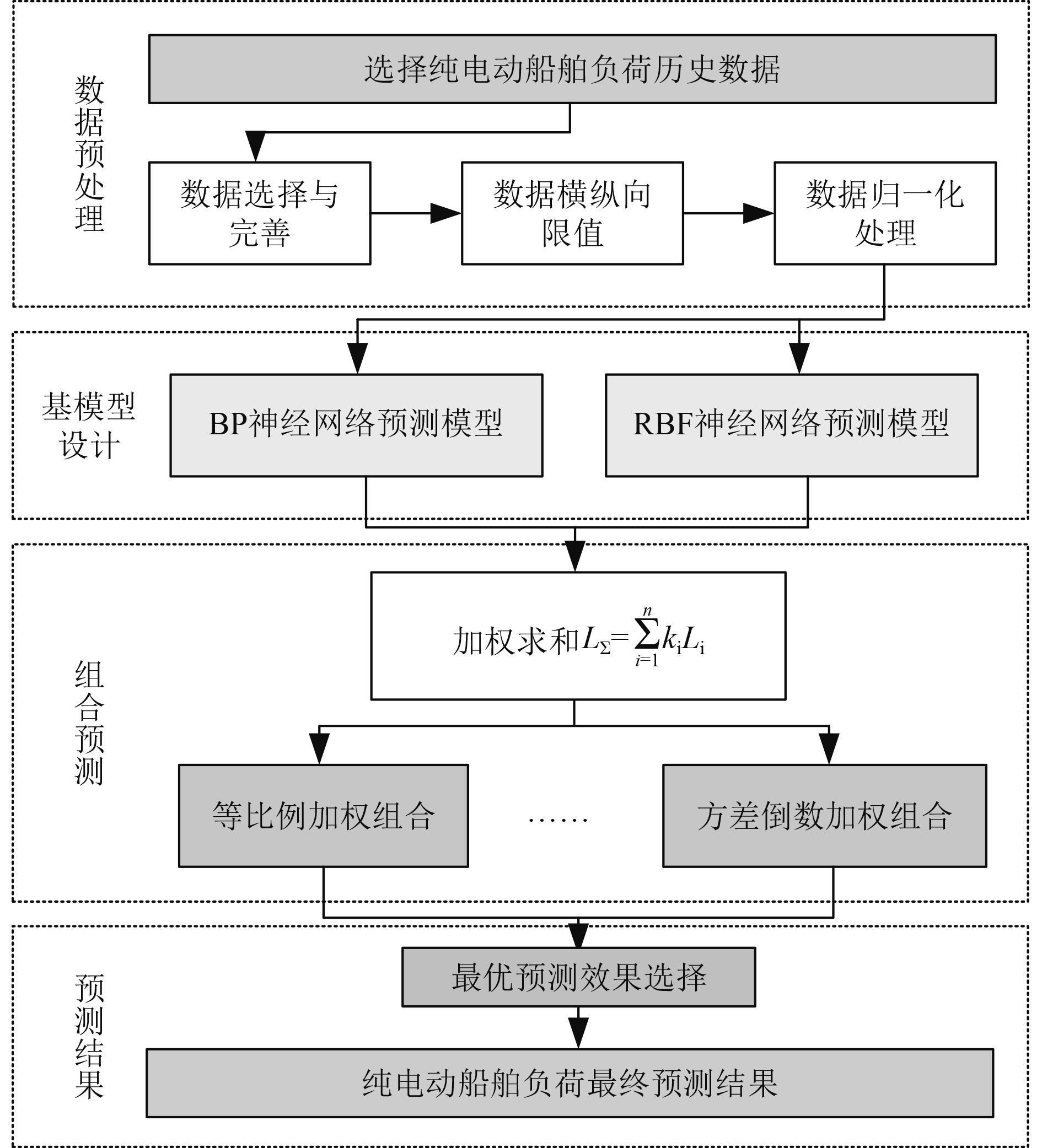
在组合模型中将预处理后的数据输入至BP和RBF神经网络模型中,预测完成后对2个模型的预测结果进行加权求和,求和结果反归一化后作为组合模型的最终预测结果。组合预测方法示意图如图4所示。
|
图 4 组合型神经网络负荷预测方法示意图 Fig. 4 Schematic diagram of combined neural network load forecasting method |
综合考虑纯电动船舶运行的实际环境和BP神经网络预测的基本原理对BP网络结构进行具体设计,本文选择输入变量为四维数据信息,包括载重量、水流速度、吃水深度和实际船舶电力系统负荷值,输出为电力系统负荷预测值,因此,对应的输入层神经元数为4,输出层神经元数为1。对于隐含层神经元个数的确定,并没有严格的理论计算方法,对此本文采用经验公式法和试凑法结合计算,公式如下:
| $ N = \sqrt {X + Y} + M。$ | (12) |
式中:
学习率取较大值虽可以在训练开始时加快网络收敛速度,但在临近最佳点时会产生振荡以至于最终网络无法收敛,综合考虑后设定学习率为0.020。最大训练次数为5000,误差精度要求为1e-5,其他参数设置为默认值。BP神经网络具体参数设置如表2所示。
|
|
表 2 BP神经网络参数设置 Tab.2 BP neural network parameter setting |
RBF神经网络不同于BP神经网络,其学习率设置分为3个层面,分别为隐含层至输出层的权值学习率、节点基宽学习率和基函数中心学习率,设置为0.090、0.015、0.015。除此之外,设置动量因子为0.1,变步长调整系数为0.1,最大训练次数设置为20000,误差精度要求为1e-4,其他参数均为默认值。
对上述设计的BP和RBF神经网络模型的结果进行加权组合预测,公式如下:
| $ {L_\Sigma } = \sum\limits_{{{i = }}1}^{{n}} {{{{k}}_{{i}}}{L_{{i}}}},{{ }}i = 1,2, \cdots \cdots ,n 。$ | (13) |
式中:
本文针对纯电动船舶的负荷特性选择基模型为BP和RBF神经网络模型,故n值取2。对于加权系数
方差倒数加权法也称为预测误差平方和倒数法,其通过误差平方和的大小分配权重,计算公式如下:
| $ {k_i} = \frac{{D_i^{ - 1}}}{{\sum\limits_{i = 1}^m {D_i^{ - 1}} }}{\text{ }}i = 1,2, \cdots \cdots ,n。$ | (14) |
其中,
| $ {D_i} = \sum\limits_{t = 1}^N {{{\left( {{F_r}\left( t \right) - {F_{ip}}\left( t \right)} \right)}^2},t = 1,2, \cdots \cdots ,n}。$ | (15) |
式中:
本文仿真数据来源于江苏省某纯电动船舶自2020年5月下水后,从2020年6月至2021年2月开展的每月一次短途试航,其中,7月丰水期运河水位太高,影响船舶通过连江桥;11−12月上海新冠疫情,公司取消试航计划,因此上述3个月无对应的数据样本信息。
考虑该船舶试航运行较为恶劣的运行环境和复杂工况,选取试航数据中具有代表性的工况数据集,例如空载、轻载、重载、满载且水流湍急情况下相对应的的启航、巡航、加减速等工作状态,对其中一组单次短途航行电力系统负荷情况进行验证,外界客观影响因素包括载重量、吃水深度和水流速度。
4.2 纯电动船舶综合电力系统负荷预测仿真评价指标对于此类预测问题,应当引入评价指标衡量预测精度[21]。本文采用平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)、MAE(Mean Absolute Error)平均绝对误差以及均方根误差(Root Mean Square Error,RMSE)对纯电动船舶电力系统的负荷预测效果进行评价,其公式如下:
| $ {{{{{e}}}}_{\rm{MAPE}}}{{ = }}\left( {\frac{1}{{{n}}}} \right) \times \sum\limits_{{{i = 1}}}^{{n}} {\left( {\frac{{\left| {{{{x}}_{{i}}} - {{{y}}_{{i}}}} \right|}}{{{{{y}}_{{i}}}}}} \right)} \times 100{{\% }} ,$ | (16) |
| $ {{{{{e}}}}_{\rm{MAE}}} = \left( {\frac{1}{{{n}}}} \right) \times \sum\limits_{{{i = }}1}^{{n}} {\left| {{{{x}}_{{i}}} - {{{y}}_{{i}}}} \right|} ,$ | (17) |
| $ {{{{{e}}}}_{\rm{RMSE}}}{{ = }}\sqrt {\left( {\frac{1}{{{n}}}} \right) \times \sum\limits_{{{i = 1}}}^{{n}} {{{\left( {{{{x}}_{{i}}} - {{{y}}_{{i}}}} \right)}^2}} } 。$ | (18) |
式中:
针对船舶试验中的3组实际运行情况进行负荷预测仿真,第1组外界输入环境特征为:载重量600 t、吃水深度2 m、水流速度−2 km/h;第2组外界输入环境特征为:载重量660 t、吃水深度2.4 m、水流速度−2 km/h;第1组外界输入环境特征为:载重量1000 t、吃水深度3.1 m、水流速度−2 km/h。
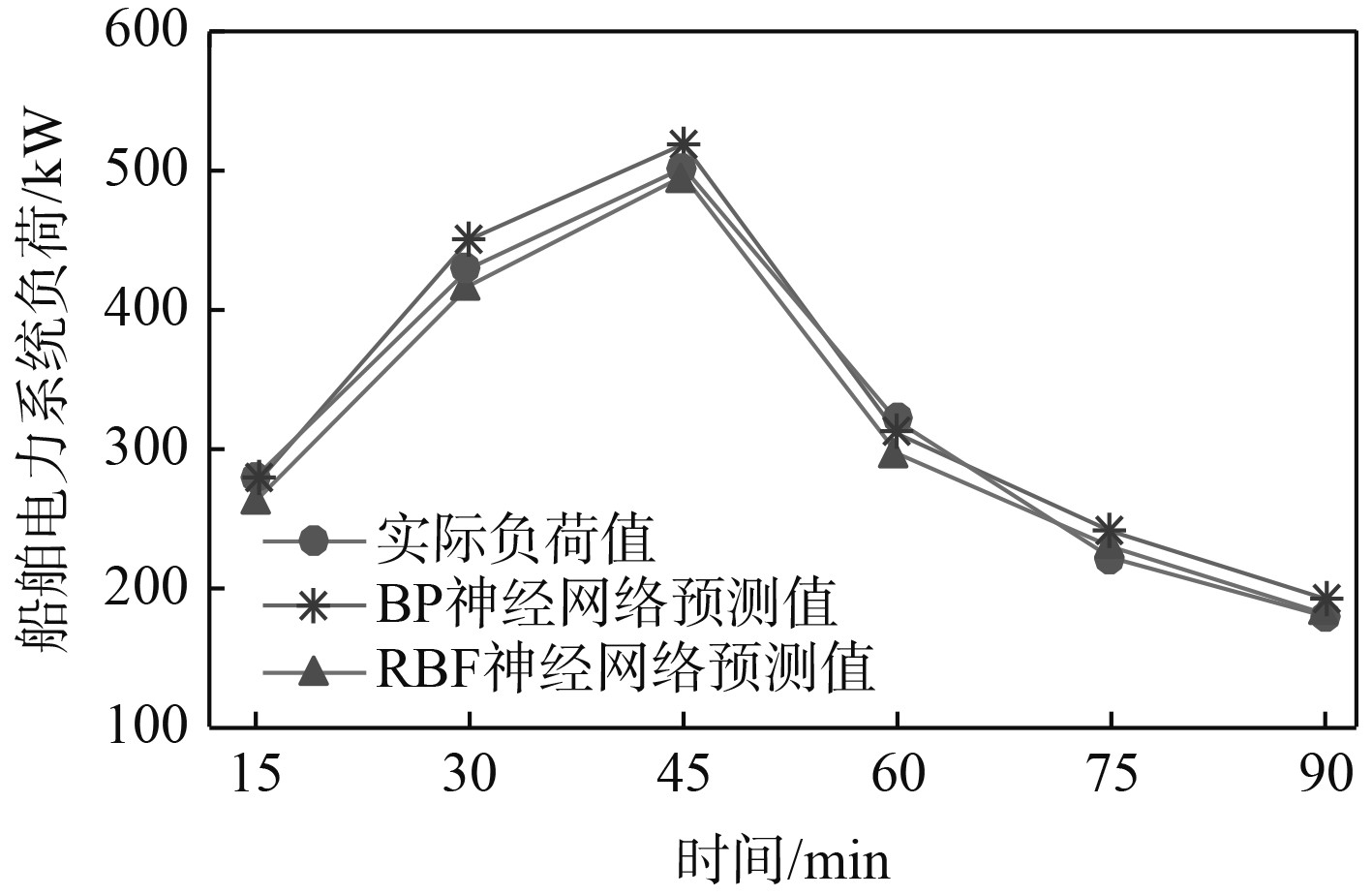
对第1组运行情况单一预测方法下的预测结果如图5所示。可知:BP神经网络模型和RBF神经网络模型都可较好地拟合船舶实际负荷值,但相比之下RBF神经网络的拟合效果更好,基本没有误差过大的预测点。计算二者的评价指标,BP神经网络模型的MAPE为4.73,MAE为12.21,RMSE为15.02,明显高于RBF神经网络模型的MAPE为3.65,MAE为11.35,RMSE为13.43。
|
图 5 第1组单一方法预测结果 Fig. 5 The first group of single method prediction results |
对BP神经网络模型和RBF神经网络模型的预测结果分别作等比例加权和方差倒数加权处理,得到组合预测方法与实际负荷值的对比如图6所示。可知:等比例加权方法和方差倒数加权方法得到的组合预测结果几乎完全一样,2条曲线近乎重叠,相比之下方差倒数加权方法更加接近实际负荷值,预测准确率高达96.62%。因此,选择方差倒数加权法作为最优的组合预测加权方法。

|
图 6 第一组组合预测方法结果 Fig. 6 Results of the first group of combined forecasting methods |
第1组试验各种预测方法对应时刻的预测结果如表3所示。其中,组合预测1为方差倒数加权预测,组合预测2为等比例加权预测。
|
|
表 3 第一组各种方法预测时刻(min)的结果(kW) Tab.3 Results of the first group of prediction time (min) by various methods (kW) |
对比单一方法和最优组合预测方法即方差倒数加权组合方法各点对应的相对误差,如图7所示。由图可知:组合预测方法显著降低了单点的相对误差,且没有出现某一点相对误差过大的问题,其中有2个时刻的预测值甚至完全逼近真实负荷值。

|
图 7 第一组单一方法和组合预测方法相对误差对比 Fig. 7 Comparison of the relative error of the first group of single method and combined prediction method |
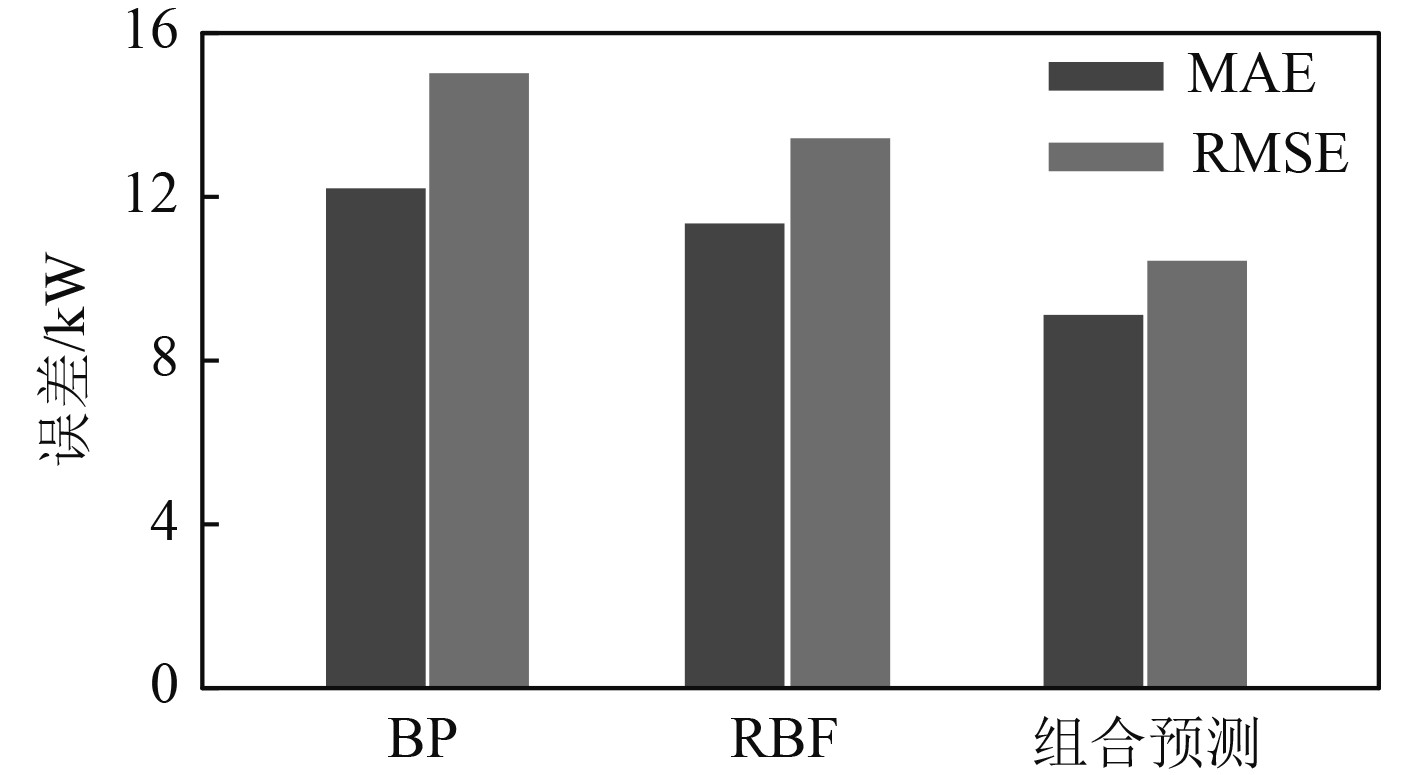
计算3种方法对应的评价指标如表4所示。其中,各预测方法对应的MAE和RMSE如图8所示。
|
|
表 4 第1组3种方法的评价指标 Tab.4 Evaluation indicators of the first group of three methods |
|
图 8 第1组3种预测方法相应的误差值 Fig. 8 The corresponding error values of the first group of three prediction methods |
对第2组运行情况单一预测方法下的预测结果如图9所示。计算二者的评价指标,BP神经网络模型的MAPE为3.35,MAE为8.47,RMSE为10.10,RBF神经网络模型的MAPE为3.37,MAE为7.63,RMSE为7.83。二者的平均百分比误差基本相同而RBF预测的平均绝对误差和均方根误差明显优于BP神经网络预测,说明RBF神经网络预测效果更好。
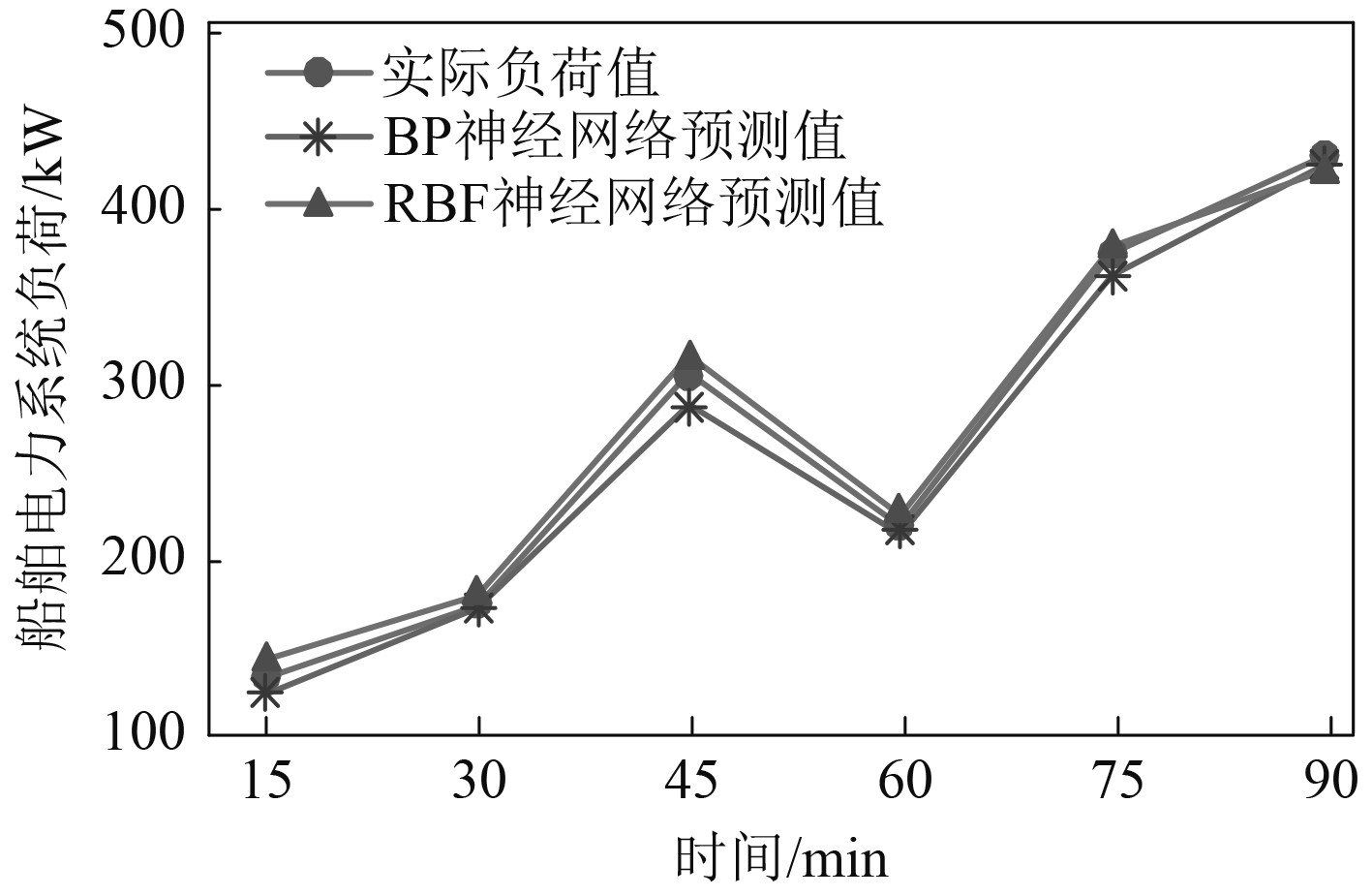
|
图 9 第2组单一方法预测结果 Fig. 9 The second group of single method prediction results |
同理,分别加权处理得到组合预测方法与实际负荷值的对比图,如图10所示。可知:等比例加权方法和方差倒数加权方法得到的组合预测结果基本吻合,但此时等比例加权方法更加逼近实际值。因此,选择等比例加权法作为最优的组合预测加权方法。
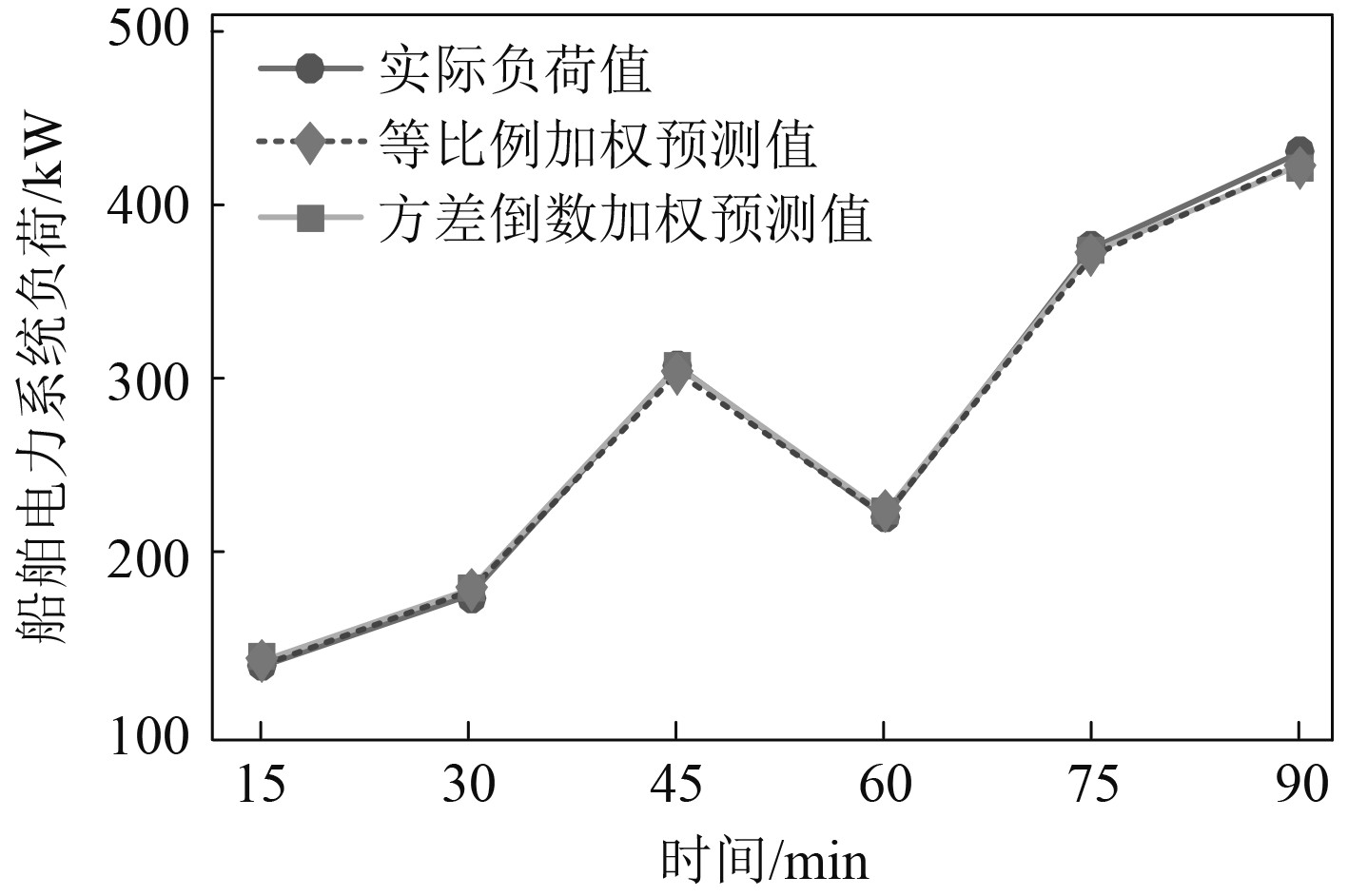
|
图 10 第2组组合预测方法结果 Fig. 10 Results of the second group of combined forecasting method |
第2组试验各种预测方法对应时刻的预测结果如表5所示。
|
|
表 5 第2组各种方法预测时刻(min)的结果(kW) Tab.5 Results of the second group of prediction time (min) by various methods (kW) |
同样对比单一方法和最优组合预测方法各点对应的相对误差,如图11所示。可知:组合预测方法依然显著降低了单点的相对误差,且没有出现某一点相对误差过大的问题。
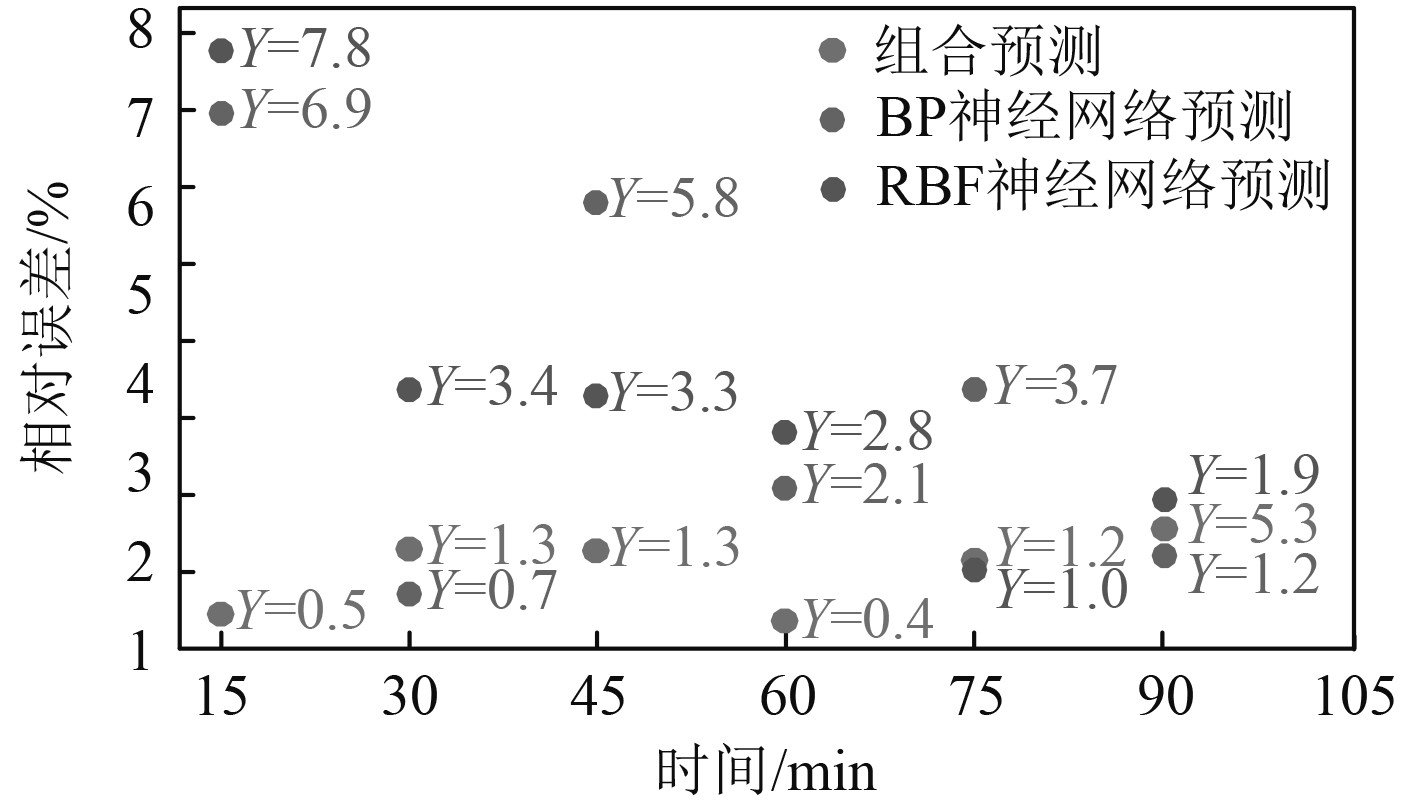
|
图 11 第2组单一方法和组合预测方法相对误差对比 Fig. 11 Comparison of the relative error of the second group of single method and combined prediction method |
计算3种方法对应的评价指标如表6所示。其中,各预测方法对应的MAE和RMSE如图12所示。
|
|
表 6 第2组3种方法的评价指标 Tab.6 Evaluation indicators of the second group of three methods |

|
图 12 第2组3种预测方法相应的误差值 Fig. 12 The corresponding error values of the second group of three prediction methods |
对第3组运行情况单一预测方法下的预测结果如图13所示。可知,RBF神经网络预测方法可大致逼近实际负荷值,而BP神经网络预测的结果误差过大,显然不符合预测要求。由于其中一个基模型的预测出现偏离问题,所以此时再对基模型得到的预测结果进行组合预测没有太大意义。由此说明对于复杂工况下的船舶在载重过大吃水过深的情况下,BP神经网络预测可能会失效。
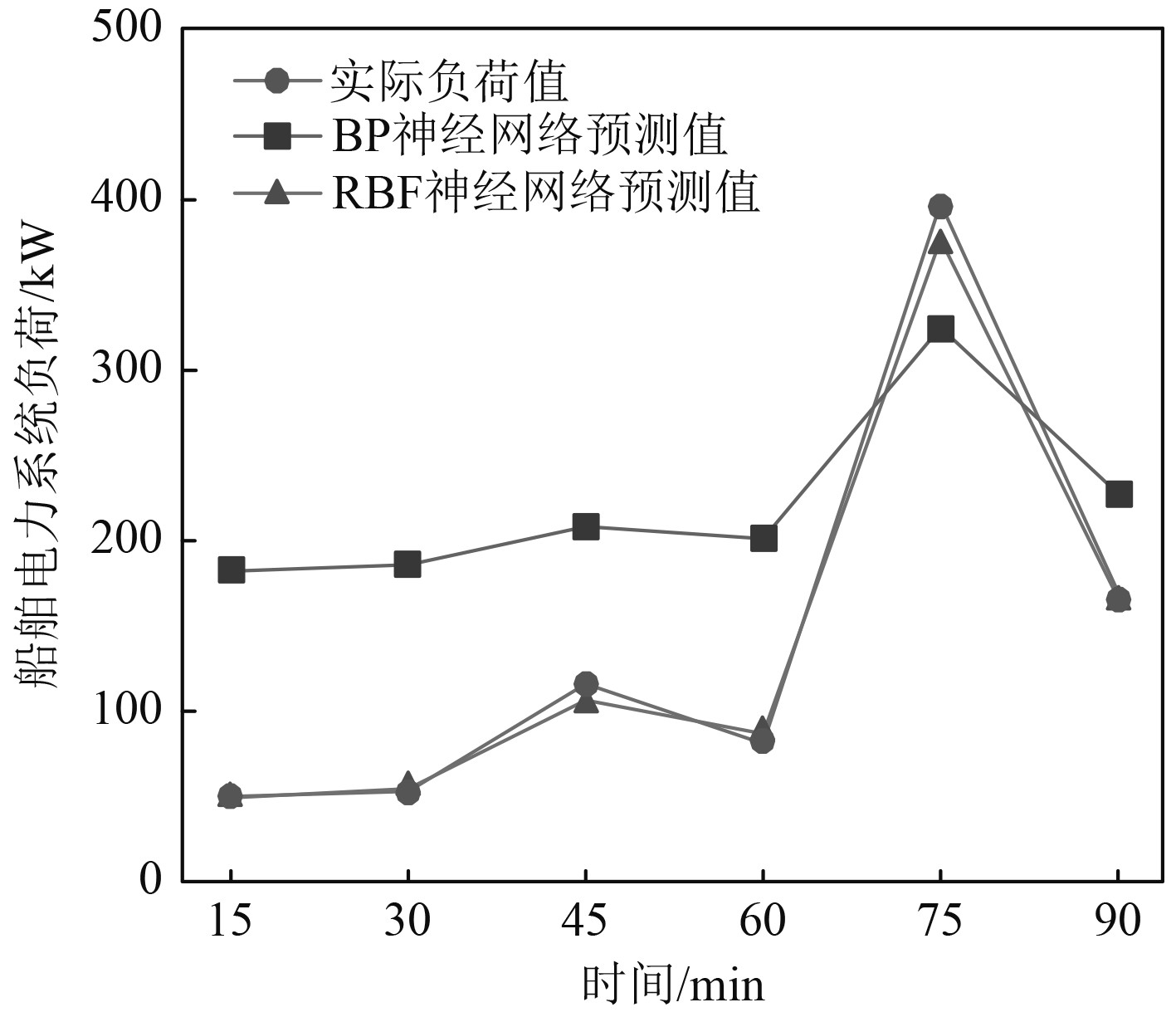
|
图 13 第3组单一方法预测结果 Fig. 13 The third group of single method prediction results |
结合上述3组试验得出,对于单一预测方法而言,RBF神经网络比BP神经网络更加适合于短期船舶综合电力系统负荷预测。本文提出的组合预测模型提高了预测点的稳定性,组合预测方法的各项评价指标均优于单一预测方法,在2次试验中,相比单一BP神经网络预测精度分别提高1.35%和2.33%,相比单一RBF神经网络预测精度分别提高0.27%和2.35%。说明针对复杂工况下,纯电动船舶综合电力系统的负荷预测本文提出的组合预测方法具有预测效果的优越性。
5 结 语针对纯电动船舶综合电力系统的负荷预测问题,本文提出一种基于BP神经网络和RBF神经网络模型的组合预测方法。该方法通过对BP神经网络模型和RBF神经网络模型的预测结果进行加权求和处理,充分利用了2种模型的优点,进而提高了预测的准确性和泛化性,从而提升预测精度。本方法通过船舶实际运行数据的负荷预测仿真,证明了该方法的优越性。通过负荷预测仿真分析对比,可得出以下结论:
1)基于典型神经网络的船舶综合电力系统负荷预测方法泛化性弱、容错率低,并不适合于复杂工况,特别在载重过大吃水过深的情况下可能预测失效。
2)基于BP神经网络和RBF神经网络模型的组合预测方法解决了复杂工况下单一预测方法出现的个别预测值偏差过大的问题,各项预测评价指标均超过单一预测方法。
3)本文提出的最优组合预测方法在两次不同运行环境的复杂工况试验条件下,预测精度分别为96.62%和98.98%,证明组合预测模型的泛化程度很高且稳定性好。
| [1] |
包育德. 双碳背景下清洁能源调度优化及排放分析[J/OL]. 电测与仪表, 1−10
|
| [2] |
王力波. 我国电动船舶产业现状与发展对策研究[J]. 中国海事, 2022(8): 65-68. WANG Libo. Study on the current situation and countermeasures of the development of china's electric ship industry[J]. Shipping Horizon, 2022(8): 65-68. |
| [3] |
陆振华. 全电力推进船舶能量管理优化研究[D]. 大连: 大连海事大学, 2020.
|
| [4] |
张旭, 张宏立, 范文慧, 等. 基于数据分析和改进Chebyshev神经网络的风速时间序列预测[J]. 电测与仪表, 2020, 57(22): 33-39. ZHANG Xu, ZHANG Hongli, FAN Wenhui, et al. Time series prediction of wind speed based on data analysis and improved Chebyshev neural network[J]. Electrical Measurement & Instrumentation, 2020, 57(22): 33-39. |
| [5] |
韩富佳, 王晓辉, 乔骥, 等. 基于人工智能技术的新型电力系统负荷预测研究综述[J/OL]. 中国电机工程学报: 1-24
|
| [6] |
侯文君, 汪英英, 姚艺新, 等. 支持向量机的船舶短期电力负荷预测方法[J]. 舰船科学技术, 2018, 40(18): 79-81. HOU Wen-jun, WANG Ying-ying, YAO Yi-xin, et al. Short term load forecasting method based on support vector machine[J]. Ship Science and Techology, 2018, 40(18): 79-81. |
| [7] |
刘静. 最小二乘SVM在电力推进船舶电力负荷短期预测的应用[J]. 舰船科学技术, 2021, 43(24): 61-63. LIU Jing. Application of least square SVM in short-term forecasting of electric load of electric propulsion ship[J]. Ship Science and Technology, 2021, 43(24): 61-63. DOI:10.3404/j.issn.16727649.2021.12A.021 |
| [8] |
刘银波, 吕越. RBF神经网络在船舶电力负荷预测中的应用[J]. 舰船科学技术, 2021, 43(18): 121-123. LIU Yin-Bo, LV Yue. Application of RBF neural network in ship power load forecasting[J]. Ship Science and Techology, 2021, 43(18): 121-123. DOI:10.3404/j.issn.1672-7649.2021.9A.041 |
| [9] |
阳曾, 丁施尹, 叶萌, 等. 基于变分模态分解和深度学习的短期电力负荷预测模型[J]. 电测与仪表, 2023, 60(2): 126-131+146. YANG Zeng, DING Shiyin, YE Meng, et al. Short-term load forecasting model based on VMD and LSTM[J]. Electrical Measurement & Instrumentation, 2023, 60(2): 126-131+146. |
| [10] |
张宇涵, 高海波, 商蕾, 等. 基于神经网络模型的船舶电网短期电力负荷预测[J]. 应用科技, 2021, 48(5): 12-15+22. ZHANG Yuhan, GAO Haibo, SHANG Lei, et al. Short-term load forecasting for marine electric network based on neural network models[J]. Applied Science and Technology, 2021, 48(5): 12-15+22. DOI:10.11991/yykj.202101010 |
| [11] |
张博山, 乔显辉. 全电力推进船舶的运行维护与管理[J]. 机电设备, 2022, 39(4): 12-19. ZHANG Boshan, QIAO Xianhui. Operation, maintenance and management of all-electric propulsion ships[J]. Electromechanical Equipment, 2022, 39(4): 12-19. |
| [12] |
杨光雨, 李晓航. 基于最大信息挖掘宽度学习系统短期电力负荷预测研究[J]. 电测与仪表, 2022, 59(3): 38-45. YANG Guangyu, LI Xiaohang. The short-term power load forecast in wide area learning system based on maximum information mining[J]. Electrical Measurement & Instrumentation, 2022, 59(3): 38-45. |
| [13] |
王克杰, 张瑞. 基于改进BP神经网络的短期电力负荷预测方法研究[J]. 电测与仪表, 2019, 56(24): 115-121. WANG Kejie, ZHANG Rui. Research on short-term power load forecasting method based on improved BP neural network[J]. Electrical Measurement & Instrumentation, 2019, 56(24): 115-121. |
| [14] |
归三荣, 郭燚, 高松, 等. 靠港后船舶电力系统负荷分析[J]. 上海海事大学学报, 2017, 38(2): 61-65. GUI Sanrong, GUO Yi, GAO Song, et al. Load analysis of power system of ships berthed in ports[J]. Journal of Shanghai Maritime University, 2017, 38(2): 61-65. |
| [15] |
ATANASOVSKI M, KOSTOV M, VELJANOVSKI G, et al. Short-Term load forecast in power systems: a comparison of different practical algorithms[C]//2022 18th International Conference on the European Energy Market, 2022.
|
| [16] |
董雷, 陈振平, 韩富佳. 基于图卷积神经网络与K-means聚类的居民用户集群短期负荷预测[J/OL]. 电网技术, 1-11
|
| [17] |
孙国良, 伊力哈木·亚尔买买提, 张宽, 等. 基于小波变换与IAGA-BP神经网络的短期风电功率预测[J/OL]. 电测与仪表, 1-11
|
| [18] |
党存禄, 杨海兰, 武文成. 基于LSTM和CatBoost组合模型的短期负荷预测[J]. 电气工程学报, 2021, 16(3): 62-69. DANG Cunlu, YANG Hailan, WU Wencheng. Short-term load forecasting based on LSTM and catboost combined model[J]. Journal Of Electrical Engineering, 2021, 16(3): 62-69. |
| [19] |
杜昆. 基于BP神经网络短期负荷预测研究[D]. 石家庄: 河北科技大学, 2021.
|
| [20] |
吴嘉竣, 徐文辉. 基于RBF神经网络的电力信息网络安全态势感知[J]. 自动化技术与应用, 2022, 41(9): 103-105. WU Jiajun, XU Wenhui. Power Information network security situation awareness based on RBF neural network[J]. Internet of Things and Network Technology, 2022, 41(9): 103-105. |
| [21] |
A T S, A. PRAVEEN, H M S. Comparison of deep learning-based methods for electrical load forecasting[C]//2022 Third International Conference on Intelligent Computing Instrumentation and Control Technologies, 2022. 1598-1602.
|
 2024, Vol. 46
2024, Vol. 46
