2. 武汉理工大学 船海与能源动力工程学院,湖北 武汉 430063;
3. 国家水运安全工程技术研究中心 可靠性工程研究所,湖北 武汉 430063
2. School of Naval Architecture, Ocean and Energy Power Engineering, Wuhan University of Technology, Wuhan 430063, China;
3. Reliability Engineering Institute, National Engineering Research Center Water Transport Safety, Wuhan University of Technology, Wuhan 430063, China
因多相电机的低压大功率传动,容错能力强和控制自由度多等特点,在船舶推进电机领域得到了广泛研究[1-3]。其中六相永磁同步电机具有转矩脉动小,动态性能良好,容错能力强等优点,在船舶推进电机领域中具有广阔的应用前景,其控制方式也逐渐成为国内外研究的热点之一[4]。
在船舶推进电机的控制中,空间矢量控制和直接转矩控制是2种较为成熟的控制策略[5-6]。空间矢量控制是基于矢量空间解耦方法,将各个变量分解到基波子空间和谐波子空间,采用1个PI转速调节器和4个PI电流调节器,对电机参数要求较高,需要大量的参数整定时间[7]。直接转矩控制策略是通过计算观测转矩和磁链给定值和实际值的插值,通过滞环比较器后查找开关表确定能够使差值变小的电压矢量[8]。相比空间矢量控制,直接转矩控制省去了复杂的坐标变换,仅采用1个PI转速调节器,节省了大量参数整定时间并减少了对电机参数的要求,具有更强的鲁棒性和响应速度。但是直接转矩控制使用的电压矢量较少,会带来较大的转矩波动和谐波电流[9]。因此,本文引入一种基于虚拟电压矢量合成的模型预测转矩控制策略,利用α-β子空间中同向的大矢量和中矢量与z1-z2子空间中反向的小矢量和中矢量恰好对应原理,通过适当地调节一个PWM周期内大矢量和中矢量的占空比,可以使z1-z2子空间中的合成电压矢量幅值为0。通过选取合适的代价函数的方法,可以使选择的电压矢量为最优选择。仿真结果表明,该方法可以有效降低电机的谐波电流,显著降低转矩脉动。
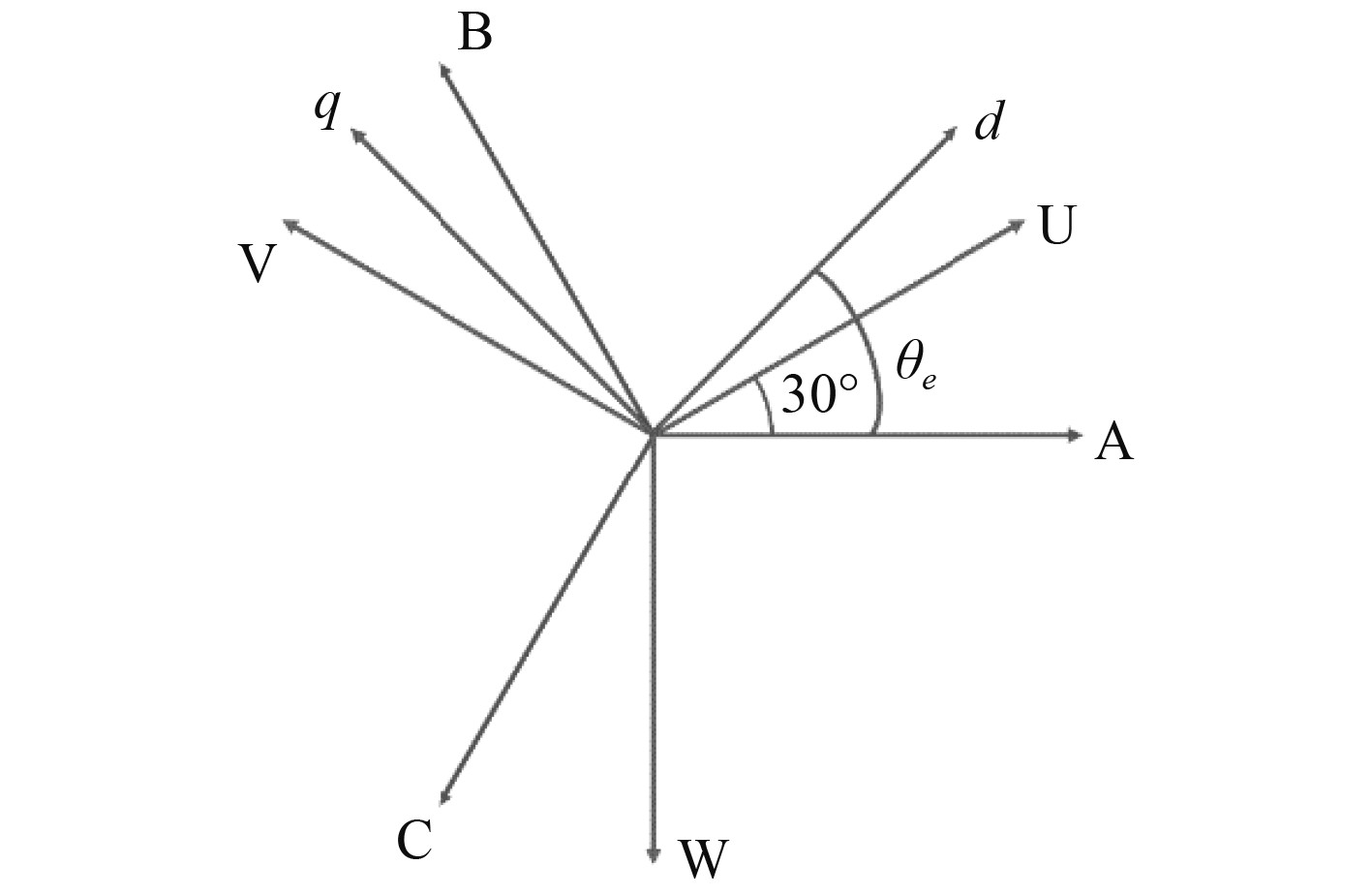
1 船舶六相永磁同步电机数学模型船舶六相永磁同步电机的定子绕组可以等效为2套Y型连接的绕组(ABC和UVW),彼此中性点隔离,相位角相差30°,如图1所示。船舶六相永磁同步电机是一个高阶、非线性的系统,为了简化分析,实现电机模型的完全解耦,本文采用空间矢量解耦坐标变换(Vector Space Decomposition,VSD)的方法,将船舶六相永磁同步电机的各个变量分别映射到3个相互正交的二维子空间,分别是α-β、z1-z2、o1-o2,其中α-β为基波子平面其分量会在气隙中产生旋转磁动势,参与机电能量转换,z1-z2为谐波子平面,包含6n±1(n=1,3,5···)次谐波该平面不参与机电能量转换,但会产生较大的谐波电流,o1-o2为零序子平面,由于电机2套绕组中性点互相隔离,不产生零序电流,所以控制时不考虑该平面[10]。矢量空间解耦变换矩阵[11]如下式:
|
图 1 船舶六相永磁同步电机结构图 Fig. 1 Structure diagram of marine six-phase permanent magnet synchronous motor |
| $ { \dfrac{1}{3}\left[ \begin{array}{*{20}{c}} {\cos \theta }&{\cos \left(\theta - \dfrac{2}{3}{\text{π }}\right)}&{\cos \left(\theta + \dfrac{2}{3}{\text{π }}\right)}&{\cos \left(\theta - \dfrac{{\text{π }}}{6}\right)}&{\cos \left(\theta - \dfrac{5}{6}{\text{π }}\right)}&{\cos \left(\theta + \dfrac{{\text{π }}}{2}\right)}\\ { - \sin \theta }&{ - \sin \left(\theta - \dfrac{2}{3}{\text{π }}\right)}&{ - \sin \left(\theta + \dfrac{2}{3}{\text{π }}\right)}&{ - \sin \left(\theta - \dfrac{{\text{π }}}{6}\right)}&{ - \sin \left(\theta - \dfrac{5}{6}{\text{π }}\right)}&{ - \sin \left(\theta + \dfrac{{\text{π }}}{2}\right)}\\ 1&{ - \dfrac{1}{2}}&{ - \dfrac{1}{2}}&{ - \dfrac{{\sqrt 3 }}{2}}&{\dfrac{{\sqrt 3 }}{2}}&0\\ 0&{ - \dfrac{{\sqrt 3 }}{2}}&{\dfrac{{\sqrt 3 }}{2}}&{\dfrac{1}{2}}&{\dfrac{1}{2}}&{ - 1} \\ 1&1&1 &0&0&0\\ 0&0&0 & 1&1&1 \end{array} \right] }$ | (1) |
忽略o1-o2子空间中的分量,可以得到旋转坐标系下的电压和磁链方程为:
| $ \left[ {\begin{array}{*{20}{c}} {{u_d}} \\ {{u_q}} \\ {{u_{z1}}} \\ {{u_{z2}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{R_s}}&0&0&0 \\ 0&{{R_s}}&0&0 \\ 0&0&{{R_s}}&0 \\ 0&0&0&{{R_s}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{i_d}} \\ {{i_q}} \\ {{i_{z1}}} \\ {{i_{z2}}} \end{array}} \right] + {{p}}\left[ {\begin{array}{*{20}{c}} {{\psi _d}} \\ {{\psi _q}} \\ {{\psi _{z1}}} \\ {{\psi _{z2}}} \end{array}} \right] + {\omega _m}\left[ {\begin{array}{*{20}{c}} { - {\psi _q}} \\ {{\psi _d}} \\ 0 \\ 0 \end{array}} \right] ,$ | (2) |
| $ \left[ {\begin{array}{*{20}{c}} {{\psi _d}} \\ {{\psi _q}} \\ {{\psi _{z1}}} \\ {{\psi _{z2}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{L_d}}&0&0&0 \\ 0&{{L_q}}&0&0 \\ 0&0&{{L_z}}&0 \\ 0&0&0&{{L_z}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{i_d}} \\ {{i_q}} \\ {{i_{z1}}} \\ {{i_{z2}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\psi _f}} \\ 0 \\ 0 \\ 0 \end{array}} \right] ,$ | (3) |
电磁转矩可通过下式计算:
| $ {T_e} = 3{p_n}[({L_d} - {L_q}){i_d}{i_q} + {\psi _f}{i_q}] 。$ | (4) |
式中:ud、uq, uz1、uz2、id、iq、iz1、iz2、Ld、Lq、Lz分别对应定子电压基波、电流基波和电感在d-q和z1-z2子空间上的投影;
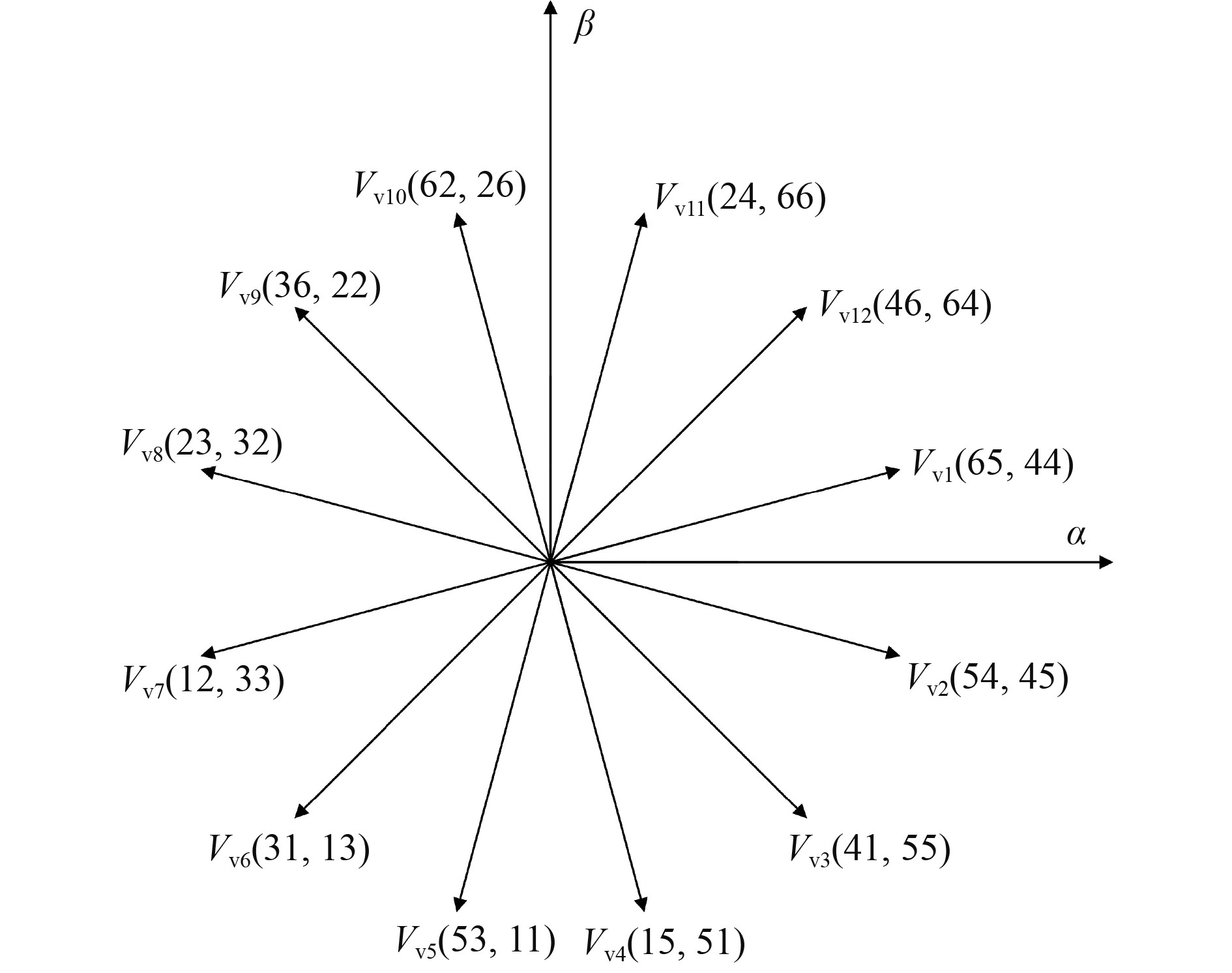
船舶六相永磁同步电机控制采用滞环比较器,通过定子磁链位置、转矩、磁链的误差计算开关表,从而保持磁链幅值不变和转矩快速响应。与三相电机的逆变器不同,六相逆变器为六相电机提供了64个电压矢量,如图2所示。其中包含了60个非零矢量和4个零矢量,按照幅值大小可以将非零矢量分为4组:大矢量vL

|
图 2 电压矢量分布 Fig. 2 Voltage vector distribution |
以12个大矢量vL 为界限将船舶六相永磁同步电机电压矢量分为12个扇区,同时作为开关表建立的参考电压矢量,以转矩响应最快作为目标,建立六相PMSM直接转矩控制系统的开关表,如表1所示。其中τ为转矩增减,φ为磁链增减,1为需要增加,−1为需要减少。
|
|
表 1 船舶六相永磁同步电机直接转矩控制系统开关表 Tab.1 Switch table of DTC system for marine six-phase permanent magnet synchronous motor |
传统的DTC不需要进行旋转坐标变换,具有很快的转矩响应速度,但滞环比较器的存在带来了较大的转矩脉动,并且由于开关表仅使用12个大电压矢量作为参考,且查询控制方法较为简单,所选出的电压矢量未必是系统的最优选择。模型预测控制作为一种先进控制算法,结构简单,响应迅速,可设置不同权重对不同控制目标进行优化,相比传统直接转矩控制具有一定的优越性。但是传统的模型预测转矩控制(MPTC)控制集中仅包含大矢量vL,控制范围仅限于α-β子空间,无法抑制z1-z2子空间的谐波[12]。因此,本文提出虚拟电压矢量模型预测直接转矩控制(VMPTC),即引入中矢量vM合成虚拟电压矢量,利用α-β子空间中同向的大矢量和中矢量与z1-z2子空间中反向的小矢量和中矢量恰好对应原理,通过适当地调节一个PWM周期内大矢量和中矢量的占空比d,可以使z1-z2子空间中的合成电压矢量幅值为0。该方法可以使选择的电压矢量为最优选择,有效降低电机的谐波电流,显著降低转矩脉动。
首先,通过前向欧拉法将式(5)~式(6)离散化,分别选择电流矢量、电压矢量、磁链和转矩作为状态变量、输入变量和输出变量,得到系统预测模型:
| $ {{\boldsymbol{I}}_s}(k + 1) = {{\boldsymbol{A}}_1}{{\boldsymbol{I}}_s}(k) + {{\boldsymbol{B}}_1}{\boldsymbol{U}}(k) + {\boldsymbol{E}} ,$ | (5) |
| $ {{\boldsymbol{\psi }}_s}(k + 1) = {{\boldsymbol{L}}_s}{{\boldsymbol{I}}_s}(k + 1) + {{\boldsymbol{\psi }}_f} ,$ | (6) |
| $ {T_e}(k + 1) = 1.5{p_n}({\psi _{sd}}(k){i_q}(k) - {\psi _{sq}}(k){i_d}(k)) ,$ | (7) |
式中:k为当前时刻采样值,k+1为下个时刻预测值,
| $ \begin{split}&{{\boldsymbol{A}}_1} = \left[ {\begin{array}{*{20}{c}} {1 - \dfrac{{{R_s}{T_s}}}{{{L_d}}}}&{\dfrac{{{L_q}{T_s}{\omega _e}(k)}}{{{L_d}}}}&0&0 \\ { - \dfrac{{{L_d}{T_s}{\omega _e}(k)}}{{{L_q}}}}&{1 - \dfrac{{{R_s}{T_s}}}{{{L_q}}}}&0&0 \\ 0&0&{1 - \dfrac{{{R_s}{T_s}}}{{{L_z}}}}&0 \\ 0&0&0&{1 - \dfrac{{{R_s}{T_s}}}{{{L_z}}}} \end{array}} \right] ,\end{split}$ |
| $ \begin{split} {{\boldsymbol{B}}_1} = \left[ {\begin{array}{*{20}{c}} {\dfrac{{{T_s}}}{{{L_d}}}}&0&0&0 \\ 0&{\dfrac{{{T_s}}}{{{L_q}}}}&0&0 \\ 0&0&{\dfrac{{{T_s}}}{{{L_z}}}}&0 \\ 0&0&0&{\dfrac{{{T_s}}}{{{L_z}}}} \end{array}} \right] ,{\boldsymbol{E}} = \left[ {\begin{array}{*{20}{c}} 0 \\ { - \dfrac{{{T_s}{\psi _f}{\omega _e}(k)}}{{{L_q}}}} \\ 0 \\ 0 \end{array}} \right] 。\end{split}$ |
由图2可知,α-β子空间中同向的大矢量vL和中矢量vM与z1-z2子空间中反向的小矢量vS和中矢量vM恰好对应。根据这2组矢量的特点,适当地调节一个PWM周期内大矢量和中矢量的占空比d,可以使z1-z2子空间中的合成电压矢量幅值为0,以大矢量44和中矢量65为例,设控制周期为Tmpc,大矢量44作用的时间为dTmpc,则中矢量65的作用时间为(1-d)Tmpc,合成的虚拟电压矢量Vv在α-β子空间和z1-z2子空间中的幅值如下式:
| $ \left\{ {\begin{array}{*{20}{l}} {\left| {{V_{v\_\alpha \beta }}} \right| = {\text{d}}\left| {{v_L}} \right| + (1 - {\text{d}})\left| {{v_M}} \right|} ,\\ {\left| {{V_{v\_z1z2}}} \right| = {\text{d}}\left| {{v_S}} \right| - (1 - {\text{d}})\left| {{v_M}} \right|} 。\end{array}} \right. $ | (8) |
可知,通过对一个周期内大矢量vL和中矢量vM的作用时间控制,可合成为在α-β子空间中幅值为0.598Vdc和z1-z2子空间幅值为0的虚拟电压矢量Vv,合成的电压矢量图如图3所示。同时为了表达清晰,对每个虚拟电压矢量进行定义,如Vv1表示(65,44)为2个电压矢量进行合成的虚拟电压矢量合成,以此类推。VMPTC将合成后的12个电压矢量作为预测电压矢量控制集,然后代入预测模型中进行迭代计算,相比64个电压矢量,预测矢量减少至12个,可以有效降低系统总的运算量。
|
|
表 2 虚拟电压矢量与原始电压矢量对比 Tab.2 Comparison between virtual voltage vector and original voltage vector |
|
图 3 虚拟电压矢量α-β子空间中的分布情况 Fig. 3 Distribution of the virtual voltage vector α-β subspace |
在理想的模型预测控制过程中没有考虑到数字处理器的采样延时和计算时间,在实际控制系统中,一个采样周期内无法完成控制。为了消除延时影响,采用提前2步预测的方式进行补偿,即在第k个采样时刻,预测第k+1个采样时刻的状态量,再据此预测第k+2个采样时刻的状态量。同时由于永磁同步电机的机械时间常数远大于电气时间常数,在一个采样时刻内转速几乎不发生变化,即ωe(k+1) = ωe(k),进而可以得到第k+1个采样时刻到第k+2个采样时刻的预测公式为:
| $ {{\boldsymbol{I}}_s}(k + 2) = {\boldsymbol{A}}{{\boldsymbol{I}}_s}(k + 1) + {\boldsymbol{BU}}(k + 1) + {\boldsymbol{C}} 。$ | (9) |
模型预测转矩控制的控制目标为电磁转矩和磁链,同时由于电压矢量合成后,z1-z2子空间中电流的理论幅值为0,代价函数不再需要考虑对谐波磁链的控制,因此设计代价函数如下式:
| $ J = {\left| {T_e^* - {T_e}(k + 2)} \right|^2} + \lambda {\left| {\psi _{sdq}^* - {\psi _{sdq}}(k + 2)} \right|^2} 。$ | (10) |
其中:Te*和ψsdq*分别为电磁转矩,d-q子空间磁链的参考值;Te (k+2)和ψsdq(k+2)分别为第k+2个采样时刻电磁转矩;d-q子空间磁链的预测值;λi为权重系数。由于权重系数的选择取决于对电磁转矩和磁链控制的优先级,在仿真过程中发现转矩脉动远大于磁链脉动,同时在合理的范围内调整权重系数,电机的稳态性能基本不发生改变。为了更大程度地减小转矩脉动,选择减少磁链控制的权重系数。
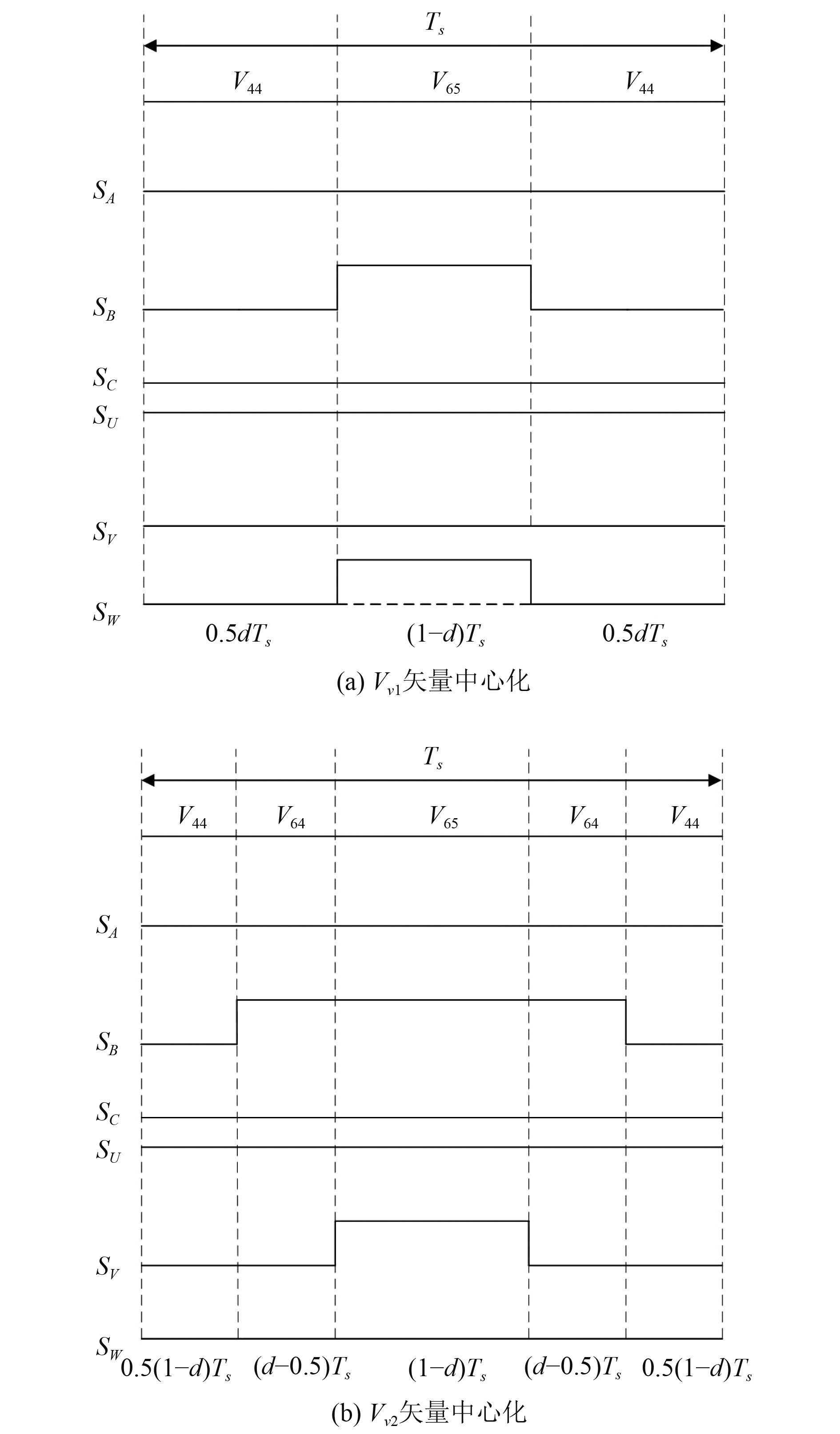
3.4 电压矢量中心化虚拟电压矢量在硬件中的实现方式为,调节大矢量和中矢量在一个控制周期内的占空比。然而无论是先使用大矢量,后使用中矢量还是先使用中矢量,后使用大矢量,虚拟电压矢量的波形都不是对称的,这不利于数字处理器的实现,还会引入偶数次谐波增加逆变器开关损耗,因此需要进行电压矢量中心化,将有效脉冲序列移动至控制周期的中心的同时保持电压平均值不变。对于图2中的虚拟电压矢量,奇数编号的虚拟电压矢量Vvi(i=1, 3, … 11)中心化方法与偶数编号的虚拟电压矢量Vvi(i=2, 4, … 12)中心化实现方法有所区别。以Vv1和Vv2为例,具体实现方法如图4所示。
|
图 4 电压矢量中心化实现 Fig. 4 Realization of voltage vector centralization |
基于虚拟电压矢量的模型预测转矩控制(VMPTC)的具体控制方法为:1)速度外环采用PI控制器,通过设置适当的比例和积分系数,得到给定转矩。2)将采样获得的电流进行坐标变换并利用公式对定子磁链进行观测,以确定预测电压的控制集。3)将电流和预测电压代入到预测模型中进行转矩和磁链的预测。4)利用代价函数计算最优电压矢量,将开关序列发送给六相逆变器,实现对电机的控制,控制框图如图5所示。

|
图 5 船舶六相永磁同步电机 VMPTC控制框图 Fig. 5 VMPTC control block diagram of Marine six-phase permanent magnet synchronous motor |
分别对传统DTC、MPTC、VMPTC进行仿真验证,为了合理分析3种方法的优劣,仿真过程中所使用的仿真参数一致。在Matlab/Simulink中搭建船舶六相永磁同步电机控制系统仿真模型。其中船舶六相永磁同步电机基于VSD变换下的数学模型搭建并进行封装,六相逆变器由2个三相逆变器组合而成,扇区判断模块采用s-function编写,VMPTC算法通过matlab function的形式实现开关表通过2-D Look-up Table模块实现,仿真模型中定子磁链参考值为0.3 Wb,磁链和转矩滞环宽度分别为0.004 Wb和0.2 N∙m,PI控制器参数为kp=0.1, ki=5。设置转速突变、转矩突变2种工况进行仿真,模拟船舶电机在运行过程中的加速、负载突增情况。
4.1 转速恒定转矩突变工况设置电机参考转速恒定为600 r/min,在空载下启动,在0.2 s时突加3 N∙m负载,仿真相关波形。从图6可以看出,在启动时刻电磁转矩都达到最大值,相比传统DTC,MPTC的电磁转矩较大一些,约10 N∙m,但转矩波动和响应速度具有明显提升;VMPTC的转速仿真结果与MPTC基本相同,转速超调与传统DTC相比有一定的降低,只有74 r/min,跟踪速度也有所提升。在突加负载后,电磁转矩迅速增加,在0.01 s内匹配上负载转矩,但VMPTC的转速下降约14 r/min,但在0.06 s后恢复到参考值。MPTC磁链脉动较大,为0.035 Wb,带载后降低至0.03 Wb,但仍是DTC磁链脉动的10倍以上,磁链轨迹也出现了一定程度的波动。这是由于使用的权重系数更侧重对转矩的控制,牺牲了部分磁链控制性能。VMPTC的转矩脉动略小于MPTC,磁链脉动在空载和加载后基本不发生变化,为0.02 Wb,磁链轨迹也比MPTC更加光滑。说明传统直接转矩控制方法采用开关表查询电压矢量的方法比较粗略,不能准确的对转矩进行控制。VMPTC采用预测转矩和磁链的方法,并通过权重系数的设定,可以达到对转矩、磁链精确的控制。

|
图 6 转矩突变工况下电机启动相关波形 Fig. 6 Related waveforms of motor startup under torque mutation condition |
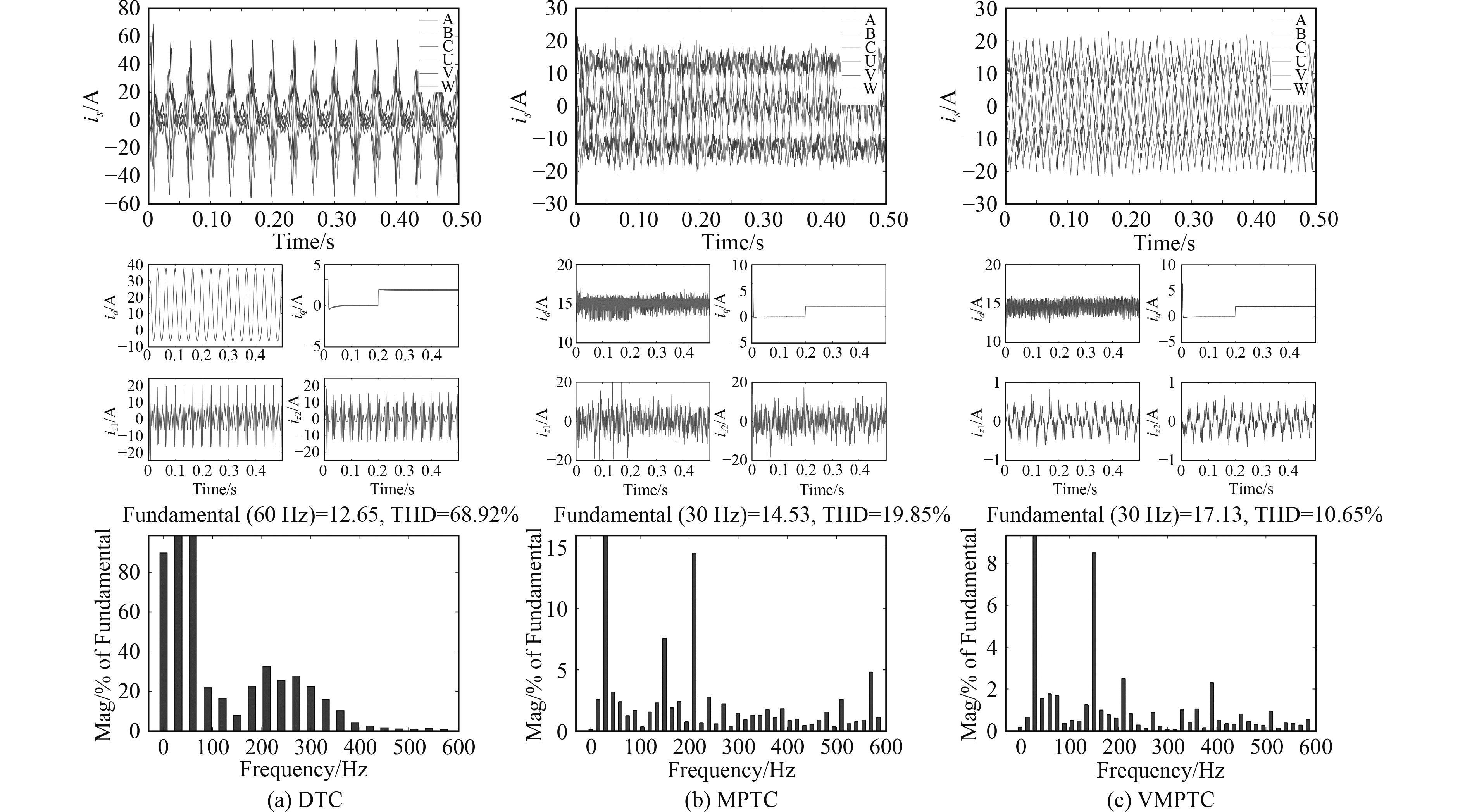
由图7可以看出,q轴电流的变化趋势与电磁转矩相同,证明了本文所搭建电机模型的正确性。还可以看出,在传统DTC控制中,由于谐波电流的原因使得相电流波形发生严重畸变,谐波电流幅值可达±20 A。采用powergui模块中的FFT Analysis功能可以发现,理论上基波频率为30 Hz,由于谐波含量过高,60 Hz成为基频,A相电流THD高达68.92%。当采用MPTC后,相电流波形畸变程度大幅降低,谐波电流得到有效抑制,幅值从±20 A降低至±5 A,THD降低至19.85%。VMPTC在3种控制算法中谐波电流幅值最小,幅值降低至±1 A以内,THD降低至10.65%,说明所提算法有效抑制了谐波电流。
|
图 7 转矩突变工况下电机电流相关波形 Fig. 7 Motor current correlation waveform under torque mutation condition |
系统带3 N∙m负载启动,参考转速初始值为400 r/min,在0.2 s时突变为600 r/min,由图8可以看出,相比DTC,MPTC系统带载启动更加稳定,超调量仅有43 r/min,并在0.08 s到达参考转速;与转矩突变工况类似,电磁转矩在启动时达到最大值约10 N∙m,在0.06 s时匹配上负载转矩。参考转速突变后,转速迅速上升,超调量为12 r/min,并在0.25 s时跟踪上新的参考转速;转矩在转速突变时刻再次上升至最大值,之后迅速下降,在0.26 s时再次匹配上负载转矩。系统转矩脉动为0.05 N·m,磁链脉动在低速时较大,达到0.04 Wb,在速度上升后下降至0.03 Wb,磁链轨迹波动大于转矩突变工况。

|
图 8 转速突变工况下电机启动相关波形 Fig. 8 Related waveforms of motor startup under speed change |
VMPTC的转速仿真结果与MPTC基本相同,转矩脉动略小于MPTC,为0.04 N∙m。磁链脉动在两次加速过程中基本不发生变化,为0.025 Wb,磁链轨迹也比MPTC更加光滑。
由图9可以看出,在转速较低的时候,MPTC系统谐波含量较高,转速达到600 r/min后,谐波电流幅值降低至±5 A。VMPTC系统谐波含量则不受转速影响,在整个仿真过程中均保持在±1 A以内。3种控制策略性能对比如表3所示。
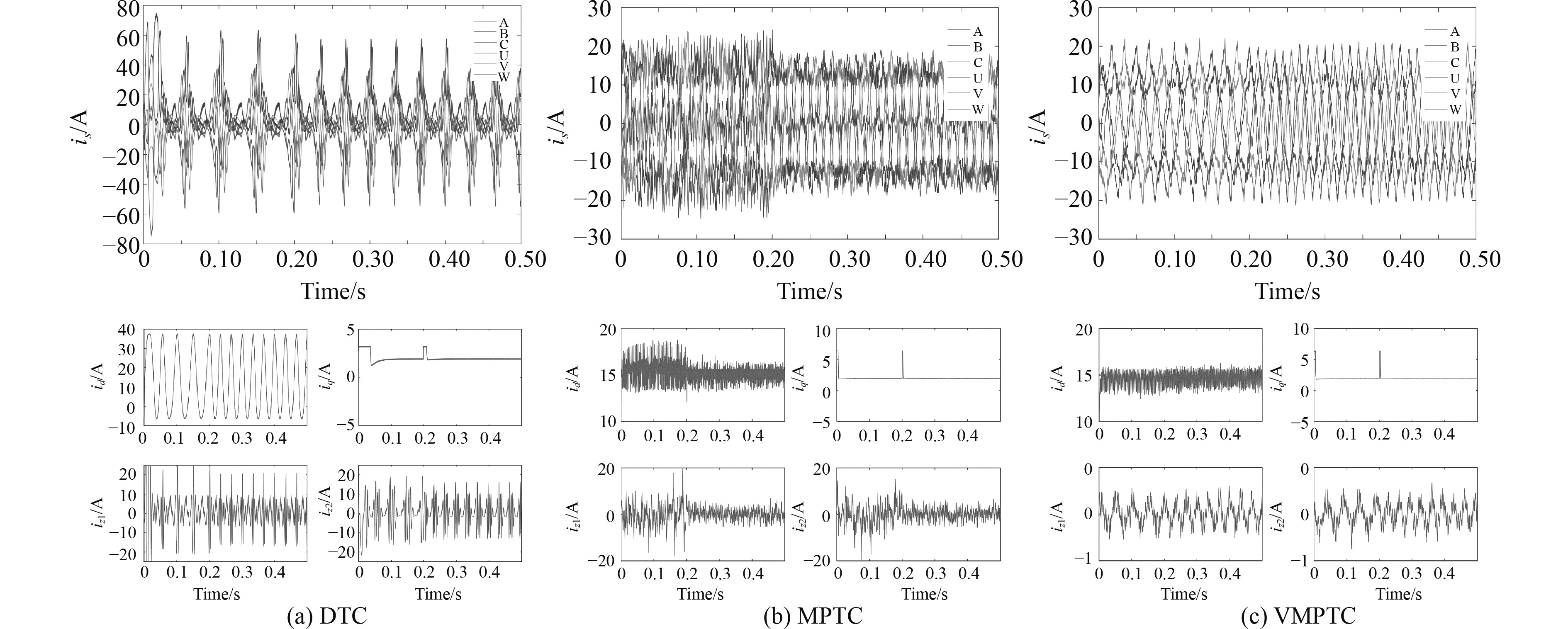
|
图 9 转速突变工况下电机电流相关波形 Fig. 9 Motor current correlation waveform under speed change condition |
|
|
表 3 船舶六相永磁同步电机3种控制策略性能对比 Tab.3 Performance comparison of three control strategies for marine six-phase permanent magnet synchronous motor |
本文对船舶电力推进系统中船舶六相永磁同步电机直接转矩控制策略进行深入研究,针对传统DTC中存在的不足,提出一种基于虚拟电压矢量模型预测转矩控制策略,并通过仿真研究了该方法的正确性,得到有关结论如下:
1)由于构建开关表时选择的电压矢量在z1-z2子空间上的投影不为0,传统DTC不能对谐波电流进行控制,谐波电流会产生电机发热严重、效率降低等问题,因此需要提出新的控制策略以降低谐波电流。
2)提出基于虚拟电压矢量的控制策略,通过合理分配电压矢量作用时间,将同一方向大矢量和中矢量合成,使z1-z2子空间平均电压幅值为0,并采用延迟2步预测方法和电压矢量中心化处理,便于硬件实现和进一步抑制电机转矩脉动和电流谐波。
3)传统MPTC仅使用大矢量作为控制集减少转矩脉动和谐波抑制效果较为有限,无法满足实际应用需求。因此提出VMPTC控制策略,结果表明所提方法可以有效抑制系统转矩脉动,谐波抑制效果更好且更稳定,是一种在船舶电力推进系统中对六相永磁同步电机控制进一步深入研究的控制方案,但仿真试验结果只是对于所提算法的一种验证,具有一定的参考意义,对于实际情况还需试验进行验证。
| [1] |
李浩, 王川, 郭昊昊, 等. 船舶推进电机运动控制系统仿真研究[J]. 舰船科学技术, 2020, 42(13): 114-119. DOI:10.3404/j.issn.1672-7649.2020.07.024 |
| [2] |
刘自程, 李永东, 郑泽东. 多相电机控制驱动技术研究综述[J]. 电工技术学报, 2017, 32(24): 17-29. DOI:10.19595/j.cnki.1000-6753.tces.l70304 |
| [3] |
张丙楠, 杜博超, 赵天旭, 等. 舰船电力推进电机研究现状与发展综述[J]. 中国电机工程学报, 2022, 42(20): 7608–7623.
|
| [4] |
王妍旖. 双三相永磁同步电机模型预测直接转矩控制研究[D]. 哈尔滨: 哈尔滨工业大学, 2019.
|
| [5] |
FENG G, LAI C, KELLY M, et al. Dual three-phase pmsm torque modeling and maximum torque per peak current control through optimized harmonic current injection[J]. IEEE Transactions on Industrial Electronics, 2019, 66(5): 3356-3368. DOI:10.1109/TIE.2018.2854550 |
| [6] |
HU Y, ZHU Z Q, ODAVIC M. Comparison of two-individual current control and vector space decomposition control for dual three-phase PMSM[J]. IEEE Transactions on Industry Applications, 2017, 53(5): 4483-4492. DOI:10.1109/TIA.2017.2703682 |
| [7] |
宋文祥, 任航, 杨煜, 等. 双三相永磁同步电机的双矢量模型预测转矩控制[J]. 电机与控制学报, 2022, 26(9): 97-107. |
| [8] |
张华强, 秦秀敬, 于亚新, 等. 双三相永磁同步电机直接转矩控制[J]. 电气传动, 2017, 47(2): 3-8. DOI:10.19457/j.1001-2095.20170201 |
| [9] |
HU H M, XU Z W, LIU X J, et al. Model predictive direct torque control of permanent magnet synchronous motor with reduced torque ripple[C]//IEEE International Conference on Applied Superconductivity and Electromagnetic Devices (ASEMD), 2015: 448–449.
|
| [10] |
张志锋, 朱春海. 双三相永磁同步电机占空比直接转矩控制[J]. 沈阳工业大学学报, 2020, 42(4): 361-367. |
| [11] |
GONCALVES P F C, CRUZ S M A, MENDES A M S, et al. Comparison of model predictive control strategies for six-phase permanent magnet synchronous machines[C]//44th Annual Conference of the IEEE Industrial-Electronics-Society (IECON), 2018: 5801–5806.
|
| [12] |
GONCALVES P F C, CRUZ S M A, MENDES A M S. Multistage predictive current control based on virtual vectors for the reduction of current harmonics in six-phase PMSMs[J]. IEEE Transactions on Energy Conversion, 2021, 36(2): 1368-1377. DOI:10.1109/TEC.2021.3055340 |
 2024, Vol. 46
2024, Vol. 46
