2. 中船澄西船舶修造有限公司, 江苏 无锡 214433;
3. 江苏大学 流体机械工程技术研究中心, 江苏 镇江 212013
2. Chengxi Shipyard Co. Ltd., Wuxi 214433, China;
3. Fluid Machinery Engineering Technology Research Center, Jiangsu University, Zhenjiang 212013, China
常见的风力发电机都是基于固定结构,不能安装在非常深或复杂的海底位置,但随着海上浮式平台的出现,这一点有了极大的改变。风力发电机现在可以安装在浮式平台上,这些平台通过灵活的锚、链条或钢索固定在海底。同时随着海上风电技术的发展,风电行业在实现大规模部署浮式海上风电方面仍然面临着重大的技术挑战。海上风力发电机的单机功率预计将达到20 MW左右,需要更大的海上浮式平台来支撑,因此对海上浮式平台[1 − 3]的研究是国内外学者研究的一个热点。
袁培银等[4]采用有限元软件建立浮式风力发电平台三维模型,分析其在不规则波作用下,浮式风力发电平台动力响应特性,实现海上风力发电平台工作状态的准确预报。王禅等[5]通过AQWA二次开发实时调用耦合平台运动的风荷载计算程序进行海上TLP浮式风机全耦合动态响应分析,研究了风、浪作用下TLP浮式风机平台及张力筋腱响应特性。邓小康等[6]对一种新型深水浮式平台进行频域和时域的计算,分析不同工况下该平台的运动响应和锚链力特性,并与试验数据相对比以验证数值方法的正确性。孔令海等[7]设计四浮筒浮式平台来搭载DTU 10 MW风机,通过AQWA建立水动力计算模型,进行频域与时域计算,来分析四浮筒基础的水动力性能。
Azcona等[8]提出了一种用于支撑10 MW风力发电机的系泊系统设计方法,使平台保持在预定位置,避免风、水流和非线性流体力学引起的漂移,同时采用钢链和聚酯纤维相结合的半紧系泊系统结构来降低系泊系统成本。Qao等[9]设计了一种新型浮式风机,并在上海交通大学深水池进行了模型试验,分析了在选定的风、浪、流条件和偏航误差情况下的响应。对各种极端响应进行了评估,并与标准推荐的限值进行了比较,以验证该设计在中等水深的可行性。Karimirad等[10]研究了不同设计案例对应的不同几何参数对半潜式支撑平台静水稳定性的影响,然后以一个设计案例为例,介绍了V型半潜式风力发电机的动力特性和性能,研究结果表明,此设计可以提高海上风力发电效率。Roddier等[11]总结了WindFloat技术的可行性,表明大型风机的平台设计必须利用与石油和天然气海上平台技术的协同作用,同时考虑到风机的不同设计要求和功能。
本文设计了一种新型的10 MW级的海上浮式平台,通过AQWA软件对其进行频域计算以及在极限工况下的时域计算来分析其运动性能及其系泊张力,为之后大型海上浮式平台的研究提供借鉴意义。
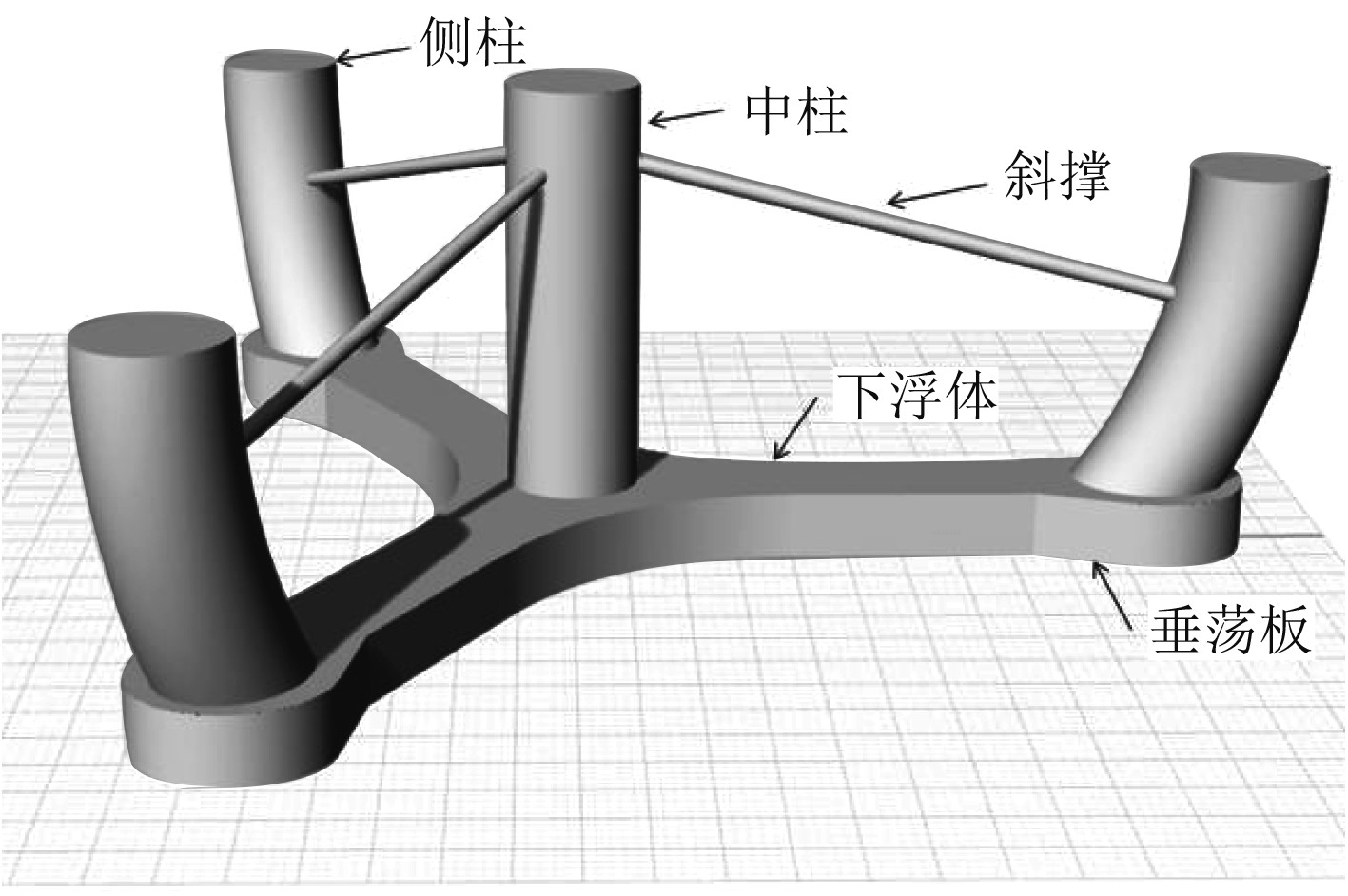
1 数值模型 1.1 浮式平台的基本参数本文针对10 MW级风机设计了一种新型的浮式平台结构。平台设计吃水27 m,用钢量4900 t,浮筒间距100 m。主要由中间柱、侧边曲柱、下浮体和斜撑组成,侧柱的曲度为22°,浮式平台的具体参数如表1所示,几何模型如图1所示。
|
|
表 1 平台主要参数 Tab.1 Main parameters of platform |
|
图 1 浮式平台的几何模型 Fig. 1 Geometric model of a floating platform |
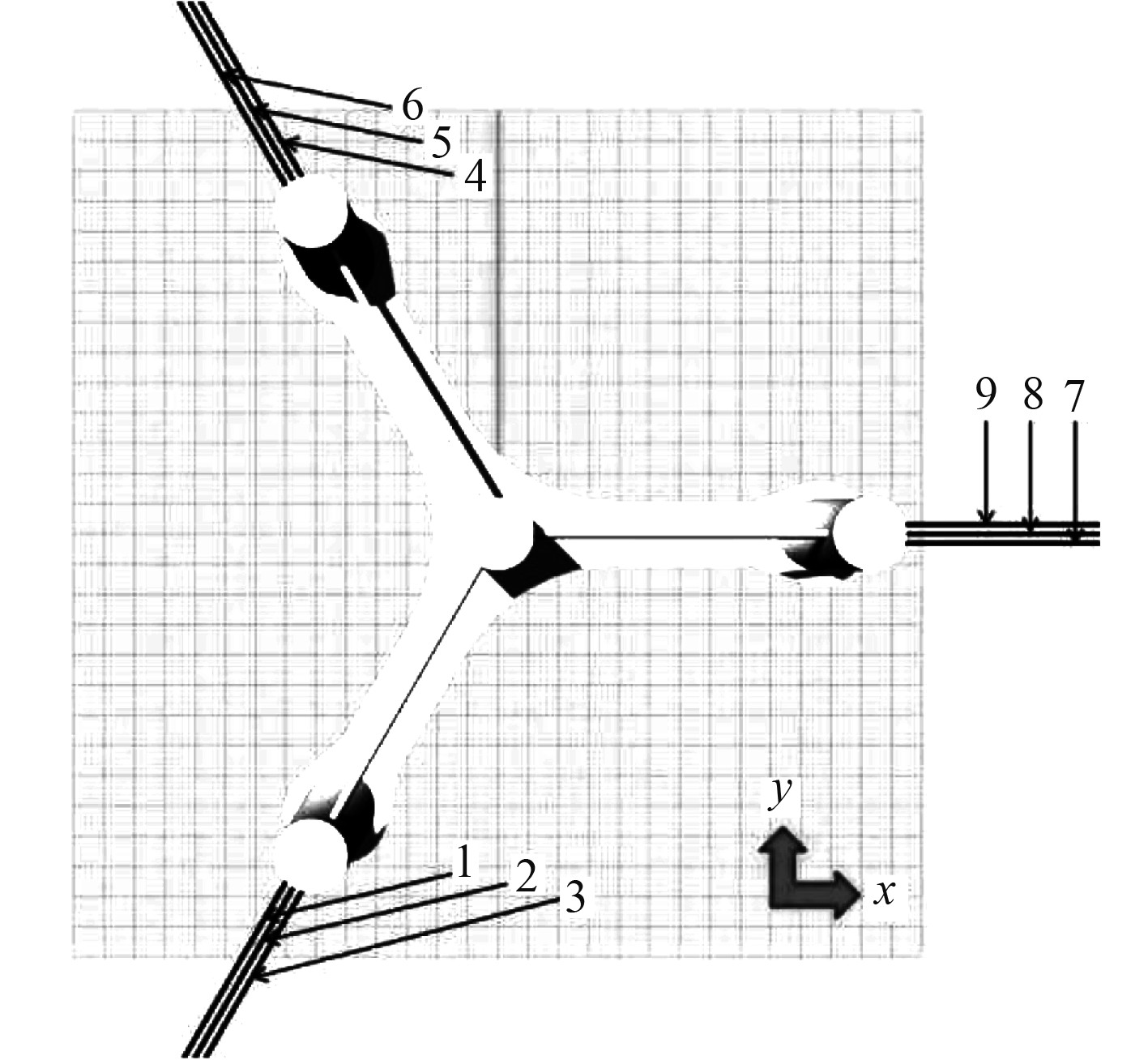
针对我国南海海域水深60 m,为该新型浮式平台设计了悬链式系泊系统。由于浮式风机的系泊系统要求具有良好的运动控制效果,而多点系泊方式又能有效控制浮体的平面运动和旋转运动,故采用多点系泊方式。同时,本文设计的浮式平台有3个侧柱,因此设计了3组9根系泊缆和锚点的系泊方案,其中每组中3根系泊缆都是平行式从导缆孔连接到海底的锚点,系泊系统的布置图如图2所示,基于吃水27 m,系泊半径540 m,系泊缆的导缆孔和锚点坐标如表2所示,系泊缆的物理参数如表3所示。
|
图 2 系泊系统布置图 Fig. 2 Layout of the mooring line |
|
|
表 2 系泊系统导缆孔和锚点坐标 Tab.2 Coordinates of fairlead and anchor points of the mooring system |
|
|
表 3 系泊缆的物理参数 Tab.3 Physical parameters of mooring line |
1)频域分析
AQWA的频域水动力分析可以求解浮式结构物静水刚度、附加质量、辐射阻尼、一阶波浪力(包括绕射力)、二阶定常波浪载荷。在求解二阶差频、和频载荷中可以考虑二阶速度势的影响,频域分析公式为:
| $ \left({M}+{A}\left(\omega \right)\right)\ddot{q}+{B}\left(\omega \right)\dot{q}+{C}q=F\left(\omega \right) 。$ | (1) |
式中:M为惯量;A为频率相关的附加质量;B为频率相关的辐射阻尼;C为静水刚度(及系泊刚度);F为振荡激励力。
2)时域分析
AQWA的时域分析分为2种。基于平均湿表面的时域求解可以分析浮式结构在风、流、一阶波浪载荷和二阶波浪载荷作用下的运动响应及连接部件的响应状态。基于非线性瞬时湿表面时域分析可以考虑浮体瞬时湿表面变化的影响,时域分析公式为:
| $ \left({M}+{{A}}_{\infty }\right)\ddot{q}+{\int }_{0}^{t}{K}\left(t-\tau \right)\dot{q}\left(\tau \right){\mathrm{d}}\tau +{C}q=F,$ | (2) |
| $ {K}\left(t\right)=\frac{2}{{\text{π}} }{\int }_{0}^{\infty }{B}\left(\omega \right)\cos\left(\omega t\right){\mathrm{d}}\omega。$ | (3) |
式中:
通过AQWA软件导入浮式风机平台模型,进行频域计算,分析其6个自由度方向上的RAO,由于整个平台对称,方向上选取了浪向角0~180°,每隔30°浪向角得到一个频域解。这里选取该平台最主要的三自由度的运动情况,如图3所示,分别为垂荡、横摇以及纵摇的RAO。

|
图 3 三自由度方向上的RAO Fig. 3 RAO of three degrees of freedom |
图3(a)中可以看到垂荡随着周期的增加,先增大后减小,最大的峰值点是在周期为22.4 s时,最大值为1.82 m,同时随着角度的变化,各个曲线几乎重叠在一起。图3(b)中浪向角在0°和180°时横摇值为0,整个曲线的趋势同样先增大后减小,在角度为120°时出现了最大值2.21 °,此时周期为25.7 s。图3(c)的曲线类似于图3(b),区别在于在角度为180°时出现了最大值2.55 °,此时周期为25.7 s,以上可以发现垂荡、横摇和纵摇的固有周期分别为22.4 s、25.7 s和25.7 s,因此所设计的新型浮式平台垂荡、横摇和纵摇的固有周期可以有效避开海上波浪波浪能量集中的周期范围[12](4~12 s),有良好的运动性能。
在分析固有周期的基础上,提取6个不同自由度附加质量数据,研究其随着周期的变化规律,如图4所示。纵荡和横荡中随着周期的增加,附加质量先增大到一个峰值,其值都为1.78×107 kg,此时周期都为8.4 s,而后减小逐渐趋于稳定。垂荡的附加质量也同样随着周期的增加而增大到一个峰值为2.79×107 kg,此时周期都为12.6 s,而后先减小再缓慢增加一部分。横摇、纵摇和首摇随着周期增长到最大值的过程中都出现了多个极值点。横摇和纵摇中的附加质量都在周期为11 s时出现了峰值为1.77×1010 kg·m2,首摇则是在9.3 s时出现了峰值为4.69×1010 kg·m2。横摇、纵摇和首摇都是先呈增长趋势,同样在增长前期都出现了多个极值点,而后呈下降趋势逐渐到趋于稳定。通过上述分析可知:平台在6个自由度方向的附加质量随着周期的增加,前期产生了多个极值,而后期趋于稳定。

|
图 4 六自由度方向上的附加质量 Fig. 4 Added mass of six degrees of freedom |
我国南海海域面积约3.5×106 km2,为中国近海中面积最大、水最深的海区,平均水深1212 m,最大深度5559 m。南海在海浪和海流方面,特点是浪小流大。所以本文选取南海中水深为60 m的开阔海域来对该新型10 MW海上浮式平台进行时域分析,同时想要验证所设计平台的运动性能的好坏,需选用极限海况下进行研究。因此在极限海况下,波浪谱类型选取JONSWAP谱,有义波高为5.76 m,谱峰提升因子为1.0~3.3,这里取2。此外,南海大部分海域的风能密度基本都在200 W/m2以上,风速55 m/s(10 min平均风速),海流流速为1 m/s。研究总时长为10800 s,时间步长为0.1 s,截取0~3500 s作为分析时段。同样在方向上选取了浪向角0~180°,每隔30°浪向角得到一个时域解,本研究假设风、浪和流是同向的。
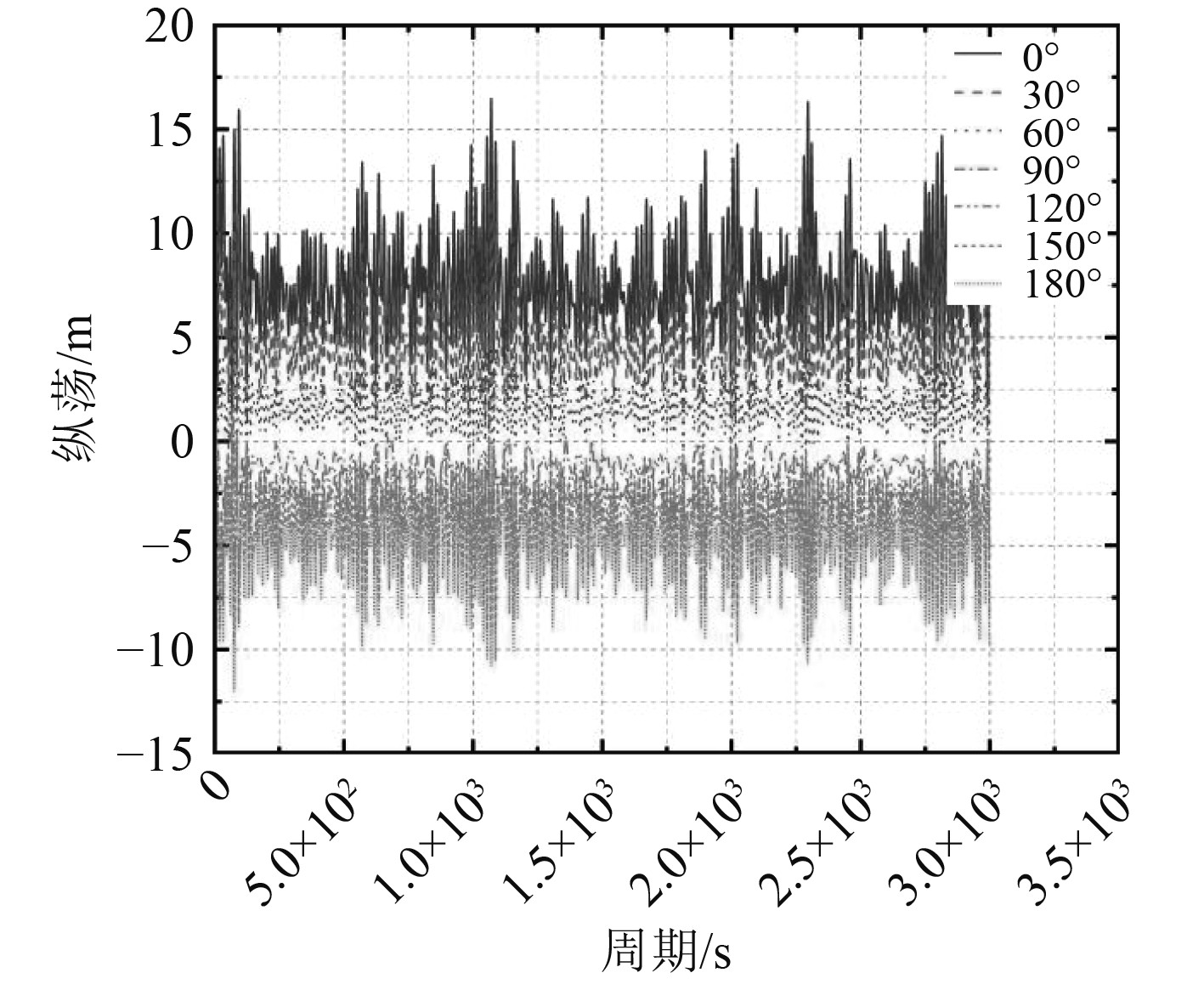
表4为极限海况下平台的运动统计结果,可以发现,平台平动最大位移出现在纵荡运动,而转动的最大角度出现在纵摇。图5为各个浪向角下平台的纵荡运动,可以发现分别在浪向角为0°和180°时出现了最大值和最小值,对应到表4中分别为16.83 m和−11.21 m。图6为各个浪向角下平台的纵摇运动,可以发现最大值和最小值都出现在浪向角为180°时,对应到表4中分别为11.81°和−7.795°,同时从表4中也能看到最小垂荡值为−6.213 m。所以结合以上运动数据分析,新型平台在极限工况下仍具有良好的运动性能。
|
|
表 4 极限海况下平台的运动统计结果 Tab.4 The motion statistics of platform with extreme sea condition |
|
图 5 不同浪向角下平台的纵荡运动 Fig. 5 The surge motion of platform under different wave direction |

|
图 6 不同浪向角下平台的纵摇运动 Fig. 6 The pitch motion of platform under different wave direction |
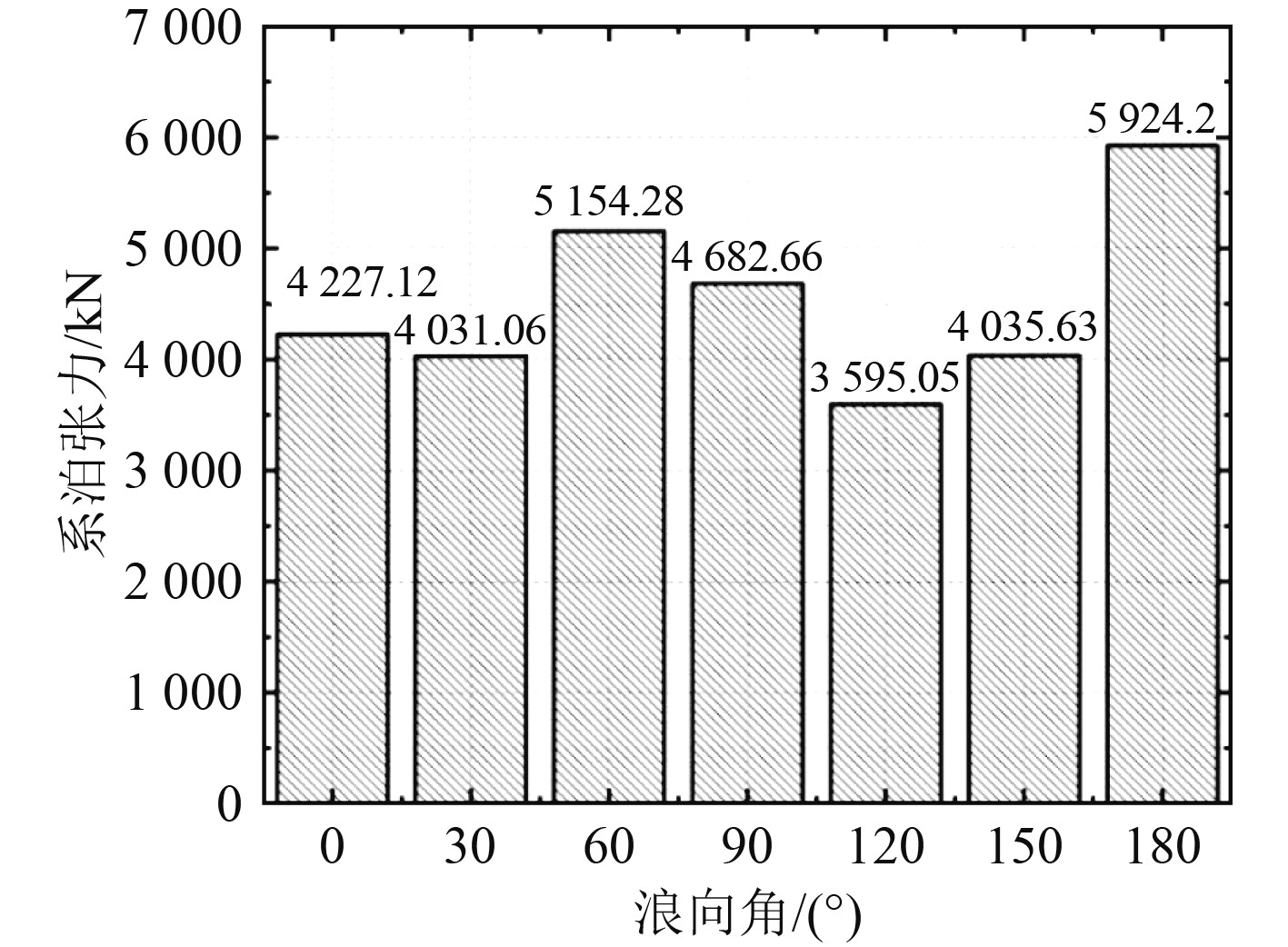
平台的所有系泊缆的系泊张力也是判断该平台运动性能的重要指标。一般情况下系泊破断力与系泊张力的比值为安全系数,设计平台需满足允许安全系数1.67。图7为各个浪向角下平台的所有系泊缆中的最大系泊张力,图中可以看到在浪向角为180°时,整个平台在各个浪向角下的最大系泊张力为5924.2 kN,该系泊张力作用在系泊缆9上。由表3中系泊缆的物理参数可知系泊缆的破断载荷为1.136×104 kN,所以安全系数为1.92,大于允许安全系数1.67,能够保证平台安全运行。
|
图 7 不同浪向角下平台的最大系泊张力 Fig. 7 The maximum mooring tension of platform under different wave direction |
通过在不同浪向角下对频域计算的幅值响应算子、附加质量,以及时域计算的运动响应、系泊张力的分析,得到的主要结论如下:
1)平台垂荡、横摇和纵摇的固有周期分别为22.4 s、25.7 s和25.7 s,可以有效避开海上波浪能量集中的周期范围,具备良好的运动性能。
2)平台在6个自由度方向的附加质量随着周期的增加,前期产生了多个极值,后期趋于稳定。
3)平台在极限工况下纵荡、纵摇以及垂荡的最值分别为16.83 m、11.81°以及−6.213 m,仍具有良好的运动性能。
4)平台系泊缆的安全系数为1.92,大于允许安全系数1.67,能够保证平台安全运行。
综上所述,本研究证明了该新型海上浮式平台的可行性和安全性,也为之后超大型浮式平台的研究提供了借鉴。
| [1] |
胡天宇, 朱仁传, 范菊. 海上浮式风机平台弱非线性耦合动力响应分析[J]. 哈尔滨工程大学学报, 2018, 39(7): 1132-1137. DOI:10.11990/jheu.201611064 |
| [2] |
徐思远, 张淑华. 海上浮式风机平台的水动力分析[J]. 水道港口, 2018, 39(2): 195-199. DOI:10.3969/j.issn.1005-8443.2018.02.012 |
| [3] |
蔡新, 张洪建, 王浩, 等. 面向深远海的新型海上风力机浮式平台水动力性能研究[J]. 中国电机工程学报, 2022, 42(12): 4339-4352. |
| [4] |
袁培银, 赵宇, 王平义, 等. 海上风力发电平台概念设计及系泊系统特性研究[J]. 舰船科学技术, 2017, 39(7): 79-83. DOI:10.3404/j.issn.1672-7619.2017.04.016 |
| [5] |
王禅, 金辉, 王腾. 风浪联合作用下海上TLP浮式风机动态响应分析[J]. 舰船科学技术, 2019, 41(19): 75-79. DOI:10.3404/j.issn.1672-7649.2019.10.014 |
| [6] |
邓小康, 谢文会, 李阳, 等. 一种新型深水浮式平台及其系泊系统动力响应分析[J]. 舰船科学技术, 2021, 43(5): 95-101. DOI:10.3404/j.issn.16727649.2021.03.019 |
| [7] |
孔令海, 容学苹, 窦培林, 等. 海上风机四浮筒基础运动响应分析[J]. 舰船科学技术, 2022, 44(17): 90-95. DOI:10.3404/j.issn.1672-7649.2022.17.018 |
| [8] |
AZCONA J, VITTORI F. Mooring system design for the 10 MW triple spar floating wind turbine at a 180 m sea depth location [C]//16th Deep Sea Offshore Wind R&D conference. Norway, 2019.
|
| [9] |
CAO Q, XIAO L, CHENG, Z, et al. Operational and extreme responses of a new concept of 10 MW semi-submersible wind turbine in intermediate water depth: An experimental study[J]. Ocean Engineering, 2020, 217: 108003. DOI:10.1016/j.oceaneng.2020.108003 |
| [10] |
KARIMIRAD M, MICHAILIDES C. V-shaped semisubmersible offshore wind turbine: an alternative concept for offshore wind technology[J]. Renewable Energy, 2015, 83: 126-143. DOI:10.1016/j.renene.2015.04.033 |
| [11] |
RODDIER D, CERMELLI C. WindFloat: A floating foundation for offshore wind turbines[J]. Journal of Renewable and Sustainable Energy, 2010, 2: 033104. DOI:10.1063/1.3435339 |
| [12] |
阮胜福, 樊冰, 王涛, 等. 半潜式海上风电平台运动特性研究[J]. 海洋工程装备与技术, 2016, 3(6): 371-375. DOI:10.3969/j.issn.2095-7297.2016.06.008 |
 2024, Vol. 46
2024, Vol. 46
