加快建设智能化、高效化、绿色化的船舶运载工具是海洋经济发展的硬件基础之一。无人水面船/艇(USV)是指没有船员参与控制情况下能够在水面上自主航行的智能化船舶。这类船舶具有速度快、体积小、成本低和自主航行的优势,使得USV能够在诸如海洋搜索、救援、军事行动等多场景中备受欢迎。受船体固有属性限制,这种小型船舶方便控制的同时也使其易受到外部环境干扰,因此对运动控制系统鲁棒性有着较高的要求。
Kose等[1]第一次通过计算机辅助控制,借助拖船是现实船舶的自动靠离泊。Mizuno等[2]基于多重打靶法,提出一种准实时自动靠离泊位的控制方法,该方法能够在较短的时间内给出解决方案。张强等[3]基于MMG船舶模型提出一种基于双极性S-PID的非线性反馈算法,抑制了靠港过程中噪声和外部干扰使船舶保持理想航向,有利于靠港过程的安全。徐海洋等[4]为了解决岸壁效应对船舶靠泊控制的影响,提出一种鲁棒自适应控制的控制算法,通过补偿岸壁效应对船舶的干扰,消除控制输出的抖振现象。韩周周[5]融合神经网络与自抗扰控制算法,能够无超调地完成船舶的航向控制,实现船舶的靠泊控制任务。贾玉鹏等[6]利用ANN神经网络重新训练系统控制器,提高了控制输出精度,解决靠泊过程船首偏差问题。王世凯等[7]设计了结合GA的LQR(Linear Quadratic Regulator,LQR)控制器,减小了系统因俯仰角和垂荡运动产生的附加阻力。
杨胜飞[8]基于协方差自适应调整的学习机制(Covariance Matrix Adaptation Evolution Strategy,CMA-ES),提出一种学习机制更新方法,降低了算法的时间复杂度,解决了多目标优化问题过早收敛的问题。Maki等[9]将CMA-ES进化策略应用在自动靠泊系统的控制参数优化过程中,得到了最小化船舶在靠泊过程中的轨迹与期望路径之间的偏差。Maniyappan等[10]利用CMA-ES对舵角变化时间序列进行PD优化控制,实验表明优化后的控制器有效避免了横甩问题。Miyauchi等[11]用CMA-ES算法优化描述了船舶在靠港过程中运动学行为的Nomoto模型参数,可以获得更高精度的控制效果。
由于船舶自动靠泊系统是在受限水域下的低速运动控制,外界环境对船舶的操纵控制的干扰具有不可忽略性。即便目前船舶已经初步实现开阔水域的自主避碰、航路规划等一系列自动化操纵,但船舶的自主靠泊依旧是目前智能化船舶技术发展较大的难点,自主船舶的“最后一公里”的问题仍未得到很好解决,还有很多研究工作需要开展。
LQR在MIMO控制领域具有较好的兼容性,这为复杂的船舶靠泊过程控制提供了一个新的思路;CMA-ES在模型参数优化和控制律的优化上,也展现出较好的优化效果。图1为基于目前船舶自动靠泊研究现状提出的自主靠泊系统架构,其涵盖了船舶智能化要求的路径规划、智能算法、最优控制、动力分配等指标,能够实现船舶自动靠泊“最后一公里”的运动控制目标。根据2018年中国船级社发布的《自主货物运输船舶指南》[12]中关于船舶智能靠泊要求,表1总结了上述文献研究中被忽略或未及深入的问题,给出了相应的解决方案。

|
图 1 船舶自主靠泊系统架构图 Fig. 1 Architecture of ship autonomous berthing system |
|
|
表 1 本文针对现阶段研究问题提出的解决方案 Tab.1 Solutions proposed in this paper for the current research problems |
本文研究对象为USV靠泊过程,为了研究方便,依据Fossen[13]提出的船舶状态空间模型,选择三自由度(surge,sway,yaw)进行处理,得到本文控制的三自由度船舶模型。
| $ \begin{gathered} {\boldsymbol{M}}{{\dot {\boldsymbol{v}} }_r} + {\boldsymbol{C}}({{\boldsymbol{v}} _r}){{\boldsymbol{v}} _r} + {\boldsymbol{D}}({{\boldsymbol{v}} _r}){{\boldsymbol{v}} _r} = \tau + {\tau _{{\text{wind}}}} + {\tau _{{\text{current}}}},\\ \dot \eta = {J_\Theta }(\eta ){{\boldsymbol{v}} _r} + {{\boldsymbol{V}}_c} 。\end{gathered} $ | (1) |
| $ \upsilon ={[u,v,r]}^{{\mathrm{T}}}\text{,}\eta ={[x,y,\varphi ]}^{{\mathrm{T}}} 。$ | (2) |
式中:
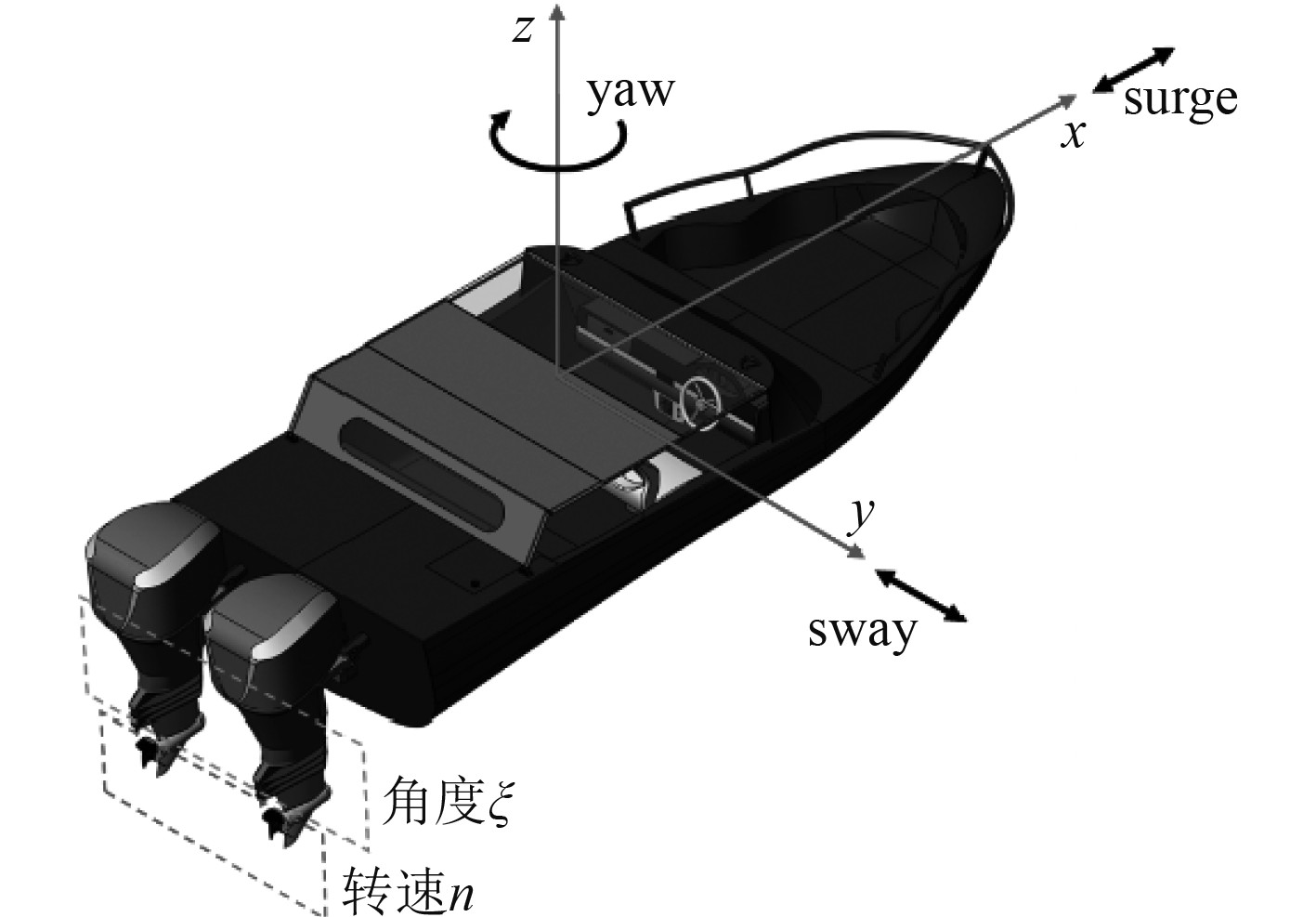
|
图 2 USV的三自由度示意图 Fig. 2 A schematic of USV 's three degrees of freedom |
根据船舶流体动力学与运动控制手册[13],风和流的叠加力通过下式计算得到。
| $ \begin{split} {\tau _{{\text{wind}}}} = & \frac{1}{2}{\rho _a}V_a^2{[{C_X}\left( {{\mu _{wd}}} \right){A_T},{C_Y}\left( {{\mu _{wd}}} \right){A_L},L{C_N}\left( {{\mu _{wd}}} \right){A_L}]^{\mathrm{T}}} ,\\ {\tau _{{\text{current}}}} = & \frac{1}{2}\rho V_{cd}^2[{C_{XC}}\left( {{\mu _{cd}}} \right){A_{TC}},{C_{YC}}\left( {{\mu _{cd}}} \right){A_{LC}},\\ & {C_{NC}}\left( {{\mu _{cd}}} \right){A_{LC}}]^{\mathrm{T}}。\\[-5pt] \end{split} $ | (3) |
文献[14]实现了基于LQR的大型邮轮的船舶运动控制,在一定风速情况下的船舶实验操纵性实验效果良好。文献[15 − 18]的仿真实验均验证了LQR在船舶运动控制上的优势。
根据Michał Brasel[15]提出的控制模型,LQR控制系统的状态方程为式(4),性能指标J由式(5)给出。
| $ \left\{ \begin{array}{l} \dot x = {\boldsymbol{A}}x + {\boldsymbol{B}}u + {\boldsymbol{H}},\\ y = {\boldsymbol{C}}x 。\end{array}\right. $ | (4) |
| $ J = \frac{1}{2}\mathop \int \nolimits_0^T \left( {{x^{\text{T}}}{\boldsymbol{Q}}x + {u^{\text{T}}}{\boldsymbol{R}}u} \right){\mathrm{d}}t。$ | (5) |
式中:x和u分别对应系统状态和控制向量;A为控制对象状态矩阵;B为u对x的线性控制矩阵;H为系统的干扰矩阵;C为系统输出矩阵;Q为x的半正定对称加权矩阵;R为对u的加权正定对称矩阵。
CMA-ES是Hansen等在演化策略(ES)算法上衍生而来的一种全局优化的进化策略计算方法,能够寻找非线性、非凸问题下的全局最优解。CMA-ES算法的搜索性能良好,与传统的线性规划方法相比,该方法不需要梯度计算,减小了计算代价。文献[9, 10, 19 − 21]利用该方法在船舶横向运动控制的优化上取得了不错的实验效果。文献[22]使用CMA-ES进行优化处理,以适应模型不确定下的靠泊问题;文献[23]利用该方法优化靠泊的轨迹,提高航行控制的鲁棒性和灵活性。CMA-ES方法通过自适应地调整协方差矩阵自动调整搜索空间,从而实现高效的全局搜索,在路径规划和运动控制过程中均能起到较好的优化作用。
3 基于CMA-ES的USV自主靠泊模型在船舶复杂控制领域里,多输入多输出、强耦合的非线性系统数学模型难以准确建立,使得控制器设计变得非常困难。Fossen[24]、张显库[25]等在大型船舶上已取得了一定的成果,但全驱动船靠泊过程中的低速大漂角模型还有待深入研究。外界干扰和船舶的运动约束也限制着船舶运动控制,目前的研究主要聚焦在最短路径、耗时等方面,自身运动约束和干扰限制还有待深入研究。
图3(a)是本文选择的路径规划算法—人工势场(APF),APF路径规划方法是计算目标的引力和障碍物的斥力,通过势力场梯度下降方向移动更新。CMA-ES优化的流程是计算适应度函数是否属于阈值区间,否则重新更改权重计算引力和斥力。在使用APF算法路径规划中,合力场用
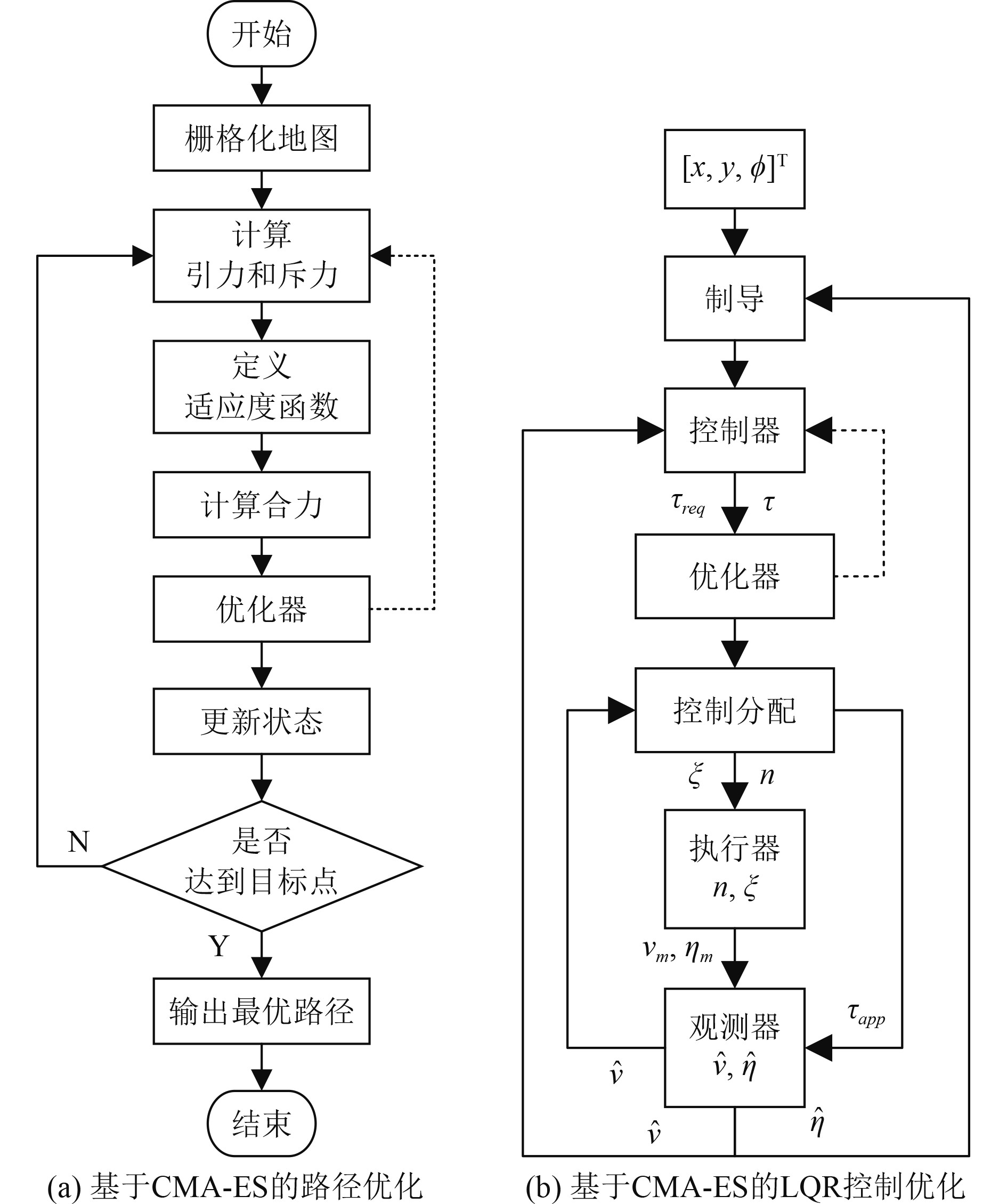
|
图 3 控制系统优化策略 Fig. 3 Control system optimization strategy |
| $ U(q) = {U_{att}}(q) + {U_{rep}}(q)。$ | (6) |
图3(b)是本文使用的LQR控制算法。优化器CMA-ES通过调整状态量和控制量的权重矩阵参数,计算寻找符合约束条件的最优值。
根据式(1)和式(4)得到式(7),其中状态矩阵
| $ \begin{gathered} {{\dot v}_r} = {\boldsymbol{A}}({v_r}){v_r} + {\boldsymbol{B}}(\tau + {\tau _{{\rm{wind}}}} + {\tau _{{\rm{current}}}}),\\ \dot \eta = {J_\Theta }(\eta ){v_r} + {V_c}。\\ \end{gathered} $ | (7) |
根据芳村康男的大漂角流体动力模型,对船舶模型的修正为式(8),详细的推导过程及参数解释见文献[26]。
| $ \left\{ \begin{array}{l} {X_{{H}}} = {X_{{H}}}(r = 0) + {X_{vr}}vr + {X_{rr}}{r^2},\\ {Y_{{H}}} = {Y_{{H}}}(r = 0) + {Y_r}|u|r +\\ \qquad \dfrac{1}{2}\rho d{C_d}\left( {Lv|v| - \int_{ - L/2}^{L/2} {\left( {v + {C_{ry}}xr} \right)} \left| {v + {C_{ry}}xr} \right|{\text{d}}x} \right) ,\\ {N_{{H}}} = {N_{{H}}}(r = 0) + {N_r}|u|r +\\ \qquad \dfrac{1}{2}\rho d{C_d}\int_{ - L/2}^{L/2} {\left( {v + {C_{rr}}xr} \right)} \left| {v + {C_{rn}}xr} \right|x{\text{d}}x 。\end{array} \right. $ | (8) |
当船舶完成靠泊时,需要满足的基本状态约束为:
| $ P1 - {P_1} \leqslant {[d\_ref,d\_ref,\psi \_ref]^{\mathrm{T}}}。$ | (9) |
式中:
位置约束是为了减小优化的搜索空间,设定的泊位停靠区域
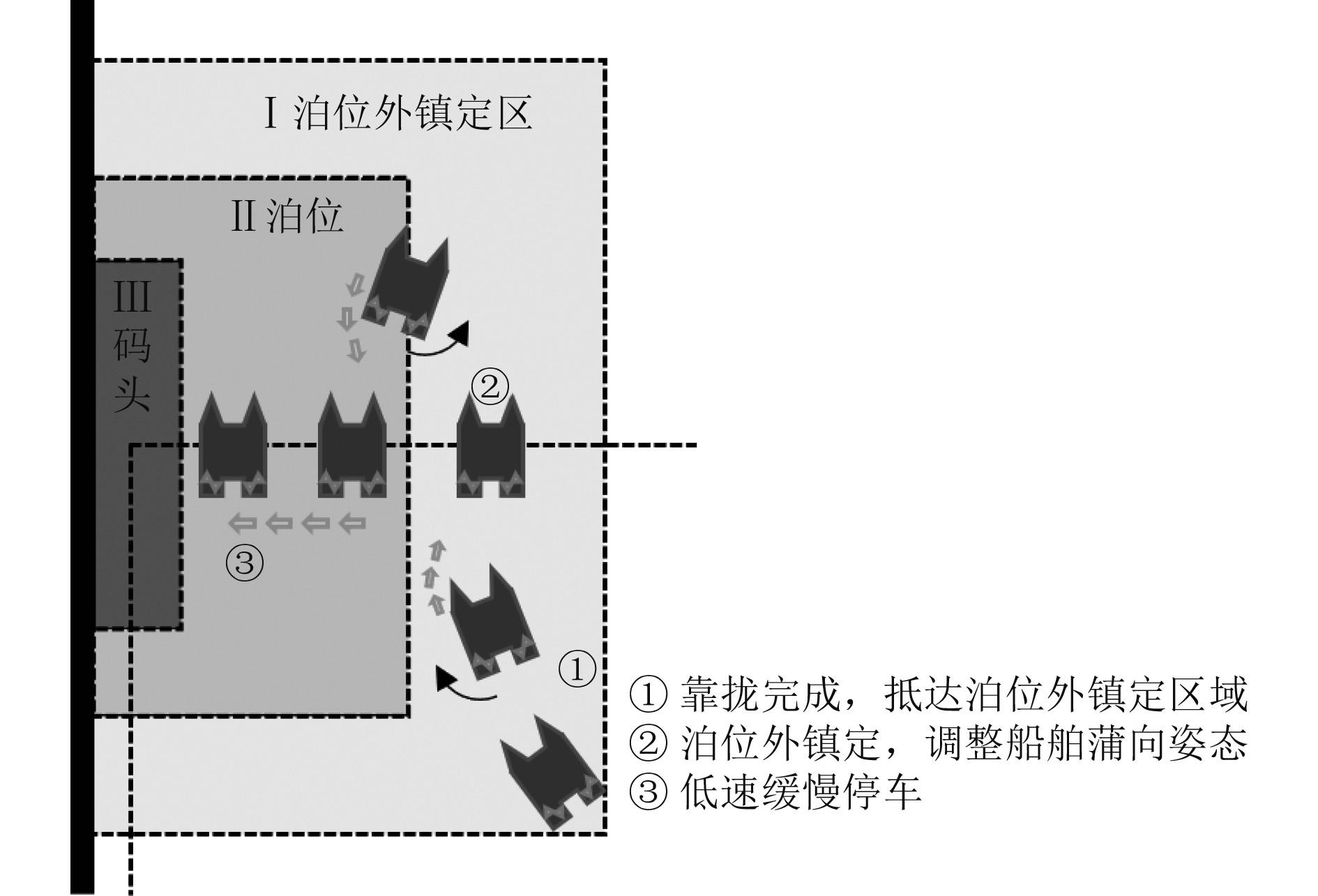
|
图 4 靠泊区域设定 Fig. 4 Berthing area |
| $ {\text{Ⅱ}}_{C}=\displaystyle \sum _{i=1}^{4}{{\displaystyle \int }}_{{p}_{i}\in {C}_{\text{berth}}}\left|{Y}_{i}-{Y}_{\text{berth}}\right|\text{d}t。$ | (10) |
本文主要考虑USV螺旋桨舵角
| $ \begin{split} &{C}_{\min}=[{{\delta }_{\mathrm{min}}}\text{,}n_{\min}]^{\mathrm{T}},C'_{\min}=[{{\delta }'_{\mathrm{min}}}\text{,}n'_{\min}]^{\mathrm{T}},\\ &{C}_{\max}=[{{\delta }_{\mathrm{max}}}\text{,}n_{\max}]^{\mathrm{T}},C'_{\min}=[{{\delta }'_{\mathrm{max}}}\text{,}n'_{\max}]^{\mathrm{T}}。\end{split} $ | (11) |
根据船舶靠泊安全要求,对船舶停靠速度约束:
| $ \left|{u}_{t}\right|\leqslant {u}_{\mathrm{max}}\text{,}\left|{v}_{t}\right|\leqslant {v}_{\mathrm{max}}。$ | (12) |
式中:
对于船舶航向的约束:
| $ \left| {rot} \right| = \left| {\frac{{\Delta \psi }}{{\Delta t}}\times\frac{{180}}{\text{π}}} \right| \leqslant RO{T_{\max }} 。$ | (13) |
式中:
假定系统状态向量
| $ \begin{split} \dot x = & {{\boldsymbol{M}}^{ - 1}}(u + {\tau _{{\mathrm{wind}}}} + {\tau _{{\mathrm{current}}}} - {\boldsymbol{C}}x + {{\boldsymbol{d}}}x + \Phi (x)\vartheta ) = \\ & {{\boldsymbol{M}}^{ - 1}}({\boldsymbol{d}} - {\boldsymbol{C}})x + {{\boldsymbol{M}}^{ - 1}}(u + {\Phi }\left( x \right)\vartheta ) +\\ & {{\boldsymbol{M}}^{ - 1}}({\tau _{{\text{wind}}}} + {\tau _{{\text{current}}}}) =\\ & {\boldsymbol{f}}\left( x \right) + {{\boldsymbol{M}}^{ - 1}}\left( {u + {\Phi }\left( x \right)\vartheta } \right) + {\boldsymbol{H}}, \\ \dot y = & {\boldsymbol{R}}(\psi )x + {V_c}。\\[-1pt] \end{split} $ | (14) |
式中:
| $ J = \frac{1}{2}{e^{\mathrm{T}}}(T){\boldsymbol{S}}e(T) + \frac{1}{2}\mathop \smallint \nolimits_0^{\mathrm{T}} \left( {{e^{\mathrm{T}}}(t){\boldsymbol{Q}}(t)e(t) + {u^{\text{T}}}(t){\boldsymbol{R}}(t)u(t)} \right){\mathrm{d}}t。$ | (15) |
将船舶停泊过程中对舵角和螺旋桨的控制量作为系统广义上的耗能指标。
| $ F(n,\delta ) = \mathop \sum \limits_{t = 0}^{T - 1} ({\lambda _1}n_t^2 + {\lambda _2}\delta _t^2) 。$ | (16) |
系统的控制目标函数:
| $ {K_J}\cdot J + {K_F}\cdot F \text{,}{H_U}\cdot U + {H_F}\cdot F $ | (17) |
式中:
综上,靠泊系统总体的优化目标函数和约束条件为:
| $ \min \left\{ \begin{gathered} {H_U}\cdot U + {H_F}\cdot F ,\\ {K_J}\cdot J(P,C) + {K_F}\cdot F(n,\delta ) 。\end{gathered} \right. $ | (18) |
| $ s.t.\left\{ \begin{aligned} & P1 - {P_1} \leqslant {[d\_ref,d\_ref,\psi \_ref]^{\mathrm{T}}},\\ &\left| {{u_t}} \right| \leqslant {u_{\max }},\left| {{v_t}} \right| \leqslant {v_{\max }},\\ &\left| {rot} \right| \leqslant RO{T_{\max }},\\ & {C_{\min }} \leqslant C \leqslant {C_{\max }},\\ & C{'_{\min }} \leqslant C' \leqslant C{'_{\max }} 。\end{aligned} \right. $ | (19) |
实验用到的船舶为全驱动的USV小船,模型水动力系数参考了Fossen[13]的Otter船体模型。本文设置2组仿真实验:实验1是使用LQR在无风无流的环境下船舶自动靠泊,实验2是利用本文提出的综合控制系统在一定风流环境下的自动靠泊仿真,同时2组实验均未设置有动态障碍物。实验的仿真环境配置为Win11教育版 Intel(R) Core(TM) i5-9500 CPU @ 3.00 GHz 16 GRAM。实验用到的仿真船舶模型初始参数见表2,相关参数取值见表3。
|
|
表 2 USV实验船模参数 Tab.2 USV experimental ship model parameters |
|
|
表 3 USV实验仿真参数 Tab.3 USV experimental simulation parameters |
当泊位附近水域不存在风流干扰时(
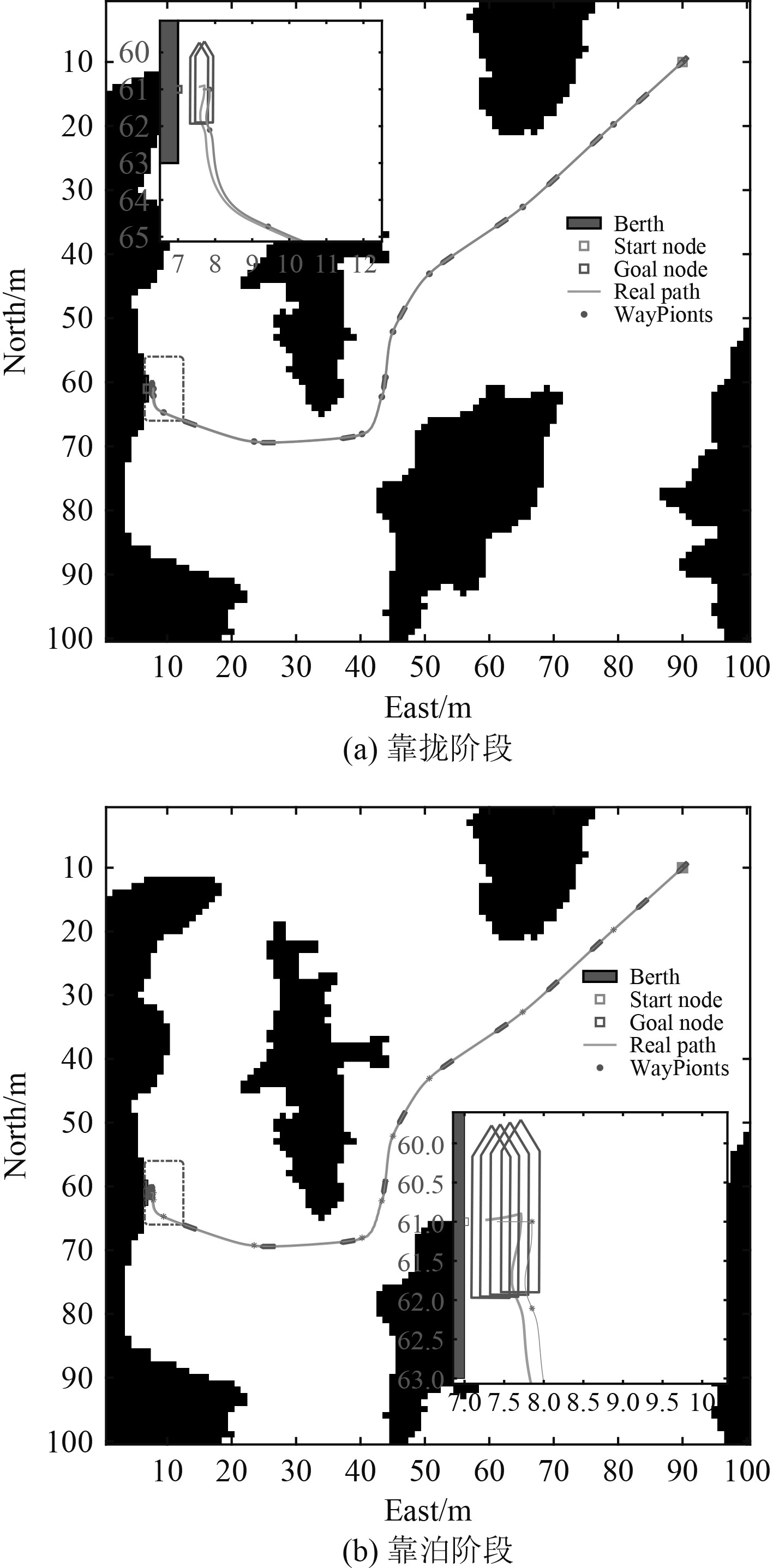
|
图 5 基于LQR船舶自动靠泊过程(无风无流) Fig. 5 USV auto-berthing process based on LQR (without wind or current) |
图5(a)是理想环境下利用LQR控制船舶运动至泊位外镇定的实验结果,控制器跟随效果良好。对于靠泊的第二阶段图5(b),已经完成泊位外镇定的船舶,根据船载传感器对泊位码头的距离检测数据,完成横向靠泊过程。在这个过程中,船舶需要根据LQR控制器输出的最优控制灵活变动,实现船舶横向靠泊,最终完成自主靠泊。
4.2 基于CMA-ES优化的USV自动靠泊当泊位水域存在北向和东向的风流干扰时(
|
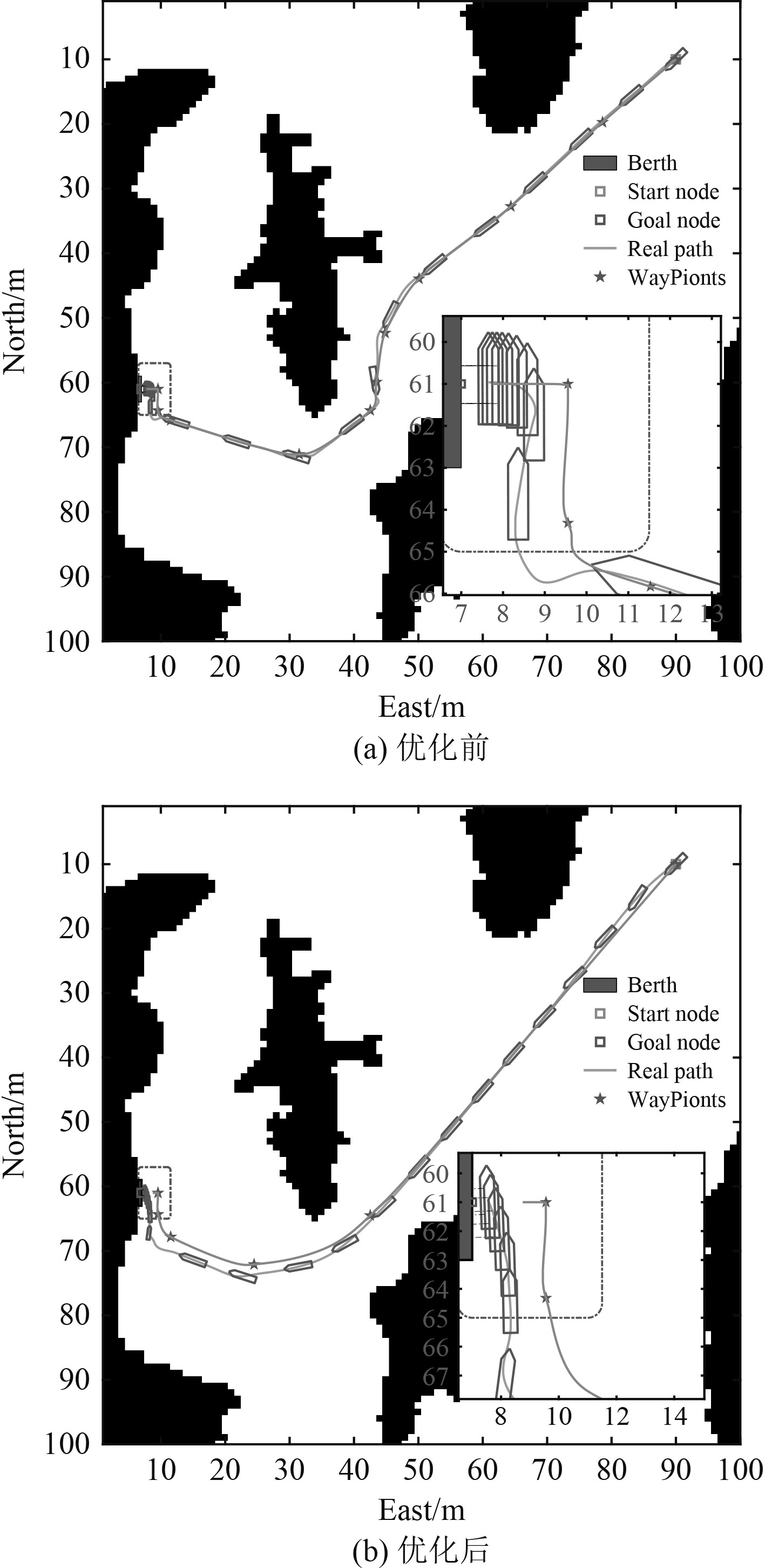
图 6 优化前后的靠泊过程 Fig. 6 The auto-berthing process before and after optimization |
对比图5和图6,说明风流的影响对于船舶的运动影响很大,从靠泊阶段图5(b)和图6(a)能够看到风流对船舶低速运动下的影响:风流的干扰会使得船舶,特别是USV这种小型船只在低速的运动状态下出现较大的轨迹偏差。图6是存在一定风流干扰下USV的自主靠泊过程。对比图5发现,即便是存在不能忽略的风流,加入了CMA-ES优化后的控制系统在对船舶运动姿态突变的抑制上表现良好。通过图5和图6,在整个控制过程的实验效果,CMA-ES的优化显著。
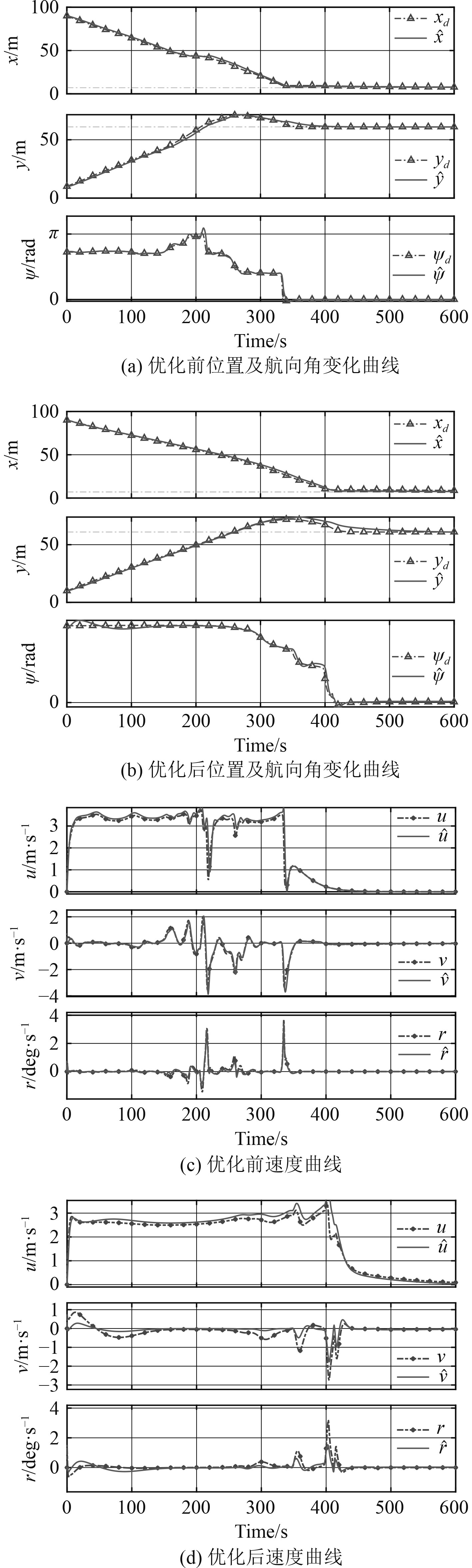
对比图7(a)和图7(b)可知,加入了对路径的优化后,航行过程中船首向的突变明显减少,在仿真时间0~300 s期间,优化后更加平滑。在300~500 s期间船舶进入靠泊第二阶段停靠期间,优化函数的加入使得船舶的姿态调整在满足目标状态时尽可能减小,航向角和位置的变化更加平滑,没有瞬间的突变。同时也能发现优化后的路径与控制器的输入更加适配,实际船舶运动和规划的路径符合度更高。
|
图 7 靠拢阶段的运动参数对比 Fig. 7 Comparison of motion parameters in the approaching stage |
对比图7(c)和图7(d)可知,在靠泊第一阶段的靠拢过程中,优化函数让船舶的输出控制具有更大的容错率。图7(c)中的速度频繁变化,瞬时间的极性变化明显存在,而通过优化后的图7(d)则有效避免了这种突变。同时发现在靠泊第二阶段优化函数的加入让LQR控制器的输出更加平稳,相比于图7(c)的剧增剧减,图7(d)的曲线反映出整个过程都没有造成转速、舵角的急速变化,这与实际船舶靠泊的操作是一致的。
对比图7中优化前后的运动参数曲线,还发现优化之后的船舶靠泊过程用时增加,在前期靠拢阶段的速度也有所减小,猜测原因可能是控制精度较高无法自适应船舶运动阶段性要求,这也是本文下一步的研究工作。
由图8可知,优化后的舵角变化显著减少,变化的幅度也明显减小;航向角的突变消失,变动更为平滑。优化后的航路总体上更加平滑,减少了船舶在航行过程中操舵改向的次数。

|
图 8 船首向和航向角的变化 Fig. 8 Changes of ship heading and heading angle |
本文提出了完整的靠泊控制系统框架,使用CMA-ES优化包括LQR控制器在内的靠泊控制系统,实验过程中充分考虑了船舶的动力学因素、自然环境干扰和运动能耗,结果显示能够很好地对船舶靠泊过程进行良好控制,符合实验预期。通过仿真实验结果证明本文提出的基于CMA-ES船舶自动靠泊系统可行的。但在目前的实验过程中,仍存在未考虑船舶的岸基效应,控制器的增益参数不能完全自适应跟随模型变化等些许不足。后期将继续深入开展USV船自主靠泊研究,结合实船完成真实环境的算法试验。
| [1] |
KOSE K, FUKUDO J, SUGANO K, et al. Study on a computer aided manoeuvring system in harbours[J]. Naval Architecture and Ocean Engineering, 1987, 25: 105-113. |
| [2] |
MIZUNO N, UCHIDA Y, OKAZAKI T. Quasi real-time optimal control scheme for automatic berthing[J]. IFAC Papers on Line, 2015(16).
|
| [3] |
ZHANG Q, ZHANG X, IM N. Ship nonlinear-feedback course keeping algorithm based on MMG model driven by bipolar sigmoid function for berthing[J]. International Journal of Naval Architecture and Ocean Engineering, 2017, 9(5): 525-536. DOI:10.1016/j.ijnaoe.2017.01.004 |
| [4] |
徐海祥, 朱梦飞, 余文曌, 等. 面向智能船舶的自动靠泊鲁棒自适应控制[J]. 华中科技大学学报(自然科学版), 2020, 48(3): 25-29. |
| [5] |
韩周周. 基于自抗扰-神经网络控制的船舶自动靠泊仿真研究[D]. 大连: 大连海事大学, 2020.
|
| [6] |
贾玉鹏, 神和龙, 尹勇, 等. 基于神经网络的无人船自主靠泊模拟研究[J]. 中国航海, 2021, 44(4): 107-111. |
| [7] |
WANG S, JIN H, MENG L, et al. Optimize motion energy of AUV based on LQR control strategy[C]//2016 35th Chinese Control Conference (CCC). IEEE, 2016: 4615-4620.
|
| [8] |
杨胜飞. 基于协方差矩阵自适应学习机制的多目标优化研究[D]. 贵阳: 贵州大学, 2019.
|
| [9] |
MAKI A, SAKAMOTO N, AKIMOTO Y, et al. Application of optimal control theory based on the evolution strategy (CMA-ES) to automatic berthing[J]. Journal of Marine Science and Technology, 2020, 25(1): 221-233. DOI:10.1007/s00773-019-00642-3 |
| [10] |
MANIYAPPAN S, UMEDA N, MAKI A, et al. Effectiveness and mechanism of broaching-to prevention using global optimal control with evolution strategy (CMA-ES)[J]. Journal of Marine Science and Technology, 2021, 26(2): 382-394. DOI:10.1007/s00773-020-00743-4 |
| [11] |
MIYAUCHI Y, MAKI A, UMEDA N, et al. System parameter exploration of ship maneuvering model for automatic docking/berthing using CMA-ES[J]. Journal of Marine Science and Technology, 2022, 27(2): 1065-1083. DOI:10.1007/s00773-022-00889-3 |
| [12] |
《自主货物运输船舶指南(2018)》发布[J]. 船舶标准化工程师, 2018, 51(5): 53.
|
| [13] |
FOSSEN T I. Handbook of marine craft hydrodynamics and motion control[M]. John Wiley & Sons, 2011.
|
| [14] |
邵闯. 基于LQR的大型船舶操纵运动控制研究[D]. 上海: 上海交通大学, 2017.
|
| [15] |
BRASEL M. ADATPIVE LQR control system for the nonlinear 4-DoF model of a container vessel[C]//2013 18th International Conference on Methods & Models in Automation & Robotics (MMAR). IEEE, 2013: 711-716.
|
| [16] |
FARZANEGAN B, MALEKIZADEH H, GHASSEMI H, et al. Control system design for a surface effect ship by linear-quadratic regulator method[J]. Journal of Marine Engineering, 2017, 13(25): 47-56. |
| [17] |
田涛. 基于鲁棒最优控制的舵减摇控制系统研究[D]. 哈尔滨: 哈尔滨工程大学, 2021.
|
| [18] |
ZHAO Y, ZHANG Z, WANG J, et al. Fin-rudder joint control based on improved linear-quadratic-regulator algorithm[J]. IEEE Access, 2022: 1.
|
| [19] |
陈佳云. 基于改进的CMA-ES的仿真足球机器人的行走优化[D]. 南京: 南京邮电大学, 2020.
|
| [20] |
MAKI A, SAKAMOTO N, AKIMOTO Y, et al. On broaching-to prevention using optimal control theory with evolution strategy (CMA-ES)[J]. Journal of Marine Science and Technology, 2021, 26(1): 71-87. DOI:10.1007/s00773-020-00722-9 |
| [21] |
MAKI A, AKIMOTO Y, NAOYA U. Application of optimal control theory based on the evolution strategy (CMA-ES) to automatic berthing (part: 2)[J]. Journal of Marine Science and Technology, 2021, 26(3): 835-845. DOI:10.1007/s00773-020-00774-x |
| [22] |
AKIMOTO Y, MIYAUCHI Y, MAKI A. Saddle point optimization with approximate minimization oracle and its application to robust berthing control[J]. ACM Transactions on Evolutionary Learning and Optimization, 2022, 2(1): 1-32. |
| [23] |
MIYAUCHI Y, SAWADA R, AKIMOTO Y, et al. Optimization on planning of trajectory and control of autonomous berthing and unberthing for the realistic port geometry[J]. Ocean Engineering, 2022, 245: 110390. DOI:10.1016/j.oceaneng.2021.110390 |
| [24] |
FOSSEN T I. A nonlinear unified state-space model for ship maneuvering and control in a seaway[J]. International Journal of Bifurcation and Chaos, 2005, 15(9): 2717-2746. DOI:10.1142/S0218127405013691 |
| [25] |
张显库, 张国庆. 船舶港内掉头操纵的简捷鲁棒控制[J]. 中国航海, 2014, 37(2): 31-34. |
| [26] |
YASUO Y. Study on mathematical model of steering motion in shallow water (Part 2): fluid forces acting on main hull during low-speed steering[J]. Journal of Kansai Shipbuilding and Ocean Engineering, 1988: 77−84.
|
 2024, Vol. 46
2024, Vol. 46
