2. 中国科学院 机器人与智能制造创新研究院,辽宁 沈阳 110169;
3. 中国科学院大学,北京 100049
2. Institutes for Robotics and Intelligent Manufacturing, Chinese Academy of Sciences, Shenyang 110169, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
AUV作为一种极为重要的探索海洋工具,在海洋勘测、军事等领域中广泛应用,其性能在近几年的发展中得到了极大的提高,AUV携带多种先进的传感器,具有很强的获取海洋相关数据的能力[1]。传统的水下航行器通常采用鱼雷形体来减小航行阻力,鱼雷形体尾端装有主螺旋桨和鳍舵控制面来驱动和控制水下航行器[2]。面对复杂多变的海洋环境,对水下机器人的稳定性、机动性都提出了很高的要求,然而传统的AUV在悬停状态或慢速状态下很难实现有效的控制,因为在这种操作条件下,控制面的效果有下降甚至完全失效的趋势[3]。这些缺点限制了AUV在许多领域的发展和应用。
为了提高AUV的机动性,通常可以为其配备矢量推进器,以提供矢量推力作为低速运行时的驱动力和控制力[3]。推力矢量技术在飞机、火箭等运载工具中展现出了优越性,在AUV领域,国外在这方面研究起步较早,如Bluefin、MBARI等矢量推进AUV在实际作业中均取得了积极成果[4],国内在这方面相关研究大多停留在理论分析和概念模型阶段,投入实际使用的成果较少,故对矢量推进器进行结构设计与性能分析对国内AUV矢量推进技术的发展有着重要意义。
受并联机器人机动性好、结构紧凑等优点的启发,设计了一种并联机构矢量推进器,为了对其进行系统、全面的研究,建立了矢量推进器的运动学和动力学模型。本文提出一种基于PUS-PRS-S并联机构的矢量推力器的新设计,并通过计算和仿真,验证其在运动性能方面的优越性。
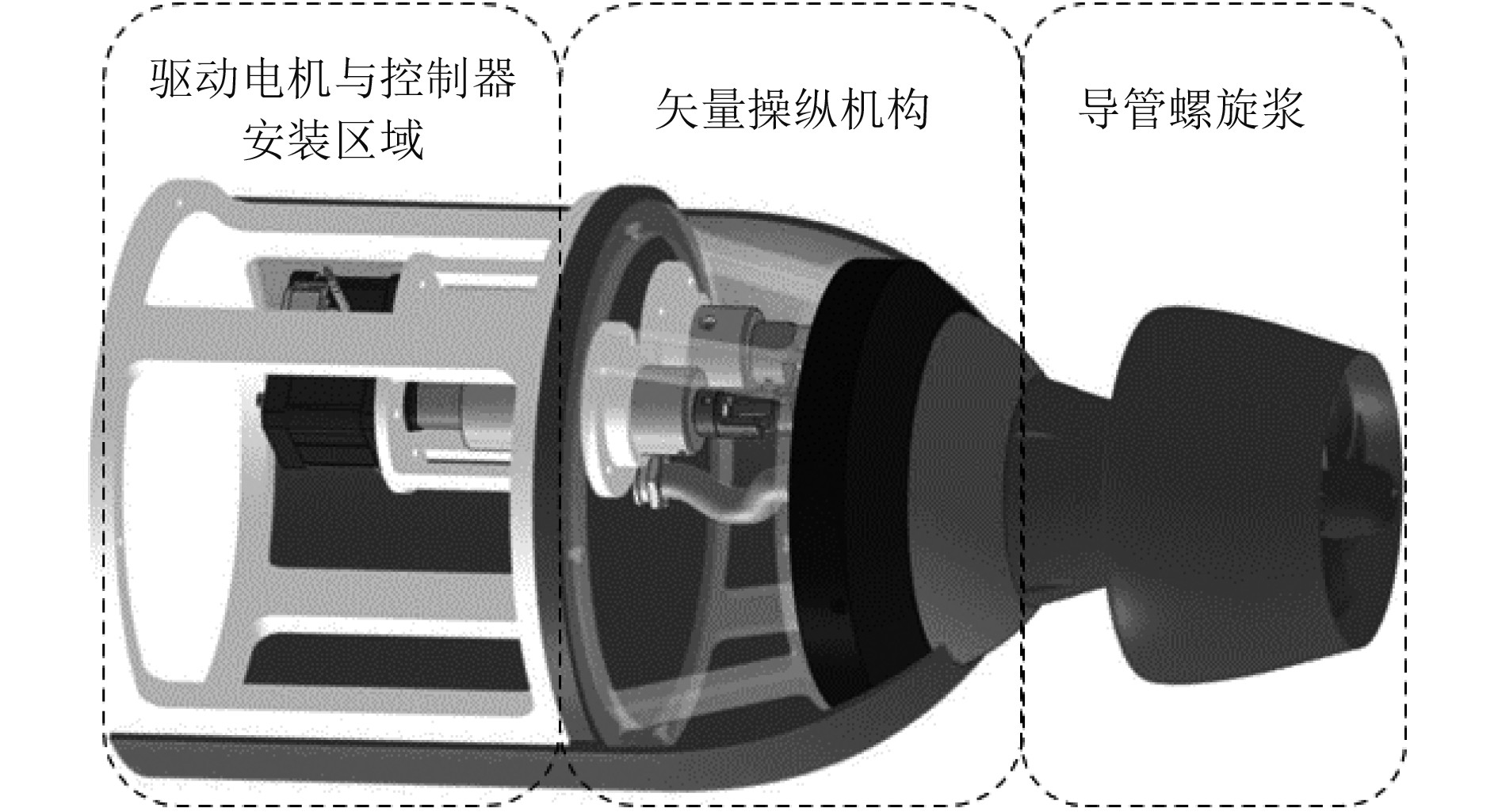
1 矢量推进器结构设计考虑到AUV的尾锥部分空间有限,设计一种既不会降低整体动力学性能又不会使结构过于复杂的矢量推进器是非常重要的。并联机构具有一系列固有的优势,如结构紧凑、承载能力高、控制精度高和响应速度快等,并联机构已经广泛应用于各领域中[5]。鉴于并联机构的诸多优势,为AUV设计了一种基于并联机构的矢量推进装置,如图1所示,采用模块化设计的矢量推进器可以很容易地作为一个整体安装在AUV的尾部。
|
图 1 矢量推进器模块 Fig. 1 Vectored thruster module |
矢量推进器由导管螺旋桨、偏转球台、支架和2条驱动支链组成,导管螺旋桨固连在旋转球台上,螺旋桨驱动电机安装在球台内部,球台在支架的包裹下可视为一个球面关节。2条驱动支链穿过舱壁通过球铰与顶部偏转球台相连,将顶部偏转球台限制在3个旋转自由度内。舱壁固连于AUV尾部,在2条支链的作用下,限制了顶部球台绕机身轴线的旋转自由度,当2支链按照一定规律运动时,顶部球台可以进行俯仰和偏摆运动,从而实现导管螺旋桨推力的矢量化。
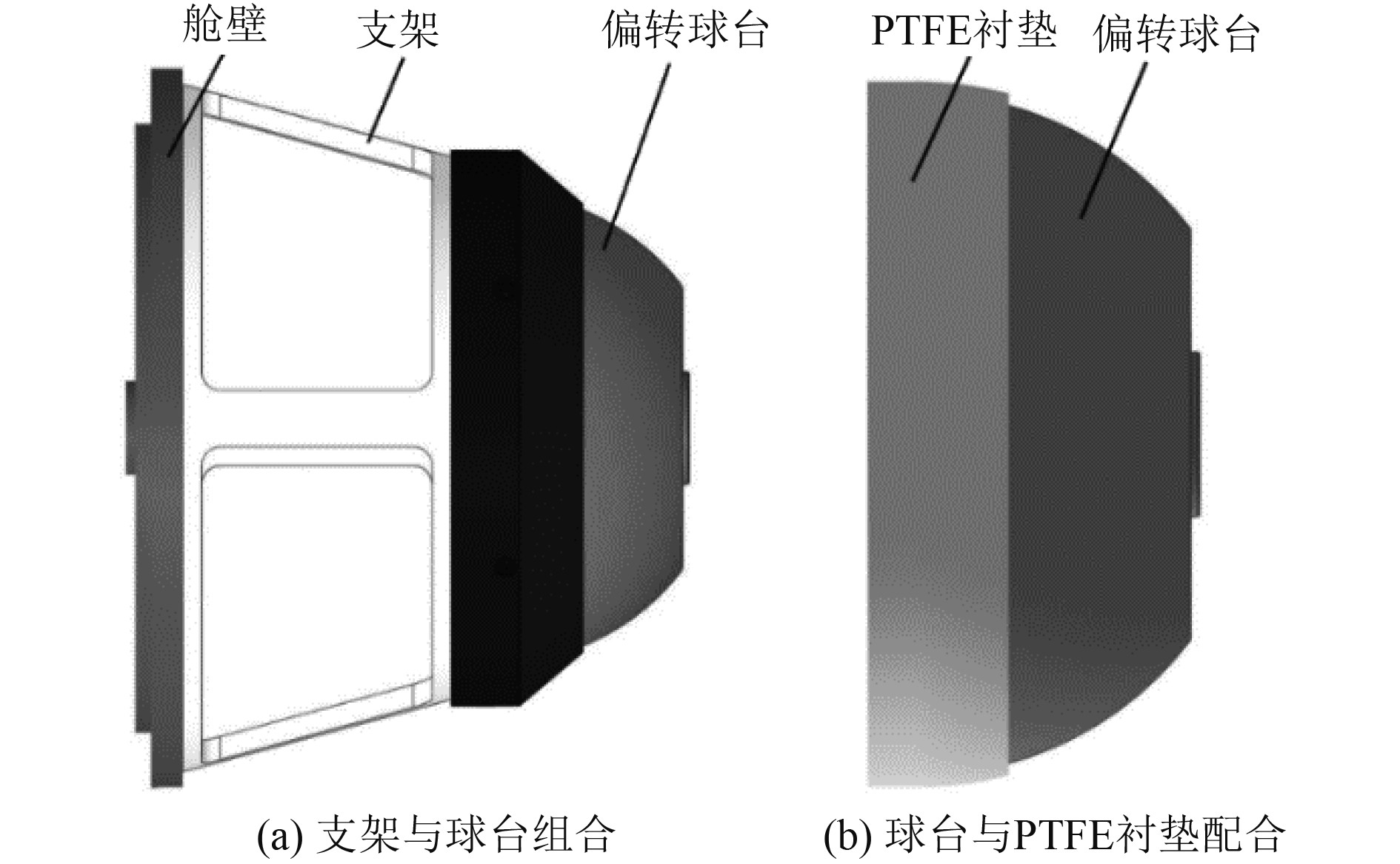
支架与偏转球台的组合约束了导管螺旋桨的移动自由度,也可以将作用在球台上的力分散到AUV的壳体上,如图2所示。考虑到加工制造的误差,并且矢量推进器安装在水下机器人尾部工作时,随着球台的转动,球台大部分表面都会与水接触,若采用支架内球面和球台外球面直接配合的形式,一方面加工困难,另一方面不方便对球台与内球面接触部分进行润滑,因此在球台转动时会存在很大的摩擦力。故采用PTFE衬垫与球台形成球面配合的方式,由于PTFE具有极佳的自润滑形式,无需添加润滑剂,当球台使用铝合金材料时,查表可知PTFE与其动摩擦因素仅为0.05。在这种设计下,推力矢量机构的运动更加灵活可靠,可以产生良好的推力矢量化效果。
|
图 2 球台的装配组合 Fig. 2 The assembly of the ball |
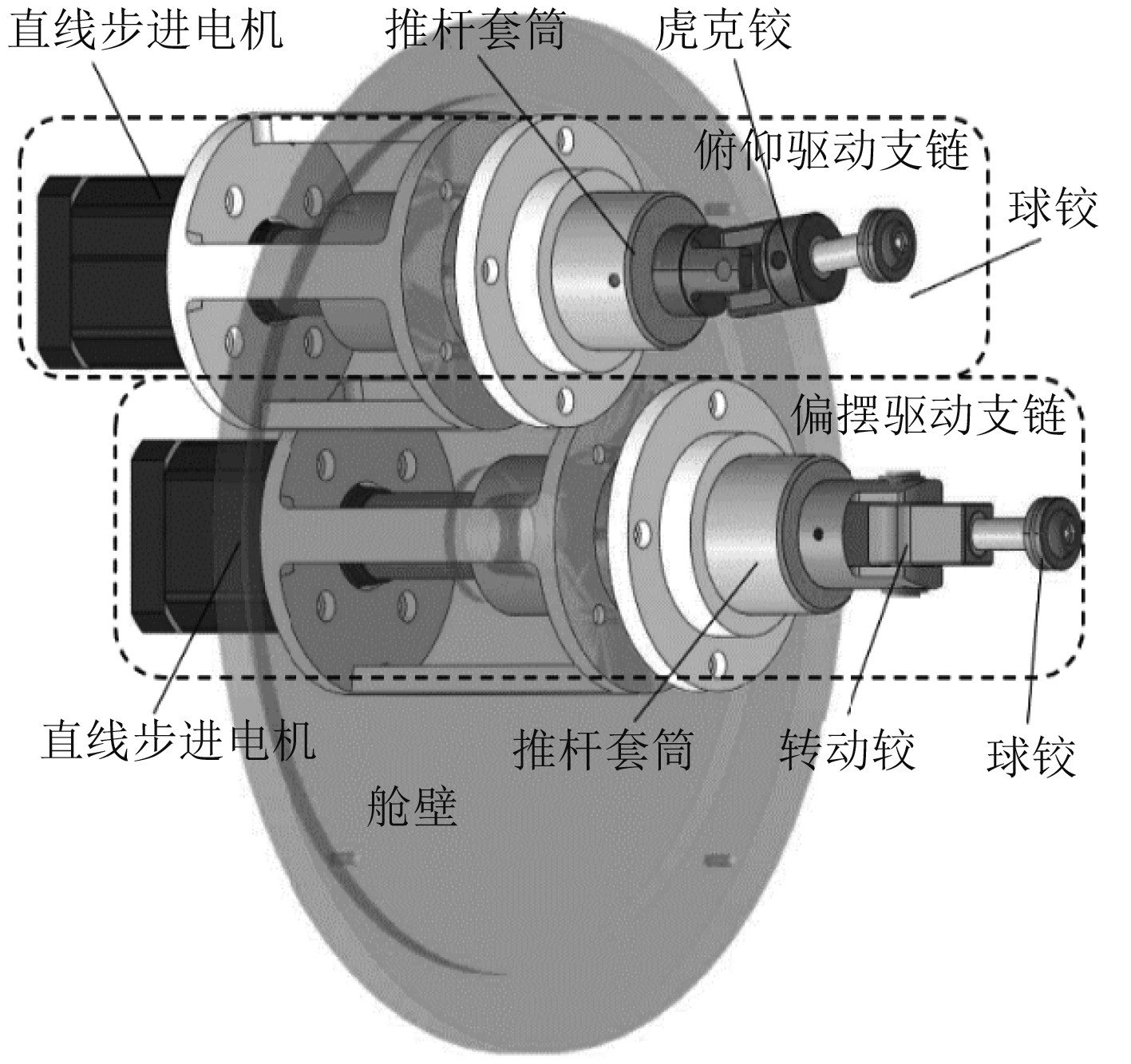
驱动支链整体结构如图3所示,两支链分别由驱动电机、电机固定座、推杆套筒、虎克铰(转动铰)和球铰构成。矢量推进器在水下机器人整体控制系统当中充当受控对象的角色,在AUV航行过程收到改变航向指令时,矢量推进器控制螺旋桨轴进行偏转运动,从而对AUV施加扰动。在实际控制过程中,通常使用角度闭环控制,根据水下机器人机身角度的反馈对矢量推进器偏转角度进行实时调整,且考虑到水下流场具有不确定性,矢量推进器球台的偏转角度无需达到很高的控制精度,角度误差范围一般在±1°左右。
|
图 3 驱动支链结构图 Fig. 3 Structure diagram of driving chain |
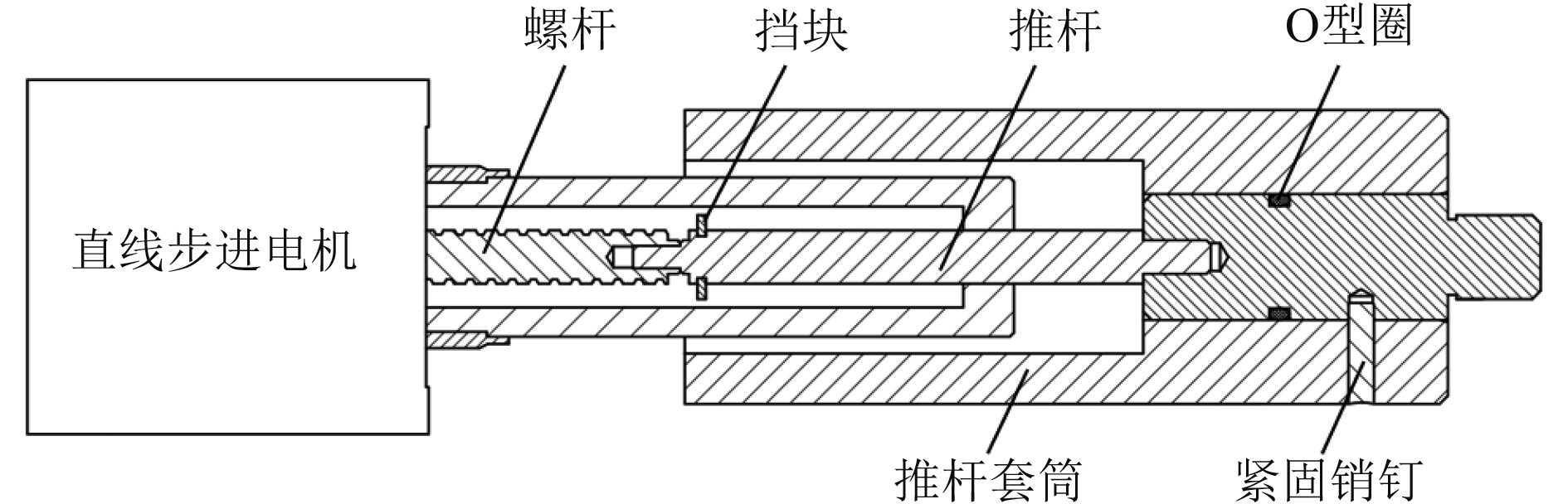
因此,选择步进电机作为矢量推进器运动支链的驱动电机。传统线性驱动器内,丝杆通过联轴器与电机转轴相连,整体安装尺寸较大,为节省安装尺寸,决定选用固定轴式直线步进电机。直线电机通过在电机内置一个带内螺纹的转子,转子的内螺纹和螺杆相啮合,螺杆连接推杆可以直接输出直线往复运动。考虑到直线步进电机主体部分难以进行防水处理,若使用防水型电机则成本较高,故将直线电机机身后半部分置于密封舱体中,但直线电机螺杆与推杆部分不方便安装动密封,故额外加工一推杆套筒将电机推杆包裹,如图4所示。
|
图 4 直线电机推杆套筒装配图 Fig. 4 Assembly drawing of Linear motor’s push rod sleeve |
由于驱动支链前端置于进水舱体中,需要考虑其密封问题。密封主要分静密封和动密封。静密封选用O型圈密封,推杆套筒与舱壁之间为直线往复运动,须进行动密封。由于推杆直线运动速度较低,选用格莱圈即可达到动密封效果。格莱圈是由一个橡胶材质O型圈和PTFE环组合而成,动摩擦阻力小,保险起见选用两组前后串联的格莱圈[6],如图5所示,A为进水区,B为密封舱体。为减小推杆套筒运动过程中的摩擦力,在套筒与舱壁之间安装一无油衬套,套筒的内表面层为PTFE,进一步减小往复运动摩擦力。
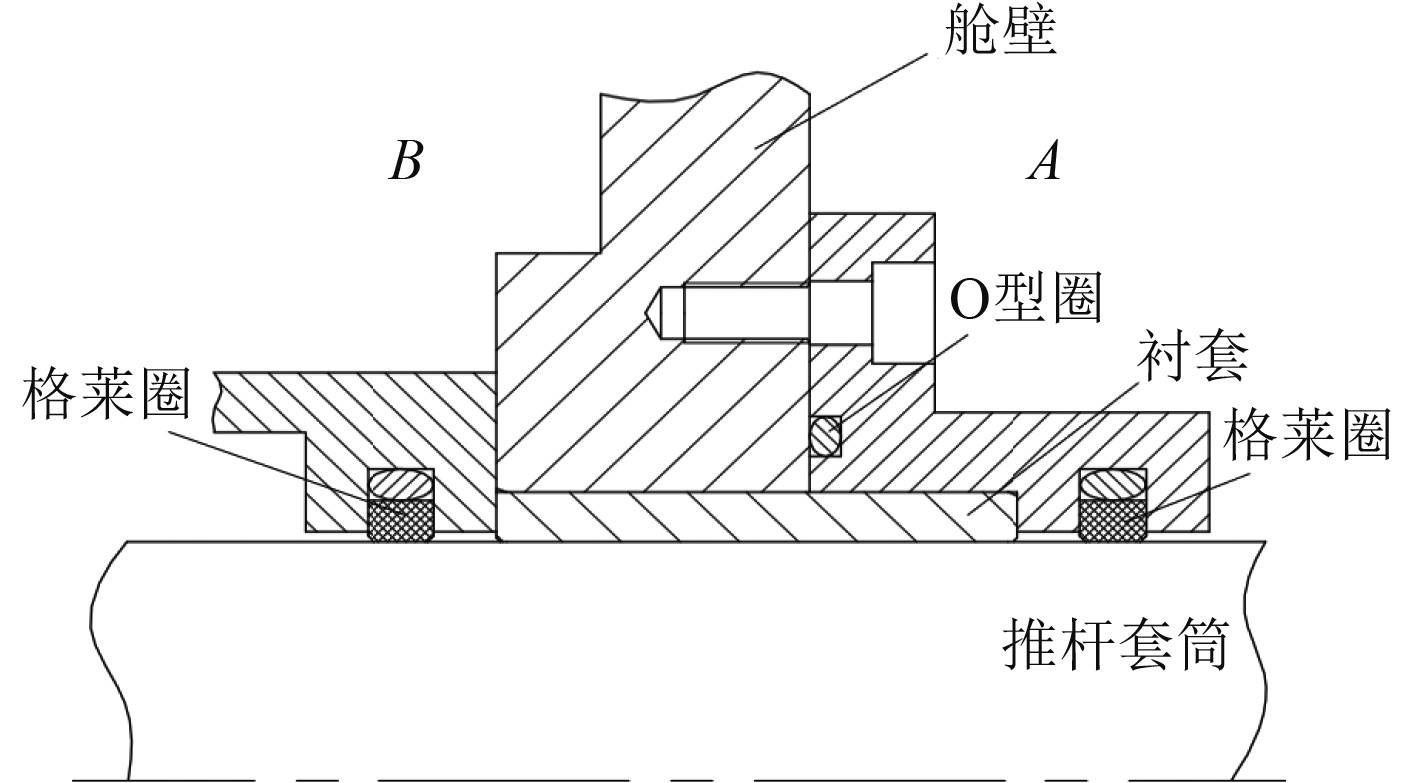
|
图 5 推杆套筒密封 Fig. 5 Sealing of push rod sleeve |
矢量推进器的机构构型基于PUS-PRS-S并联机构,如图6所示,机构由静平台、动平台、PRS驱动支链和PUS驱动支链组成。图中,静平台和动平台中心分别为
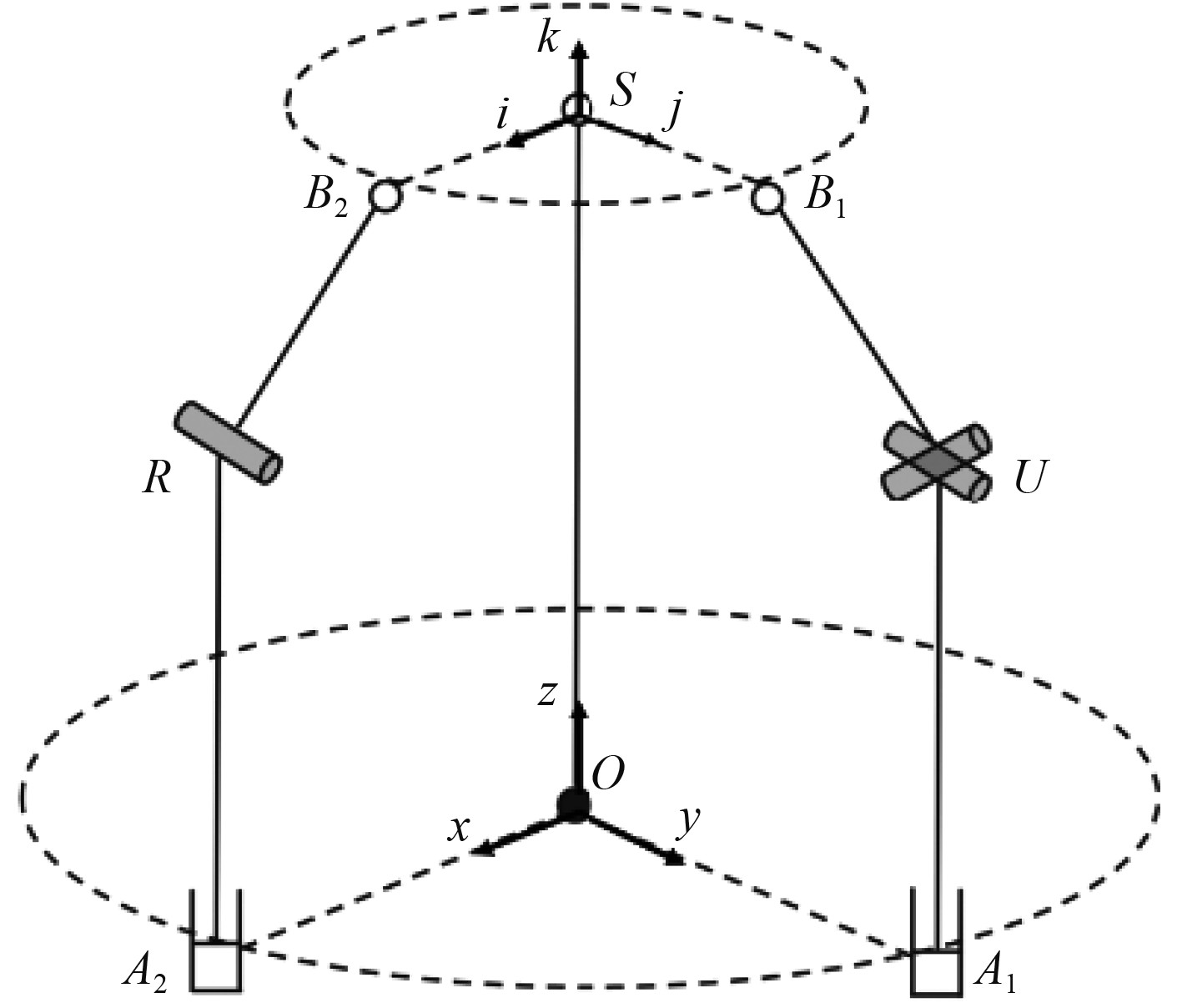
|
图 6 并联机构简图 Fig. 6 Schematic diagram of parallel mechanism |
为研究该机构的运动学性能,建立
机构简图中
| $P_A^{S_1} = \left[ {\begin{array}{*{20}{c}} {A_1^{S_1}}&{A_2^{S_1}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0&{{r_1}} \\ {{r_1}}&0 \\ 0&0 \end{array}} \right]。$ | (1) |
同样,在动平台局部坐标系
| $ P_B^{S_2} = \left[ {\begin{array}{*{20}{c}} {B_1^{S_2}}&{B_2^{S_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0&{{r_2}} \\ {{r_2}}&0 \\ 0&0 \end{array}} \right]。$ | (2) |
局部坐标系
| $ {\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} {\cos \beta }&{\sin \alpha \sin \beta }&{\cos \alpha \sin \beta } \\ 0&{\cos \alpha }&{ - \sin \alpha } \\ { - \sin \beta }&{\sin \alpha \cos \beta }&{\cos \alpha \cos \beta } \end{array}} \right]。$ | (3) |
使用旋转矩阵
| $ P = {\left[ {\begin{array}{*{20}{c}} {{P_x}}&{{P_y}}&{{P_z}} \end{array}} \right]^{\rm{T}}} = {\left[ {\begin{array}{*{20}{c}} 0&0&h \end{array}} \right]^{\rm{T}}}。$ | (4) |
通过式(3)和式(4),在局部坐标系
| $ \begin{split} {\boldsymbol{P}}_B^{S_1} = & {\boldsymbol{TP}}_B^{S_2} + P = [\begin{array}{*{20}{c}} {B_1^{S_1}}&{B_2^{S_1}} \end{array}] =\\ & \left[ {\begin{array}{*{20}{c}} {{r_2}\sin \alpha \sin \beta }&{{r_2}\cos \beta } \\ {{r_2}\cos \alpha }&0 \\ {{r_2}\sin \alpha \cos \beta + h}&{ - {r_2}\sin \beta + h} \end{array}} \right] 。\end{split}$ | (5) |
式中,右上标表示坐标所在的坐标系。设PUS支链中线性执行器长度为
| $ \left[ {\begin{array}{*{20}{c}} {{U^{S1}}}&{{R^{S1}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0&{{r_1}} \\ {{r_1}}&0 \\ {{d_1}}&{{d_2}} \end{array}} \right] 。$ | (6) |
则两支链中定长连杆的长度可以表示为:
| $ {l_1} = \left\| {B_1^{S1} - {U^{S1}}} \right\|,$ | (7) |
| $ {l_2} = \left\| {B_2^{S1} - {R^{S1}}} \right\| 。$ | (8) |
根据式(7)和式(8)可以得到线性执行器长度与动平台转角之间的函数关系为:
| $ \begin{split} & {(h + + {r_2}\sin \alpha \cos \beta - {d_1})^2} =\\ & \quad\quad l_1^2 - {({r_2}\cos \alpha - {r_1})^2} - r_2^2{\sin ^2}\alpha {\sin ^2}\beta,\end{split}$ | (9) |
| $ {(h - {r_2}\sin \beta - {d_2})^2} = l_2^2 - {({r_2}\cos \beta - {r_1})^2} 。$ | (10) |
整理可得线性执行器长度计算公式为:
| $ {d_1} = h + {r_2}\sin \alpha \cos \beta - \sqrt {l_1^2 - {{({r_2}\cos \alpha - {r_1})}^2} - r_2^2{{\sin }^2}\alpha {{\sin }^2}\beta },$ |
| $ {d_2} = h - {r_2}\sin \beta - \sqrt {l_2^2 - {{({r_2}\cos \beta - {r_1})}^2}}。$ | (11) |
两线性执行器的行程变化可以通过式(11)、式(12)和表1中的参数计算得到。式中,
|
|
表 1 几何参数 Tab.1 Geometric parameters |
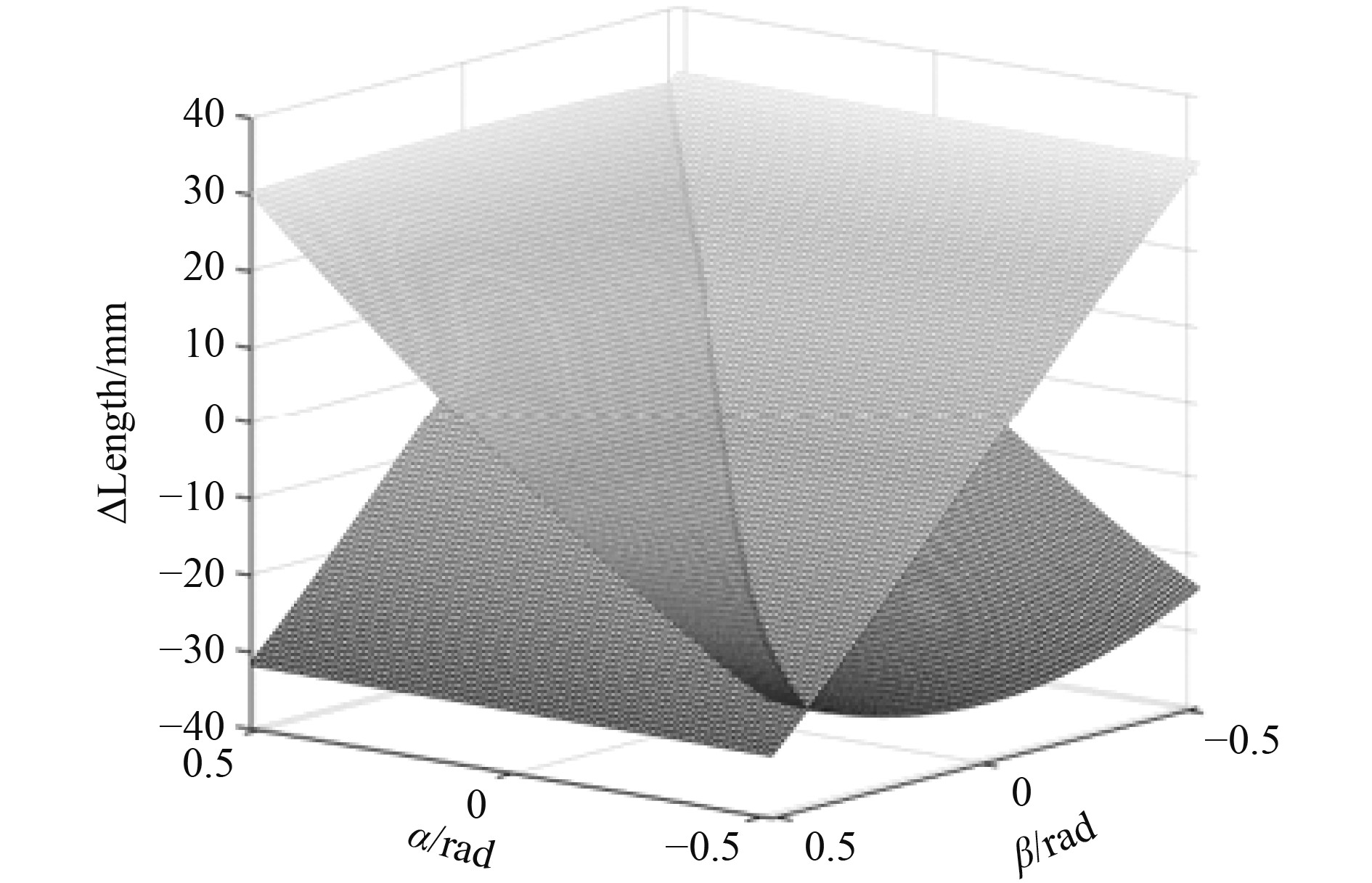
|
图 7 线性执行器行程变化三维图 Fig. 7 Three-dimensional graph of the length changes of actuators |
| $ \Delta {d_1} = {d_1} - {d_{01}},$ |
| $ \Delta {d_2} = {d_2} - {d_{02}}。$ | (12) |
为了研究矢量推进器的周期运动性能,令顶部平台的法线绕
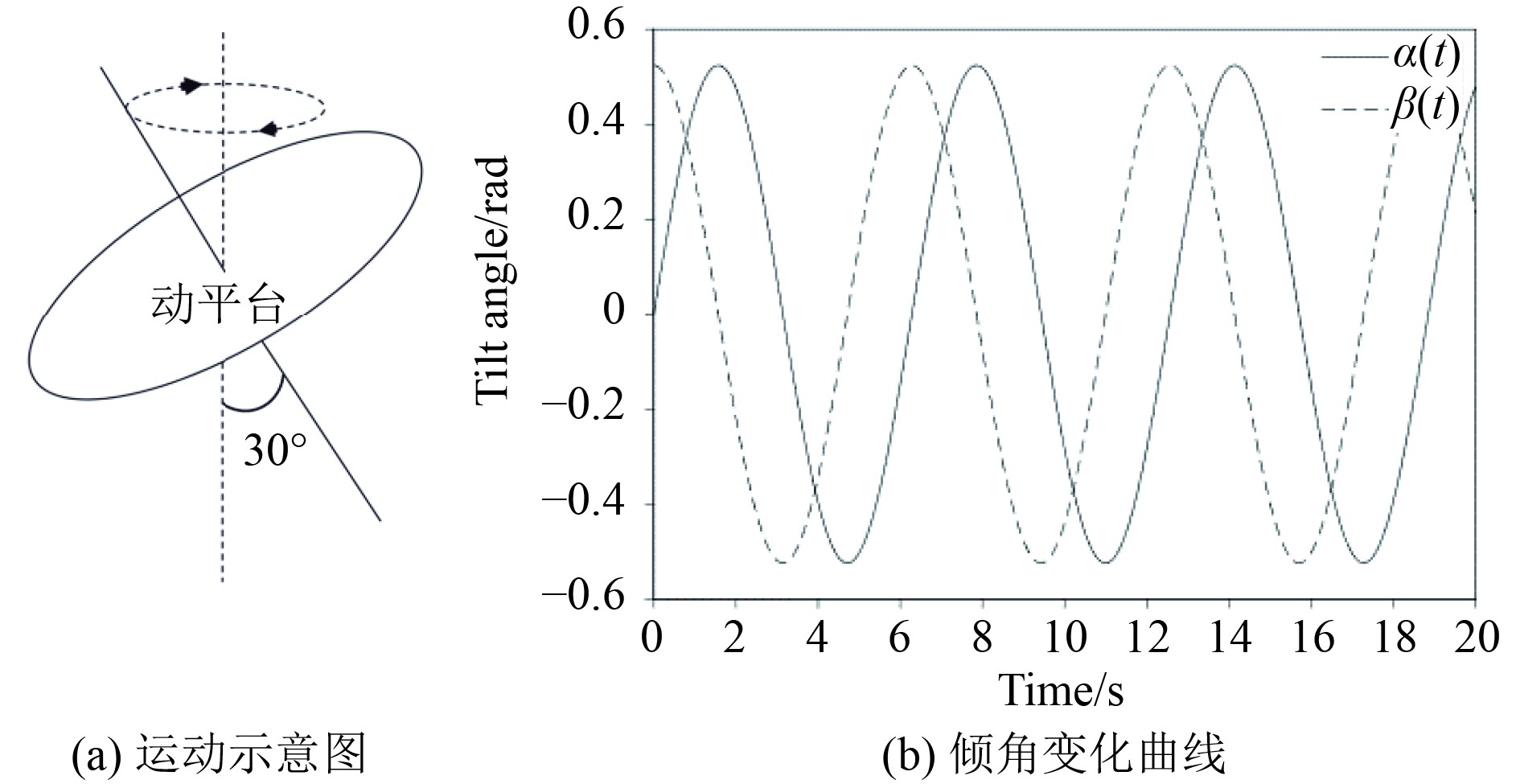
|
图 8 动平台运动分析 Fig. 8 Motion analysis of the moving platform |
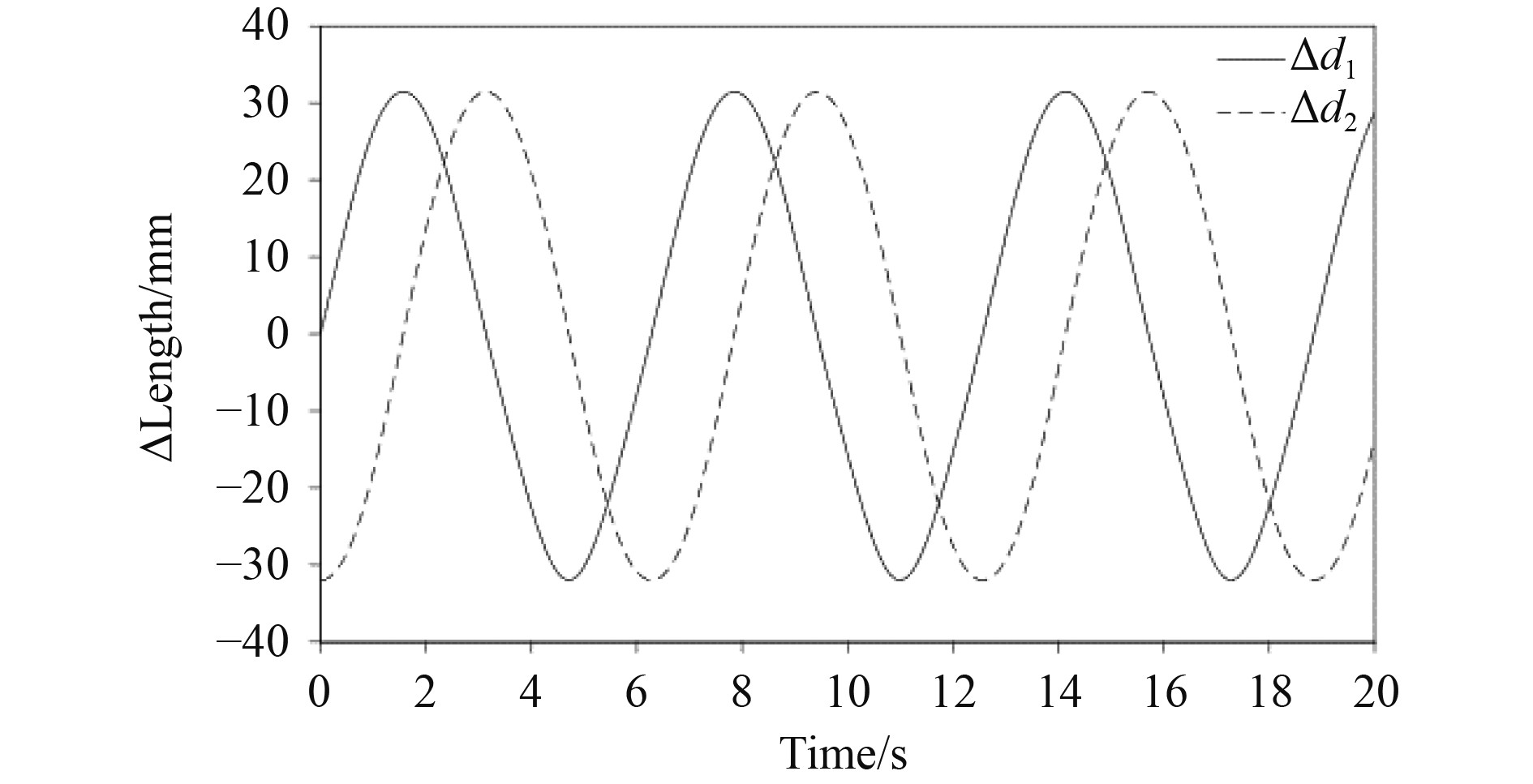
|
图 9 线性执行器行程变化 Fig. 9 Length changes of actuators |
动平台在2个线性执行器驱动下,保持顶部动平台法向量与
为验证运动学理论推导的正确性,将机构模型简化后导入虚拟样机仿真软件。对动平台设置驱动,即
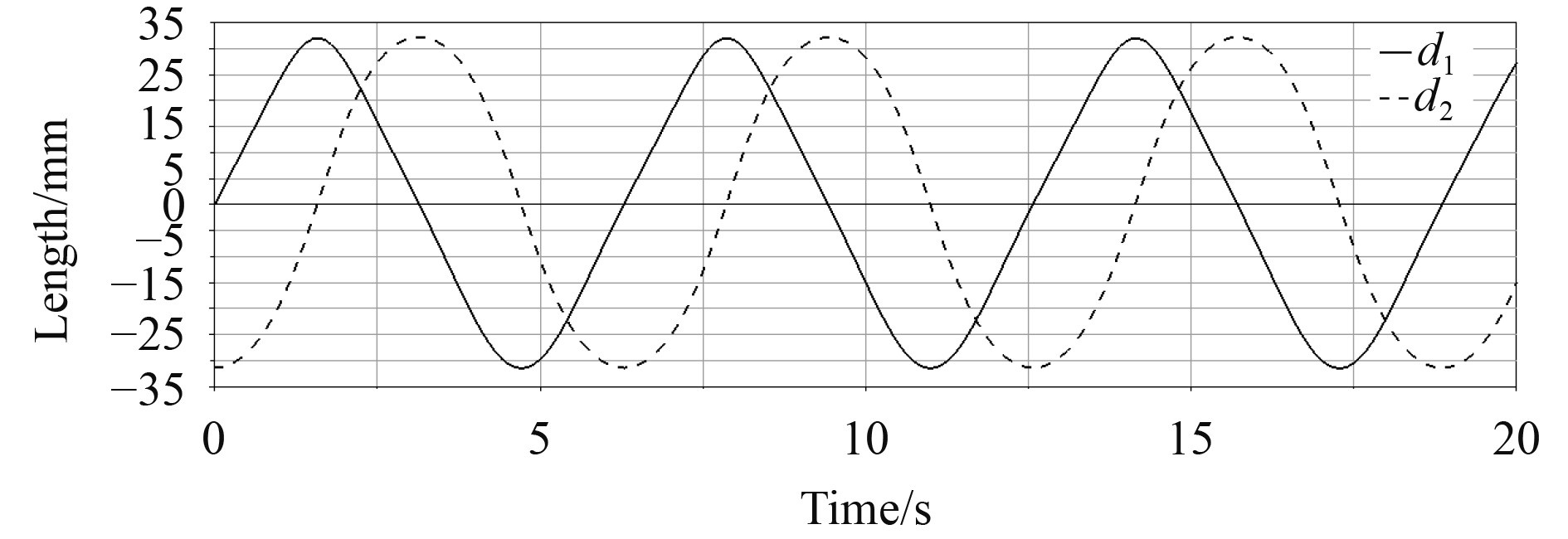
|
图 10 线性执行器行程变化仿真 Fig. 10 Length changes of actuators |
动力学分析主要是研究机构在非平衡状态运动过程中,各构件受力运动的关系,其理论基础是牛顿运动定律。目前研究动力学的方法有牛顿-欧拉法、拉格朗日方程法、虚功原理法等,这些方法各有优劣与其适用场合[7]。牛顿-欧拉法是研究并联机构动力学最常用的方法,递推逻辑清晰,易于理解和推导[8]。牛顿方程描述构建受力与运动加速度的关系,欧拉方程描述构件所受力矩与转动角速度、角加速度的关系,忽略摩擦力的牛顿-欧拉方程一般形式如下:
| $ \Sigma F = ma ,$ | (13) |
| $ \Sigma M + \Sigma (r \times F) = {r_{cg}} \times ma + I\dot \omega 。$ | (14) |
以PRS支链为例,对机构部件进行受力分析如图11所示,由于动平台无移动自由度,故忽略动平台牛顿方程,建立全局坐标系下动平台欧拉方程:
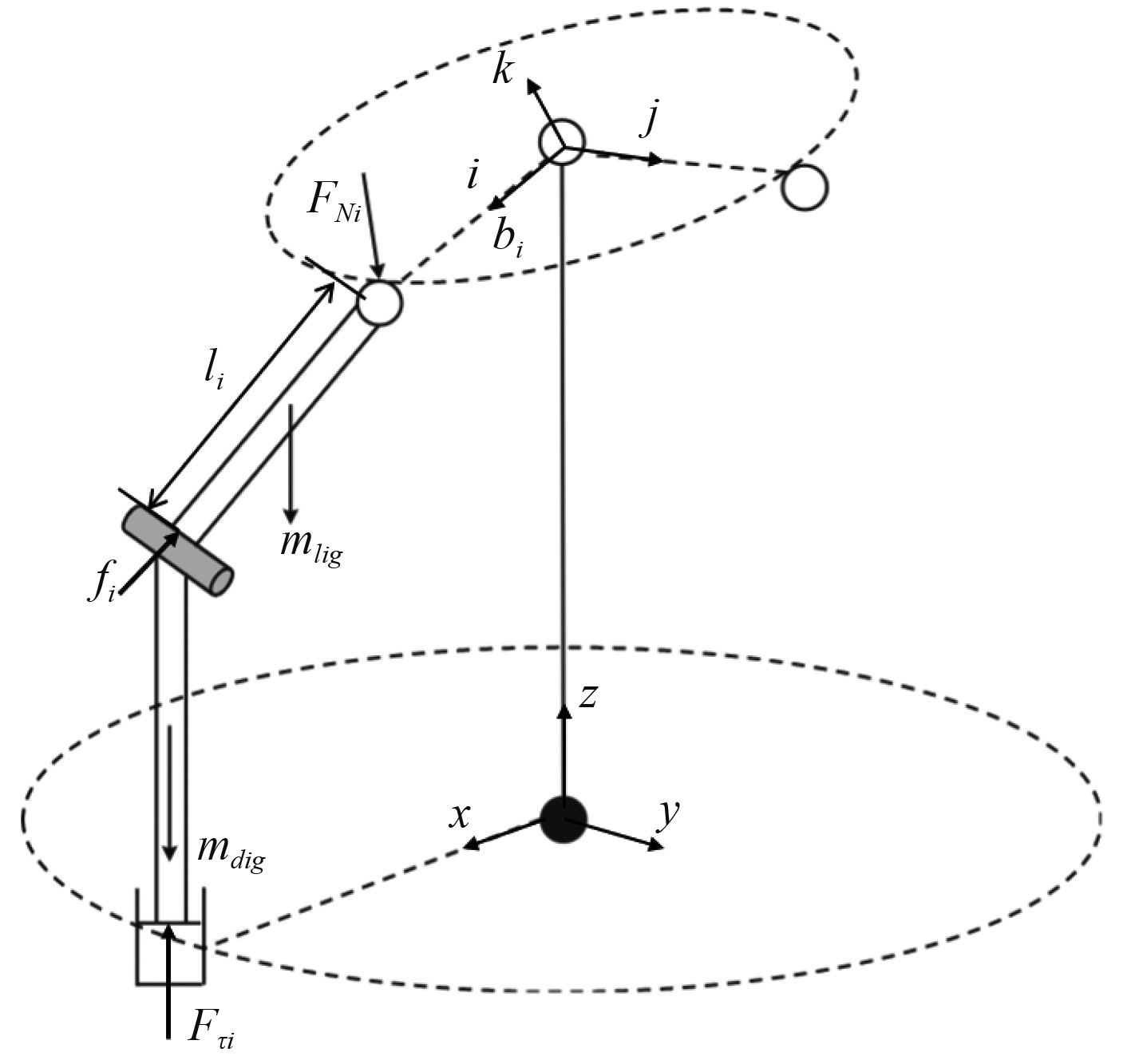
|
图 11 机构受力分析图 Fig. 11 Force analysis diagram of the mechanism |
| $ {I_p}{\dot {\boldsymbol{\omega}} _p} + {{\boldsymbol{\omega}} _p} \times {I_P}{{\boldsymbol{\omega}} _p} = T{{\boldsymbol{M}}_e} + \Sigma [(T{{\boldsymbol{b}}_i}) \times {{\boldsymbol{F}}_{Ni}}]。$ | (15) |
式中:
建立转动副与球副之间定长连杆的牛顿方程与欧拉方程如下:
| $ {m_{li}}{\dot {\boldsymbol{v}}_{li}} = {{\boldsymbol{f}}_i} - {{\boldsymbol{F}}_{Ni}} + {m_{li}}{\boldsymbol{g}},$ | (16) |
| $ {I_P}{\dot {\boldsymbol{\omega}} _{li}} + {{\boldsymbol{\omega}} _{li}} \times {I_{li}}{{\boldsymbol{\omega}} _{li}} = 0.5{{\boldsymbol{l}}_i} \times {{\boldsymbol{f}}_i} + 0.5{{\boldsymbol{l}}_i} \times {{\boldsymbol{F}}_{Ni}} 。$ | (17) |
式中:
| $ \begin{split} &\left[ {\begin{array}{*{20}{c}} {{m_{li}}{I_3}}&0 \\ 0&{{I_P}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\dot {\boldsymbol{v}}}_{li}}} \\ {{{\dot {\boldsymbol{\omega}} }_{li}}} \end{array}} \right] =\\ & \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{f}}_i} - {{\boldsymbol{F}}_{Ni}} + {m_{li}}{\boldsymbol{g}}} \\ { - {{\boldsymbol{\omega }}_{li}} \times {I_{li}}{{\boldsymbol{\omega}} _{li}} + 0.5{{\boldsymbol{l}}_i} \times {{\boldsymbol{f}}_i} + 0.5{{\boldsymbol{l}}_i} \times {{\boldsymbol{F}}_{Ni}}} \end{array}} \right]。\end{split} $ | (18) |
由于线性执行器仅输出直线运动,故忽略其推杆的欧拉方程,建立推杆的牛顿方程:
| $ {m_{di}}{\dot v_{di}} = {F_{\tau i}} - {{\boldsymbol{s}}_i}{{\boldsymbol{f}}_i} + {m_{li}}g。$ | (19) |
式中:
| $ \begin{split} \left[ {\begin{array}{*{20}{c}} {{F_{\tau 1}}} \\ {{F_{\tau 2}}} \end{array}} \right] =\,& {{\boldsymbol{D}}_1}\left[ {\begin{array}{*{20}{c}} {\ddot \alpha } \\ {\ddot \beta } \end{array}} \right] + {{\boldsymbol{D}}_2}\left[ {\begin{array}{*{20}{c}} {\alpha \dot \beta } \\ {\dot \alpha \beta } \end{array}} \right] + {{\boldsymbol{D}}_3}\left[ {\begin{array}{*{20}{c}} {{{\dot \alpha }^2}} \\ {{{\dot \beta }^2}} \end{array}} \right] +\\ & {{\boldsymbol{D}}_4}\left[ {\begin{array}{*{20}{c}} {{m_{d1}}g} \\ {{m_{d2}}g} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{M_{ex}}} \\ {{M_{ey}}} \end{array}} \right]。\end{split} $ | (20) |
式中:
同样令动平台完成
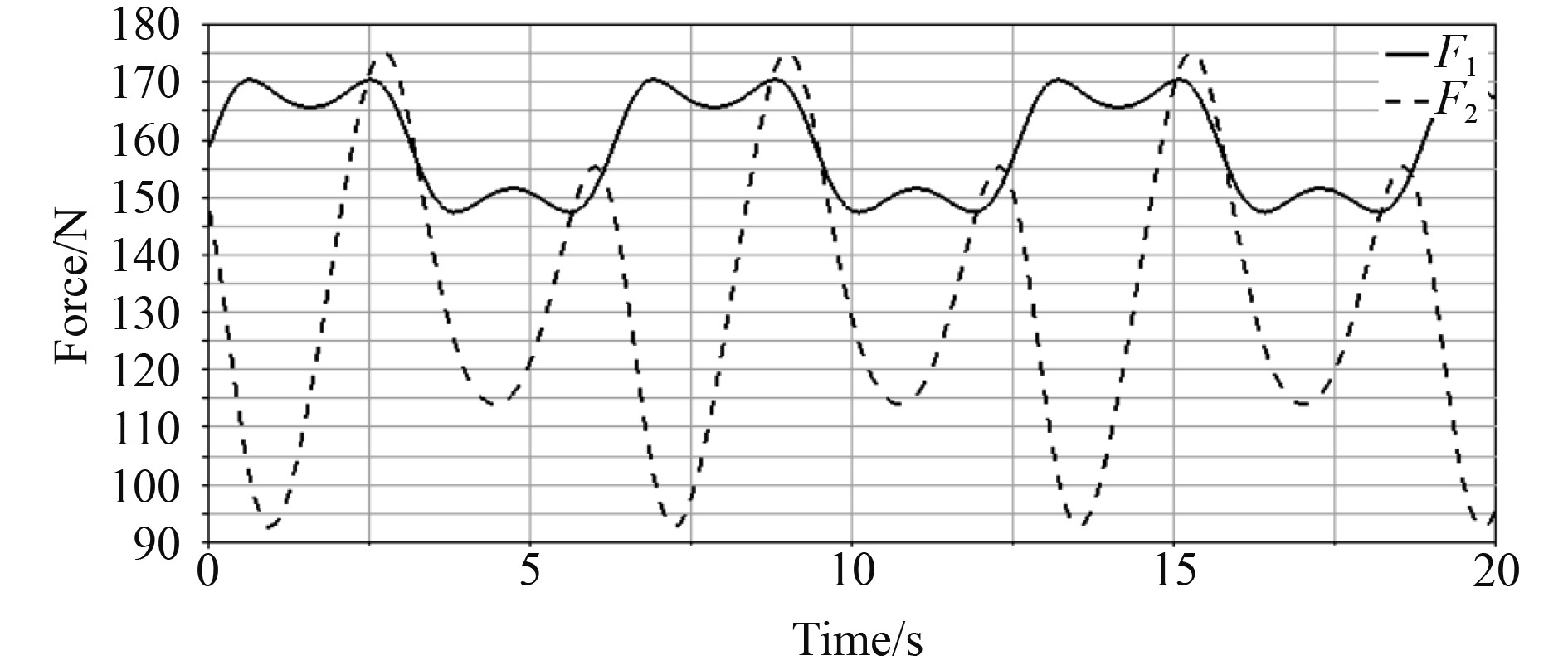
|
图 12 驱动力曲线图 Fig. 12 Driving force diagram |
图中,
传统AUV螺旋桨的方向始终与AUV机身中轴线方向对齐,本文研究的矢量推进器安装与水下机器人尾部,具备2个自由度,推力
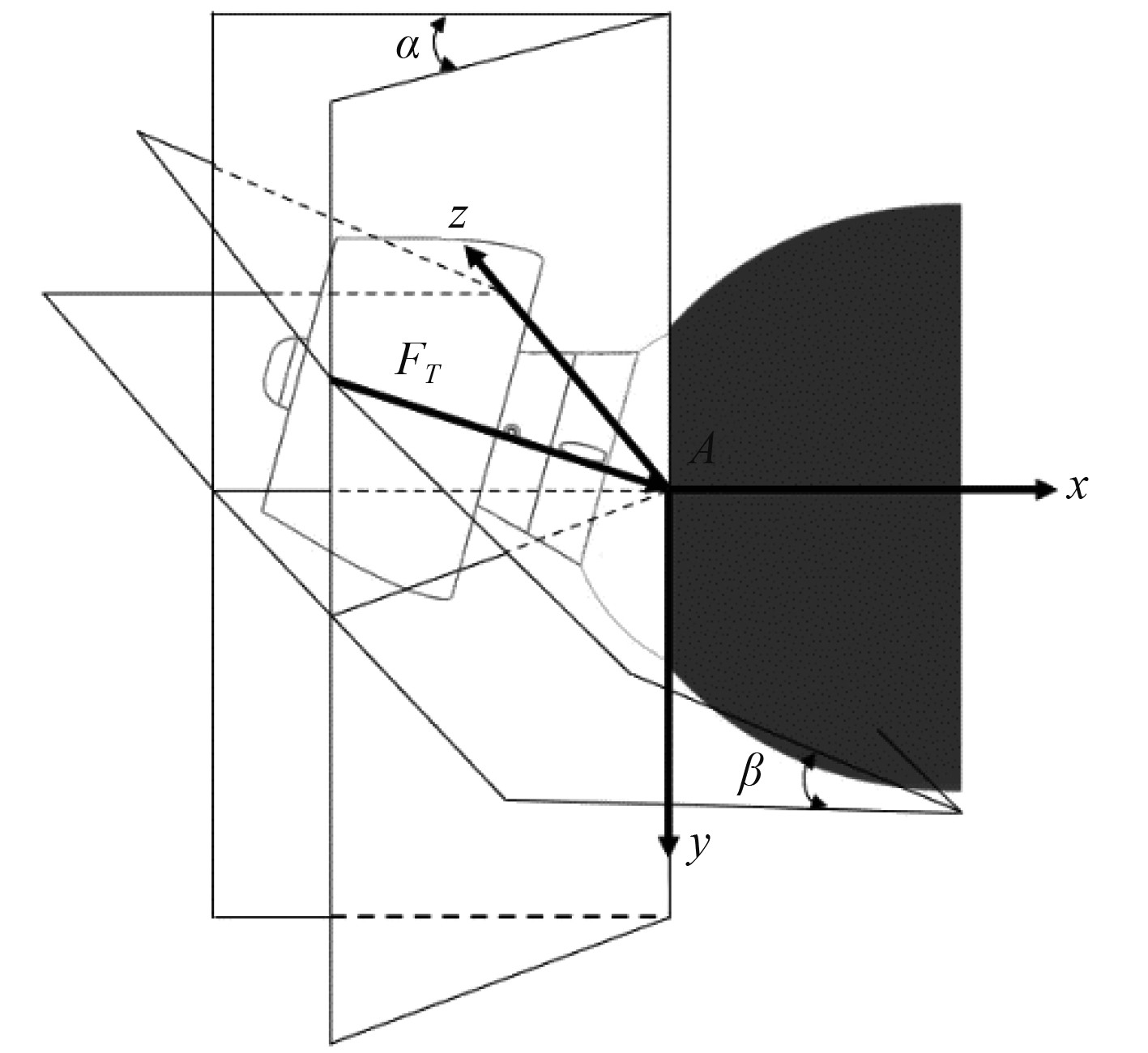
|
图 13 矢量推力分解 Fig. 13 Diogram of vectored thrust |
基于空间几何学可得到螺旋桨推力的3个分量
| $ {F_T} = \left[ \begin{gathered} {F_{Tx}} \\ {F_{Ty}} \\ {F_{Tz}} \\ \end{gathered} \right] = \left[ \begin{gathered} - {T_P}\cos \beta \cos \alpha \\ {T_P}\sin \beta \\ {T_P}\cos \beta \sin \alpha \\ \end{gathered} \right] 。$ | (21) |
为方便研究推力矢量与偏转角之间的关系,即螺旋桨产生的推力在在各方向的权重,定义单位矢量
| $ \left\{ \begin{gathered} {\delta _x} = - \cos \beta \cos \alpha,\\ {\delta _y} = \sin \beta,\\ {\delta _z} = \cos \beta \sin \alpha 。\\ \end{gathered} \right. $ | (22) |
比例因子量化了推力矢量大小在三维空间中的分布情况,其本身是无量纲数据,图14为使用Matlab绘制的各比例因子随水平摆角
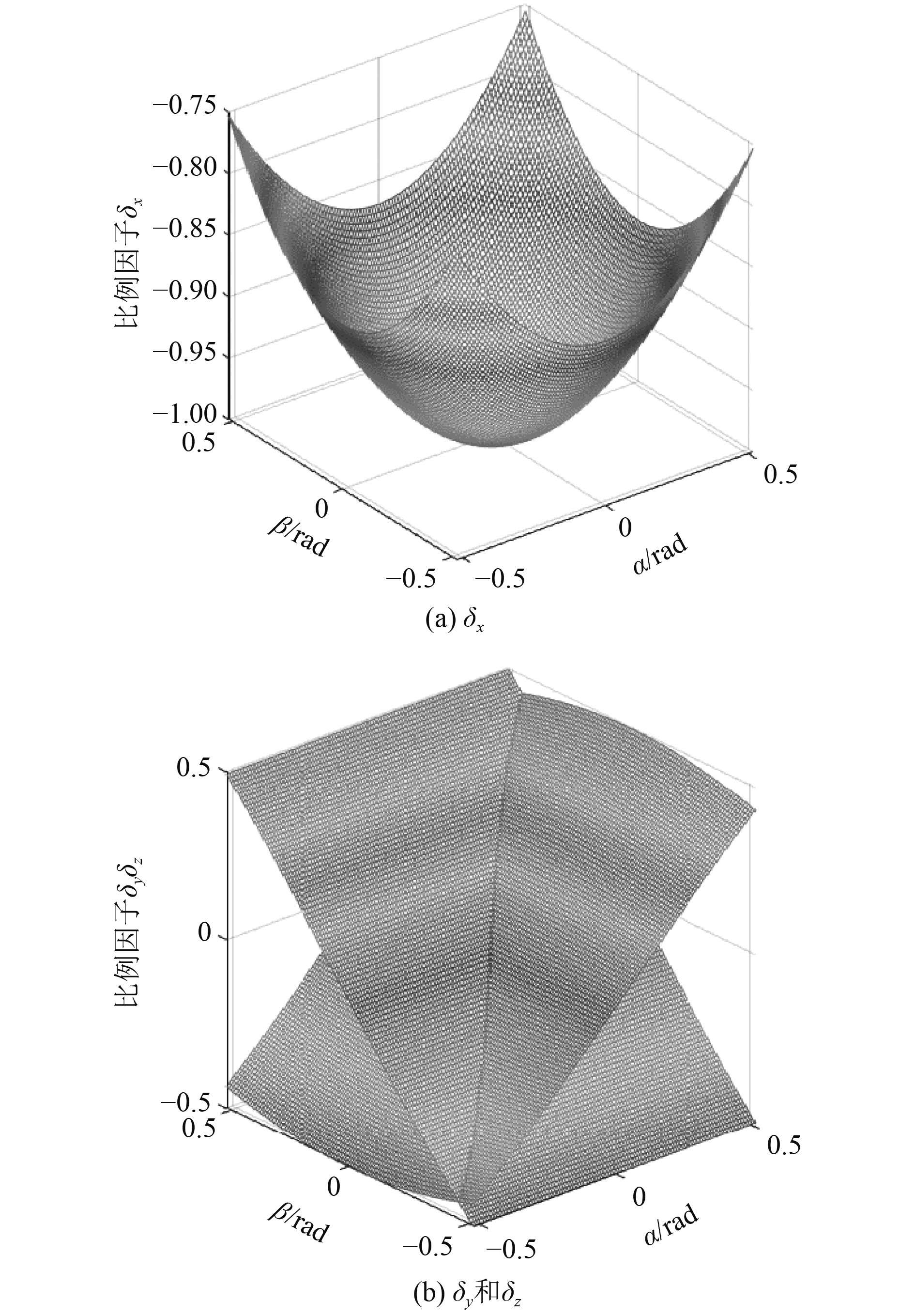
|
图 14 比例因子空间分布图 Fig. 14 Spatial distribution of vectored thrust |
矢量推进AUV 的俯仰和偏航运动分别由推力分量
| $ {\boldsymbol{M}} = {\boldsymbol{r}} \times {{\boldsymbol{F}}_T} = {\boldsymbol{r}} \times {T_p}\delta ,$ | (23) |
| $ {T_p} = {K_T}\rho {n^2}{D^4}。$ | (24) |
式中:
传统推进方式AUV的姿态和侧向机动分别由2个水平尾翼和2个垂直尾翼(方向舵)控制,尾翼升力和阻力的经验公式为[9]:
| $ \left\{ \begin{split}&L = \frac{1}{2}\rho {C_L}{A_R}{\delta _e}v_e^2,\\ &D = \frac{1}{2}\rho {D_L}{A_R}{\delta _e}v_e^2 。\end{split}\right.$ | (25) |
式中:
根据等式(25),垂尾升力和阻力与有效垂尾速度
本文设计了并联机构形式的螺旋桨矢量推进器,这种矢量推进器具备俯仰、偏摆两自由度,且产生的推力仅受导管螺旋桨的转速和倾角的影响。矢量推力可以控制水下机器人的俯仰和偏航运动,矢量推力由矢量推进器进行定向调节。这种推进形式具有机动性好、效率高、结构简化等优点。因此,在要求高机动性、高可靠性AUV海洋勘探领域具有明显的潜力和优势。
对基于PUS-PRS-S并联机构的矢量推进器进行了具体的结构设计,总体结构紧凑,模块化的设计方式使得该机构具备较好的普适性,可以很容易地作为一个整体安装在AUV的尾部。经过对该机构的运动学和动力学分析,建立了运动学和动力学方程,经过数值计算与仿真,证明设计的矢量推进器能够较好的完成俯仰、偏摆运动,符合设计需求。
研究了矢量推进器螺旋桨推力在不同矢量角度下的比例分布,矢量推进方式既可以保证水下机器人在前进方向上的绝大部分动力,也可以为水下机器人的转向提供足够的转向力矩,且与水下机器人的速度和姿态无关,对比传统推进方式AUV,矢量推进方式在低速航行时具备天然的机动性优势。
在未来的研究中,将建立矢量推进AUV水动力模型和数值模拟,以研究航行器在不同姿态下对推进器的水动力响应。此外,还将对矢量推进器的运动轨迹进行分析和优化,以提高其性能。最终,还将建造配备矢量推进器的AUV原型机来验证设计原理,在水池或开放水域进行测试,以检查其性能。
| [1] |
ZHANG Y, LI Y, SUN Y, et al. Design and simulation of x-rudder AUV's motion control[J]. Ocean Engineeringr, 2017, 204–214.
|
| [2] |
张继威, 于复生, 隽志龙, 等. 水下推进形式应用现状及发展趋势[J] . 船舶工程, 2021, 43(6): 61–78. ZHANG Ji-wei, YU Fu-sheng, JUAN Zhi-long, et al. Application status and development trend of underwater promoting form[J]. Ship Engineering, 2021, 43(6): 61–78. |
| [3] |
韦荣伟. 水下机器人发展趋势及前景[J]. 现代制造技术与装备, 2018(2): 175–176. WEI Rong-wei. Research on development tendency and prospect for underwater robot[J]. Modern Manufacturing Technology and Equipmen, Modern Manufacturing Technology and Equipmen, 2018(2): 175–176. |
| [4] |
张帅, 肖晶晶. 水下矢量推进器研究综述[J]. 舰船科学技术, 2019, 41(7): 1-5. ZHANG Shuai, XIAO Jing-jing. Review of underwater vector propulsion devices[J]. Ship Science and Technology, 2019, 41(7): 1-5. DOI:10.3404/j.issn.1672-7649.2019.07.001 |
| [5] |
杜小强, 赵世豪, 贺磊盈. 2转动高精度重载并联机构构型综合[J]. 浙江理工大学学报(自然科学版), 2023, 49(1): 115–123.
|
| [6] |
吕爱平. O型圈的选型与应用[J]. 黑龙江造纸, 2020, 48(3): 29-32+36. |
| [7] |
李永泉, 郭雨, 张阳, 等. 基于牛顿欧拉法的一种空间被动过约束并联机构动力学建模方法[J]. 机械工程学报, 2020, 56(11): 48-57. DOI:10.3901/JME.2020.11.048 |
| [8] |
杨飞雪, 康绍鹏, 刘凯磊, 等. 基于牛顿-欧拉法的三轴线连杆转向机构数学建模与仿真优化[J]. 制造技术与机床, 2022(3): 9-16. |
| [9] |
高伟, 谷海涛, 冯萌萌, 等. 水下机器人舵翼参数设计与优化[J]. 海洋技术学报, 2021, 40(4): 74–83.
|
 2024, Vol. 46
2024, Vol. 46

