随着海洋资源开发的迫切需求,水下滑翔机作为一种专业的海底勘察设备而受到极大重视。其中,圆碟形水下滑翔机是一种新式水下滑翔机,具有能耗低和长续航等特点。它可通过调节重、浮力来实行上升、下潜等机动运动,能够高效地完成海洋环境参数收集等任务[1]。伴随着圆碟形水下滑翔机功能的多元化需求,其结构和功能性更新设计也在不断突破中。20世纪90年代以来,美国相继开发了Slocum、Seaglider和Spray[2],以及九州大学设计的BOOMERANG和LUNA[3]等圆碟形水下滑翔机。
对于圆碟形水下滑翔机而言,耐压壳是其重要组成部分。除了抵抗海水浸蚀外,耐压壳还需要在一定的工作水深下能够正常完成探测任务,从而需要对水下滑翔机的构造强度和密封特性设置严苛的设计标准[4]。同时,耐压壳体的自重占到了滑翔机重量的25%~50%[5],其结构设计必须满足轻量化要求。面对作业环境的复杂性和恶劣性,低成本、多功能和远程无人化操作平台的架设都对圆碟形滑翔机耐压壳的设计提出了较高的要求。张代雨等[6]以FFD参数化方法为核心,以CFD 为求解器,优化算法,完成了翼身融合水下滑翔机的外形优化设计。董华超等[7]运用基于数据驱动的离散优化思路,对翼身融合水下滑翔机舱体骨架耦合结构进行优化设计。李天博等[8]提出将航空领域先进的联翼布局与传统水下滑翔机相结合,提出一种新型的联翼式水下滑翔机,并通过外形优化设计使得联翼式水下滑翔机具有更优的升阻特性。张宁等[9]对传统克里金-高维模型表示(Kriging-HDMR)优化方法进行改进,以达到更准确的预测精度和更高效的优化效率,提高了滑翔机的升阻比。这些结构优化设计方法对于水下滑翔机的性能提升具有积极意义。除此之外,刘德良等[10]对圆盘水下滑翔机中的球-环-环压力壳开展了灵敏度分析和响应面分析,并且用挑选法对压力壳开展优化,在满足刚度要求的同时质量较原始设计方案缓解了30%。甄春博等[11]运用多总体目标进化算法和灵敏度分析对水下滑翔机中的圆筒半经和耐压壳壁厚开展了优化,并将组成优化算法与单体目标优化算法结合实现了较为优化的设计。何雪浤等[12]根据正交实验和有限元对水中航行器壳体开展优化,获得了最好计划方案,大大减少了试验测算。伍莉等[13]根据概念估算和有限元分析测算,优化了球型潜泳器耐压壳的设计方案。程妍雪等[14]对潜水器电池舱进行非均匀加肋设计,并对耐压舱进行结构轻量化控制,并进行了稳健性优化设计。张凡[15]通过Ansys对圆碟形耐压壳的屈曲模态进行了线性屈曲分析,给出了耐压壳各个缺陷参数的影响公式。于鹏垚等[16]在传统滑翔机的外形设计思路上进行突破,设计了圆碟形水下滑翔机并分析了水动力性能,建立了外形设计的分析方法。甄春博等[17]运用Ansys APDL参数化设计语言对圆碟形滑翔机进行参数化分析,进行了耐压壳体的轻量化设计。除了壳体构造、材料、孔径和高度等构型可靠性要求外,圆碟形水下滑翔机耐压壳的结构设计仍存在较大的优化空间以满足内部空间和外部壳体强度的要求。
本文主要从不同机身直径、不同机身高度与不同机身表面饱和度3个方面对圆碟形水下滑翔机耐压壳体表面的变形与压力分布情况进行研究,得出在100 m、200 m和300 m水深下的壳体表面受压情况,并结合材料的特性对机身外形进行综合优化,使其在不同水深环境下具有更好的力学性能。
1 计算模型及研究方法圆碟形水下滑翔机耐压壳体由上下对称的圆碟形薄壳结构构成,内部有加强环。圆碟形水下滑翔机耐压壳体材料一般选择7075航空铝合金,适用于水下潜器等对强度和抗腐蚀性能有较高要求的情况,也被许多水下滑翔机选为耐压壳体的首选材料。为了研究在不同水深下耐压壳体的应变特征和应力分布情况,主要通过调整机身直径、机体高度与机身表面饱和度来分析表面剪应力与变形情况,从而得到圆碟形水下滑翔机外部壳体的优化设计目标。
本文所设计的水下滑翔机最大工作深度为300 m,根据CCS中国潜水系统与潜水器入级规范,取安全系数K=1.5,极限载荷为4.9 MPa,耐压壳体壁厚为4.5 mm。
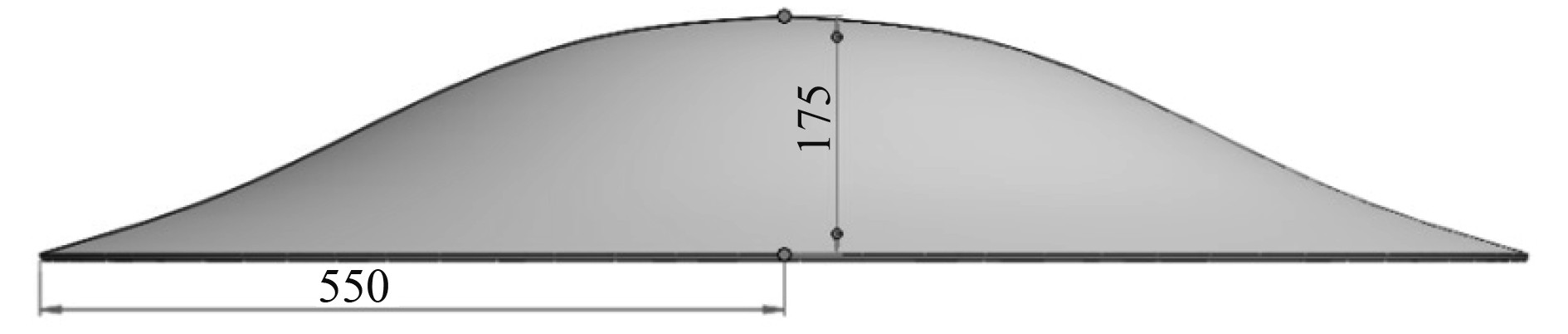
1.1 计算模型圆碟形水下滑翔机机身原始设计如图1所示。根据机身前主视图的几何图形特征,创建直角坐标。图上原始设计方案的机身截面曲线方程如下式:
|
图 1 圆碟型水下滑翔机原型 Fig. 1 Original shape design of DSUG |
| $ y= -3.563\;4x^4 -1.563\;4x^3-0.039\;4x+275。$ | (1) |
为了进行耐压壳体优化研究,本文设计了不同机身高度、不同机身直径与不同机身表面饱和度等9种圆碟形水下滑翔机,包括了3个不同机身直径、3个不同机身高度和3个不同机身表面饱和度的耐压壳体,具体结构设计如图2所示。在机身高度保持在h=350 mm时,设计水下滑翔机耐压壳体机身直径为d1=1 000 mm、d2=1050 mm、d3=1 200 mm。

|
图 2 不同机身直径的设计图 Fig. 2 Shapes of different diameters of DSUG |
如图3所示,机身直径d=1 100 mm时,耐压壳体机身高度设计为h1=340 mm、h2=360 mm、h3=380 mm。

|
图 3 不同机身高度的设计图 Fig. 3 Shapes of different heights of DSUG |
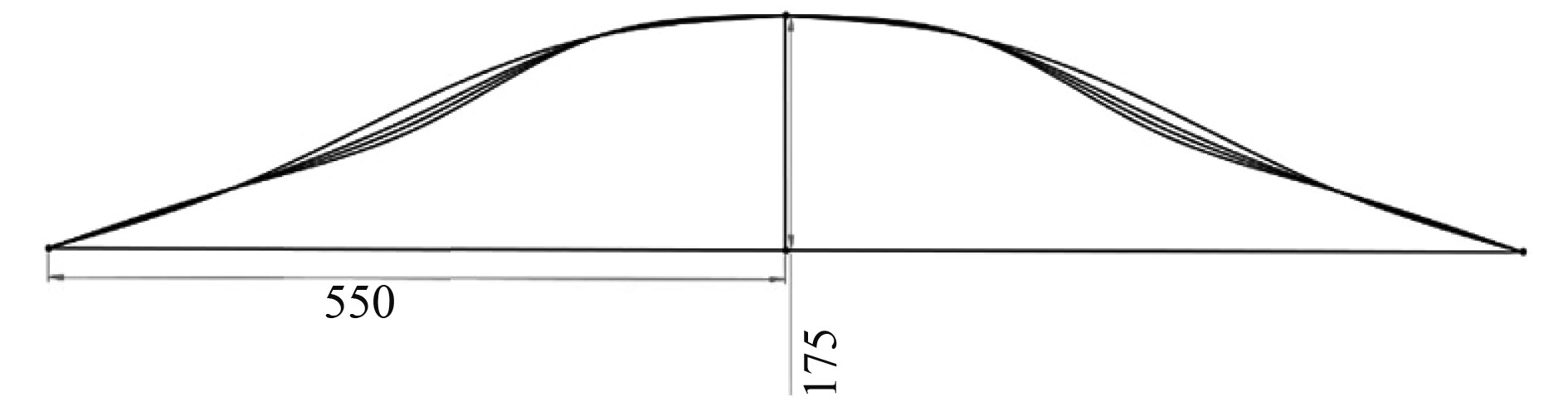
如图4所示,以机身正视图几何中心为原点,建立直角坐标系,维持机身高度350 mm和孔径1 100 mm不变,选择不同饱和度曲线Ω1、Ω2和Ω3来设计不同构型曲线的圆碟形水下滑翔机,分别命名为B1、B2和B3。3种不同饱和度曲线方程分别为:
|
图 4 不同机身表面饱和度设计示意图 Fig. 4 Shapes of different surface saturations of DSUG |
| $ \begin{split} B_1\quad\Omega_1=& -9.5914x^4- 15.7463x^3-\\ & 0.036x^2-0.2576x+175,\end{split} $ | (2) |
| $ \begin{split} B_2\quad\Omega_2= &-20.4645x^4+ 2.2817x^3-\\ & 0.0049x^2-0.3667x+175,\end{split} $ | (3) |
| $ \begin{split} B_3\quad \Omega_3=& 5.2817x^4- 0.4366x^3-\\ & 0.0049x^2-0.3667x+175。\end{split} $ | (4) |
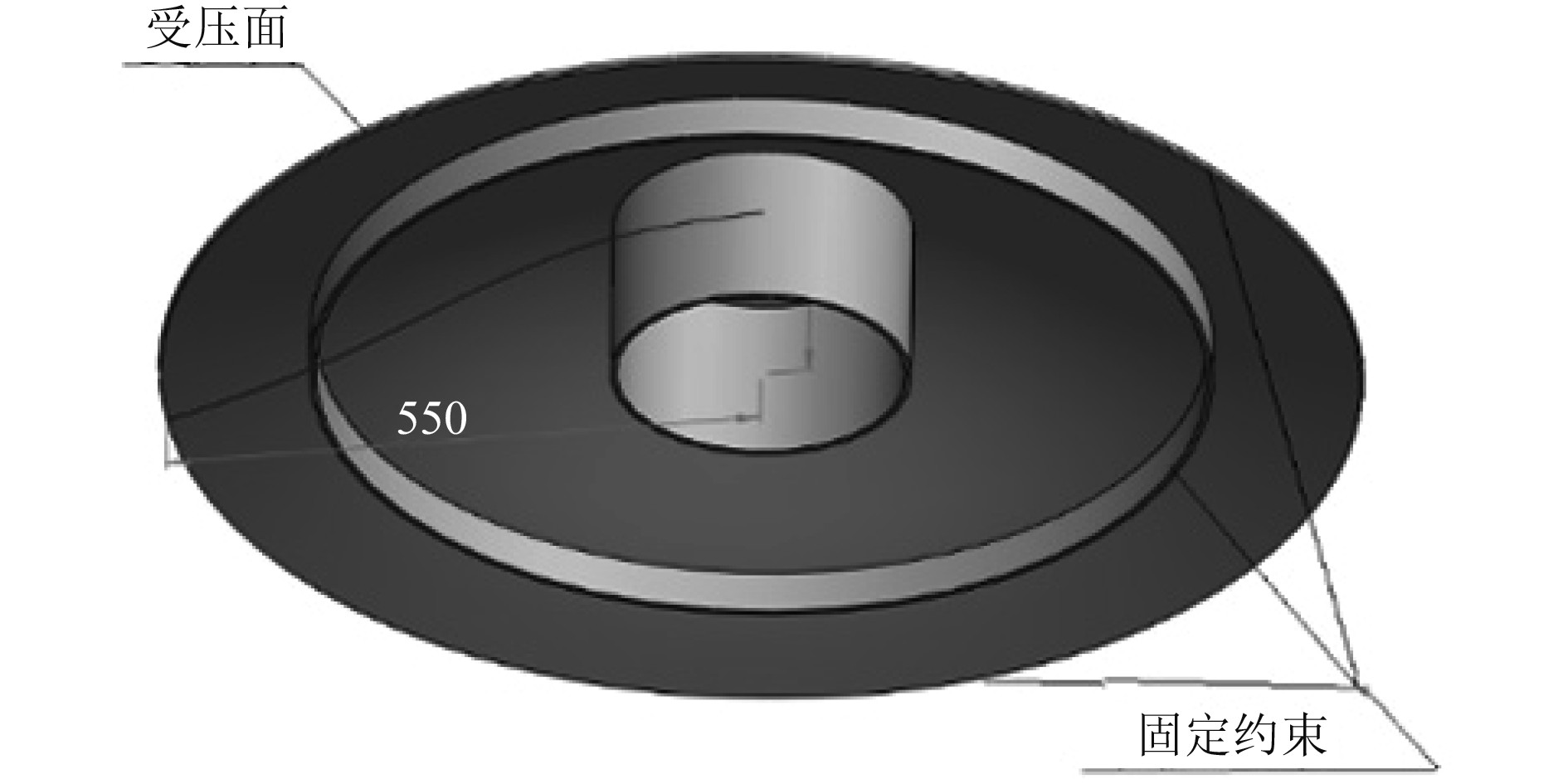
本文使用Ansys Workbench中的静力学结构模块进行有限元分析,在Static Structural模块中对7075航空铝合金的材料特性进行定义,定义密度ρ=2 800 kg/m3,弹性模量E=71 700 MPa,泊松比v=0.33,该材料的屈服强度为505 MPa。由于碟型水下滑翔机的耐压壳体对称性设计,故本文选择上部壳体结构作为研究对象,同时把耐压壳体的边缘和2个加强环的接触面积设定为固定约束,耐压面为全部耐压壳体的外表面,如图5所示。
|
图 5 边界条件设定示意图 Fig. 5 Boundary loading setting |
圆碟形耐压壳体机身直径普遍小于1100 mm,机身高度低于350 mm,基于误差和计算可行性的考虑,本文在保证计算精度的前提下采取5 mm的最大网格尺寸,网格划分情况如图6所示。

|
图 6 网格划分 Fig. 6 Mesh generation |
在进行静力学应力分析时分别在不同设计上进行静力学加载,模拟100 m、200 m和300 m水深情况。在计算中实际加载的载荷是Pj100=0.98 MPa、Pj200=1.96 MPa与Pj300=2.94 MPa。
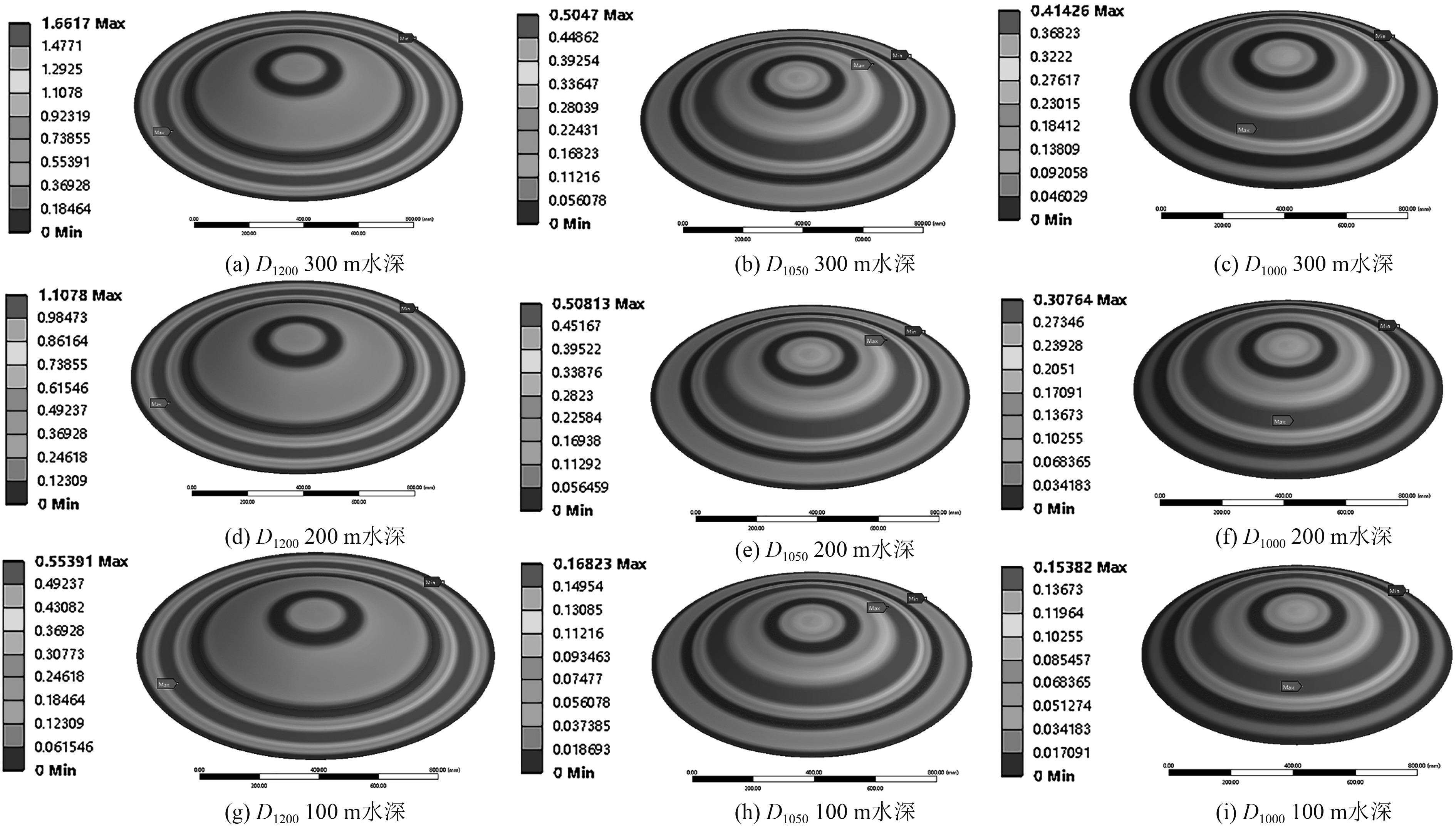
2 数值结果及分析 2.1 不同机身直径对壳体设计的影响图7为不同水深下不同机身直径圆蝶形滑翔机壳体最大变形云图。当保持机身的高度不变时,机身直径在100~300 m范围内,壳体的最大变形会随着机身直径的增大而增大。在300 m水深下,D1000型滑翔机外壳最大变形数值最小,为0.4142 mm,D1200型滑翔机外壳最大变形数值最大,为1.661 7 mm。D1000型设计的最大变形优于原始设计,其他机身直径模型则变形大于原始设计。在200 m水深时,D1000型滑翔机外壳最大变形的数值为0.3076 mm,D1200型滑翔机外壳最大变形数值为1.1078 mm。在100 m水深时,D1000型滑翔机外壳最大变形最小,为0.1538 mm,而D1200型滑翔机外壳最大变形最大,为0.5539 mm。从计算结果可以看出,耐压壳的直径越小,其在100 ~300 m范围内的最大变形就越小,因此 D1000与D1050型的滑翔机壳体设计更符合较小变形量的要求。
|
图 7 不同水深下不同机身直径圆蝶形滑翔机壳体最大变形云图 Fig. 7 Maximum deformation of pressure shell of different diameters in different water depths |
图8为不同水深下不同机身直径圆蝶形滑翔机壳体最大剪应力分布云图。在300 m深度时,最大剪切应力也随着机身直径的增大而逐渐增大,D1000型滑翔机外壳最大应力数值最小,为348.36 MPa;D1200型滑翔机外壳最大应力数值最大,为699.79 MPa,甚至超过了7075航空铝合金材料的屈服强度。200 m水深时,机身高度保持不变,D1000型滑翔机外壳最大应力的数值为237.17 MPa,而D1200型滑翔机外壳最大应力为466.53 MPa。在100 m水深时,D1000型滑翔机外壳最大应力最小,为118.5 MPa;D1000型滑翔机外壳最大应力最大,为233.26 MPa。可以看出,在深度到达300 m时D1200的应力明显超过了材料的屈服强度,这说明在100~300 m水深的蝶形滑翔机的设计过程中机身的直径长度的选择不能过大,与之相比D1000与D1050型滑翔机从表面应力分布上也较为优秀。同时,较大应力和较小应力呈现对称分布的特点。为了保障在更深的水下环境下工作,耐压壳必须增加壳体厚度且在满足内部空间的前提下尽量选择较小的机身直径。

|
图 8 不同水深下不同机身直径圆蝶形滑翔机壳体剪应力分布图 Fig. 8 Shear stress distribution of pressure shell of different diameters in different water depths |
图9为不同水深下不同机身高度圆蝶形滑翔机壳体最大变形云图。在100 m、200 m和300 mm水深下,H360型滑翔机外壳最大变形量分别为0.1862 mm、0.3725 mm、0.55879 mm;而H340型滑翔机和H380型滑翔机最大变形量均较为接近,分别为0.3146 mm和0.3139 mm、0.6293 mm和0.6279 mm、0.9472 mm和0.9439 mm。从计算结果上来看,H340型滑翔机和H380型滑翔机最大形变程度相似,在水深增大的过程中最大变形增长速率比H360型增长快,并且在同等水深下H360型滑翔机外壳最大变形数值仅为它们的60%左右。同时,H340型滑翔机和H380型滑翔机的最大变形区域在圆碟型滑翔机的顶部,而H360型滑翔机则位于接近边缘的区域。

|
图 9 不同水深下不同机身高度圆蝶形滑翔机壳体最大变形云图 Fig. 9 Maximum deformation of pressure shell of different heights in different water depths |
图10为不同水深下不同机身高度圆蝶形滑翔机壳体最大剪应力分布云图。在300 m深度时,H360型滑翔机外壳最大应力数值最小,为494.74 MPa,而H380型滑翔机外壳最大应力数值最大,为535.65 MPa,也超过了7075航空铝合金材料的屈服强度。在200 m深度时,H360型滑翔机外壳最大应力数值也最小,为329.83 MPa,而H340型滑翔机和H380型滑翔机最大应力数值接近,分别为340.36 MPa和333.63 MPa。在100 m深度时,H360型滑翔机外壳最大剪应力数值最小,为164.91 MPa,H340型滑翔机和H380型滑翔机最大应力分别为170.1 MPa和166.82 MPa。以上分析说明:H360型滑翔机外壳最大剪应力量明显优于H340型滑翔机和H380型滑翔机,且最大变形也优于它们。因此,在100~300 m水深范围内应根据机身直径选择合适的机身高度,机身高度与机身直径的匹配在一个合适的取值范围内,且在较深的水下设计环境下不宜选取较高的机身高度。

|
图 10 不同水深下不同机身高度圆蝶形滑翔机壳体剪应力分布图 Fig. 10 Shear stress distribution of pressure shell of different heights in different water depths |
图11为不同水深下不同机身饱和度圆蝶形滑翔机壳体最大变形云图。B1、B2和B3在100 m、200 m和300 mm水深下,B1型滑翔机外壳最大变形量分别为0.2655 mm、0.5311 mm、0.7967 mm;而B2型滑翔机和B3滑翔机最大变形量均较为接近,分别为0.3447 mm和0.4266 mm、0.6894 mm和0.8533 mm、1.0341 mm和1.28 mm。从计算结果来看,从B1→B2→B3,随着饱和度不断增加,耐压壳在100~300 m水深范围内的最大变形量越来越大,B3型滑翔机的最大变形量甚至是B1和B2的2倍左右。B1即使在300 m时最大变形程度也小于1 mm,B2型滑翔机外壳最大变形处于B1型和B3型之间。从整体上看3种不同饱和度圆碟形水下滑翔机的最大变形部位都在顶部,且饱和度较小的B1型滑翔机的最大变形量更加合理。

|
图 11 不同水深下不同机身饱和度圆蝶形滑翔机壳体最大变形云图 Fig. 11 Maximum deformation of pressure shell of different surface saturations in different water depths |
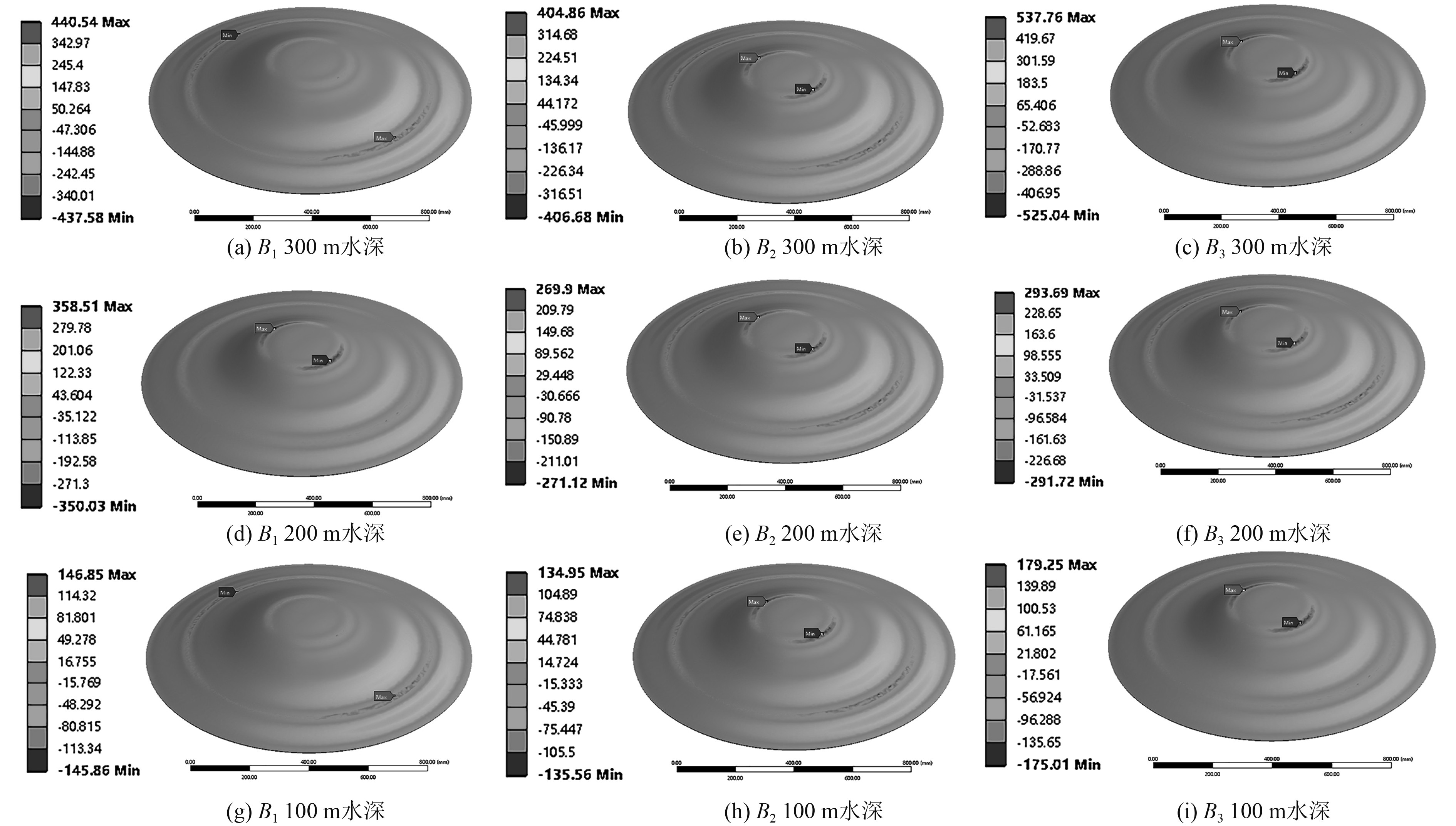
图12为不同水深下不同机身饱和度圆蝶形滑翔机壳体最大剪应力分布云图。在300 m深度时,B2型滑翔机外壳最大应力的数值最小,为404.86 MPa,B1型滑翔机为440.54 MPa,而B3型滑翔机外壳最大应力数值最大,为537.76 MPa,超过了7075航空铝合金材料的屈服强度。在200 m深度时,B2型滑翔机外壳最大应力的数值最小为269.9 MPa,B1型滑翔机和B3型滑翔机外壳最大应力数值分别为293.69 MPa和358.51 MPa。在100 m深度时,B2型滑翔机外壳最大应力最小,为134.95 MPa;B1型滑翔机和B3型滑翔机外壳最大应力数值分别为146.85 MPa和179.25 MPa。显然,B2与B1型水下滑翔机的最大应力接近原始设计,而设计B3的最大应力则较大。虽然B1型滑翔机外壳最大应力的数值在100~300 m水深范围内并不是最小的,但B1型滑翔机外壳最大变形处于较为明显的优势。因此,机身饱和度较低的B1型滑翔机的综合性能较优。
|
图 12 不同水深下不同机身饱和度圆蝶形滑翔机壳体剪应力分布图 Fig. 12 Shear stress distribution of pressure shell of different surface saturations in different water depths |
图13为不同水深下不同蝶形滑翔机壳体最大变形和最大剪应力分布趋势图。从机身直径方面分析,随着机身直径的增加,最大变形和最大剪应力均会增加,而D1200型滑翔机在300 m水深下的最大剪应力超过了屈服强度,D1050型滑翔机随着水深增加最大剪应力增加速率明显高于D1000型滑翔机,因此为了优化设计,应在100~300 m水深范围内的碟形滑翔机直径应在1000 mm左右选取,从而降低机身的最大变形量和剪应力。

|
图 13 不同水深下蝶形滑翔机壳体最大变形和最大剪应力分布趋势图 Fig. 13 Distribution trend of maximum deformation and shear stress of DSUG in different water depths. |
从机身高度进行分析,可以观察到随着机身身高的增加,最大变形量和最大剪应力的变化会呈现先增后减的变化,并且随着水深的增加,这种趋势越发明显。在100~300 m水深时,H360型滑翔机壳体的变形量和剪应力数值均优于H340型滑翔机和H380型滑翔机。因此对于机身身高的选取,圆碟形水下滑翔机均存在一个最优解。
对于不同机身表面饱和度圆碟型水下滑翔机,外壳的最大变形和最大剪应力分布规律并不统一。B2型滑翔机外壳最大应力的数值在100~300 m水深范围内是最小,但B2型滑翔机外壳最大变形处于B1型和B3型的中间位置。B3型滑翔机的最大变形和最大剪应力均较大。而B1型滑翔机耐压壳的最大变形量最小,且相较于B2和B3具有较为明显的优势。虽然B1型滑翔机耐压壳剪应力略高于B2型滑翔机,但也在合理的范围区间,且完全满足材料屈服强度的限制。综合来看,机身饱和度较低的B1型滑翔机的综合性能较优。
3 结 语本文利用有关CCS规范与薄壳形变理论对耐压壳体的壁厚进行设计。结合圆碟形水下滑翔机耐压壳体的优缺点和工作环境的特点,选择7075航空铝合金作为耐压壳体材料。通过CCS潜水系统与潜水器入级规范中设计并校核圆碟形耐压壳体的厚度,确定了水下滑翔机耐压壳体壁厚为4.5 mm。为了使圆碟形滑翔机结构在不同水深下的受力更加均匀,确定了包括原始设计在内,不同机身直径、不同机身高度和不同机身表面饱和度的9种水下滑翔机机身外形结构。通过有限元方法分析了圆碟形水下滑翔机的结构,为优化设计提供了理论数据与参考。具体结论为:
1)在100~300 m水深范围内应减小机身直径,从而降低机身的最大变形量和最大应力,D1000型滑翔机外壳的最大变形和最大应力分布更为合理。
2)随着机身高度的增加,最大变形量和最大应力的变化规律是先减后增,且随着工作水深的增加,这种趋势越发明显。H360型滑翔机外壳在100~300 m水深范围内最大变形和最大应力数值均优于H340型滑翔机和H380型滑翔机,因此机身高度的选取对圆碟型水下滑翔机的优化设计有一定影响。
3)对于不同机身表面饱和度圆碟型水下滑翔机,其外壳的最大变形和最大应力分布规律并不统一。饱和度较低的B1型滑翔机耐压壳剪应力略高于B2型滑翔机,但也在合理的范围区间,且完全满足材料屈服强度的限制。综合来看,机身饱和度较低的B1型滑翔机的综合性能较优。
| [1] |
沈新蕊, 王延辉, 杨绍琼, 等. 水下滑翔机技术发展现状与展望[J]. 水下无人系统学报, 2018, 26(2): 89−106. SHEN Xin-rui, WANG Yan-hui , YANG Shao-qiong, et al. Development of underwater gliders: an overview and prospect[J]. Journal of Unimanned Undersea System 2018, 26(2): 89−106. |
| [2] |
LEONARD N E, PALEY D A, LEKIEN F, et al. Collective motion, sensor networks, and ocean sampling[J]. Proceeding of the IEEE, 2007, 95(1): 48-74. DOI:10.1109/JPROC.2006.887295 |
| [3] |
NAKAMURA M, ITO Y, INADA M, et al. Development of disk type underwater glider for virtual mooring: Part 3, Construction of prototype vehicle and field experiments[J]. Journal of the Japan Society of Naval Architects& Ocean Engineers, 2013, 18: 157-166. |
| [4] |
WOODS, ALLENT, KUHNS, et al. The development of an autonomous underwater powered glider for deep-sea biological, chemical and physical oceanography[C]//Oceans. Aberdeen, UK: IEEE, 2007, 4302217.
|
| [5] |
俞铭华, 王仁华, 王自力, 等. 深海载人潜水器有开孔耐压球壳的极限强度[J]. 中国造船, 2005, 92-96. YU Min-hua, WANG Ren-hua, WANG Zi-Li, et al. Deep-sea manned submersibles have the ultimate strength of a perforated pressure-resistant ball shell[J]. Shipbuilding of China, 2005, 92-96. DOI:10.3969/j.issn.1000-4882.2005.04.015 |
| [6] |
张代雨, 王志东, 凌宏杰, 等. 基于FFD和轴变形方法的翼身融合水下滑翔机外形参数化建模[J]. 舰船科学技术, 2021, 43(3): 89−92+125. ZHANG Dai-yu, WANG Zhi-dong, LING Hong-jie, et al. Shape parameterization of blended-wing-body underwater glider based on FFD and axis deformation method[J]. Ship Science and Technology, 2021, 43(3): 89−92+125. |
| [7] |
董华超, 王鹏, 张益进. 翼身融合水下滑翔机舱体−骨架耦合 结构的离散优化设计[J]. 中国舰船研究, 2021, 16(4): 70-78. DONG H C, WANG P, ZHANG Y J. Discrete optimization design for cabin-skeleton coupling structure of blended-wingbody underwater glider[J]. Chinese Journal of Ship Research, 2021, 16(4): 70-78. |
| [8] |
李天博, 王鹏, 孙斌, 等. 一种联翼式水下滑翔机外形优化设计方法[J]. 哈尔滨工业大学学报, 2019, 51(4): 26−32. LI Tianbo, WANG Peng, SUN Bin, et al. A shape optimization design method of the joined-wing underwater glider[J]. Journal of Harbin Institute of Technology, 2019, 51(4): 26−32. |
| [9] |
张宁, 王鹏, 宋保维. 基于改进型 Kriging-HDMR 的翼身融合水下滑翔机外形优化设计[J]. 水下无人系统学报, 2019, 27(5): 496−502. ZHANG Ning, WANG Peng, SONG Bao-wei. Shape Optimization for blended-wing-body underwater glider using improved Kriging-HDMR[J]. Journal of Unmanned Undersea Systems, 2019, 27(5): 496−502. |
| [10] |
刘德良, 曹淑华, 王天霖, 等. 碟形水下滑翔器耐压壳的结构优化[J]. 大连海事大学, 2018, 37(3): 1−7. LIU De-liang, CAO Shu-hua, WANG Tian-lin, et al. Optimized design of the pressure-proof shell of disk-shaped underwater gliders[J]. Dalian Maritime University, 2018, 37(3): 1−7. |
| [11] |
甄春博, 邱吉廷, 英扬, 等. 基于组合优化算法的碟形水下滑翔机结构优化[J]. 科学技术与工程, 2019, 19(9): 240-244. ZHEN Chunbo, QIU Jiting, YING Yang, et al. Structure optimization of round dish-shaped underwater glider based on combinatorial optimization method[J]. Science Technology and Engineering, 2019, 19(9): 240-244. DOI:10.3969/j.issn.1671-1815.2019.09.038 |
| [12] |
何雪浤, 刘新猛, 郭珍珍, 等. 基于正交试验的潜水器耐压壳体的结构优化设计[J]. 机械科学与技术, 2015(1): 8-12. HE Xuehong, LIU Xinmeng, GUO Zhenzhen, et al. Structural optimization design of underwater vehicle shell based on orthogonal experimen[J]. Mechanical Science and Technology for Aerospace Engineering, 2015(1): 8-12. |
| [13] |
伍莉, 徐治平, 张涛, 等. 球形大深度潜水器耐压壳体优化设计[J]. 船舶力学, 2010, 14(5): 509−515. WU Li, XU Zhi-ping, ZHANG Tao, et al. Optimum design of spherical deep—submerged pressure hull[J]. Journal of Ship Mechanics, 2010, 14(5): 509−515. |
| [14] |
程妍雪, 庞永杰, 杨卓懿, 等. 基于径向基神经网络模型的耐压壳 6σ 设计[J]. 上海交通大学学报, 2014, 48(4): 493-497. CHENG Yan-xue, PANG Yong-jie, YANG Zhuo-yi, et al. 6σ design for pressurized cylindrical shells based on RBF[J]. Journal of Shanghai Jiaotong University, 2014, 48(4): 493-497. |
| [15] |
张凡. 碟形水下滑翔机结构稳定性与强度研究[D]. 大连: 大连海事大学, 2017.
|
| [16] |
于鹏垚, 沈聪, 王天霖, 等. 圆碟形水下滑翔机外形设计研究[J]. 中国造船, 2018, 59(4): 42-50. YU Peng-yao, SHENG Cong, WANG Tian-lin, et al. Design of disc-shaped underwater glider[J]. Shipbuilding of China, 2018, 59(4): 42-50. DOI:10.3969/j.issn.1000-4882.2018.04.005 |
| [17] |
甄春博, 王强, 王晓旭, 等. 基于参数化方法的圆碟形水下滑翔机结构轻量化设计[J]. 机械设计与制造, 2021(4): 231−234. ZHENG Chun-bo, WANG Qiang, WANG Xiao-xu et al. The lightweight design for the structure of round disk-shaped underwater glider based on parameterization method[J]. Machinery Design & Manufacture, 2021(4): 231−234. |
 2024, Vol. 46
2024, Vol. 46
