水下辐射噪声的主要来源通常有螺旋桨噪声、机械噪声、水动力噪声3种[1]。其中,稳态机械噪声,即水下结构的稳态辐射噪声的预报方法已成熟。然而,近年来水下结构的瞬态辐射噪声也渐渐引起了国内外学者的重视。典型的水下结构瞬态噪声包括舰艇内部机器的启动、转向时的舵角变化、鱼雷发射出管等过程产生的时域上持续时间短暂的宽带噪声等。水下结构瞬态噪声因其独有的突发性、随机性、突变性等性质,利用过去处理稳态噪声的方法计算结果并不准确,亦无法描述瞬态辐射噪声的声场特性[2]。因此,对水下结构瞬态噪声的研究仍不够充分,需进行更为深入的探索研究。
目前,时域有限元法[3]、时域边界元法[4]、时域有限差分法[5]、时域有限元结合时域边界元法[6]、虚拟模态结合统计能量法[7]等作为水下瞬态结构噪声计算的重要方法,在求解时长较短的情况下可得到较为准确的收敛结果。然而,在求解过程中需对维数等离散自由度数的矩阵求逆,且由于收敛性要求数值计算的时间步长不能取得很大,计算效率受到很大制约。此外,由于有限元法和边界元法等数值方法适用于归一化波数较小时的低频噪声计算,而瞬态噪声的带宽较宽,归一化波数较大时的高频噪声计算无法使用上述数值方法得到较为准确的结果。
为了提高水下结构瞬态噪声的计算效率,特别是归一化波数较大的高频噪声计算准确性,本文提出一种基于时域冲激响应的瞬态噪声预报方法。它通过目标辐射声场与散射声场的互易定理,利用基于物理声学近似方法的时域散射声场的快速算法,求解时域冲激响应,进而对在结构表面各离散单元处时域冲激响应与法向振速的时域卷积的面积加权求和,以获得结构的瞬态辐射噪声。本文通过2种典型的解析模型验证了该方法的准确性,并利用该方法计算了复杂刚性目标的瞬态结构噪声,并分析了其时域声场的时间特性和能量的空间指向性。
1 基础理论 1.1 已知结构表面振速的时域辐射声场Kirchhoff公式在理想流体中、小振幅声压假设前提下,基于时域格林函数的时域辐射声场的Kirchhoff公式[8]如下:
| $ \begin{split} p(\stackrel{\rightharpoonup }{r},t)=\,& -\displaystyle {\int }_{-T}^{T}\displaystyle {\int }_{S}\left[G(\stackrel{\rightharpoonup }{r},t;\stackrel{\rightharpoonup }{{r}^{\prime }},\tau )\frac{\partial p(\stackrel{\rightharpoonup }{{r}^{\prime }},\tau )}{\partial n}- \right.\\[-4pt] & \left. p(\stackrel{\rightharpoonup }{{r}^{\prime }},\tau )\frac{\partial G(\stackrel{\rightharpoonup }{r},t;\stackrel{\rightharpoonup }{{r}^{\prime }},\tau )}{\partial n}\right]{\rm{d}}S{\rm{d}}\tau 。\end{split} $ | (1) |
式中:
对于时域格林函数
| $ \left\{\begin{aligned} & {\nabla }^{2}G(\stackrel{\rightharpoonup }{r},t;\stackrel{\rightharpoonup }{{r}^{\prime }},\tau )-\dfrac{1}{{c}^{2}}\dfrac{{\partial }^{2}G(\stackrel{\rightharpoonup }{r},t;\stackrel{\rightharpoonup }{{r}^{\prime }},\tau )}{\partial {t}^{2}}=\\ & \qquad-\delta (\stackrel{\rightharpoonup }{r}-\stackrel{\rightharpoonup }{{r}^{\prime }})\delta (t-\tau ),\\ & {G(\stackrel{\rightharpoonup }{r},t;\stackrel{\rightharpoonup }{{r}^{\prime }},\tau )|}_{t\leqslant \tau }=0,\\ & {\frac{\partial G(\stackrel{\rightharpoonup }{r},t;\stackrel{\rightharpoonup }{{r}^{\prime }},\tau )}{\partial t}|}_{t\leqslant \tau }=0,\\ & {G(\stackrel{\rightharpoonup }{r},t;\stackrel{\rightharpoonup }{{r}^{\prime }},\tau )|}_{\left|\stackrel{\rightharpoonup }{r}\right|\to \infty }=0。\end{aligned}\right. $ | (2) |
时域格林函数的选取方式有很多种。常见的自由场中的时域格林函数[9]为:
| $ G(\stackrel{\rightharpoonup }{r},t;\stackrel{\rightharpoonup }{{r}^{\prime }},\tau )=\frac{1}{4{\text{π}} R}\delta (t-\tau -\frac{R}{c})\text{ },\text{ }R=\left|\stackrel{\rightharpoonup }{r}-\stackrel{\rightharpoonup }{{r}^{\prime }}\right|。$ | (3) |
自由场中的时域格林函数表示
对于已知结构体表面
| $ {\frac{\partial G(\stackrel{\rightharpoonup }{r},t;\stackrel{\rightharpoonup }{{r}^{\prime }},\tau )}{\partial n}|}_{\stackrel{\rightharpoonup }{r}\in S}=0。$ | (4) |
满足式(4)边界条件的时域格林函数,即为已知结构表面法向振速时,结构体辐射声场的时域冲激响应函数。将式(4)代入式(1),可得已知结构表面法向振速时,结构体产生的时域辐射声场:
| $ p(\stackrel{\rightharpoonup }{r},t)=-{\displaystyle {\int }_{-T}^{T}{\displaystyle {\int }_{S}G(\stackrel{\rightharpoonup }{r},t;\stackrel{\rightharpoonup }{{r}^{\prime }},\tau )\frac{\partial p(\stackrel{\rightharpoonup }{{r}^{\prime }},\tau )}{\partial n}{\rm{d}}S}{\rm{d}}\tau } 。$ | (5) |
基于该时域冲激响应函数,只需给结构体表面
互易定理为线性声学中的一条普适法则。本研究基于该法则,将构建已知结构表面法向振速时的辐射声场与散射声场之间的声学互易关系。
对本文涉及的2种不同声系统进行互易性分析:一种是在声场中位置A处施加单极子声源
| $ \frac{{{p_1}(\omega )}}{{Q(\omega )}} = \frac{{{p_2}(\omega )}}{{{v_n}(\omega ){\rm{d}}S}}。$ | (6) |
将式(6)写成乘积形式,并作逆傅里叶变换:
| $ {{\mathcal{F}}}^{-1}[{p}_{2}(\omega )Q(\omega )]={{\mathcal{F}}}^{-1}[{p}_{1}(\omega ){v}_{n}(\omega ){\rm{d}}S]。$ | (7) |
由于2个时域信号卷积的傅里叶变换结果等于二者信号频谱的乘积,因此式(7)可写成:
| $ {p_2}(t) \times Q(t) = {p_1}(t) \times {v_n}(t) \times {\rm{d}}S 。$ | (8) |
式(8)是用于描述已知结构法向振速时结构体的时域辐射问题与点源激励下满足刚性边界条件的结构体的时域散射问题互易关系式。其中,
若
| $ Q(t) = {Q_0}\delta (t) 。$ | (9) |
即声场中位置A处的
| $ {p_2}(t) = \frac{1}{{{Q_0}}} \cdot {p_1}(t) \times {v_n}(t) \cdot {\rm{d}}S 。$ | (10) |
由此,可得出基于互易定理的已知结构法向振速时,结构体的时域辐射声压表达式:
| $ p(\stackrel{\rightharpoonup }{r},t)=\frac{1}{{Q}_{0}}{\displaystyle {\int }_{S}{p}_{1}(\stackrel{\rightharpoonup }{{r}^{\prime }},t)\times {v}_{n}(\stackrel{\rightharpoonup }{{r}^{\prime }},t){\rm{d}}S} 。$ | (11) |
事实上,若交换式(5)的积分次序,时域积分项即为时域格林函数
| $ p(\stackrel{\rightharpoonup }{r},t)=-{\displaystyle {\int }_{S}G(\stackrel{\rightharpoonup }{r},t;\stackrel{\rightharpoonup }{{r}^{\prime }})\times \frac{\partial p(\stackrel{\rightharpoonup }{{r}^{\prime }},t)}{\partial n}{\rm{d}}S}。$ | (12) |
再由声压的法向导数与法向振速关系式:
| $ \frac{\partial {v}_{n}(\stackrel{\rightharpoonup }{r},t)}{\partial t}=-\frac{1}{\rho }\frac{\partial p(\stackrel{\rightharpoonup }{r},t)}{\partial n}。$ | (13) |
其中:
| $ p(\stackrel{\rightharpoonup }{r},t)=\rho {\displaystyle {\int }_{S}\frac{\partial G(\stackrel{\rightharpoonup }{r},t;\stackrel{\rightharpoonup }{{r}^{\prime }})}{\partial t}\times {v}_{n}(\stackrel{\rightharpoonup }{{r}^{\prime }},t){\rm{d}}S} 。$ | (14) |
比较式(11)与式(14),不难发现基于点源散射与面元辐射互易关系的时域格林函数
| $ \frac{\partial G(\stackrel{\rightharpoonup }{r},t;\stackrel{\rightharpoonup }{{r}^{\prime }})}{\partial t}=\frac{1}{\rho {Q}_{0}}{p}_{1}(\stackrel{\rightharpoonup }{{r}^{\prime }},t)。$ | (15) |
因此,首先利用散射问题中满足刚性边界条件的结构表面入射声压与散射声压之和
数值计算时,通过剖分网格的方式将目标表面离散成
| $ p(\stackrel{\rightharpoonup }{r},t)=\frac{1}{{Q}_{0}}{\displaystyle \sum _{j=1}^{N}{p}_{1}(\stackrel{\rightharpoonup }{{{r}^{\prime }}_{j}},t)\times {v}_{n}(\stackrel{\rightharpoonup }{{{r}^{\prime }}_{j}},t)\Delta {S}_{j}}。$ | (16) |
式中:
本节以单个脉动球、脉动球与刚性球阵列这2种典型模型作为研究对象,开展基于互易定理时域冲激响应的瞬态噪声近似预报方法验证。其中,脉动球与刚性球阵列模型中,包含沿直线等距排列的1个脉动球和2个刚性球,脉动球位于中间。2种典型模型中的脉动球表面均施加信号形式为单频正弦信号的法向振速。
2.1 单个脉动球的瞬态辐射声场验证与分析该脉动球的半径为1 m。施加于球体表面的法向振速信号为单频正弦信号,频率为2 kHz,信号长度为5 ms,幅值为1 m/s。考察场点定为距球心10 m处同心球面上的某一点,不妨取为(10 m,0,0)。球表面的网格划分,以法向振速信号频率对应的1/6波长的三角形网格进行划分。图1为单个脉动球及考察场点的几何示意图。
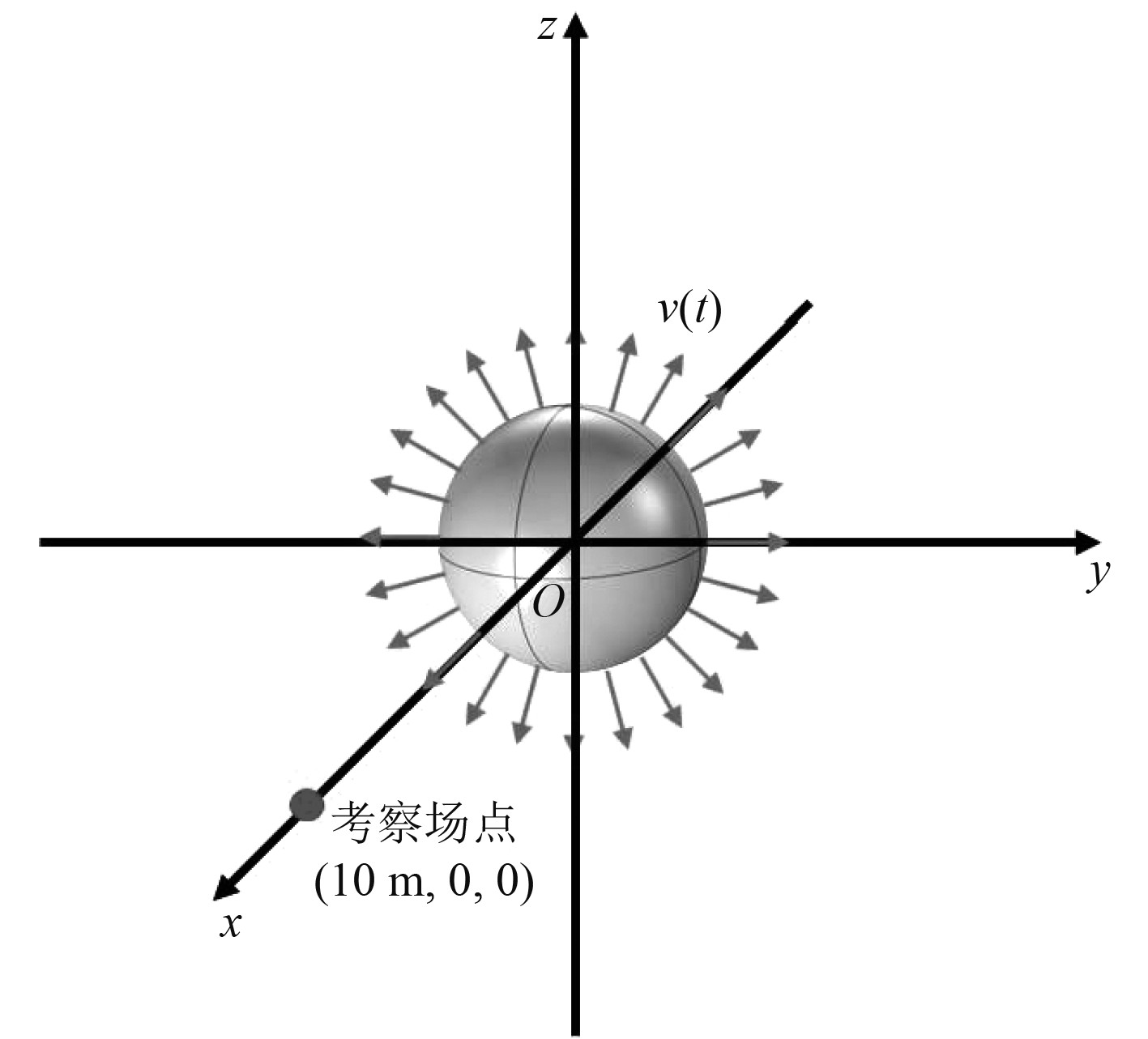
|
图 1 单个脉动球及考察场点几何位置 Fig. 1 Geometric position of the single pulsating sphere and the field point |
首先,进行与辐射声场相互易的散射声场的计算。在距球心10 m处的(10 m,0,0)点处设置一个单极点源,激励信号为带宽包含2 kHz的脉冲函数。通过时域快速算法求得该球表面网格每一中心点处的入射声压
为了验证该近似预报算法的正确性,需将该结果与时域解析解对比。该时域解析解是基于单个脉动球的频域解析解,运用频域间接法计算得到。
图2为时域近似预报方法与时域解析解的计算结果对比图。
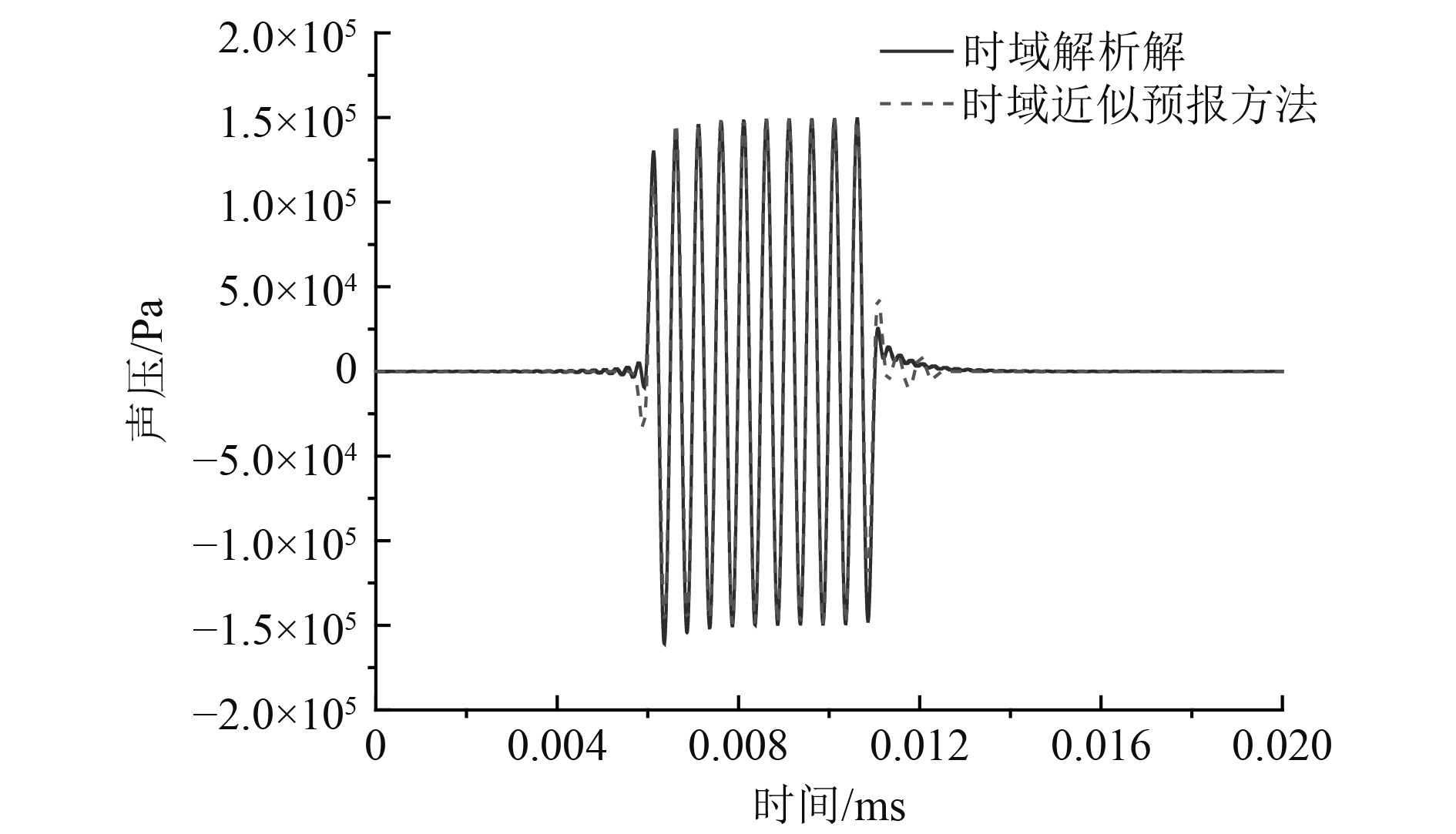
|
图 2 单个脉动球时域辐射声场的计算结果对比 Fig. 2 Comparison of calculation results of time domain radiated sound field of the single pulsating sphere |
可知,二者波形吻合较好。二者考察点接收到辐射声压波形的时延一致,波形的形状与幅值略有不同。时域近似预报方法的波形幅值相对解析解较小,是由于时域快速算法中冲击响应的激励波形是以瑞克脉冲为近似波形进行计算导致的,即会有一定程度的能量泄露。此外,近似预报方法的波形在首位两端与解析解的差异是由于瑞克脉冲的波形调制导致的。
为了进一步定量比较时域近似预报方法计算结果与时域解析解计算结果的优劣,表1列出了二者所花费的计算时间以及二者时域波形的包络相关系数。
|
|
表 1 单个脉动球结果的计算时间及包络相关系数 Tab.1 Calculation time and envelope correlation coefficient of the single pulsating sphere results |
可以看出,时域近似预报方法的计算时间比时域解析解要少很多,该近似方法的计算效率更高。此外,时域近似预报方法和时域解析解的包络相关系数为0.9974,相关系数接近于1,说明时域近似预报方法的结果与时域解析解的结果符合得很好。
综上,在一定的误差范围内,可以验证该时域近似预报方法的准确性和合理性。
2.2 脉动球与刚性球阵列的瞬态辐射声场验证与分析排列于同一直线的3个球体半径均为1 m。相邻球体的球心间距为3 m。其中,对位于中心位置的脉动球表面施加法向振速信号。信号形式为单频正弦信号,频率为4 kHz,信号长度为2.5 ms,幅值为1 m/s。以中心脉动球的球心为坐标原点,以3个球的球心连线作为z轴。考察场点选取距坐标原点100 m处的同心球面上的3个点,其坐标分别为
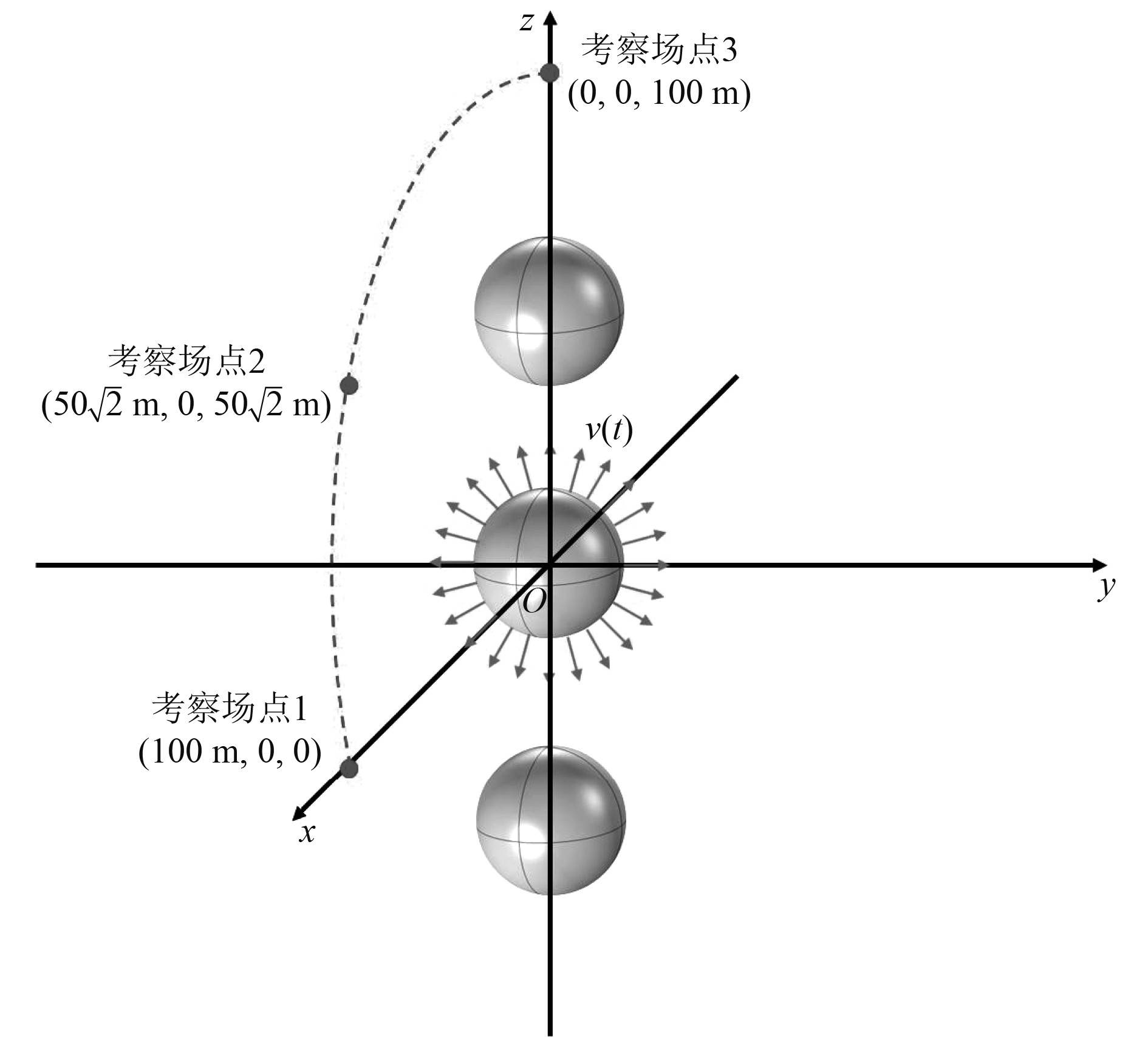
|
图 3 脉动球与刚性球阵列及考察场点几何位置 Fig. 3 Geometric positions of the array consisting of one pulsating sphere and two rigid spheres and field points |
划分好网格后,首先进行与辐射声场相互易的散射声场计算。根据辐射声场考察点的数量决定了其对应散射声场的计算次数。将分别在距球心100 m处的
同样地,计算完成后将3种工况下的每一网格中心点处的入射、散射声压相加得到总声压
基于该脉动球与刚性球阵列的频域解析解的推导公式见附录,再利用频域间接法计算得到该脉动球与刚性球阵列模型辐射问题的时域解析解。
将以上3个考察点时域近似预报方法与解析解的计算结果进行对比。图4分别为考察点
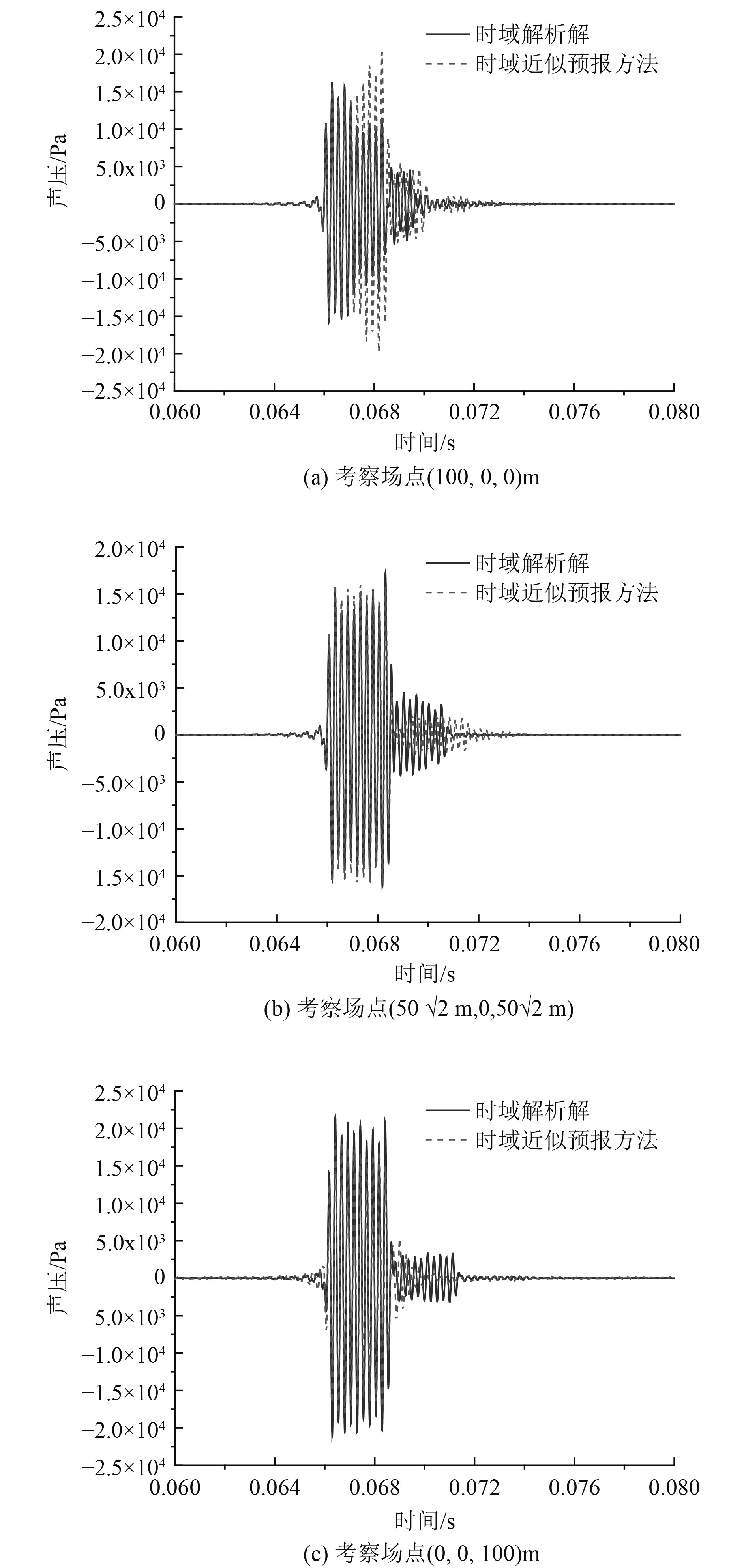
|
图 4 脉动球与刚性球阵列所有考察场点的时域辐射声场计算结果对比 Fig. 4 Comparison of time domain radiated sound field calculation results for all field points of the array consisting of one pulsating sphere and two rigid spheres |
从图4(a)和图4(b)可知,2个考察点的波形总体吻合较好。对每一考察点而言,时域近似预报方法得到波形相应的时延均与解析解一致。然而,近似预报方法的波形形状与幅值相较解析略有不同,特别是在二者直达接收信号的末尾处。末尾处的信号是由于中上下刚性球对脉动球辐射声场的一次散射甚至多次散射影响而产生的信号延迟效应。因为近似预报方法虽然考虑了多次散射,但未考虑到更复杂的多次散射,所以其波形与解析解的实际波形在幅值与相位上有所区别。
图4(c)中,时域近似预报方法的波形与解析解波形的直达信号拟合较好,直达信号后端毗连的波包有些差异。第1个直达波包,时域近似预报方法比解析解的幅值略低;第2个毗连波包,时域近似预报方法的信号长度小于解析解,分析是由于在求解冲激响应时受时域快速算法本身的影响,无法得到实际情况下因球体遮挡而产生的衍射效应所产生的时域波形,造成二者波形不一致。
表2列出了时域近似预报方法与时域解析解所花费的计算时间以及二者在3个考察场点时域波形的包络相关系数。
|
|
表 2 脉动球与刚性球阵列结果的计算时间及3个场点的包络相关系数 Tab.2 Calculation time and envelope correlation coefficients of three field points for the results of the array consisting of one pulsating sphere and two rigid spheres |
可知,时域近似预报方法的计算时间与时域解析解相比大幅降低,该近似方法的计算效率显著提高。此外,考察场点(100, 0, 0) m、
综上,在一定的误差范围内,该时域近似预报方法对脉动球与刚性球阵列的时域辐射声场实现预报的准确性得到了验证。
3 复杂结构瞬态辐射特性分析利用该近似预报方法对结构稍复杂的模型进行时域辐射声场计算。
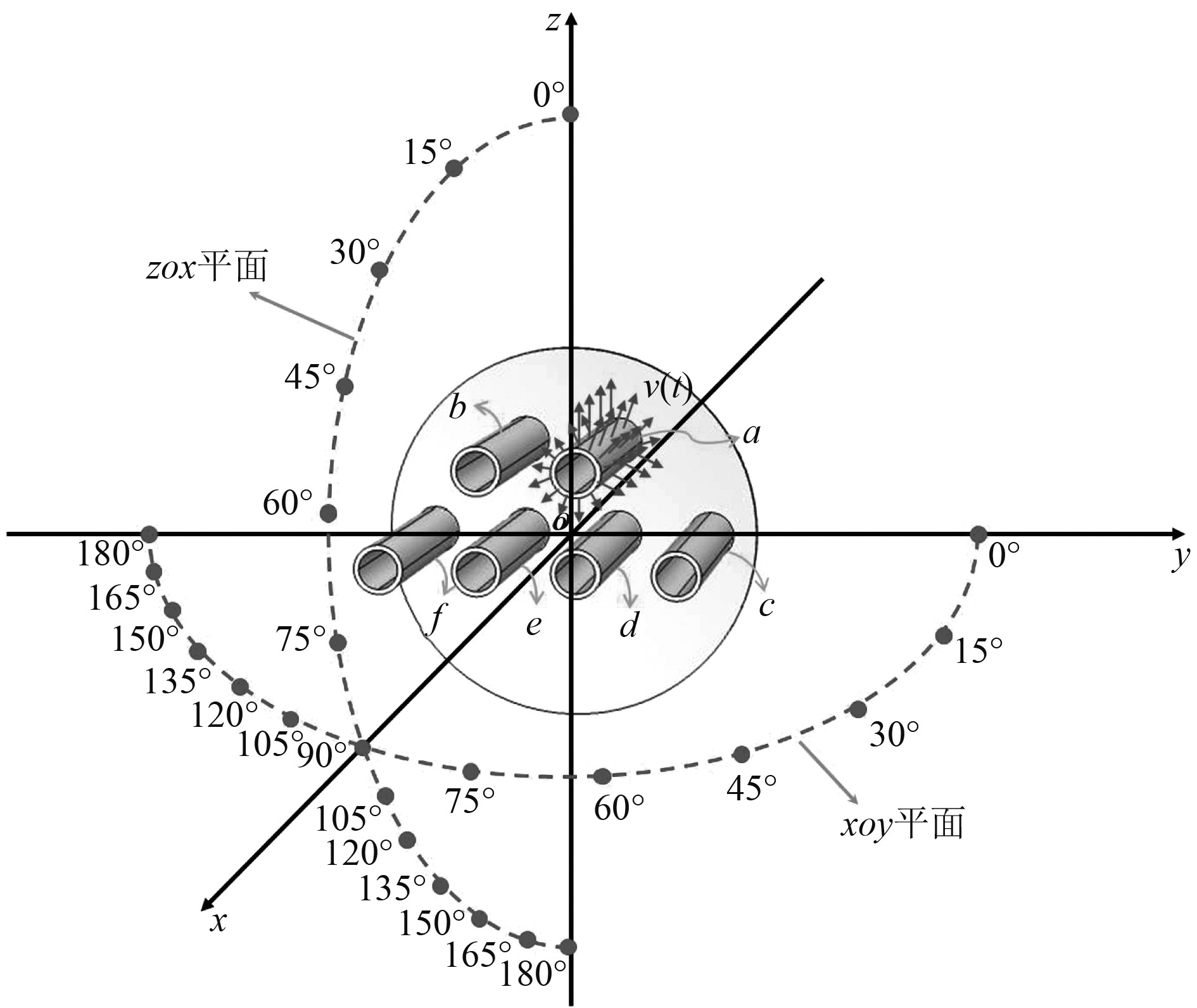
该复杂结构及考察场点的几何示意图如图5所示。该模型由6根完全相同且相互平行的圆柱管和一个圆形障板组成。其中,圆柱管的长度为6 m、管外直径为1 m、管厚为100 mm。圆形障板的半径为4 m、厚度为100 mm。以圆形障板的前圆端面中心作为坐标原点,并令该模型的对称平面为ZOX平面,以圆柱管的轴向方向作为X轴。a号管、b号管、c号管、d号管、e号管、f号管的轴向投影圆心分别位于(0,1 m,2 m)、(0,−1 m,2 m)、(0,3 m,0 m)、(0,1 m,0 m)、(0,−1 m,0 m)、(0,−3 m,0 m)。
|
图 5 复杂结构及考察场点几何位置 Fig. 5 Geometric positions of the complex structure and field points |
本文将距坐标原点20 m,
其中,对模型中a号管的内外表面均施加法向振速信号。信号形式为单频正弦信号,频率为4 kHz,信号长度为2.5 ms,幅值为1 m/s。对该模型表面利用三角形网格进行网格划分,其中圆柱管的网格尺寸定为该法向振速信号频率对应的1/6波长,圆形障板的网格最大尺寸定为1/3波长。
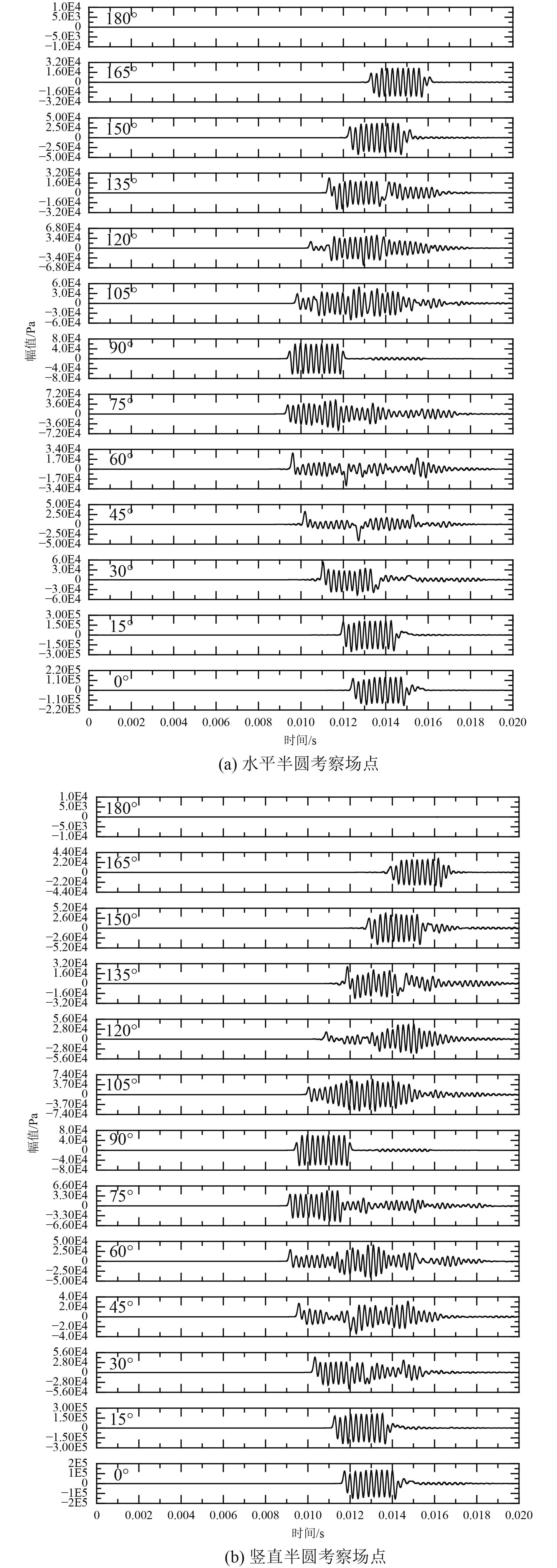
3.1 近似预报方法的时域计算结果图6为利用时域近似预报方法计算得到的水平、竖直半圆间隔15°的考察点、辐射声压时域波形对比图。
|
图 6 复杂结构所有考察场点时域声压计算结果 Fig. 6 Time domain sound pressure calculation results for all field points of the complex structure |
可知,无论是水平方向还是竖直方向的考察场点,辐射声压信号的最早到达时刻都随着考察场点的角度变化而不同,并且其波形展宽随着角度的不同而变化。这是由于施加法向振速激励的a号管及其余结构相对于各考察场点的相对空间位置不同而造成的。
辐射声压信号的最早到达时刻取决于a号管直达辐射波的最早到达时刻和a号管的初始辐射波经模型其他结构产生的一次散射波的最早到达时刻的最小值。需注意的是,只有当考察场点与a号管之间未被模型其他结构遮挡时,a号管的直达辐射波才能被考察场点接收到。
同样地,辐射声压信号的时间延展与a号管的直达辐射波最晚到达时刻、a号管的初始辐射波,经模型其他结构产生的一次、二次甚至多次散射波最晚到达时刻有关。辐射声压信号的实际脉宽为前述两类最晚到达时刻的最大值与激励信号的脉冲宽度之和。这里,在考虑a号管直达辐射波的最晚到达时刻时,亦需判断考察场点与a号管是否被其他结构所遮挡。
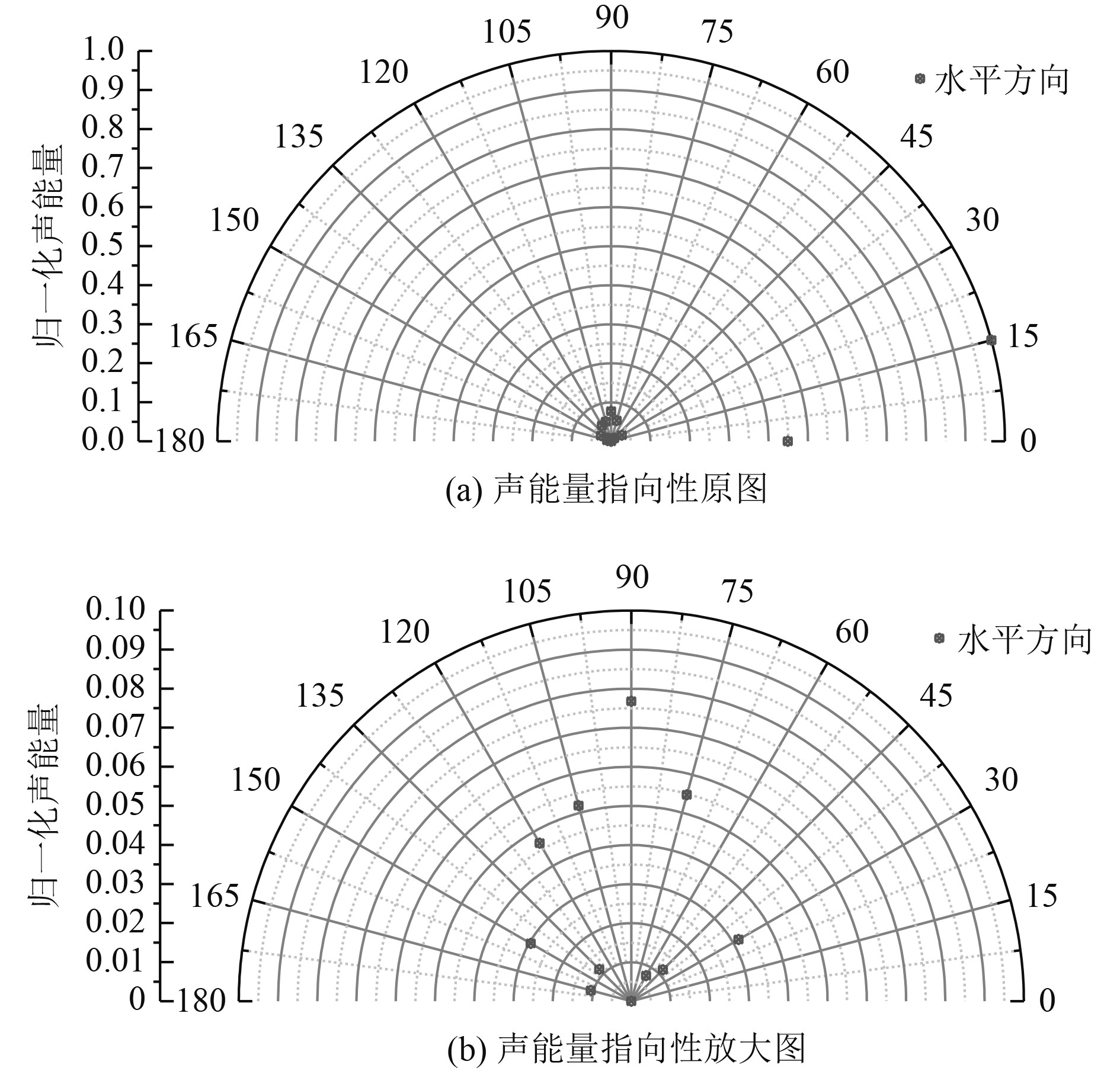
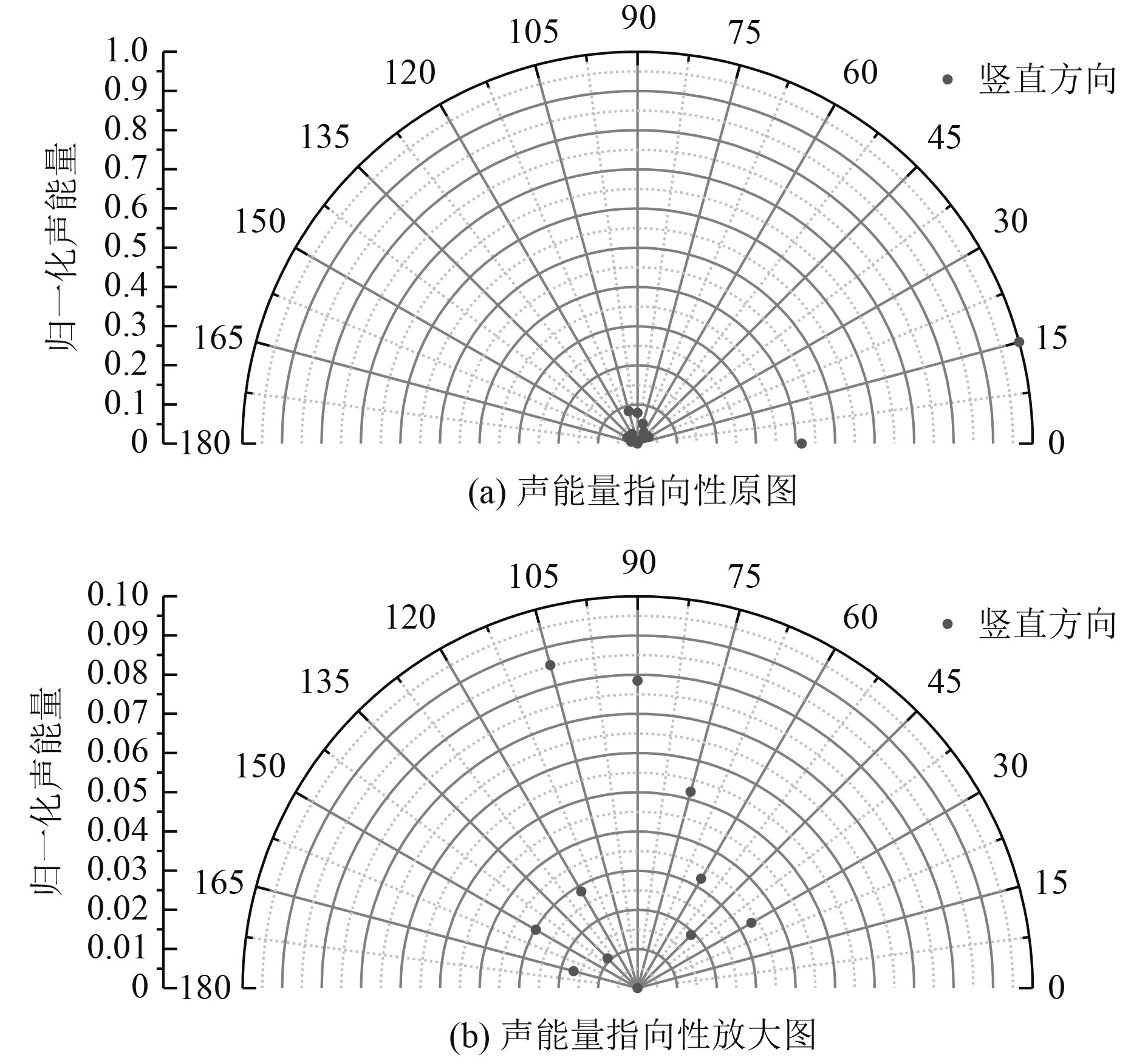
3.2 声场能量的空间指向性考察该模型在a号管施加4 kHz的单频振速信号激励下产生的辐射声场的水平方向及竖直方向的声能量空间指向性。对每一组时域声压取平方在有效时间内进行时域积分,并将归一化后的相对声能量大小作为声能量空间指向性的考察指标。图7和图8分别为水平、竖直半圆间隔15°考察点辐射声能量的指向性散点图。
|
图 7 复杂结构辐射声能量水平方向指向性 Fig. 7 Horizontal directivity of radiated sound energy from the complex structures |
|
图 8 复杂结构辐射声能量竖直方向指向性 Fig. 8 Vertical directivity of radiated sound energy from the complex structures |
从图7可知,水平方向上,在0°及15°方向的辐射声能量显著大于其他角度方向的辐射声能量。并且,在15°方向达到了最大值。是因为在0°和15°方向上,考察点位于相对于a号管的正横方向附近,且未有其他管子的遮挡影响。特别地,在180°方向上,a号管完全被与其平行的b号管遮挡,b号管的衍射效应微弱,所以其幅值接近于0。
从30°方向开始,其辐射声能量明显下降,且随着角度的能量增加呈现无规律地时增时减波动。在这些角度上,考察点远离a号管的正横方向,其振动产生的直达辐射波幅值本身较弱。另外,其5根刚性管会对a号管振动产生的辐射声场的散射效应,即由于一次散射波、二次散射波甚至多次散射波与考察点之间声程的不同,分别对考察点的直达辐射波形在时间上以不同的幅值与时延进行叠加调制。
其中,在90°方向上,辐射声能量较其他角度较大,主要是由于圆形障板对a号管振动产生的直接辐射波及其他管子的散射波散射作用,使得该考察点的辐射声能量增强。若不考虑180°方向,在45°、60°、135°以及165°方向上,其辐射声能量相对较小,这是由于管子间的互散射效应十分明显,这些方向考察点位置处的原直达辐射波的幅值被大大削减。
从图8可知,竖直方向上,在0°及15°方向的辐射声能量显著大于其他角度方向的辐射声能量,并且在15°方向达到了最大值。是因为在0°和15°方向上,考察点位于相对于a号管的正横方向附近,且未有其他管子的遮挡影响。特别地,在180°方向上,a号管完全被其正下方的d号管遮挡,且d号管与e号管的衍射效应微弱,所以其声能量接近于0。
从30°方向开始,其辐射声能量明显下降,且随着角度声能量的增加呈现无规律地时增时减的波动。在这些角度上,考察点远离a号管的正横方向,其振动产生的直达辐射波幅值本身较弱。另外,其余5根刚性管及圆形障板会对a号管振动产生辐射声场的散射效应,即由于一次散射波、二次散射波甚至多次散射波与考察点之间声程的不同,分别对考察点的直达辐射波形在时间上以不同的幅值与时延进行叠加调制。
其中,在75°、90°、105°方向上,辐射声能量较其他角度较大,主要是由于圆形障板对a号管振动产生的直接辐射波及其他管子的散射波散射作用,使得该考察点的辐射声能量增强。若不考虑180°方向,在45°、135°以及165°方向上,其辐射声能量相对较小,这是由于管子与管子、管子与障板间的互散射效应十分明显,这些方向考察点位置处的原直达辐射波的幅值被大大削减。
4 结 语1)提出一种基于时域冲激响应的瞬态噪声近似预报方法。其中,结构表面各处之于考察场点的时域冲激响应是运用时域快速算法,通过计算在考察场点设置脉冲点源激励下,结构表面各处的时域表面声压响应得到的。
2)以2种典型模型为例,通过对比该瞬态噪声近似预报方法与时域解析解的计算结果,验证了该近似预报方法的准确性,并且该近似预报方法适用于工程上对瞬态噪声的快速预报。
3)运用瞬态噪声近似预报方法,对镶嵌于圆形障板的管阵列这一复杂结构进行瞬态辐射声场的计算,并分析了所选取考察场点辐射声压信号的时间特征及声能量空间指向性。
| [1] |
张勇, 张福民, 刘庆亮, 等. “深海一号”载人潜水器支持母船水下辐射噪声控制关键技术[J]. 舰船科学技术, 2022, 44(10): 49-54. ZHANG Y, ZHANG F M, LIU Q L, et al. Research on key technologies of underwater radiated noise control of Shen Hai 1 manned submersible supporting ship[J]. Ship Science and Technology, 2022, 44(10): 49-54. |
| [2] |
张峻铭. 水下瞬态声源声能量计算与测量方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2019.
|
| [3] |
彭志. 水下目标声散射频域/时域特性仿真及应用研究[D]. 武汉: 华中科技大学, 2020.
|
| [4] |
HU F Q, PIZZO M E, NARK D M. On a time domain boudary integral equation formulation for acoustic sacttering by rigid bodies in uniform mean flow[J]. Journal of the Acoustical Socirty America, 2017, 142: 3624-3636. DOI:10.1121/1.5017734 |
| [5] |
刘佳琪, 郭永超, 朴胜春. 海洋涡旋地震成像的时域有限差分仿真[J]. 声学技术, 2022, 41(3): 426-431. |
| [6] |
庞福振, 王洪富, 缪旭弘, 等. 瞬态冲击载荷下双层加筋圆柱壳水下声辐射研究[C]//第十八届船舶水下噪声学术讨论会论文集. 中国昆明, 2021. PANG F Z, WANG H F, MIAO X H, et al. Study on underwater acoustic radiation of double stiffened cylindrical shells under transient impact loading[C]//Proceedings of the 18th Symposium on Ship Underwater Noise. Kunming, China, 2021. |
| [7] |
温华兵, 吴俊杰, 马正刚, 等. 浮冰碰撞下船舶舱室瞬态噪声分析及控制[J]. 中国造船, 2020, 61(3): 121-130. |
| [8] |
BENNETT C L, MIERAS H. Time domain integral equation solution for acoustic scattering from fluid targets[J]. Journal of the Acoustical Socirty America, 1981, 69(5): 1261-1265. DOI:10.1121/1.385808 |
| [9] |
WU S F. Transient sound radiation from impulsively accelerated bodies[J]. Journal of the Acoustical Socirty America, 1993, 94(1): 542-553. DOI:10.1121/1.407066 |
| [10] |
FAHY F J. Some applications of the reciprocity principle in experimental vibroacoustics[J]. Acoustical Physics, 2003, 49(2): 217-229. DOI:10.1134/1.1560385 |
| [11] |
GAUNAURD G C, HUANG H. Acoustic scattering by a spherical body near a plane boundary[J]. Journal of the Acoustical Socirty America, 1994, 96(4): 2526-2536. DOI:10.1121/1.410126 |
 2024, Vol. 46
2024, Vol. 46
