2. 武汉理工大学 高性能船舶技术教育部重点实验室,湖北 武汉 430063
2. Key Laboratory of High Performance Ship Technology, Ministry of Education, Wuhan University of Technology, Wuhan 430063, China
夹芯复合材料T型节点作为复合材料船体结构中常见的连接结构,主要用于顶甲板与舱壁、内甲板与舷侧以及舷侧与主甲板之间的连接,因此这类节点强度对复合材料船体结构强度有着直接的影响。不同传统金属材料,由于复合材料结构具有各向异性的特点,要想准确预测复合材料结构的强度,破坏模式,一般是通过试验进行研究[1]。但试验测试存在周期长、成本高等问题,特别是对节点进行尺寸优化后再次进行试验效率较低,因此有必要针对复合材料T型节点直接计算模型进行研究,实现对T型节点强度的快速校核。
目前国内外针对T型节点研究主要是关于T型节点的极限承载力及其影响因素的研究,而关于如何有效地对T型节点结构强度进行直接计算的研究较少。Atul等[2]对3种不同结构形式的复合材料T型节点进行拉伸试验研究,并建立与之对应的有限元计算模型,研究不同节点之间失效模式的区别。结果表明数值模拟结果与试验结果吻合度较高,能够有效表现3种不同结构形式T型节点的失效模式。陈亮等[3]针对一种新型复合材料T型节点在其梯形过渡区设置不同长度的复合材料纤维铺层,进行三点弯曲试验与剪切变形试验,研究该节点结构的失效破坏模式以及极限承载力大小。Dharmawan等[4]针对复合材料T型节点的芯材厚度以及过渡区的尺寸变化对其极限承载力的影响展开试验研究。
而在关于船体结构的直接计算中,针对局部模型的载荷与边界条件的设置,朱加刚等[5]通过在舱段模型端面施加剪力和弯矩,同时设置惯性释放的边界条件进行舱段结构强度直接计算,其结果表明舱段模型与整船模型关键部位应力结果具有一致性,证明了该计算方法的有效性。张爱青等[6]基于相关规范对复合材料整船直接计算方法进行研究,探讨不同载荷大小、载荷施加方式、工况定义以及衡准方法对复合材料船体结构的适用性,随后对总纵弯曲载荷进行修正,验证了使用应变衡准对复合材料船体结构强度校核的适用性。甄春博等[7]基于船体结构强度直接计算理论,参考相关船级社的规范,对玻璃钢双体船进行直接计算方法研究。计算结果表明玻璃钢船体结构在横向弯曲载荷作用下最容易发生失效破坏,强度校核结果满足规范要求。
本文以上层建筑结构中的T型节点作为研究对象,基于相关规范和计算结果确定T型节点直接计算模型的范围尺寸、边界条件以及强度校核标准,为T型节点复合材料船体结构上的应用提供指导意义。
1 上层建筑板架模型 1.1 模型尺寸及材料参数首先参考文献[8]中的一体化上层建筑的结构形式,得到含T型节点的上层建筑板架模型,如图1所示。板架模型主要由甲板与舷侧壁板组合而成,该上层建筑模型板架模型长3 420 mm、宽 2 120 mm、高 2 000 mm,舷侧与甲板成100°的倾斜角。其中板架模型的甲板与舷侧部分均为厚度48 mm的夹芯面板与高度为80 mm、宽度为40 mm的筋条组成的加筋板结构;另外夹芯面板的芯材为PVC泡沫材质,厚度为40 mm,上下2层蒙皮为厚度4 mm的纤维增强复合材料层合板结构,筋条的侧面与顶面同样为厚度4 mm的蒙皮结构。同时在该模型中纵向加强筋间距为500 mm,横向加强筋间距为750 mm。
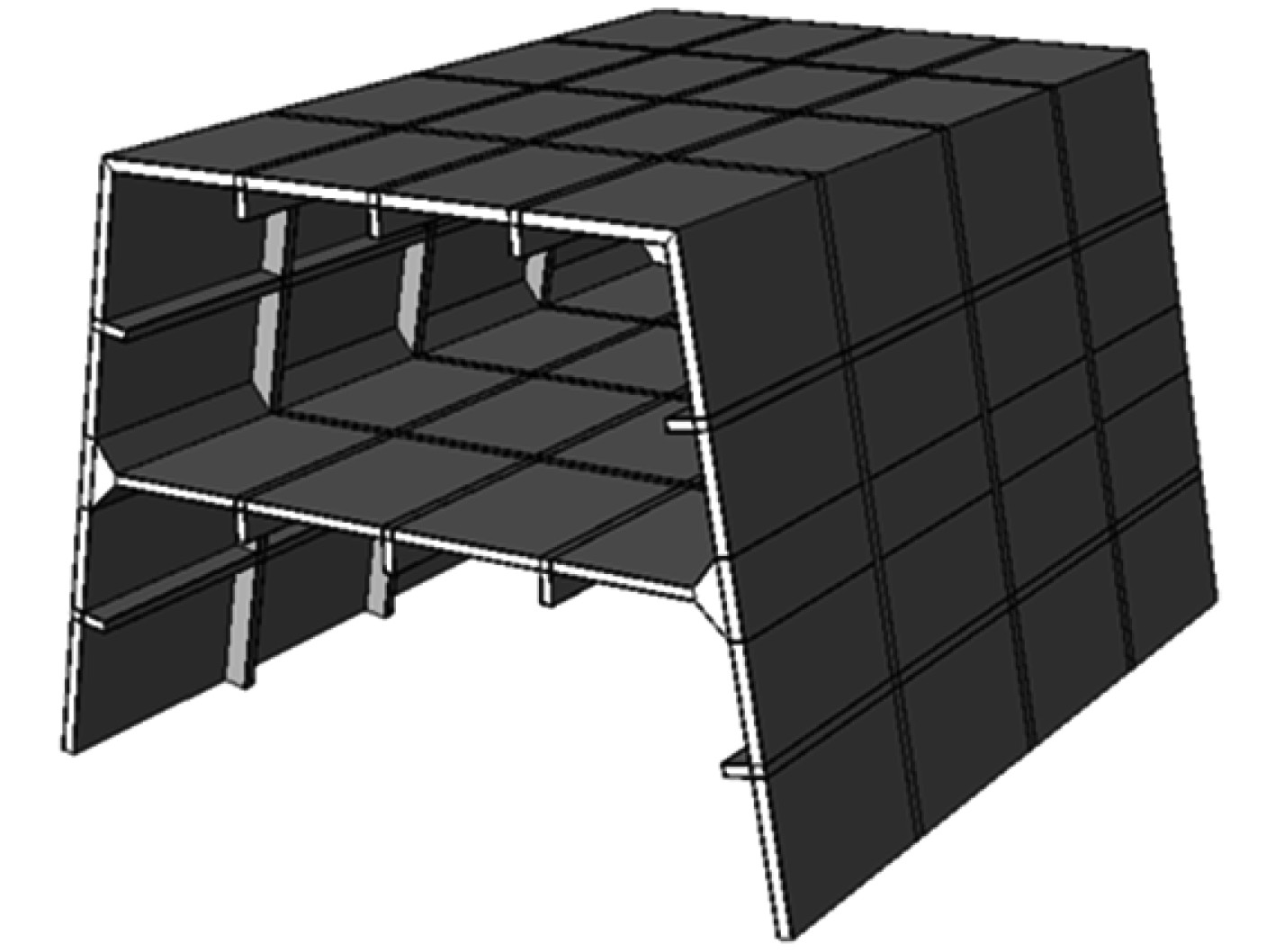
|
图 1 模型整体示意图 Fig. 1 Overall schematic diagram of the model |
在侧壁与中间连接处设置了T型节点,以文献[9]中T型节点的样式为研究对象,该节点的结构形式及尺寸如图2所示,该节点的梯形过渡区、腹板以及底部表面均为厚度4 mm的复合材料(GFRP)蒙皮,内部填充物为PVC泡沫,为提高梯形过渡区的承载能力,该节点是通过真空辅助一体化工艺成型。
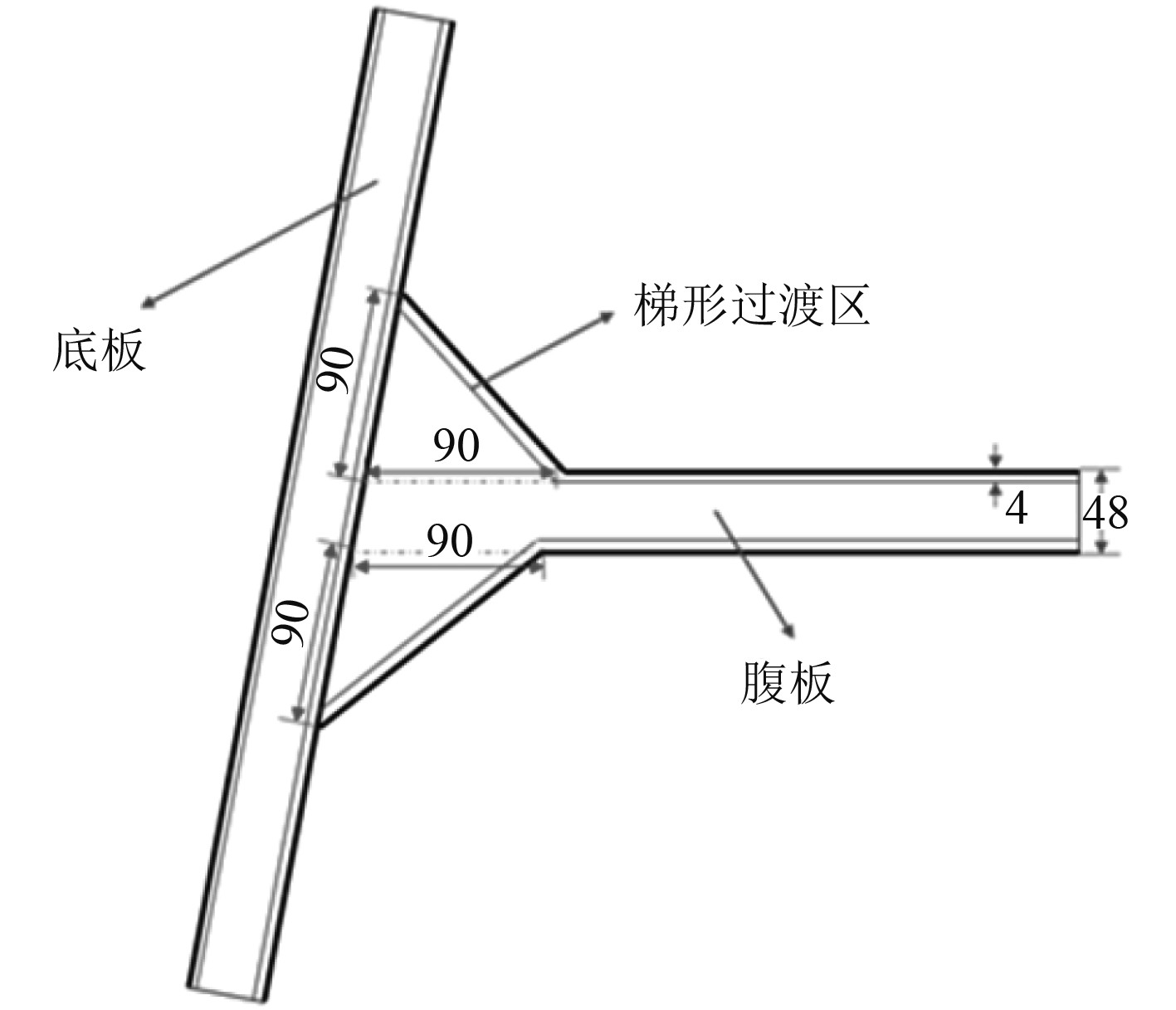
|
图 2 T型节点结构形式 Fig. 2 T-shaped node structure |
模型中复合材料结构蒙皮与泡沫芯材的相关材料参数如表1所示。对复合材料结构以长度方向定义为x方向,宽度方向定义为y方向,厚度方向定义为z方向。
|
|
表 1 材料参数 Tab.1 Material parameters |
采用 Abaqus 建立有限元模型,在建模过程中对上述结构中复合材料蒙皮与PVC芯材均采用实体单元(C3D8R)模拟,全局种子尺寸为20 mm,其总数为213246个实体单元。
根据《水面舰艇结构设计计算方法》[10]规定,在舰船上层建筑结构的设计阶段,将上浪载荷作为上层建筑强度校核的主要载荷。根据规范要求对舷侧载荷大小取为0.01 MPa;对甲板在综合考虑其重物和惯性载荷以后大小取0.01 MPa,方向均为垂直于板平面向内的均布载荷。考虑到在上浪载荷作用下其舷侧作为主要的受载面,因此主要考虑2种受载工况,工况1为甲板受到重物与惯性载荷作用,舷侧受到上浪载荷作用;工况2为只考虑甲板受重物与惯性载荷作用,舷侧无载荷作用。由于该部分模型在上层建筑结构位于横舱壁与主甲板等强力结构之间,因此对其底部和两侧采用刚性固定的约束条件。
1.3 结果分析考虑到位于板架模型中外侧的T型节点的应力分布及变形会受边界条件一定的影响,因此选取为内侧的T型节点进行单独分析。
对2种工况下T型节点计算结果进行分析可以发现在工况1中应力峰值区域位于梯形过渡区与腹板下侧面板交接处,其中Mise应力最大值为14.62 MPa;其变形特征主要为腹板右侧端部有较大变形。工况2中应力峰值区域也是位于 与腹板下侧面板交接处,Mise应力最大值为13.15 MPa,腹板右侧端部有较大变形产生。
由计算结果可知,2种工况下T型节点的应力分布与变形特征基本保持一致,只是应力峰值与腹板右侧端部变形值略有差异,因此可将2种工况简化为1种工况,即以工况1中T型节点的应力分布和变形特征作为参考标准,为下文中直接计算模型研究提供参照对象。工况1的计算结果如图3和图4所示。

|
图 3 工况1应力云图 Fig. 3 Stress nephogram in working condition 1 |
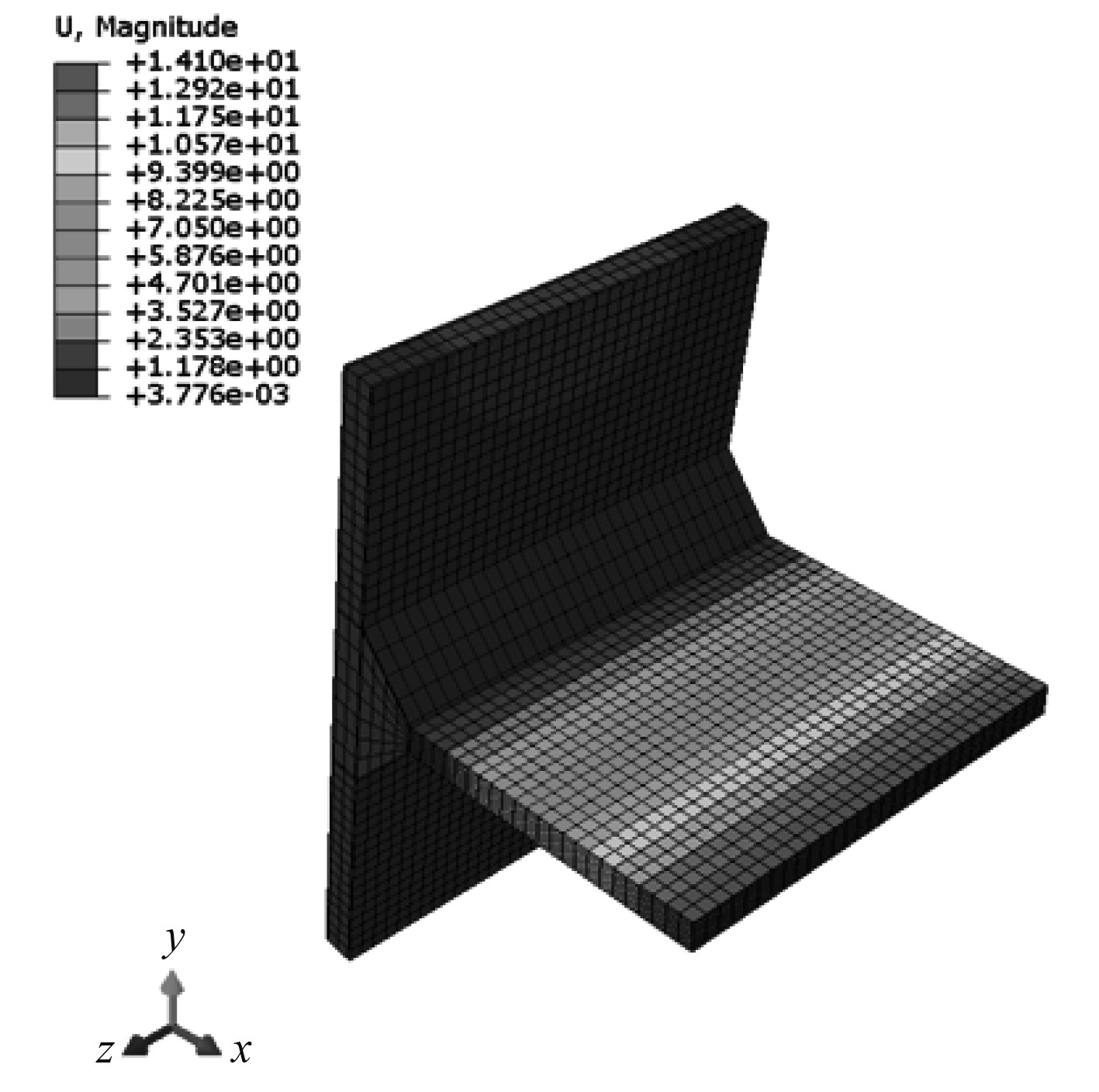
|
图 4 工况1变形云图 Fig. 4 Deformation cloud map in working condition 1 |
根据T型节点的计算结果,就T型节点直接计算模型进行研究。首先需要确定模型的尺寸范围。根据《海上高速船入级与建造规范》[11]中规定在进行局部结构强度直接计算时,局部结构分析模型应以目标结构为中心,向外扩展到强力结构处。
在本节所使用的上层建筑板架模型中横向加强筋间距为750 mm,纵向加强筋间距为500 mm,加强筋宽度为40 mm。因此在本节中T型节点宽度取为750 mm,腹板长度为500 mm,底板两侧长度相等,均为500 mm,其结构形式如图5所示。
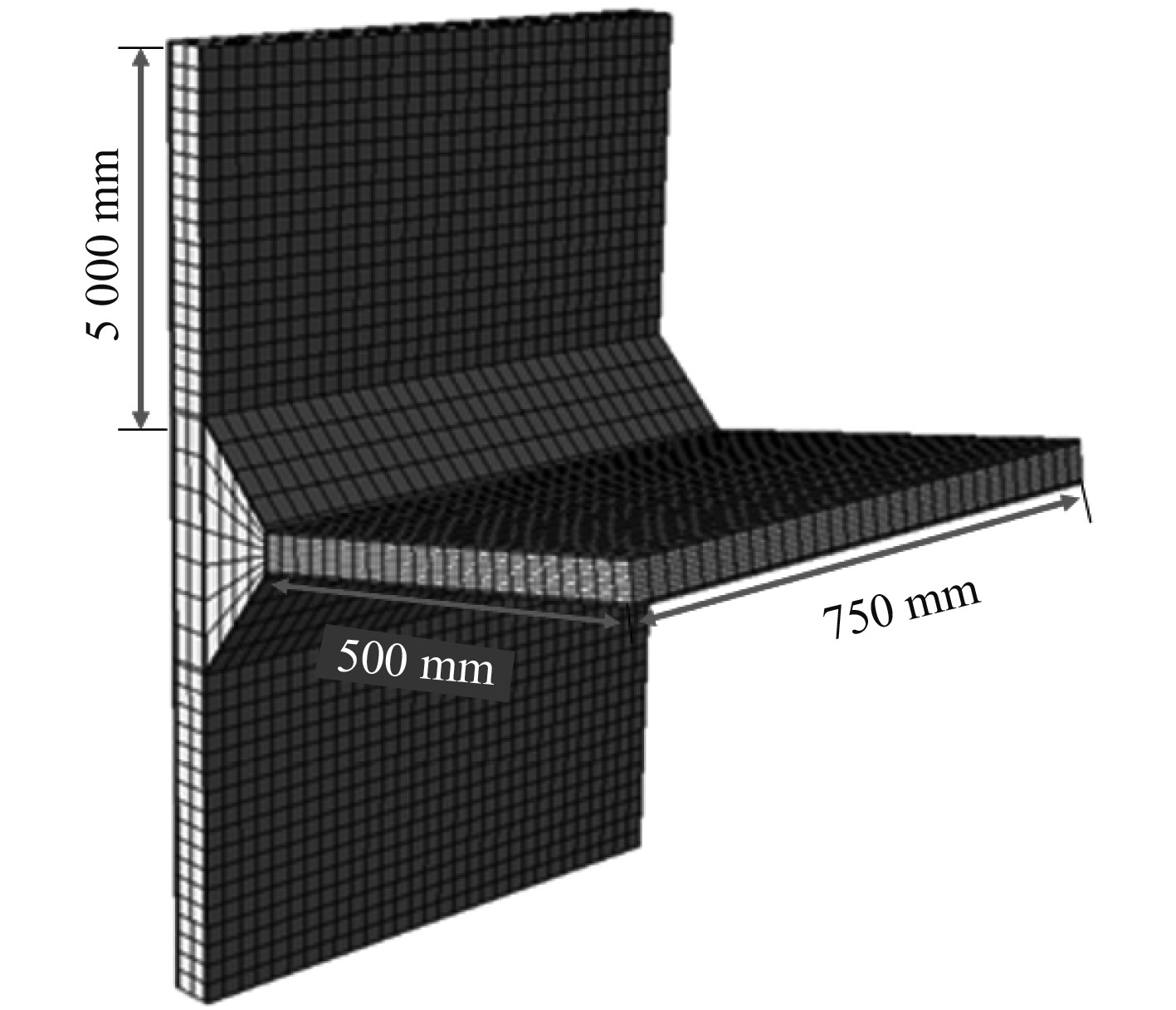
|
图 5 T型节点模型结构形式图 Fig. 5 Structure diagram of T-shaped node model |
在基于已经确定的T型节点模型范围尺寸,下面以板架模型中的T型节点设为原型,该原型的应力分布与变形特征作为参考对象,为下面T型节点模型的载荷与边界条件研究提供参考依据。
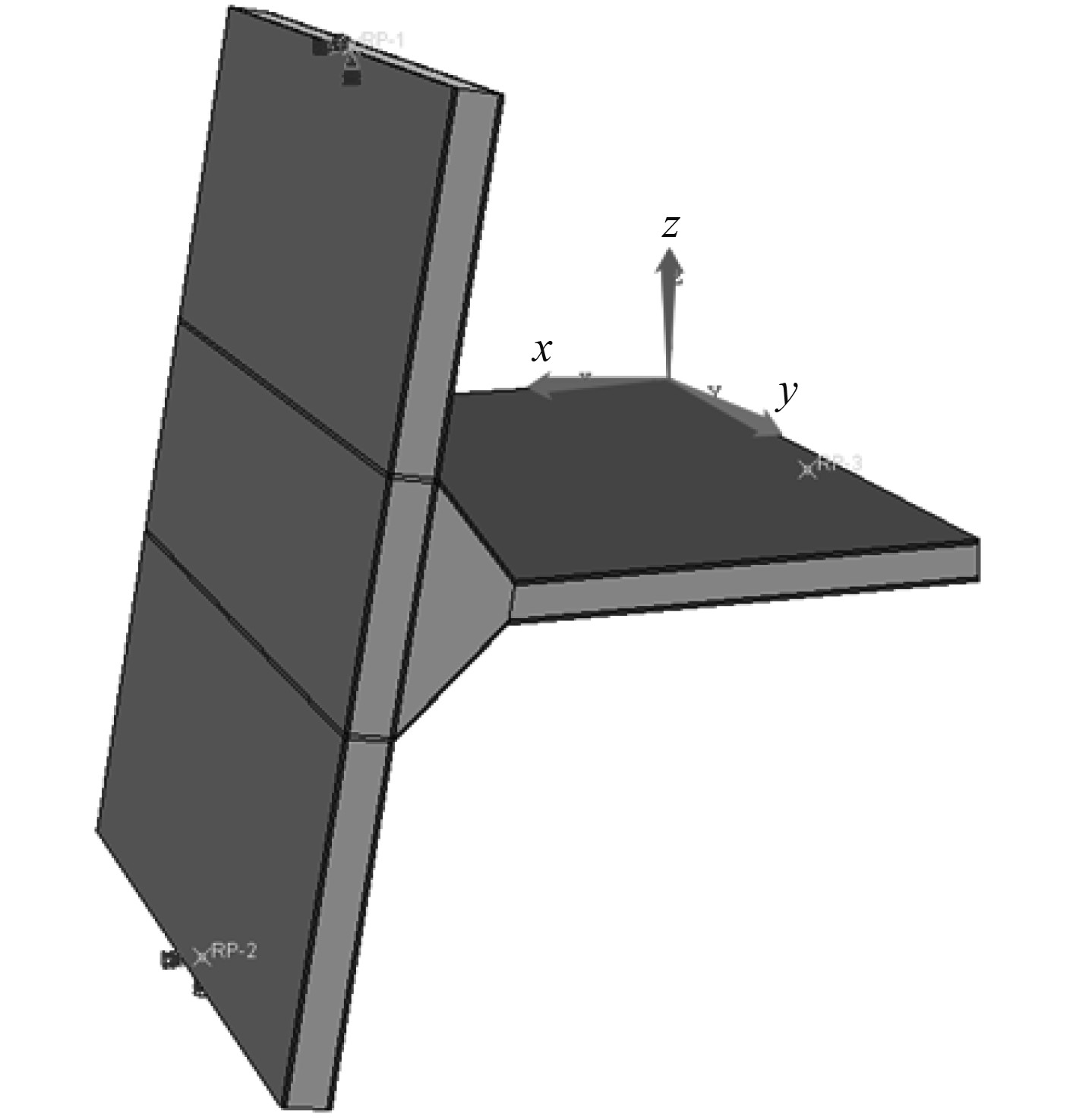
下面就T型节点模型的边界条件进行研究,建立局部坐标系csys1,定义沿腹板长度方向为X轴,沿腹板宽度方向为Y轴,沿腹板厚度方向为Z轴,其坐标系示意图如图6所示。
|
图 6 局部坐标系csys1 Fig. 6 Local coordinate system csys1 |
观察在上浪载荷作用下的T型节点的变形云图可知,位于底板区域的结构变形值基本为0,其次底板的上、下端部变形关于梯形过渡区对称分布,左右侧变形关于局部坐标系xoz平面对称分布,因此根据船体结构强度直接计算指南中模型端面的对称边界条件为垂直于端面方向的线位移为0,绕端面内两坐标轴的角位移为0,即底板两侧端部区域边界条件设置为
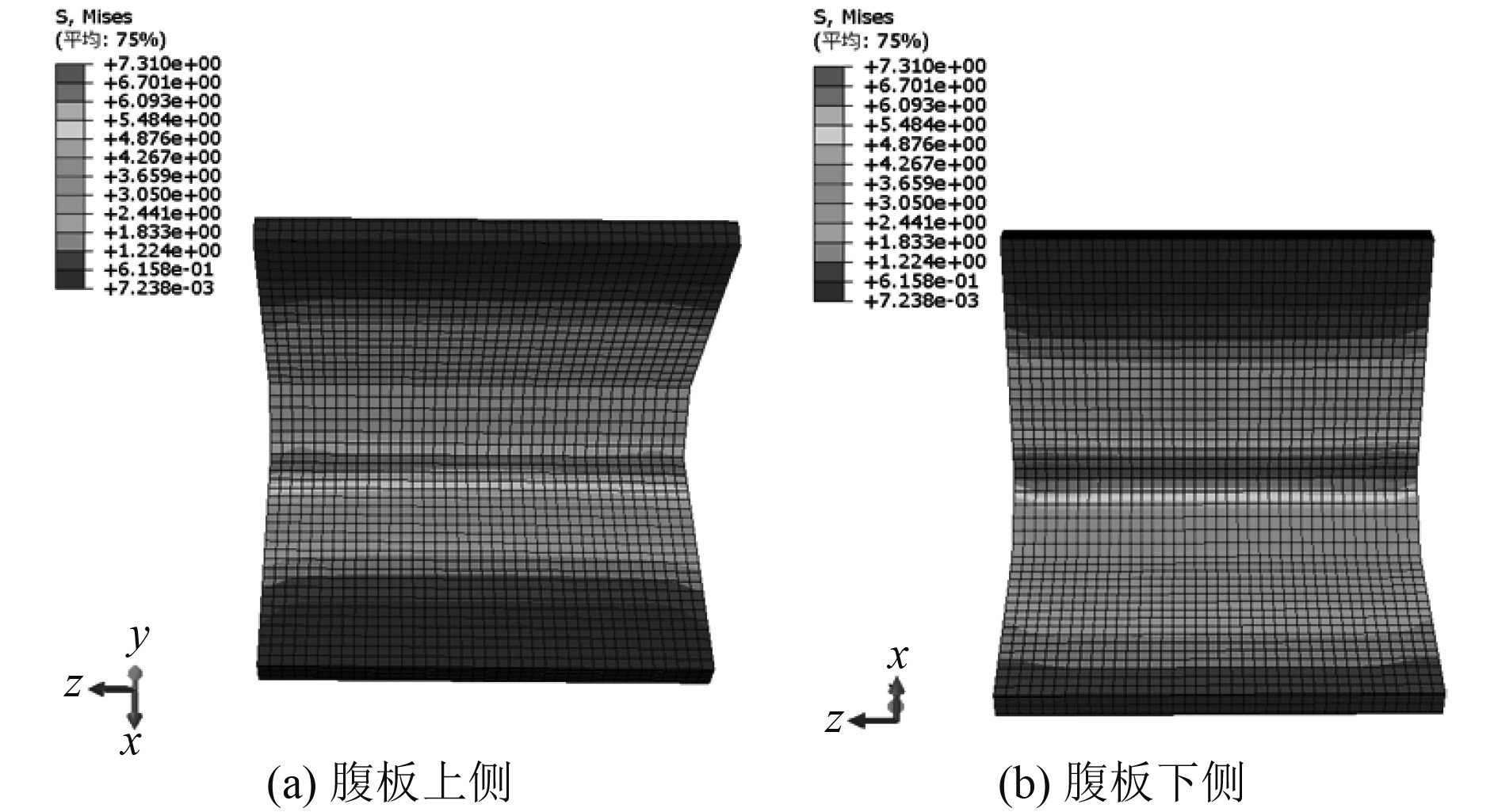
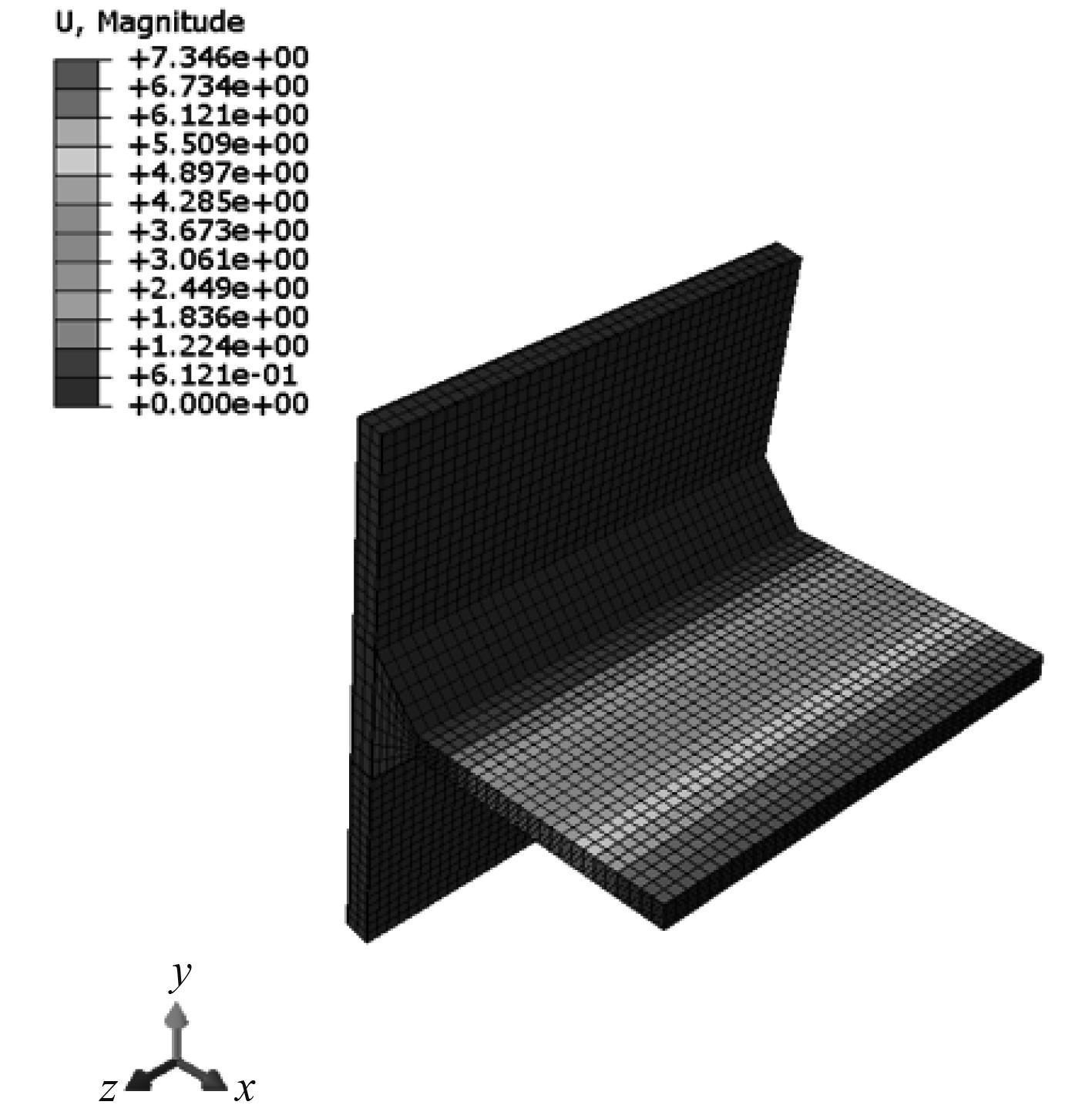
在明确了位于T型节点底板上的边界条件以后,则进行校核。考虑到T型节点原型在腹板区域受到均布载荷作用,因此对T型节点模型施加同样的载荷条件,得到计算结果如图7和图8所示。
|
图 7 节点模型应力云图 Fig. 7 Nodal model stress nephogram |
|
图 8 节点模型变形云图 Fig. 8 Nodal model deformation cloud map |
根据模型的计算结果来看,其应力分布、变形特征与T型节点原型基本保持一致,应力峰值区域为梯形过渡区与腹板下侧面板交接处。因此在底板两侧端部区域设置边界条件
针对本节中复合材料T型节点结构强度衡准,使用蔡-吴失效准则可以对结构强度进行有效的校核,精度较高。但由于在蔡-吴强度理论中设置的参数较多,无法实现对结构强度进行快速校核的目的,因此参考相关规范,选用合适的强度衡准方法对T型节点实现快速校核的目的。
在《海上高速船入级与建造规范》中指出对于纤维复合材料构件,采用“最大应变衡准”衡量结构的完整性[11]。其中针对玻璃纤维板,轴向拉伸、压缩的最大应变值为
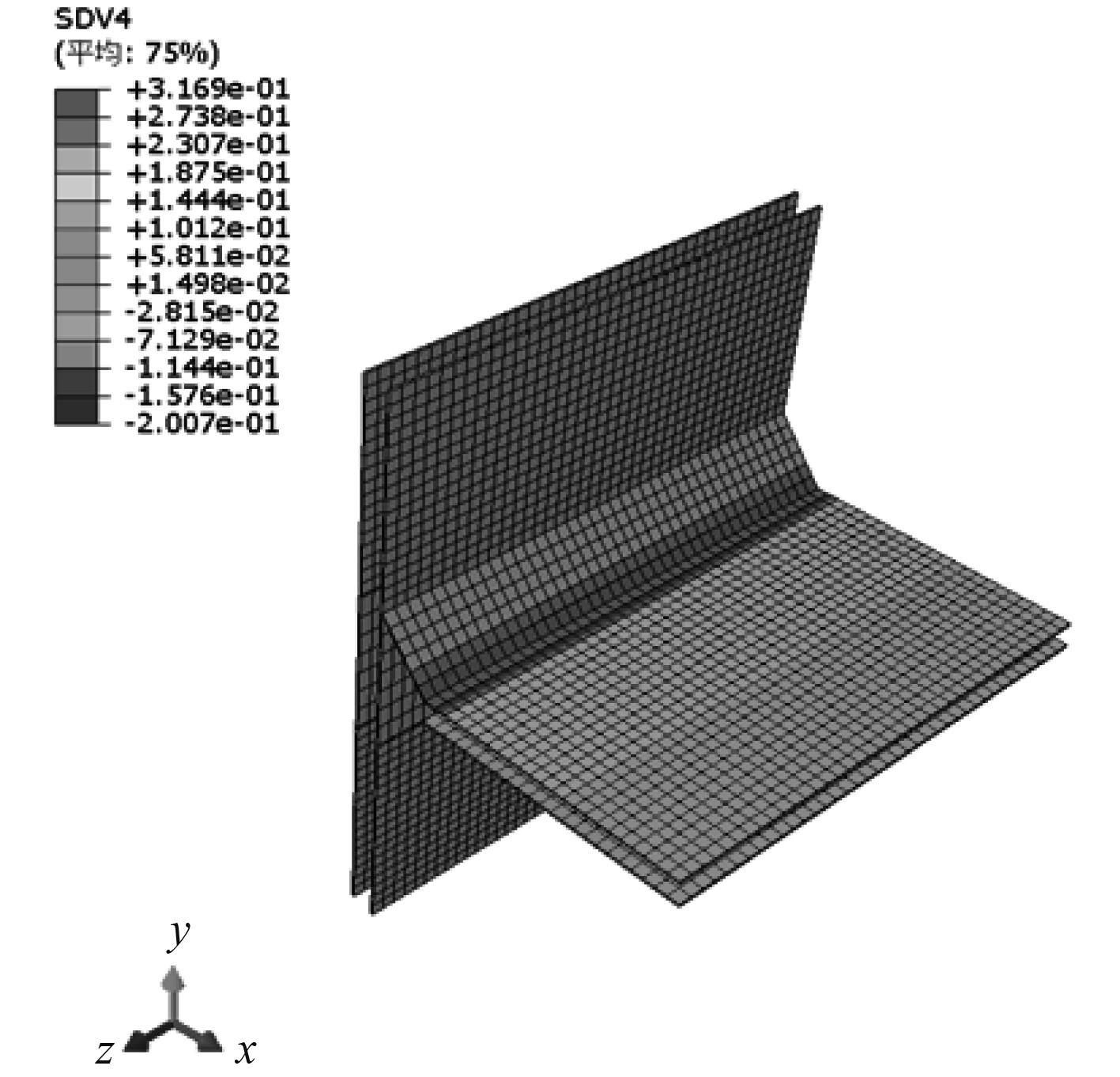
为验证上述2种强度衡准方法的适用性,首先通过基于蔡-吴失效准则对T型节点模型进行强度计算,通过编写相关子程序、选取合适的刚度退化模型输出设计载荷作用下T型节点的状态变量值CRm,得到的计算结果如图9所示。可知CRm最大值为0.31,T型节点模型并未产生损伤破坏。根据蔡-吴强度准则可知当CRm<1时,复合材料结构不产生损伤破坏。
|
图 9 状态变量云图 Fig. 9 Cloud diagram of state variables |
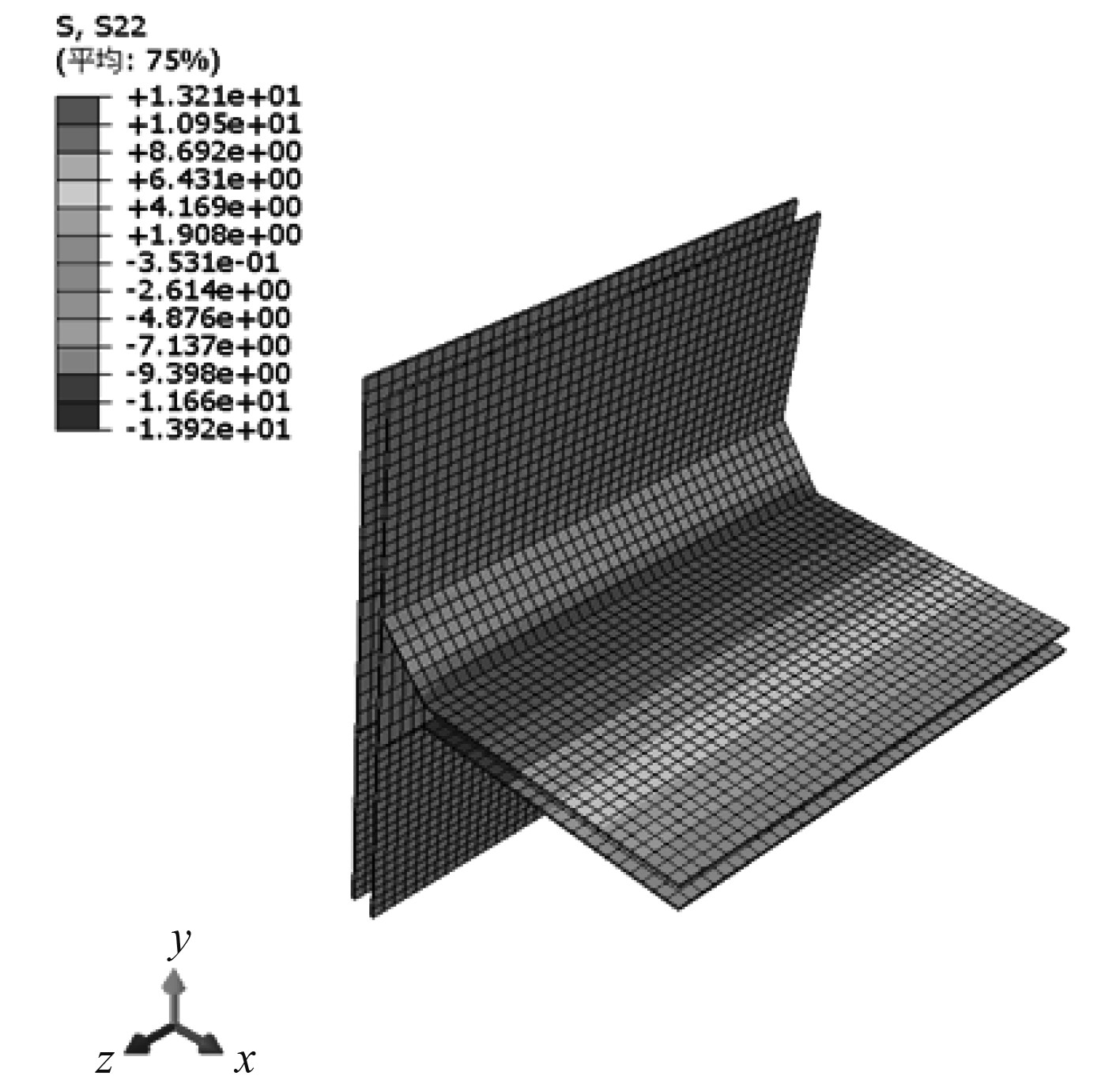
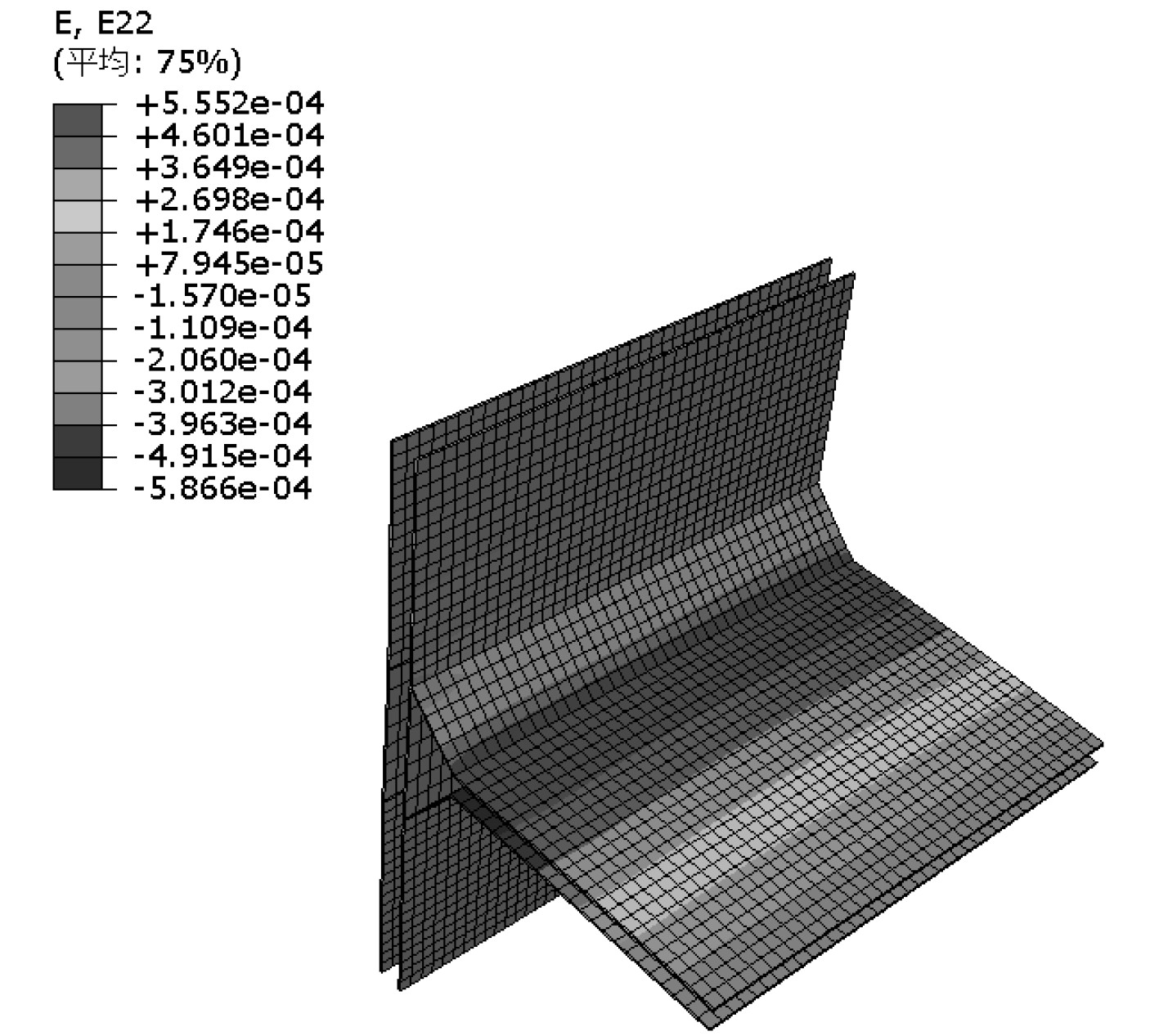
其次定义失效因子R,为计算最大应变(力)与许用应变(变)的比值。通过计算可知在设计载荷作用下使用最大应力进行衡准时T型节点模型的各方向主应力中最大应力为压应力,其值为13.92 MPa,此时失效因子为0.41(见图10);使用最大应变进行衡准时T型节点模型最大轴向应变为
|
图 10 最大主应力云图 Fig. 10 Nephogram of maximum principal stress |
|
图 11 最大应变云图 Fig. 11 Maximum strain cloud diagram |
显然对比上述2种方法中失效因子与状态变量值可知对采用最大应变进行T型节点模型的强度校核时误差更小,因此对T节点模型进行直接计算时采用最大应力衡准进行强度校核。
3 结 语本文以上浪载荷作用下上层建筑板架模型的T型节点的应力分布及变形特征作为参考对象,结合相关规范对T型节点的直接计算模型进行研究,得到以下结论:
1)T型直接计算模型中腹板长度取为500 mm,节点宽度取为400 mm,底板长度为500 mm。
2)当甲板与舷侧受到相同大小的均布载荷作用或只有甲板一侧受到均布载荷作用时2种工况下的T型节点模型边界条件的设置方式相同,均为底板两侧端部设置固定约束即
3)T型直接计算模型中对T节点模型进行直接计算时采用最大应力进行强度校核误差更小。
| [1] |
聂海民. 船体夹芯复合材料典型节点强度试验考核方法研究[D]. 武汉: 武汉理工大学, 2020.
|
| [2] |
ATUL U S, PRAMOD M P, MANJUNATHA C M, et al. Mixed mode cohesive zone modelling and analysis of adhesively bonded composite T-joint under pull-out load[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2018, 40(3): 167-170. DOI:10.1007/s40430-018-1056-1 |
| [3] |
陈亮, 杨坤. 夹芯复合材料T型接头制备工艺及力学性能试验研究[J]. 中国舰船研究, 2014, 9(4): 70-75. DOI:10.3969/j.issn.1673-3185.2014.04.011 |
| [4] |
DHARMAWAN F, THOMSON R S, LI H, et al. Geometry and damage effects in a composite marine T-joint[J]. Composite Structures, 2004, 66(1): 181-187. |
| [5] |
朱加刚, 肖渤舰, 肖曙明, 等. 舱段有限元分析等效计算总纵强度研究[J]. 船海工程, 2008. 37(6): 27−29.
|
| [6] |
张爱青, 蒲映超, 胡代荣. 复合材料船全船有限元分析方法[J]. 上海海事大学学报, 2017. 38(4): 68−72.
|
| [7] |
甄春博, 周清婉, 王晓鹏, 等. 玻璃钢双体船结构强度直接计算研究[J]. 复合材料科学与工程, 2022(04): 50−55.
|
| [8] |
郭占一. 一体化复合材料上层建筑力学性能及其连接结构设计研究[D]. 哈尔滨: 哈尔滨工程大学, 2016.
|
| [9] |
肖雪瑞, 邱伟强, 马武伟, 等. 夹芯复合材料T型节点悬臂弯曲强度特性分析[J]. 玻璃钢/复合材料, 2018, 292(5): 42-48. |
| [10] |
国防科学技术工业委员会. GJB Z119-99, 水面舰艇结构设计计算方法[S]. 北京: 中国标准出版社, 2001.
|
| [11] |
中国船级社技术委员会. 海上高速船入级与建造规范[S]. 北京: 中国船级社, 2022.
|
| [12] |
中国船级社技术委员会. 纤维增强塑料船建造规范[S]. 北京: 中国船级社, 2015.
|
 2024, Vol. 46
2024, Vol. 46
