0 引　言

模型预测控制（Model Predictive Control, MPC）由于采用了多步预测、滚动优化以及反馈校正等控制策略，使得其一般具有控制效果好、鲁棒性强等优点。同时其可有效的处理执行机构约束问题和多变量控制问题，使得其被广泛应用于石油化工等过程控制系统^[1]，其中具有代表性的MPC控制算法主要有基于对象的脉冲响应模型算法控制^[2]、基于对象的阶跃响应模型的动态矩阵控制^[3]、基于对象的CARIMA（Controlled Suto-regressive Integrated Moving-average−受控自回归积分滑动平均）模型的广义预测控制^[4]以及基于对象的状态空间模型滚动时域控制。SteenSon^[5]基于MPC提出了一种过驱动悬停水下机器人的的深度、纵倾和航速的控制策略，李光磊等^[6]采用了基于Laguerre函数的船舶航向DMPC控制方法实现了高海情下船舶航向控制，刘程^[7]对比了PID、LQR、MPC这3种控制律下的船舶航向控制问题，验证了舵角舵速约束条件下MPC控制律相比LQR和PID具有很好的控制效果，范朗等^[8]采用了广义预测控制算法设计了船舶航向控制器，并通过仿真验证了所设计控制器在风浪流干扰下相交于PID控制具有更好的控制效果。

为保证船舶航行时的平稳性和安全性，船舶需要根据不同的航速限制一定的最大操舵舵角，当船舶遭遇较差的海况，海浪干扰将引起操舵系统的频繁操舵，通过频繁的操舵纠正航向不仅达不到目的，反而会增加航行的附加阻力并增加舵机的磨损。

针对上述问题，本文采用了一种基于内环航向速率的航向控制策略，并通过基于Laguerre函数和状态空间模型的模型预测控制算法，研究了舵角舵速约束下的航向速率控制器，通过对转向过程中的航向速率进行限幅形成了舵角、舵速、航向速率多约束下的航向控制算法。针对海浪带来的频繁操舵问题，通过忽略舵角舵速的约束条件得到了航向控制器的线性表达形式，并在此基础上引入辅助滤波器对航向控制器进行校正。

1 船舶运动数学模型

参照目前国际上普遍采用的ITTC（International Towing Tank Conference）推荐的坐标系，并依据牛顿运动定律和流体力学原理，结合MMG船舶操纵性方程^[9]并忽略船舶在垂直面的运动以及横倾，得到船舶的三自由度运动动力学及运动学方程如下：

$ \left\{ \begin{array}{l} {\dot u = \dfrac{{X + mvr}}{m}}，\\ {\dot v = \dfrac{{Y - mur}}{m}} ，\\ {\dot r = \dfrac{{{N_z}}}{{{I_{zz}}}}} ，\\ {\dot \psi = r} 。\end{array} \right. $

(1)

$ \left\{ {\begin{array}{*{20}{l}} {X = {X_H} + {X_T} + {X_R} + {X_D}}，\\ {Y = {Y_H} + {Y_T} + {Y_R} + {Y_D}} ，\\ {{N_z} = {N_H} + {N_T} + {N_R} + {N_D}} 。\end{array}} \right. $

(2)

式中：X、Y、N_z分别为纵向合力、横向合力、转首合力矩；$m$为船舶的质量；$u$、$v$、$r$分别为船舶的纵向速度、横向速度和航向速率；$\dot u$、$\dot v$、$\dot r$分别为纵向加速度、横向加速度以及转艏角加速度；$ {I_{zz}} $为船舶的转动惯量，$\psi $分别为船舶的航向角。下标 H，T，R，D分别为船体流体水动力和力矩，螺旋桨推力和推力矩，舵力和舵力矩，风、浪、流等干扰的合力和合力矩。

2 航向控制器设计 2.1 航向控制策略

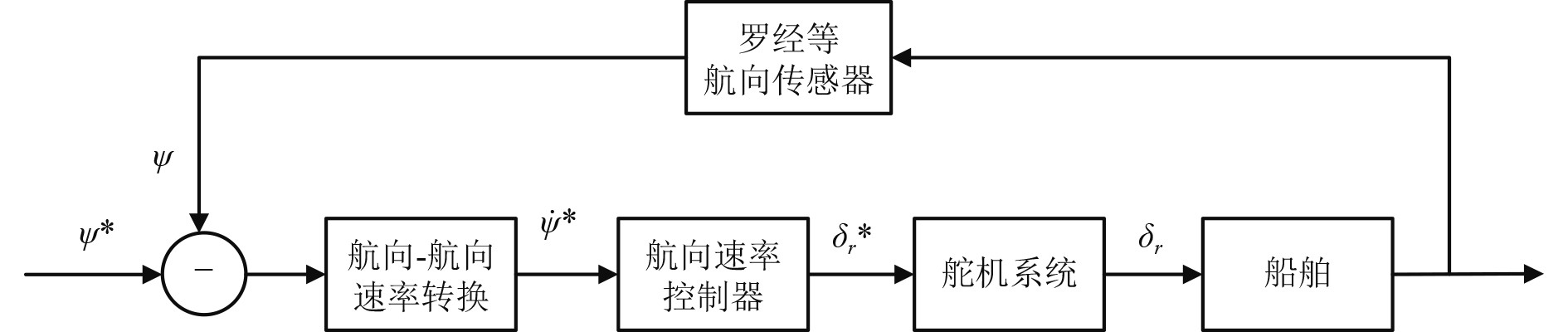
本文设计了一种航向-航向速率内外环的控制策略，如图1所示。

图中$ {\psi ^*} $为指令航向，$ {\dot \psi ^*} $为指令航向速率，$ \delta _r^* $为指令方向舵舵角，$ {\delta _r} $为实际方向舵舵角。航向与航向速率的转换方法如下：

$ {\dot \psi ^*} = \lambda ({\psi ^*} - \psi )。$

(3)

其中，转换系数$ \lambda $与船舶的当前航速相关，为避免船舶在转向过程中出现过大转向速率和横倾，可对内环控制中的航向速率进行限幅，限幅方式如下：

$ \left\{ {\begin{array}{*{20}{c}} {{{\dot \psi }^*} = {{\dot \psi }_{\max }}}，& {{\rm{if}}({{\dot \psi }^*} > {{\dot \psi }_{\max }})}，\\ {{{\dot \psi }^*} = {{\dot \psi }_{\min }}}，& {{\rm{if}}({{\dot \psi }^*} < {{\dot \psi }_{\min }})}。\end{array}} \right. $

(4)

2.2 线性化模型

其中以航向速率为控制目标的状态空间模型形式如下：

$ \begin{split} & \left[ {\begin{array}{*{20}{c}} {\dot v} \\ {\dot r} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}} \\ {{a_{21}}}&{{a_{22}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} v \\ r \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{b_1}} \\ {{b_2}} \end{array}} \right]{\delta _r} ，\\[-3pt] & r = \left[ {\begin{array}{*{20}{c}} 0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} v \\ r \end{array}} \right] 。\end{split} $

(5)

式中：a₁₁、a₁₂、a₂₁、a₂₂均为航速u的一次函数；b₁、b₂均为航速u的二次函数。式（5）记成标准的状态空间形式，即：

$ \dot x = {{\boldsymbol{A}}_o}x + {{\boldsymbol{B}}_o}u ，y = {{\boldsymbol{C}}_o}x 。$

(6)

将其转换为离散时间的线性状态空间模型：

$ {x_m}(k + 1) = {{\boldsymbol{A}}_m}{x_m}(k) + {{\boldsymbol{B}}_m}u(k)，y(k) = {{\boldsymbol{C}}_m}{x_m}(k) 。$

(7)

式中：$ x = {\left[ {v,r} \right]^{\rm{T}}} $为系统的状态量；$ u = {\delta _r} $即方向舵角为被控系统的控制输入量；$ y = r $即航向速率为被控系统的输出量。$ {{\boldsymbol{A}}_m} $、$ {{\boldsymbol{B}}_m} $、$ {{\boldsymbol{C}}_m} $分别为离散化后的状态空间模型矩阵。当外部环境存在干扰时，由于典型的状态反馈控制律${\boldsymbol{u}}(k) = - K{\boldsymbol{x}}(k)$中不包含积分环节，所以针对式（7）所示的状态空间模型采用典型的状态反馈控制，状态量会存在静态误差，考虑到实际建模的偏差带来的误差以及船舶易遭遇风浪流等外部干扰，为消除稳态时的静差，可采用状态增量形式的状态空间模型，用$ \Delta {\boldsymbol{u}}(k) $（其中，$ \Delta {\boldsymbol{u}}(k) = {\boldsymbol{u}}(k) - {\boldsymbol{u}}(k - 1) $为控制输入的增量）代替$ {\boldsymbol{u}}(k) $作为控制输入量使系统能实现无静差控制^[10]，故将状态空间方程改写成如下形式：

$ \begin{split} & \underbrace {\left[ {\begin{array}{*{20}{c}} {\Delta {x_m}(k + 1)} \\ {y(k + 1)} \end{array}} \right]}_{x(k + 1)} = \underbrace {\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{A}}_m}}&{o_m^{\rm{T}}} \\ {{c_m}{{{A}}_m}}&1 \end{array}} \right]}_{{A}}\underbrace {\left[ {\begin{array}{*{20}{c}} {\Delta {x_m}(k)} \\ {y(k)} \end{array}} \right]}_{x(k)} +\\[-3pt] & \underbrace {\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{B}}_m}} \\ {{{\boldsymbol{C}}_m}{{\boldsymbol{B}}_m}} \end{array}} \right]}_{{B}}\Delta u(k)，\\[-3pt] & y(k) = \underbrace {\left[ {\begin{array}{*{20}{c}} {{o_m}}&1 \end{array}} \right]}_{{C}}\left[ {\begin{array}{*{20}{c}} {\Delta {x_m}(k)} \\ {y(k)} \end{array}} \right] 。\end{split} $

(8)

其中：

$ \begin{split} & \Delta {x}_{m}(k+1) = {x}_{m}(k+1) - {x}_{m}(k)\text{；}\Delta {x}_{m}(k) = {x}_{m}(k) - {x}_{m}(k-1);\\ & \Delta {x}_{m}(k+1)={A}_{m}\Delta {x}_{m}(k)+{B}_{m}\Delta u(k);{o}_{m}=[\begin{array}{cc}0& 0\end{array}];\\ & y(k+1) - y(k)={C}_{m}({x}_{m}(k+1) - {x}_{m}(k))={C}_{m}\Delta {x}_{m}(k+1)。\\[-1pt] \end{split} $

(9)

由于系统中有些状态量并不一定可测量，因此可通过Luenberger状态观测器或卡尔曼滤波器的方法得到状态量的观测值$ \hat x = {\left[ {\hat v,\hat r} \right]^{\rm{T}}} $，令$ z = {\left[ {\Delta {{\hat x}_m}(k),\hat y(k)} \right]^{\rm{T}}} $。其中状态观测器或卡尔曼滤波器的形式如下：

$ z(k + 1) = ({\boldsymbol{A}} - {\boldsymbol{LC}})z(k) + {\boldsymbol{B}}\Delta u(k) + {\boldsymbol{L}}y。$

(10)

式中：$ {\boldsymbol{L}} $为观测器增益矩阵或卡尔曼滤波器增益矩阵。

2.3 未来状态预测

设定预测步长为$ {N_p} $以及控制步长${N_c}$，则通过迭代式（9）并将状态观测值$ z $代入式（9）可得到，在$ {k_i} $时刻系统未来$ {N_p} $步长内的输出值为：

$ Y = Fz({k_i}) + \Phi \Delta U ，$

(11)

其中：

$ \begin{split} & Y =\\[-3pt] & {[ \begin{array}{*{20}{c}} {y({k_i} + 1\left| k \right.)} & {y({k_i} + 2\left| k \right.)} & {y({k_i} + 3\left| k \right.)} & \cdots & {y({k_i} + {N_p}\left| k \right.)} \end{array} ]^{\rm{T}}}s，\\[-1pt] \end{split} $

(12)

$ \begin{split} & \Delta U = \\[-3pt] & {[ \begin{array}{*{20}{c}} {\Delta u({k_i})} & {\Delta u({k_i} + 1)} & {\Delta u({k_i} + 2)}& \cdots &{\Delta u({k_i} + {N_c} - 1)} \end{array} ]^{\rm{T}}}，\end{split} $

(13)

$ \begin{split} & F=\left[\begin{array}{c}CA\\ C{A}^{2}\\ C{A}^{3}\\[-3pt] \vdots\\ C{A}^{{N}_{p}}\end{array}\right]\text{，}\\[-4pt] & \Phi =\left[ \begin{array}{ccccc}CB& 0& 0& \cdots & 0\\ CAB& CB& 0& \cdots & 0\\ C{A}^{2}B& CAB& CB& \cdots & 0\\[-3pt] \vdots & \vdots& \vdots & \vdots &\vdots\\ C{A}^{{N}_{p}-1}B& C{A}^{{N}_{p}-2}B& C{A}^{{N}_{p}-3}B& \cdots & CB\end{array} \right]。\end{split} $

(14)

对于指令信号$ r({k_i}) $，通过设定输入的权值系数$ {r_w} $($ {r_w} \geqslant 0 $)可如式（15）描述的目标函数：

$ \begin{split} J =\,& \sum\limits_{m = 1}^{{N_p}} {{{(r({k_i}) - y({k_i} + m|{k_i}))}^{\rm{T}}}} (r({k_i}) - y({k_i} + m|{k_i})+ \\[-3pt] & \sum\limits_{m = 1}^{{N_p}} {{{(\Delta u({k_i} + m))}^{\rm{T}}}} {r_w}(\Delta u({k_i} + m)) ，\end{split} $

(15)

记成向量形式也即：

$ J = {({R_s} - Y)^{\rm{T}}}({R_s} - Y) + \Delta {U^{\rm{T}}}\bar R\Delta U，$

(16)

其中：

$ R_s^{\rm{T}} = \underbrace {[ {\begin{array}{*{20}{c}} 1&1& \ldots &1 \end{array}} ]}_{{N_p}}r({k_i}) \text{，} \bar R = {r_w}{I_{{N_c} \times {N_c}}} 。$

(17)

2.4 Laguerre函数引入

Laguerre函数在控制领域最初被用来对系统的脉冲响应进行系统辨识，由于其易实现性和正交性，由离散时间的拉盖尔函数组成的网络也被引入到模型预测控制算法当中，离散拉盖尔函数网络的Z变换为：

$ \begin{split} & {\Gamma _1}(z) = \frac{{\sqrt {1 - {a^2}} }}{{1 - a{z^{ - 1}}}}，\\[-3pt] & {\Gamma _2}(z) = \frac{{\sqrt {1 - {a^2}} }}{{1 - a{z^{ - 1}}}}\frac{{{z^{ - 1}} - a}}{{1 - a{z^{ - 1}}}}，\\[-6pt] & \vdots \\[-6pt] & {\Gamma _N}(z) = \frac{{\sqrt {1 - {a^2}} }}{{1 - a{z^{ - 1}}}}{\left(\frac{{{z^{ - 1}} - a}}{{1 - a{z^{ - 1}}}}\right)^{N - 1}} 。\end{split} $

(18)

其中，$ a $为离散拉盖尔网络的极点，上述离散拉盖尔网络的Z反变换满足以下关系：

$ L(k + 1) = {A_l}L(k)，$

(19)

$ \begin{split} & {A_l} = {\left[ {\begin{array}{*{20}{c}} a&0&0&0&0 \\ \beta &a&0&0&0 \\ { - a\beta }&\beta &a&0&0 \\ [-4pt] \vdots & \vdots & \vdots & \ddots & \vdots \\ {{{( - a)}^{N - 2}}\beta }&{{{( - a)}^{N - 3}}\beta }& \ldots &\beta &a \end{array}} \right]_{N \times N}}，\\[-4pt] & L(0) = \sqrt \beta \left[ {\begin{array}{*{20}{c}} 1 \\ { - a} \\ {{a^2}} \\ [-4pt] \vdots \\ {{{( - a)}^{N - 1}}} \end{array}} \right]。\end{split} $

(20)

其中：$ L(k) = {\left[ {\begin{array}{*{20}{c}} {{l_1}(k)}&{{l_2}(k)}& \ldots &{{l_N}(k)} \end{array}} \right]^{\rm{T}}} $；$ {l_1}(k) $为$ {\Gamma _1}(z) $的Z反变换；$ {l_2}(k) $为$ {\Gamma _2}(z) $的Z反变换并以此类推。

在模型预测控制算法中，在$ {k_i} $时刻，未来时刻的控制轨迹$ \Delta u({k}_{i}){\text{、}}\Delta u({k}_{i}+1){\text{、}} $$ \Delta u({k}_{i}+2){\text{、}}\cdots {\text{、}}\Delta u({k}_{i}+k) $可看成是一个稳定动态系统的脉冲响应，因此可引入离散拉盖尔网络对未来输入变量序列$ \Delta U $进行近似处理并能有效减少算法的计算负担^[11]。具体来讲，在任意一个未来的采样时刻$ k $，$ \Delta u({k_i} + k) $可表达为：

$ \Delta u({k_i} + k) = \sum\limits_{j = 1}^N {{c_j}({k_i})} {l_j}({k_i})。$

(21)

式中：$ N $为拉盖尔多项式的阶数；$ {c_j} $为待求的拉盖尔函数系数。

将式（21）记为$ \Delta u({k_i} + k) = L{(k)^{\rm{T}}}\eta $，其中$ L(k) $可由式（19）和式（20）迭代计算得到，$ \eta = $ $ {\left[ {\begin{array}{*{20}{c}} {{c_1}}\;{{c_2}}\; \cdots \;{{c_N}} \end{array}} \right]^{\rm{T}}} $。将$ \Delta u({k_i} + k) = L{(k)^{\rm{T}}}\eta $代入到模型中进行预测，得到：

$ z({k_i} + m|{k_i}) = {A^m}z({k_i}) + \sum\limits_{i = 0}^{m - 1} {{A^{m - i - 1}}BL{{(i)}^{\rm{T}}}\eta }，$

(22)

$ y({k_i} + m|{k_i}) = C{A^m}z({k_i}) + \sum\limits_{i = 0}^{m - 1} {C{A^{m - i - 1}}BL{{(i)}^{\rm{T}}}\eta }。$

(23)

将式（21）和式（23）代入到代价函数式（16）中，并由拉盖尔函数的正交性：

$ \sum\limits_{m = 1}^{{N_p}} {{l_i}(m)} {l_j}(m) = 0,i \ne j ，\sum\limits_{m = 1}^{{N_p}} {{l_i}(m)} {l_j}(m) = 1,i = j 。$

(24)

得到：

$ J = \sum\limits_{m = 1}^{{N_p}} {{{(r({k_i}) - y({k_i} + m|{k_i}))}^{\rm{T}}}} (r({k_i}) - y({k_i} + m|{k_i})) + {\eta ^{\rm{T}}}{R_L}\eta。$

(25)

其中，$ {R_L} = diag(\underbrace {{r_w} \cdots {r_w}}_N) $。将式（25）描述成离散型LQR控制器的代价函数形式，则得到如式描述的代价函数形式：

$ J = \sum\limits_{m = 1}^{{N_p}} {{{(z({k_i} + m|{k_i}))}^{\rm{T}}}} Q(z({k_i} + m|{k_i})) + {\eta ^{\rm{T}}}{R_L}\eta。$

(26)

2.5 舵角舵速约束处理及最优求解 2.5.1 无约束限制下的优化问题求解

式（22）可记为：

$ z({k_i} + m|{k_i}) = {A^m}z({k_i}) + {\phi ^{\rm{T}}}(m)\eta 。$

(27)

其中，$ {\phi ^{\rm{T}}}(m) =\displaystyle \sum\limits_{i = 0}^{m - 1} {{A^{m - i - 1}}BL{{(i)}^{\rm{T}}}} $，将式（27）代入式（26），得到代价函数为：

$ \begin{split} J =\,& {\eta ^{\rm{T}}}\left(\sum\limits_{m = 1}^{{N_p}} {\phi (m)} Q\phi {(m)^{\rm{T}}} + {R_L}\right)\eta + 2{\eta ^{\rm{T}}} \left(\sum\limits_{m = 1}^{{N_p}} {\phi (m)} Q{A^m}\right)z({x_i}) +\\[-4pt] & \sum\limits_{m = 1}^{{N_p}} {z{{({x_i})}^{\rm{T}}}{{({A^{\rm{T}}})}^m}Q{A^m}} z({x_i})。\\[-1pt] \end{split} $

(28)

将式（28）对输入$ \eta $求偏导，当$ {{\partial J} \mathord{\left/ {\vphantom {{\partial J} {\partial \eta }}} \right. } {\partial \eta }} = 0 $时，则得到此时的最优控制输入为：

$ \eta = - {\Omega ^{ - 1}}\varPsi z({x_i})。$

(29)

其中：$ \Omega ={\displaystyle \sum _{m=1}^{{N}_{p}}\varphi (m)}Q\varphi {(m)}^{{\mathrm{T}}}+{R}_{L}\text{；}\varPsi ={\displaystyle \sum _{m=1}^{{N}_{p}}\varphi (m)}Q{A}^{m} $。

由预测控制滚动优化的思想，取控制输入的第一项$ \Delta u(k) = L{(0)^{\rm{T}}}\eta $作为实际输入值，由此可见不考虑各种约束条件下的DMPC控制器可线性化为全状态反馈控制器的形式$ \Delta u(k) = - Kz(k) $。其中$ K = L{(0)^{\rm{T}}}{\Omega ^{ - 1}}\varPsi $。

实际船舶航行时，舵角的幅值和舵速的幅值受到固有的物理条件限制，因此可将其看成一种硬约束条件。其中，舵速的限制为$ \Delta {u^{\min }} \leqslant \Delta u(k) \leqslant \Delta {u^{\max }} $，舵角的限制为$ {u^{\min }} \leqslant u(k) \leqslant {u^{\max }} $。在模型预测控制算法中，要求在整个控制步长内，输入满足约束条件$ \Delta {u^{\min }} \leqslant \Delta u(k) \leqslant \Delta {u^{\max }} $与$ {u^{\min }} \leqslant u(k) \leqslant {u^{\max }} $。

2.5.2 舵角限制：$ {u^{\min }} \leqslant u(k) \leqslant {u^{\max }} $

舵角约束不等式为：

$ {u^{\min }} \leqslant \sum\limits_{i = 0}^{m - 1} {{L_1}{{(i)}^{\rm{T}}}} \eta + u({k_i} - 1) \leqslant {u^{\max }}。$

(30)

将$ m = 1,2, \ldots ,{N_c} $对应的舵角约束整理成矩阵不等式，则可得：

$ \underbrace {\left[ \begin{gathered} L{(0)^{\rm{T}}} \\[-4pt] \sum\limits_{i = 0}^1 {L{{(i)}^{\rm{T}}}} \\[-4pt] \vdots \\[-4pt] \sum\limits_{i = 0}^{m - 1} {L{{(i)}^{\rm{T}}}} \\ \end{gathered} \right]}_{{M_u}}\eta \leqslant \underbrace {\left[ \begin{gathered} {u^{\max }} - u({k_i} - 1) \\[-4pt] {u^{\max }} - u({k_i} - 1) \\[-4pt] \vdots \\[-4pt] {u^{\max }} - u({k_i} - 1) \\ \end{gathered} \right]}_{{U^{\max }} - \bar u({k_i} - 1)} \text{，} $

$ - \underbrace {\left[ \begin{gathered} L{(0)^{\rm{T}}} \\[-4pt] \sum\limits_{i = 0}^1 {L{{(i)}^{\rm{T}}}} \\[-4pt] \vdots \\[-4pt] \sum\limits_{i = 0}^{m - 1} {L{{(i)}^{\rm{T}}}} \\ \end{gathered} \right]}_{{M_u}} \eta \leqslant \underbrace {\left[ \begin{gathered} {u^{\min }} + u({k_i} - 1) \\[-4pt] {u^{\min }} + u({k_i} - 1) \\[-6pt] \vdots \\[-4pt] {u^{\min }} + u({k_i} - 1) \\ \end{gathered} \right]}_{ - {U^{\min }} + \bar u({k_i} - 1)}。$

(31)

简记为：

$ {M_u}\eta \leqslant {U^{\max }} - \bar u({k_i} - 1) ，- {M_u}\eta \leqslant - {U^{\min }} + \bar u({k_i} - 1) 。$

(32)

2.5.3 舵速限制：$\Delta {U_{\min }} \leqslant \Delta U \leqslant \Delta {U_{\max }} $

舵速约束不等式为：

$ \Delta {u^{\min }} \leqslant L{(m)^{\rm{T}}}\eta \leqslant \Delta {u^{\max }} 。$

(33)

则将$ m = 1,2, \ldots ,{N_c} $对应的舵速约束整理为矩阵不等式形式，则有

$ \underbrace {\left[ \begin{gathered} L{(1)^{\rm{T}}} \\[-3pt] L{(2)^{\rm{T}}} \\[-3pt] \vdots \\[-3pt] L{({N_c})^{\rm{T}}} \\ \end{gathered} \right]}_{{M_\Delta }}\eta \leqslant \underbrace {\left[ \begin{gathered} \Delta {u^{\max }} \\[-3pt] \Delta {u^{\max }} \\[-3pt] \vdots \\[-3pt] \Delta {u^{\max }} \\ \end{gathered} \right]}_{\Delta {U^{\max }}} \text{，} \underbrace {\left[ \begin{gathered} - L{(1)^{\rm{T}}} \\[-3pt] - L{(2)^{\rm{T}}} \\[-3pt] \vdots \\[-3pt] - L{({N_c})^{\rm{T}}} \\ \end{gathered} \right]}_{ - {M_\Delta }}\eta \leqslant \underbrace {\left[ \begin{gathered} - \Delta {u^{\min }} \\[-3pt] - \Delta {u^{\min }} \\[-3pt] \vdots \\[-3pt] \Delta {u^{\min }} \\ \end{gathered} \right]}_{ - \Delta {U^{\min }}} 。$

(34)

简记为：

$ {M_\Delta }\eta \leqslant \Delta {U^{\max }}，- {M_\Delta }\eta \leqslant - \Delta {U^{\min }}。$

(35)

将式（32）和式（35）联立后简记为：

$ M\eta \leqslant \gamma 。$

(36)

联立式（36）和式（25），则航向速率控制器的求解即被转换为二次规划问题：

$ \left\{ \begin{gathered} J = \sum\limits_{m = 1}^{{N_p}} {{{(r({k_i}) - y({k_i} + m|{k_i}))}^{\mathrm{T}}}} (r({k_i}) - y({k_i} + m|{k_i})) + {\eta ^{\rm{T}}}{R_L}\eta，\\[-4pt] M\eta \leqslant \gamma 。\\ \end{gathered} \right. $

(37)

该二次规划问题可利用Hildreth二次规划方法等二次规划方法求解^[11]。且由预测控制滚动优化的思想，在当前时刻只采样控制输入的第一项作为实际的输入值，也即

$ \Delta u(k) = L{(0)^{\rm{T}}}\eta 。$

(38)

2.6 海浪干扰下的滤波处理

文献[12]采用扩展海浪观测器的方法设计了滤波器，本文采用辅助校正器的思想来校正控制器在波浪干扰频率处的响应特性，从而避免在波浪干扰下船舶直航时的频繁打舵问题。首先，依据上述推导航向速率控制器的方式，将被控变量替换为航向并将整个系统的状态空间进行改写为：

$ \begin{split} & \left[ {\begin{array}{*{20}{c}} {\dot v} \\[-2pt] \begin{gathered} {\dot r} \\[-2pt] {\dot \psi } \\[-2pt] \end{gathered} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}&0 \\[-2pt] {{a_{21}}}&{{a_{22}}}&0 \\[-2pt] 0&1&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} v \\[-2pt] \begin{gathered} r \\[-2pt] \psi \\[-2pt] \end{gathered} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{b_1}} \\[-2pt] \begin{gathered} {b_2} \\[-2pt] 0 \\[-2pt] \end{gathered} \end{array}} \right]{\delta _r}，\\ & \psi = \left[ {\begin{array}{*{20}{c}} 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} v \\[-2pt] \begin{gathered} r \\[-2pt] \psi \\[-2pt] \end{gathered} \end{array}} \right] 。\end{split} $

(39)

为了得到线性解的形式，近似认为船舶在直航时将不会触发舵速、舵角的约束条件也即忽略舵角、舵速约束条件，得到此时的DMPC航向控制器形式$ \Delta u(k) = - Kz(k) $。其中$ K = L{(0)^{\rm{T}}}{\Omega ^{ - 1}}\varPsi $，此处的$ z(k) = [ {\Delta \hat v}\;{\Delta \hat r}\; {\Delta \hat \psi }\;{\hat \psi } ] $，为便于分析，将其转换成连续时域下的控制表达形式$ \dot u = \bar Kz + {K_0}u + {k_3}y + \xi $。其中$ z = [ {\begin{array}{*{20}{c}} {\hat v}\;{\hat r}\;{\hat \psi } \end{array}} ] $，$ \bar K = [ {\begin{array}{*{20}{c}} {{k_1}}\;{{k_2}}\;{{k_3}} \end{array}} ] $，$ {K_0} $与$ \bar K $控制系数矩阵通过$ K $与系统的状态空间方程进行转换得到，$ \xi $为引入的辅助滤波器校正量，另外由状态观测器的连续时域表达形式$ \dot z = (A - LC)z + Bu + Ly $。此处$ u $为指令舵角$ {\delta _r} $，综合考虑航向控制器和状态观测器：

$ \left[ {\begin{array}{*{20}{c}} {\dot z} \\[-2pt] {\dot u} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {A - LC}&B \\[-2pt] {\bar K}&{{K_0}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} z \\[-2pt] u \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} L&0 \\[-2pt] {{k_3}}&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} y \\[-2pt] \xi \end{array}} \right]。$

(40)

令$ \zeta = y - Cz $为观测器观测误差，得到以下系统模型状态空间形式：

$ \left[ {\begin{array}{*{20}{c}} {\dot z} \\[-2pt] {\dot u} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {A - LC}&B \\[-2pt] {\bar K}&{{K_0}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} z \\[-2pt] u \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} L&0 \\[-2pt] {{k_3}}&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} y \\[-2pt] \xi \end{array}} \right] ，$

(41)

$ \left[ {\begin{array}{*{20}{c}} u \\[-2pt] \zeta \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0&1 \\[-2pt] { - C}&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} z \\[-2pt] u \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0&0 \\[-2pt] 1&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} y \\[-2pt] \xi \end{array}} \right] 。$

(42)

则以输入为$ {[ {\begin{array}{*{20}{c}} y&\xi \end{array}} ]^{\rm{T}}} $，以输出为$ {[ {\begin{array}{*{20}{c}} u&\zeta \end{array}} ]^{\rm{T}}} $的系统的传递函数为：

$ \left[ {\begin{array}{*{20}{c}} u \\[-2pt] \zeta \end{array}} \right] = T(s)\left[ {\begin{array}{*{20}{c}} y \\[-2pt] \xi \end{array}} \right]，\begin{array}{*{20}{c}} {}&{T(s) = \left[ {\begin{array}{*{20}{c}} {{T_{11}}(s)}&{{T_{12}}(s)} \\[-2pt] {{T_{21}}(s)}&{{T_{22}}(s)} \end{array}} \right]}。\end{array} $

(43)

其中，输入为$ \zeta $、输出为$ \xi $的部分$ \xi = F(s)\zeta $为需设计的滤波器。

从船舶输出航向$ y $至指令舵角$ u $之间的传递函数为：

$ G(s) = [{T_{11}}(s) + {T_{12}}(s)F(s){(I - {T_{22}}(s)F(s))^{ - 1}}{T_{21}}(s)。$

(44)

为达到波浪主频率点附近尽量少操舵的目的，可令$ {G_{{\delta _r}\varphi }}(j\omega ) = 0 $。其中，$ \omega $为船舶遭遇的波浪主频率，则可推出：

$ \begin{split} F(j\omega ) =\,& {\left\{ {{T_{12}}(j\omega ) + [ - {T_{11}}(j\omega )]{T_{21}}^{ - 1}(j\omega ){T_{22}}(j\omega )} \right\}^{ - 1}} \times\\[-4pt] & [ - {T_{11}}(j\omega )]{T_{21}}^{ - 1}(j\omega )。\\[-1pt] \end{split} $

(45)

得到由式（45）描述的传递函数结果后，即可设计状态空间方程对$ F(s) $进行最小实现或标准化实现。

3 仿真示例

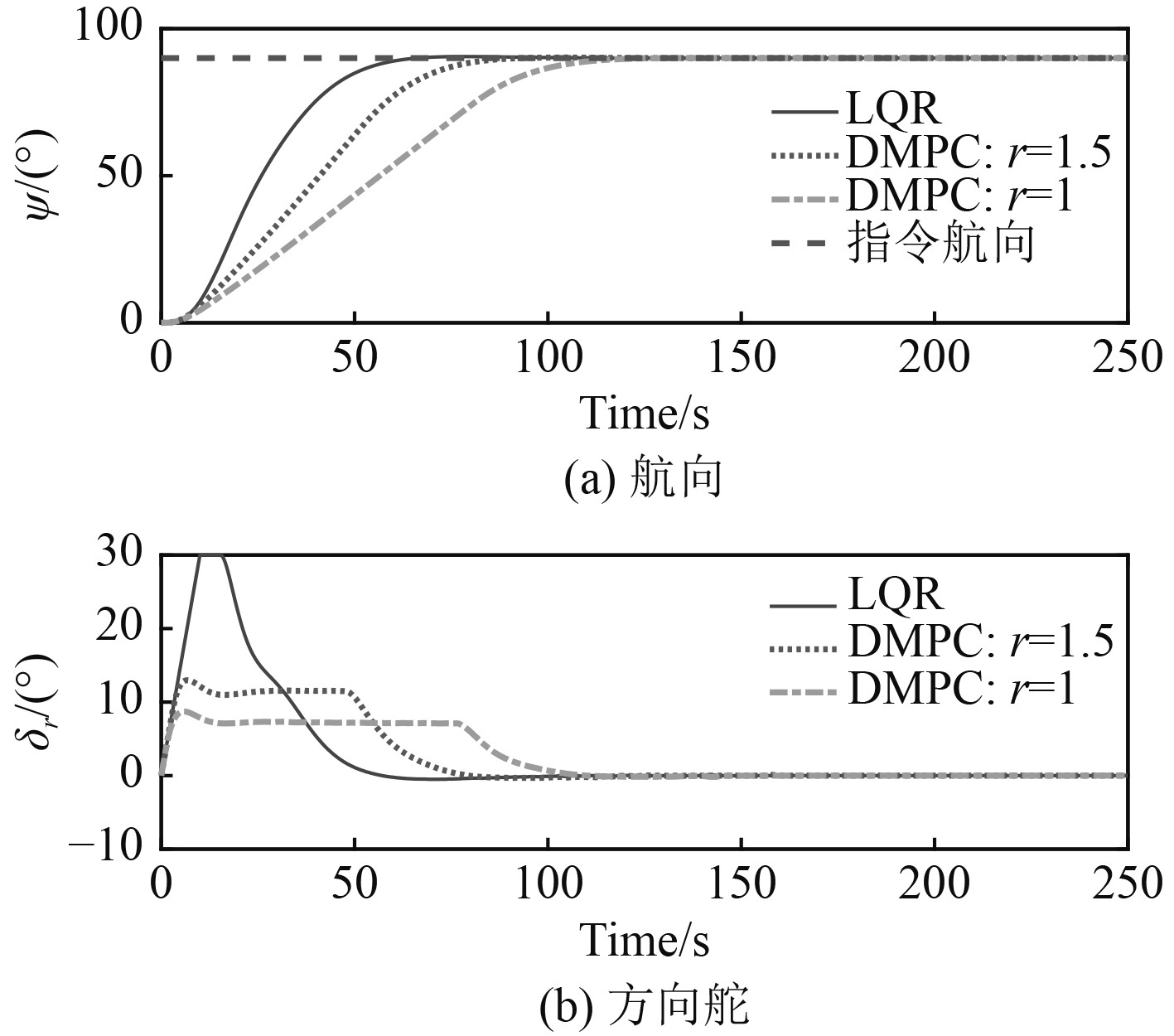
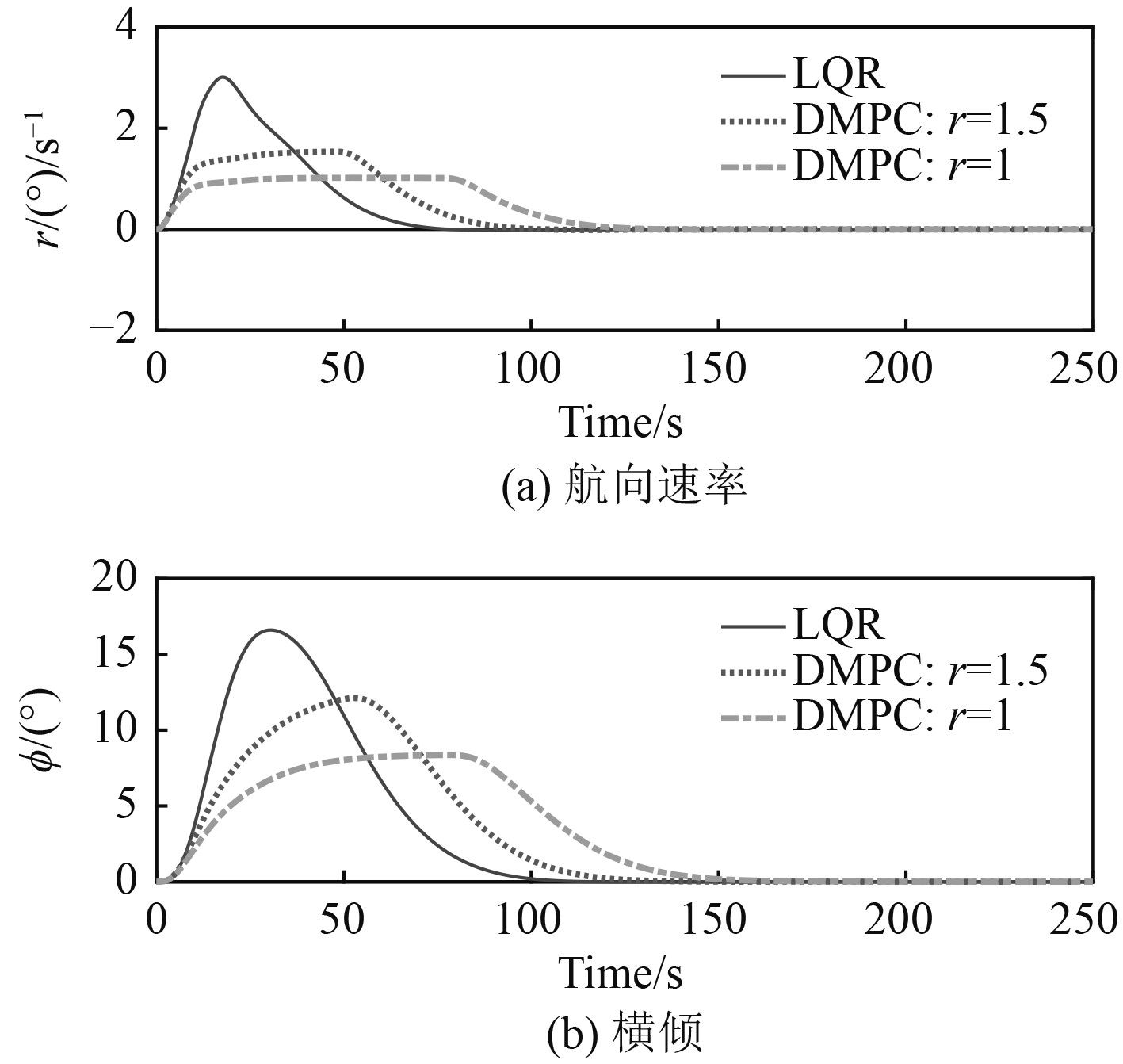
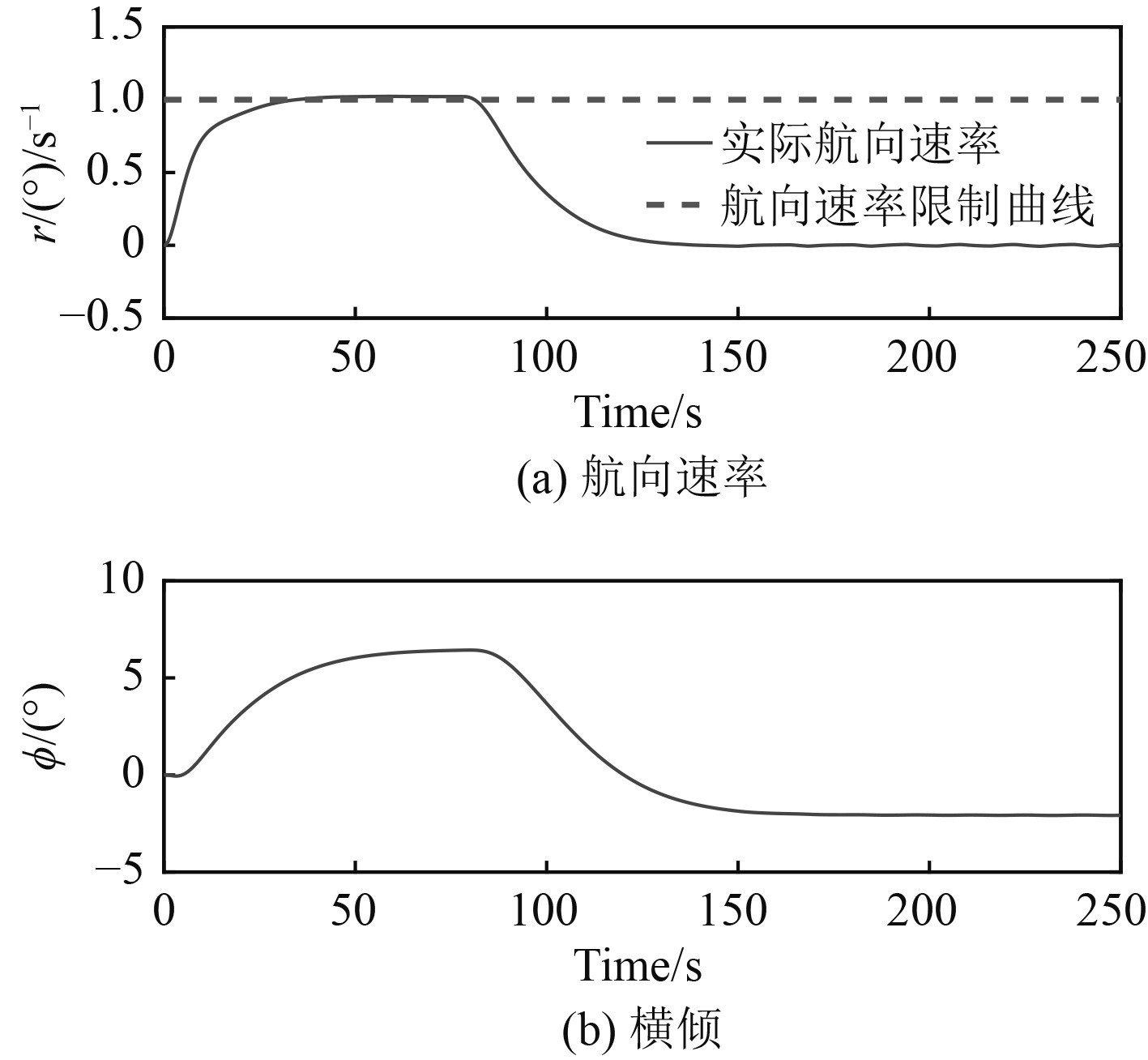
仿真工况1：为了验证所设计的航向——航向速率控制算法的有效性，对某型船舶航向机动过程进行仿真验证。航速20 kn仿真结果如图2和图3所示。其中实际航向测量值精度和舵角测量精度都取为0.05°，航向速率限定值分别设定为1.5°/s和1°/s，指令航向设定为90°，舵角约束为$ {{ - 3}}{{\text{0}}^ \circ } \leqslant {\delta _r} \leqslant 3{{\text{0}}^ \circ } $，舵速约束为$ {{{{ - }}{{\text{3}}^ \circ }} \mathord{\left/ {\vphantom {{{{ - }}{{\text{3}}^ \circ }} {\rm{s}}}} \right. } {\rm{s}}} \leqslant {\dot \delta _r} \leqslant {{{{\text{3}}^ \circ }} \mathord{\left/ {\vphantom {{{{\text{3}}^ \circ }} {\rm{s}}}} \right. } {\rm{s}}} $，控制器采样时间为0.1 s，并采用常规LQR航向控制器作为对比仿真。

统计上述仿真试验结果，其中稳定时间为航向由初始航向达到稳态值的±2%之内（也即航向达到88°）的时间值。

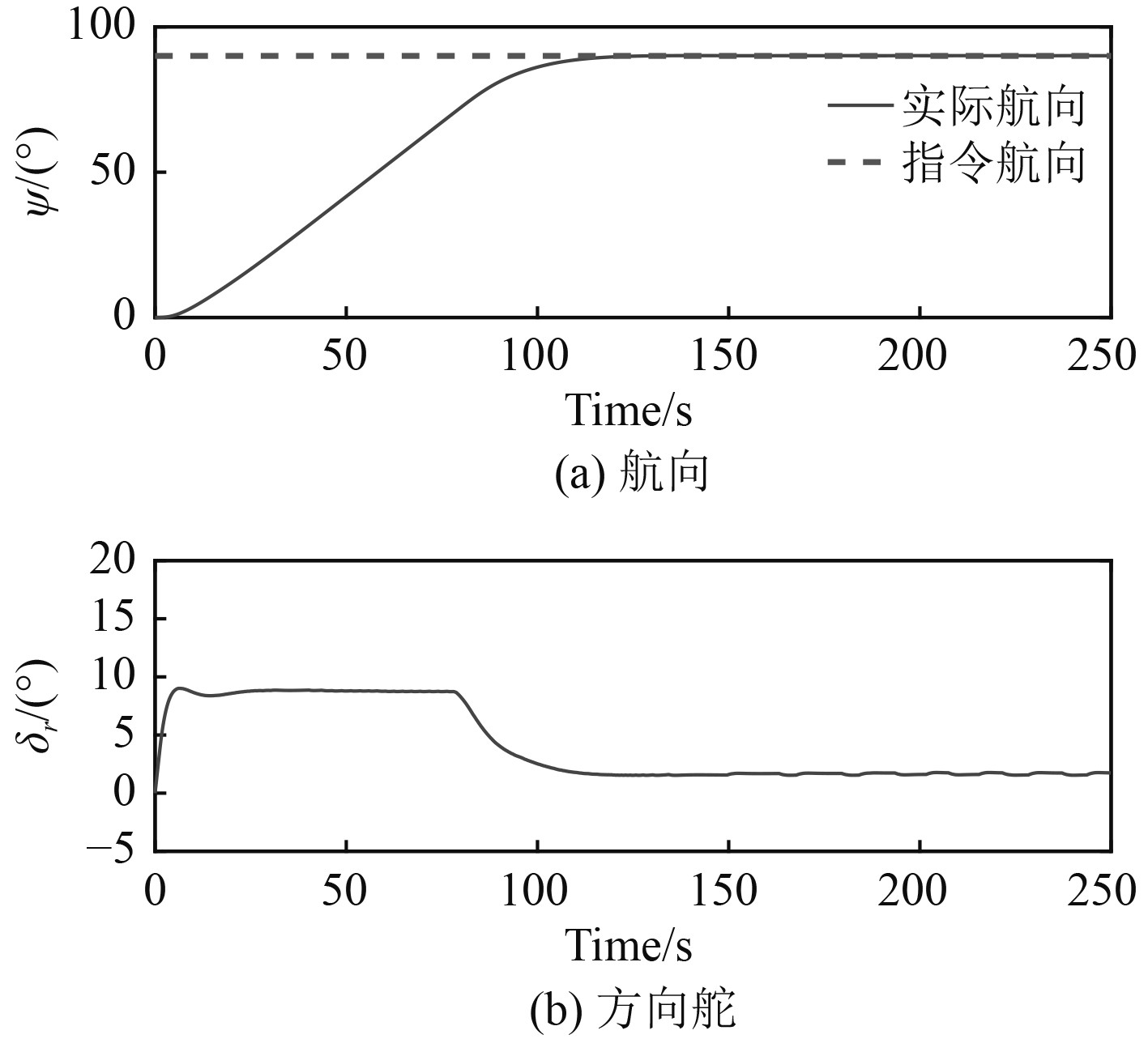
仿真工况2：为验证所设计控制算法控制航向的无静差性，加入定常恒值干扰，并设定航向速率为1°/s，在与上述仿真结果同等的约束条件和指令航向条件下进行仿真。其中仿真结果如图4～图5所示。

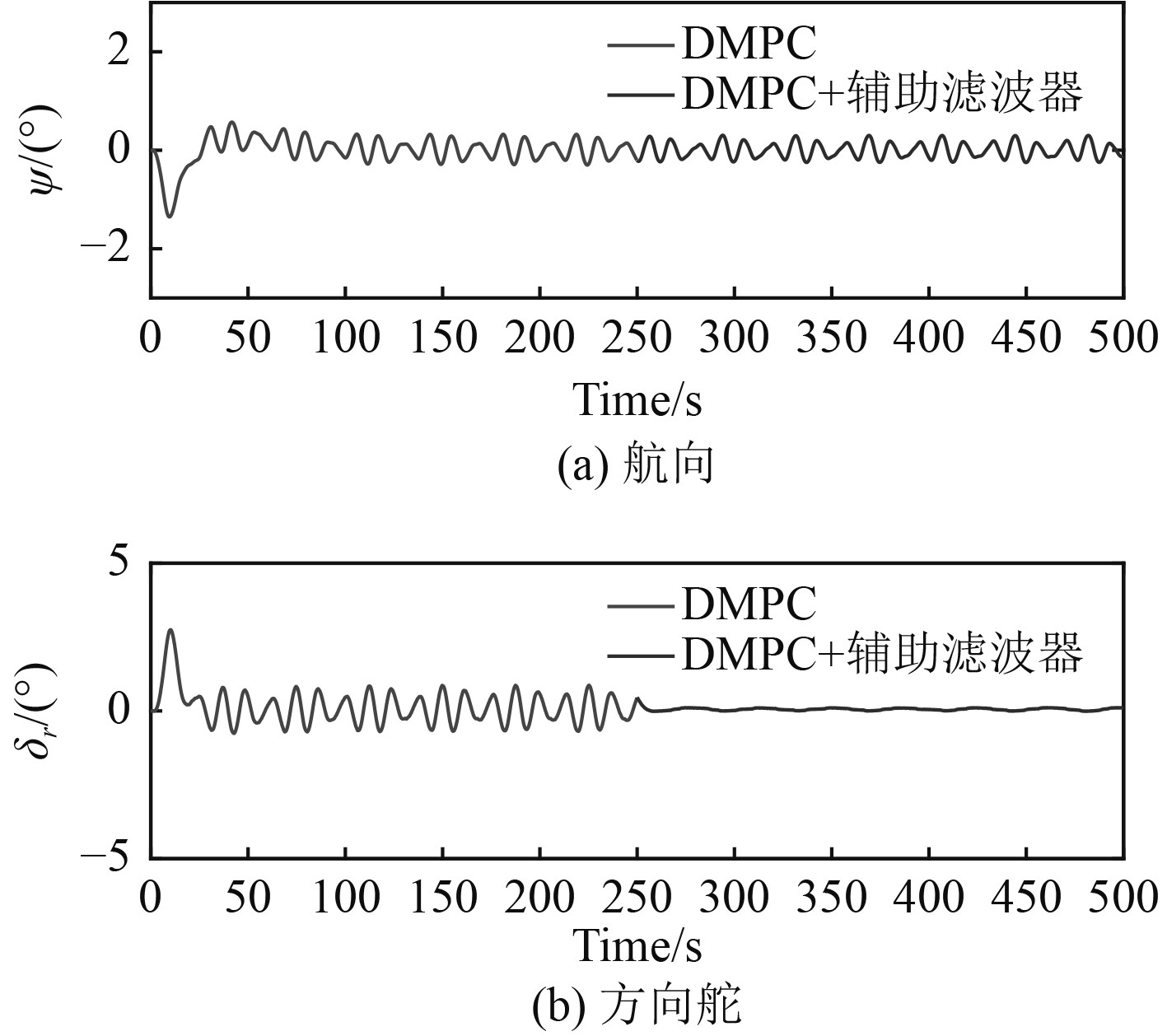
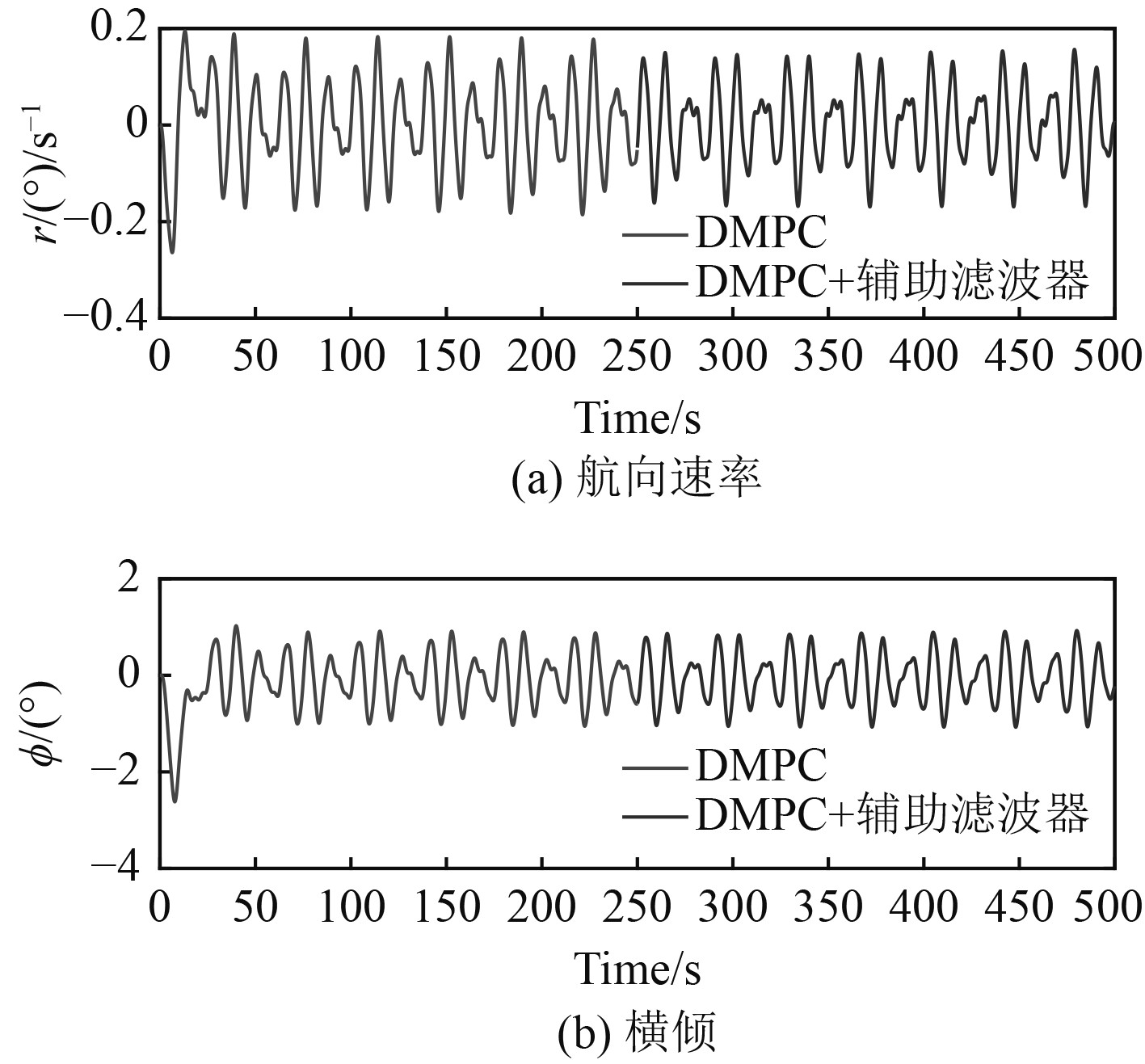
仿真工况3：为验证DMPC航向控制器综合辅助滤波器的有效性，在上述仿真工况1的基础上添加主频w=0.8 rad/s的海浪干扰，依据时间对控制器进行切换。其中，前250 s不引入辅助滤波器进行正常的直航操纵，后250 s引入辅助滤波器。其中仿真结果如图6～图7所示。

4 结　语

由图2和图3及表1可知，所设计的基于内环航向速率限幅的DMPC航向控制方法能有效限制船舶航向机动过程中的最大航向速率，且与LQR航向控制方法进行对比可看出，所设计的航向控制策略相比LQR控制方法而言，响应时间稍长但能有效降低机动过程中的最大横倾。其中，限定转向速率r=1.5°/s后，稳定时间增大约20 s，最大横倾降低了约26%，限定转向速率r=1°/s后，稳定时间增大约48 s，最大横倾降低了约50%。由图4和图5可知，在船舶遭遇定常恒值干扰情况下，上述控制算法依然可达到不错的控制效果，并实现了航向控制最终状态的无静差性。由图6～图7可知，对比250 s以前的和250 s以后的方向舵曲线，可看出通过改变控制器结构和引入辅助滤波器，在很大程度上降低了海浪干扰下的操舵频率，有利于船舶驾驶整体的安全性和舒适性，但上述控制器都采用了被控对象精确的状态空间模型，如何提高所设计控制器的鲁棒性和自适应性为随后研究的重点。