2. 中船邮轮科技发展有限公司,上海 200120;
3. 上海市船舶工程重点实验室,上海 200011
2. CSSC Cruise Technology Development Co., Ltd., Shanghai 200120, China;
3. Shanghai Key Laboratory of Ship Engineering, Shanghai 200011, China
随着计算机技术的跨越式发展,基于计算流体力学(CFD)技术的船体线型设计方法得到广泛应用[1]。通过粘、势流数值方法预报船舶航行阻力,指导船体线型设计、优化的技术手段,逐渐成为国内外船舶工作者的研究热点。陈红梅等[2, 3]通过自由曲面变形(FFD)技术、CFD技术和试验设计(DOE)方法组成的集成优化系统对某集装箱船多工况下的阻力性能进行优化,经试验证明优化船型有效功率明显下降。Kim等[4,5]将基于径向基函数(RBF)的变形方法与基于船体横截面积曲线的插值方法相结合,对KCS船型进行了阻力线型优化,验证了该方法的可行性。
作为造价高昂、建造难度大的高技术、高附加值船舶,豪华邮轮设计资料获取难度大,其阻力线型优化研究相对较少,现有文献多局限于球首的设计[6 − 8],针对全船线型的优化则是少之又少。为提高船舶营运经济性,本文针对某8万总吨级豪华邮轮,基于CAESES集成优化平台开展了线型优化工作,同时在优化线型的基础上进行了截流板的设计。研究工作分为船体线型优化、截流板方案设计及模型试验验证,其中船体线型优化的具体流程如图1所示。

|
图 1 船型优化流程 Fig. 1 Hull form optimization process |
优化过程中的船体曲面变形通过CAESES软件的CAD模块完成。CAESES中包含多种三维曲面半参数化变形方法可供选用,其中应用最多的有3种:Lackenby方法、FFD方法以及Delta shift方法,本文在优化过程中运用了其中的FFD方法与Delta shift方法。
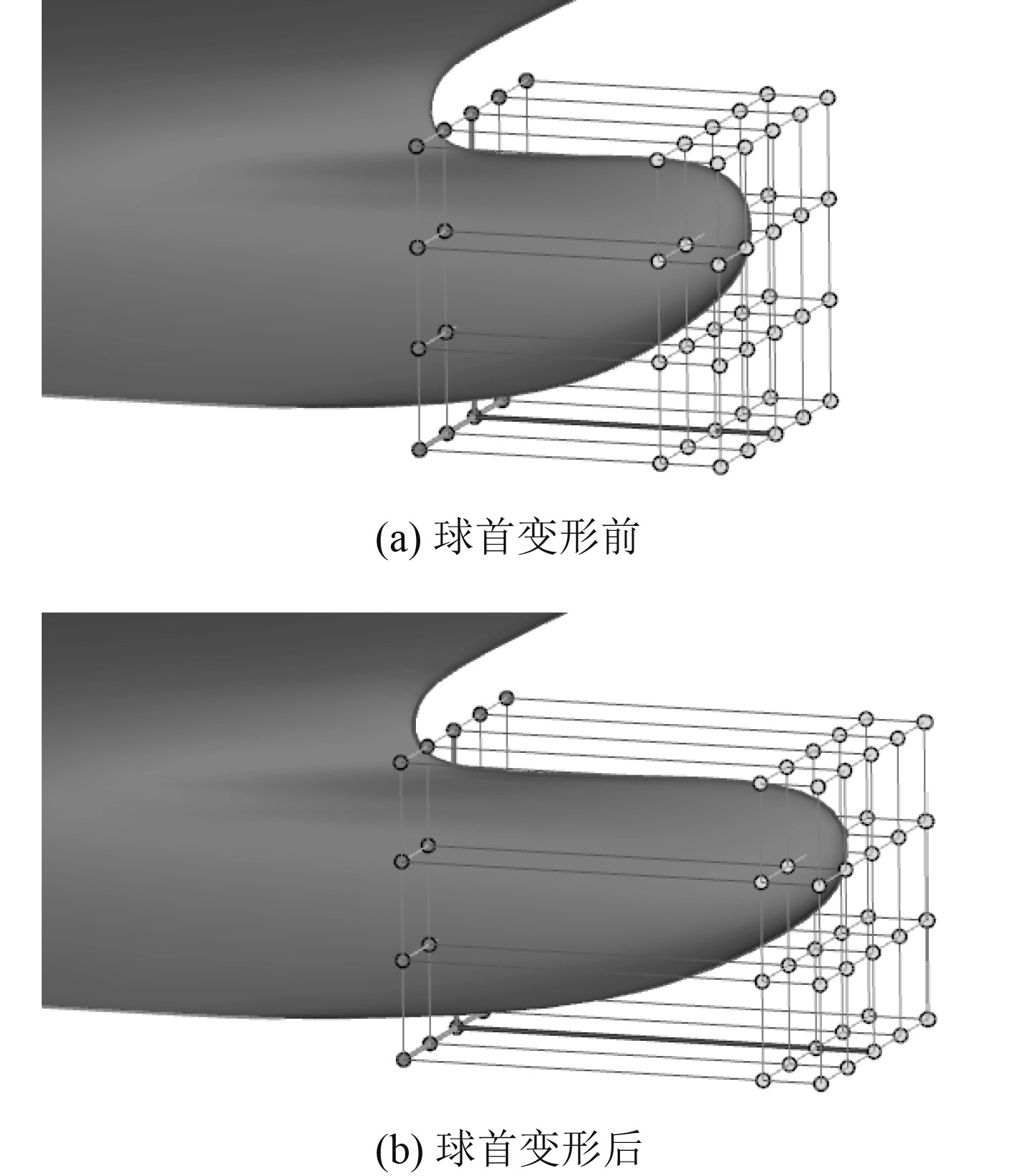
Sederberg和Parry于1986年提出了曲面自由变形(FFD)方法[10],其变形方式简单灵活,变形效果直观,在船舶领域应用广泛。采用FFD方法基本思想是:首先针对拟变形区域的大小以及空间位置构建变形控制体;根据Bernstein多项式建立船体表面型值点与变形控制体的各控制点坐标间的函数关系;选定控制点,以控制点位移量作为设计变量,通过改变控制点的空间位置即可实现船体曲面的变形(见图2)。由于简单实用的控制体嵌入式设计,FFD方法既可以实现全船线型的总体变化,也可以用于船体曲面的局部变形,变形后的曲面几何连续。该方法的缺点是变形控制点多,需要大量测试来确定不同控制点位移量之间的耦合关系才能实现目标曲面区域的光顺变形,不便于船型优化过程中设计变量的选取。
|
图 2 FFD方法示意图 Fig. 2 Diagram of the FFD method |
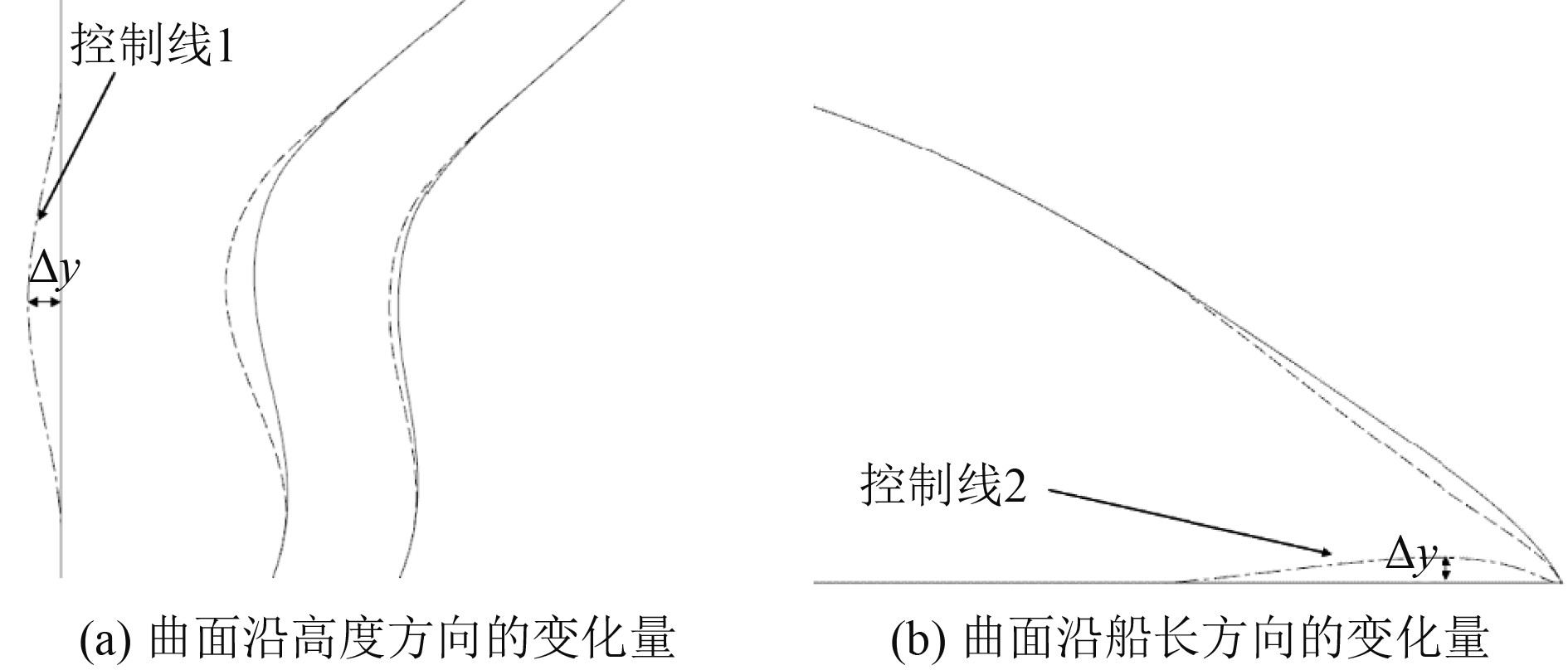
采用Delta shift方法进行船壳曲面变形,其变形区域、变形方向和变形量主要通过控制线控制。如图3所示,将曲面变形方向选定为y方向,控制线1表征了其长度范围内曲面沿高度方向上y方向变化量,由于控制线1上的控制点y坐标值为负,因此目标区域朝y轴负方向移动,控制点的y坐标值绝对值越大变形量越大;同理,控制线2表征了其长度范围内曲面沿船长方向上y方向变化量,由2条曲线的共同控制实现船壳曲面局部的变形。相比于其他变形方法,Delta shift方法变形控制较为复杂,一般需要通过多个方向上的控制线耦合以实现船壳曲面的光顺变形;其优势在于各控制线对应的变形效果清晰可控,可以直接选取控制点位移量作为优化设计变量,无需考虑参数之间的耦合关系。
|
图 3 Delta shift方法原理图 Fig. 3 Diagram of the Delta shift method |
在势流理论体系下,计算域流体无旋、无粘、不可压缩且有速度势,速度势方程为:
| $ \varPhi (x,y,z)=U_x+\varphi(x,y,z) 。$ | (1) |
式中:Ux为均匀来流的的速度势;
流场速度势满足Laplace方程:
| $ \nabla^2\varPhi=0。$ | (2) |
由于理想流体中没有剪切力作用,物体表面上的流体法向速度为0,可得物面边界条件:
| $ \frac{\partial \varphi}{\partial n}+Un_x=0 。$ | (3) |
在自由液面上,流体质点的法向速度与自由面本身的法向速度相同,联合兴波区域以及无限远处自由面伯努利方程,可得自由面边界条件:
| $ \frac{1}{2}\varPhi_x(\nabla \varPhi\cdot \nabla \varPhi)_x+\frac{1}{2}\varPhi_y(\nabla \varPhi\cdot \nabla \varPhi)_y+g\varPhi_z=0。$ | (4) |
联立式(2)~式(4),采用高阶面元法,结合伯努利方程求解波阻力系数CW。
2.2 STAR-CCM+粘流计算粘流计算中,坐标系原点取为船体基平面与尾垂线的交点,从船尾指向船首为X轴正向,由船中指向船体左舷为Y轴正向,由基平面法线方向向上为Z轴正向。采用RANS方法中时,非定常、不可压缩的粘性流体的控制方程为连续性方程及RANS方程,如下:
| $ \frac{\partial u_x}{\partial x}+\frac{\partial u_y}{\partial y}+\frac{\partial u_z}{\partial z}=0 ,$ | (5) |
| $ \frac{\partial u_i}{\partial t}+\frac{\partial (u_iu_j)}{\partial x_j}=-\frac{1}{\rho}\frac{\partial p}{\partial x_i}+\frac{\partial }{\partial x_j}\left[ v\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right) \right]+f_i 。$ | (6) |
式中:u为时均化速度;p为时均化压力;ν为流体运动粘性系数;fi为体积力。
采用Realizable k-ε模型封闭控制方程,采用有限体积法离散控制方程,采用SIMPLE算法对压力速度耦合解耦,采用VOF方法模拟自由液面。
3 线型优化本文针对某8万总吨级邮轮(见图4),采用基于CAESES平台的船型集成优化方法进行线型优化及截流板的方案设计,主要参数见表1。目标船推进形式为双吊舱桨推进,设计吃水状态下,Fr=0.219对应本船能达到的最高航速,线型优化及截流板方案设计基于此工况进行。

|
图 4 8万总吨级邮轮三维模型示意图 Fig. 4 CAD model of the 80,000 ton cruise ship |
|
|
表 1 8万总吨级邮轮船模尺度主要参数 Tab.1 Main particulars of the 80,000 ton cruise ship at model scale |
对目标船带首侧推孔船型阻力性能进行粘流数值计算。计算域大小如图5所示,长度方向取为5LPP,其中船首前方取1.5LPP,船尾后方2.5LPP;宽度方向为2.5LPP;高度方向空气部分取1.5LPP,液体部分取2.5LPP。

|
图 5 计算域设置示意图 Fig. 5 The computational domain |
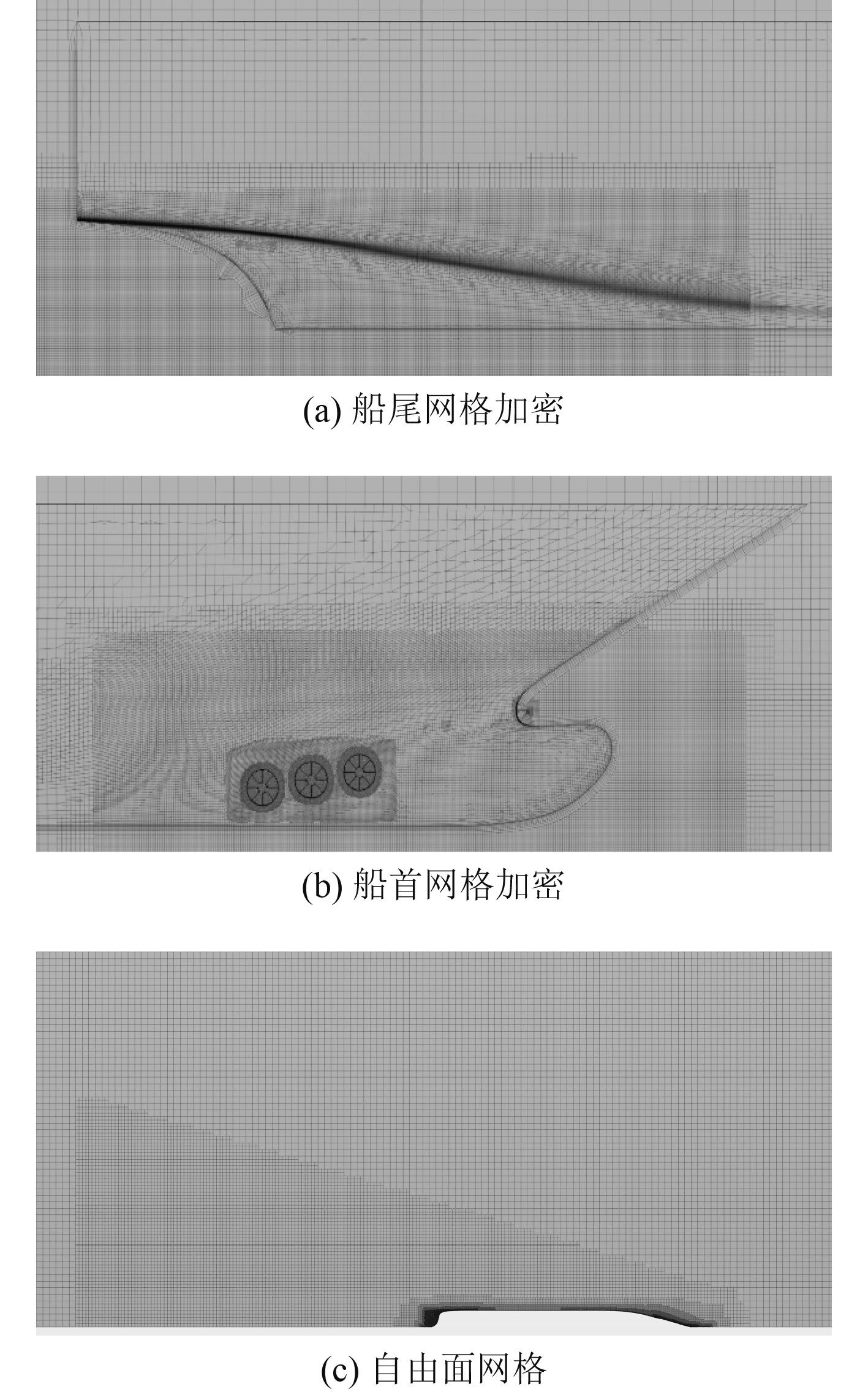
通过切割体网格生成器划分非结构化网格,对船首、船尾以及船体附近区域进行了局部网格加密(见图6(a)和图6(b)),对首侧推孔附近区域设置了更小尺寸的网格。考虑到船舶航行过程中的自由面兴波,对设计吃水自由面附近以及船后兴波区域进行了局部网格加密(见图6(c))。目标船原型在设计吃水、Fr=0.219(计算水温15°C)状态下阻力计算结果见表2。
|
图 6 计算域网格划分 Fig. 6 Mesh generation for the computational domain |
|
|
表 2 原型阻力计算结果 Tab.2 CFD results of the original hull form |
以降低兴波阻力系数CW为目标,通过CAESES与SHIPFLOW耦合对目标船(不带首侧推孔)进行全船线型优化。首先通过FFD、Delta shift方法实现船壳曲面的半参数化变形,提取控制点的位移量作为设计变量;然后通过CAESES内嵌算法控制设计变量的变化,生成不同的线型方案,同时运用SHIPFLOW进行势流计算,求解兴波阻力系数CW;选取典型方案通过STAR-CCM+软件进一步计算线型优化方案总阻力,分析优化结果。
对于首部线型优化,一方面,考虑到对于Fr>0.2的中高速船舶,首部水线半进角的大小对兴波阻力影响较为敏感[11],在CAESES软件中,通过自由变形(FFD)方法实现首部水线半进角的参数化控制(见图7(a));另一方面,考虑到球鼻首有降低兴波阻力的作用,而球首长度直接影响球首的减阻效果,同样通过FFD方法实现球首的半参数化变形(见图7(b)),选取水线半进角变化量(Delta_HalfEntranceAngle)、球首长度变化量(Delta_BulbLength)作为设计变量进行首部线型优化。

|
图 7 船体曲面的半参数化变形 Fig. 7 Semi-parametric deformation of the hull surface |
对于尾部线型优化,尾封板高度以及船尾横剖面形状的变化会引起去流段水线形状的变化,从而影响船尾兴波。分别采用Delta shift方法、FFD方法实现尾封板以及船尾横剖面形状的半参数化变形(如图7(c)、图7(d)),选取尾封板高度变化量(DeltaZ_transom)、尾部横剖面UV度变化量(stern_UV)作为设计变量进行尾部线型优化。优化算例的定义见表3,根据设计要求需保证优化前后船型排水量∆变化在0.7%以内,不满足约束条件的样本方案将不进行计算。
|
|
表 3 优化算例定义 Tab.3 Configurations of the optimization |
CAESES-SHIPFLOW计算结果如图8所示,可以看出,兴波阻力系数CW随变量Delta_HalfEntranceAngle的增大而增大、随变量Delta_BulbLength和DeltaZ_transom的增大而减小,即减小首部水线半进角、增大球首长度、降低尾封板距基平面高度有利于降低船型兴波阻力;兴波阻力系数CW随stern_UV的变化趋势不明显,即尾部横剖面形状对于本船兴波阻力影响不显著。

|
图 8 兴波阻力系数随各设计变量变化散点图 Fig. 8 Scatter plot of the wave making resistance coefficient with design variables |
基于以上结果,本文针对首部线型优化方案OPT1以及全船线型优化方案OPT2进行了总阻力CFD计算,优化方案OPT1和OPT2设计变量取值见表4。阻力计算结果见表5,从中可以看出首部线型优化方案OPT1实船有效功率较原型下降了4.3%,全船线型优化方案OPT2实船有效功率较原型下降了8.4%。
|
|
表 4 优化方案设计变量取值 Tab.4 The values of design variables for the optimized hull form |
|
|
表 5 原型与优化方案总阻力对比 Tab.5 Comparisons of the ship resistance between the original hull form and the optimized hull forms |
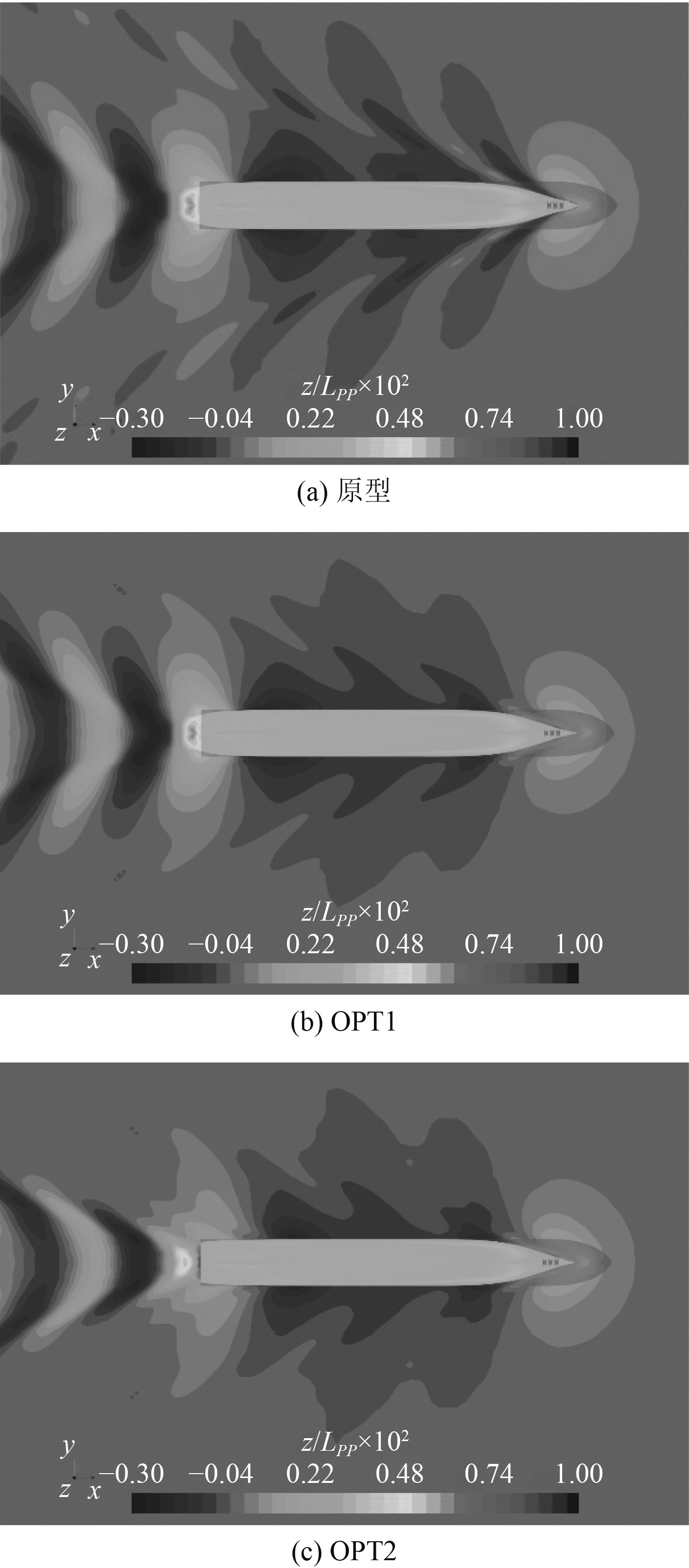
图9和图10分别为原型与优化方案舷侧波高对比图、原型与优化方案自由面兴波示意图。对比原型与优化方案OPT1,可以看出首部线型优化后首波峰高度明显降低,自由面散波明显减弱;对比优化方案OPT1与OPT2,可以看出尾部线型优化后尾波峰高度降低,船后兴波区域面积减小。图11为原型与优化方案船体表面压力分布图,相比于原型,优化方案OPT1和OPT2球鼻首高压区面积有所减小,首肩附近曲面压力梯度更均匀;优化方案OPT2尾部高压区面积较原型有所减小。
|
图 9 原型与优化方案舷侧波高对比 Fig. 9 Comparisons of the wave height on the hull between the original hull form and the optimized hull forms |

|
图 10 原型与优化方案自由面兴波示意图 Fig. 10 Free surface elevations for the original hull form and the optimized hull forms |
|
图 11 原型与优化方案船体表面压力分布 Fig. 11 Distributions of the hydrodynamic pressure for the original hull form and the optimized hull forms |
为进一步改善目标船设计状态阻力性能,本文针对线型优化方案OPT2进行了截流板的多方案设计和优选。截流板是安装在船尾的一块薄板,它紧贴着尾封板垂直下伸,其主要尺寸参数有截流板深度h以及宽度b。共设计5种不同宽度和深度的截流板方案(见表6),并对加装截流板的船型进行了总阻力CFD计算,计算结果见表7。
|
|
表 6 不同方案截流板尺寸 Tab.6 Dimensions of the interceptor for different design candidates |
|
|
表 7 阻力计算结果 Tab.7 CFD results of the ship resistance for different design candidates of the interceptor |
从表7可知截流板方案1减阻效果最好,因此选择方案1作为截流板的最终设计方案,线型优化方案OPT2安装截流板后实船有效功率下降了1.5%;对比原型,OPT2(带截流板)实船有效功率下降了9.8%。
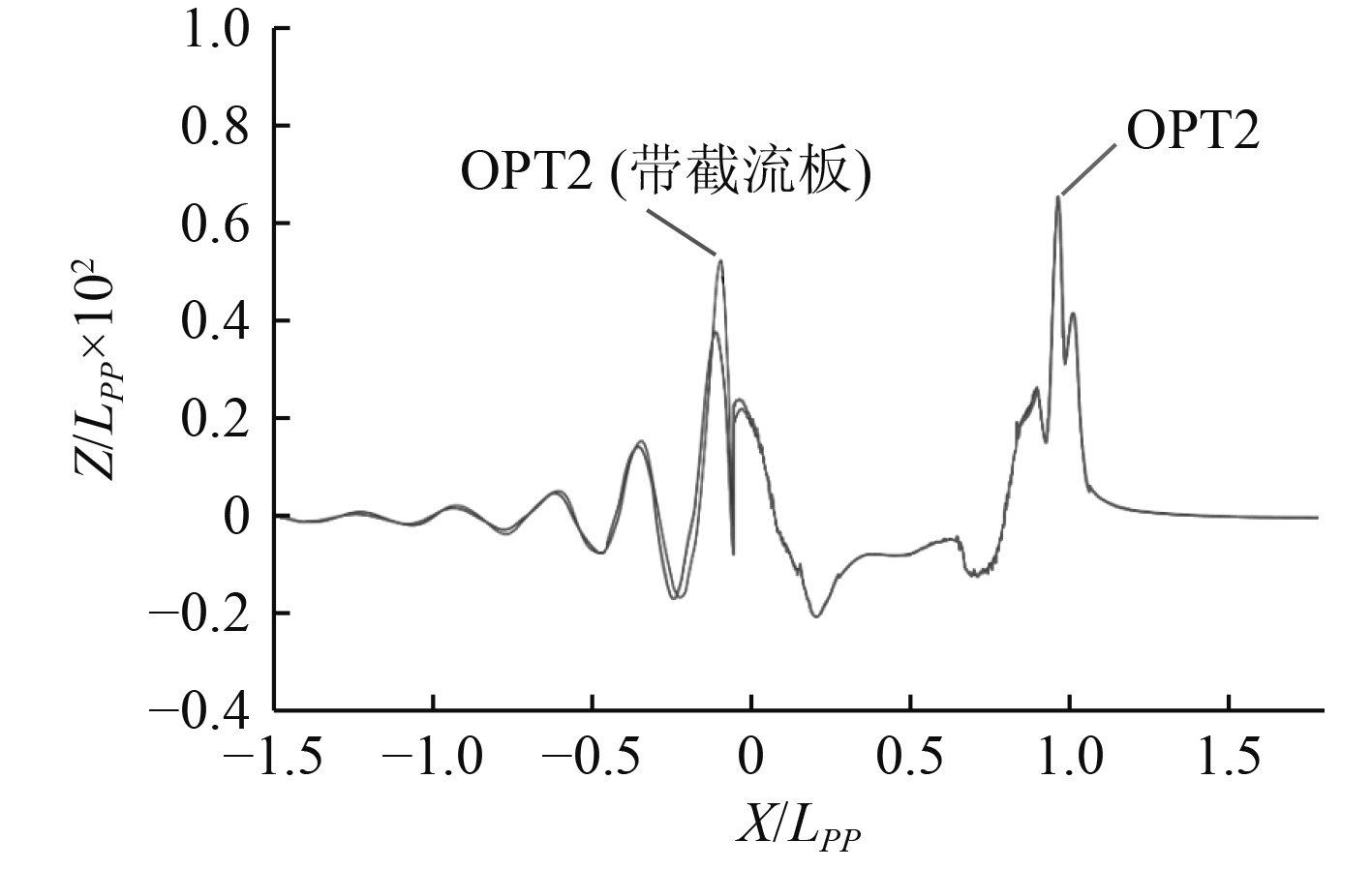
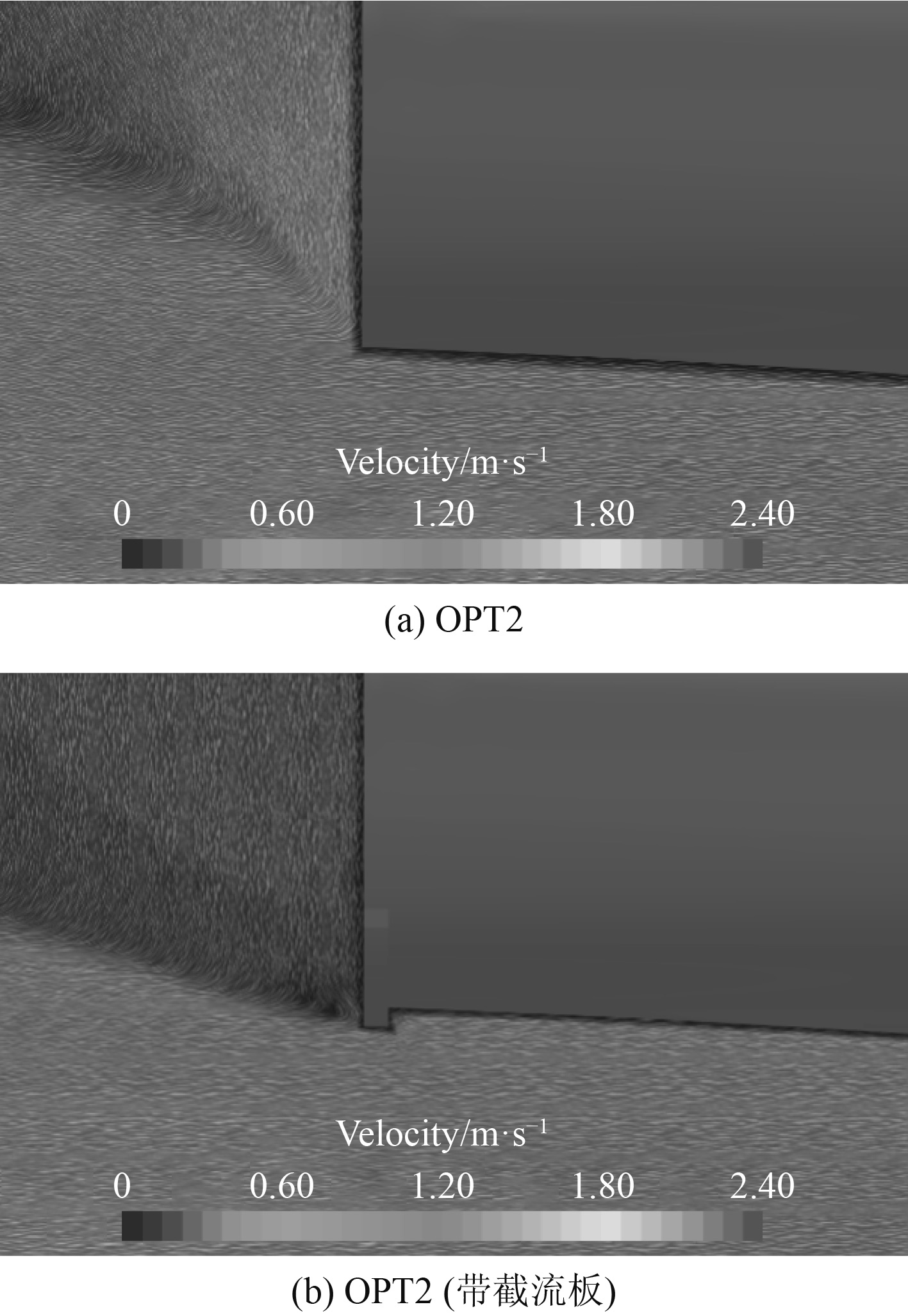
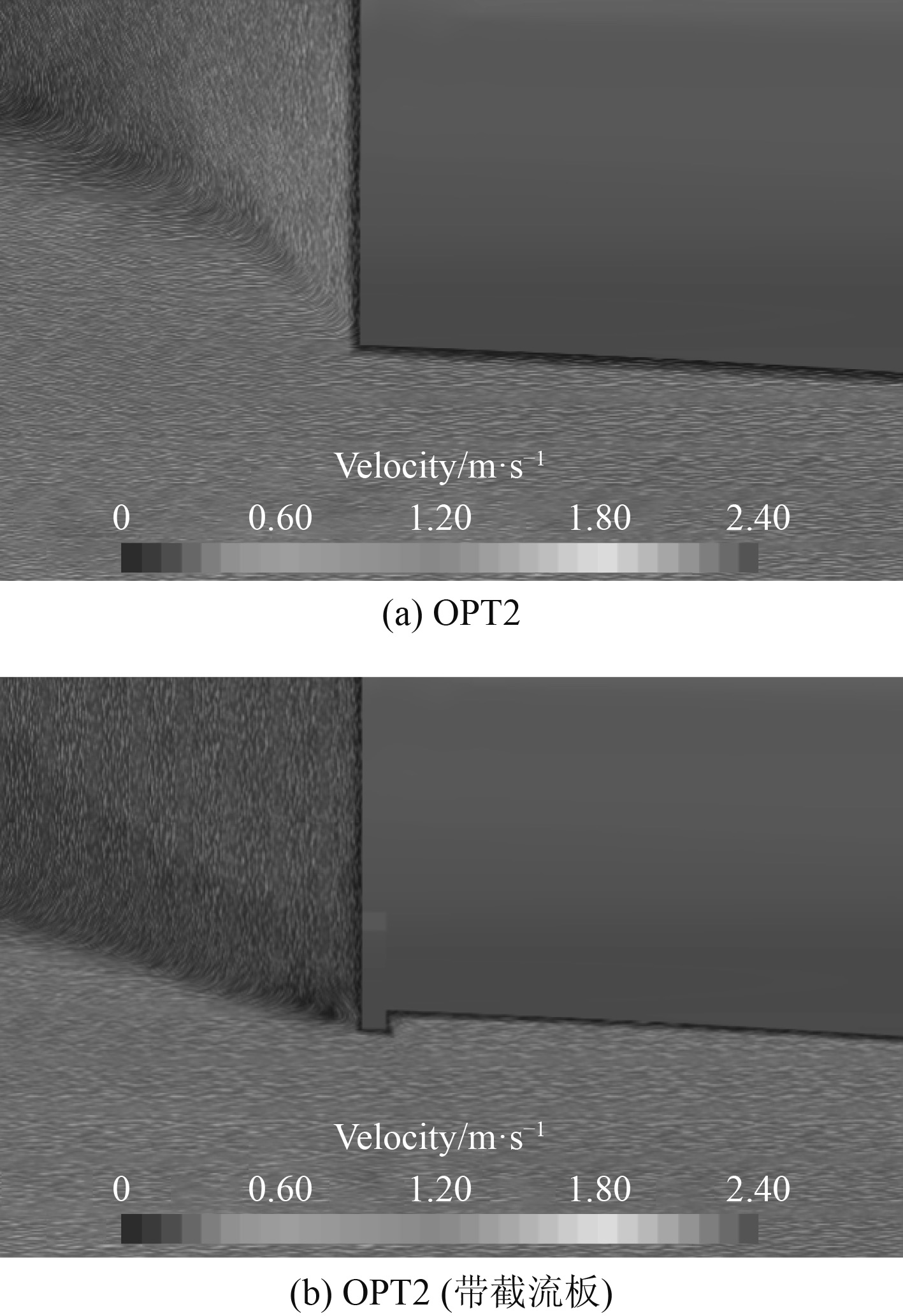
图12为线型优化方案OPT2带与不带截流板情况下舷侧波高对比图,从中可以看出安装截流板后船尾波峰高度进一步降低。这是由于截流板会对其前方的流体产生阻滞作用(见图13),降低尾封板下方来流速度,同时对船体尾部形成向上的升力和纵倾力矩,改变了船体的受力和姿态(见表7),从而减小了船体的兴波阻力。
|
图 12 OPT2带与不带截流板的舷侧波高对比 Fig. 12 Comparisons of the wave height on the hull for OPT2 with and without the interceptor |
|
图 13 OPT2带与不带截流板的尾部流场示意图 Fig. 13 The flow field near the stern for OPT2 with and without the interceptor |
为了对线型优化及CFD计算结果进行验证,本文针对目标船开展了模型试验相关工作。在相同环境条件下进行阻力试验,设计状态下阻力试验结果见表8。
|
|
表 8 模型试验结果 Tab.8 Results of the model test |
可知,优化后船型实船有效功率下降了7.8%,对比前文计算结果可知,剩余阻力系数及总阻力系数CFD计算值相较于试验值均偏小,但CFD计算与模型试验结果表明优化方案的阻力优化效果接近,可认为本文针对目标船进行的线型优化及截流板设计成功。
6 结 语本文基于CAESES集成优化平台对某8万总吨级邮轮进行了阻力线型优化,其次针对优化方案进行了截流板的设计,进一步降低了目标船设计状态的实船有效功率。从模型试验结果来看,本文所采用的线型优化及截流板设计方法切实可行,可为相关船型的线型优化以及附体设计提供有力参考。
对比目标船不同方案阻力CFD计算和试验结果,得到了以下结论:
1)设计状态下,减小船型首部水线半进角、增大球首长度、降低尾封板高度有利于降低兴波阻力;
2)安装截流板可以改善尾部流场,降低船尾波峰高度,进而降低船型总阻力;
3)对比舷侧波高图可知,经全船线型优化,目标船首、尾波峰高度明显降低,安装截流板后,船尾波峰高度进一步降低;
4)阻力模型试验结果表明,优化线型安装截流板后,实船有效功率相对于原型降低了7.8%。
| [1] |
万德成, 缪爱琴, 赵敏. 基于水动力性能优化的船型设计研究进展[J]. 水动力学研究与进展(A辑), 2019, 34(6): 693-712. |
| [2] |
陈红梅, 熊小青, 吴琼, 等. 超巴拿马型集装箱船球艏型线优化研究[J]. 中国造船, 2015, 56(1): 80-86. |
| [3] |
陈红梅, 冯毅, 于海, 等. 集装箱船型线多速度点的数值优化[J]. 船舶, 2015, 26(6): 8-12. |
| [4] |
KIM Hyunyul, YANG Chi. Hull form optimization for reduced resistance and improved seakeeping via practical designed-oriented CFD tools[C]//Conference on Grand Challenges in Modeling & Simulation. Ottawa, Canada, 2010.
|
| [5] |
KIM Hyunyul, YANG Chi. A new surface modification approach for cfd-based hull form optimization[J]. Journal of Hydrodynamics, Ser. B, 2010, 22(5): 520-525. |
| [6] |
章新智, 王驰明, 郭昂. 豪华邮轮球艏的新型设计[J]. 船舶工程, 2014, 36(S1): 12-15. |
| [7] |
王杉, 王艳霞, 赵强, 等. 参数化方法的中型豪华游船特殊球艏线型优化[J]. 江苏科技大学学报(自然科学版), 2017, 31(5): 646-649. |
| [8] |
熊小青, 何佳益, 于海, 等. 中型豪华游船直立艏型线设计和优化研究[J]. 中国造船, 2019, 60(1): 88-96. |
| [9] |
LAEKENBY H. On the systematic geometrical variation of ship forms[J]. RINA Transaction, 1950, 92: 289-315. |
| [10] |
THOMAS W S, SCOTT R P. Free-form deformation of solid geometric models[J]. ACM SIGGRAPH Computer Graphics, 1986, 20(4): 151-160. DOI:10.1145/15886.15903 |
| [11] |
何佳益, 封培元, 沈兴荣, 等. 兼顾静水阻力和波浪增阻的船舶型线优化[C]// 第十四届全国水动力学学术会议暨第二十八届全国水动力学研讨会文集(下册), 2017.
|
 2024, Vol. 46
2024, Vol. 46
