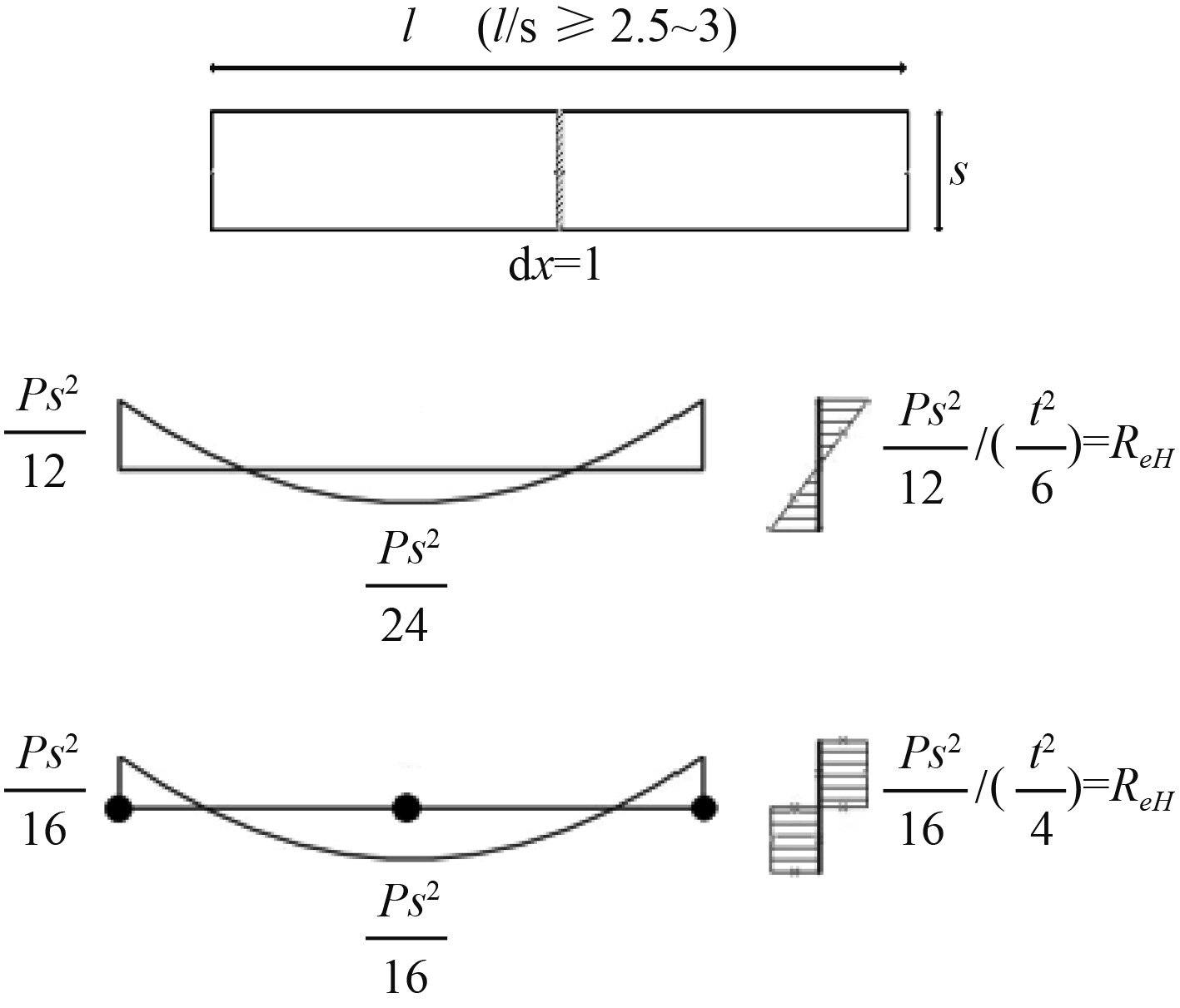
船体结构设计过程中,板厚的合理选取是结构重量控制的重要因素。共同规范在其技术背景文件[1-2]中给出了简化的力学模型,认为船体基本板格由骨材支撑,承受船体梁总弯曲引起的面内力和海水和货物引起的侧向压力。其板格局部强度评估模型是基于经典的板条梁理论,即在板格中心沿长边选取单位宽度为l(mm)、高度为t(mm)、跨长为s(mm)的板条梁,不同失效模式的梁端剖面应力分布如图1所示。
|
图 1 板条梁弹性和塑性失效模式对比图 Fig. 1 Comparison of elastic and plastic failure modes of slatted beam |
假定板格长宽比不小于2.5~3,板条梁两端刚性固定,均布压力为P(kN/m2)。若以弹性失效作为控制条件,在板条梁的两端形成最大弯矩,板的上下表面发生屈服,则板厚要求如式(1)所示,参考LR舰船规范[3-4]。若以塑性失效作为控制条件,在板条梁的两端和中点先后出现3个塑性铰,则板厚要求如式(2)所示,参考DNVGL民船规范[5]。2套规范体系下,板格局部强度校核公式在基本形式上相差
| $ {t}_{r}=0.0224s\sqrt{\frac{P}{{R}_{eH}}},$ | (1) |
| $ {t}_{r}=0.0158s\sqrt{\frac{P}{{R}_{eH}}}。$ | (2) |
式中:s为骨材间距;P为板格承受的侧向压力;ReH为板材的屈服极限,MPa。
共同规范结合国际修造船质量控制标准[6],采用了塑性变形控制模式,引入板格侧向弯曲许用应力折减系数
| $ {t}_{r}=0.0158s\sqrt{\frac{P}{{C}_{a}{R}_{eH}}}。$ | (3) |
式中:
以往船体板格强度的研究,大多是针对面内力[7]或侧向力[8]单独作用情况,缺少联合应力对塑性变形影响的分析。本文采用非线性有限元方法,考虑板格面内应力,分析规范中侧向许用应力折减系数的拟合方法,并与共同规范校核公式中的折减曲线进行对比。再结合设计经验,针对舰船上典型的高强度、小间距的薄板格结构形式进行了总纵应力折减方法研究,可为舰船纵骨架式板的局部强度评估提供参考。
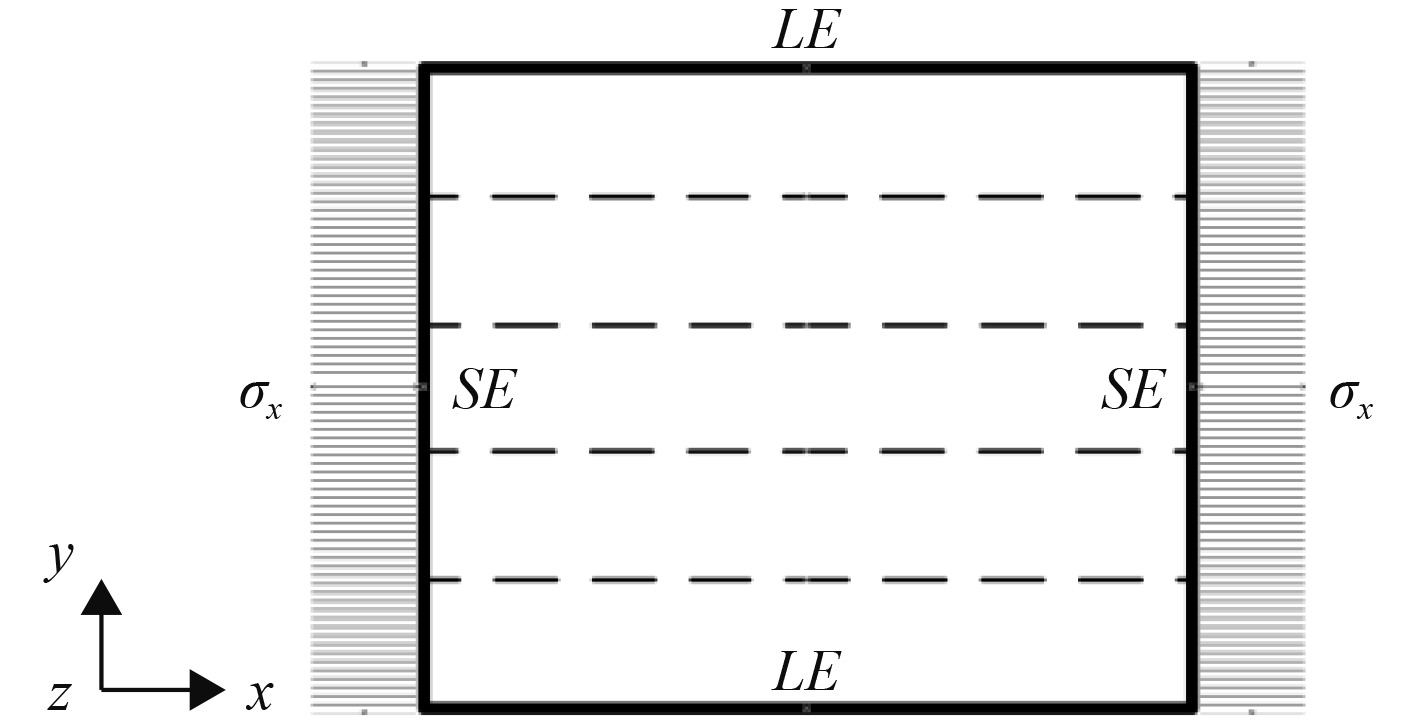
1 许用应力折减系数分析 1.1 力学简化模型加筋板基础模型采用非线性有限元软件Abaqus建立,虚线代表骨材,假定LE和SE被主要构件有效支撑,面内应力
|
图 2 模型边界和加载示意图 Fig. 2 Illustration of model boundary and loading pattern |
出于保守考虑,计算和拟合过程中均假定面内应力
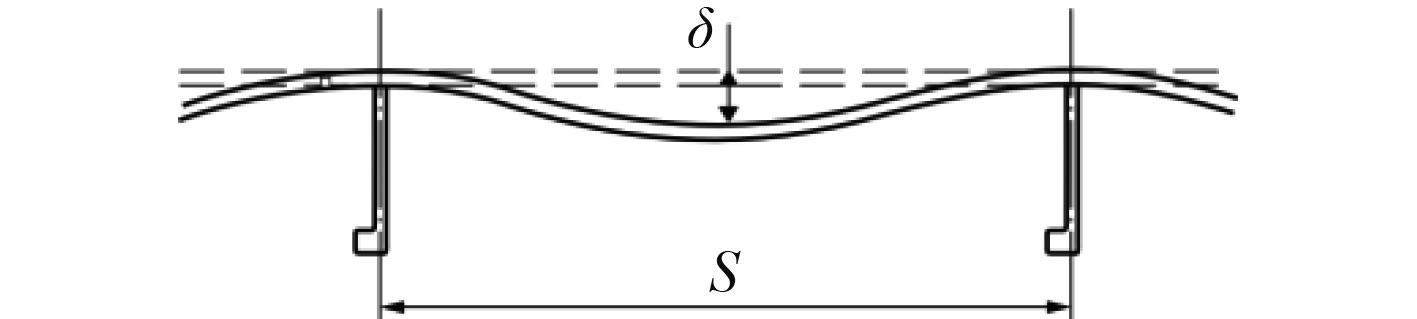
|
图 3 板的塑性变形示意图 Fig. 3 Illustration of panel plastic deformation |
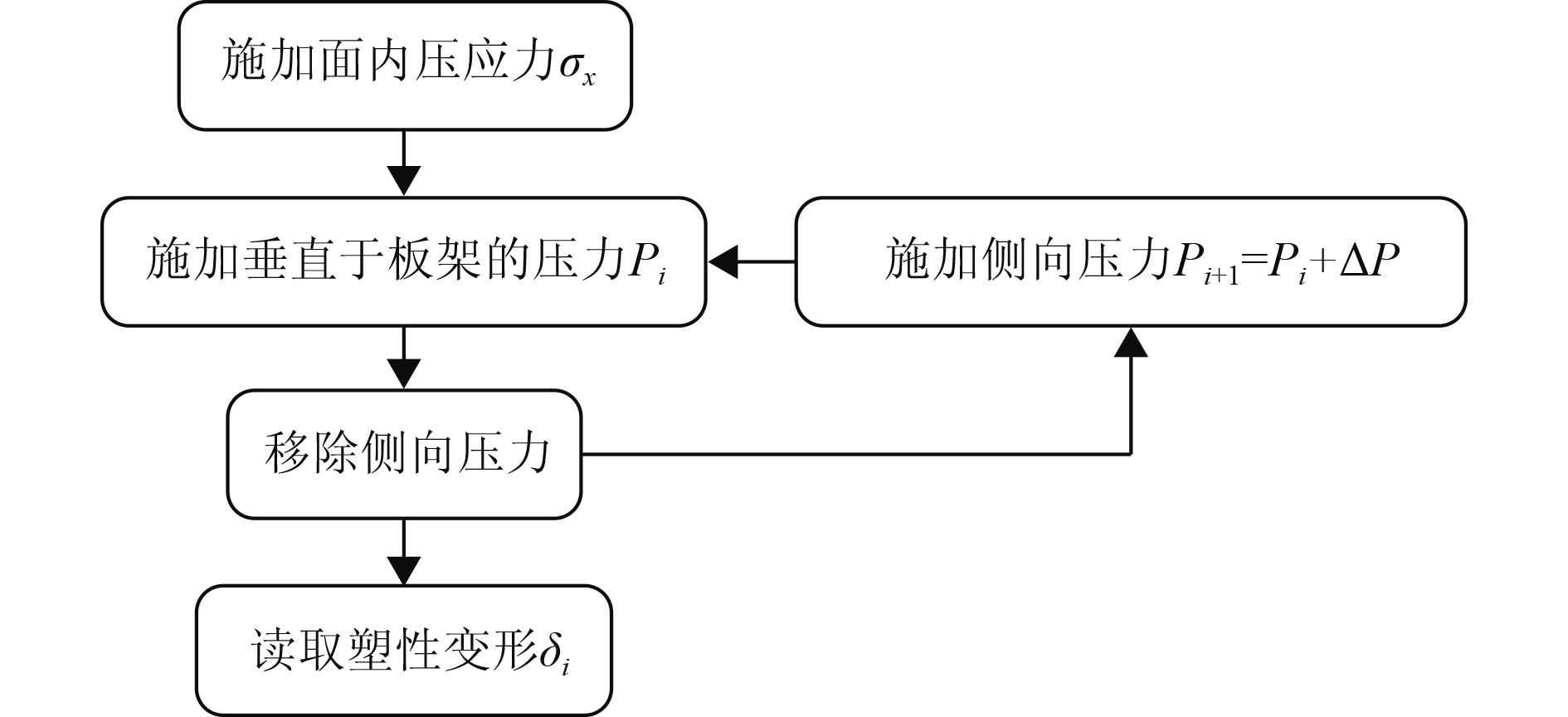
|
图 4 塑性变形计算流程图 Fig. 4 Flow diagram of deformation calculation |
对于静态压力、晃荡压力以及回归周期短的功能性载荷(AC-S),共同规范的塑性变形控制衡准为

|
图 5 许用侧向压力插值示意图 Fig. 5 Illustration of interpolation for permissible pressure |
式(4)可由共同规范的公式(3)转化而成,定义许用应力折减系数为
| $ {C}_{a\_FEM}=\frac{{P}_{FEM-\delta }}{{R}_{eH}}\cdot {\left(\frac{0.0158s}{t}\right)}^{2} 。$ | (4) |
参考共同规范背景文件提供的基本参数[2],建立板厚为13 mm,短边为800 mm,长边为4 800 mm,材料为HT32的加筋板有限元模型。该板架仅SE边界受压时,发生屈曲的临界应力约为
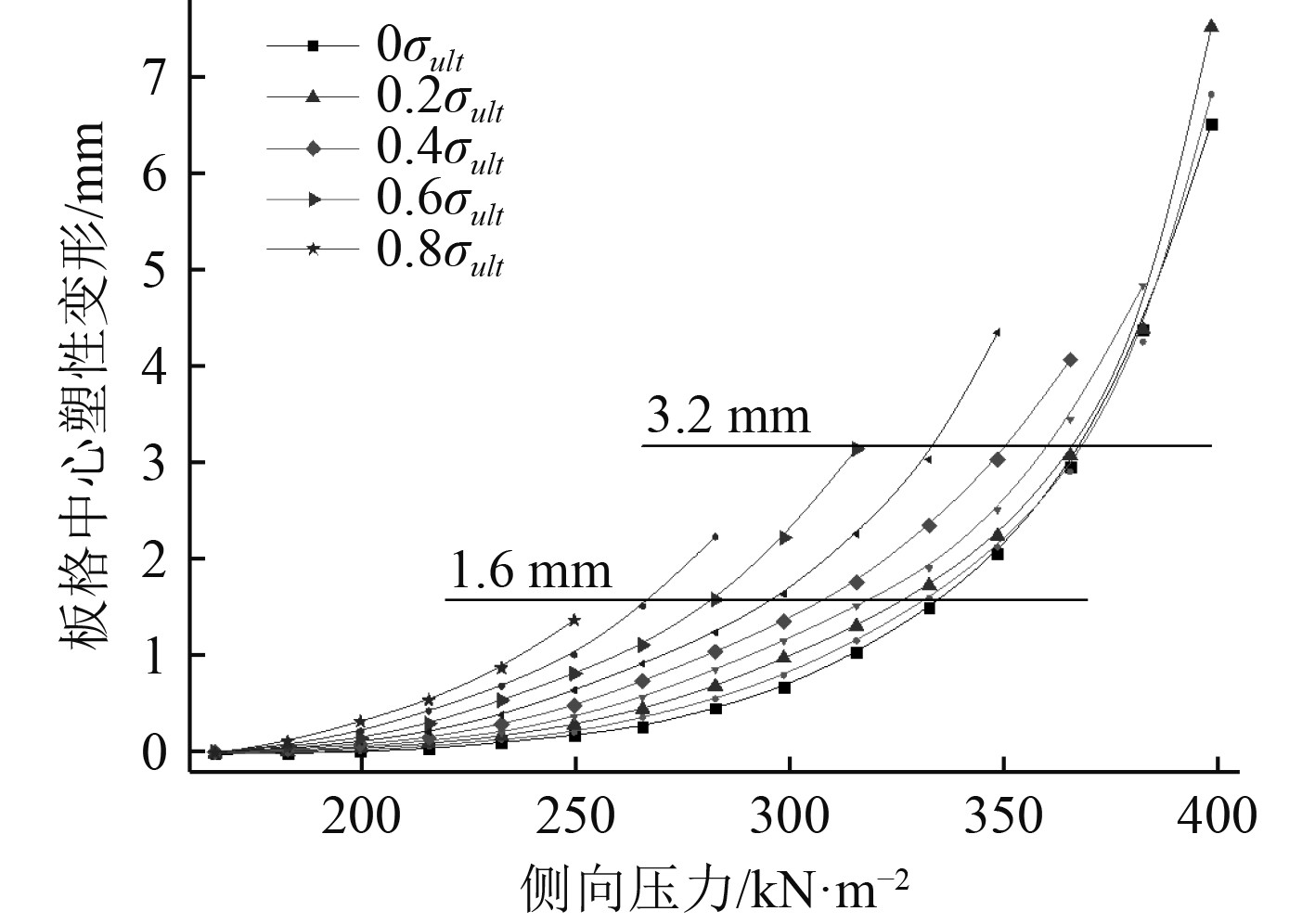
|
图 6 基于非线性有限元计算的许用侧向压力插值图 Fig. 6 Interpolation for permissible pressure based on nonlinear finite element calculation |
结合塑性变形控制衡准,即δ1=0.002s和δ2=0.004s,插值读取对应衡准和面内应力下的许用侧向压力PFEM-δ,并根据理论公式推导出折减系数Ca_FEM,插值和计算结果如表1所示。在相同总纵应力作用下,非线性有限元分析和共同规范给出的折减曲线对比如图7的上半端所示。圆形散点连线表示非线性有限元插值推导结果,方形散点连线为共同规范给定公式的计算结果。
|
|
表 1 基于非线性有限元计算的许用应力折减系数 Tab.1 Reduction factor of permissible stress based on nonlinear finite element calculation |
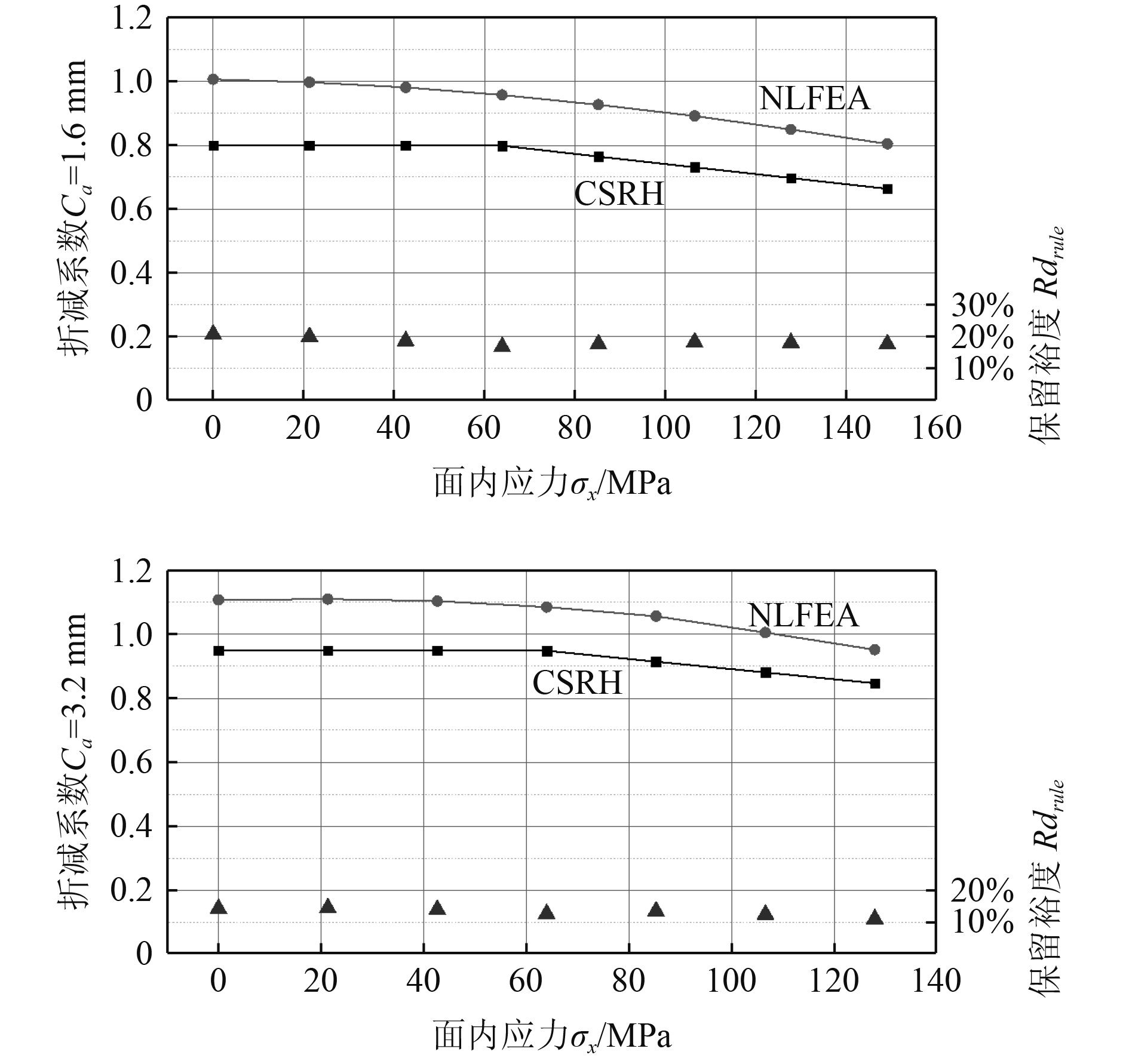
|
图 7 非线性有限元分析和共同规范的折减曲线对比图 Fig. 7 Comparison of reduction factor for nonlinear finite element calculation and rule formula |
对比2种控制衡准下的折减曲线,变化趋势吻合良好。共同规范选取的折减系数小于非线性有限元的分析值,为实船设计留出了一定的安全裕度。定义i为不同面内力所对应的计算点,Ca-FEM(i)和Ca-rule(i)分别为该计算点折减系数的理论推导值和规范选取值。2组衡准下,各计算点,处保留裕度基本持平且稳定性良好,如图7下半端三角形散点所示。求取所有计算点保留裕度的平均值,对于准静态的AC-S(
| $ R{d}_{rule}=\frac{1}{n}{\sum }_{i=1}^{n}\frac{{C}_{a-FEM}\left(i\right)-{C}_{a-rule}\left(i\right)}{{C}_{a-FEM}\left(i\right)}。$ | (5) |
英国LR舰船规范根据船长、排水量和肩负任务使命的不同,将入级舰船分为NS1、NS2和NS3三类。如英劳规范所述[3],使用船级符号NS1的舰船船长在140 m以上,排水量在10000 t以上;船级符号NS2的舰船船长在70~140 m,排水量在1300~20000 t;船级符号NS3的舰船排水量在1500 t以下。由于大型重要舰船通常不宜入级商用的船级社,实际上选择NS3船级符号的中小型舰船建造数量最多、运营分布最广。
结构主规范的总布置章节指出,NS3船级符号的舰船主要横向构件间距不得大于1.5 m。由于长边长度通常对板格强度影响不大,本文样本模型板格长边固定取为1 500 mm。根据设计经验,板格短边长度通常为长边的1/4左右,考虑一定变异性,样本模型板格短边取为350 mm、375 mm和400 mm,板厚取为6 mm、8 mm和10mm。相比造价因素,舰船更关注重量控制,很少选择普通钢建造,因此样本模型材料固定取为高强度钢
|
|
表 2 样本模型主要参数 Tab.2 Main parameters of the sample model |
利用共同规范公式,首先假定
海上航行的舰船主要承受波浪引起的船体梁载荷和海水侧向压力载荷。与民用船型不同,舰船规范中对腐蚀余量没有严格的规定。因此本文出于保守考虑,对舰船AC-SD工况选用
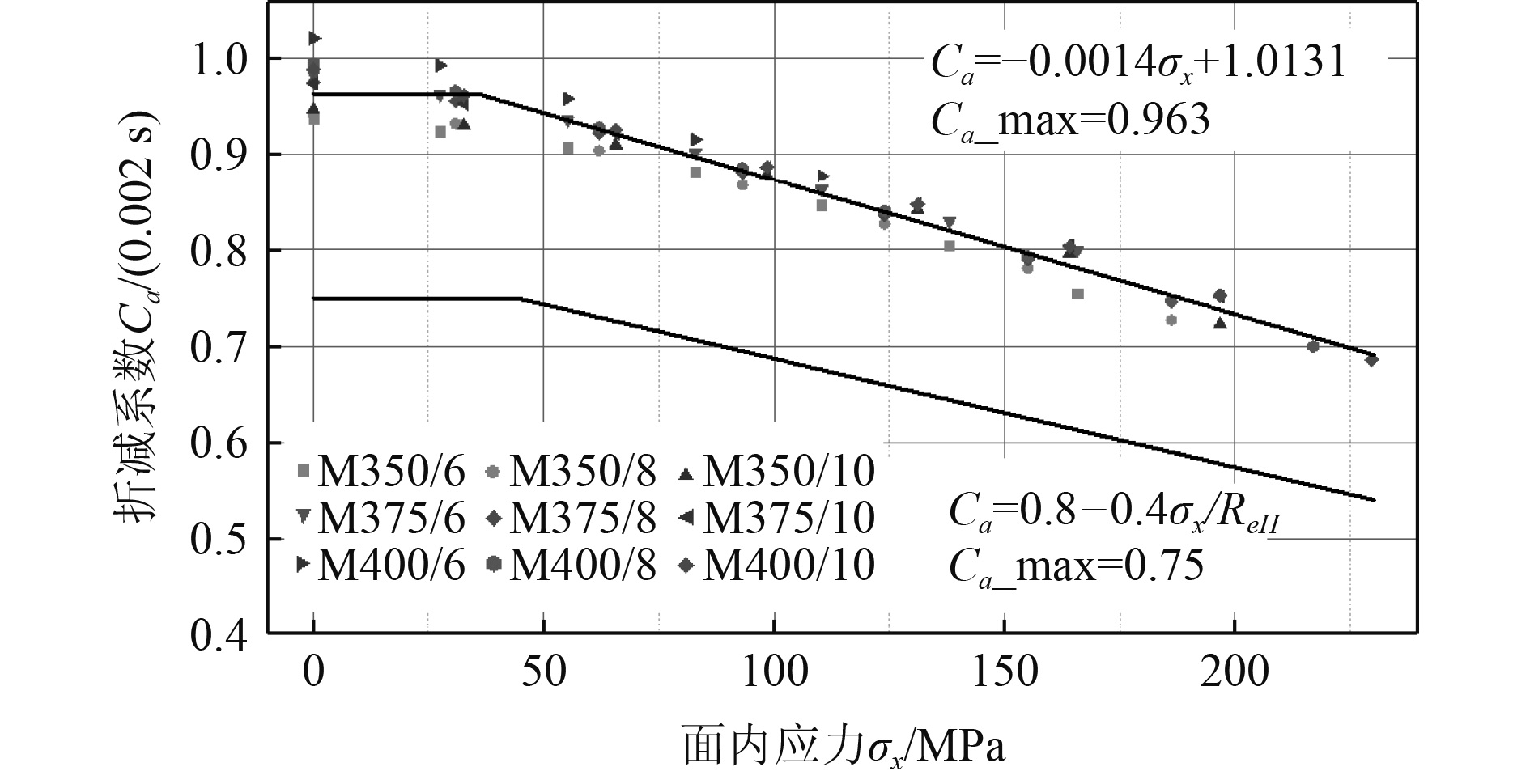
|
图 8 基于非线性有限元分析的折减曲线图 Fig. 8 Fitted curve of reduction factor based on nonlinear finite element calculation |
| $ {C}_{a}=1.0131-0.0014{\sigma }_{x},{C}_{a-{\mathrm{max}}}=0.963 ,$ | (6) |
| $ {C}_{a}=0.8-0.4\frac{\left|{\sigma }_{x}\right|}{{R}_{eH}}\text{,} {C}_{a-{\mathrm{max}}}=0.75。$ | (7) |
本文采用非线性有限元方法,通过控制板格中心塑性变形,分析了船体板格在不同总纵面内应力作用下,同时承受来自海水和货物侧向压力时的板格许用应力折减系数拟合方法,并得到如下结论:
1)通过折减曲线对比分析,基于塑性变形控制的折减系数拟合方法,能够较好地还原共同规范板格校核公式。不同面内应力下的插值计算结果显示,对于板格大、尺寸厚的民用船型,共同规范在AC-S和AC-SD工况下的保留裕度分别约为18%和13%。
2)针对水面舰船的典型的密加筋结构,基于63组有限元数值计算,采取同样的折减系数分析方法,得到了不同面内应力和构件尺寸下的折减系数。基于上述散点给出的拟合曲线与共同规范公式存在差异,可见民船公式不能直接应用于舰船设计。本文研究结果对符合NS3要求的纵骨架式舰船结构校核评估具有一定参考价值。
| [1] |
IACS. Common structural rules for bulk carriers and oil tankers[S]. London: IACS, 2019.1.
|
| [2] |
IACS. CSR-H technical background of rule reference[S]. London: IACS, 2014.1.
|
| [3] |
LR. Rules and regulations for the classification of naval ships[S]. London: LR, 2018.1.
|
| [4] |
LR. Rules and regulations for the classification of special service craft[S]. London: LR, 2018.1.
|
| [5] |
DNV GL. Rules for classification of Ships[S]. Oslo: DNV, 2019.1.
|
| [6] |
IACS. Shipbuilding and repair quality standard, Rev. 7[S]. London: IACS, 2013.6.
|
| [7] |
路春晖, 师桂杰, 彭文科, 等. 邮轮船体的总纵弯曲强度分析[J]. 船舶与海洋工程, 2019, 35(1): 1-7. |
| [8] |
赵超, 蔡伟, 朱凌, 等. 不同位置处多次轮印载荷作用下甲板板格塑性变形评估方法[J]. 船舶力学, 2022, 26(7): 1030-1038. DOI:10.3969/j.issn.1007-7294.2022.07.009 |
 2024, Vol. 46
2024, Vol. 46
