2. 浙江东海岸船业有限公司,浙江 舟山 316123
2. Zhejiang East Coast Shipping Industry Co., Ltd., Zhoushan 316123, China
液舱晃荡常见于造船业和海洋工程领域,是一种复杂的液体流动现象,具有很强的非线性和随机性[1]。晃荡会对舱壁产生冲击力,不仅会损坏结构,还会影响船舶稳定性。尤其是当晃荡频率接近液舱自身的固有频率时,晃荡会变得更为剧烈,巨大的冲击将对船舶的安全构成极大的危害[2]。
早期,学者们研究晃荡问题经常采用的是传统的网格法。但是当处理一些具有大变形的自由表面流动时,传统的网格法无法对大变形精确描述,仿真结果往往以失败告终[3]。即便某些网格法可以通过自由表面捕获法或者进一步完善大变形区域中的网格2种方式来克服这一问题,但同时又会产生更为复杂的算法且需要更长的计算时间。
MPS方法是一种基于拉格朗日粒子的无网格方法,最早是由日本学者Koshizuka等[4]于1995年提出来的。它采用估计修正法来求解不可压缩粘性流的控制方程,可以有效地避免对流项离散引起的数值差异[5 − 8]。与传统的网格方法相比,MPS法在解决变形较大的自由表面流动问题方面具有更大的优势。
在液舱晃荡问题研究中,许多学者均倾向于通过添加挡板来增强抑制液体晃荡的效果,鉴于此,本文在基于MPS方法的基础上,将水平挡板对称地放置在矩形液舱底部,通过改变对称挡板的宽度和高度,研究抑制液舱晃荡的规律。
1 理论方法 1.1 控制方程对于不可压缩的粘性流体,MPS的控制方程包括连续方程和N-S方程,具体如下:
| $ \left\{ \begin{aligned} & \frac{{\rm{d}}\rho }{{\rm{d}}t} = \frac{\partial \rho }{\partial t} + \nabla(\rho v) = 0,\\ & \frac{{\rm{d}}v}{{\rm{d}}t} = f - \frac{1}{\rho }\nabla p + \upsilon \nabla^2 v。\end{aligned} \right. $ | (1) |
式中:v为流场速度矢量;f为流体的单位质量力;p为流体的压力;ρ为流体密度;υ为运动粘性系数。
在MPS方法中,核函数主要用于平衡粒子之间的相互作用。本文采用MPS方法中使用最广泛的核函数,其表达式如下:
| $ w(r) = \left\{ \begin{gathered} \frac{{{r_e}}}{r} - 1,{r < {r_e}},\\ 0,{r > {r_e}}。\\ \end{gathered} \right.$ | (2) |
在MPS方法中,粒子数密度即核函数及其周围粒子核函数的控制域中的粒子累积,表达式如下:
| $ {\left\langle n \right\rangle _i} = \sum\limits_{j = 1}^N w\left(\left| {r_i} - {{r_j}} \right| \right)。$ | (3) |
式中:N为相邻粒子的数量;ri和rj为粒子i和粒子j的位置矢量。
用以描述权重函数离散化的Gradient运算符和Laplacian运算符的模型,表达式如下:
| $ {\left\langle {\nabla \varphi } \right\rangle _i} = \frac{d}{{{n^0}}}\sum\limits_{j = i} \left[({\varphi _j} - {{\hat \varphi }_i} )\frac{{({r_j} - {r_i})}}{{{{\left| {{r_j} - {r_i}} \right|}^2}}}w\left(\left| {{r_j} - {r_i}} \right|\right)\right],$ | (4) |
| $ {\left\langle {{\nabla ^{\text{2}}}\varphi } \right\rangle _i} = \frac{{2d}}{{{n^0}\lambda }}\sum\limits_{j \ne i}^N \left[({\varphi _j} - {\varphi _i} )w\left(\left| {{r_j} - {r_i}} \right|\right)\right] ,$ | (5) |
| $ {\left\langle {\nabla \varphi } \right\rangle _i} = \frac{d}{{{n^0}}}\sum\limits_{j = i} \left[({\varphi _j} - {{\hat \varphi }_i} )\frac{{({r_j} - {r_i})}}{{{{\left| {{r_j} - {r_i}} \right|}^2}}}w\left(\left| {{r_j} - {r_i}} \right|\right)\right],$ | (6) |
| $ {\left\langle {{\nabla ^{\text{2}}}\varphi } \right\rangle _i} = \frac{{2d}}{{{n^0}\lambda }}\sum\limits_{j \ne i}^N \left[({\varphi _j} - {\varphi _i} )w\left(\left| {{r_j} - {r_i}} \right|\right)\right] 。$ | (7) |
式中:
另外,
| $ \lambda = \frac{{\displaystyle\int\limits_V {w(r){r^2}{\mathrm{d}}V} }}{{\displaystyle\int\limits_V {w(r){\mathrm{d}}V} }} \cong \frac{{\displaystyle\sum\limits_{j \ne i}^N {[W(\left| {{r_j} - {r_i}} \right|} ){{\left| {{r_j} - {r_i}} \right|}^2}]}}{{\displaystyle\sum\limits_{j \ne i}^N {W(\left| {{r_j} - {r_i}} \right|)} }} 。$ | (8) |
边界条件包含自由表面边界条件和实体壁边界条件。
相邻粒子的数量和自由表面粒子的粒子数密度均小于流体内部粒子的相应值[9],因此自由表面粒子的判断条件为:
| $ {N_i} \leqslant \beta {N^0}。$ | (9) |
式中:Ni为控制域中相邻粒子的数量;N0为流体内部粒子的控制域中相邻粒子的数量;β为一个小于1.0的参数,通常选取β=0.97。
最靠近流体粒子的粒子层是流体边界粒子,而且这些粒子还参与泊松方程中的压力计算。在这层粒子之外的2层,则是固体壁粒子,除了可以避免流体粒子被误判之外,这2层粒子还可以有效地防止流体粒子渗入固体壁。施加在流体粒子上的力可以近似表达为:
| $ f(r) = D\left[{\left(\frac{{{r_0}}}{r}\right)^{{p_1}}} - {\left(\frac{{{r_0}}}{r}\right)^{{p_2}}}\right]\frac{r}{{{r^2}}},r \gt {r_0}。$ | (10) |
式中:r0为初始粒子距离L ;D=5gh,h为水柱高度;指数 p1和 p2 分别取值4和2 。
1.3 MPS计算流程1)引入中间速度v*和中间位移r*,并分两步求解N-S方程。可以使用以下表达式:
| $ {r^*} = {r^n} + \Delta t\cdot {v^*}。$ | (11) |
2)确定自由表面粒子并定义压力为0 Pa。
3)计算泊松方程以获得下一个压力值。
4)根据粒子的压力分布情况修改中间速度v*和中间位移r*。
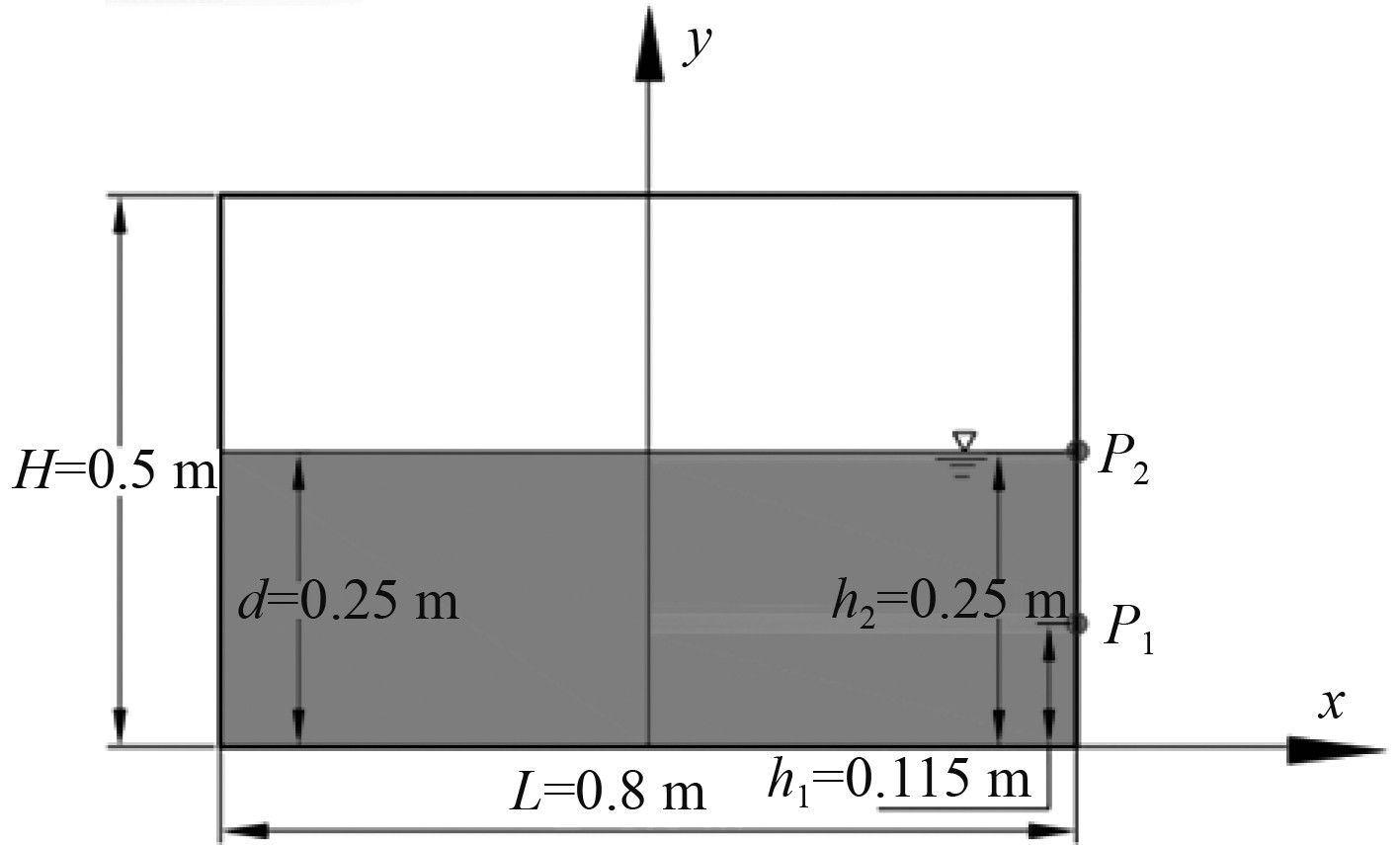
2 数值模型的验证 2.1 数值模型采用MPS方法研究对称水平挡板液舱晃荡,首先需要建立液舱晃荡模型。图1为二维矩形液舱的验证模型,液舱的宽度L= 800 mm,高度H= 500 mm,水深 d=250 mm,充水率为50%[10]。在二维矩形液舱右侧壁面上设置2个压力监测点P1和P2,分别距离液舱底部距离h1=115 mm和h2=250 mm。P1点和P2点的选择具有代表性和普遍性,其中P2点设置在液面上,能够模拟出晃荡过程中监测点在与不在液体中的压力,P1点设置在液体中,距离液舱底部距离h1=115 mm,具有普遍性,能够模拟晃荡过程中舱壁所受到的抨击压力。
|
图 1 矩形验证模型示意图 Fig. 1 Schematic diagram of rectangular verification model |
矩形液舱在外部激励作用下做水平方向上的简谐运动,运动方程为:
| $ x = - A\cos (\omega t) 。$ | (12) |
式中,振幅A=20 mm,激励频率
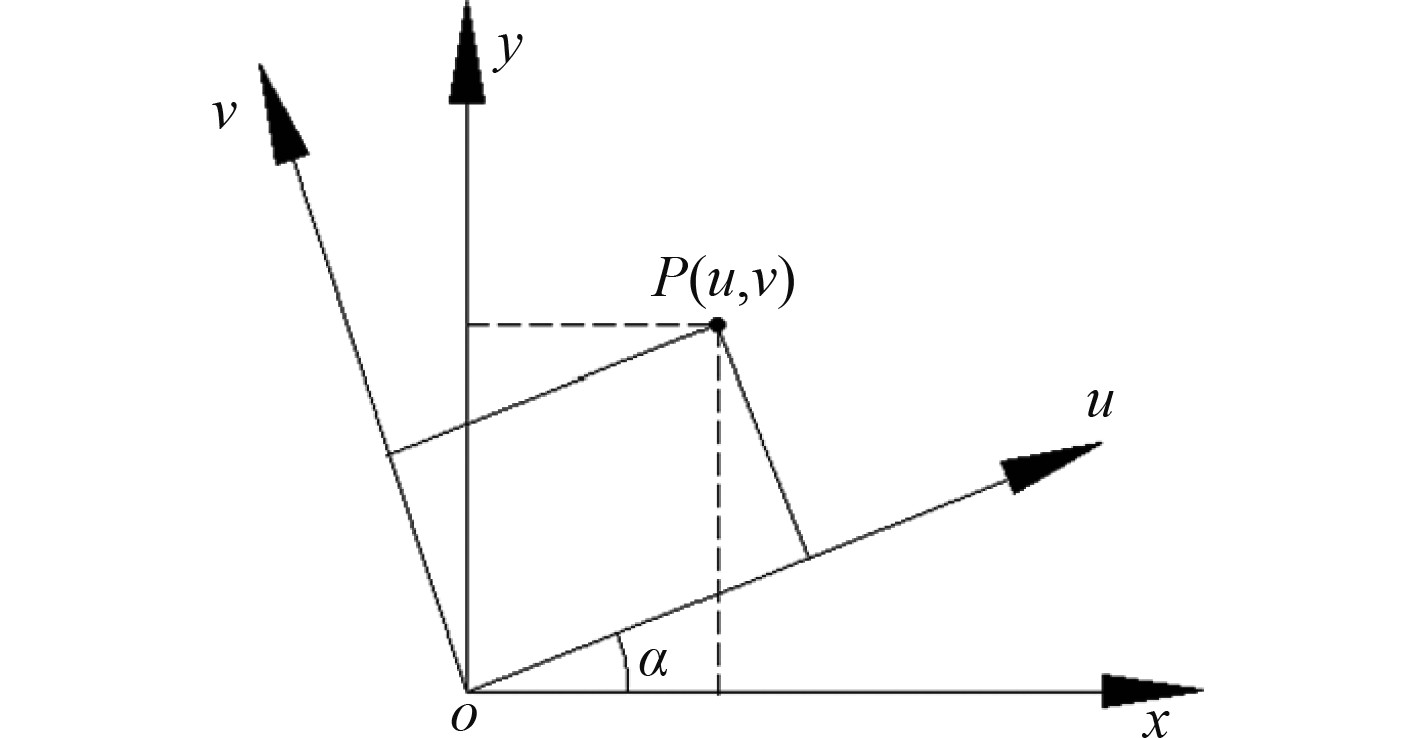
由于在液舱晃荡问题中需要用到坐标转换,在此先介绍二维坐标转换的相关理论。如图2所示,oxy为原直角坐标系,ouv为直角坐标系绕oxy绕坐标原点
|
图 2 坐标转换示意图 Fig. 2 Illustration of coordinate transformation |
| $ \left[\begin{array}{cc}x\\y\end{array}\right]=\left[\begin{array}{cc}\cos\alpha&-\sin \alpha\\ \sin \alpha&\cos\alpha\end{array}\right]\cdot \left[\begin{array}{cc}u\\v\end{array}\right]。$ | (13) |
如果ouv坐标系绕坐标原点o旋转α角后,然后按照向量(a,b)进行平移,即ouv坐标系新的原点
| $ \left[\begin{array}{cc}x\\y\end{array}\right]=\left[\begin{array}{cc}a\\b\end{array}\right]+\left[\begin{array}{cc}\cos\alpha&-\sin \alpha\\ \sin \alpha&\cos\alpha\end{array}\right]\cdot \left[\begin{array}{cc}v\\s\end{array}\right]。$ | (14) |
对于本文的液舱晃荡离散模型,其坐标原点位于模型的左下方,如果液舱离散模型的中心点(横摇的中心点)坐标为(a,b),则在数值模拟中的任意时刻,在液舱离散时的坐标系下粒子的坐标为:
| $ \left[\begin{array}{cc}x\\y\end{array}\right]=\left[\begin{array}{cc}a\\b\end{array}\right]+\left[\begin{array}{cc}\cos\alpha&-\sin \alpha\\ \sin \alpha&\cos\alpha\end{array}\right]\cdot \left[\begin{array}{cc}u-a\\v-b\end{array}\right]。$ | (15) |
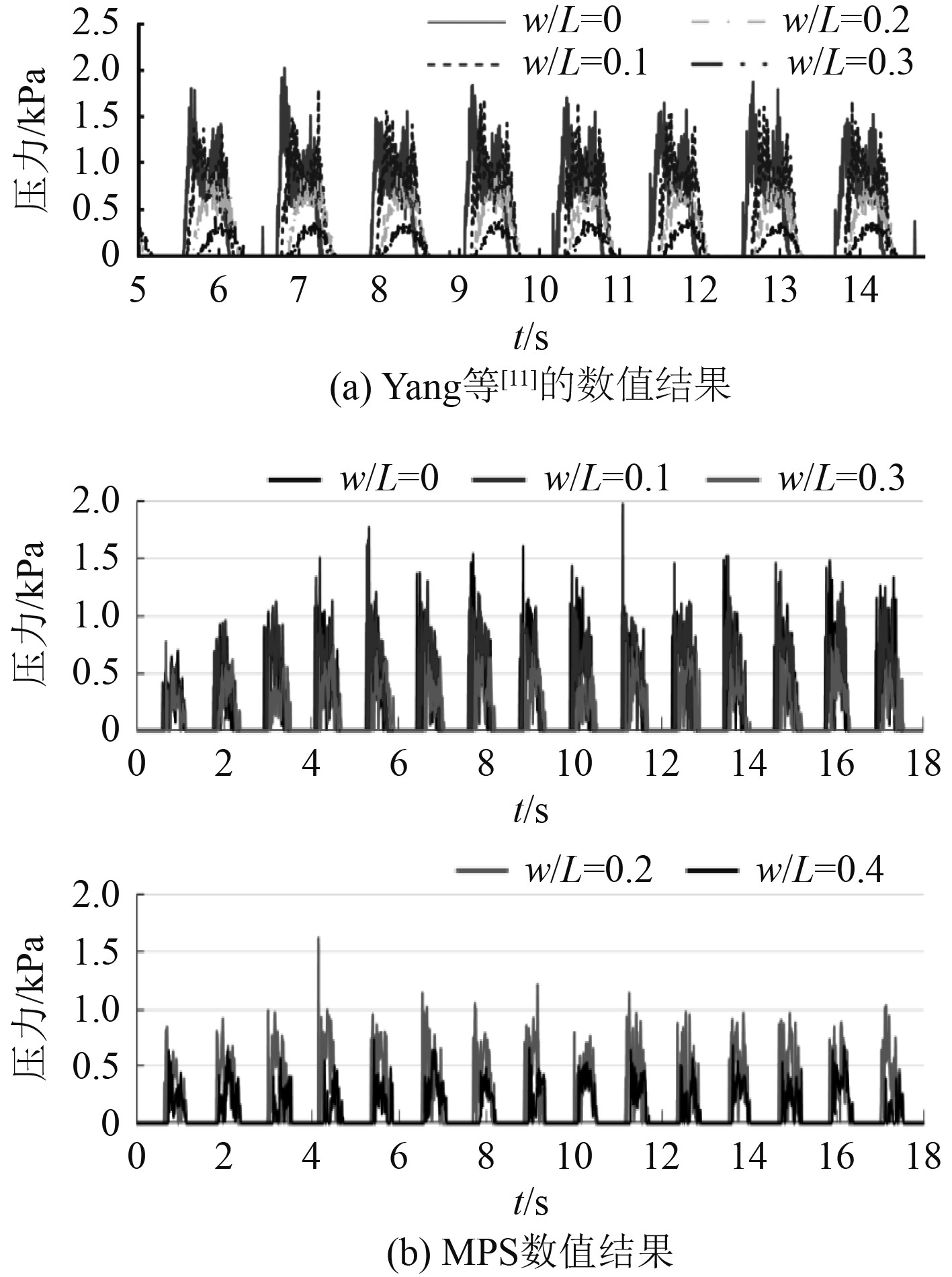
建立液舱晃荡模型以及给出坐标转换后需要验证MPS方法在研究液舱晃荡现象中的可靠性与准确性。图3为不同挡板宽度下,P2点所受到的冲击压力的大小,在不同时间点的变化。图3(a)为Yang等[11]的数值模拟结果,图3(b)为采用MPS方法的分析结果。可知,随着挡板宽度的增加,压力曲线呈周期性变化,相位略有延迟。当挡板宽度w/L=0(即没有挡板的情况)时,冲击压力的最大值可达到2 kPa。虽然在w/L=0.1时,冲击压力最大值也接近2 kPa,但平均压力变小。在w/L=0.2的情况下,平均压力降低多达50%,大约为1 kPa。显然,当宽度增加到w/L=0.3时,平均压力降低到0.5 kPa,曲线呈凸形。综上所述,MPS方法的数值结果与Yang等[11]的结论具有良好的一致性。因此,可以说MPS方法对于解决液舱晃荡问题有效。
|
图 3 挡板高度为h/d=0.5的压力-时间曲线 Fig. 3 The time history of the pressure with the baffle height of h/d = 0.5 |
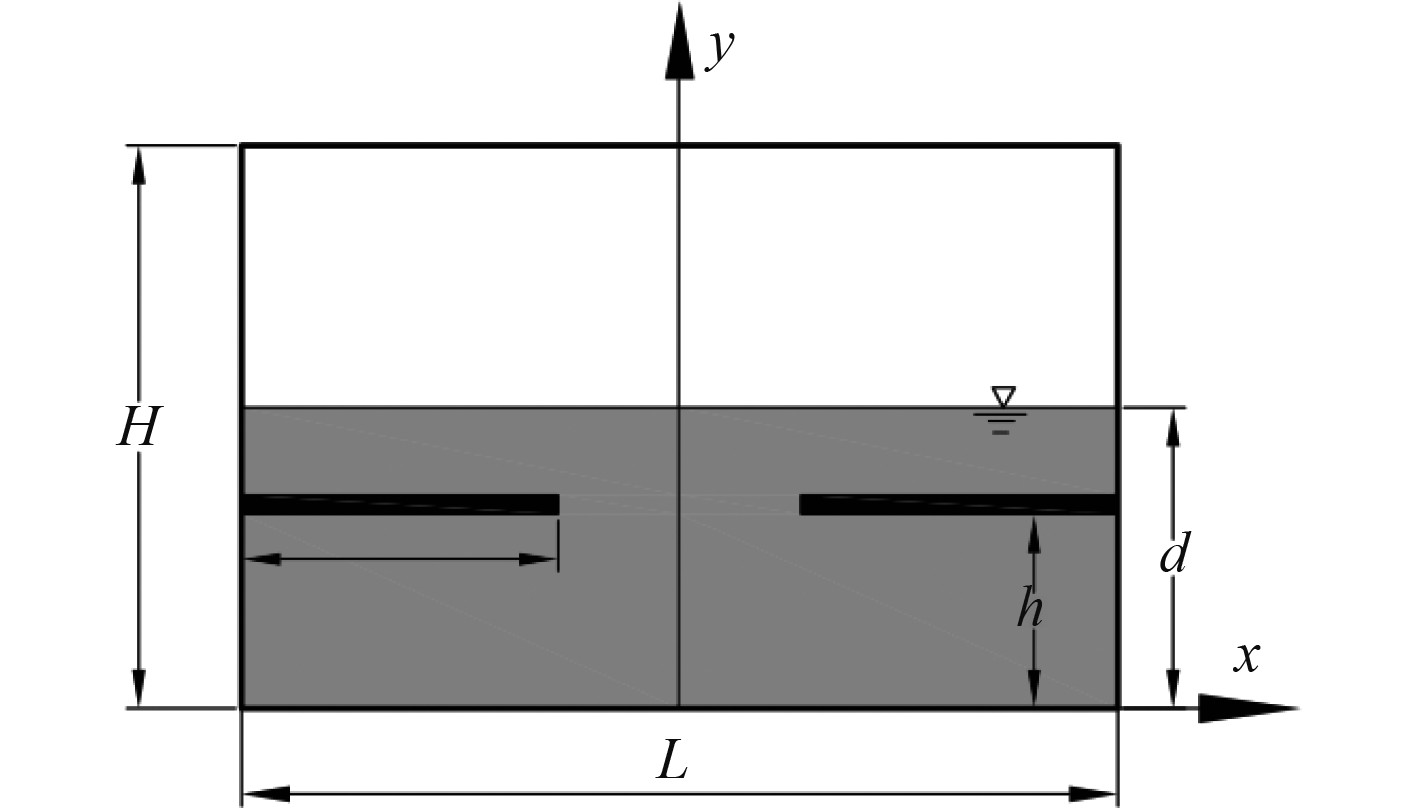
基于模型的验证,将运用MPS方法研究在二维矩形液舱中添加对称水平挡板的晃荡现象。在液舱中加入对称水平挡板,如图4所示,h为挡板的高度,w为挡板的宽度,在下文中用挡板的相对高度和相对宽度来表示挡板的位置,相对高度即是挡板高度与水深之比,相对宽度即是挡板宽度与液舱宽度之比,挡板的相对高度为h/d,相对宽度为w/h。在矩形w/L液舱的右端壁面上设置2个压力监测点P1和P2,分别距离液舱底部距离为h1=115 mm和h2=250 mm。
|
图 4 液舱晃荡模型 Fig. 4 Sloshing model of liquid tank |
运用MPS方法进行数值模拟需采用粒子化的模型,在本文中运用Matlab编程生成粒子化模型。研究对称水平挡板对液舱晃荡的减晃效果时选用12种工况,如表1所示。
|
|
表 1 工况明细 Tab.1 Details of working conditions |
上述对称水平挡板的粒子化模型,共12种情况,在此模型基础上运用MPS方法进行数值模拟,将得出的数据进行后期处理,分别为流场分布、自由液面变形和各压力监测点的压力曲线。
3.1 流场分布图5为不同高度和不同宽度时的液体流场变化情况。总体而言,在上半周期液体从右边运动至左边,在后半周期液体运动方向相反。在没有挡板时流场分布较为均匀,不产生涡流现象,当设置挡板后速度分布产生较大的变化,挡板的尖端产生涡流,分离了部分流场。随着挡板的宽度越来越大,挡板有将二维矩形液舱分割成上下两半的趋势,流场的分布也在变化,液体在爬壁时挡板上方的流场相比没有任何挡板时的流场要小很多,只有在靠近壁面时有流场。由图5(c)和图5(d)可知,在挡板下方的流场则非常大,这也是加了挡板后可以减晃的原因,挡板的存在分割了流场。

|
图 5 流场分布 Fig. 5 Flow field distribution |
通过对晃荡过程中流场分析能够清晰地看出液体在液舱内的走势和晃荡过程中流场分布,从流场的分布可看出晃荡的一些现象。同时自由液面变形也在一定程度上反映出一些晃荡现象,图6为自由液面变形情况,其由可视化与后期处理软件EnSight处理完善。

|
图 6 自由液面变形 Fig. 6 Free surface deformation |
图6为在液舱晃荡过程中加入不同高度和不同宽度挡板的自由液面变形和压力分布情况。图6(a)中没有加入挡板时的自由液面变形较大,在晃荡过程中自由液面能够爬到液舱壁面很大的高度,自由液面中蕴藏着很大的能量,并有冲高到液舱顶部的趋势,晃荡过程中流体的流动出现非线性。图6(b)~图6(d)是在液舱中加入不同参数的对称水平挡板,在液舱中加入对称水平挡板后可以很明显地看出随着挡板的高度越来越高和宽度越来越宽,在晃荡过程中自由液面的起伏越来越小,自由液面的波形变得越来越平缓,当挡板的高度达到h/d=0.6挡板的宽度达到h/d=0.4时自由液面的起伏很小,变的非常平滑,基本上和水平面无差别。这是因为对称水平挡板阻止了液体的晃荡,导致在晃荡过程中液体的能量减小,故而不能到达液舱壁面很大的高度。从而得出结论,设置水平挡板对液舱的减晃具有很好的效果。挡板高度h/d≤0.4、挡板宽度w/L≤0.2时,减晃效果不是很理想。挡板高度h/d≥0.6、挡板宽度w/L≥0.4时,晃荡幅度极小,几乎达到饱和。
3.3 各压力监测点的压力曲线本文设计2种工况来详细研究水平挡板对液体晃荡现象的影响:一种是将挡板高度设置为特定的参数,分析不同挡板宽度产生的压强变化;另一种是将挡板宽度设定为特定的参数,分析不同挡板高度下的压强变化。
图7为控制挡板高度一定,给出P1点压力随挡板宽度变化的压力-时间曲线。图8为特定挡板宽度下P1点压力随挡板高度变化的压力-时间曲线。不难看出,在液体晃荡过程中,P1点的静压力为1 kPa,并随时间呈周期性变化。对于没有挡板的情况,压力最大值约为2 kPa。当挡板高度控制在h/d=0.6时,不同宽度下的压力曲线波动情况基本一致,而当h/d=0.5时,不同宽度下的压力曲线波动情况有很大区别。造成这一现象的原因是压力监测点P1设置的位置(115 mm)恰好低于挡板位置(125 mm),导致压力变得更小。

|
图 7 P1点压力随挡板宽度变化的时间曲线 Fig. 7 The time history of the pressure at P1 with different baffle widths |
如图8所示,水平挡板对墙体的冲击压力明显降低。而在无挡板的情况下,压力曲线峰值较大,以至于出现了双峰现象。设置挡板后,压力峰值大约减少60%,为1.4 kPa。当挡板宽度为w/L=0.4,高度h/d=0.5的情况下,平均压力低于1 kPa。除此之外,由图7和图8可知,随着挡板高度和宽度的增加,挡板对舱中液体的影响力也在增加。

|
图 8 P1点的压力随挡板高度变化的时间曲线 Fig. 8 The time history of the pressure at P1 with different baffle heights |
考虑当压力监测点离挡板非常近的时候,监测结果会更加明显有效,所以在P2设置监测点可以有效避免误差。
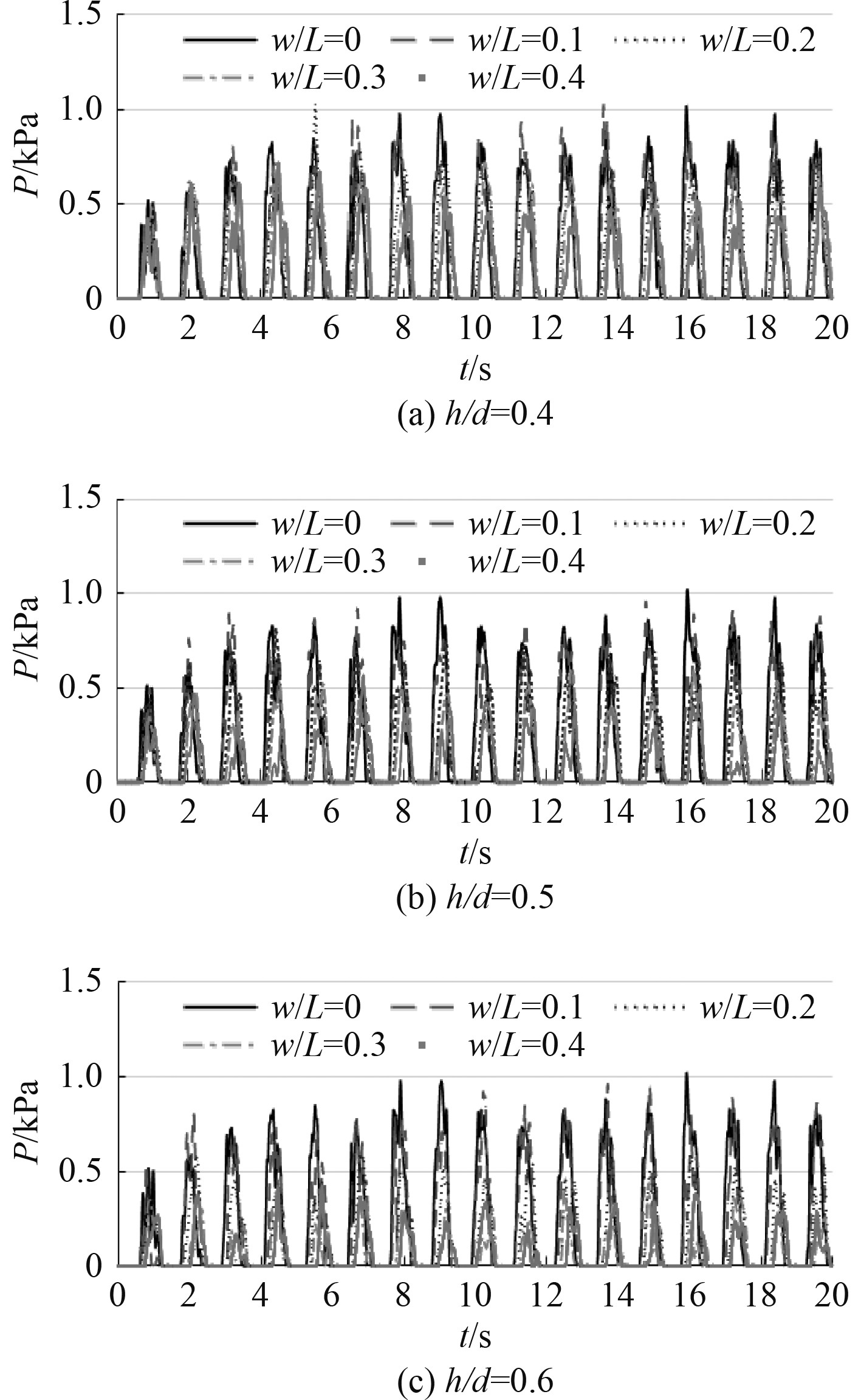
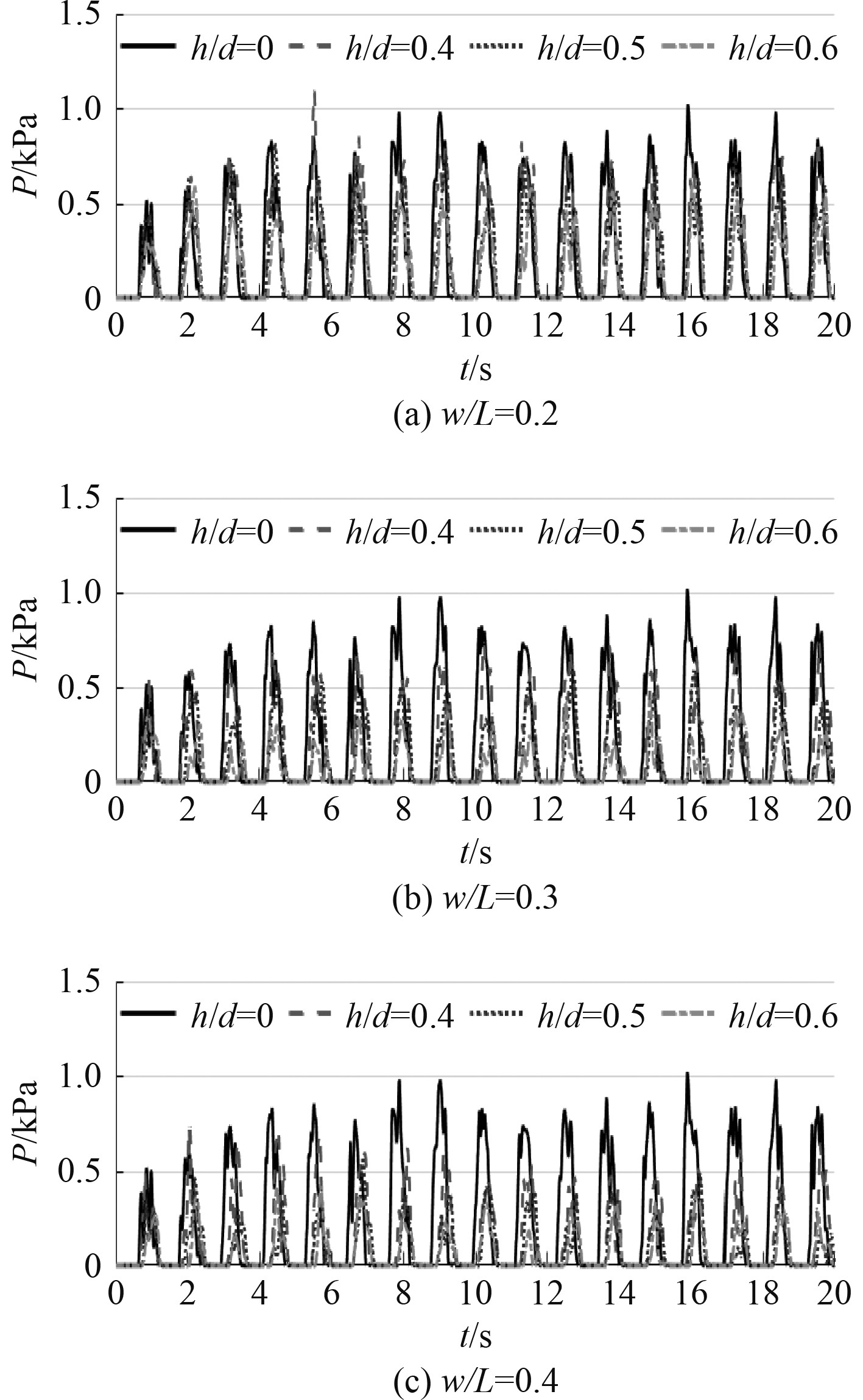
图9和图10为在液舱中设置不同高度和宽度的挡板时,相应P2点的压力变化曲线,其中静力值约为0.25 kPa。在h/d=0、w/L=0时的最大冲击压力约为1 kPa,而h/d=0.5、w/L=0.4时的最大冲击压力降到了0.7 kPa。当挡板设置为h/d=0.6、w/L=0.4时,最大冲击压力约为0.5 kPa,相对下降50%。此外,由于P2点高于P1点,可以明显看出P2点处的最小压力为0,这意味着在液舱晃荡过程中P2点有时高于水面。
|
图 9 P2点压力随时间和挡板宽度变化的曲线 Fig. 9 The time history of the pressure at P2 with different baffle widths |
|
图 10 P2点压力随时间和挡板高度变化的曲线 Fig. 10 The time history of the pressure at P2 with different baffle heights |
由图10可知,水平挡板的存在可以有效改善液舱晃荡的现象,P1点的压力值大约可以减少60%;同时点P2处的压力值下降约50%。当h/d=0.6和w/L=0.4时,自由液面几乎不存在晃荡。另外,随着挡板高度和宽度的增加,对称水平挡板对舱内流场的干扰在逐渐增大,最终解决了液体晃荡的问题。
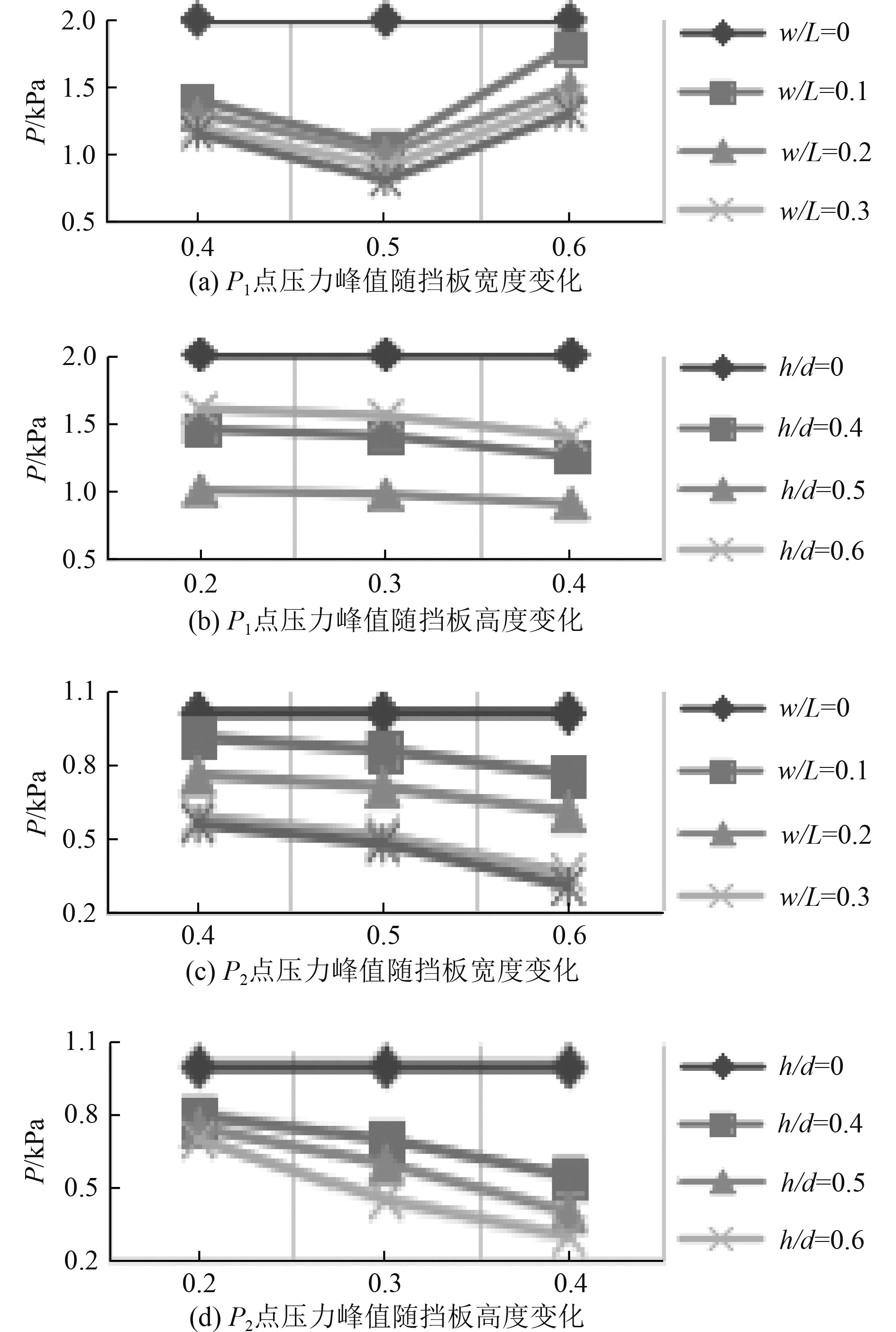
3.4 压力峰值随挡板宽度、高度变化分析本文首先建立二维液舱模型,在外部激励作用下做水平方向上的简谐运动,将数值模拟的结果与其他学者实验研究的结果作对比,验证方法的准确性和可靠性。在此基础上,在液舱中加入不同参数跟不同位置的对称水平挡板研究减晃机理,并在液舱右侧壁面上设置2个不同的压力监测点P1和P2,来检测液舱晃荡过程中压力的变化情况,同时研究的还有自由液面变形和流场分布。图11为P1和P2点的压力峰值随挡板变化情况。
|
图 11 P1、P2两点压力峰值变化曲线 Fig. 11 The variation curve of pressure peaks at P1 and P2 |
对比图11(a)和图11(c)可知,挡板宽度越大,监测点压力峰值越小,尤其是在没有挡板的情况下,压力峰值最大。P1点在有挡板的情况下,压力峰值呈现先减小后增大的趋势,4条曲线的变化情况一致,在h/d=0.5时,各条线的压力峰值都在最低的;不同的是,P2点在有挡板的时候,压力峰值随高度一直减小,且在h/d=0.5和h/d=0.6区间的减小幅度更大。
对比图11(b)和图11(d)可知,3种情况的峰值变化有很大区别。在图11(b)图中,h/d=0.4和h/d=0.6这2种情况下的曲线比较接近,在h/d=0.5时曲线出现了明显的下降,说明在挡板高度为h/d=0.5时,P1点挡板的减摇效果最佳;在图11(d)图中,峰值随挡板高度增大呈减小趋势,且各条曲线随挡板宽度增加逐渐减小。
4 结 语本研究采用MPS方法来解决液体晃荡的问题。主要可以得出以下结论:
1)不同参数跟不同位置的对称水平挡板能够有效的抑制晃荡幅度,减小晃荡的拍击压力。且随着挡板的高度和宽度越大,液体晃荡的幅度将大幅减小,隔板的阻尼效果更加明显,减晃效果越好。
2)当在液舱中没加挡板时,液体晃动剧烈,并伴随有液面翻卷和破碎的趋势,随着挡板的高度和宽度的增加,改善液体晃动的效果变得越来越明显。当h/d=0.6且w/L=0.4时,液舱中的自由水平挡板晃动很小,几乎没有晃动。
3)在液舱中加入挡板后能改变压力曲线的相位,并随着挡板的高度和宽度的增加,相位迟滞现象更明显。
| [1] |
JIN Xin, LIN Pengzhi. Viscous effects on liquid sloshing under external excitations[J]. Ocean Engineering, 2019, 171: 695-707. DOI:10.1016/j.oceaneng.2018.10.024 |
| [2] |
WANG L, WAN Z H, HUANG J H, et al. Research on key technologies of LNG carriers [J]. Ship Science and Technology. 2015, 6: 37(6): 1−5.
|
| [3] |
HOSAIN M L, SAND U, FDHILA R B. Numerical investigation of liquid sloshing in carrier ship fuel tanks[J]. IFAC-Papers On Line, 2018, 51(2): 583-588. DOI:10.1016/j.ifacol.2018.03.098 |
| [4] |
KOSHIZUKA S, TAMAKO H, OKA Y. A particle method for incompressible viscous flow with fluid fragmentation[J]. Journal of Computational Fluid Dynamics, 1995, 4(1): 29-46. |
| [5] |
WU Qiao-rui, TAN M Y, XING J T. An improved particle semi-implicit method for dam break simulation[J]. Journal of Ship Mechanics, 2014, 18(9): 1044-1054. |
| [6] |
WU Qiao Rui, WANG L, XIE Y H, et al. Effect of elastic support wall on dam break based on improved MPS method[J]. Journal of Zhejiang Ocean University, 2019, 38(1): 76-82. |
| [7] |
WANG Jianqiang , ZHANG Xiaobing. Improved moving particle semi-implicit method for multiphase flow with discontinuity[J]. Computer Methods in Applied Mechanics and Engineering, 2019, 346: 312-331.
|
| [8] |
HAN Fenglei, WANG Chunhui. Bow flare water entry impact prediction and simulation based on moving particle semi-implicit turbulence method[J]. Shock and Vibration, 2018, 2018(3): 1-16. |
| [9] |
KOSHIZUKA S, IKEDA H, OKA Y. Numerical analysis of fragmentation mechanisms in vapor xxplosions[J]. Nuclear Engineering and Design, 1999, 189: 423-433. DOI:10.1016/S0029-5493(98)00270-2 |
| [10] |
吴巧瑞, 王化明. 一种无网格方法——移动粒子半隐式方法MPS[D]. 上海: 上海交通大学, 2018.
|
| [11] |
YANG Yaqiang, TANG Z Y, WAN D C. Simulation of liquid tank sloshing with horizontal partition based on MPS method[J]. Research and Progress in Hydrodynamics (Part )A, 2015, 30(2): 146-153. |
| [12] |
黄松兴, 焦甲龙, 孙树政, 等. 基于CFD的单体复合船水动力性能分析[J]. 哈尔滨工程大学学报, 2021, 42(1): 105−111.
|
| [13] |
张珍, 陈明辉, 邵菲, 等. 外部激励对刚弹性液舱晃荡影响的数值模拟[J]. 青岛科技大学学报:自然科学版, 2022(4): 97. |
| [14] |
王宁, 鹿玮川, 孙士艳. 基于完全非线性边界元方法的楔形液舱入水问题研究[J]. 舰船科学技术, 2022, 44(6): 29. |
 2024, Vol. 46
2024, Vol. 46
